Тематические тесты для контроля качества усвоения теоретического материала по геометрии для учащихся 8 класса.

Пояснительная записка
Тематические тесты  для контроля качества усвоения теоретического материала по геометрии для учащихся 8 класса. Тематика и содержание тестов соответствуют требованиям программы по геометрии для учащихся 8 класса.
 Тесты содержат два варианта, состоящих из трёх уровней:

 Уровень А является базовым(4 задания), это задания с выбором одного правильного ответа из четырёх предложенных.

Уровень В - более сложный (2задания)-задания, ответ для которых учащиеся должны получить сами.

Уровень С включает задания повышенной сложности (1 задание), требующее подробного решения задачи.

Критерии оценки ответов.

За каждое верно выполненное задание части  А начисляется 1 балл, в части В - 2 балла, в части С - 3 балла.

Примерное соответствие количества баллов и отметки.

80—100% от максимальной суммы баллов — оценка «5»;

60-80% - оценка «4»;

40-60% - оценка «3»;

0—40% — оценка «2».

 

 

 

 

 

 

 

 

 

 

Содержание                                                                                     страница

1.Пояснительная записка                                                                                    1

2.Тест №1 «Параллелограмм»                                                                          3-4

3.Тест№2 «Прямоугольник.Ромб.Квадрат»                                                    5-6

4.Тест№3 «Средняя линия треугольника и трапеции. Теорема Фалеса.Теорема о пропорциональных отрезках»                                                         7-8

5.Тест№4 «Трапеция»                                                                                        9-10

6.Тест№5 «Четыре замечательные точки треугольника»                                11

7.Тест№6 -Теоретический тест по теме «Четырёхугольники»                      12-15

8.Тест №7 «Соотношения между сторонами и углами прямоугольного треугольника»                                                                                                     16-19

9.Тест№8 «Теорема Пифагора»                                                                        20-21

10.Тест№9 «Декартовы координаты на плоскости»                                       22-23

11.Тест№10 «Площадь прямоугольника»                                                        24-25

12.Тест№11 «Площадь параллелограмма, ромба, треугольника»                 26-27

13.Тест№12 «Площадь трапеции»28-29

14.Тест№13  Теоретический тест по теме «Площадь»                                   30-31

15.Тест№14 Обобщающий тест по теме «Площадь»                                      32-35

16.Тест№15   Итоговый тест за курс 8 класса                                                  36-37

17.Литература                                                                                                     38

 

 

 

 

 

 

ТЕМА: ПАРАЛЛЕЛОГРАММ

ВАРИАНТ 1

  А1. Периметр параллелограмма равен 24 см, а одна из сторон в два раза больше другой. Чему равна наименьшая из его сторон?

1) 4 см  2) 12 см  3) 9 см 4) 6 см

  Ответ: 1.

   А2. Если в параллелограмме ABCD угол А + угол В + угол D = 272^°, то чему равен угол А?

  1) 80^°  2) 72^°  3) 56^°  4) 92^°

  Ответ: 4.

   А3. В параллелограмме ABCD диагональ АС со сторонами АВ и ВС образует углы, равные соответственно 40^° и 35^°. Чему равна величина угла С?

  1) 25^°  2) 105^°  3) 70^°  4) 110^°

  Ответ: 2.

   А4. В параллелограмме ABCD биссектриса угла А пересекает сторону ВС в точке К так, что ВК = 9 см, КС = 3 см. Чему равен периметр параллелограмма?

  1) 24 см  2) 42 см  3) 34 см  4) 38 см

  Ответ: 2.

   В1. В параллелограмме ABCD высота, опущенная на сторону CD, делит ее пополам и образует с диагональю BD угол 30^°, АВ = 10 см. Найдите периметр параллелограмма.

  Ответ: 40 см.

   В2. В параллелограмме ABCD биссектрисы углов B и D пересекают стороны AD и ВС в точках М и Е соответственно так, что MD = 5 см, ЕС = 7 см. Найдите периметр ABCD.

  Ответ: 38 см.

   С1. На сторонах ВС и CD параллелограмма ABCD отмечены точки Р и Н соответственно так, что отрезки ВН и РD пересекаются в точке О; угол BHD = 95^°, угол DРC = 90^°, угол BOD = 155^°. Найдите углы параллелограмма.

  Ответ: угол С = угол А = 30^°, угол В = угол D = 150^°.

 

 

Вариант 2

  А1. Периметр параллелограмма равен 40 см, а две из его сторон относятся как 3 : 1. Чему равна наибольшая из его сторон?

  1) 15 см  2) 10 см  3) 6 см  4) 4 см

  Ответ: 1.

   А2. Если в параллелограмме ABCD угол А + угол В + угол С = 221^°, то чему равен угол В?

  1) 57^°  2) 79^°  3) 139^°  4) 90^°

  Ответ: 3.

   А3. В параллелограмме ABCD диагональ BD со сторонами АВ и AD образует углы, равные соответственно 54^° и 22^°. Чему равна величина угла В?

  1) 54^°  2) 26^°  3) 102^°  4) 76^°

  Ответ: 4.

   А4. В параллелограмме ABCD биссектриса угла В пересекает сторону AD в точке М так, что АМ = 6 см, MD = 4 см. Чему равен периметр параллелограмма?

  1) 40 см  2) 24 см  3) 32 см  4) 36 см

  Ответ: 3.

   В1. В параллелограмме ABCD высота, опущенная на сторону CD, делит ее пополам и образует со стороной ВС угол 30^°, АВ = 12 см. Найдите периметр параллелограмма.

  Ответ: 48 см.

   В2. В параллелограмме ABCD биссектрисы углов А и С пересекают стороны ВС и AD в точках М и К соответственно так, что АК = 4 см, ВМ = 6 см. Найдите периметр ABCD.

  Ответ: 32 см.

   С1. На сторонах ВС и CD параллелограмма ABCD взяты точки К и М соответственно. Отрезки ВМ и KD пересекаются в точке О; угол BOD = 140^°, угол DKB = 110^°, угол ВМС = 90^°. Найдите углы параллелограмма.

  Ответ: угол С = угол А = 60^°; угол В = угол D = 120^°.

 

 

 

ТЕМА: ПРЯМОУГОЛЬНИК. РОМБ. КВАДРАТ

ВАРИАНТ 1

  А1. Диагонали ромба составляют с его стороной углы, один из которых на 10^° меньше другого. Чему равен больший угол ромба?

  1) 55^°  2) 100^°  3) 110^°  4) 80^°

  Ответ: 2.

   А2. В прямоугольнике ABCD диагонали пересекаются в точке О. Е - середина стороны АВ, угол ВАС = 40^°. Чему равен угол EOD?

  1) 140^°  2) 130^°  3) 120^°  4) 150^°

  Ответ: 4.

   А3. В ромбе ABCD угол А равен 60^°, АВ = 8 см. Из вершины В на стороны AD и CD проведены перпендикуляры ВМ и ВК соответственно. Чему равна сумма длин отрезков MD и СК?

  1) 8 см  2) 10 см  3) 12 см  4) 4 см

  Ответ: 1.

   А4. На сторонах АВ, ВС, CD и AD квадрата ABCD отмечены соответственно точки Р, М, Е и К так, что АР = ВМ = СЕ = DK = 5 см, угол АРК = 60^°. Чему равен периметр четырехугольника РМЕК?

  1) 20 см  2) 36 см  3) 24 см  4) 40 см

  Ответ: 4.

   В1. В ромбе ABCD высота АК, проведенная к стороне ВС, пересекает диагональ BD в точке Е, угол ADE = 40^°. Найдите величину угла ЕАС.

  Ответ: 40^°.

   В2. Внутри квадрата ABCD выбрана точка М так, что треугольник AMD равносторонний. Найдите величину угла АМВ.

  Ответ: 75^°.

   С1. Через середину диагонали КМ прямоугольника KLMN перпендикулярно этой диагонали проведена прямая, пересекающая стороны KL и MN в точках А и В соответственно. Известно, что АВ = ВМ = 6 см. Найдите большую сторону прямоугольника.

  Ответ: 9 см.

Вариант 2

   А1. Диагонали ромба составляют с его стороной углы, один из которых на 35^° меньше другого. Чему равен меньший угол ромба?

  1) 70^°  2) 55^°  3) 60^°  4) 85^°

  Ответ: 2.

   А2. В прямоугольнике МРКН диагонали пересекаются в точке О. Отрезок ОА является высотой треугольника МОР, угол АОР = 15^°. Чему равен угол ОНК?

  1) 105^°  2) 150^°  3) 135^°  4) 75^°

  Ответ: 4.

   А3. В ромбе ABCD угол А равен 30^°. Из вершины В на стороны AD и CD проведены перпендикуляры ВМ и ВК соответственно. ВМ = 4 см. Чему равен периметр ромба?

  1) 40 см  2) 24 см  3) 32 см  4) 50 см

  Ответ: 3.

   А4. На сторонах АВ, ВС, CD и AD квадрата ABCD отмечены соответственно точки Р, М, Е и К так, что АР = ВМ = СЕ = DK = 3 см, угол ВМР = 60^°. Чему равен периметр четырехугольника РМЕК?

  1) 32 см  2) 18 см  3) 24 см  4) 8 см

  Ответ: 3.

   В1. В ромбе ABCD биссектриса угла ВАС пересекает сторону ВС и диагональ BD соответственно в точках М и N, угол АМС = 120^°. Найдите величину угла ANB.

  Ответ: 110^°.

   В2. Внутри квадрата ABCD выбрана точка Е так, что треугольник ВЕС равносторонний. Найдите величину угла EAD.

  Ответ: 15^°.

   С1. Через середину диагонали АС прямоугольника ABCD перпендикулярно этой диагонали проведена прямая, пересекающая стороны ВС и AD в точках К и Е соответственно. Известно, что КЕ = АЕ = 8 см. Найдите большую сторону прямоугольника.

  Ответ: 12 см.

 

 

ТЕМА: СРЕДНЯЯ ЛИНИЯ ТРЕУГОЛЬНИКА И ТРАПЕЦИИ

ТЕОРЕМА ФАЛЕСА

ТЕОРЕМА О ПРОПОРЦИОНАЛЬНЫХ ОТРЕЗКАХ

ВАРИАНТ 1

 А 1. В треугольнике АВС, ВС = 36 см. Через точку М, которая делит сторону АС так, что АМ : МС = 5 : 7, проведена прямая ML параллельно прямой АВ, пересекающая ВС в точке L. Найдите LC.

  1) 11  2) 18  3) 20  4) 21  5) невозможно найти

  Ответ: 4.

   А2. Боковая сторона AD трапеции ABCD равна 51 см. Через точку М, которая делит боковую сторону ВС так, что ВМ : МС = 11 : 6, проведена прямая MN параллельно основанию АВ, пересекающая AD в точке N. Найдите AN.

  1) 33  2) 22  3) 11  4) 6  5) невозможно найти

  Ответ: 1.

   А3. Диагонали четырёхугольника равны 120 см и 248 см. Найдите периметр четырёхугольника, вершинами которого являются середины сторон данного четырёхугольника.

  1) 240  2) 368  3) 496  4) 128  5) невозможно найти

  Ответ: 2.

   А4. Дан произвольный четырёхугольник АВМТ (никакие пары противоположных сторон не параллельны). Точки L и Н - середины отрезков АМ и МВ. Точки G и Y - середины отрезков АТ и ВТ. Найдите периметр четырёхугольника LHYG, если АВ + МТ = 20.

  1) 40  2) 30  3) 20  4) 10  5) невозможно найти

  Ответ: 3.

   В1. В трапеции ABCD на боковой стороне CD отмечена точка Н так, что СН : HD = 2 : 5. Прямая HG, параллельная основаниям ВС и AD, пересекает сторону АВ в точке G. Найдите GH, если ВС = 14, AD = 21.

  Ответ: 16.

   В2. В треугольнике АВС на стороне ВС отмечена точка D так, что CD : DB = 1 : 2. В каком отношении прямая, проходящая через точку В и середину отрезка AD делит сторону АС, считая от точки А.

  Ответ: 2 : 3.

ВАРИАНТ 2

А1. В треугольнике ВЕС,ЕС=56см.Через точку М, которая делит сторону ВС так, что ВМ:ВС=3:8,проведена прямая МК параллельно прямой ВЕ, пересекающая ЕС в точке К. Найдите КС .

  1) 10  2) 25  3) 20  4) 35

  Ответ: 4.

  А2.Боковая сторонаАВ трапеции АВСD равна 28см.Через точку М,которая делит боковую сторону СD так,что СМ:МD =5:9,проведена прямая МЕ параллельно основанию АD,пересекающаяАВ в точке Е.Найдите ВЕ.

  1) 10  2) 28  3) 18  4) 9

  Ответ: 1.

  А3.Диагонали четырёхугольника равны320см и 68см.Найдите периметр четырёхугольника, вершинами которого являются середины сторон данного четырёхугольника.

  1) 640  2) 388  3) 136  4) 252

  Ответ: 2.

  А4.Дан произвольный четырёхугольник  АВРС(никакие пары противоположных сторон не параллельны).Точки Д и Е- середины отрезковАР и РВ.Точки M и N – середины отрезков АС и ВС.Найдите периметр четырёхугольника MДЕN, если АВ+РС=40

  1) 10  2) 20  3) 30  4) 40

  Ответ: 4.

 В1.В трапеции АВСД на боковой стороне СД отмечена точка Е так, что СЕ:ЕД=7:2.Прямая ЕК, параллельная основаниям ВС и АД, пересекает сторонуАВ в точке К. Найдите КЕ, еслиВС=9,АД=36.

  Ответ: 30.

  В2.В треугольнике АВС на стороне АВ отмечена точка Е так, что АЕ:ЕВ=4:3. В каком отношении прямая, проходящая через точку А и середину отрезка СЕ делит сторону ВС,считая от точки В.

 

  Ответ: 7 : 4. 

 

 

ТЕМА: ТРАПЕЦИЯ

ВАРИАНТ 1

  А1. В трапеции ABCD основания равны 12 см и 16 см. Чему равна ее средняя линия?

  1) 26 см  2) 14 см  3) 8 см  4) 6 см

  Ответ: 2.

   А2. В трапеции ABCD угол В = 116^°, угол С = 125^°. Чему равна сумма градусных мер углов А и D?

  1) 119^°  2) 241^°  3) 193^°  4) 166^°

  Ответ: 1.

   А3. В трапеции ABCD из вершины угла В проведена прямая, параллельная стороне CD и пересекающая сторону AD в точке К так, что угол АКВ = 60^°, угол А = 35^°. Чему равен угол BCD?

  1) 65^°  2) 35^°  3) 120^°  4) 115^°

  Ответ: 3.

   А4. В равнобедренной трапеции высота образует с боковой стороной угол 30^°, а ее основания равны 10 см и 6 см. Чему равен периметр трапеции?

  1) 28 см  2) 24 см  3) 26 см  4) 32 см

  Ответ: 2.

   В1. В трапеции ABCD AD и ВС - основания, AD > ВС. На стороне AD отмечена точка М так, что МBCD - параллелограмм. Периметр трапеции равен 22 см, DМ = 5 см. Найдите периметр треугольника АВМ.

  Ответ: 11 см.

   В2. В равнобедренной трапеции ABCD диагональ BD перпендикулярна боковой стороне, угол А = 60^°, AD = 14 см, ВС = 12 см. Найдите периметр трапеции.

  Ответ: 40 см.

   С1. В прямоугольной трапеции диагональ перпендикулярна боковой стороне, острый угол равен 45^°. Найдите отношение оснований.

  Ответ: 1 : 2.

 

 

Вариант2

   А1. В трапеции ABCD основания равны 10 см и 16 см. Чему равна ее средняя линия?

  1) 26 см  2) 13 см  3) 8 см  4) 6 см

  Ответ: 2.

   А2. В трапеции ABCD угол В = 128^°, угол С = 115^°. Чему равна сумма градусных мер углов А и D?

  1) 117^°  2) 243^°  3) 193^°  4) 167^°

  Ответ: 1.

   А3. В трапеции ABCD из вершины угла В проведена прямая, параллельная стороне CD и пересекающая сторону AD в точке К так, что угол АКВ = 65^°, угол А = 35^°. Чему равен угол BCD?

  1) 65^°  2) 35^°  3) 100^°  4) 115^°

  Ответ: 4.

   А4. В равнобедренной трапеции высота образует с боковой стороной угол 30^°, а ее основания равны 11 см и 5 см. Чему равен периметр трапеции?

  1) 28 см  2) 27 см  3) 26 см  4) 32 см

  Ответ: 1.

   В1. В трапеции ABCD AD и ВС - основания, AD > ВС. На стороне AD отмечена точка Е так, что EBCD - параллелограмм. Периметр трапеции равен 32 см, DЕ = 5 см. Найдите периметр треугольника АВЕ.

  Ответ: 22 см.

   В2. В равнобедренной трапеции ABCD диагональ BD перпендикулярна боковой стороне, угол А = 60^°, AD = 24 см, ВС = 12 см. Найдите периметр трапеции.

  Ответ: 60 см.

   С1. В прямоугольной трапеции диагональ перпендикулярна боковой стороне, острый угол равен 45^°. Найдите отношение оснований.

  Ответ: 1 : 2.

 

 

 

Тест по теме: «Четыре замечательные точки треугольника»  вариант 1 Теорема: Каждая точка биссектрисы неразвернутого угла _______________________ от его сторон. Серединным перпендикуляром к отрезку называется ____________, проходящая через _________________ данного отрезка и перпендикулярна к нему. Обратная теорема: Каждая точка, ______________________ от концов отрезка, лежит на серединном _________________________ к нему. Серединные перпендикуляры к сторонам треугольника пересекаются ___________________________. Нарисуйте в треугольнике АВС серединные перпендикуляры и отметьте их точку пересечения буквой О. Тест по теме: «Четыре замечательные точки треугольника»  вариант 2 Обратная теорема: Каждая точка, лежащая внутри угла и ______________________ от сторон угла, лежит наего _______________________. Биссектрисы треугольника пересекаются ______________________ . Теорема: Каждая точка серединного ____________________ к отрезку ____________________ от концов этого отрезка. Высоты треугольника (или их продолжения) пересекаются ______________________. Нарисуйте в треугольнике АВС высоты и отметьте их точку пересечения буквой О.

 

 

 

ТЕОРЕТИЧЕСКИЙ ТЕСТ ПО ТЕМЕ: ЧЕТЫРЕХУГОЛЬНИКИ

  А1. Сумма углов выпуклого n-угольника равна:

  1) 180°(n − 2)  2) 360°  3) 180° · n  4) 360° · n

  Ответ: 1.

   А2. Четырехугольник является параллелограммом, если у него:

  1) две стороны равны, а две другие параллельны

  2) диагонали пересекаются и точкой пересечения делятся пополам

  3) две пары равных сторон

  4) все стороны параллельны

  Ответ: 2.

   А3. Трапеция называется равнобедренной, если у нее:

  1) две стороны равны  2) два угла равны  3) основания параллельны и равны

  4) боковые стороны равны

  Ответ: 4.

   А4. Прямоугольником называется:

  1) параллелограмм, у которого все стороны равны

  2) параллелограмм, у которого все углы прямые

  3) четырехугольник, у которого диагонали равны

  4) четырехугольник, у которого противолежащие стороны равны

  Ответ: 2.

   А5. Четырехугольник является ромбом, если у него:

  1) диагонали перпендикулярны

  2) диагонали равны

  3) диагонали перпендикулярны и точкой пересечения делятся пополам

  4) диагонали точкой пересечения делятся пополам

  Ответ: 3.

   А6. Квадратом является:

  1) параллелограмм, у которого все углы прямые

  2) ромб, у которого все углы прямые

  3) параллелограмм, у которого диагонали равны

  4) прямоугольник, у которого диагонали равны

  Ответ: 2.

   А7. Всякий прямоугольник является:

  1) квадратом  2) ромбом  3) трапецией  4) параллелограммом

  Ответ: 4.

   А8. Выберите верное утверждение:

  1) если в четырехугольнике диагонали равны и точкой пересечения делятся пополам, то этот четырехугольник - прямоугольник

  2) если в четырехугольнике две стороны параллельны и равны, то этот четырехугольник - ромб

  3) если в четырехугольнике две стороны равны, а два угла прямые, то этот четырехугольник - прямоугольник

  4) если в четырехугольнике диагонали равны, а один из углов прямой, то этот четырехугольник - квадрат

  Ответ: 1.

   А9. Внешний угол правильного n-угольника равен:

  1) 180° / n  2) 180° (n − 2)/n  3) 360° (n − 2)/n  4) 360° / n

  Ответ: 4.

   А10. Многоугольник называется выпуклым, если:

  1) все его стороны являются выпуклыми

  2) его нельзя разрезать на два других многоугольника

  3) он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины

  4) все его углы являются выпуклыми

  Ответ: 3.

Тест:  «Четырехугольники»

1.Какая фигура обладает следующими свойствами:

- все углы прямые;

- диагонали равны;

- диагонали пересекаются под прямым углом и является биссектрисами его углов?

А. Прямоугольник        Б. Ромб          В. Квадрат    Г. Параллелограмм

Ответ:В

2. Прямоугольник, у которого все стороны равны – это

А. Прямоугольник        Б. Ромб          В. Квадрат    Г. Параллелограмм

Ответ:В

3.Четырехугольник,  вершины которого находятся в серединах сторон прямоугольника.

А. Произвольный параллелограмм  Б. Прямоугольник    В. Ромб        Г. Квадрат

Ответ:В

4.Из каких двух равных треугольников можно сложить квадрат?

А.  Прямоугольных   Б. Правильных   В. Равнобедренных   Г. Равнобедренных прямоугольных

Ответ:Г

5. В ромбе одна из диагоналей равна его стороне. Углы ромба:

А. 30°, 60°, 30°, 60°        Б. 45°, 45°, 135°, 135°        В.  60°, 60° ,  120°, 120° 

 Г. 30°, 150°, 30°, 150°

Ответ:В

6. Сумма двух углов параллелограмма  134°. Найдите его углы.

А. 134°, 134°, 46° 46°      Б. 67°, 67°, 113°, 113°       В.  67°, 67°, 134°, 134° 

 Г. 67°, 113°, 134°, 46°

Ответ:Б

7. В прямоугольнике перпендикуляры, проведенные из точки пересечения диагоналей к его сторонам, равны соответственно 3см и 5 см. Найдите периметр прямоугольника.

А. 16см         Б. 24см       В. 32см          Г. 48 см

Ответ:В

8. Периметр параллелограмма 36см. Одна из сторон 12см. Найти остальные стороны.

А. 12, 12, 6, 6        Б. 12, 18, 12, 6   В. 12,  6, 10, 8    Г. 12,  12, 8, 8

Ответ:А

9. В равнобокой трапеции диагональ перпендикулярна к ее боковой стороне и образует с основанием угол 15°. Найдите углы трапеции.

А. 30° , 150° ,  30°, 150°        Б. 75°, 105°, 75°, 105°           В. 45°, 135°, 45°, 135°

Ответ:Б

10. В ромбе перпендикуляр, проведенный из вершины тупого угла, делит сторону пополам. Найдите углы ромба.

А. 60°, 60°, 120°, 120°        Б. 45°, 45°, 135°, 135°        В.  90°, 90° ,  90°, 90° 

 Г. 30°, 30°, 150°, 150°

Ответ:А

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ТЕМА: СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ

ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА

ВАРИАНТ 1

  А1. В треугольнике АВС угол С = 90°, угол А = 32°, ВС = 4 см. Найдите длину АС.

  1) 4 · cos32°  2) 4 : tg32°  3) 4 · tg32°  4) 4 : sin32°

  Ответ: 2.

   А2. sin α = 5/13. Найдите tg α.

  1) 5/12  2) 12/13  3) 12/5  4) 13/12

  Ответ: 1.

   А3. В треугольнике КСР (КС = СР) угол С = 70°, КС = 12 см. Найдите длину КР.

  1) 12 · cos35°  2) 6 · cos35°  3) 24 · sin35°  4) 24 : sin35°

  Ответ: 3.

   А4. Вычислите значение выражения sin²60° − 3tg45°.

  1) −2,25  2) −1,25  3) −0,75  4) −1,5

  Ответ: 1.

   В1. В треугольнике АВС угол С = 90°, CD - высота, угол А = α, АВ = k. Найдите длины АС, ВС, AD.

  Ответ: АС = k · cosα; BC = k · sinα; AD = k · cos²α.

   В2. Стороны параллелограмма равны 4 см и 5 см, угол между ними 45°. Найдите высоты параллелограмма.

  Ответ: 2√2 см; 2,5√2 см.

   С1. В прямоугольной трапеции меньшее основание равно 6, а меньшая боковая сторона - 2√3. Найдите площадь трапеции, если один из ее углов равен 120°.

  Ответ: 14√3 см².

   С2. В равнобедренном треугольнике АВС (АВ = ВС) угол А = 30°. Найдите высоту, опущенную к основанию, если AD = 20 см (D принадлежит прямой АВ, а CD перпендикулярен АВ).

  Ответ: 20/3 см.

 

Вариант2

   А1. В треугольнике АВС угол С = 90°, угол В = 40°, ВС = 9 см. Найдите длину АС.

  1) 9 : tg40°  2) 9 · cos40°  3) 9 : sin60°  4) 9 · tg40°

  Ответ: 4.

   А2. cos α = 8/17. Найдите tg α.

  1) 9/8  2) 15/8  3) 8/15  4) 8/9

  Ответ: 2.

   А3. В треугольнике CDE (CD = DE) угол D = 68°, СЕ = 10 см. НайдитедлинуCD.

  1) 5 · sin34°  2) 10 :sin68°  3) 8 · cos51°  4) 5 : sin34°

 Ответ: 4.

   А4. Вычислите значение выражения cos²45° − 4sin30°.

  1) −2  2) −3  3) −1,5  4) −2,5

  Ответ: 3.

   В1. В треугольнике MNP угол Р = 90°, РК - высота, угол N = β, PN = b. Найдите длины MN, MP, KN.

  Ответ: MN = b :cosβ; MP = b · tgβ; KN = b · cosβ.

   В2. Стороны параллелограмма равны 6 см и 7 см, угол между ними 60°. Найдите высоты параллелограмма.

  Ответ: 3√3 см; 3,5√3 см.

   С1. В равнобедренной трапеции меньшее основание равно 8, а высота - √3. Найдите площадь трапеции, если один из ее углов равен 150°.

  Ответ: 11√3 см².

   С2. В равнобедренном треугольнике АВС с основанием АС угол при вершине равен 120°, CD - высота. Найдите длину AD, если высота, проведенная к основанию, равна 10 см.

  Ответ: 30 см.

 

 

ВАРИАНТ 1

1.Вставьте пропущенные  слова, чтобы получилось верное высказывание

Косинусом острого угла ….. треугольника называется отношение ….. катета к гипотенузе.

2. В прямоугольном треугольнике один из острых углов 30°, а гипотенуза равна 12 см. Найдите меньший катет этого треугольника.

а) 6 см    б) 6√3 см   в) 18 см г) другой ответ

3. В прямоугольном треугольнике угол С =90, АС=28 см,  АВ=35 см.

    Найти     sin В.

а)другой ответ.   б)      в);     г).

4. В треугольнике АВС, угол С равен 90°, sin А=  . Найти cosA.

а) ;  б)  ;   в) ;

  5. В треугольнике АВС угол  С равен 90°,  АС = 7, АВ = 25

    Найти  cosA.

а) ;   б)  ;     в)  ;      г) .

6. В треугольнике АВС угол  С=90,  АС=4,8  cosA=.  Найти АВ.

7. В треугольнике АВС угол С=90°. СА= 6 см,  СВ=2см.  Найти угол A

 

а) 30;             в) 60;

б) 45              г) 10°.

8. Напишите соотношение

1) соs -30: 2)  60; 3)sin 30; 4) sin45.

a);           в:

б) ;         г) .

 

 ВАРИАНТ 2

1.      Вставьте пропущенное слово, чтобы получилось верное высказывание

Синусом острого угла треугольника называется отношение ….. катета к гипотенузе.

2.      В прямоугольном треугольнике один из острых углов 60°, а прилежащий катет равен 8. Найти гипотенузу

                  а)  4;                  б)  10;

                  б)  6;                  в)  16.

3.      В  треугольнике угол С=90, АВ=50, ВС=30. Найти cosА.

                 а)  0,6                в) 0,75

                 б) 0,8                б) 0,5

4.      В треугольнике АВС, угол С=90, cos А=0,4. Найти sin А.

                а) 0,6                в)

                б) 0,8               г) 2

5.      В треугольнике АВС,  угол С=90, АВ=20, ВС=16. Найти sin А.

               а) 0,7                   в) 0,8

               б) 1                     г) 0,5

6.      В треугольнике АВС угол С=90, sinA=  , ВС=. Найти АВ.

               а)                в)

               б) 0,5                 г) другой ответ.

7.      В треугольнике АВС угол С=90  АС=12 см, СВ=15. Найти tgA

              а) 0,8    б) 5/4   в) 4/3   г) 3/4

8.      Написать соотношение

1)      сos 60   2)   tg  60   3)  sin  60   4) cos 45

               а) ;    б)     в)     г)

 

 

ТЕМА: ТЕОРЕМА ПИФАГОРА

ВАРИАНТ 1

  А1. В прямоугольном треугольнике катеты равны 6 см и 8 см. Чему равна его гипотенуза?

  1) 9 см  2) 10 см  3) 11 см  4) 12 см

  Ответ: 2.

   А2. В прямоугольнике ABCD смежные стороны относятся как 12 : 5, а его диагональ равна 26 см. Чему равна меньшая сторона прямоугольника?

  1) 24 см  2) 20 см  3) 16 см  4) 10 см

  Ответ: 4.

   А3. Один из внешних углов прямоугольного треугольника равен 135°, а его гипотенуза - 6см. Чему равны катеты данного треугольника?

  1) 4 см и 4 см  2) 2 см и 2 см  3) 3 см и 3 см  4) 3√2 см и 3√2 см

  Ответ: 4.

   А4. Диагонали ромба равны 12 см и 16 см. Чему равна сторона ромба?

  1) 21 см  2) 10 см  3) 15 см  4) 20 см

  Ответ: 2.

   В1. Большая диагональ прямоугольной трапеции равна 25 см, а большее основание - 24 см. Найдите площадь трапеции, если ее меньшее основание равно 8 см.

  Ответ: 112 см².

   В2. Основания равнобедренной трапеции равны 10 см и 26 см, а боковая сторона равна 17 см. Найдите площадь трапеции.

  Ответ: 270 см².

   С1. В параллелограмме ABCD BD = 2√41 см, АС = 26 см, AD = 16 см. Через точку пересечения диагоналей параллелограмма О проведена прямая, перпендикулярная стороне ВС. Найдите отрезки, на которые эта прямая разделила сторону AD.

  Ответ: 4 см; 12 см.

 

 

 

 Вариант2

   А1. В прямоугольном треугольнике катеты равны 12 см и 5 см. Чему равна его гипотенуза?

  1) 14 см  2) 11 см  3) 13 см  4) 12 см

  Ответ: 3.

   А2. В прямоугольнике ABCD смежные стороны относятся как 3 : 4, а его диагональ равна 20 см. Чему равна большая сторона прямоугольника?

  1) 16 см  2) 12 см  3) 14 см  4) 15 см

  Ответ: 1.

   А3. Один из внешних углов прямоугольного треугольника равен 135°, а его гипотенуза - 5√2 см. Чему равны катеты данного треугольника?

  1) 4 см и 4 см  2) 5 см и 5 см  3) 3 см и 3 см  4) 5√2 см и 5√2 см

  Ответ: 2.

   А4. Диагонали ромба равны 12 см и 16 см. Чему равна сторона ромба?

  1) 10 см  2) 20 см  3) 15 см  4) 14 см

  Ответ: 1.

   В1. Большая диагональ прямоугольной трапеции равна 17 см, а большее основание - 15 см. Найдите площадь трапеции, если ее меньшее основание равно 9 см.

  Ответ: 96 см².

   В2. Основания равнобедренной трапеции равны 10 см и 24 см, а боковая сторона равна 25 см. Найдите площадь трапеции.

  Ответ: 408 см².

   С1. Две окружности радиусов 13 см и 15 см пересекаются. Расстояние между их центрами О₁ и О₂ равно 14 см. Общая хорда этих окружностей АВ пересекает отрезок О₁О₂ в точке К. Найдите О₁К и КО₂ (О₁ - центр окружности радиуса 13 см).

  Ответ: О₁К = 5 см; КО₂ = 9 см.

 

Тест по теме «Декартовы координаты на плоскости»

Вариант 1

№1. Точка С – середина отрезка АВ. найдите ее координаты, если А(-2; -2), В(3; 2).

А) (-0,5; 0);     Б) (0; 1);     В) (0,5; 0);     Г) (1; 0).

Ответ: В

№2. Найдите диагональ квадрата АВСD,  если А(0; 4), В(4; 4), С(4; 0), D(0; 0).

А) ;     Б) 32;      В) 16;       Г) 8.

Ответ: А

№3.  Найдите координаты центра и радиус окружности

+.

А) О(0;0), R=2;    Б) О(5;0), R=2; 

В)  О(-5;0), R=4;   Г) О(0;-5), R=4.

Ответ:Б

№4. 

Найдите точку пересечения прямых, которые заданы уравнениями: 2х+3у+5=0 и 2х+2у+6=0.

Ответ: х= -4 у=1

№5

Даны точки  А(0; 1), В(2; 5), С(4; 1), D(2; -3).

Докажите, что АВСD -ромб.

 

 

 

 

 

 

 

 

Вариант 2

№1. Точка С – середина отрезка АВ. найдите ее координаты, если А(-4; 2), В(6; -8).

А) (1; -3);     Б) (-3; 1);     В) (-1; -3);     Г) (2; -6).

Ответ:А

№2. Найдите диагональ квадрата АВСD,  если А(-2; 3), В(0; 5), С(2; 3), D(0; 1).

А) 6;     Б) 4;      В) 8;       Г) 10.

Ответ:Б

№3.  Найдите координаты центра и радиус окружности

=49.

А) О(1;1), R=49;    Б) О(0;1), R=7; 

В)  О(0;-1), R=7;   Г) О(-1;0), R=14.

Ответ:В

№4.

Найдите точку пересечения прямых, которые заданы уравнениями: 3х+2у+7=0 и х+у+4=0.

Ответ: х = 1 у = - 5

№5.

Даны точки  А(1; 5), В(-2; 2), С(0; 0), D(3; 3).

Докажите, что АВСD -прямоугольник.

 

 

 

 

 

 

 

 

 

ТЕМА:  ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА

ВАРИАНТ 1

  А1. Периметр прямоугольника равен 22 см, а одна из его сторон на 1 см больше другой. Чему равна площадь прямоугольника?

  1) 30 см²  2) 72 см²  3) 16 см²  4) 25 см²

  Ответ: 1.

   А2. Площадь квадрата равна 16 см². Чему равен его периметр?

  1) 12 см  2) 16 см  3) 24 см  4) 36 см

  Ответ: 2.

   А3. В прямоугольнике ABCD сторона АВ равна 12 см. Расстояние от точки пересечения диагоналей до этой стороны равно 8 см. Найдите площадь треугольника АВС.

  1) 48 см²  2) 192 см²  3) 24 см²  4) 96 см²

  Ответ: 4.

   А4. Периметр прямоугольника равен 40 см, а одна из его сторон равна 4 см. Прямоугольник имеет такую же площадь, что и квадрат. Чему равен периметр квадрата?

  1) 16 см  2) 40 см  3) 64 см  4) 32 см

  Ответ: 4.

   В1. Найдите сумму площадей квадратов, построенных на сторонах прямоугольника со сторонами 5 см и 7 см.

  Ответ: 148 см².

   В2. Через вершину А прямоугольника ABCD проведена прямая, пересекающая продолжение стороны ВС в точке Е так, что ВС = СЕ. Периметр прямоугольника равен 46 см, а сторона ВС на 5 см больше АВ. Найдите площадь треугольника АВЕ.

  Ответ: 126 см².

   С1. Высота BD треугольника АВС равна 8 см и делит сторону АС на отрезки, равные 5 см и 6 см. Найдите площадь треугольника.

  Ответ: 44 см².

 

 

 

ВАРИАНТ 2

  А1. Периметр прямоугольника равен 24 см, а одна из его сторон в два раза меньше другой. Чему равна площадь прямоугольника?

  1) 18 см²  2) 32 см²  3) 36 см²  4) 9 см²

  Ответ: 2.

   А2. Периметр квадрата равен 36 см. Чему равна его площадь?

  1) 12 см²  2) 36 см²  3) 81 см²  4) 24 см²

  Ответ: 3.

   А3. В прямоугольнике ABCD сторона ВС равна 18 см. Расстояние от точки пересечения диагоналей до этой стороны равно 7 см. Найдите площадь треугольника BCD.

  1) 126 см²  2) 252 см²  3) 63 см²  4) 64 см²

  Ответ: 1.

   А4. Периметр квадрата равен 24 см. Прямоугольник имеет такую же площадь, что и квадрат, а одна из его сторон равна 9 см. Чему равен периметр прямоугольника?

  1) 32 см  2) 26 см  3) 24 см  4) 28 см

  Ответ: 2.

   В1. Найдите сумму площадей квадратов, построенных на сторонах прямоугольника со сторонами 4 см и 9 см.

  Ответ: 194 см².

   В2. Через вершину В прямоугольника ABCD проведена прямая, пересекающая продолжение стороны AD в точке К так, что AD = DK. Периметр прямоугольника равен 42 см, а сторона ВС на 3 см больше АВ. Найдите площадь треугольника АВК.

  Ответ: 108 см².

   С1. Высота BD треугольника АВС делит сторону АС на отрезки, равные 7 см и 4 см. Площадь треугольника равна 55 см². Найдите длину BD.

  Ответ: 10 см.

 

 

 

ТЕМА: ПЛОЩАДЬ ПАРАЛЛЕЛОГРАММА, РОМБА И ТРЕУГОЛЬНИКА

 ВАРИАНТ 1

  А1. Стороны параллелограмма равны 10 см и 6 см, а угол между этими сторонами равен 150°. Чему равна площадь этого параллелограмма?

  1) 60 см²  2) 30 см²  3) 15 см²  4) 120 см²

  Ответ: 2.

   А2. Чему равна площадь ромба, диагонали которого равны 8 см и 6 см?

  1) 12 см²  2) 48 см²  3) 96 см²  4) 24 см²

  Ответ: 4.

   А3. Две стороны треугольника равны 10 см и 14 см, а угол между ними 30°. Чему равна площадь треугольника?

  1) 27 см²  2) 108 см²  3) 54 см²  4) 35 см²

  Ответ: 4.

   А4. Стороны параллелограмма 10 см и 8 см, меньшая высота 4 см. Найдите большую высоту параллелограмма.

  1) 3 см  2) 5 см  3) 6 см  4) 4 см

  Ответ: 2.

   В1. В треугольнике АВС угол А = 45°, ВС = 10 см, а высота BD делит сторону АС на отрезки AD = 6 см, DC = 8 см. Найдите площадь треугольника и высоту, проведенную к стороне ВС.

  Ответ: 42 см²; 8,4 см.

   В2. В треугольнике АВС угол А = 75°, угол В = 30°, АВ = 12 см. Найдите площадь треугольника.

  Ответ: 36 см².

   С1. Высоты, проведенные из вершины тупого угла параллелограмма, составляют угол, равный 45°. Одна из высот делит сторону, на которую она опущена, на отрезки 3 см и 7 см, считая от вершины острого угла. Найдите площадь параллелограмма.

  Ответ: 30 см².

 

 

Вариант2

  А1. Стороны параллелограмма равны 12 см и 8 см, а угол между этими сторонами равен 30°. Чему равна площадь этого параллелограмма?

  1) 192 см²  2) 96 см²  3) 24 см²  4) 48 см²

  Ответ: 4.

   А2. Чему равна площадь ромба, диагонали которого равны 10 см и 12 см?

  1) 60 см²  2) 120 см²  3) 30 см²  4) 240 см²

  Ответ: 1.

   А3. Найдите площадь треугольника, две стороны которого равны 6 см и 8 см, а угол между ними 30°.

  1) 48 см²  2) 12 см²  3) 96 см²  4) 24 см²

  Ответ: 2.

   А4. Высоты параллелограмма 6 см и 8 см, большая сторона 12 см. Найдите меньшую сторону параллелограмма.

  1) 10 см  2) 9 см  3) 16 см  4) 4 см

  Ответ: 2.

   В1. В треугольнике АВС угол С = 45°, АВ = 10 см, а высота AD делит сторону СВ на отрезки CD = 8 см, DВ = 6 см. Найдите площадь треугольника и высоту, проведенную к стороне АВ.

  Ответ: 56 см²; 11,2 см.

   В2. В треугольнике АВС угол А = углу В = 75°. Найдите длину ВС, если площадь треугольника равна 25 см².

  Ответ: 10 см.

   С1. Высоты, проведенные из вершины тупого угла параллелограмма, составляют угол, равный 45°. Одна из высот делит сторону, на которую она опущена, на отрезки 5 см и 8 см, считая от вершины острого угла. Найдите площадь параллелограмма.

  Ответ: 65 см².

 

ТЕМА: ПЛОЩАДЬ ТРАПЕЦИИ

ВАРИАНТ 1

  А1. Основания трапеции равны 5 см и 9 см, ее высота - 5 см. Чему равна площадь трапеции?

  1) 45 см²  2) 35 см²  3) 42 см²  4) 84 см²

  Ответ: 2.

   А2. В равнобедренной трапеции основания равны 6 см и 12 см, а угол при основании равен 45°. Чему равна площадь трапеции?

  1) 16 см²  2) 32 см²  3) 27 см²  4) 24 см²

  Ответ: 3.

   А3. В прямоугольной трапеции основания равны 5 см и 9 см, а меньшая боковая сторона - 4 см. Чему равна площадь трапеции?

  1) 36 см²  2) 56 см²  3) 14 см²  4) 28 см²

  Ответ: 4.

   А4. Диагонали трапеции взаимно перпендикулярны и равны 10 см и 15 см. Чему равна площадь трапеции?

  1) 75 см²  2) 216 см²  3) 54 см²  4) 162 см²

  Ответ: 1.

   В1. В равнобедренной трапеции высота, проведенная из вершины тупого угла, делит большее основание на два отрезка, больший из которых равен 26 см. Найдите площадь трапеции, если ее высота равна 10 см.

  Ответ: 260 см².

   В2. В равнобедренной трапеции диагонали взаимно перпендикулярны, высота трапеции равна 12 см. Найдите площадь трапеции.

  Ответ: 144 см².

   С1. Основания и высота трапеции относятся как 5 : 6 : 2. Найдите меньшее основание трапеции, если площадь трапеции равна 44 см².

  Ответ: 10 см.

   С2. В трапеции ABCD BC и AD - основания, BC : AD = 3 : 4. Площадь трапеции равна 70 см². Найдите площадь треугольника АВС.

  Ответ: 30 см².

Вариант2

   А1. Основания трапеции равны 4 см и 8 см, ее высота - 9 см. Чему равна площадь трапеции?

  1) 54 см²  2) 27 см²  3) 108 см²  4) 72 см²

  Ответ: 1.

   А2. В равнобедренной трапеции основания равны 8 см и 16 см, а угол при основании равен 45°. Чему равна площадь трапеции?

  1) 24 см²  2) 96 см²  3) 72 см²  4) 48 см²

  Ответ: 4.

   А3. В прямоугольной трапеции основания равны 6 см и 10 см, а меньшая боковая сторона - 5 см. Чему равна площадь трапеции?

  1) 80 см²  2) 40 см²  3) 20 см²  4) 30 см²

  Ответ: 2.

   А4. Диагонали трапеции взаимно перпендикулярны и равны 14 см и 12 см. Чему равна площадь трапеции?

  1) 168 см²  2) 224 см²  3) 56 см²  4) 84 см²

  Ответ: 4.

   В1. В равнобедренной трапеции высота, проведенная из вершины тупого угла, делит большее основание на два отрезка, больший из которых равен 18 см. Найдите площадь трапеции, если ее высота равна 12 см.

  Ответ: 216 см².

   В2. В равнобедренной трапеции диагонали взаимно перпендикулярны, высота трапеции равна 11 см. Найдите площадь трапеции.

  Ответ: 121 см².

   С1. Высота трапеции равна меньшему основанию и в два раза меньше большего основания. Найдите высоту трапеции, если ее площадь равна 54 см².

  Ответ: 6 см.

   С2. В трапеции ABCD BC и AD - основания, ВС : AD = 4 : 5. Площадь треугольника ACD равна 35 см². Найдите площадь трапеции.

  Ответ: 63 см².

ТЕОРЕТИЧЕСКИЙ ТЕСТ ПО ГЕОМЕТРИИ

ТЕМА: ПЛОЩАДЬ

  А1. Выберите верное утверждение:

  1) если два многоугольника имеют равные площади, то они равны

  2) если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников

  3) квадратный сантиметр - это фигура, стороны которой равны 1 см

  4) площадь квадрата равна произведению его сторон

  Ответ: 2.

   А2. Высотой трапеции называется:

  1) перпендикуляр, проведенный к его основанию  2) отрезок, пересекающий основание трапеции под прямым углом  3) перпендикуляр, опущенный из вершины трапеции

  4) перпендикуляр, проведенный из любой точки одного из оснований к прямой, содержащей другое основание

  Ответ: 4.

   А3. Если высоты двух треугольников равны, то:

  1) их площади относятся как основания  2) их площади равны

  3) эти треугольники равны  4) основания, к которым они проведены, равны

  Ответ: 1.

   А4. Площадь параллелограмма равна:

  1) произведению стороны параллелограмма на высоту  2) произведению его основания на высоту, проведенную к данному основанию  3) половине произведения его основания на высоту, проведенную к данному основанию

  4) произведению смежных сторон параллелограмма

  Ответ: 2.

   А5. Площадь прямоугольного треугольника равна:

  1) произведению его катетов  2) произведению его гипотенузы на один из его катетов

  3) половине произведения его катетов  4) произведению стороны на высоту

  Ответ: 3.

   А6. Площадь трапеции равна:

  1) произведению полусуммы оснований на половину высоты  2) произведению суммы оснований на высоту  3) произведению суммы оснований на половину высоты

  4) произведению оснований и высоты

  Ответ: 3.

   А7. Теорема Пифагора гласит:

  1) в прямоугольном треугольнике гипотенуза равна сумме катетов

  2) в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

  3) в прямоугольном треугольнике квадрат гипотенузы равен сумме катетов

  4) если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный

  Ответ: 2.

   А8. Если в треугольнике АВС АС² = АВ² + ВС², то:

  1) угол В прямой  2) угол С прямой  3) угол А прямой  4) угол С или угол А прямой

  Ответ: 1.

   А9. Египетским называется треугольник, длины сторон которого:

  1) удовлетворяют теореме Пифагора  2) удовлетворяют теореме, обратной теореме Пифагора

  3) равны 3, 4 и 5  4) равны целым числам

  Ответ: 3.

   А10. Как записывается формула Герона для вычисления площади треугольника АВС со сторонами a, b и с?

 

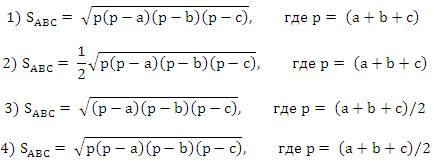
  Ответ: 4.

ОБОБЩЕНИЕ ТЕМЫ "ПЛОЩАДЬ"

ВАРИАНТ 1

  А1. Сторона ромба равна 5 см, а одна из его диагоналей - 6 см. Чему равна площадь ромба?

  1) 30 см²  2) 24 см²  3) 15 см²  4) 12 см²

  Ответ: 2.

   А2. Биссектриса угла А прямоугольника ABCD пересекает сторону ВС в точке Е так, что ВЕ = 4,5 см, СЕ = 5,5 см. Чему равна площадь прямоугольника?

  1) 55 см²  2) 100 см²  3) 110 см²  4) 45 см²

  Ответ: 4.

   А3. Чему равна площадь ромба со стороной 8 см и углом, равным 60°?

  1) 32 см²  2) 32√3 см²  3) 38 см²  4) 16√3 см²

  Ответ: 2.

   А4. Чему равна площадь прямоугольного треугольника с гипотенузой 26 см, один из катетов которого равен 24 см?

  1) 120 см²  2) 60 см²  3) 312 см²  4) 240 см²

  Ответ: 1.

   А5. Одна из сторон треугольника равна 16 см, а высота, проведенная к ней, - 9 см. Чему равна высота, проведенная к стороне треугольника, равной 24 см?

  1) 5 см  2) 12 см  3) 13 см  4) 6 см

  Ответ: 4.

   А6. Площадь квадрата равна 48 см². Чему равен периметр данного квадрата?

  1) 12√3 см  2) 8√3 см  3) 16√3 см  4) 144 см

  Ответ: 3.

   А7. Площадь ромба равна 36 см², а одна из его диагоналей в два раза меньше другой. Чему равна сторона ромба?

  1) 3 см  2) 3√5 см  3) 3√3 см  4) 3√2 см

  Ответ: 2.

 

  В1. В трапеции ABCD угол А = 60°, угол D = 45°, основание ВС равно 3 см, BF и СЕ - высоты трапеции, ED = 4 см. Найдите площадь трапеции.

  Ответ: S_ABCD = 4(5 + 2√3/3)см².

   В2. В треугольнике АВС биссектриса AD равна 7 см, АВ = 6 см, АС = 8 см. Найдите S_ABD : S_ACD.

  Ответ: S_ABD : S_ACD = 3 : 4.

   В3. В трапеции ABCD основания ВС и AD равны 8 см и 12 см, диагональ АС равна 40 см и пересекает диагональ BD в точке О. Найдите разность АО и СО.

  Ответ: 8 см.

   С1. В параллелограмме ABCD диагональ BD перпендикулярна стороне АВ, один из углов параллелограмма равен 120°, AD = 12 см, О - точка пересечения диагоналей. Найдите диагонали параллелограмма и площадь треугольника CDO.

  Ответ: АС = 6√7; BD = 6√3 см; S_CDO = 9√3 см².

   С2. В прямоугольной трапеции ABCD меньшее основание равно меньшей боковой стороне. Диагональ, проведенная из вершины тупого угла, перпендикулярна большей боковой стороне, равной 8√2 см. Найдите периметр и площадь трапеции.

  Ответ: P_ABCD = 8(4 + √2) см; S = 96 см².

 

 

 

 

 

 

 

 

 

 

 

 

 

Вариант2

   А1. Чему равна площадь квадрата со стороной 5√2 см?

  1) 50 см²  2) 25 см²  3) 75 см²  4) 100 см²

  Ответ: 1.

   А2. Биссектриса угла В прямоугольника ABCD пересекает сторону AD в точке К так, что АК = 6,5 см, KD = 3,5 см. Чему равна площадь прямоугольника?

  1) 35 см²  2) 100 см²  3) 65 см²  4) 32,5 см²

  Ответ: 3.

   А3. Чему равна площадь ромба со стороной 10 см и углом, равным 60°?

  1) 50 см²  2) 50√3 см²  3) 100 см²  4) 25√3 см²

  Ответ: 2.

   А4. Чему равна площадь равнобедренной трапеции с основаниями 10 см и 16 см и боковой стороной 5 см?

  1) 104 см²  2) 52 см²  3) 42 см²  4) 65 см²

  Ответ: 2.

   А5. Одна из сторон параллелограмма равна 14 см, а высота, проведенная к ней, - 12 см. Чему равна высота, проведенная к смежной стороне, равной 21 см?

  1) 8 см  2) 12 см  3) 10 см  4) 19 см

  Ответ: 1.

   А6. Периметр квадрата равен 20√2 см. Чему равна площадь данного квадрата?

  1) 200 см²  2) 25 см²  3) 100 см²  4) 50 см²

  Ответ: 4.

   А7. Площадь прямоугольника равна 24 см², а его стороны относятся как 2 : 3. Чему равна диагональ прямоугольника?

  1) √13 см  2) 3√13 см  3) 2√13 см  4) 13 см

  Ответ: 3.

 

  В1. В трапеции ABCD угол А = 60°, угол D = 45°, основание ВС равно 5 см, BF и СЕ - высоты трапеции, ED = 4 см. Найдите площадь трапеции.

  Ответ: S_ABCD = 4(7 + 2√3/3) см².

   В2. В треугольнике АВС биссектриса АН равна 8 см, АВ = 6 см, АС = 9 см. Найдите S_ABH : S_ACH.

  Ответ: 2 : 3.

   В3. В параллелограмме MNKP диагональ МК равна 20 см. Точки В и С - середины сторон NK и КР соответственно. Отрезок ВС пересекает диагональ МК в точке Е. Найдите разность МЕ и ЕК.

  Ответ: 10 см.

   С1. В треугольнике АВС через точку пересечения медиан проведена прямая, параллельная стороне АС и пересекающая стороны АВ и ВС в точках К и Е соответственно. Найдите АС, если КЕ = 12 см. Найдите площадь треугольника ВКЕ, если площадь треугольника АВС = 72 см².

  Ответ: АС = 18 см; S_BKE = 32 см².

   С2. В равнобедренной трапеции MNKP диагональ МК является биссектрисой угла при нижнем основании МР. Меньшее основание NK равно 8 см. Найдите площадь трапеции, если один из углов в два раза меньше другого. В каком отношении высота КЕ делит основание МР?

  Ответ: S_MNKP = 48√3 см²; МЕ : ЕР = 3 : 1.

 

 

 

 

 

 

 

 

 

 

 

 

ИТОГОВЫЙ ТЕСТ ПО ГЕОМЕТРИИ ЗА 8 КЛАСС

ВАРИАНТ 1

  А1. Чему равна площадь равностороннего треугольника со стороной 8см?

  1) 9 см²  2) 9√3 см²  3) 18 см²  4) 16√3 см²

  Ответ: 4.

   А2. Биссектриса угла А параллелограмма ABCD делит сторону ВС на отрезки ВК = 5 см и КС = 3 см. Чему равен периметр параллелограмма?

  1) 28 см  2) 15 см  3) 24 см  4) 30 см

  Ответ: 1.

   А3. В равнобедренной трапеции ABCD высота, опущенная из вершины В на большее основание AD, равна 4 см и делит AD на отрезки, равные 5 см и 9 см. Чему равна площадь трапеции?

  1) 36 см²  2) 72 см²  3) 18 см²  4) 38 см²

  Ответ: 1.

   А4. ABCD - квадрат со стороной 4 см. На сторонах АВ и CD отложены отрезки АМ и СК так, что АМ = СК = 3 см. Найдите периметр четырехугольника MBKD.

  1) 14 см  2) 12 см  3) 10 см  4) 16 см

  Ответ: 2.

   В1. В трапеции ABCD основание ВС перпендикулярно боковой стороне АВ, угол D равен 60°, диагональ АС перпендикулярна стороне CD, равной 10 см. Найдите длину основания ВС.

  1) 8 см  2) 15 см  3) 16 см  4) 4 см

  Ответ: 2.

   В2. В трапеции ABCD основания ВС и AD равны соответственно 6 см и 10 см. Диагональ АС, равная 32 см, пересекает диагональ BD в точке К. Найдите длину КС.

  Ответ: 12 см.

   С1. В параллелограмме ABCD АВ = 8 см, ВС = 12 см. Точки К и Е лежат соответственно на сторонах ВС и CD так, что СК = 3 см, СЕ = 2 см. Отрезок КЕ пересекает диагональ АС в точке Р. Найдите отношение АР к РС.

  Ответ: 7 : 1.

Вариант2

   А1. Чему равна площадь равностороннего треугольника, высота которого 9 см?

  1) 13,5 см²  2) 13,5√3 см²  3) 6,75 см²  4) 27√3 см²

  Ответ: 4.

   А2. Биссектриса угла В параллелограмма ABCD делит сторону AD на отрезки АЕ = 7 см и ED = 4 см. Чему равен периметр параллелограмма?

  1) 28 см  2) 22 см  3) 36 см  4) 30 см

  Ответ: 3.

   А3. В равнобедренной трапеции ABCD высота, опущенная из вершины В на большее основание AD, равна 6 см и делит AD на отрезки, равные 3 см и 7 см. Чему равна площадь трапеции?

  1) 84 см²  2) 42 см²  3) 21 см²  4) 26 см²

  Ответ: 2.

   А4. ABCD - квадрат со стороной 8 см. На сторонах АВ и CD отложены отрезки АМ и КС так, что АМ = КС = 6 см. Найдите периметр четырехугольника MBKD.

  1) 24 см  2) 32 см  3) 28 см  4) 36 см

  Ответ: 1.

   В1. В трапеции ABCD основание AD перпендикулярно боковой стороне АВ, диагональ АС перпендикулярна стороне CD. Найдите длину стороны CD, если ВС = 6 см, угол ВСА = 30°.

  1) 6 см  2) 4√3 см  3) 12 см  4) 4 см

  Ответ: 4.

     В2. В трапеции ABCD основания ВС и AD равны соответственно 8 см и 12 см. Диагональ BD, равная 25 см, пересекает диагональ АС в точке Е. Найдите длину ВЕ.

  Ответ: 10 см.

   С1. В параллелограмме ABCD АВ = 6 см, ВС = 9 см. Точки К и Е лежат соответственно на сторонах ВС и CD так, что СК = 6 см, СЕ = 4 см. Отрезок КЕ пересекает диагональ АС в точке Р. Найдите отношение АР к РС.

  Ответ: 2 : 1.