
3.7. Теплопередача
3.7.1. Теплопередача при постійних температурах теплоносіїв.
А. Плоска стінка. Визначимо кількість тепла, яке передається в одиницю часу від більш нагрітого середовища (теплоносія з температурою t1=const) до менш нагрітого середовища (теплоносія з температурою t2=const) через тверду стінку, яка їх розділяє (рис.3.10).
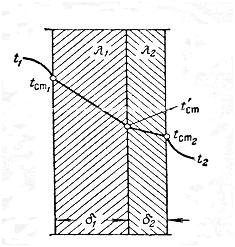
Рис. 3.10. До виведення рівняння теплопередачі через плоску стінку
Нехай стінка складається з двох шарів з різною теплопровідністю, наприклад, власне стінки з товщиною δ1, коефіцієнт теплопровідності якої дорівнює λ1, і шару теплової ізоляції товщиною δ2, що має коефіцієнт теплопровідності λ2. Робоча поверхня стінки F.
Процес теплообміну сталий. Отже, від більш нагрітого середовища до стінки, крізь стінку і від стінки до менш нагрітого середовища за однаковий час передається одна й та ж кількість тепла.
Кількість тепла, переданого за час τ від більш нагрітого середовища до стінки, за рівнянням тепловіддачі (3.19) становить:
![]()
Кількість тепла, що проходить шляхом теплопровідності через окремі шари стінки відповідно до рівняння (3.14) дорівнює:
![]() і
і ![]()
Кількість тепла, що віддається стінкою менш нагрітому середовищу
![]()
Отримані вираження для Q можуть бути представлені у вигляді
![]() ;
;![]()
![]()
![]() ;
; ![]()
Склавши ці рівняння, отримаємо
![]() .
.
або
![]() (3.53)
(3.53)
Відповідно при τ=1
![]() (3.53а)
(3.53а)
Якщо порівняти отримані рівняння (3.53) та (3.53а) з основним рівнянням теплопередачі (3.1), то можна зробити висновок, що перший множник правої частини цих рівнянь є коефіцієнтом теплопередачі:
![]() (3.54)
(3.54)
Відповідно, рівняння теплопередачі для плоскої стінки при постійних температурах теплоносіїв має вигляд
![]() (3.55)
(3.55)
і для безперервних процесів
![]() (3.55a)
(3.55a)
Відповідно до рівняння (3.55) розмірність коефіцієнту теплопередачі:
![]() .
.
Величина, зворотна
К, називається загальним термічним опором ![]() . Із рівняння (3.54) випливає, що
загальний
термічний
опір
. Із рівняння (3.54) випливає, що
загальний
термічний
опір
![]() . (3.56)
. (3.56)
де ![]() і
і ![]() – термічний опір більш нагрітого і
менш нагрітого середовища відповідно;
– термічний опір більш нагрітого і
менш нагрітого середовища відповідно; ![]() - термічний опір багатошарової плоскої
стінки.
- термічний опір багатошарової плоскої
стінки.
Термічні опори окремих шарів багатошарової стінки можуть значно відрізнятися за величиною, і той з них, який відповідає шару із значно нижчою ніж у інших теплопровідністю, є визначальним.
За умов теплопередачі через чисту металеву стінку (без забруднень і теплової ізоляції) термічний опір стінки невеликий і в першому наближенні ним можна знехтувати, прийнявши
![]() .
.
Якщо
значення коефіцієнтів тепловіддачі α1 і α2 значно
відрізняються один від одного,
наприклад ![]() >>
>> ![]() , то
, то ![]() у багато разів більше
у багато разів більше ![]() і величина К
практично визначається значенням
і величина К
практично визначається значенням ![]() . У цьому випадку
. У цьому випадку
![]() .
.
Ha підставі рівняння (3.56) можна зробити деякі висновки про можливості
інтенсифікації процесів теплопередачі. Для збільшення К і, відповідно, теплового навантаження Q для даного теплообмінного апарату необхідно збільшувати менший з коефіцієнтів тепловіддачі, оскільки К завжди менше найменшого з коефіцієнтів тепловіддачі. Це може бути досягнуто, наприклад, збільшенням швидкості теплоносія з меншим α або іншими способами.
Якщо значення окремих термічних опорів різні, то для інтенсифікації
теплопередачі слід зменшувати найбільше з них. При цьому досягається ефект тим більший, чим значніше цей опір перевищує інші. Так, наприклад, якщо визначальним є термічний опір шару забруднень на стінці апарату, то збільшити теплопередачу можна шляхом зменшення товщини шару за рахунок, наприклад, періодичного очищення поверхні нагрівання.
Б. Циліндрична стінка. Цей випадок теплопередачі має істотне практичне значення у зв'язку з тим, що в хімічній технології передача тепла часто відбувається через поверхні труб.
Припустимо, що всередині труби (рис. 3.11а) знаходиться більш нагрітий
теплоносій з температурою t1 і коефіцієнт тепловіддачі від нього до внутрішньої поверхні циліндричної стінки α1. Ззовні труби - холодніший теплоносій, що має температуру t2. Коефіцієнт тепловіддачі від зовнішньої поверхні стінки до більш холодного теплоносія α2.
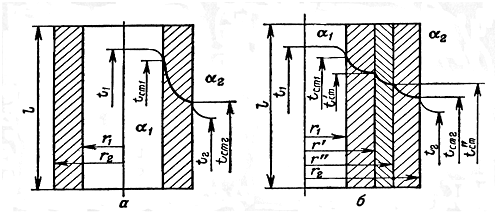
Рис. 3.11. До виведення рівняння теплопередачі через циліндричну стінку
а - одношарова циліндрична стінка; б - багатошарова циліндрична стінка
Кількість тепла, що передається від більш нагрітого теплоносія до стінки,
становить:
![]() .
.
Кількість тепла, що проходить крізь стінку шляхом теплопровідності, знаходимо у відповідності з рівнянням (3.16):
![]() .
.
Кількість тепла, що передається від стінки до більш холодного теплоносія, дорівнює
![]() .
.
Наведені вище рівняння можуть бути представлені у вигляді
![]() ,
,
![]() ,
,
![]() .
.
Склавши ці рівняння, отримаємо
![]() .
.
Звідки
![]() =
=![]() (3.57)
(3.57)
При теплопередачі
через циліндричну стінку зазвичай визначають кількість тепла, що передається через
одиницю довжини труби
![]() . Рівняння (3.57) при цьому
представляється наступним
чином:
. Рівняння (3.57) при цьому
представляється наступним
чином:
![]() , (3.57а)
, (3.57а)
де
величина ![]() виражається рівнянням
виражається рівнянням
![]() =
= ![]() (3.58)
(3.58)
або для багатошарової стінки (рис. 3.11б)
![]() =
= ![]() , (3.58a)
, (3.58a)
де і – відповідні діаметри багатошарової стінки.
Величина ![]() називається
лінійним коефіцієнтом теплопередачі, який, на відміну від К, віднесений до одиниці довжини
труби, а не до одиниці її поверхні. Відповідно,
називається
лінійним коефіцієнтом теплопередачі, який, на відміну від К, віднесений до одиниці довжини
труби, а не до одиниці її поверхні. Відповідно, ![]() виражається у Вт/(м·K).
виражається у Вт/(м·K).
Величину ![]() називають лінійною густиною теплового
потоку або скорочено лінійним тепловим потоком.
називають лінійною густиною теплового
потоку або скорочено лінійним тепловим потоком.
На практиці рівняння (3.57) застосовують тільки для товстостінних циліндричних стінок, наприклад, трубопроводів, покритих товстим шаром теплової ізоляції. Для труб з тонкими стінками розрахунок теплопередачі можна вести приблизно – як для плоскої стінки, що має товщину δ, рівну напів-різниці зовнішнього і внутрішнього діаметрів даної труби. Нехтувати кривизною стінки труби, зводячи задачу до наближеної до розрахунку плоскої стінки, можна при відношенні товщини стінки до внутрішнього діаметру труби, що не перевищує δ/dв= 0,3 - 0,4. При більших значеннях цього відношення слід вести розрахунок за точним рівнянням (3.57).
Позначимо поверхню теплообміну плоскої стінки через Fпл. ст. Тоді
![]() ,
,
де К
- коефіцієнт теплопередачі для плоскої стінки, що визначається за рівнянням (3.54),
в яке підставляється величина δ = 0,5(![]() -
-![]() );
); ![]() - розрахунковий
діаметр труби. За розрахунковий діаметр приймають або діаметр тієї поверхні
циліндричної стінки, з боку якої α значно менше, ніж з протилежної,
або середній діаметр dcеp, якщо
коефіцієнти тепловіддачі з обох сторін стінки розрізняються незначним чином.
- розрахунковий
діаметр труби. За розрахунковий діаметр приймають або діаметр тієї поверхні
циліндричної стінки, з боку якої α значно менше, ніж з протилежної,
або середній діаметр dcеp, якщо
коефіцієнти тепловіддачі з обох сторін стінки розрізняються незначним чином.
3.7.2. Теплопередача при змінних температурах теплоносіїв.
Процеси теплопередачі при постійних температурах (як у випадку плоскої, так і циліндричної стінок) поширені відносно мало. Такі процеси протікають, наприклад, у тому випадку, якщо з одного боку стінки конденсується пара, а з іншого - кипить рідина. Найбільш часто теплопередача в промисловій апаратурі протікає при змінних температурах теплоносіїв.
Температури теплоносіїв зазвичай змінюються уздовж поверхні теплообміну F стінки, яка їх розділяє. При цьому температури теплоносіїв можуть залишатися постійними в часі і виражатися залежністю t=f(F), що характеризує усталені процеси теплообміну.
При несталих процесах теплообміну можливі два випадки:
а) температури в кожній точці поверхні стінки змінюються тільки в часі, тобто вони є однозначною функцією часу [t=φ(τ)]; такий випадок можливий, наприклад, при обігріві рідини, що добре перемішується, через стінку насиченою водяною парою;
б) температури теплоносіїв змінюються і в часі, і уздовж поверхні теплообміну [t=ψ(τ, F)].
Теплопередача при змінних температурах залежить від взаємного напряму руху теплоносіїв.
|
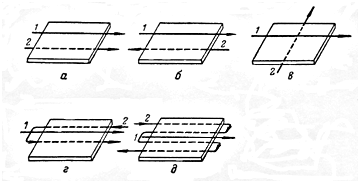
Рис. 3.12. Схеми напряму руху рідин 1 і 2 при теплообміні: а - прямотечія; б - протитечія; в - перехресна течія; г - одноразова змішана течія; д - багаторазова змішана течія. |
У безперервних процесах теплообміну можливі наступні варіанти взаємного напрямку руху рідин уздовж стінки, яка їх розділяє:
1) паралельний потік або прямотечія (рис. 3.12а), при якому теплоносії рухаються в одному і тому ж напрямі;
2) протитечія (рис. 3.12б), при якому теплоносії рухаються в протилежних напрямках;
3) перехресна течія (рис. 3.12в), при якому теплоносії рухаються взаємно перпендикулярно один одному;
4) змішана течія, при якому один з теплоносіїв рухається в одному напрямку, а інший - як прямотечією, так і протитечією до першого. При цьому розрізняють просту або одноразову змішану течію (рис. 3.12г) і багаторазову змішану течію (рис. 3.12д).
Рушійна сила процесів теплопередачі при змінних температурах змінюється в залежності від виду взаємного направлення руху теплоносіїв. Тому вираження середньої рушійної сили процесу у загальному рівнянні теплопередачі (3.1) також буде залежати від відносного напрямку руху теплоносіїв та характеру організації процесу теплопередачі (безперервний або періодичний).
Рівняння теплопередачі при прямотечії і протитечії теплоносіїв. Нехай з одного боку стінки (рис. 3.13а) рухається з масовою швидкістю G1 більш нагрітий теплоносій, що має теплоємність с1. З іншого боку стінки в тому ж напрямі рухається більш холодний теплоносій, масова швидкість якого дорівнює G2, а теплоємність с2. Припустимо, що теплоємності сталі і теплообмін між теплоносіями, що рухаються за прямотечією, відбувається тільки через стінку (поверхнею F), яка їх розділяє.
Процес теплопередачі є сталим або безперервним. У міру протікання теплоносіїв уздовж стінки їх температури будуть змінюватися внаслідок теплообміну. Відповідно, буде змінюватися і різниця температур Δt.
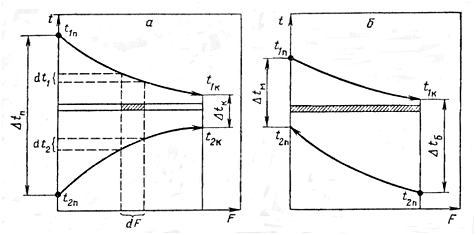
Рис. 3.13. Зміна температури теплоносіїв при прямо- та протитечії.
На елементі поверхні теплообміну dF більш нагрітий теплоносій охолоджується на dt1 град., а більш холодний нагрівається на dt2 град. Рівняння теплового балансу для елемента поверхні dF при цьому має вигляд
![]()
Знак «мінус» вказує на охолодження більш нагрітого теплоносія в процесі
теплообміну. Отже
![]() і
і ![]() .
.
Складаючи ці
вирази і позначаючи
![]() , одержимо
, одержимо
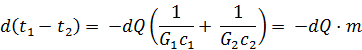
або
![]() .
.
Разом з тим ![]() , тому
, тому
![]()
Розділяємо
змінні та інтегруємо отриманий вираз у межах зміни Δt уздовж
всієї поверхні теплообміну від ![]() до
до ![]() і
і ![]() – від 0
до
– від 0
до ![]() . При цьому приймаємо коефіцієнт
теплопередачі К величиною постійною, тоді
. При цьому приймаємо коефіцієнт
теплопередачі К величиною постійною, тоді
![]() ,
,
![]() або
або ![]() , (А)
, (А)
де ![]() — початкова різниця температур (на одному
кінці теплообмінника);
— початкова різниця температур (на одному
кінці теплообмінника); ![]() - кінцева різниця температур (на
протилежному кінці теплообмінника).
- кінцева різниця температур (на
протилежному кінці теплообмінника).
Рівняння теплового балансу для всієї поверхні теплообміну
![]() ,
,
звідки
![]() .
.
Підставивши значення m в рівняння (А), одержимо
![]() ,
,
звідки знаходимо
![]() . (3.59)
. (3.59)
Зіставляючи вираз для Q, отриманий при сталих значеннях К, с1 і с2 уздовж поверхні теплообміну, з основним рівнянням теплопередачі (3.1), отримаємо, що середня рушійна сила, або середній температурний напір, представляє собою середню логарифмічну різницю температур:
![]() . (3.60)
. (3.60)
Рівняння (3.59) є рівнянням теплопередачі при прямотечії теплоносіїв. За
допомогою цього рівняння за заданим тепловим навантаженням Q і відомими
початковою та кінцевою температурами теплоносіїв визначається основна розрахункова величина - поверхня теплообміну F.
З рівняння (А) випливає, що
![]() .
.
Отже,
при прямотечії температури теплоносіїв змінюються за кривими, що асимптотично зближуються.
Якби температури теплоносіїв змінювалися прямолінійно уздовж поверхні
теплообміну, то середній температурний напір визначався б середньоарифметичною
різницею температур. При відношенні різниці температур теплоносіїв на кінцях
теплообмінника ![]() можна з достатньою для технічних
розрахунків точністю визначати середній температурний напір як
середньоарифметичну величину, тобто приймати
можна з достатньою для технічних
розрахунків точністю визначати середній температурний напір як
середньоарифметичну величину, тобто приймати
![]() .
.
За методикою, аналогічною вище наведеній, може бути отримано рівняння
теплопередачі для протитечії рідин (рис. 3.13б), аналогічне рівнянню (3.59):
![]() . (3.61)
. (3.61)
величина ![]() представляє собою різницю температур на
тому кінці теплообмінника, де вона більше;
представляє собою різницю температур на
тому кінці теплообмінника, де вона більше; ![]() менша різниця температур на протилежному
кінці
теплообмінника.
менша різниця температур на протилежному
кінці
теплообмінника.
Середня рушійна сила при перехресній і змішаній течії. Середня різниця температур при перехресній і змішаній течії нижче, ніж при протитечії, і вище, ніж при прямотечії. Тому зазначені види взаємного направлення руху теплоносіїв займають проміжне положення між протитечією і прямотечією.
При
перехресній і змішаній течії середню різницю температур ![]() найчастіше знаходять, виходячи зі
середньологарифмічної різниці температур при протитечії
найчастіше знаходять, виходячи зі
середньологарифмічної різниці температур при протитечії ![]() При цьому використовують
співвідношення
При цьому використовують
співвідношення
![]() , (3.62)
, (3.62)
де f — поправочний множник, менший одиниці.
Величина f є функцією двох величин:
-
відносних перепадів
температур теплоносіїв ![]() і
і ![]()
![]() ;
;
- ступеня нагріву більш холодного теплоносія, яка визначається відношенням його перепаду температур до різниці початкових температур обох теплоносіїв:
![]() .
.
Графіки для визначення значень поправочного
множника f,
а також рівняння для
аналітичного
визначення середньої різниці температур (у тих випадках, коли необхідне
більш точне
обчислення
![]() ) наводяться у довідковій
літературі.
) наводяться у довідковій
літературі.
Вибір взаємного направлення руху теплоносіїв. Правильний вибір взаємного направлення руху теплоносіїв має істотне значення для найбільш економічного проведення процесів теплообміну.
 Для
порівняльної оцінки прямотечії і протитечії можна порівняти ці види взаємного направлення
руху теплоносіїв з точки зору витрат теплоносіїв та середньої різниці
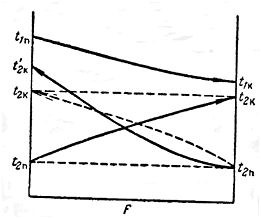
температур. У випадку прямотечії (рис. 3.14) кінцева температура більш
холодного теплоносія t2к не може бути вище
кінцевої температури більш нагрітого теплоносія t1к тому що практично
для здійснення процесу теплообміну на виході з теплообмінника повинна бути
деяка різниця температур.
Для
порівняльної оцінки прямотечії і протитечії можна порівняти ці види взаємного направлення
руху теплоносіїв з точки зору витрат теплоносіїв та середньої різниці
температур. У випадку прямотечії (рис. 3.14) кінцева температура більш
холодного теплоносія t2к не може бути вище
кінцевої температури більш нагрітого теплоносія t1к тому що практично
для здійснення процесу теплообміну на виході з теплообмінника повинна бути
деяка різниця температур.
Рис.3.14. Порівняльна характеристика прямотечії і протитечії теплоносіїв
При протитечії
більш холодний теплоносій з тією ж початковою температурою що і при прямотечії,
може нагрітися до більш високої температури ![]() , близької до початкової температури
більш нагрітого теплоносія. При однаковій тепловій потужності в умовах
охолодження це дозволяє скоротити витрату більш холодного теплоносія, але одночасно приводить до
деякого зменшення середньої різниці температур і, відповідно, до збільшення
потрібної поверхні теплообміну при протитечії в порівнянні з прямотечією. Проте
економічний ефект, що досягається внаслідок зменшення витрат теплоносія при
протитечії, перевищує додаткові витрати, пов'язані зі збільшенням розмірів
теплообмінника. Звідси випливає, що застосування протитечії при теплообміні є більш
економічним, аніж прямотечії.
, близької до початкової температури
більш нагрітого теплоносія. При однаковій тепловій потужності в умовах
охолодження це дозволяє скоротити витрату більш холодного теплоносія, але одночасно приводить до
деякого зменшення середньої різниці температур і, відповідно, до збільшення
потрібної поверхні теплообміну при протитечії в порівнянні з прямотечією. Проте
економічний ефект, що досягається внаслідок зменшення витрат теплоносія при
протитечії, перевищує додаткові витрати, пов'язані зі збільшенням розмірів
теплообмінника. Звідси випливає, що застосування протитечії при теплообміні є більш
економічним, аніж прямотечії.
Тепер порівняємо протитечію з прямотечією при одних і тих же початкових і кінцевих температурах теплоносіїв. Зміна температури більш холодного теплоносія показана на рис. 3.14 пунктиром. Розрахунки показують, що в даному випадку середня різниця температур при протитечії буде більше, ніж при прямотечії, а витрата теплоносіїв однаковою. Отже, швидкість теплообміну при протитечії буде більше, що й обумовлює перевагу протитечії перед прямотечією.
Разом з тим, в окремих випадках вибір напрямку руху теплоносіїв прямотечією диктується технологічними міркуваннями. Так, наприклад, в барабанних сушарках (див. розділ 5) висушуваний матеріал і гріючий агент (топкові гази, нагріте повітря) направляють прямотечією з тим, щоб не піддавати перегріву висушений матеріал, щоб уникнути його окислення, осмоления і т. п.
Зазначені вище переваги протитечії відносяться до процесів теплообміну без зміни агрегатного стану теплоносіїв. Якщо температура одного з теплоносіїв (наприклад, насиченої пари, що конденсується) залишається постійною уздовж поверхні теплообміну, а температура теплоносія по інший бік стінки змінюється, або обидва теплоносії мають постійні температури, що не змінюються в часі і уздовж поверхні теплообміну, то напрям руху теплоносіїв не впливає на різницю їх температур, середню різницю температур і витрати теплоносіїв.
Визначення
температури стінок. Як видно з вищевикладеного, в ряді випадків визначення
коефіцієнта тепловіддачі α неможливе без знання температури більш нагрітої
поверхні стінки (![]() ) або температури менш нагрітої її
поверхні (
) або температури менш нагрітої її
поверхні (![]() ).
).
Температуру стінки
знаходять методом послідовних наближень: задаються довільно цією температурою,
визначають α, розраховують К за формулою (3.54), а потім, за наведеними
нижче формулами, перевіряють збіжність розрахованої величини ![]() з попередньо прийнятою; розрахунок
повторюють до задовільного збігу розрахованого і прийнятого значень
з попередньо прийнятою; розрахунок
повторюють до задовільного збігу розрахованого і прийнятого значень
![]() Розрахунок
Розрахунок ![]() і
і ![]() проводять виходячи з рівнянь
тепловіддачі і теплопередачі.
проводять виходячи з рівнянь
тепловіддачі і теплопередачі.
Кількість тепла, що віддається гарячим теплоносієм
![]() ,
,
де F — поверхня
теплообміну;
![]() — температура гарячого теплоносія.
— температура гарячого теплоносія.
Кількість тепла, що отримується холодним теплоносієм
![]() ,
,
де ![]() — температура холодного теплоносія.
— температура холодного теплоносія.
З цих рівнянь тепловіддачі знаходимо
![]() ,
(А)
,
(А)
![]() .
(Б)
.
(Б)
Відповідно до загального рівняння теплопередачі
![]()
де ![]() - середня різниця температур між
теплоносіями.
- середня різниця температур між
теплоносіями.
Підставляючи значення Q з рівняння теплопередачі в рівняння (А) і (Б) та
скорочуючи F, остаточно отримаємо
![]() , (3.63)
, (3.63)
![]() .
(3.64)
.
(3.64)
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.