ТЕПЛОПРОВІДНІСТЬ ЗА НЕСТАЦІОНАРНИХ УМОВ.

ТЕПЛОПРОВІДНІСТЬ ЗА НЕСТАЦІОНАРНИХ УМОВ.

1.8.1. Розрахункові формули і приклад розрахунку.

Температурне поле за нестаціонарних умов описується як функція:

                                             (1.50)

де Q - безрозмірна температура:

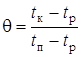,                                       (1.51)

 – кінцева та початкова температури виробу, що нагрівається (охолоджується), ºC;

 - температура охолодного середовища, ºC.

У рівнянні (1.50) критерій Біо:

,                                           (1.52)

де      α – інтенсивність тепловіддачі залежно від виду теплообміну, Вт/м²К;

l – визначальний розмір (для пластини, товщина якої ),

λ_м – середньоінтегральне значення коефіцієнта теплопровідності матеріалу виробу в діапазоні температур охолодження (нагрівання).

Критерій Фур’є:

,                                     (1.53)

де      _м - середньоінтегральне значення коефіцієнта теплопровідності матеріалу виробу, м²/с;  – час охолодження (нагрівання), с.

Для труб, у яких відношення внутрішнього діаметра до зовнішнього більше як 0,7, за зовнішнього охолодження слід користуватись розрахунковими формулами для пластин з визначальним розміром в критеріях , який дорівнює товщині труби.

Приклад. Труба з поліетилену низького тиску (ПНТ), зовнішній діаметр якого = 160 мм, товщина  = 14,6 мм, охолоджується в умовах вільної конвекції від початкової температури  =140 ºС до кінцевої  = 40 ºС. Температура охолоджувальної води стала  ºС. Знайти час охолодження труби.

Відношення:

.

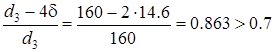Безрозмірна температура за (1.51):

Перепад температур між трубою і водою:

= 70ºC.

Критерій Грасгофа:

,

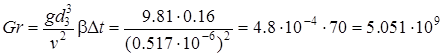За визначальної температури:

;

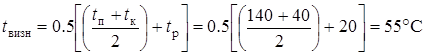з таблиці теплофізичних властивостей води ;  м²/с.

Добуток , де  = 3,26 за .

Критерій Нуссельта за (1.15):

 = 343.

Коефіцієнт тепловіддачі:

                                            Вт/м^2.К,

де  = 0.653 Вт/м^.К  для води, якщо .

Критерій Біо за (1.52):

де _м = 0.253 Вт/м К – середньоінтегральне значення в інтервалі температур охолодження.

З графічної залежності  для центру пластини критерій

Час охолодження труби за (1.53):

,

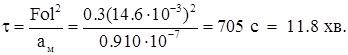де а_м – середньоінтегральне значення в інтервалі температур охолодження.