Тест по математике для 12 класса "Площадь криволинейной трапеции и интеграл"

Тест по математике (алгебре) для 12 класса "Площадь криволинейной трапеции и интеграл"

Тест по математике, 12 класс

«Площадь криволинейной трапеции и интеграл»

1. Как называют операцию нахождения первообразной для данной функции? ________________________________________________

2. Какая из формул является формулой Ньютона - Лейбница?

1) ;

2) ;

3) .

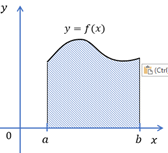3. Как называют отрезок [a; b]?

1) основание криволинейной трапеции;

2) отрезок криволинейной трапеции;

3) средняя линия криволинейной трапеции.

4. Как называют фигуру, изображённую на рисунке? _____________________________________

5. По какой формуле можно вычислить площадь криволинейной трапеции, F(x) - любая первообразная функции f(x)?

1) ;

2) ;;

3) ;.

6. Чему равна площадь фигуры, ограниченной осью Ox и параболой y=1-x²?

1) 1;

2) ;

3) 2;

4) .

7. Чему равна площадь фигуры, ограниченной осью Ox и параболой y=4-x²?

1) 10;

2) ;

3) 21;

4) .

8. Чему равна площадь криволинейной трапеции, ограниченной прямыми x=0, x=2, осью Ox и графиком функции f(x)=x³+1?

Ответ: _________________

9. Чему равна площадь фигуры, ограниченной прямой x=2, осью Ox и графиком функции f(x)=x³?

Ответ: _________________

10. Чему равна площадь фигуры, ограниченной прямой x=3, осью Ox и графиком функции y=x²+2x?

Ответ: _________________

Теоретический материал для самостоятельного изучения

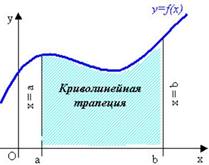Криволинейной трапецией называется фигура, ограниченная графиком непрерывной на отрезке [a; b] функции y=f(x), прямыми x=a, x=b и отрезком [a; b] находящимся на оси Ox.

Отрезок [a; b] называют основанием этой криволинейной трапеции.

Для вычисления площади криволинейной трапеции применяется формула Ньютона – Лейбница: ,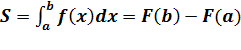

где F(x) - первообразная функции f(x).

Если в задаче требуется вычислить площадь, то ответ всегда будет положительным.

Если требуется, используя чертеж, вычислить интеграл, то его значение может быть любым (зависит от расположения криволинейной трапеции).

Пример решения задачи

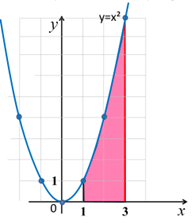Найти площадь криволинейной трапеции, изображенной на рисунке

Решение:

Для вычисления площади криволинейной трапеции воспользуемся формулой Ньютона – Лейбница:

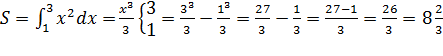(кв. ед.)

Ответ: (кв. ед.)

Тест по математике, 12 класс «Площадь криволинейной трапеции и интеграл» 1

Теоретический материал для самостоятельного изучения

Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

14.12.2020