Тренировочная работа по МАТЕМАТИКЕ

9   класс

2019 год

Вариант МА9003

 

 

 

 

 

Район	______________________________________________
Город	______________________________________________
Школа	______________________________________________
Класс	______________________________________________
Фамилия	______________________________________________
Имя	______________________________________________
Отчество	______________________________________________

 

 

 

 

 

    

 

 

 

 

Инструкция по выполнению работы

 

Работа состоит из двух модулей: «Алгебра» и «Геометрия». Всего в работе 26 заданий. Модуль «Алгебра» содержит семнадцать заданий: в части 1 — четырнадцать заданий; в части 2 — три задания. Модуль «Геометрия» содержит девять заданий: в части 1 — шесть заданий; в части 2 — три задания.

     На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).

      Ответы к заданиям 2, 3, 14 запишите в виде одной цифры, которая соответствует номеру правильного ответа. 

      Для остальных заданий части 1 ответом является число или последовательность цифр. Если в ответе получена обыкновенная дробь, обратите её в десятичную. 

      Решения заданий части 2 и ответы к ним запишите на отдельном листе бумаги. Задания можно выполнять в любом порядке, начиная с любого модуля. Текст задания переписывать не надо, необходимо только указать его номер. 

      Сначала выполняйте задания части 1. Начать советуем с тех заданий, которые вызывают у Вас меньше затруднений, затем переходите к другим заданиям. Для экономии времени пропускайте задание, которое не удаётся выполнить сразу, и переходите к следующему. Если у Вас останется время, Вы сможете вернуться к пропущенным заданиям. 

      При выполнении части 1 все необходимые вычисления, преобразования выполняйте в черновике. Записи в черновике не учитываются при оценивании работы. Если задание содержит рисунок, то на нём непосредственно в тексте работы можно выполнять необходимые Вам построения. Рекомендуем внимательно читать условие и проводить проверку полученного ответа. 

      При выполнении работы Вы можете воспользоваться справочными материалами, выданными вместе с вариантом. 

      Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.

 

 

 

Желаем успеха!

 

 

 

 

 

 

Часть 1

 

Ответами        к      заданиям      1–20     являются   последовательность цифр.	цифра,	число	или
Модуль «Алгебра»

 

 

1

Найдите значение выражения 7,65 4,5.

          

            Ответ: ___________________________.

 

 

2

Студентка Цветкова выезжает из Наро-Фоминска в Москву на занятия в университет. Занятия начинаются в 9:00. В таблице приведено расписание утренних электропоездов от станции Нара до Киевского вокзала в Москве.

                ^{Номер поезда}        Отправление от ст. Нара        Прибытие на Киевский в.

038А 6:17    7:13 020У     6:29    7:50 016А     6:35    7:59 116С     7:05    8:23

Путь от вокзала до университета занимает 45 минут. Укажите время отправления от станции Нара самого позднего из электропоездов, которые подходят студентке.

1) 038А                   2) 020У                  3) 016А                        4) 116С

 

             Ответ:         

 

 

3

Какому из данных промежутков принадлежит число ?

 

1) [0,1; 0,2]        2)  [0,2; 0,3]        3)  [0,3; 0,4]        4)  [0,4; 0,5]                          

 

             Ответ:         

 

 

4

14⁸

Найдите значение выражения 2₅ 77 .

            Ответ: ___________________________.

 

5

При работе фонарика батарейка постепенно разряжается, и напряжение в электрической цепи фонарика падает. На рисунке показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечается время работы фонарика в часах, на вертикальной    оси — напряжение в вольтах. Определите по рисунку, на сколько вольт упадет напряжение c 6-го по 30-й час работы фонарика.

 

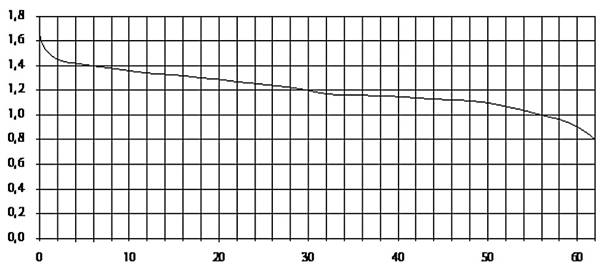
            Ответ: ___________________________.

 

6

Решите уравнение ^х2 7х18  0.

Если уравнение имеет более одного корня, в ответе запишите больший из корней.

             Ответ: ___________________________.

 

7

В начале учебного года в школе было 1250 учащихся, а к концу года их стало 950. На сколько процентов уменьшилось за год число учащихся?           

  

Ответ: ___________________________.

  

 

 

8

Завуч школы подвёл итоги контрольной работы по математике в 9-х классах. Результаты представлены на круговой диаграмме.

 

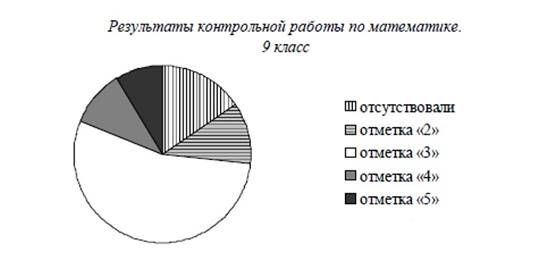
Какие из утверждений относительно результатов контрольной работы верны, если всего в школе 120 девятиклассников? В ответе укажите номера верных утверждений.

 

1)  Более половины учащихся получили отметку «3».

2)  Около половины учащихся отсутствовали на контрольной работе или получили отметку «2».

3)  Отметку «4» или «5» получила примерно шестая часть учащихся. 4) Отметку «3», «4» или «5» получили более 100 учащихся.

 

В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

 

             Ответ: ___________________________.

 

 

9

В магазине канцтоваров продаётся 206 ручек: 20 красных, 8 зелёных,    12 фиолетовых, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или синей.

 

       

             Ответ: ___________________________.

 

 

10

На рисунках изображены графики функций вида у^ах2 bxc .               Установите соответствие между графиками функций и знаками коэффициентов a и c .

ГРАФИКИ

 

 

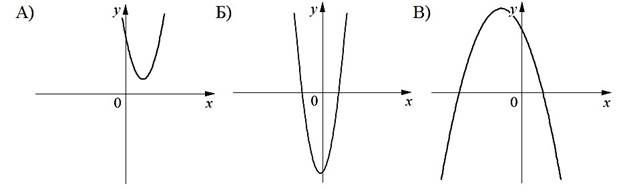
          КОЭФФИЦИЕНТЫ

 

                1)           а 0, c 0                2)     а 0, c 0              3) а 0, c 0     

 

В таблице под каждой буквой укажите соответствующий номер.

 

 

А	Б	B

 

 Ответ:  

 

 

11

Выписаны первые три члена геометрической прогрессии:  80;  20;  5; … Найдите её пятый член.

 

Ответ: ___________________________.

 

12

9b a² ab

 Найдите значение выражения    при a83, b5,4 a b 45b

 Ответ: ___________________________.

 

13

Перевести значение температуры по шкале Фаренгейта в шкалу Цельсия

5

позволяет формула t_C  t_F 32, где t_C — температура в градусах 9

Цельсия, t _F — температура в градусах Фаренгейта. Скольким градусам по шкале Цельсия соответствует 59 градуса по шкале Фаренгейта?

          

          Ответ: ___________________________.

 

 

14

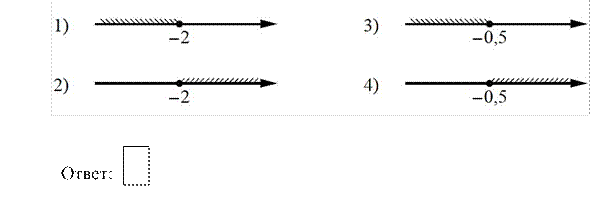Укажите решение неравенства   3х2х9.

 

 

 

 

15

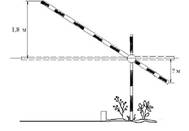Короткое плечо шлагбаума имеет длину 1 м, а длинное плечо – 3 м. На какую высоту (в метрах) опустится конец короткого плеча, когда конец длинного плеча поднимается  на 1,8 м?

 

Ответ: ___________________________.

 

 

 

16

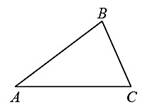В треугольнике АВС известно, что АВ = 14, ВС = 12, sinABC. Найдите площадь треугольника АВС.

 

Ответ: ___________________________.

 

 

 

17

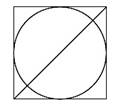Радиус вписанной в квадрат окружности равен  8 2 . Найдите диагональ этого квадрата.

 

Ответ: ___________________________.

 

 

 

18

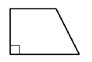Один из углов прямоугольной трапеции равен 107^о.  Найдите меньший угол этой трапеции. Ответ дайте в градусах.

 

Ответ: ___________________________.

 

19

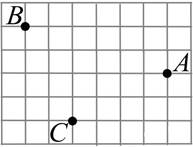На клетчатой бумаге с размером клетки  1см × 1см отмечены точки А, В и С. Найдите расстояние от точки А до середины отрезка ВС. Ответ выразите в сантиметрах.

 

Ответ: ___________________________.

 

 

 

20

Какое из следующих утверждений верно?

1)  Если угол равен 45°, то вертикальный с ним угол равен 45°.

2)  Через любые три точки проходит ровно одна прямая.

3)  Если расстояние от точки до прямой меньше 1, то и длина любой наклонной, проведенной из данной точки к прямой, меньше 1. В ответе запишите номер выбранного утверждения.

 

          Ответ: ___________________________.

 

 

 При выполнении заданий 21–26 используйте отдельный лист бумаги.  Сначала укажите номер задания, а затем запишите его решение и  ответ. Пишите чётко и разборчиво.

 

Часть 2

 

 

 

21

Решите уравнение х⁴  4х5².

 

 

22

Имеются два сосуда, содержащие 4 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 57 % кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 60% кислоты. Сколько килограммов кислоты содержится в первом растворе?

  

23

Постройте график функции

^{х2 } 4х1 при х3,                                     у_

                                                                                     _х1               при х3.

Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.

 

 

 

 

24

Прямая, параллельная основаниям трапеции ABCD, пересекает её  боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF , если AD = 45, BC =20, CF : DF = 4 : 1.

 

 

25

Через точку O пересечения диагоналей параллелограмма ABCD проведена прямая, пересекающая стороны AB и CD в точках P и Q соответственно. Докажите, что отрезки BP и DQ равны.

 

 

26

В равнобедренную трапецию, периметр которой равен 200, а площадь равна 1500, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.