
_______________________________________________________
(наименование организации образования)
Поурочный план или краткосрочный план
для педагога организаций среднего образования
Тригонометрические функции острого угла в прямоугольном треугольнике. Теорема Пифагора. (тема урока)
|
Раздел: |
8.2A Соотношения между сторонами и углами прямоугольного треугольника |
|
|
ФИО педагога |
Хамитов Р.Х |
|
|
Дата: |
14.11.23 |
|
|
Класс: 8 |
Количество присутствующих: |
Количество отсутствующих: |
|
Тема урока: |
Тригонометрические функции острого угла в прямоугольном треугольнике. Теорема Пифагора Урок №21 |
|
|
Цели
обучения в соответствии |
8.1.3.3 доказывать и применять теорему Пифагора;
|
|
|
Цели урока: |
Ознакомить и обеспечить овладение учащимися основными алгоритмическими приемами при нахождении сторон прямоугольного треугольника при помощи теоремы Пифагора; показать практическое применение теоремы Пифагора в жизни; способствовать развитию математической речи, оперативной памяти, произвольного внимания, наглядно-действенного мышления.
|
|
Ход урока
|
Этап урока/ Время |
Действия педагога |
Действия ученика |
Оценивание |
Ресурсы |
||||||||||||
|
Организационно-мотивационный этап. (5 мин) |
Приветствие учащихся, проверяет готовность учащихся к уроку. Мотивирует учащихся на восприятие нового материала: - Сегодня у нас с вами необычный день и необычный урок. Какие дни для себя вы считаете необычными? - А какие уроки вы считаете необычными? - А что необычное вы заметили сегодня в классе? - Прочитайте их и выберите три наиболее вам подходящие.
- А кто такой - Пифагор? Где вы раньше слышали это имя?
Значит, Пифагор имеет отношение к математике, и наш урок необычен тем, что мы сегодня не только изучим одну из самых известных геометрических теорем древности, называемую теоремой Пифагора, но и познакомимся с древнегреческим учёным Пифагором Самосским. Кто же такой Пифагор? / использовать сообщения учащихся , подготовленные заранее или презентацию /
- Подведем итог, кто же такой Пифагор? Пифагорейцами было сделано много важных открытий в арифметики и геометрии. Например, известная нам теорема о сумме углов треугольника, теорема о соотношении сторон в прямоугольном треугольнике.
|
Приветствуют учителя, настраиваются на урок
Ответы учащихся: дни рождения, семейные праздники, дни, когда, происходят события, значимые для вас. Нестандартные уроки, когда узнаём что-то очень интересное. На доске висят заповеди Пифагора.
Учащиеся высказывают свое мнение. Называют таблицу Пифагора, портрет Пифагора в кабинете математики.
Ученики воспринимают информацию.
Учёный, мыслитель, философ, поборник нравственности, поклонник ЗОЖ. |
Устная обратная связь учителя |
Презентация « Пифагор –великий математик » |
||||||||||||
|
Постановка учебной задачи. (3 мин.) |
Создает проблемную ситуацию: В 4 м друг от друга растут два дерева. Высота одного 5 м, а другого – 2 м. Найдите расстояние (в метрах) между их верхушками.
- Попробуйте сформулировать тему урока - В тетрадях запишите число и тему урока.
|
Выдвигаются версии, какую формулу применить при ответе на вопрос. Фиксируется затруднение в деятельности. Целеполагание. Самостоятельное выделение и формулирование проблемы. Перед учащимися возникает проблема: как найти расстояние между верхушками дерева..
Участвуют в формулировке темы урока и постановке целей. |
Устная обратная связь учителя
|
раздаточный материал /задача/ |
||||||||||||
|
Построение проекта выхода из затруднения. (9 мин)
|
Организует учащихся по исследованию проблемной ситуации с помощью решения исследовательской задачи практического содержания Задача. Построить прямоугольные треугольники с катетами 12 см и 5 см; 6 см и 8 см; 8 см и 15 см и измерить гипотенузу. Результаты занести в таблицу:
-Какой можно сделать вывод? -Попробуйте сами сформулировать теорему Пифагора. - Корректирует формулировку, данную учениками, советует сравнить ее с формулировкой в учебнике , обращая внимание на то, что теорема свойственна только для прямоугольных треугольников. - Рассмотрим доказательство теоремы Пифагора.
Запускает и демонстрирует МЭО.
Учащиеся прослушивают, а затем конспектируют в тетрадь (если что- то не понятно учитель комментирует по ходу). |
Учащиеся строят прямоугольные треугольники с заданными катетами и измеряют гипотенузу
Учащиеся формулируют теорему.
Анализируют, насколько правильно была составлена ими формулировка, сравнив ее с формулировкой, найденной в тексте учебника
Оформляют в тетрадях чертеж и записывают дано. Делают необходимые записи в тетрадь. После записи доказательства один из «сильных» учащихся пробует сам без звука и текста воспроизвести доказательство теоремы Пифагора. |
ФО . Устная обратная связь учителя
Самоанализ работы |
таблица
видео объяснение доказательства теоремы https://www.youtube.com/watch?v=529Rj_xaS9Q |
||||||||||||
|
Первичное закрепление новых знаний. (9 мин.) |
-Теперь, зная зависимость между катетами и гипотенузой в прямоугольном треугольнике, ответим на вопрос: какое расстояние между верхушками дерева./ возвращаемся к решению задачи про деревья/ Предлагает учащимся ознакомиться с иными формулировками теоремы Пифагора. Запускает ЭОР.
-Многие писатели прошлого обращались к этой замечательной теореме и посвящали ей свои строки.
Устанавливает осознанность восприятия учебного материала. Рассматривается решение типовых задач из учебника. №1-2(а) с 66. №8 |
У доски сильный ученик решают задачу с пояснением, все остальные учащиеся работают в тетрадях. На основании решения делают вывод (как найти гипотенузу, зная два катета и как найти катет, зная гипотенузу и катет). Воспринимают информацию, сравнивают формулировки. Читают стихотворение.
Решают типовые задачи. Работа по учебнику (Применение теоремы Пифагора к решению задач). Задачи решаются на доске и в тетради |
Взаимооценив. Прием « Две звезды одно пожелание «
ФО . Устная обратная связь учителя
|
Презентация ЭОР https://www.youtube.com/watch?v=EFB9z304j3k
Геометр.8кл «Мектеп» 2018
|
||||||||||||
|
Контроль и оценка результатов деятельности. (8 мин,) |
Организует деятельность по контролю усвоения приобретенных знаний.
|
Выполняют проверочную самостоятельную работу. 1. Найти гипотенузу прямоугольного треугольника, если известны катеты.
2. Найти катет, если известна гипотенуза и другой катет.
|
Взаимооценивание
|
|
||||||||||||
|
Домашнее задание (2 мин.) |
Объясняет домашнее задание. №3,6 с66. Инструктирует по выполнению заданий. Творческое задание: - Существует более 100 способов доказательства теоремы. Найдите другие способы доказательства этой теоремы.
|
Записывают домашнее задание в дневники. |
|
|||||||||||||
|
Организует рефлексию - Чем необычный был для вас сегодняшний урок? - Что нового и интересного вы узнали на уроке? - Что научились делать? - Оцените удовлетворенность своей работой на уроке с помощью карточек. И закончить урок я
бы хотела словами Пифагора:
|
Отвечают, на вопросы с аргументацией, оценивают свою работу на уроке (показывают карточки: синяя – удовлетворены, красная - нет). |
|
|
Приложение
|
Приведем различные формулировки теоремы Пифагора в переводе с греческого, латинского и немецкого языков. У Евклида эта теорема гласит (дословный перевод): "В прямоугольном треугольнике квадрат стороны, натянутой над прямым углом, равен квадратам на сторонах, заключающих прямой угол". Латинский перевод арабского текста Аннаирици (около 900 г. до н. э. ), сделанныйГерхардом Клемонским (начало 12 в.), в переводе на русский гласит: "Во всяком прямоугольном треугольнике квадрат, образованный на стороне, натянутой над прямым углом, равен сумме двух квадратов, образованных на двух сторонах, заключающих прямой угол". В Geometria Culmonensis (около 1400 г.) в переводе теорема читается так : "Итак, площадь квадрата, измеренного по длинной стороне, столь же велика, как у двух квадратов, которые измерены по двум сторонам его, примыкающим к прямому углу". В первом русском переводе евклидовых "Начал", сделанном Ф. И. Петрушевским, теорема Пифагора изложена так: "В прямоугольных треугольниках квадрат из стороны, противолежащей прямому углу, равен сумме квадратов из сторон, содержащих прямой угол". В настоящее время известно, что эта теорема не была открыта Пифагором. Однако одни полагают, что Пифатор первым дал ее полноценное докзательство, а другие отказывают ему и в этой заслуге. Некоторые приписывают Пифагору доказательство, которое Евклид приводит в первой книге своих "Начал". С другой стороны, Прокл утверждает, что доказательство в "Началах" принадлежит самому Евклиду. Как мы видим, история математики почти не сохранила достоверных данных о жизни Пифагора и его математической деятельности. |
Таблица
|
A |
12 |
6 |
8 |
|
B |
5 |
8 |
15 |
|
c |
|
|
|
|
A |
12 |
6 |
8 |
|
B |
5 |
8 |
15 |
|
c |
|
|
|
Задача
В 4 м друг от друга растут два дерева.
Высота одного 5 м, а другого – 2 м.
Найдите расстояние (в метрах) между их верхушками.
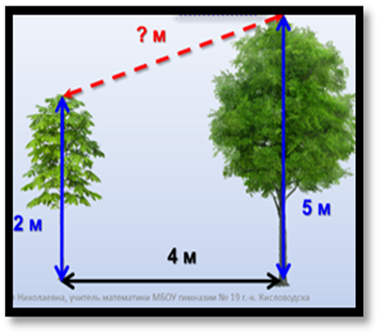
Решение
5м – 2м = 3м
3 2 + 4 2 = 9 + 16 = 25
√25 = 5 м расстояние между их верхушками.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.