Тригонометриялық функциялардың графигі мен қасиеттері. у=сtgx

Сабақ жоспары Сабақ нөмірі: №25 Пәні: алгебра Сыныбы: 10  Күні:  Сабақтың  тақырыбы:     Тригонометриялық функциялардың   графигі мен қасиеттері. у=сtgx Сабақтың міндеттері: Білімділігі:  Оқушыларды  тригонометриялық функциялардың  графигін салу   арқылы қасиеттерімен                             таныстыру.Есеп шығаруда қолдана білуге үйрету Дамытушылығы:  Оқушының   график салу шеберлігін   қалыптастыру және практикамен                              ұштастыруға үйрету, шығармашылығын  және ойлау қабілетін дамыту Тәрбиелігі: Оқушыны графикті тануға үйрету, сұрақтарға нақты жауап беруге баулу. Сабақтың түрі:  Жаңа сабақты меңгерту Сабақтың көрнекілігі: Компьютер, видеопроектор, карточка, слайдтар Сабақтың барысы:  1. Ұйымдастыру кезеңі 2. Үй тапсырмасын тексеру: §7, №67(б)  3. Жаңа сабақты түсіндіру:    4. 1.  y   функциясын қарастырамыз: tgx жиынынан басқа барлық нақты сандар жиыны,    себебі 1) анықталу облысы     x   2  ,     y  tgx , cos x  ,0 x   ,  ; sin cos x x  2 2) мәндер жиыны ­ барлық нақты сандар жиыны, яғни     3)  4) функция тақ, өйткені  функция периодты, себебі ең кіші оң периоды  саны;   x  , tgx  ; R ; tgx tgx tg tg x     5)       2   n ;  ,0;0 Енді      аралығында    nn   ,      интервалында функция бірсарынды өспелі.  2  6 y   графигін саламыз.  (1­сурет)                                             3  3  tgx   ,1;   3  4 3;       ; ,  бақылау нүктелерін координаталық жазықтықта белгілеп,    ;0  2      tgx 1­сурет                                                                                                                                             y  функциясы тақ функция болғандықтан, оның графигі бас нүктеге қарағанда симметриялы қисық екенін ескеріп,       интервалындағы графигі шығады. (2­сурет)                                  аралығында графикті жалғастырамыз. 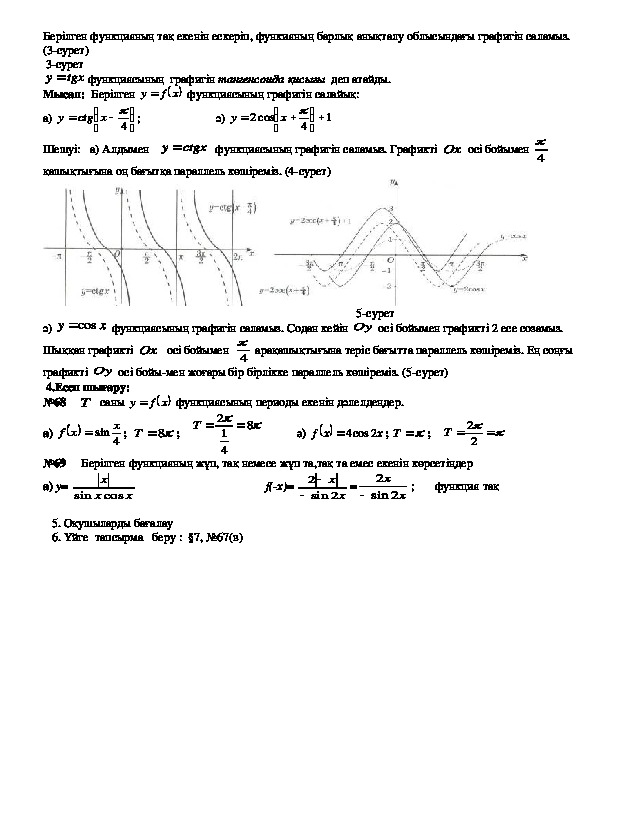Сонда  y  функциясының  2 2  2     tgx 0;      ; Берілген функцияның тақ екенін ескеріп, функияның барлық анықталу облысындағы графигін саламыз.  (3­сурет)  3­сурет y  функциясының  графигін тангенсоида қисығы  деп атайды. tgx Мысал:  Берілген      функциясының графигін салайық: ;                         ә)     cos x      4  xf  4 y        ctg а)       1 2 x y y  Шешуі:   а) Алдымен    y  ctgx   функциясының графигін саламыз. Графикті  Ox  осі бойымен  қашықтығына оң бағытқа параллель көшіреміз. (4­сурет)  4   y cos x ә)   функциясының графигін саламыз. Содан кейін  Oy  осі бойымен графикті 2 есе созамыз.  Шыққан графикті  Ox   осі бойымен    арақашықтығына теріс бағытта параллель көшіреміз. Ең соңғы   4 5­сурет y   xf  функциясының периоды екенін дәлелдеңдер. графикті  Oy  осі бойы­мен жоғары бір бірлікке параллель көшіреміз. (5­сурет)  4.Есеп шығару: №68    T   саны  х 4  2 2 №69     Берілген функцияның жұп, тақ немесе жұп та,тақ та емес екенін көрсетіңдер а) у=                                             f(­х)=   2   8 1 4            ә)  8T ;  T T  xf  xf ;     ;     4 cos sin а)  ;    = T 2 x   ;       функция тақ     x 2 2sin x  x 2 2sin x  x cos x x sin    5. Оқушыларды бағалау    6. Үйге  тапсырма   беру :  §7, №67(в)