
|
Тема: |
Целые и рациональные числа. |
||||||||||||||
|
Тип занятия: |
Урок овладения новым материалом. |
||||||||||||||
|
Вид занятия: |
Аудиторное теоретическое занятие |
||||||||||||||
|
Цели занятия: |
|
||||||||||||||
|
Образовательные: |
- рассмотреть множество натуральных чисел; - рассмотреть множество целых чисел; - рассмотреть множество рациональных чисел; - ввести понятие конечной и бесконечной десятичной дроби; - дать определение бесконечной периодической десятичной дроби. - сформировать умениепереводить обыкновенную дробь в десятичную; - сформировать умение переводить бесконечную периодическую дробь в обыкновенную; - сформировать желание самостоятельно изучать материал; |
||||||||||||||
|
Воспитательные: |
- воспитывать положительное отношение к приобретению новых знаний; - воспитывать ответственность за свои действия и поступки; - вызвать заинтересованность новым для студентов подходом изучения математики. |
||||||||||||||
|
Развивающие: |
- формировать навыки познавательного мышления; - формировать умения и навыки учебного труда. |
||||||||||||||
|
Методы обучения: |
Лекция объяснительно - иллюстрированная |
||||||||||||||
|
Планируемый результат: |
Студент знает: Определение бесконечной периодической десятичной дроби. Знает множество натуральных чисел. Знает множество целых чисел. Знает множество рациональных чисел. Умеет представлять обыкновенную дробь в виде десятичной. Умеет представлять бесконечную периодическую дробь в виде обыкновенной дроби. |
||||||||||||||
|
Структура занятия: |
1. Устная работа |
||||||||||||||
|
2. Объяснение темы «Целые и рациональные числа» 1. Множество натуральных чисел 2. Множество целых чисел 3. Множество рациональных чисел 4. Конечные десятичные дроби 5. Бесконечные десятичные дроби 6. Бесконечная периодическая десятичная дробь |
|||||||||||||||
|
3. Решение ключевых задач. 1. Представить обыкновенную дробь в виде десятичной. 2. Представить бесконечную периодическую дробь в виде обыкновенной дроби. |
|||||||||||||||
|
4. Решение упражнений (нечетные пункты) на закрепление темы (№1,2,4,5) |
|||||||||||||||
|
5. Самостоятельная работа. 6.Домашнее задание |
|||||||||||||||
|
1 |
Устная работа: |
||||||||||||||
|
|
Вычислите:
|
Вычислите:
|
Вычислите:
|
Вычислите:
|
|||||||||||
|
|
Объединить числа в группы по общим признакам (подсказка: 4 группы, в каждой группе по три числа):
Ожидаемый ответ: 1 группа: 4; 7; 12 2 группа: 3 группа: 4 группа: 2). Назвать одним словом полученные группы чисел. Ожидаемый ответ: 1 группа: положительные числа 2 группа: 3 группа: 4 группа: |
||||||||||||||
|
|
Учащиеся отвечают на наводящие вопросы, самостоятельно формулируют тему урока. 1) Представителями какого множества чисел являются числа из группы №1? 2) Представителями какого множества чисел являются числа из групп №1 и №2 вместе? 3) Представителями какого множества чисел являются числа из групп №3 и №4 вместе? |
||||||||||||||
|
2 |
Объяснение новой темы: |
||||||||||||||
|
|
1. Множество натуральных чисел: |
Числа, которые мы используем при счете предметов, называются натуральными. При сложении и умножении натуральных чисел всегда получаются натуральные числа. Однако разность и частное натуральных чисел не всегда являются натуральными числами.
|
|||||||||||||
|
2. Множество целых чисел
|
Дополним множество натуральных чисел, нулем и отрицательными числами(т.е. числами противоположными натуральным). Мы получим множество целых чисел. Надо заметить, что при сложении, вычитании, умножении целых чисел, всегда образуются целые числа. Однако частное двух целых чисел, не обязятельно будет целым числом.
|
||||||||||||||
|
|
|||||||||||||||
|
3. Множество рациональных чисел
|
Введение рациональных чисел, то есть чисел вида Каждое целое число При выполнении четырех арифметических действий (кроме деления на нуль) над рациональными числами всегда получаются рациональные числа. |
||||||||||||||
|
|
|||||||||||||||
|
|
Остановимся на десятичных и обыкновенных дробях более подробно (т.е. на множестве рациональных чисел) В предыдущих классах вы научились записывать обыкновенную дробь в виде десятичной и наоборот – десятичную дробь записывать в виде обыкновенной. Рассматриваются и разбираются следующие примеры: 8,75 = 8
II способ – деление уголком 2 на 5. При делении уголком 13 на 19 получаем: 0,68421… Ученики дают название полученной дроби (бесконечная десятичная дробь). Разберем другой пример: - перевести - при делении
уголком находим - замечаем повторяющуюся цифру, называем ее периодом. - а полностью дробь – десятичная периодическая. - запись и чтение: |
||||||||||||||
|
4. Конечные десятичные дроби |
Если рациональное число можно представить в виде дроби Например,
Например,
|
||||||||||||||
|
|
5. Бесконечные десятичные дроби
|
Существуют рациональные числа, которые нельзя записать в виде
конечной десятичной дроби, например Если, например, попытаться записать число Бесконечную деятичную
дробь Коротко записывают так: |
|||||||||||||
|
|
6. Бесконечная периодическая десятичная дробь.
|
Определение Периодическая дробь – это бесконечная десятичная дробь, у которой начиная с некоторого десятичного знака повторяется одна и та же цифра или несколько цифр – период дроби.
|
|||||||||||||
|
3 |
Решение ключевых задач. |
Задача 1. Записать число Решение: |
|||||||||||||
|
Задача 2. Представить бесконечную периодическую десятичную
дробь Решение: 1.Пусть
2)Период этой дроби состоит из двух
цифр. Поэтому, умножая обе части последнего равенства на
3)Вычитая из равенства (2) равенство (1), получаем
|
|||||||||||||||
|
4 |
Решение тренировочныхупражнений из учебника «Алгебра и начала анализа 10-11» на закрепление темы: нечетные пункты |
||||||||||||||
|
|
№1.
Записать в виде десятичной дроби: Решение: |
||||||||||||||
|
|
|
|
|
|
|
||||||||||
|
№2. Выполнить действия и записать результат в виде десятичной дроби:
|
|||||||||||||||
|
|
|
|
|||||||||||||
|
|
|||||||||||||||
|
|
|
|
|||||||||||||
|
№4.Вычислить: |
|||||||||||||||
|
|
|||||||||||||||
|
1)
|
|||||||||||||||
|
|
|||||||||||||||
|
1)
|
|||||||||||||||
|
№5.Вычислить: |
|||||||||||||||
|
|
|||||||||||||||
|
5 |
Самостоятельная работа |
||||||||||||||
|
1 вариант |
2 вариант |
||||||||||||||
|
Закончите предложения таким образом, чтобы высказывание стало истинным |
|||||||||||||||
|
1. Натуральное число делится на 3 если, …….сумма цифр этого числа делится на 3 |
1. Натуральное число делится на 4 если, …….две его последние цифры нули или число, кратное 4. |
||||||||||||||
|
2. Натуральное число делится на 5 если, …….если число оканчивается на цифру ноль или цифру 5 |
3. Натуральное число делится на 9 если, ……. сумма цифр этого числа делится на 9 |
||||||||||||||
|
4. Каждое натуральное число можно записать в виде бесконечной периодической дроби с периодом…..ноль |
2. Каждое целое число можно записать в виде бесконечной периодической дроби с периодом….. ноль |
||||||||||||||
|
Представьте бесконечную периодическую десятичную дробь в виде десятичной |
|||||||||||||||
|
|
Решение:
1) Период нашей дроби состоит из одной
цифры. Поэтому, умножая обе части последнего равенства на 2) Вычитая из равенства (2) равенство (1), получаем 3)
|
Решение:
1) Период нашей дроби состоит из одной
цифры. Поэтому, умножая обе части последнего равенства на 2) Вычитая из равенства (2) равенство (1), получаем 3)
|
|||||||||||||
|
|
Решение:
1) Период нашей дроби состоит из двухцифр.
Поэтому, умножая обе части последнего равенства на 2) Вычитая из равенства (2) равенство (1), получаем 3)
|
Решение:
1) Период нашей дроби состоит из двухцифр.
Поэтому, умножая обе части последнего равенства на 2) Вычитая из равенства (2) равенство (1), получаем 3)
Итак,
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
Рефлексия. Закончить предложение «На сегодняшнем уроке»: - Тема… - Цель… - Я узнал… - Я научился… - Я выполнял задания… - Особенно мне понравилось… - Было трудно… - Я считаю, нужно запомнить… - Я считаю, что нужно еще поработать над… - На следующем уроке я хотел бы научиться… |
||||||||||||||
|
6 |
Домашнее задание: Учебник №1, №2, №4, №5 – четные пункты. |
||||||||||||||
|
|
|
||||||||||||||


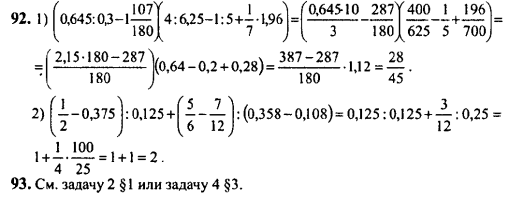




Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.