Составитель 

Даниелян Ц.М., преподаватель БПОУ «Омавиат»

             Учебное пособие «Исследование функции с помощью производной. Монотонность, экстремумы функции» предназначено для студентов 1 курса. Содержит тренировочные и диагностические  работы, ориентированные на закрепления и контроль знаний по задачам исследования функций с помощью производной.

                                       Исследование функции с помощью производной

                                                          Тренировочные задания

№1         На рисунке изображен график функции у=f^/(x) определенной на интервале (-1;10). Найдите промежутки убывания функции f(x). В ответе укажите сумму целых точек , входящих в эти промежутки.

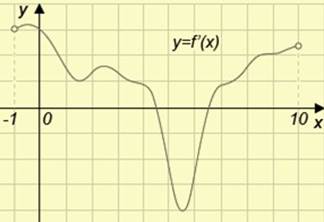
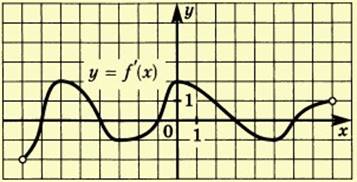
№2         На рисунке изображен график функции у=f(x), определенной на интервале (-4;9). Определите количество целых точек, в которых производная функции отрицательна.

№3         На рисунке изображен график дифференцируемой функции у= f(x). На оси абсцисс отмечены девять точек х₁,х₂,…х_9. Среди этих точек найдите все точки в которых производная функции отрицательна. В ответе укажите количество точек.

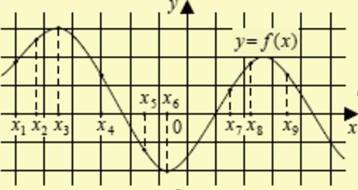
№4         Функция f(x) определена на интервале (-8;8). На рисунке изображён график её производной. Найдите длину наибольшего промежутка возрастания функции y=f(x).

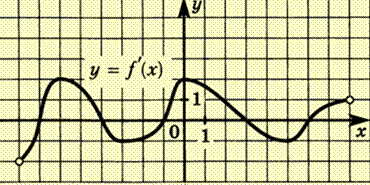
№5        На рисунке изображен график производной функции f(x), определенной на интервале (-4;13). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.

№6         Функция определена на отрезке [-4;4].На рисунке изображён её график. Найдите точку минимума этой функции на интервале (-3;3).

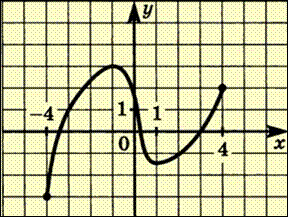
№7         На рисунке изображен график функции у= f(x), определенной на интервале (-9;4). Найдите сумму точек экстремума функции f(x).

№8         На рисунке изображен график производной функции f(x), определенной на интервале (-8;3). Найдите точку экстремума функции  f(x) на отрезке [-5;2]

№9         Найдите точки экстремума функции .

№10      Найдите точки экстремума функции  на промежутке .

№11 На рисунке изображён график производной функции у=f’(x).           Найдите точку максимума функции у=f(x)  на отрезке  [-6;6].

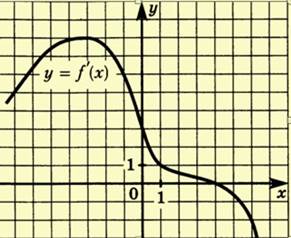
№12      На рисунке изображен график производной функции f^/(x) на интервале (-8;8)

а) сколько промежутков возрастания имеет функция у=f(x);

б) укажите длину наибольшего из них;

в) сколько точек экстремума имеет функция;

г) укажите количество точек максимума функции минимума функции

д) укажите количество точек, в которых касательная параллельна прямой у=2х+3

Исследование функции с помощью производной

                                         Диагностическая работа

                                                                                                               Вариант 1

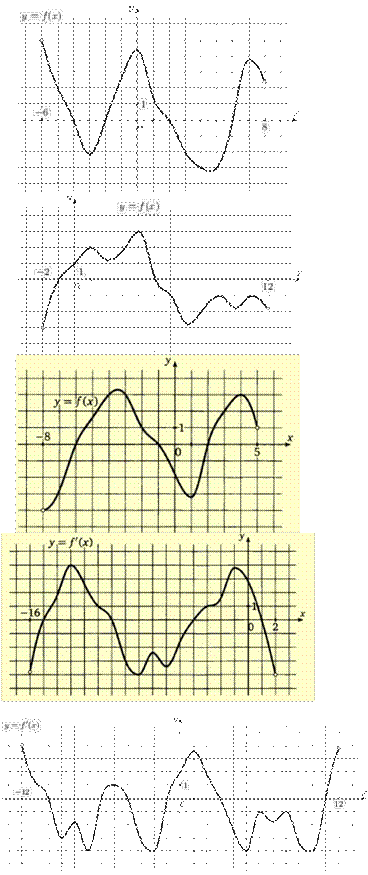№1 На рисунке изображен

график функции ,

определенной на интервале  

(-6;8) . Определите количество целых точек, в которых производная функции положительна.

№2 На рисунке изображен

график функции ,

определенной на интервале (-2;12) . Найдите сумму

точек экстремума функции

 .

№3     На рисунке изображен график функции y=f(x), определенной на интервале

(-8;5).Определите количество целых чисел x_i, для которых f’(x_i)отрицательно.

№4 На рисунке изображен график производной функции f(x), определенной на интервале (-

16;2).Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.

№5 На рисунке изображен график  y=f ^'(x) - производной функции f(x), определенной на интервале (-12;12). Найдите  сумму точек

экстремума функции f(x) на

               отрезке [-8;7]                             

            Вариант 2 №1  

На рисунке изображен

график функции ,

определенной на интервале  (-1;12) . Определите количество целых точек, в которых производная функции отрицательна.

№2

На рисунке изображен

график функции,

определенной на интервале  (-7;5) . Найдите сумму точек экстремума функции .

№3 На рисунке изображен график функции y=f(x), определенной на интервале

(-6;8).Определите количество целых чисел x_i, для которых f’(x_i)отрицательно.

№4 На рисунке изображен  

график производной функции f(x), определенной на интервале

 (-12;2).Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.

№5 На рисунке изображен  

график y=f ^'(x) - производной функции f(x), определенной на интервале (-9;5). Найдите  сумму точек экстремума функции f(x) на отрезке [-6;4].