Учебное пособие «Исследование функции с помощью производной. Монотонность, экстремумы функции»

Составитель

Даниелян Ц.М., преподаватель БПОУ «Омавиат»

                         Учебное пособие «Исследование функции с помощью производной. Построение графиков» предназначено для студентов 1 курса. Содержит тренировочные и диагностические работы, ориентированные на закрепления и контроль знаний по задачам   исследования функции с помощью производной. 

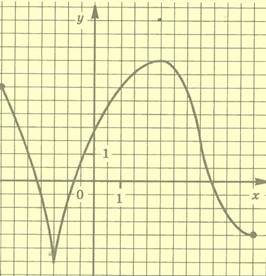
№1     Функция у=f(x) задана своим графиком.  Укажите:

а) область определения функции;

б) при каких значениях x f^/(x)<0

                                            f^/(x)>0;

в) наибольшее и наименьшее значения функции;

г) в какой точке графика касательная к нему параллельна оси абсцисс.

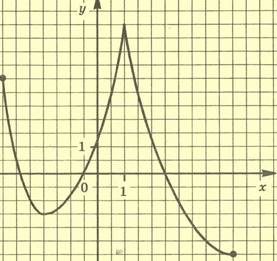№2     Функция у=f(x) задана своим графиком. 

Укажите: 

а) область определения функции;

б) при каких значениях x  

 -2< f(x)≤1; 

в) при каких значениях x   f^/(x)=0;

г) промежутки возрастания и   промежутки убывания функции.

№3     Дана функция f(x)=3-3х-2х². Найдите координаты точки графика этой функции, в которой угловой коэффициент касательной к нему равен 5.

№10     Изобразите график непрерывной функции у=f(x), зная, что:

а) область определения функции есть промежуток [-4;3];

б) значения функции составляют промежуток [-2;4];

в) производная функции на промежутке (-1;1) принимает положительные значения, а на промежутках  (-4;-1) и (1;3) – отрицательные значения;

г) график функции  имеет единственную касательную, параллельную оси абсцисс.

Вариант 1

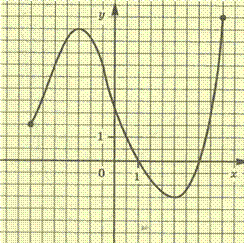
№1 Функция у=f(x) задана своим графиком.  Укажите:

а) область определения функции;

б) при каких значениях x f(x)<-1;

в) при каких значениях x f^/(x)<0           f^/(x)>0;

г) в каких точках  графика касательные к нему параллельны оси абсцисс;

д) наибольшее и   наименьшее  значения функции.

№2 Изобразите график непрерывной функции у=f(x), зная, что:

а) область определения функции есть промежуток [-1;6];

б) значения функции составляют промежуток [-4;4];

в) производная функции на промежутках (-1;1) и (1;3) принимает положительные значения, а на промежутке (3;6) – отрицательные значения;

г) нули производной функции: 1 и 3.

№3 Изобразите эскиз графика функции у=f(x), если промежутки постоянства знака производной f^/(x) представлены на схеме:

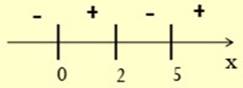
№4 Дана функция f(x)= 3+5x+3x². Найдите координаты точки ее графика, в которой угловой коэффициент касательной ему равен -7.

Вариант 2

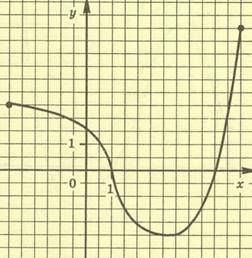№1 Функция у=f(x) задана своим графиком.  Укажите:

а) область определения функции;

б) при каких значениях x f(x)>1;

в) промежутки возрастания и   промежутки убывания функции; г) в какой точке графика касательная к нему параллельна оси абсцисс;

д) наибольшее и наименьшее значения функции.

№2 Изобразите график непрерывной функции у=f(x), зная, что:

а) область определения функции есть промежуток [-5;2];

б) значения функции составляют промежуток [-2;5];

в) f^/(x)<0 для любого х из промежутка (-3;-1), f^/(x)>0 для любого х из промежутков (-5;-3) и (-1;2), f^/(x)=0 при х=-3; г) нули функции: х=-4 и х=-1.

№3 Изобразите эскиз графика функции у=f(x), если промежутки постоянства знака производной f^/(x) представлены на схеме:

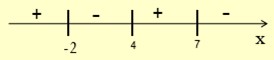
№4 Дана функция f(x)= 3x² -8x+1. Найдите координаты точки ее графика, в которой угловой коэффициент касательной ему равен -2.