
Публикация является частью публикации:

Большая часть вопросов практики приводится к задачам наибольших и наименьших величин, … и только решением этих задач мы можем удовлетворить требованиям практики, которая везде ищет самого лучшего, самого выгодного.
П.Л. Чебышев
Составитель
Даниелян Ц.М., преподаватель БПОУ «Омавиат»
Учебное пособие «Исследование функции с помощью производной. Наибольшее и наименьшее значение функции» предназначено для студентов 1 курса. Содержит тренировочные и диагностические работы, ориентированные на закрепления и контроль знаний по задачам исследования функции с помощью производной.

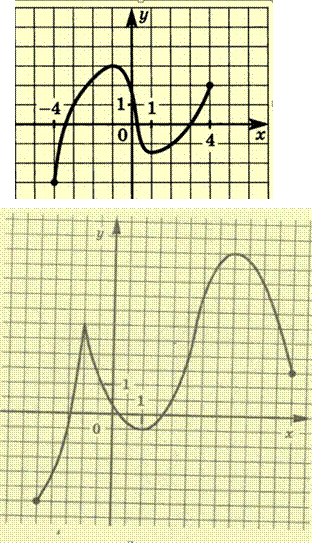 №1 Функция
определенна на отрезке [-4;4]. На рисунке изображен ее график. В какой точке
она принимает свое наименьшее значение.
№1 Функция
определенна на отрезке [-4;4]. На рисунке изображен ее график. В какой точке
она принимает свое наименьшее значение.
№2 Функция у=f(x) задана своим графиком.
Укажите:
а) область определения функции;
б) при каких значениях x f(x) ![]() -0,5;
-0,5;
в) точки экстремума функции;
г) промежутки возрастания и убывания функции;
д) наибольшее и наименьшее значения функции.
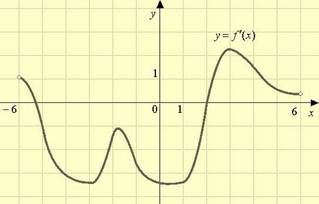 №3 На рисунке
изображен график /(x)- производной функции
№3 На рисунке
изображен график /(x)- производной функции
у=f f(x), определенной на интервале (-6;6). В какой точке отрезка [3;5]
 функция f(x)
принимает наибольшее значение? №4 На рисунке изображен график
производной функции f(x),определенный на интервале (-3;9). В какой
точке отрезка[-2;3] f(x) принимает наибольшее значение?
функция f(x)
принимает наибольшее значение? №4 На рисунке изображен график
производной функции f(x),определенный на интервале (-3;9). В какой
точке отрезка[-2;3] f(x) принимает наибольшее значение?
№5 Найдите наибольшее и
наименьшее значения функции ![]() на отрезке [3;4].
на отрезке [3;4].
|
№6 |
Найдите наименьшее значение функции f(x)=3х2-12х+1 на промежутке [1;4]. |
|
№7 |
Сумма удвоенного числа и квадрата этого же числа имеет наименьшее значение. Найдите это число. |
|
№8 |
Разделить число 24 на два положительных слагаемых так, чтобы их произведение было наибольшим.
|
|
№9 |
Материальная точка движется прямолинейно по закону |
s![]() какой момент времени из промежутка[1;4]
скорость точки будет наибольшей?
какой момент времени из промежутка[1;4]
скорость точки будет наибольшей?
№10 Периметр прямоугольника равен 72 см. При каких длинах сторон площадь прямоугольника будет наибольшей?
№11 На странице книги печатный текст должен занимать 15осм2.
Верхнее и нежнее поля страницы по 3 см, а правое и левое – по 2 см. Если принимать во внимание только экономию бумаги,то каковы должны быть наиболее выгодные размеры страницы?
№12 Найдите наибольшее и наименьшее значения функции
3-3х2-12х+1 на отрезке [4;5].
у=2х

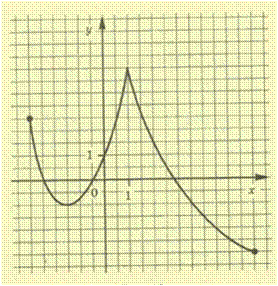 №1 Функция у=f(x)
задана своим графиком. Укажите:
№1 Функция у=f(x)
задана своим графиком. Укажите:
а) область определения функции;
б) при каких значениях x f(x) ![]() -1;
-1;
в) при каких значениях x f’(x)=0;
г) промежутки возрастания и убывания функции;
д) наибольшее и наименьшее значения функции.
|
|
|
|
№2 |
Найдите наибольшее и наименьшее значения функции у=2х -3х2-12х+1 на отрезке [4;5]. 3
|
|
№3 |
Забором, длиной 80, м нужно огородить прямоугольную площадку наибольшей площади. Найдите размеры площадки.
|
|
№4 |
Разбейте число 18 на два неотрицательных слагаемых так, чтобы произведение квадрата первого и второго слагаемого было бы наибольшим.
|
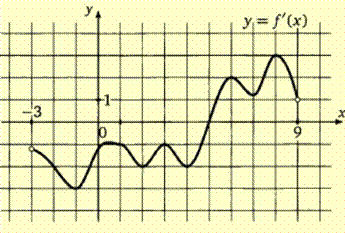
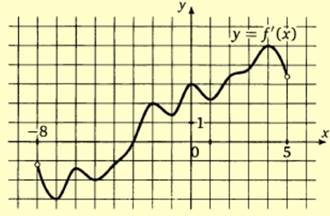 №5 На рисунке
изображен график у=f/(x)- производной функции f(x), определенной на
интервале (-8;5). В какой точке отрезка [0;4] функция f(x) принимает наименьшее
значение?
№5 На рисунке
изображен график у=f/(x)- производной функции f(x), определенной на
интервале (-8;5). В какой точке отрезка [0;4] функция f(x) принимает наименьшее
значение?
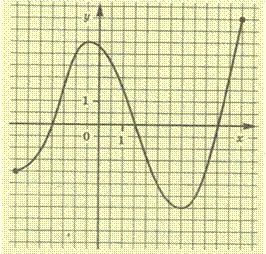 №1 Функция у=f(x)
задана своим графиком.
№1 Функция у=f(x)
задана своим графиком.
Укажите:
а) область определения функции;
б) при каких значениях x f(x) ![]() 3,5;
3,5;
в) при каких значениях x f’(x)=0;
г) промежутки возрастания и убывания функции;
д) наибольшее и наименьшее
|
|
значения функции.
|
|
№2 |
Найдите наибольшее и наименьшее значения функции у= -х3+3х2+4 на отрезке [-3;3]
|
|
№3 |
Забором, длиной 16, м требуется огородить с трех сторон прямоугольный палисадник наибольшей площади. Найдите размеры палисадника.
|
|
№4 |
Число 86 представлено в виде суммы двух слагаемых так, что их произведение максимально. Найти эти слагаемые.
|
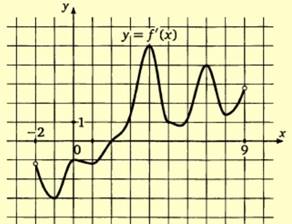 №5 На рисунке
изображен график у=f/(x) - производной функции f(x), определенной на
интервале (-2;9). В какой точке отрезка [3;8] функция f(x) принимает наименьшее
значение?
№5 На рисунке
изображен график у=f/(x) - производной функции f(x), определенной на
интервале (-2;9). В какой точке отрезка [3;8] функция f(x) принимает наименьшее
значение?
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.