УМНОЖЕНИЕ ОДНОЧЛЕНА НА МНОГОЧЛЕН

умножение  одночлена на многочлен

Цели: изучить правило умножения одночлена на многочлен; формировать умение применять это правило при преобразовании выражений.

Ход урока

I. Устная работа.

1. Раскройте скобки.

а) 3 (2х – 5);                              в) (4 + 2y);                               д) 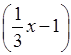 · (–3);

б) (5а – 1) 4;                              г) –5 (3р – 8);                    е) 0,7 (3а – 10).

2. Упростите выражение.

а) а⁵ · а⁷;                                     в) аа²а³;                                             д) (п³)² п⁴;

б) х⁸ : х³;                                     г) (х²)⁵;                                е) у² у³(у⁴)².

II. Объяснение нового материала.

При объяснении этого материала достаточно привести несколько примеров умножения одночлена на многочлен и сформулировать соответствующее правило.

III. Формирование умений и навыков.

1. № 614; № 615 (а, в, д).

2. № 616.

Решение:

(На первых порах желательно, чтобы учащиеся (особенно слабые) вели подробные записи, это позволит избежать ошибок в преобразованиях.)

в)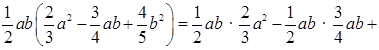

г)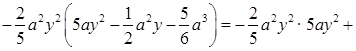

3. № 618 (а, в).

Решение:

(Здесь важно ещё раз напомнить учащимся о том, что перед нахождением значения любого выражения его сначала упрощают.)

в) 4у – 2 (10у – 1) + (8у – 24) = 4у – 20у + 2 + 8у – 24 = –8у – 22

при у = –0,1:       –8у – 22 = –8 · (–0,1) – 22 = 0,8 – 22 = –21,2.

4. № 619.

IV. Итоги урока.

– Как выполнить умножение одночлена на одночлен?

– Перемножьте одночлены –2х² и 5х⁴.

– Сформулируйте правило умножения одночлена на многочлен.

– Умножьте одночлен 4а³ на многочлен 2а – 3.

Домашнее задание: № 617;  618 (б, г); № 620.