УМНОЖЕНИЕ РАЗНОСТИ ДВУХ ВЫРАЖЕНИЙ НА ИХ СУММУ

умножение разности двух выражений на их сумму

Цели: вывести формулу умножения разности двух выражений на их сумму; формировать умение применять эту формулу.

Ход урока

I. Устная работа.

1. Выполните возведение в квадрат.

а) (–3х²у)²;                                г) 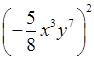;                   ж) (–3m + 2)²;

б) 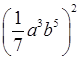;                           д) (2х – 1)²;                         з) (–у – 9)².

в) (0,9p⁴q¹⁰)²;                           е) (а + 11)².

2. Выполните умножение.

а) –3a² (5a – a⁴);                     в) (y – 3) (x + 4);

б) x³ (2x – x⁵);                       г) (a – 1) (2b – 5).

II. Объяснение нового материала.

Объяснение  проводить  согласно  пункту  34  учебника  в  несколько этапов.

1. Вспомнить формулу

2.

3. Сделать выводы, сформулировать правило умножения разности двух выражений на их сумму, разобрать примеры 1 и 2 из учебника.

III. Формирование умений и навыков.

1. № 854.

После преобразования нескольких выражений учащиеся зачастую начинают делать распространенную ошибку: возводят в квадрат выражения в том порядке, в котором они записаны в первой скобке. Например:

е) (7 + 3y) (3y – 7) = 7² – (3y)² = 49 – 9y².

1) (x + 2y) (2y – x);                  3) (4a + 1) (1 – 4a);

2) (6 + 5n) (5n – 6);                 4) .

2. № 859.

Решение:

а)

б)

в)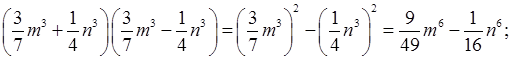

г) 25a⁴ – 0,16y⁶;

д) 1,44c⁴ – 49a⁴;

е)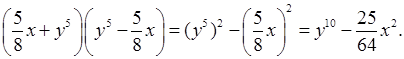

3. № 858 (устно).

4. № 860.

Решение:

г) 74 · 66 = (70 + 4) (70 – 4) = 70² – 4² = 4900 – 16 = 4884;

е) 1,05 · 0,95 = (1 + 0,5) (1 – 0,5) = 1 – 0,5² = 1 – 0,25 = 0,75.

IV. Итоги урока.

– Для чего нужны формулы сокращенного умножения?

– С какой формулой вы познакомились на этом уроке?

– Выполните умножение:

а) (х + 1) (1 – х);

б) (3у + 1) (1 – 3у);

в) (п + 7) (7 – п).

Домашнее задание: № 855; № 857; № 861 (б, г, е).