Универсальная формула статья

УДК 628413                 Амбарцумян Егине Гамлетовна,

ученица 11 «Б» класса

МОУ СОШ № 12 с углубленным изучением отдельных предметов

Город Сургут, Ханты-Мансийский автономный округ, Россия

Зотова Рита Ямилевна,

Научный руководитель: учитель математики, первая категория,

МОУ СОШ № 12 с углубленным изучением отдельных предметов

Город Сургут, Ханты-Мансийский автономный округ, Россия

rita_zotova@mail.ru

УНИВЕРСАЛЬНАЯ ФОРМУЛА

Аннотация.     

Формул для вычисления объёма геометрических тел: призмы, пирамиды, конуса, цилиндра, шара, параллелепипеда очень много. Цель моей работы найти универсальную формулу для вычисления объёма этих тел, и я нашла: это формула Симпсона. Возникла необходимость доказать, что формула действительно справедлива для разного рода геометрических фигур. Полученные результаты подтвердили мои ожидания: я очень легко убедилась в правильности этой формулы путём её применения к простым телам.

Содержание

Введение

Глава 1. Применение формулы Симпсона

1.1 Формула Симпсона

1.2 Нахождение объёма правильных геометрических тел.

1.3 Практическое применение формулы

Заключение

Список используемой литературы

Введение

Часто нам в жизни приходится сталкиваться с нахождением объёма геометрических тел. Думаю, всем знакома ситуация, когда с одной стороны все данные измерения нам известны, а формулу вспомнить довольно тяжело.  И в школе, казалось бы, так недавно проходили.… В связи с многообразием геометрических тел существует огромное количество формул для нахождения объёма (на каждое тело приходится своя формула). Оттого в голове может возникнуть каша.

Я задалась вопросом: а существует ли такая универсальная формула для нахождения объёма геометрических тел?

Для того чтобы найти ответ на этот вопрос я поставили перед собой  цели:

·             Найти в литературе эту формулу и доказать на практике, что она действительно универсальна;

·             Доказать, что найденной формулой можно пользоваться не только на практике, но и на экзаменах, в том числе и на ЕГЭ.

Для достижения целей необходимо выполнить следующие задачи:

·             Вспомнить изученные ранее основные характеристики геометрических тел: призмы, пирамиды, конуса, цилиндра, шара;

·             Доказать, что формулу можно применять в жизни;

·             Ознакомить учащихся старших классов с этой формулой и выяснить с помощью анкетирования, удобно ли применять её на экзаменах.

Я считаю тему данного проекта актуальной не только среди учащихся, но и среди взрослых, т.к. школьная программа со временем забывается, и мало кому известно о том, что существует такая формула, которая объединила в себе все другие многочисленные и тяжело запоминающие формулы для нахождения объёма.

Практическая значимость моей работы: Результаты данной работы могут иметь применение в школьной практике при работе со старшеклассниками, а именно использоваться на занятиях по геометрии и алгебре.

1.1 Формула Симпсона

Такая формула существует; более того: она пригодна не только для цилиндра, полного конуса и усеченного конуса, но также и для всякого рода призм, пирамид полных и усеченных и даже для шара. Вот эта замечательная формула, известная в математике под названием формулы Симпсона:

[6]

Следующий этап – исследование. Возникла необходимость доказать, что формула действительно справедлива для разного рода геометрических фигур.

1.2 Нахождение объёма правильных геометрических тел.

Пирамида.Пирамидой называется многогранник, который состоит из плоского многоугольника – основания пирамиды, точки не лежащей в плоскости основания – вершины пирамиды и всех отрезков соединяющих вершину пирамиды с точками основания.

Я измерила пирамиду и нашла её объём по обычной формуле [1]

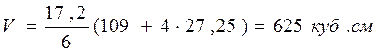
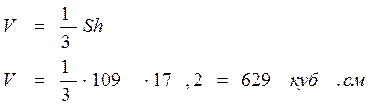
Объём по формуле Симпсона [6]

Цилиндр.

Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя равными кругами, которые находятся в параллельных плоскостях.

Я измерила цилиндр и нашла его объём по обычной формуле [1]

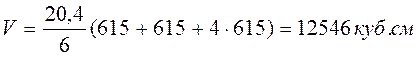
         Ообъем по формуле Симпсона [6]

Шар.

Шар – геометрическое тело ограниченное сферой.

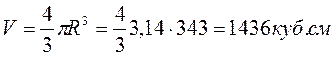Я измерила шар и нашла его объём по обычной формуле [1]

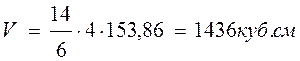Объём по формуле Симпсона [6]

Шестигранная призма.

Призмой называется многогранник, у которого две грани (основания) лежат в параллельных плоскостях, а все рёбра вне этих граней параллельны между собой.

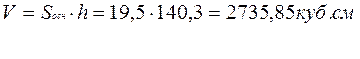Я измерила призму и нашла её объём по обычной формуле [1]

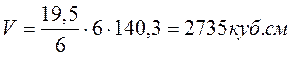
Объём по формуле Симпсона [6]

Куб

Куб – призма, основаниями которой являются квадраты.

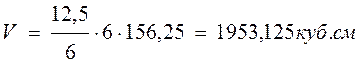
       Я измерила куб и нашла его объём по обычной формуле [1]

Объём по формуле Симпсона [6]

Конус

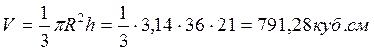Конус – геометрическое тело, ограниченное конической поверхностью и кругом.  Я измерила конус и нашла его объём по обычной формуле [1]

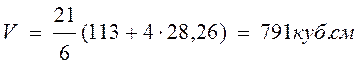
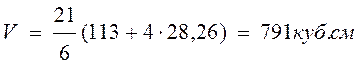
             Объём по формуле Симпсона [6]

Вывод:  Проведя исследование я доказала, что формула Симпсона универсальна для таких тел, как пирамида, призма, цилиндр, шар, куб и конус.

1.3 Практическое применение формулы

Следующим этапом моего исследования является практическое применение. Я располагаю формулой, по которой можно приближенно вычислить объем ствола дерева, не задаваясь вопросом о том, на какое геометрическое тело оно похоже: на цилиндр, на полный конус или на усеченный конус. Зная плотности различных пород древесины, можно вычислить вес дерева на корню. Я решила эту задачу с помощью вычисления объема ствола , как объем цилиндра, диаметр основания которого равен диаметру ствола посредине длины: при этом результат получается, однако, преуменьшенный, иногда на 12 %. Без большой ошибки можно принимать объем дерева на корню половину объема цилиндра той же высоты с диаметром, равным поперечнику дерева на высоте груди.[6]

Проделав расчеты, по известным нам ранее формулам, я вычислила объем ствола дерева на корню. [6]

1. 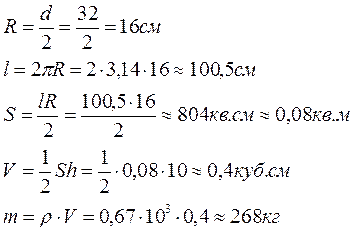         Расчёт для берёзы:

2. Расчёт для осины.

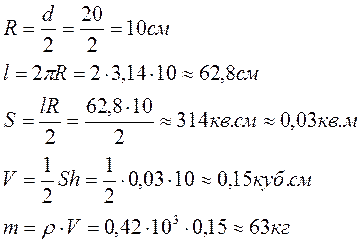
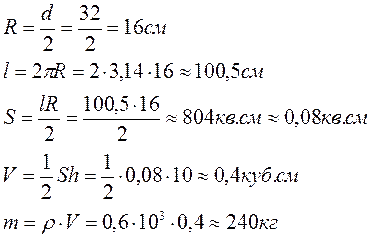3. Расчёт для сосны.

Вывод: Из всего исследования можно сделать вывод о том, что я располагаю формулой, по которой можно приближённо вычислить объём ствола дерева и, зная плотность различных пород древесины, можно определить вес дерева на корню.

Заключение

Теперь прогуливаясь по лесу, вам наверно будет, вероятно, интересно определить объём любого дерева. Вычислить  сколько в нём кубических метров древесины, а заодно и взвесить его – узнать, можно ли было бы, например, увезти такой ствол на одной телеге.

 Я располагаю формулой, по которой можно приближенно вычислить объем ствола дерева, не задаваясь вопросом о том, на какое геометрическое тело оно похоже: на цилиндр, на полный конус или на усеченный конус

Проведя исследование, я доказала, что формула Симпсона универсальна для таких тел, как пирамида, призма, цилиндр, шар, куб и конус.

Из всей проделанной работы можно сделать вывод о том, что я располагаю формулой, по которой можно приближённо вычислить объём ствола дерева и, зная плотность различных пород древесины, можно определить вес дерева на корню.

Из результатов анкетирования убедилась, что формула Симпсона достаточно проста для запоминания, и её стоит включить в школьную программу.

Эту формулу так же можно применять на экзаменах, включая ЕГЭ.

Список использованных источников.

1.          Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия, 10-11 : Учеб. для общеобразоват. учреждений – 13-ое изд. – М.: Просвещение, 2007.- 206 с. : ил.-ISBN/

2.          Л Интернет. Геометрические фигуры: параллепипед, призма, куб и т.д.geometricheskie.narod.ru

3.          Интернет. Фигура (геометрия) – Векипедия. Свободная энциклапедия www.ru.wikipedia.org›Геометрия

4.          Лаппо.Л.Д. , Попов М.А.. Математика. Подготовка к ЕГЭ-2010. Вступительные испытания – М.: Издательство «Экзамен», 2010.- 334. [2] c. E- mail: по общим вопросам: info@eхamen.biz;

5.          Математика. Школьная энциклопедия/ Гл. ред. М34 Никольский С.М.- М.: Научное издательство «Большая Российская энциклопедия», 1996,-527 с.: ил.

6.          Перельман Я.И; А.Л. Бондаренко. Геометрия на вольном воздухе.- М.: АСТ: Астрель; Владимир: ВКТ, 2008.- 94,[2] c.: ил. Электронный адрес: www.ast.ru E-mail: astpub@aha.ru

UDC 628413

Скачано с www.znanio.ru