УПРАВЛЕНИЕ ЗАПАСАМИ. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ

УПРАВЛЕНИЕ ЗАПАСАМИ. ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ

Задание 1

а = 8,

b = 1.

A = 2 + 0,5(a + b) = 6,5;

B = 2000 + 50(а – b) = 2350;

С = 0,15+0,01(a + b) = 0,24;

D = 5 + 0,5a – 0,2b = 8,8;

E = 2 + а = 10;

F = 14 + 0,5(b – a) = 10,5;

Р₁ = 1 + 0,5b = 1,5;

P₂ = 3 + 0,5(а + b) = 7,5;

Q₁ = 7 + 2a = 23;

Q₂ = l8 + a + b = 27;

Ситуация

Строительная фирма планирует возведение здания в течение А лет. За неделю используется примерно В отделочных кирпичей. Цена закупки одного кирпича составляет С$. Кирпичи доставляются поддонами по 264 штуки. За­траты на оформление заказа и доставку определяются в основном арендой до­ставщика и погрузчика и равны D тыс. руб. за один раз. Заказ доставляется че­рез Е рабочих дней после оформления. Хранение тысячи кирпичей обходится примерно в F тыс. руб. в месяц.

Возможно договориться с поставщиком о скидках при достаточно круп­ных партиях закупки. Размер скидки (в процентах от исходной цены) указан в следующей таблице

Таблица 1

Условия скидок

Задание

1.                 Записать условие задачи со своими конкретными данными.

2.                 Выписать основные параметры, необходимые для анализа системы управ­ления запасами, и привести их к одним единицам измерения.

3.                 Решить задачу и дать четкие ответы на все вопросы (см. ниже) для обеих ситуаций: без скидок и со скидками.

4.                 Записать четкое итоговое управленческое решение для обеих ситуаций: без скидок и со скидками.

5.                 Определить экономию на затратах относительно исходного предложения поставок по 6 поддонов за один раз. За счет чего достигается экономия?

6.                 Объяснить, почему необходимо пользоваться той или иной скидкой, или почему нужно отказаться от скидок.

Вопросы

Сколько поддонов отделочных кирпичей необходимо заказывать в одной партии?

Сколько заказов в месяц будет сделано?

Какой интервал времени (в днях) будет между заказами?

При каком количестве оставшихся поддонов кирпичей надо делать очеред­ной заказ?

Каковы минимальные суммарные затраты на закупку, доставку и хранение отделочного кирпича за период времени строительства здания?

Замечания

1.                 Считать, что:

-                     в неделе 7 дней;

-                     в месяце 30,5 дней:

-                     в году 365 дней. 12 месяцев. 52 недели.

2.                 Курс доллара принять равным 1$ = 60 руб.

Решение:

1.                 Ситуация

Строительная фирма планирует возведение здания в течение 6,5 лет. За неделю используется примерно 2350 отделочных кирпичей. Цена закупки одного кирпича составляет 0,24 $. Кирпичи доставляются поддонами по 264 штуки. За­траты на оформление заказа и доставку определяются в основном арендой до­ставщика и погрузчика и равны 8,8 тыс. руб. за один раз. Заказ доставляется че­рез 10 рабочих дней после оформления. Хранение тысячи кирпичей обходится примерно в 10,5 тыс. руб. в месяц.

Возможно договориться с поставщиком о скидках при достаточно круп­ных партиях закупки. Размер скидки (в процентах от исходной цены) указан в следующей таблице

2.                 Т = 6,5 лет = 2372,5 дней

0,24 $ = 14,4руб. С = 14,4·264 = 3801,6 руб. = цена 1 поддона

C₁ = 3744,58 руб. С₂ = 3516,48 руб.

К = 8,8 тыс. руб. = 8800 руб.

1000 кирпичей = 3,8 поддонов

s = 10,5 тыс. руб. / 30,5 дней / 3,8 под. = 90,6 руб. – хранение 1 поддона в день.

v = 2350 кир./нед. = 335,7 кир./день / 264 = 1,3 поддона/день

t_д = 10 дней.

1 поддон = 264 кирпича,

Q₁ = 23 поддона

Q₂ = 27 поддонов

3.                

Q_опт. =  = 16 поддонов

L_min =  + 3801,6·1,3·2372,5 =

= 1 696 337,5 + 1 719 588 + 11 725 084,8  = 15 141 010,3 руб. =

= 15 141 тыс. руб.

n_опт  =  = 192,77 поставок за 6,5 лет.

 =  = 0,08 поставок в день = 2,5 поставок в месяц = 5 поставок в 2 месяца

 =  = 12,3 дней ≈ 12 дней

q_зак = 10·1,3 = 13 поддонов

Вывод: при отсутствии скидок необходимо организовать поставки примерно по 16 поддонов каждые 12 дней (с частотой 2,5 поставки в месяц). Заказ необходимо делать в момент, когда в наличие осталось 13 поддонов. Суммарные расходы на поставку и хранение платьев составят  15 141 тыс. руб. за 6,5 лет.

Рассмотрим сначала задачу с первой скидкой. Q₁ = 23 поддона,  C₁ = 3744,58руб. Найдем L₁ по формуле

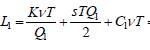
L₁ =  + 3744,58·1,3·2372,5 =

= 1 180 060,87 + 2 471 907,75 + 11 459 220,87 = 15 111 189,5 руб. =

= 15 111 тыс. руб.

Рассмотрим теперь задачу со второй скидкой. Q₂ = 27 поддонов,  C₁ = 3516,48 руб. Найдем L₂ по формуле

L₂ =  + 3516,48·1,3·2372,5 =

= 1 005 237 + 2 901 804,75 + 10 845 703,44 = 14 752 745 руб. =

= 14 753 тыс. руб.

Наименьшее из значений расходов равно

L_min = 14 753 тыс. руб.

Тогда

Q_опт. = Q₂ = 27 поддонов

Находим остальные параметры

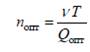
n_опт =  = 114 поставок за 6,5 лет.

 =  = 0,05 поставок в день = 1,5 поставок в месяц = 3 поставок в 2 месяца

 =  = 20,7 дней ≈ 21 день

q_зак = 10·1,3 = 13 поддонов

Управленческое решение: при имеющейся системе скидок выгодно пользоваться второй скидкой. Необходимо организовать поставки ровно по 27 поддонов кирпичей примерно каждые 20 дней (с частотой 1,5 поставки в месяц). Заказ необходимо делать в момент, когда в наличие осталось 13 поддонов кирпичей. Суммарные расходы на поставку и хранение платьев составят примерно 14 753  тыс. руб. за 6,5 лет.

Заметим, что все получившееся параметры оптимальной поставки являются примерными и могут быть скорректированы под реальную ситуацию – выходные дни, режим работы заказчика и транспортной компании и т.п. Однако число партий в заказе, равное 27, в этом случае достаточно четкая величина, обусловленная системой скидок.

Скачано с www.znanio.ru