Уравнение Бернулли для реальной и идеальной жидкости.

Уравнение Бернулли для реальной жидкости

Уравнение Бернулли для потока реальной жидкости несколько отличается от уравнения

Дело в том, что при движении реальной вязкой жидкости возникают силы трения, на преодоление которых жидкость затрачивает энергию. В результате полная удельная энергия жидкости в сечении 1-1 будет больше полной удельной энергии в сечении 2-2 на величину потерянной энергии (рис.1). 

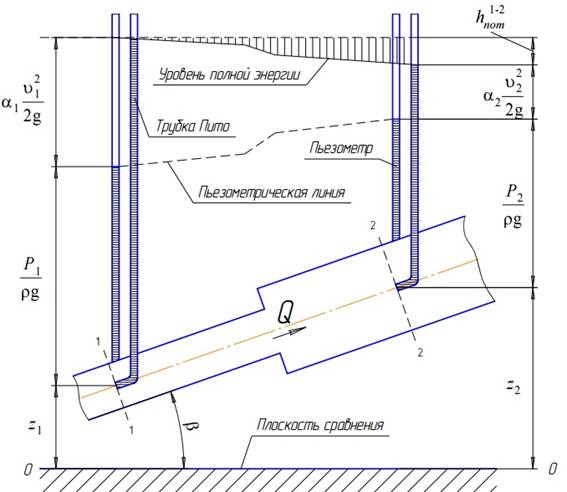
Рис.1. Схема к выводу уравнения Бернулли для реальной жидкости

Потерянная энергия или потерянный напор обозначаются   и имеют также линейную размерность.

Уравнение Бернулли для реальной жидкости будет иметь вид:

Из рис.1 видно, что по мере движения жидкости от сечения 1-1 до сечения 2-2 потерянный напор все время увеличивается (потерянный напор выделен вертикальной штриховкой). Таким образом, уровень первоначальной энергии, которой обладает жидкость в первом сечении, для второго сечения будет складываться из четырех составляющих: геометрической высоты, пьезометрической высоты, скоростной высоты и потерянного напора между сечениями 1-1 и 2-2.

Кроме этого в уравнении появились еще два коэффициента α₁ и α₂, которые называются коэффициентами Кориолиса и зависят от режима течения жидкости (α = 2 для ламинарного режима, α = 1 для турбулентного режима ).

Потерянная высота  складывается из линейных потерь, вызванных силой трения между слоями жидкости, и потерь, вызванных местными сопротивлениями (изменениями конфигурации потока)

С помощью уравнения Бернулли решается большинство задач практической гидравлики. Для этого выбирают два сечения по длине потока, таким образом, чтобы для одного из них были известны величины Р, ρ, g, а для другого сечения одна или величины подлежали определению. При двух неизвестных для второго сечения используют уравнение постоянства расхода жидкости υ₁ω₁ = υ₂ω₂.