Уравнения с параметром вида f (x)=g(a;x)

Конспект урока

Тема занятия: Уравнения с параметром вида .

Тип занятия: занятие изучения нового

Учебная задача занятия: В совместной деятельности с учащимися изучить определение функционально-графический метода решений задач с параметрами; способ решения уравнений с параметром вида .

Диагностируемые цели занятия:

В результате занятия ученик

знает:

- определение функционально-графического метода; теорему о принадлежности всех точек функции к ее графику на плоскости ;

- способы преобразования графиков элементарных функций (параллельный перенос, сжатие/растяжение, симметрия);

умеет:

- решать уравнения с параметром вида  графическим способом;

- преобразовывать графики функций, изображать их на плоскости ;

понимает:

- когда применять КП-метод, а когда функционально-графический.

Учебные действия, формируемые на занятии:

•        Личностные: умение учащегося устанавливать связи между целью учебной деятельности и её мотивом, т.е. между результатом учения, и тем, что побуждает деятельность, ради чего она осуществляется, таким образом, должна осуществляться осмысленная организация собственной деятельности ученика.

•        Регулятивные: целеполагание как постановка учебной задачи на основе соотнесения того, что уже известно и усвоено учащимся, и того, что ещё неизвестно; планирование - определение последовательности промежуточных целей с учётом конечного результата; оценка - выделение и осознание учащимся того, что уже усвоено и что ещё подлежит усвоению, осознание качества и уровня усвоения; волевая саморегуляция как способность к мобилизации сил и энергии,  способность к волевому усилию к выбору в ситуации мотивационного конфликта и  к преодолению препятствий.

•        Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками, т. е. определение цели сотрудничества, функций участников, способов взаимодействия, в том числе совершенствование навыков работы в группе, умение с достаточно полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации, владение монологической и диалогической формами речи в соответствии с грамматическими и синтаксическими нормами родного языка, умение доказывать собственное мнение.

•        Познавательные: анализ объектов с целью выделения признаков (существенных, несущественных); построение логической цепи рассуждений, доказательство; подведение под понятие; выведение следствий; установление причинно-следственных связей, структурирование знаний, выбор наиболее эффективных способов решения задач в зависимости от конкретных условий.

Методы обучения: репродуктивный, частично-поисковый

Форма работы: фронтальная.

Средства обучения: традиционные.

Структура занятия:

•        Мотивационно-ориентировочная часть (8 минут).

- Актуализация знаний.

- Мотивация.

- Постановка учебной задачи (цели) урока.

•        Операционно-познавательная часть (35 минуты).

•        Рефлексивно-оценочная часть (2 минуты).

Ход занятия:

Мотивационно – ориентировочная часть.

Актуализация знаний.

Задача №1. При каких значениях параметра  уравнение   имеет ровно три корня?

Решение:

Для начала упростим исходное выражение до вида, т.е. чтобы параметр а являлся функцией координаты .

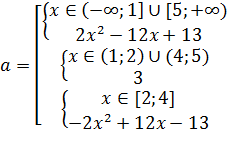
Т.к. , то можно рассматривать КП-плоскость  с вертикальной параметрической осью .

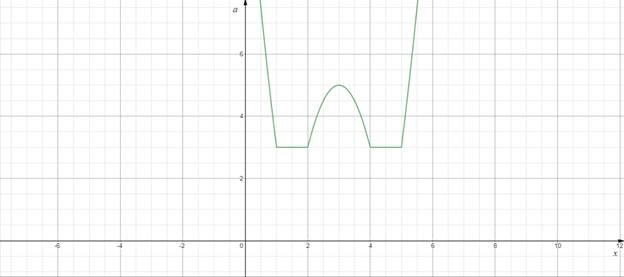
Рисунок 1

«Считывая» информацию с графика, видим

Ответ: .

Задача №2. При каких значениях па­раметра  уравнение  имеет три решения?

Решение:

Для начала упростим исходное выражение до вида, т.е. чтобы параметр а являлся функцией координаты : .

Несмотря на то, что 1 и 2 задачи похожи по условию

Мотивация.

полученная функция очень сложна для построения, но все же графическим способом это уравнение решить можно.

Постановка учебной задачи (цели) занятия.

Поэтому сегодня на занятии мы изучим функционально-графический способ решения уравнений с параметрами.

Операционно-познавательная часть.

Опр.: Функционально-графический метод – это метод, основанный на использовании графических иллюстраций или каких-либо их свойств.

Теорема: Если дана функция ,то все точки  координатной плоскости  принадлежат графику этой функции.

В этом методе решаются задачи, существенной частью которых является построение графика некоторой функции, в том числе при помощи элементарных преобразований графика известной функции.

Поэтому вспомним возможные преобразования графиков.

Сводная таблица преобразований графиков.

- Решим задачу №2 функционально-графическим способом.

Решение:

Введем функции - «уголок» с  вершиной в точке , ветви которого направлены вниз, и функцию  задает семейство парабол с вер­шиной  при  и прямую  при . Изменение параметра  влияет на направление ветвей параболы.

I. Если а = 0, то прямая  и график функции  имеют одну общую точку, а следовательно данное уравнение – один корень. Значение  не удовле­творяет условию задачи.

Рисунок 2

II. Если , то ветви параболы направ­лены вверх, и графики не имеют общих точек.

Рисунок 3

III.  Пусть , тогда ветви параболы бу­дут направлены вниз. Рассмотрим случай касания.

«Считывая» информацию с графика, видим

при   - два решения

при  - три решения

при   - четыре решения

Рисунок 4

Ответ: .

Задача №3. Найдите все значения параметра , при каждом из которых уравнение  имеет ровно три различных корня.

Решение:

Введем функции  и .

График функции  получается из графика функции  (это парабола, ветви которой направлены вверх, вершина имеет координаты ) с помощью зеркального отражения (симметрии) относительно оси абсцисс части параболы, расположенной ниже этой оси, а также последующим параллельным переносом вдоль оси  на  3 единицы вниз.

График функции  получается параллельным переносом графика функции  вдоль оси  на  единиц вправо и вдоль оси  на  единицы вверх. Таким образом, графиком функции является «уголок» с вершиной в точке . Т.е. . Следовательно, вершина «уголка» лежит на прямой .

Рисунок 5

Уравнение имеет ровно три различных корня, если графики функций имеют ровно три общие точки, что возможно в двух случаях.

В первом случае, сторона «уголка»   касается параболы  в точке, лежащей на отраженном участке параболы, отсюда , также .

 .

Во втором случае сторона «уголка», расположенная слева от его вершины, поэтому , проходит через точку . Поэтому .

Ответ: .

Задача №4. (ЕГЭ 2013). Найти при каком значении параметра  уравнение  имеет имеет единственный корень.

Решение:

Введем функции  и .

График функции :

; 

 - верхняя полуокружность с центром  и радиусом . При этом .

График функции  - пучок прямых, проходящих через точку с координатами .

Уравнение имеет ровно один корень, если графики функций имеют ровно одну общую точку, что возможно в следующих случаях.

График функции  проходит через точку с координатами , тогда .

Рисунок 6

График функции  проходит через точку с координатами , тогда .

Рисунок 7

График функции  проходит через точку с координатами , тогда .

Рисунок 8

при

Ответ:

Рефлексивно-оценочная часть.

-Какова была цель урока?

- (Изучить способ решения уравнений с параметром вида )

- Достигли мы её?

- (Да)

- Как мы её достигли?

-(Изучили функционально-графический метод решения уравнений с параметром вида, вспомнили способы преобразования графиков, практиковались применять теорию при решении задач)

Домашнее задание.

1. Найти при каких значениях параметра  уравнение имеет единственный корень.

Ответ: 

2. Найти при каких значениях параметра  уравнение  имеет единственное решение.

Ответ:

Скачано с www.znanio.ru