Урок 27
РЕШЕНИЕ ЗАДАЧ. ПОДГОТОВКА К КОНТРОЛЬНОЙ РАБОТЕ.
Цели: закрепить навыки в решении задач на применение признаков равенства треугольников; проверить знания учащихся; подготовить учащихся к предстоящей контрольной работе.
Ход урока
I. Анализ самостоятельной работы.
II. Устный опрос учащихся по карточкам.
Вариант I
1. Сформулируйте первый признак равенства треугольников.
2. На рисунке 1 АВ = DВ, 
1 = 2.
Докажите, что 
АВС = DВС.
3. В треугольниках АВС и А1В1С1
АВ = А1В1; АС = А1С1;
А
= А1. На сторонах АС и
А1С1 отмечены точки D и D1
так, что СD = С1D1. Докажите, что АВD
= А1В1D1.
Вариант II
1. Сформулируйте второй признак равенства треугольников.
2. На рисунке 2 1 = 2, 3 = 4.
Докажите, что АВD =
= СВD.
3. В треугольниках АВС и А1В1С1
проведены биссектрисы АD и А1D1.
Докажите, что АВС = А1В1С1,
если DС = D1С1, С = С1,
АDС
=
= А1D1С.
Вариант III
1. Сформулируйте третий признак равенства треугольников.
2. На рисунке 3 АВ = DС, ВС =
АD. Докажите, что АВС =СDА.
3. На рисунке 4 АВ = DС, ВK
= DМ, АМ = СK. Докажите, что АDМ =СВK.
Вариант IV
1. Сформулируйте свойство углов равнобедренного треугольника.
2. На рисунке 5 АВ = ВС, АD =
DС. Докажите, что ВАD =ВСD.
3. В равнобедренном треугольнике АВС на основании АС взяты точки D и Е так, что АD = СЕ. Докажите, что треугольник DВЕ равнобедренный.
Вариант V
1. Сформулируйте свойство биссектрисы, проведенной к основанию равнобедренного треугольника.
2. В равнобедренном треугольнике АВС с
основанием АС проведена биссектриса ВD, АВD =
37°, АС = 25 см. Найдите В, ВDС и DС.
3. В равнобедренном треугольнике СDЕ с основанием DЕ проведена биссектриса СF. Найдите СF, если периметр треугольника СDЕ равен 84 см, а треугольника СFE равен 56 см.
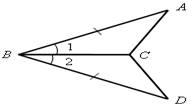
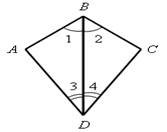
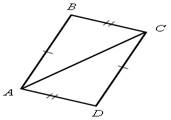
Рис. 1 Рис. 2 Рис. 3
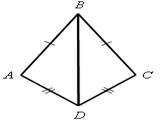
Рис. 4 Рис. 5
III. Решение задач.
1. Задача 1 (решение объясняет учитель на доске).
В равнобедренном треугольнике основание относится к боковой стороне как 3 : 4. Найдите стороны этого треугольника, если периметр его равен 33 см.
|
|
Дано: Р = 33 см. Найти: МK, МD, DK. Решение Пусть на одну часть приходится х см, тогда МK = 3х см, МD = DK = 4х см. |
По условию Р = 33 см, значит, 3х + 4х + 4х = 33; 11х = 33; х = 3.
МK = 9 см, МD = DK = 12 см.
Ответ: 9 см; 12 см; 12 см.
2. Задача 2 (самостоятельно).
В равнобедренном треугольнике боковая сторона относится к основанию как 2 : 3. Найдите стороны треугольника, если периметр его равен 28 см.
3. Решить задачу № 175*.
Запись решения задачи значительно упрощается, если ввести цифровые обозначения углов, как показано на рисунке 1.
Решение
|
Рис. 1 |
1) 2) Углы 3 и 5, а также 4 и 6 являются смежными,
поэтому из равенства 3) |
4) ОАЕ = ОВЕ по трем сторонам,
значит, 7 = 8, то есть ОЕ –
биссектриса угла ХОY.
|
Рис. 2 |
Для построения биссектрисы произвольного угла М на его сторонах откладываем отрезки МА = МВ, АС = ВD, как показано на рисунке 2, и проводим отрезки АD и ВС. Затем проводим искомый луч МЕ, где Е – точка пересечения отрезков АD и ВС. |
IV. Итоги урока.
Домашнее задание: подготовиться к контрольной работе, повторив материал пунктов 15–23; решить задачи №№ 170, 171.
Урок 27 РЕШЕНИЕ ЗАДАЧ. ПОДГОТОВКА
Рис. 1
ОАЕ = ОВЕ по трем сторонам, значит, 7 = 8, то есть
© ООО «Знанио»
С вами с 2009 года.
