Урок 44. ВНЕШНИЙ УГОЛ ТРЕУГОЛЬНИКА. ТЕОРЕМА О ВНЕШНЕМ УГЛЕ ТРЕУГОЛЬНИКА

Урок 44
ВНЕШНИЙ УГОЛ ТРЕУГОЛЬНИКА.
Теорема о внешнем угле треугольника

Цели: закрепить знания учащихся о сумме углов треугольника при решении задач; ввести понятие внешнего угла треугольника; доказать теорему о внешнем угле треугольника; учить решению задач.

Ход урока

I. Проверка усвоения изученного материала.

1. Один учащийся на доске доказывает теорему о сумме углов треугольника.

2. Второй учащийся решает на доске задачу № 230.

3. Устно со всем классом решаем задачи по готовым чертежам.

Вычислите все неизвестные углы треугольника (по рис. 1–8).

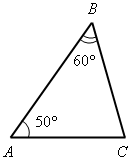
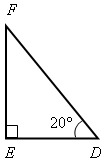
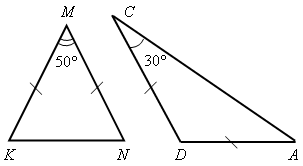
 Рис. 1                      Рис. 2                          Рис. 3                              Рис. 4

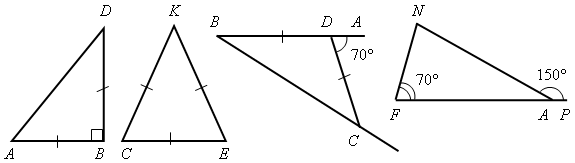
Рис. 5                   Рис. 6                          Рис. 7                                  Рис. 8

II. Изучение нового материала.

1. Ввести понятие внешнего угла треугольника.

2. Доказать теорему  о  внешнем  угле  треугольника  (рис. 125 учебника).

3. Устно решить задачу: в треугольнике АВС В = 110°. Чему равны: а) сумма остальных внутренних углов треугольника? б) внешний угол при вершине В?

4. По готовому чертежу на доске устно решить задачу:

III. Решение задач.

1. Решить задачу  № 232  под  руководством  учителя  на  доске  и в тетрадях.

ВF || АС,  так  как 1 = 2 = 3, а углы 1 и 3 соответственные при пересечении прямых ВF и  АС  секущей  АВ. ВD  АС,  так как ВD ВF, а ВF || АС. В треугольнике АВС биссектриса ВD является высотой, следовательно, треугольник АВС – равнобедренный (см. задачу № 133).

2. Обратное утверждение также верно, а именно: если треугольник равнобедренный, то внешний угол при вершине, противолежащей основанию треугольника, в два раза больше угла при основании.

Действительно,  этот  внешний  угол  равен  сумме  двух  углов  при основании равнобедренного треугольника, а так как углы при основании равны, то данный внешний угол в два раза больше угла при основании треугольника.

3. Решить задачу  № 234  на  доске  и  в  тетрадях  (рассмотреть два случая).

IV. Самостоятельная работа обучающего характера (15–20 мин).

Вариант I

1. Один из углов равнобедренного треугольника равен 96°. Найдите два других угла треугольника.

2. В треугольнике СDЕ с углом Е = 32° проведена биссектриса CF, СFD = 72°. Найдите D.

Вариант II

1. Один из углов равнобедренного треугольника равен 108°. Найдите два других угла треугольника.

2. В  треугольнике  СDЕ  проведена биссектриса CF, D = 68°, Е =
= 32°. Найдите СFD.

Вариант III

1. В  равнобедренном  треугольнике  MNP  c  основанием  МР  и углом N = 64° проведена высота МН.  Найдите РМН.

2. В треугольнике СDЕ проведены биссектрисы CK и DР, пересекающиеся в точке F, причем DFK = 78°. Найдите СЕD.

Вариант IV

1. В равнобедренном треугольнике CDЕ c основанием СЕ и D = 102° проведена высота СН.  Найдите DСН.

2. В треугольнике АВС проведены биссектрисы АМ и ВN, пересекающиеся в точке K, причем АKN = 58°. Найдите АСВ.

V. Итоги урока.

Домашнее задание: изучить пункты 30–31; ответить на вопросы 1–5 на с. 89; решить задачи №№ 233, 235.