Урок алгебры 11 класс "Определенный интеграл"

Подготовил учитель математики

Бакаева Наталья Александровна

Разработка урока по теме «Определённый интеграл»

Цель урока: ввести понятие определённого интеграла и получить формулу для его вычисления.

Задачи урока: Образовательные – повторить формулы площадей многоугольников и круга; вывести формулу площади криволинейной трапеции, тем самым подойдя к понятию определённого интеграла.  Развивающие – развивать память, воображение и логическое мышление учащихся;  Воспитательные – воспитывать у учащихся трудолюбие и усидчивость, умение доводить начатое дело до конца.

Тип урока: урок – изучение нового материала.

Оборудование: учебник, интерактивная доска, проектор.

Ход урока

Организационный момент

Приветствие учащихся, фронтальная проверка домашнего задания, сообщение темы и плана урока.

Повторение ранее изученного материала

Учитель отмечает, что к новому понятию мы придём через решение геометрической задачи, а именно через вычисление площади. Таким образом, мы строим очередной «мостик» между математическим анализом и геометрией (подчёркивание межпредметных связей). До сих пор мы умели вычислять площади только многоугольников и круга. С использованием презентации (слайды №2 - №7), организуется повторение соответствующих формул в форме фронтального опроса.

Этап создания мотивации

Как поступить, если требуется отыскать площадь фигуры, изображённой на слайде? (слайд №9) Заметим, что данную фигуру нельзя представить в виде объединения некоторого конечного числа многоугольников и кругов или их частей. Учащимся предлагается выдвинуть гипотезу. В случае успешного выдвижения учащимися гипотезы (о приближённой замене криволинейной трапеции ступенчатой фигурой) учитель эту гипотезу одобряет и разъясняет её смысл, используя презентацию (слайды №10 - №12).

Новый материал

Учащиеся должны уяснить основную идею – чем больше прямоугольников и чем меньше длина их оснований, тем точнее площадь ступенчатой фигуры приближает площадь криволинейной трапеции. Записываются формулы площади отдельно взятого прямоугольника и всей ступенчатой фигуры (слайды №13, №14).

Каким бы ни было количество прямоугольников, в любом случае площадь будет приближённой. Для получения точного значения площади необходимо выполнить предельный переход – устремить к бесконечности количество прямоугольников (соответственно, устремить к нулю дины их оснований).

Если теперь отвлечься от геометрического смысла этой задачи и проделать описанные действия с произвольной непрерывной функцией, то можно придти к нашему новому понятию. Ту сумму, которая была нами составлена, называют интегральной суммой Римана для функции  на отрезке , а предел интегральных сумм называют определённым интегралом от функции   на отрезке . На слайде №15 демонстрируется обозначение определённого интеграла. Следует обратить внимание учащихся на обозначение – символ интеграла представляет собой вытянутую букву S, что символизирует площадь.

Учитель отмечает, что вычисление интегралов путём составления интегральных сумм и последующего перехода к пределу – задача исключительно трудная. Есть гораздо более простой способ вычисления – вычисление по формуле Ньютона-Лейбница (имена выдающихся учёных, создателей математического анализа, интегрального исчисления в частности). На слайде №16 появляется эта формула.

Для доказательства этой формулы вспомним, что переменная площадь  подграфика функции  является одной из первообразных этой функции. Проверим справедливость формулы для этой первообразной.

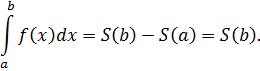
Равенство справедливо. Пусть теперь  произвольная первообразная функции . Как известно, любые две первообразные отличаются друг от друга на константу K. Следовательно, приращения будут одинаковыми:

Следовательно, формула доказана. Демонстрация и комментирование слайдов №17 и №18.

Исторические сведения

         Отметим, что метод  нахождения площади криволинейной трапеции уходит своими корнями в глубокую древность. Речь идёт о методе исчерпывания. Появляется слайд №19. В течение 5-7 минут заранее подготовленный учащийся зачитывает краткое сообщение о методе исчерпывания, о создателе этого метода – Евдоксе Книдском и о его выдающемся преемнике – Архимеде.

Применение полученных знаний на практике

         На слайде №20 приведены три интеграла, которые мы вычислим по формуле Ньютона-Лейбница. Первые два примера демонстрируются учителем, третий пример предлагается проделать у доски  одному из учащихся.

Подведение итогов урока, запись домашнего задания.