Урок алгебры в 8 классе. Решение текстовых задач с помощью квадратных уравнений.

Урок алгебры для 8-го класса по теме "Решение задач с помощью квадратных уравнений
Тема урока: Решение задач с помощью квадратных уравнений.
Цели урока:
- Закрепить навыки решения текстовых задач с помощью квадратных уравнений;
- Развивать у учащихся внимание при чтении условия задачи и выборе способа решения уравнения;
- Воспитание ответственности и коллективизма у учащихся.
Оборудование: мультимедийный проектор, экран, графопроектор, шесть конвертов с шестью карточками, на каждой из которых написана задача.
Структура урока:
- Организационный момент: замена тетрадей, учащиеся рассаживаются по группам: 6 групп по 5-6 человек в каждой, группы составлены разноуровневые– 3 мин.
- Мотивация учебной деятельности через осознание учащимися практической значимости применяемых знаний и умений, сообщение темы, цели и задач урока -2 мин
- Актуализация изученного материала:
- Вопросы:
o
- Какое уравнение называется квадратным?
- Что показывает дискриминант?
- Формулы корней квадратного уравнения?
- Задания для устного решения Презентация 1 – 7 мин:
o
- Решить уравнения;
- Найти натуральный корень уравнения.
- Решение задач (работа в группах):
Каждой группе
предлагается конверт с 6 задачами. Набор задач у каждой группы одинаков. Каждый
ученик выбирает себе задачу и решает ее. В первую очередь выбирать задачи №
1-5. Возможно советоваться с ребятами из своей группы. Учитель контролирует
процесс и, в случае необходимости, оказывает помощь – 7 мин.
От каждой группы выходят по 1 человеку (те, кто раньше решил свою задачу) и
оформляют свои решения на доске (3 чел.), на пленках для графопроектора (2
чел). Учитель контролирует, чтобы задачи были различны (задачи 1-5).
Весь класс сверяет свои решения с теми, которые представлены на доске. Те
задачи, которых у учеников нет в тетрадях, они записывают. Для удобства текст
проверяемой на доске задачи представлен в виде слайдов Презентации 2.
В ходе проверки задач, записанных на доске, остальные ребята, решавшие эти же
задачи, вносят свои коррективы, если необходимо. Задачу 6 проверяет учитель в
тетрадях, если есть время, то – разбор на доске. (15 мин.)
- Подведение итогов урока, обобщение и систематизация результатов выполненных заданий. (4 мин.)
- Постановка домашнего задания: № 656, 651, составить свою задачу, аналогичную одной из решенных в классе, и решить ее. (2 мин)
Задачи (в порядке разбора их у доски):
1. Несколько подруг решили обменяться фотографиями на память. Чтобы каждая девочка получила по одной фотографии каждой своей подруги, потребовалось 30 фотографий. Сколько было подруг?
Решение:
Пусть было х подруг, тогда каждая должна получить по (х – 1) фотографии. Всего фотографий было х(х – 1), что по условию задачи равно 30. Составим и решим уравнение:
х(х – 1) = 30
х2 – х – 30 = 0,
D = 1 + 120 = 121,
х = ![]() ,
,
х1 = – 5 – не удовлетворяет смыслу задачи,
х2 = 6.
По смыслу ясно, что х – натуральное число, и существует только два последовательных натуральных числа, произведение которых равно 30. Итак, х = 6. 6 подруг обменивались фотографиями.
Ответ: 6 подруг.
2. Несколько приятелей решили сыграть турнир по шахматам. Кто-то из них подсчитал, что если каждый сыграет с каждым по одной партии, то всего будет сыграно 36 партий. Сколько было приятелей?
Решение:
Пусть х приятелей участвует в турнире, тогда каждый из них сыграет (х –
1) партию, но в этом случае партия каждой пары учтена дважды, значит всего было
сыграно ![]() х(х – 1) партий, что по
условию задачи равно 36. Составим и решим уравнение:
х(х – 1) партий, что по
условию задачи равно 36. Составим и решим уравнение:
![]() х(х – 1) = 36,
х(х – 1) = 36,
х(х – 1) = 72,
х2 – х – 72 = 0,
D = 1 + 288 = 289,
х = ![]() ,
,
х1 = 9,
х2 = – 8 – не удовлетворяет смыслу задачи.
Рассуждения, аналогичные задаче 1.
9 приятелей участвовало в турнире.
Ответ: 9 приятелей.
3. Задача Диофанта (III в.)
Найти два числа. Зная, что их сумма равна 20, а произведение – 96.
Решение:
Пусть х – одно из чисел, тогда второе число – (20 – х). Значит х(20 – х) – произведение этих чисел, что по условию задачи равно 96. Составим и решим уравнение:
х(20 – х) = 96,
20х – х2 – 96 = 0,
х2 – 20х + 96 = 0,
![]() = 100 – 96 = 4,
= 100 – 96 = 4,
х = 10 + 2,
х1 = 12,
х2 = 8.
12 – первое число, тогда 20 – 12 = 8 – второе число;
8 – первое число, тогда 20 – 8 = 12 второе число.
Ответ: 12 и 8.
4. Решение Диофанта (показывает учитель):
Пусть числа 10 + х и 10 – х (сумма их равна 20), тогда (10 + х)(10 – х) – их произведение, что равно 96. Имеем:
(10 + х)(10
– х) = 96,
100 – х2 = 96,
х2 = 4.
х = + 2.
В обоих случаях искомые числа 12 и 8.
Ответ: 12 и 8.
5. Задача Бхаскары, Индия, XII в.
Цветок лотоса возвышается над тихим озером на полфута. Когда порыв ветра отклонил цветок от прежнего места на 2 фута, цветок скрылся под водой. Определите глубину озера.
Решение.
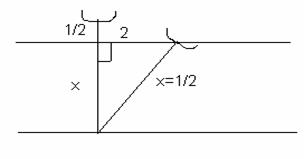
Пусть глубина озера х
ф., тогда длина стебля (х + ![]() ) ф. Учитывая, что цветок
рос вертикально, составим и решим уравнение:
) ф. Учитывая, что цветок
рос вертикально, составим и решим уравнение:
х2 + 22 = (х + ![]() )2
)2
х2 + 4 = х2 + х + ![]()
х = 3![]()
3![]() фута – глубина озера.
фута – глубина озера.
Ответ: 3 ![]() ф.
ф.
6. В море встретились два корабля. Один из них шел в восточном направлении, другой – в северном. Скорость первого на 10 узлов больше, чем второго. Через 2 часа расстояние между ними оказалось равным 100 милям. Найдите скорость каждого корабля.
Решение:
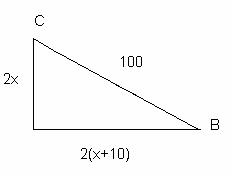
Пусть х узлов – скорость второго корабля, тогда (х – 10) узлов – скорость первого корабля, за 2 часа они пройдут 2х и 2(х – 10) миль соответственно, т.к. они идут в перпендикулярных направлениях, то, используя теорему Пифагора, составим и решим уравнение:
(2х)2 +
(2(х + 10))2 = 1002
4х2 + 4(х2 + 20х +
100) = 10000
2х2 + 20х + 100 = 2500
х2 + 10х + 50 – 1250 = 0
х2 + 10х – 1200 = 0
![]() = 25 + 1200 = 1225
= 25 + 1200 = 1225
х = – 5 + 35
х1 = – 40 – не удовлетворяет смыслу задачи,
х2 = 30
30 узлов – скорость корабля, идущего на север, тогда 30 + 10 = 40 (узлов) –
скорость корабля, идущего на восток.
Ответ: 30 узлов и 40 узлов.
7. Два равных прямоугольника сложили так, что они образуют букву Т и их общей частью является меньшая сторона одного из прямоугольников. Периметр образовавшейся фигуры равен 42 м, а площадь каждого прямоугольника равна 27 м2. Найти стороны прямоугольников.
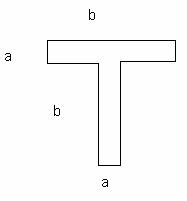
Решение.
P = 3b + 3a +
(b – a) = 4b + 2a, a = ![]() –
2b, S = ab
–
2b, S = ab
Пусть b см длина прямоугольника, тогда ширина прямоугольника (![]() –
2b) м, т.к. P = 42 м, то длина – (21 – 2b)м.
Площадь прямоугольника b(21 – 2b), что по условию равно 27 м2.
Составим и решим уравнение.
–
2b) м, т.к. P = 42 м, то длина – (21 – 2b)м.
Площадь прямоугольника b(21 – 2b), что по условию равно 27 м2.
Составим и решим уравнение.
b(21 – 2b) = 27
21b – 2b2 – 27 = 0
2b2 – 21b + 27 = 0
D = 441 – 4 * 2 * 27 = 441 – 216 = 225
b = ![]()
b1 = 9
b2 = 1![]()
Если 9 м – длина, тогда 21 – 2 * 9 = 3(м) – ширина.
Если 1![]() м – длина, тогда 21 – 2 * 1
м – длина, тогда 21 – 2 * 1![]() =
18(м) – ширина, что не удовлетворяет смыслу задачи.
=
18(м) – ширина, что не удовлетворяет смыслу задачи.
Ответ: 9 м и 3 м.
Скачано с www.znanio.ru
© ООО «Знанио»
С вами с 2009 года.
![]()

