Урок алгебры в 9 классе: "Методы решения целых уравнений"

9 КЛАСС

тема: методы Решения целых уравнений 

Цель: продолжить формирование умения применять различные методы при решении целых уравнений выше второй степени. Обобщить     значения     и     умения     по     изученной теме. Систематизировать основные понятия, которые имеют место в данной         теме         (определения,         свойства,         правила). Систематизировать свойства, как свойства, действия умножения и действия сложения.

Воспитательная   цель:   повысить   интерес к математике, способствовать развитию трудолюбия, взаимопомощи и патриотизма.

Оборудование: персональный компьютер, интерактивная доска.

Ход урока

I. Организационный момент.

II. Устная работа.

Определите, каким методом может быть решено каждое из данных целых уравнений:

а) 7х⁵ + 3х⁴ = 0;                   г) ;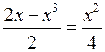

б) х⁴ + 3х² – 4 = 0;               д) (х² – 5)² + 2(х² – 5)² + 1 = 0;

в) х³ + х² + х + 1 = 0;           е) (х² – 2х) (х² + 4 – 2х) = 3.

III. Формирование умений и навыков.

На этом уроке учащиеся продолжают применять разные методы решения целых уравнений. При этом внимание уделяется не только грамотному их использованию, но и умению распознавать по внешнему виду уравнения тот метод, который целесообразно применить в данной ситуации.

Упражнения:

1. № 273 (в. д), № 279 (д), № 282 (а), № 277 (а, в), № 282 (а).

2. № 283 (а).

Р е ш е н и е

х⁵ + х⁴ – 6х³ – 6х² + 5х + 5 = 0.

Разложим выражение, стоящее слева, на множители методом группировки. Получим:

х⁴ (х + 1) – 6х² (х + 1) + 5 (х + 1) = 0;

(х + 1) (х⁴ – 6х² + 5) = 0;

О т в е т: ±1, ±.

Некоторым  сильным в учебе  учащимся  можно  дополнительно  дать  карточки-задания.

К а р т о ч к а  № 1

1. Решите уравнение:  (х + 1) (х + 2) (х + 3) (х + 4) = 360.

2. При каких значениях параметра а не имеет корней уравнение

х⁴ – 6х² + а = 0?

К а р т о ч к а  № 2

1. Решите уравнение:  (х – 1) (х – 3) (х – 5) (х – 7) = 105.

2. При каких значениях параметра а не имеет корней уравнение

х⁴ + ах² + 9 = 0?

Р е ш е н и е  задач карточки № 1.

1. Найдем произведение крайних и средних множителей, заменив их трехчленами. Получим:

(х² + 5х + 4) (х² + 5х + 6) = 360.

С д е л а е м   з а м е н у: х² + 5х + 4 = t. Получим:

t (t + 2) = 360;

t² + 2t – 360 = 0;

t₁ = –20,  t₂ = 18.

В е р н е м с я   к   з а м е н е:

О т в е т: –7; 2.

2. Биквадратное уравнение не имеет корней в двух случаях: если дискриминант полученного после замены квадратного уравнения отрицателен или если это квадратное уравнение имеет только отрицательные корни.

С д е л а е м   з а м е н у: х² = t. Получим уравнение:

t² – 6t – а = 0;

D₁ = 9 – а;

D₁ < 0, если 9 – а < 0, то есть а > 9.

Значит, при а > 9 данное биквадратное уравнение корней не имеет. При а ≤ 9 уравнение имеет корни х₁ и х₂. Предположим, что они отрицательные. Однако, по теореме Виета, имеем: х₁ + х₂ = = 6. Таким образом, полученное квадратное уравнение не может иметь одновременно двух отрицательных корней. Значит, исходное биквадратное уравнение не имеет корней только при а > 9.

О т в е т: (9; +∞).

Р е ш е н и е  задач карточки 2.

1. Так же, как и при решении уравнения из карточки 1, выполним преобразование и получим уравнение:

(х² – 8х + 7) (х² – 8х + 15) = 105.

С д е л а е м   з а м е н у:  х² – 8х + 7 = t. Получим:

t (t + 8) = 105;

t² + 8t – 105 = 0;

t₁ = –15,  t₂ = 7.

В е р н е м с я   к   з а м е н е:

О т в е т: 0; 8.

2. С д е л а е м   з а м е н у: х² = t. Получим уравнение:

t² + аt + 9 = 0;

D₁ = а² – 36;

D₁ < 0, если а² – 36 < 0, то есть а  (–6; 6).

Значит, при таких значениях а данное биквадратное уравнение корней не имеет.

Если а  (–∞; –6) (6; +∞), то квадратное уравнение t² + аt + 9 = 0 имеет два корня: х₁ и х₂. По теореме Виета, х₁ · х₂ = 9, значит, эти корни одинаковых знаков.

Чтобы данное биквадратное уравнение не имело корней, числа х₁ и х₂ должны  быть  отрицательными,  то  есть  х₁ + х₂ < 0,  а  по  теореме Виета х₁ + х₂ = –а. Имеем:

х₁ + х₂ < 0, если –а < 0, то есть а > 0.

О т в е т: (–6; 6) (6; +∞).

IV. Итоги урока.

В о п р о с ы   у ч а щ и м с я:

– Какие существуют методы решения целых уравнений?

– В чем состоит суть метода введения новой переменной при решении целого уравнения?

– В чем состоит метод разложения на множители решения целого уравнения?

Домашнее задание: № 273, № 277 (б), № 279 (е), № 282 (б), № 283 (б).