
9 КЛАСС
тЕМА: Решение систем уравнений
Цели: систематизировать знания учащихся по теме; актуализировать умения и навыки решения систем уравнений с двумя неизвестными первой и второй степени. Обобщить значения и умения по изученной теме. Систематизировать основные понятия, которые имеют место в данной теме (определения, свойства, правила).
Воспитательная цель: повысить интерес к математике, способствовать развитию трудолюбия, взаимопомощи и патриотизма.
Оборудование: персональный компьютер, интерактивная доска.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Выразите одну переменную через другую из уравнения:
а) 5х + 2у = –6; б) ху – 3 = 0.
2. Определите, из какого уравнения системы какую переменную удобнее выразить:
а) 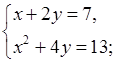 б)
б)
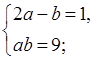 в)
в)
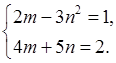
3. Решите систему уравнений:
а) 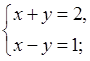 б)
б)
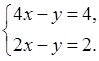
III. Формирование умений и навыков.
Перед решением упражнений следует повторить основные способы решения систем уравнений с двумя неизвестными:
1) способ подстановки;
2) способ сложения;
3) графический.
Упражнения:
№ 957 (а).
Р е ш е н и е
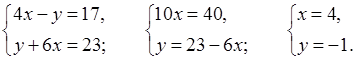
О т в е т: (4; –1).
№ 958 (б).
Р е ш е н и е
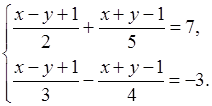
Обозначим х – у + 1 = а, х + у – 1 = b.
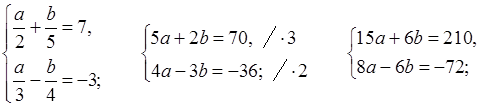
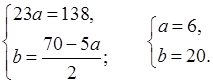
И м е е м: 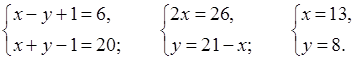
О т в е т: (13; 8).
№ 961.
Р е ш е н и е
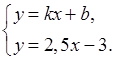
а) Чтобы система не имела решений, приравняем значения у:
kx + b = 2,5x – 3;
(k – 2,5) х = –3 – b.
Если k – 2,5 = 0, а –3 – b ≠ 0, то нет решений.
Пусть k = 2,5, b = 1.
б) Чтобы система имела бесконечно много решений, необходимо, чтобы k = 2,5, b = –3.
в) Если х = 4 – входит в решение, то у = 2,5 · 4 – 3;
у = 7, тогда 7 = k · 4 + b, например, k = 1, b = 3.
О т в е т: а) k = 2,5, b = 1; б) k = 2,5, b = –3; в) k = 1, b = 3.
№ 963 (а).
Р е ш е н и е
Прямая задается уравнением у = kx + b. Так как точки (0; 30) и (6; 0) принадлежат этой прямой, то
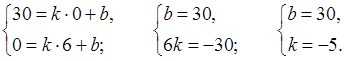
Уравнение прямой: у = –5х + 30.
О т в е т: у = –5х + 30.
№ 972 (а).
Р е ш е н и е
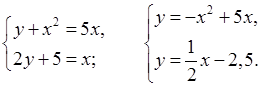
Построим
графики функций у = –х2 + 5х и у = ![]() х
– 2,5 и найдем координаты их точек пересечения.
х
– 2,5 и найдем координаты их точек пересечения.
1) у = –х2 + 5х. Графиком является парабола, проходящая через точки (0; 0), (5; 0), вершина параболы (2,5; 6,25), ветви направлены вниз.
2) у
= ![]() х
– 2,5. Графиком является прямая, проходящая через точки (0; –2,5),(5; 0).
х
– 2,5. Графиком является прямая, проходящая через точки (0; –2,5),(5; 0).
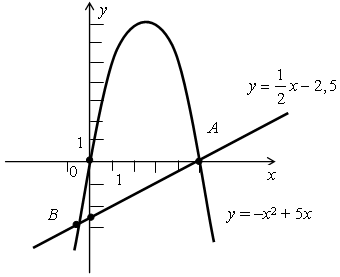
А (5; 0), В (–0,5; –2,75).
О т в е т: (5; 0), (–0,5; –2,75).
№ 973 (б).
Р е ш е н и е
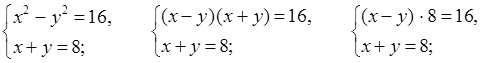
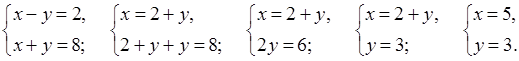
О т в е т: (5; 3).
№ 974 (а).
Р е ш е н и е
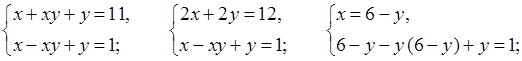
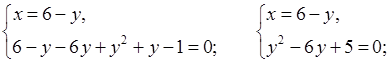
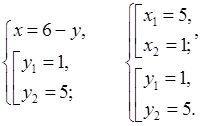
О т в е т: (5; 1), (1; 5).
№ 975 (а, б).
Р е ш е н и е
а) 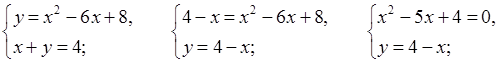
|
А (1; 3); В (4; 0) |
|
б) 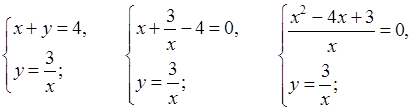
|
А (1; 3); В (3; 1) |
|
О т в е т: а) (4; 0); (1; 3); б) (1; 3); (3; 1).
IV. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Как найти координаты точек пересечения графиков уравнений?
– В чем состоит способ сложения при решении систем уравнений?
– Каков алгоритм решения систем уравнений способом подстановки?
– Любую ли систему линейных уравнений можно решить способом сложения? Способом подстановки?
– Можно ли решить способом сложения систему, содержащую нелинейные уравнения? Когда это возможно?
Домашнее задание: № 958 (а), № 962 (а), № 972 (б), № 973 (д),
№ 976*.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.