Урок геометрии в 9 классе на тему: "Признаки подобия прямоугольных треугольников"

Геометрия, 9 класс                                   

Тема: Признак подобия прямоугольных треугольников

Цели: сформулировать признак подобия прямоугольных треугольников, свойство катетов, высоты и биссектрисы прямоугольного треугольника.

Оборудование: дидактический материал, рисунки, чертежные приборы.

Ход урока

1. Организационный момент

2. Анализ практической работы

Рассматриваются задача на определение высоты предмета.

Вопросы: - Какие треугольники рассматриваются в этом случае?

-Какой признак подобия треугольников используется  в этом случае? Нужно ли измерять углы? Сколько углов надо измерить?

- Сформулируйте признак подобия прямоугольных треугольников и обоснуйте его.

3. Изучение нового материала

Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то такие треугольники подобны.

Соотношения в прямоугольном треугольнике:

Ø Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.

Ð В - общий, Ð САВ = Ð ВСD, то D АВС = D  ВСD, тогда АВ/ВС = ВС/ DВ,

ВС^2=АВ*DВ .         ВС=Ö АВ*DВ

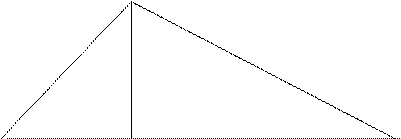Ø Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между проекциями катетов на гипотенузу.

D АВС~ D  DВС, D АВС~ D  АСD, тогда D  DВС~ D  АСD, DВ/СD = CD/АD

CD^2 = DB*AD.        CD=Ö DВ*AD

Эти свойства учащиеся доказывают самостоятельно с последующей проверкой.

Формулируется свойство биссектрисы угла треугольника:

Ø  Биссектриса треугольника делит противоположные стороны на отрезки, пропорциональные двум другим отрезкам.

AF^CD, BE ^CD, D АСF~ D  ВEС, т. К.

Ð F = Ð E = 90°. Ð ACF = Ð BCE ( CD- биссектриса), AF/BE = AD/DB, а по условию АС/ВС = AD/DB. Следовательно,      АС/ ВС=AD/DВ

4. Закрепление изученного материала

Решение задач № 39, 40, 41, 42, 43 самостоятельно. Задача № 42 ( ключевая, решается коллективно).

Докажите, что высоты подобных треугольников относятся как соответственные стороны.

5. Подведение итогов урока

- где понадобятся знания об изученных свойствах прямоугольного треугольника?

6. Домашнее задание

Повторить п. 100-106, вопросы 1-12, задачи №  44, 45 ( по желанию - № 46, 47)