Урок геометрии в 9 классе: "Решение треугольников"

Тема урока: Решение треугольников

 Цели урока:

• повторить и обобщить тему “Треугольник”;

• проверить усвоение теоремы косинусов и теоремы синусов, теоремы о сумме углов треугольника, отрабатывать умение применять теорему косинусов, теорему синусов решая задачи, тесты;

   • развивать навыки исследовательской работы учащихся;

• развивать, выработать активность, внимание, логическое мышление, монологическую речь, интерес к предмету, коллективное обучение.

Тип урока: урок систематизации и обобщения знаний и умений

ХОД УРОКА

I. Вступительная часть – 3 мин.

Треугольник… Знакомый вам с детства, и начиная с 7 класса, с уроков геометрии, геометрическая фигура, таит в себе немало интересного и загадочного, как Бермудский треугольник, в котором бесследно исчезают корабли и самолеты. Знакомые нам фигуры квадрат, параллелограмм, прямоугольник, ромб, трапеция состоят из двух треугольников, если провести одну диагональ и из четырех треугольников, если провести две диагонали. В 10-11 классах тоже применяются решения треугольников, поэтому вы должны научиться решать любой треугольник. Прежде чем решать задачи, повторим тему “Треугольник”, отправимся в путешествие в страну “Треугольник”, повторим определение, элементы, виды, свойства треугольников и каждый раз будем удивляться полученным открытиям, удивительной формой, красотой, свойствами треугольников. В путешествие отправимся рядами, будем соревноваться, кто больше знает об этой стране “Треугольник”.

Условия состязания:

• быть внимательными и сообразительными;

• не оставлять ни одного вопроса без ответа;

• на каждое задание минимум времени, но максимум усердия;

• не подглядывать, не подслушивать, не мешать соседям.

II. Первая остановка в путешествии  «Сосчитай-ка»

Часто знает и дошкольник,
Что такое треугольник,
А уж вам-то, как не знать…
Но совсем другое дело —
Очень быстро и умело
Треугольники считать!
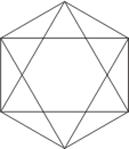
Например, в фигуре этой
Сколько разных? Рассмотри!
Все внимательно исследуй
И “по краю” и “внутри”.                                                        

Ответ: 32

III. Вторая  остановка в путешествии “Решение кроссворда” “Треугольник”. Остановка – 5 минут.

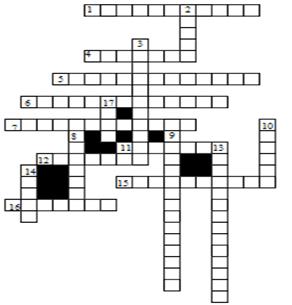
 По горизонтали: 1. Луч, делящий угол пополам. 4. Элемент треугольника. 5.6.7. Виды треугольника (по углам). 11. Математик древности. 12. Часть прямой. 15. Сторона прямоугольного треугольника. 16. Отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

По вертикали: 2. Вершина треугольника. 3. Фигура в геометрии. 8. Элемент треугольника. 9. Вид треугольника (по сторонам). 10. Отрезок в треугольнике. 13. Треугольник, у которого две стороны равны. 14. Сторона прямоугольного треугольника. 17. Элемент треугольника.

Ответы:

По горизонтали: 1. Биссектриса. 4. Сторона. 5. Прямоугольный. 6. Остроугольный. 7. Тупоугольный. 11. Пифагор. 12. Отрезок. 15. Гипотенуза. 16. Медиана.

По вертикали: 2. Точка. 3. Треугольник. 8. Вершина. 9. Равносторонний. 10. Высота. 13. Равнобедренный. 14. Катет. 17. Угол.

IV. Мы повторили немного о треугольнике, еще лучше узнаем о нем на следующей остановке. Остановка называется “Ответы на вопросы”– 7 минут

Знаменитый древнегреческий ученый Аристотель вопрос трактовал, как мыслительную форму, обеспечивающую переход от незнания к знанию.

Вопросы (команды задают друг другу):     

1. Какую фигуру называют треугольником?

2. Перечислите элементы треугольника.

3. Назовите виды треугольников по углам.

4. Назовите виды треугольников по сторонам.

5. Какой треугольник называется равносторонним?

6. Как называется третья сторона в равнобедренном треугольнике?

7. Перечислите свойства равнобедренного треугольника.

8. Перечислите свойства равностороннего треугольника.

9. Перечислите свойства прямоугольного треугольника.

10. Синусом, косинусом, тангенсом что называем?

11. Чему равна сумма углов в треугольнике?

12. Синус 30°,  синус 60°, косинус 45°, косинус 90°

13. Что значит решить треугольник?

14. Как называется треугольник со сторонами 3, 4, 5?  (Сообщение  ученика. Землемеры Древнего Египта для построения прямого угла пользовались следующим приемом. Веревку делили узлами на 12 равных частей и концы связывали. Затем веревку растягивали на земле так, чтобы получился треугольник со сторонами 3, 4, 5 делений. Угол треугольника, противолежащий стороне с пятью делениями, был прямой. В связи с указанным способом построения прямого угла, треугольник со сторонами 3, 4,5 иногда называют египетским.)

Слова знаменитого древнегреческого ученого Аристотеля подтвердили. Продолжим путешествие.

V. Работа с сигнальными карточками.

Тест на определение истинности (ложности) утверждения и правильности формулировок.

1. В треугольнике против угла в 150° лежит большая сторона. (И)
2. В равностороннем треугольнике внутренние углы равны между собой и каждый равен 60°.(И)
3. Существует треугольник со сторонами: 2 см, 7 см, 3 см. (Л)
4. Прямоугольный равнобедренный треугольник имеет равные катеты. (И)
5. Если один из углов при основании равнобедренного треугольника равен 50°, то угол, лежащий против основания, равен 90°.(Л)
6. Если острый угол прямоугольного треугольника равен 60°, то прилежащий к нему катет равен половине гипотенузы. (И)
7. В равностороннем треугольнике все высоты равны. (И)
8. Сумма длин двух сторон любого треугольника меньше третьей стороны. (Л)
9. Существует треугольник с двумя тупыми углами. (Л)
10. В прямоугольном треугольнике сумма острых углов равна 90°.(И)
11. Если сумма двух углов меньше 90°, то треугольник тупоугольный. (И)

VI. Отработка формул.

Найдите ошибку в ответе товарища:

1) а² = в² + с² + 2вc cos                             4)

2) в² = а² + с² – 2вс cos                             5)

3) а² = а² + с² - 2ас sin                               6)

VII. Геометрический диктант.

Вариант 1.

1. Один из углов прямоугольного треугольника равен 48°. Чему равен второй острый угол? (42°)
2. В равнобедренном треугольнике одна сторона равна 70 см, другая 26 см. Чему равна длина основания? (26 см)
3. В треугольнике ABC угол В — наибольший. Какая из сторон треугольника наибольшая? (АС)
4. Запишите теорему синусов для треугольника MPK. (= 2R).
5. Запишите теорему косинусов для треугольника МРК ( МР²=МК² +КР²– 2МK·РК·cosÐK)

  Вариант 2.

1. Один из углов прямоугольного треугольника равен 35°. Чему равен второй острый угол? (55°)
2. В равнобедренном треугольнике одна сторона равна 25 см, другая 58 см. Чему равна длина основания? (25 см)
3. В треугольнике ABC угол C — наибольший. Какая из сторон треугольника наибольшая? (АB)
4. Запишите теорему синусов для треугольника BCD. (= 2R).
5. Запишите теорему косинусов для треугольника BCD ( BC²=BD² +DC²– 2BD·DC·cosÐD)

 VIII. Решение задач.

Задача:    С помощью программы «Решение треугольников»  (можно свободно скачать в Интернете)  вычислите неизвестные элементы треугольника АВС (два ученика садятся за компьютеры и выполняют работу):

Ответы:

Задача № 1.   Пожарная лестница, стоящая на машине, может быть выдвинута на 20 м, а её крутизна может достигать 70⁰. Основание лестницы находится на высоте 2 м. До какого этажа можно по ней добраться, если высота этажа 3 м?

Задача № 2.   Спортивный самолёт летит по замкнутому треугольному маршруту. Два угла этого треугольника равны 60⁰ и 100⁰. Сторону, лежащую против третьего угла, он пролетел за 1 час. За сколько времени он пролетит весь маршрут, сохраняя постоянную скорость?

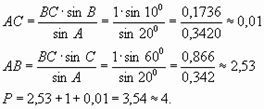
Ответ: за 4 часа самолёт пролетит весь маршрут.

Задача № 3.  Найдите длину отрезка, в концы которого упираются ножки циркуля-измерителя, длиной 15 см, если они образуют угол в 30⁰.

Закончим урок словами великого итальянского ученого Галилео Галилея: “Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает возможность правильно мыслить и рассуждать”.

6. Задание на дом.  № 1036, индивидуально 1038

Источники:

1. «Геометрия 7 – 9» Л.С.Атанасян, В.Ф.Бутузов, С.Б. Кадомцев и др. М.: Просвещение, 2012.

2. Изучение геометрии в 7-9 классах: методические рекомендации к учебнику/ Л.С.Атанасян, В.Ф.Бутузов, С.Б. Кадомцев и др. М.: Просвещение, 2000

3. http://math66.ucoz.ru/  Программа "Решение треугольников"

4. http://festival.1september.ru/ Оготоева К. П., "Уроки обобщающего повторения в 9 классе"

Скачано с www.znanio.ru