
Урок – лекция по геометрии
«Декартовы координаты в пространстве»
Учитель: Макеева О. В.
Цели урока:
1. Повторить введение и применение координат на прямой и на плоскости; формулы координат середины отрезка и расстояния между точками.
2.
 Ввести декартовы координаты в пространстве.
Ввести декартовы координаты в пространстве.
3. Развивать интерес к истории математики.
Оборудование:
1. Таблица «Декартовы координаты в пространстве».
2. Модель трёхмерной системы координат.
3. Чертежные инструменты.
4. Портрет Р. Декарта.
Ход урока
I. Введение
В 1637 г. во Франции вышла книга, которая принесла её автору невероятную известность. По обычаям того времени она имела довольно длинное название: «Рассуждение о методе, позволяющем направлять разум и отыскивать истину в науках. Кроме того, Диоптрика, Метеоры и Геометрия, которые являются приложениями этого метода». Автор книги Рене Декарт (1596 – 1650 г.). В ней он ввел прямоугольную систему координат, поставил каждой точке в соответствие пару чисел – её координаты. Этот прогрессивный метод позволил решить ряд геометрических задач алгебраическим методом, что оказалось очень удобным.
Главные правила метода гласят:
1. Не принимать за истинное что бы то ни было, прежде чем не признал это несомненно истинным, т. е. старательно избегать поспешности и предубеждения и включить в свои рассуждения только то, что представляется уму так ясно и отчетливо, что никоим образом не может дать повод к сомнению.
2. Делить каждую из рассматриваемых трудностей на столько частей, на сколько требуется, чтобы лучше их разрешить.
3. Руководить ходом своих мыслей, начиная с предметов простейших и легко познаваемых, и восходить мало – помалу, как по ступеням, до познания наиболее сложных, допуская существования порядка даже среди тех, которые в естественном порядке вещей не предшествуют друг другу.
4. Делать всюду настолько полные перечни и такие общие обзоры, чтобы быть уверенным, что ничего не пропущено.
Руководствуясь этими правилами, начнем с ранее изученного материала.
|
(4;
– 0,5), |
(– 9;
11), |
(– 3;
2), |
«Кит»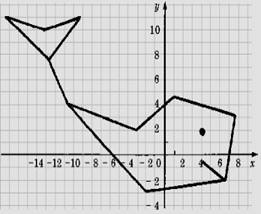
«Заяц»
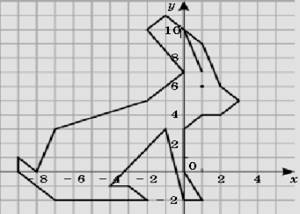
|
(1;
7) |
(–
2; 5) |
(–
7; – 2) |
(0;
– 2) |
(2;
4) |
В своё время Рене Декарт сказал: “… потомки будут благодарны мне не только за то, что я сказал, но и за то, что я не сказал и тем самым дал им возможность и удовольствие додуматься до этого самостоятельно”. Я предоставлю вам возможность и удовольствие разобраться с декартовой системой координат самостоятельно.
Предлагаю вам таблицу, которую мы с вами заполним, сделав сравнительную характеристику.
|
На плоскости |
В пространстве |
|
Определение. |
Определение. |
|
2 оси, ОУ- ось ординат, ОХ- ось абсцисс |
3 оси, ОХ - ось абсцисс, ОУ – ось ординат, ОZ - ось аппликат. |
|
ОХ перпендикулярна ОУ
|
ОХ перпендикулярна ОУ, ОХ перпендикулярна ОZ , ОУ перпендикулярна ОZ. |
|
(О;О) |
(О;О;О) |
|
(Х; У) |
(Х; У; Z) |
|
Расстояние между точками.
|
Расстояние между точками.
|
|
Координаты середины отрезка.
|
Координаты середины отрезка.
|
Вопросы для заполнения первой части таблицы.
1. Сформулируйте определение декартовой системы координат?
2. Попробуйте сформулировать определение декартовой системы координат в пространстве?
3. Назовите оси координат на плоскости? Назовите оси координат в пространстве? Название, какой оси мы не изучали? (Знакомство с новым словом “аппликата”)
4.Под каким углом располагаются оси координат друг к другу?
5. Назовите координату начала координат на плоскости (в пространстве)?
6. Как задается координата точки на плоскости и в пространстве?
7. По каким формулам находится расстояние между двумя точками на плоскости и в пространстве? (Координаты середины отрезка)
II. Повторение. Актуализация знаний
1. Сначала координаты точки ввели на луче, потом на прямой.
Координатная прямая – это прямая с выбранными на ней направлением, началом отсчета и единичным отрезком.
О А(х)
![]()
![]()
![]()
![]()
![]()
![]() =
ОА
=
ОА
0 1 х
Координатой точки А называют число, абсолютная величина которого равна расстоянию от начала отсчета до точки А.
Если точка расположена справа от точки О, то её координата положительная, если слева – то отрицательная.
2. Для определения положения точки на плоскости одной координаты недостаточно. Поэтому по примеру географических координат Декартом были введены координаты на плоскости, добавив к оси х перпендикулярную ось и выбрав на ней направление и единичный отрезок.
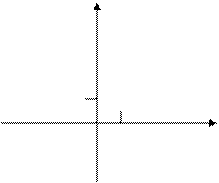 y О –
начало отсчета.
y О –
начало отсчета.
(Повторить определение абсциссы и
![]()
![]() Аy А(х,y)
ординаты точки на плоскости).
Аy А(х,y)
ординаты точки на плоскости).
ОАх = ![]() , ОАy =
, ОАy = ![]() ,
,
1 А (х;y), Ах (х;0), Аy (0;y )
![]() О 1 Ах х
О 1 Ах х
III. Введение координат в пространстве
Первое определение IX книги «Начала» Евклида гласит: «Тело есть то, что имеет длину, ширину и глубину». Тем не менее есть основание полагать, что в древности нашего понятия о трехмерном пространстве не существовало. У Декарта имелись лишь далекие намеки на возможность распространения метода координат с двумерного пространства (плоскости) на трехмерное. Потребовалось ещё почти 100 лет, чтобы идея пространственных координат была сформирована, постоянно и и широко использовалась.
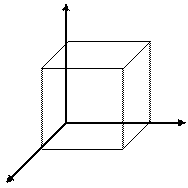 z (Объяснение
с опорой на трехмерную модель и
z (Объяснение
с опорой на трехмерную модель и
Аz Ayz таблицу №21).
Система координат в пространстве представляет
Axz A собой три взаимно перпендикулярные прямые
![]() х, y, z, пересекающиеся
в одной точке.
х, y, z, пересекающиеся
в одной точке.
О – начало отсчета,
О Ау у x, y, z – координатные оси,
Ax Axy xy, yz, xy – координатные плоскости.
x Координатные плоскости делят все пространство
на 8 октантов.
Определим координаты точки А на плоскости.
Через точку А проведем плоскость, параллельную плоскости yz. Она пересекает ось x в точке Аx . Координатой х точки А называется число, равное по абсолютной величине длине отрезка ОАх . Аналогично определяются и другие координаты. Таким образом, точке А в пространстве ставится в соответствие тройка чисел – её координаты.
Обозначение: А(x; y; z). (Название координаты z найти самостоятельно).
Рассмотрим координаты частного расположения точек в пространстве.
Ах (х;0;0) Ахy (х;y;0) О (0;0;0)
Аy (0;y;0) Аyz (0;y;z)
Аz (0;0;z) Ахz (х;0;z)
Задача 1. Дан куб с ребром, равным 4. Определите координаты его вершин.
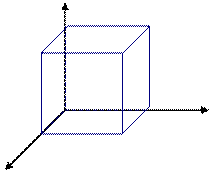 z
z
В1 С1 Ответы:
А1 D1 А (4;0;0) А1 (4;0;4)
В (0;0;0) В1 (0;0;4)
В С y С (0;4;0) С1 (0;4;4)
D (4;4;0) D1 (4;4;4)
А D
x
Задача 2. Дан прямоугольный параллелепипед, измерения которого равны 6;4;4. Определите координаты его вершин.
![]() В1
z С А1 D1
В1
z С А1 D1
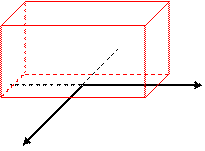 Ответы:
Ответы:
А1 D1
А (2;-3;0) А1 (2;-3;4)
В С В (-2;-3;0) В1 (-2;-3;0)
А D y С (-2;3;0) С1 (-2;3;4)
D (2;3;0) D1 (2;3;4)
x
IV. Приложение метода координат
В качестве иллюстрации приложения метода координат рассмотрим алгебраические равенства, имеющие простые геометрические истолкования. Это формулы координат середины отрезка и расстояния между точками.
Задача на повторение. Найдите координаты середины отрезка АВ и длину отрезка АВ, если:
1 вариант – А (3;-1), В (-2;4)
2 вариант – А (3;4), В (2; -1)
(Проверку работ осуществить на боковых досках).
Аналогичные формулы применяются в пространстве. По учебнику прочитать п.153, 154 и выписать формулы в тетрадь. Два ученика получают на дом задание - вывод формул.
Задача №3. Дано: А (1;-1;2), В (3;1;-2)
Найдите координаты середины отрезка АВ и его длину.
Решение:
1). Пусть С – середина отрезка АВ, тогда С (![]() ;
; ![]() ;
;
![]() ), С (2;0;0)
), С (2;0;0)
2). АВ = ![]() =
= ![]() = 2
= 2![]() .
.
V. Подведение итогов урока
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.