
Учитель математики: Евграшина Наталья Васильевна
Город: Славгород
Образовательное учреждение: МБОУ «Лицей №17»
Предмет: математика
Цель: актуализировать знания по теме «Обратная функция», закрепить при решении задач.
Задачи урока:
образовательные:
· формировать навыки нахождения обратной функции, умение решать задачи на нахождение обратной функции, применять полученные знания при решении задач.
· способствовать развитию математической речи, оперативной памяти, произвольного внимания, наглядно-действенного мышления.
воспитательные:
· воспитывать культуру поведения при фронтальной и индивидуальной работе, работе в парах, формировать положительную мотивацию;
· формировать ответственность, трудолюбие, организованность в работе на уроке.
развивающие:
· развивать компетентности: учебно-коммуникативные, учебно-интеллектуальные, учебно-организационные, учебно-информационные.
· воспитывать учебно-познавательную активность, прививать интерес к предмету
· планировать своё действие в соответствии с поставленной задачей.
Образовательные технологии: технология формирующего оценивания.
Оборудование: учебник: Алгебра и начала математического анализа 10 класс для общеобразовательных учреждений (профильный уровень), М: Мнемозина,2017 г. под редакцией А.Г. Мордковича, доска, мультимедиа проектор, компьютер, презентация «Обратная функция».
Ресурсы: мультимедийный проектор, презентация.
Основные понятия: обратная функция, график обратной функции.
Сценарий урока
|
Этапы урока |
Деятельность учителя |
Деятельность учеников |
|
1.Организационный этап (1 мин.)
|
Учитель приветствует учащихся, проверяет их готовность к уроку. -"Здравствуйте", слово какое чудесное, Давайте улыбки друг другу дарить, и в жизни всегда верный путь находить. |
Учащиеся слушают учителя. |
|
2.Мотивация учебной деятельности (1 мин.)
|
Начать урок я хочу с вопроса. Как вы думаете, что самое ценное на Земле? «Знание – самое превосходное из владений. Все стремятся к нему, само же оно не приходит». Аль – Бируни (слайд1) Эти слова будут эпиграфом нашего урока. |
Ответы учащихся.
|
|
3. Этап целепологания и постановки задач урока. |
Чем мы занимались на предыдущем уроке? Сегодня мы продолжаем работу по теме «Обратная функция». Сформулируйте цель, которую вы ставите перед собой? Хорошо, наши цели практически совпали. Сегодня на уроке мы будем закреплять знания по данной теме. (слайд 2) Давайте определим
круг задач, чтобы добиться поставленной цели. Перед вами листы самооценки, куда вы в конце урока поставите себе оценку (слайд 3). |
Ответы учащихся.
ü повторить свойства обратной функции; ü закрепить и отработать алгоритм нахождения обратной функции при решении заданий; ü проверить свои знания по теме «обратная функция».
|
|
4.Актуализация и систематизация знаний, и фиксация затруднения в пробном действии. Этап повторения теоретического материала (4 мин.)
|
На шкале продвижений отметьте свой уровень знаний по данной теме.
Какие определения и свойства нужно знать, чтобы правильно решать задания по теме урока? (слайд4) Рассматриваем картинки-перевертыши, понятия палиндрома в русском языке и свойство суммы двух положительных взаимно обратных чисел в алгебре, знакомлю, где в высшей математике применяют обратные функции.Палиндром – это текст, одинаково читающийся от начала к концу и от конца к началу. Привожу пример “А роза упала на лапу Азора”, слова русского поэта – лирика. Афанасия Афанасьевича Фета (1820 — 1892гг.).
(слайд5)Устно:
5..На столах у вас находятся карточки, отражающие шаги алгоритма нахождения обратной функции. Работая в парах, составьте алгоритм.
6.Найти ошибку в решении нахождения функции, обратную к данной: у =
|
Отмечают по 10 бальной шкале
Ответы учащихся · определение обратной функции; · алгоритм нахождения обратной функции; · построение графика обратной функции;.
1.Да.
2. Да. Монотонна, область определения и область значений взаимнообратны.
3.Возрастает 4.Убывает. 5. Алгоритм 1. Определяем монотонность функции. 2. Если функция монотонна, значит обратима. 3. Выражаем х через у. 4. Заменяем х на у. 6. у
=
|
|
5.Применение имеющихся знаний на практике § Индивидуальная работа по карточкам, два варианта, с последующей взаимопроверкой. |
(слайд 6-7) Обменяйтесь тетрадями и оцените себя. Критерии оценивания: каждое правильно выполненное задание оценивается 1 баллом. |
4. у=
Сверяют с эталоном на доске, осуществляя взаимопроверку, проставляют баллы. |
|
§ 6. Физкультминутка § (2 мин.) |
Постройте глазами график квадратичной функции, график линейной функции, график тригонометрической функции у=cos x,y=sin x. |
Выполняют упражнения для глаз. |
|
§ 7. Построение проекта коррекции выявленных затруднений
(постановка задач) |
- Подведём итоги работы: |
Высказываются по
поводу решения проблемы, ставят перед собой задачи.
Повторить: Построение графика обратной функции; Выражение одной переменной через другую; Свойства функции. |
|
8. Реализация проекта по устранению затруднений § Работа
в группах |
Работая в группах, мы составим конспект по теме «Обратная функция» для подготовки учащегося 10 класса, по которому легко будет готовиться решать задачи. Деление на группы дифференцированное: группы 2;3 выполняют задания среднего уровня, группы 1;4 выполняют задания повышенного уровня. В каждой группе свой консультант по данной теме, он поможет разобраться с вашими трудностями. (группы по 5 человек, задания на доске и на столе у каждой группы) (слайд 9) Группа 1. По алгоритму нахождения графика обратной функции найти функцию обратную данной, укажите области определения и области значений данных функций; у =
Группа 2. №10.13(в) Группа3 .№10.14;10.16 Группа 4. №10.23(в)
Ребята, вы проделали нужную работупо устранению пробелов в знаниях по теме « Обратная функция». Можем ли мы на данном этапе работы утверждать, что теперь нет вопросов по нахождению и построению графика функции, обратной данной?
|
Работают в группах.
Вывешивают свои решения, кратко комментируют.
Да. |
|
§ 8. Рефлексия (подведение итогов урока) ) § (3 мин.) |
Мы добились своей цели и выполнили все задачи урока? Как вы думаете, что нужно сделать, чтобы не допускать ошибок в заданиях по этой теме? Возьмите линейку продвижений и отметьте на ней
уровень ваших знаний по теме сейчас. Посчитайте баллы в тетради и в лист самооценки поставьте себе оценку за урок.Сдайте листы мне. С горы скатившись, камень лег в долине. Столетье за столетьем пронеслось: 19 век. Я желаю, чтобы в вашей жизни все проблемы всегда разрешались! |
Ответы учащихся
Отмечают продвижение в знаниях по теме. Поднимают шкалу вверх.
Считают баллы и выставляют оценку.
|
|
§ 9. Информация о домашнем задании с комментариями. § (1 мин.) |
П.10,творческое задание: на листе формата А4 построить графики взаимно-обратных функции: линейной и обратной пропорциональности (записано на доске) |
записывают задания в дневнике. |
Приложение 1
Лист самооценки по теме: «Обратная функция»
Ф. И. ученика _________________________
|
Отметка «5» |
Отметка «4» |
Отметка «3» |
Отметка «2» |
|
Могу объяснить, какие функции называются «Обратными». Знаю и применяю алгоритм нахождения обратной функции; Умею строить график обратной функции, но могу допустить 1ошибку по невнимательности.
( из 7 заданий допускается 1 ошибка) |
Могу объяснить, какие функции называются «Обратными». Знаю и применяю алгоритм нахождения обратной функции; Умею строить график обратной функции, но могу допустить 2 ошибки (1вычислительного характера, 1 в построении графика)
( из 7 заданий допускаются 2 ошибки) |
Понимаю, какие функции называются «Обратными» Знаю, алгоритм нахождения обратной функции, но не во всех случаях могу применить; Умею строить график обратной функции, но могу допустить ошибки.
( из 7 заданий допускаются 3 ошибки) |
Понимаю, какие функции называются «Обратными». Не знаю, алгоритм нахождения обратной функции, но могу сделать задание по образцу и допустить вычислительные ошибки. Не умею строить график обратной функции.
(из 7 заданий больше половины сделано не верно) |
Приложение 2. Линейка продвижений




Приложение 3
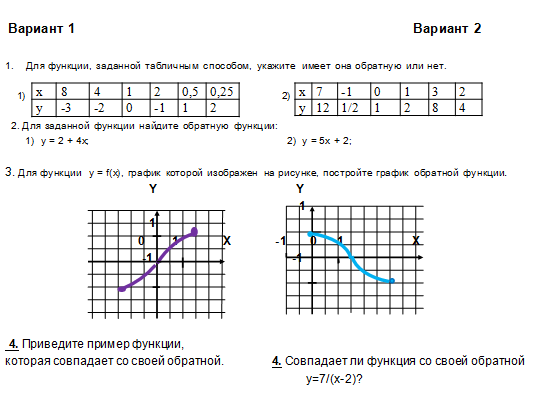
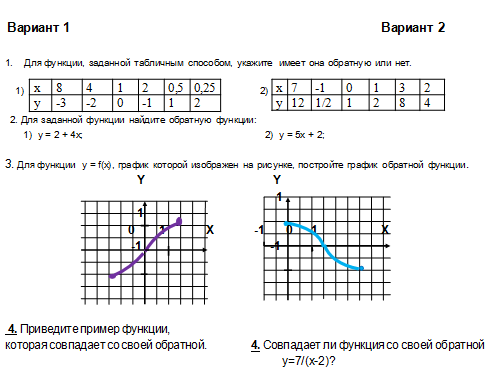
Приложение 4
Алгоритм нахождения обратной функции
Определяем монотонность.
Если функция монотонна, значит обратима.
Выражаем х через у.
Заменяем х на у.
Определяем монотонность.
Если функция монотонна, значит обратима.
Выражаем х через у.
Заменяем х на у.
Определяем монотонность. Если функция монотонна, значит обратима.
Выражаем х через у.
Заменяем х на у.
.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.