Урок математики в 6 классе в формате онлайн на тему "Наименьшее общее кратное"

Дата: 02.10.2020г.

Тема урока: Наименьшее общее кратное (НОК)

Цель: научиться находить наименьшее общее кратное нескольких натуральных чисел.

Задачи: научиться решать задачи, связанные с нахождением НОК.

На уроке

мы узнаем:

• что называется НОК;

мы научимся:

• находить НОК;

мы сможем:

• решать задачи, связанные с нахождением НОК.

Основные понятия:

– делители числа;

– кратные числа;

– признаки делимости;

– разложение на простые множители;

– НОК.

Словарь:

Кратное натурального числа – это число, которое делится на данное натуральное число без остатка.

Простое число – это такое натуральное число, которое больше 1 и делится только на 1 и само на себя.

Составные числа – это непростые натуральные числа, большие 1.

Взаимно простые числа – это числа, которые не имеют общих простых делителей

Наименьшее общее кратное (НОК) двух натуральных чисел m и n – это наименьшее натуральное число, делящееся нацело на каждое из чисел m и n.

Теоретический материал:

Ранее мы узнали, что такое кратное, ввели понятие делителя, научились находить наибольший общий делитель, а можно ли каким-либо способом найти общее кратное нескольких чисел? Оказывается, можно, этим сегодня мы и будем заниматься. Но находить не просто общее кратное нескольких чисел, а их наименьшее общее кратное – НОК.

Итак, для начала вспомним, что называется кратным. Это число, делящееся на данное натуральное число без остатка.

Теперь найдём, например, общие кратные чисел 12 и 15. Для этого выпишем все кратные чисел 12 и 15.

12 – его кратные 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, …

15 – его кратные 15, 30, 45, 60, 75, 90, 105, 120, 135, …

Из представленных чисел общие кратные – это числа 60 и 120. Меньшее из них – 60. Это и есть наименьшее общее кратное чисел.

Наименьшее общее кратное (НОК) двух натуральных чисел m и n – это наименьшее натуральное число, которое делится на m и n без остатка.

Для нахождения наименьшего общего кратного двух чисел можно использовать несколько способов. Один из них мы рассмотрели на примере нахождения НОК 12 и 15. Этот способ заключается в том, что выписываются все кратные двух чисел и затем находится наименьший общий из них.

Узнаем ещё одно правило нахождения НОК.

Во-первых, разложим числа на простые множители. Далее подчеркнём одинаковые множители этих чисел. Затем перемножим общие множители одного из чисел и добавим произведение всех остальных множителей от каждого числа. Это и будет НОК заданных чисел.

Найдём НОК (15; 16). Разложим числа на простые множители:

Видно, что из всех множителей общий лишь единица, значит, это взаимно простые числа.

НОК взаимно простых чисел – это произведение всех их множителей или произведение этих чисел.

В данном случае НОК равен 240.

Т. е. НОК любых двух простых чисел или двух соседних натуральных чисел будет равен произведению этих чисел.

Найдём НОК (10; 100). Разложим числа на простые множители:

Выделим общие делители у этих чисел, это 2 и 5.

Умножим их, а результат умножим ещё на оставшиеся простые множители от чисел 100 и 10.

НОК (10; 100) = 2 · 5 · 2 · 5 = 100

Обратите внимание на то, что 100 делится нацело на 10, и НОК тоже равен 100. Поэтому можно сделать вывод: если одно из двух чисел делится нацело на другое, то НОК этих чисел равен большему из них.

Некоторые задачи можно решить при помощи НОК проще, чем каким-либо другим способом.

Например, рассмотрим такую задачу.

Девочка решила купить несколько плиток шоколада по 38 руб. , но у неё только 5-рублёвые монеты, а в магазине нет сдачи. Какое наименьшее количество плиток шоколада она сможет купить?

Решение: чтобы решить эту задачу, нужно найти НОК (5;38).

Разложим числа на множители:

Мы видим, что НОК (5; 38) = 5 · 38 = 190 – это будет сумма покупки за шоколад.

Теперь найдём, сколько девочка купит плиток.

Для этого сумму покупки разделим на стоимость одной плитки шоколада.

190 : 38 руб. = 5 – наименьшее количество плиток шоколада, которые сможет купить девочка.

Ответ: 5 плиток.

Тренировочные задания

№ 1. Какую цифру нужно подставить в число НОК (7; 2_) вместо пропуска, чтобы получить НОК = 21?

Варианты ответов: 1; 2; 3.

Решение: для решения этой задачи, надо разложить на множители оба числа, при этом вместо пропуска нужно подставить по порядку все цифры. А далее найти подходящий НОК этих чисел, равный 21.

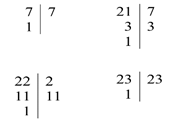
Из всех разложений на множители под НОК (7; 2_) = 21 подходит только число 21.

НОК (7; 21) =21

НОК (7; 22) =154

НОК (7; 23) =161

Ответ: искомая цифра – 1.

№ 2. Какой наименьшей длины должен быть рулон ткани, чтобы от него без остатка можно было отрезать куски по 3 м и 7 м?

Решение: чтобы решить эту задачу, нужно найти НОК заданных чисел, он и будет являться искомым ответом, т. е. наименьшей длиной рулона ткани.

НОД (3; 7) = 7 · 3 = 21 м

Ответ: 21 м.

Порядок выполнения домашнего задания:

1.     Учебник §6 чит., отв. на вопр. 1-4 устно, ВЫУЧИТЬ определения и алгоритм.

2.     Просмотр видеоурока  https://infourok.ru/videouroki/2998

3.     Выполнить в тетради №№164 (1-3), 166, 168 (1, 2).

Скачано с www.znanio.ru