Урок "Арифметическая прогрессия"

12.02.08 12.02.08 Тема урока: «Сумма  Тема урока: « Сумма nn первых   первых  членов арифметической  членов арифметической  прогрессии».». прогрессии Цель урока: повторить формулы n­го  члена и суммы n первых членов  арифметической прогрессии; учиться  применять их при решении различных  задач.

Арифметическая прогрессия Арифметическая прогрессия • 5; 10; 15; 20;… • ­ 20; ­ 16; ­ 12; ­ 8;… • ­ 24; … ; 10; … • an = 2n – 1 • a1 = 0, an+1 = an – 3     an= 5n bn+1 =  bn + 4 a2 =  ­ 7 1; 3; 5; … 0; ­3; ­6; …

Восстановите пропуски: Восстановите пропуски: an+1 – an =              xn = x1 + (    …   )∙d      a8 = a1 + … d  d n ­ 1 7 a 1 a  2 a S 5 2a1 ...  Sn n  n Sn ... a5 ...  5 1  ... 2  ( n 2 9  ... d 2 ... 2 1 x )1 d n S 10     10

Проверка домашнего задания Проверка домашнего задания №13*Вариант№1 Какое из следующих чисел является членом  арифметической прогрессии 3; 6; 9; 12;…? А. 83   Б. 95   В. 100  №13* Вариант№2  Г. 102 Какое число не является членом  арифметической прогрессии 6; 12; 18;…? А.60              В. 66   Г. 72 Б. 63 № 632(в)             №643(а)      №6.6*(1)с.132 «Да»,n = 4         S40 = 1640      S51 = 4335

ЦИР К S14 =  2 1 a 13 d  2           Задача 1 В первом ряду цирка 40  мест, а в каждом  следующем на 8 мест  больше, чем в  предыдущем. Всего в  цирке 14 рядов. Сколько  всего мест в цирке? Дано: {an} – арифм. прогрессия a1 = 40, d = 8, n = 14 Найти: S14  14  14 184 2  1288 Решение:  402 813 2  14 Ответ: 1288 мест.

Задача 2 Задача 2 В первый день после  нарушения правил дорожного  движения штраф составляет  200р.,а в каждый  последующий день он  увеличивается на 10р., по  сравнению с предыдущим.  Какой штраф заплатит  автомобилист на n день?  Дано: {an} – арифм. прогрессия a1 = 200, d = 10 Найти: an Решение: an = a1 + (n­1)d = 200 + (n­1) ∙ 10 = 200 +10n ­10=190+10n Ответ: 190 + 10n

Домашнее задание Домашнее задание №13* Вариант №3 № 13* Вариант №4 №635(а), №643(в).

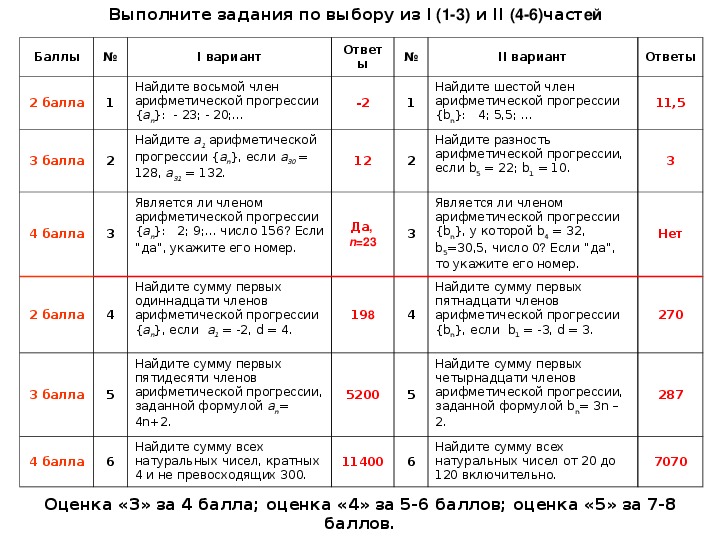
Выполните задания по выбору из I (1­3) и II (4­6)частей Баллы № I вариант Ответ ы № II вариант Ответы 2 балла 3 балла 1 2 4 балла 3 2 балла 4 3 балла 4 балла 5 6 Найдите восьмой член арифметической прогрессии {an}: - 23; - 20;… Найдите a1 арифметической прогрессии {an}, если a30 = 128, a31 = 132. Является ли членом арифметической прогрессии {an}: 2; 9;… число 156? Если “да”, укажите его номер. Найдите сумму первых одиннадцати членов арифметической прогрессии {an}, если a1 = -2, d = 4. Найдите сумму первых пятидесяти членов арифметической прогрессии, заданной формулой an= 4n+2. Найдите сумму всех натуральных чисел, кратных 4 и не превосходящих 300. -2 12 Да,  n=23 198 5200 11400 1 2 3 4 5 6 Найдите шестой член арифметической прогрессии {bn}: 4; 5,5; … Найдите разность арифметической прогрессии, если b5 = 22; b1 = 10. Является ли членом арифметической прогрессии {bn}, у которой b4 = 32, b5=30,5, число 0? Если “да”, то укажите его номер. Найдите сумму первых пятнадцати членов арифметической прогрессии {bn}, если b1 = -3, d = 3. Найдите сумму первых четырнадцати членов арифметической прогрессии, заданной формулой bn= 3n – 2. Найдите сумму всех натуральных чисел от 20 до 120 включительно. 11,5 3 Нет 270 287 7070 Оценка «3» за 4 балла; оценка «4» за 5-6 баллов; оценка «5» за 7-8   баллов.