
Публикация является частью публикации:
МОУ «Ерышовская СОШ Ртищевского района Саратовской области»
ОТКРЫТЫЙ УРОК ПО МАТЕМАТИКЕ
в 9 КЛАССЕ
по теме
Подготовка к ГИА по теме «Неравенства».
Подготовила: Тишина Е.С.,
учитель математики
Тема «Неравенства» подготовка к ГИА
Цель: обобщить и оценить знания учащихся по теме
образовательная:
-повторить и закрепить учебный материал по теме «Решения линейных неравенств с одной переменной »;
- развивать приёмы мыслительной деятельности, внимание;
-развивать коммуникативную и информационную компетенции учащихся;
-воспитывать культуру коллективной работы;
-развитие самостоятельности.
Ход урока.
1. Организационный момент, мотивация учащихся. Определение темы урока
Я рада всех вас приветствовать. Мы проводим очередной урок по подготовке к государственной итоговой аттестации.
2. Актуализация знаний
а) устная работа
В начале урока предлагаю провести небольшую устную работу (Фронтальный опрос) слайды
1 Известно, что а >в. Сравните а-b и b- а
1) а-b > b-а
2) а-b< b-а
3) а-b = b- а
2 Известно, что а>в>0.Какое из указанных утверждений верно?
1)2а+1<0
2)-а>-b
3)2b >2a
4)1-a>1-b

Тему сегодняшнего урока вы сами попробуете ее сформулировать, посмотрев на слайд 1.
Итак, тема урока «Неравенства».
№1
|
На рисунке изображен график функции Используя график, решите неравенство |
|
№2.
|
На рисунке изображен график функции Используя график, решите неравенство
|
|
№3
|
На рисунке изображен график функции Используя график, решите неравенство
|
|
3 Тренировочные упражнения:
Линейные неравенства
Какие неравенства называются линейными?
1 Решите неравенства(записаны на доске ,индив решение)
а) х-1 < 3х+2 б)4-7(х+3)<-9 в) 4+12х>7+13х
у доски классом
![]() .
.
2 Соотнеси неравенства и промежутки Самостоятельная работа
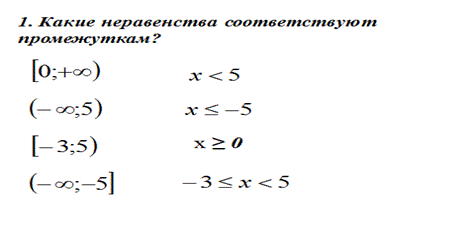
3 Тест

Квадратные неравенства ax²+bx+c>0
1. Какие из неравенств вы бы назвали неравенствами второй степени:
1) 6х2 – 13х>0; 2) х2 – 3x – 14>0; 3) (5 + x)(x – 4)>7;
4) ![]() ;
5)
;
5) ![]() ;
;
6) 8 х2>0; 7) x(x – 9) – х2>0?
– Теперь давайте сформулируем определение неравенства второй степени:
Определение: Неравенство, левая часть которого есть многочлен второй степени, а правая – нуль, называется неравенством второй степени.
2 Решите неравенства
х2 - 4х+3>0 6х2 – 13х>0; х2 -1 <0
![]()
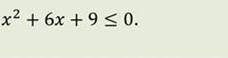

Укажите неравенство, которое не имеет решений:
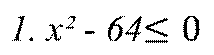
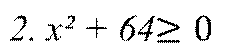
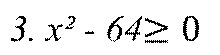
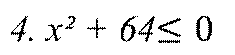
Найдите ошибки
№ 1. Решите неравенство: х2 – 5х + 6 < 0
f(х) = х2 – 5х + 6 – квадратичная функция, график – парабола,
 ветви
вверх.
ветви
вверх.
х2 – 5х + 6 = 0
х1 = 2 х2 = 3
2 3 x
Ответ: ( 2; 3 )
№ 2. Найдите множество решений неравенства:
- 0,2 х2 + х – 1,2 ≤ 0
f(х) = - 0,2 х2 + х – 1,2 - квадратичная функция, график – парабола,
ветви вниз.
- 0,2 х2 + х – 1,2 = 0 / ( - 5)
 х2 – 5х + 6 = 0
х2 – 5х + 6 = 0
х1
= 2 х2 = 3![]()
![]()
![]()
![]()
![]()
![]()
![]()
2 3 x
Ответ: (
-∞; 2 ) U![]() ( 3; + ∞)
( 3; + ∞)
№ 3. Решите неравенство: 2х > х2
2х - х2 > 0
f(х) = 2х - х2 - квадратичная функция, график – парабола,
ветви вниз.
 2х - х2 = 0
2х - х2 = 0
х ( 2 – х ) = 0
х = 0 или х = 2
0 2 x
Ответ: [ 0; 2 ]
№ 4. Найдите множество решений неравенства:
1 + 2х + х2 > 0
f(х) = 1 + 2х + х2 - квадратичная функция, график – парабола,
 ветви
вниз.
ветви
вниз.
1 + 2х + х2 = 0
х2
+ 2х +1 = 0![]()
![]()
х = - 1![]()
-1 x
Ответ: - 1
Тест.
1. На каком рисунке изображено множество решений неравенства х2 – 9 ≤ 0 ?
![]()
![]() а) б)
а) б)
-3 3 x 3 x
![]()
![]() в) г)
в) г)
-3 x -3 3 x
2. Решите неравенство: х2 – 8х + 15 > 0
а) ( 3; 5) б) [ 3; 5 ]
в) (- ∞; 3) U (5; + ∞) г) (- ∞; 3 ] U [ 5; + ∞)
3. Найдите множество решений неравенства: 5х - х2 ≥ 0
а) [ 0; 5] б) (- ∞; 0) U (5; + ∞)
в) (- 5; 0) г) (- ∞; 0 ] U [5; + ∞)
4. Решите неравенство: 6а < а2 + 10
а) ( - 4; + ∞) б) решений нет
в) ( - ∞; 4) U (36; + ∞) г) ( - ∞; + ∞ )
5. Найти область определения функции: у = ![]()
а) (- ∞; 0) U (4; + ∞) б) (0; 4)
в) (- ∞; 8 ] U [2; + ∞) г) [ 0; 4 ]
Самостоятельная работа
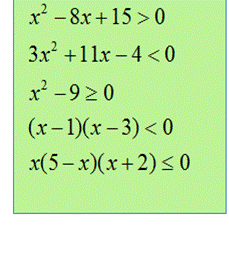
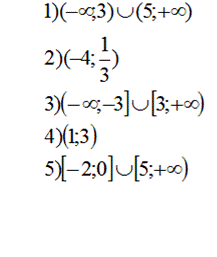
Задания на дом
1. Решите неравенство ![]() .
.
|
1) |
|
3) |
|
|
2) |
|
4) |
|
2. Решите неравенство ![]() .
.
|
1) |
|
3) |
|
|
2) |
|
4) |
|
3. Решите неравенство ![]() .
.
|
1) |
|
3) |
|
|
2) |
|
4) |
|
4. Решите неравенство ![]() .
.
|
1) |
|
3) |
|
|
2) |
|
4) |
|
Рефлексия
- Чему мы посвятили сегодняшние 45 мин своей жизни?
- Что нового узнали?
- Кто остался довольным собой на уроке?
- Добились ли мы цели поставленной нами в начале урока?
- Как вы думаете, стоит ли задержаться на решении неравенств ещё на урок ?
- Благодарю всех за работу. Всего доброго. Урок окончен.
Литература
1. Алгебра 9 класс. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова, Москва, «Просвещение», 2010 г.
2. Дидактические материалы. Алгебра 9 класс, Ю.Н. Макарычев, Н.Г. Миндюк, Л.М. Короткова, Москва, «Просвещение», 2012 г.
3. Алгебра. Сборник заданий для подготовки к итоговой аттестации в 9 классе. Л.В. Кузнецова, С.Б. Суворова, Е.А. Бунимович, Москва, «Просвещение», 2011 г.
4. Журнал «Математика в школе», № 2, 1998 г.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.