Урок математики в 6 классе "Применение распределительного свойства умножения"

Тема учебного занятия: «Применение распределительного свойства умножения».

Тип учебного занятия: урок комплексного применения знаний и способов действий.

Цель учебного занятия:

1.     повторить распределительное свойство умножения относительно сложения и вычитания;

2.     показать применение распределительного свойства умножения при работе с обыкновенными дробями и смешанными числами;

3.     совершенствовать навыки рациональных вычислений;

4.     способствовать развитию логического мышления, умению формулировать и обосновывать суждения;

5.     воспитывать аккуратность, точность и внимательность при работе с обыкновенными дробями.

6.     Организовать деятельность учащихся по самостоятельному переносу усвоенных ими комплекса знаний и способов действий  в рамках изучаемой темы в изменённую и новую ситуации.

7.     Продолжить формирование у учащихся критического отношения к получаемому результату деятельности посредством самооценки и взаимопроверки.

8.     Обеспечить оптимальное сочетание мотивации учения школьников и развитие интеллекта.

Форма учебного занятия: Урок – игра «Математические гонки».

Логика учебного занятия:  Мотивация→актуализация опорных знаний и способов            действий, необходимых для применения на творческом уровне→образец комплексного применения знаний →самостоятельное применение знаний и способов действий → самоконтроль и контроль → коррекция.

Содержание:

Средства, необходимые для проведения учебного занятия:

Дидактический материал, карточки, учебник, доска,  компьютер,

мультимедио.

1.     Организационный момент

Ø Сегодняшний урок начнём с высказывания Л.Н, Толстого: «Человек подобен дроби: в знаменателе – то, что он о себе думает, в числителе – то, что он есть на самом деле. Чем больше знаменатель, тем меньше дробь».   

Ø Как вы понимаете эти слова? (Чем больше человек о себе воображает, тем меньше он что-то из себя представляет).

2.     Постановка темы и цели урока:

Ø Как вы думаете, о чем сегодня наш урок?

Ø Какую цель поставим мы перед собой?

3.     Актуализация знаний

Устно найти значения выражений:

1).  ∙        2).  ∙         3). 6 ∙ 7          4). 2 ∙ 6            

4.     Подготовка учащихся к работе на основном этапе урока.

Ø У нас есть поговорка «Попал в тупик», то есть попал в трудное положение, аналогичная поговорка у немцев звучит так: «Попасть в дроби». Она напоминает о тех временах, когда дроби считали самым трудным разделом математики, В наше время их начинают изучать уже в младших классах.

Ø Сегодня у нас необычный урок, на этот раз мы принимаем участие в гонках, причём гонки эти – математические.

Ø В чём состоит ваша задача?

Ø Вы должны как можно быстрее и качественнее преодолеть все препятствия, которые будут попадаться по всей трассе, а препятствия эти – примеры, уравнения, задачи, которые вам надо решить.

Ø В конце гонки подведём итоги.

Ø «Зачисление в экипаж гоночной машины»

Задание. Записать на доске и « сигнальных карточках» формулы, выражающие распределительное свойство умножения (РСУ) относительно:

1.     сложения:

2.     вычитания.

Вопрос. Сформулировать правило умножения смешанного и натурального чисел.

5.     Применение знаний и способов действий, учащихся в изменённой ситуации.

Ø Что нужно сделать, прежде чем выйти на трассу?

Ø «Устранение неполадки в машине».

Задание. Найти ошибку и охарактеризовать её:

Ø Есть неполадки, их нужно устранить:

Задание.  Отгадать слово, обозначающее неполадку в машине.

Даётся установка: «Найти значение выражений и из соответствующих им букв составить слово, обозначающее неполадку в машине».

                                                         
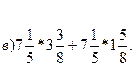
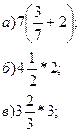
Ответы:

а) 17(Ш); б) 9(И); в) 11(Н); г) 36(А).              

Ø Неполадки вы ликвидировали, а теперь вам предстоят:

Ø «Гонки по пересечённой местности».

Участникам команд даётся установка: «Выполнить по очереди задания».  

                     Задание. а) Упростите выражение:

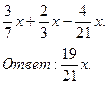
                           б) Найдите его значение при x, равном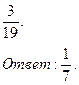                                                                      

                     Задание 5. Решите уравнение:

Ответ: x=2

6.     Применение учащимися знаний и способов действий в новой ситуации

Ø «Внезапная остановка».

Ø С 93 № 570

Ø «Финиш». Самостоятельное выполнение заданий в новой ситуации.

Даётся установка: «Чтобы успешно пересечь линию финиша, каждому нужно успешно решить задания самостоятельной работы».

                                Задание. Найдите значение выражения:

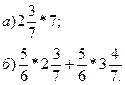
Ответ:17;   5.                                                              

     Задание. Решите уравнение:

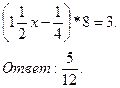
7.     Подведение итогов.

Ø Над чем работали?

Ø Цели достигли?

Ø Выставление оценок.

8.     Домашнее задание:

Ø № 539 (в, г) упростить выражение

Ø № 540 (б) решить уравнение.

 Анкета, которая позволяет осуществить самоанализ, дать качественную и количественную оценку уроку. 

9.     Этап рефлексии.

Ø Перед вами лист настроений.

Ø С каким настроением вы уходите с урока? Поднимите тот смайлик, который соответствует вашему настроению.

 Спасибо за урок! До свидания!                 

Урок математики в 6 классе по теме «Распределительное свойство умножения». Коммуникативные УУД формировались через обсуждение проблем, которые возникали в ходе выполнения заданий. Формирование познавательных действий, определяющих умение ученика выделять тип задач и способы их решения: ученикам предлагается ряд задач, в котором необходимо найти схему, отображающую логические отношения между известными данными и искомыми. Предметом ориентировки и целью решения математической задачи становится не конкретный результат, а установление логических отношений между данными и искомыми, что обеспечивает успешное усвоение общего способа решения задач. В процессе вычислений, измерений, поиска решения задач у учеников формируются основные мыслительные операции (анализа, синтеза, классификации, сравнения, аналогии и т.д.), умения различать обоснованные и необоснованные суждения, обосновывать этапы решения учебной задачи, производить анализ и преобразование информации (используя при решении самых разных математических задач простейшие предметные, знаковые, графические модели, таблицы, диаграммы, строя и преобразовывая их в соответствии с содержанием задания). Коммуникативные действия, которые обеспечивают возможности сотрудничества учеников: умение слушать и понимать партнера, планировать и согласованно выполнять совместную деятельность, распределять роли, взаимно контролировать действия друг друга и уметь договариваться. В процессе изучения математики осуществляется знакомство с математическим языком, формируются речевые умения: дети учатся высказывать суждения с использованием математических терминов и понятий, формулировать вопросы и ответы в ходе выполнения задания, доказательства верности или неверности выполненного действия, обосновывают этапы решения учебной задачи. Работая в соответствии с инструкциями к заданиям учебника, дети учатся работать в парах, выполняя заданные в учебнике проекты в малых группах.  Формирование регулятивных действий - действий контроля: приемы самопроверки и взаимопроверки заданий. В процессе работы ребёнок учится самостоятельно определять цель своей деятельности, планировать её, самостоятельно двигаться по заданному плану, оценивать и корректировать полученный результат.  Личностные действия: Самостоятельно определять и высказывать самые простые общие для всех людей правила поведения при общении и сотрудничестве (этические нормы общения и сотрудничества).