Урок по алгебре "Квадратичная функция"

Тема: «Функции у=х²,  у=ах² и их графики»

Класс: 8А

Цель: систематизация знаний по теме: «Функции у=х²,  у=ах² и их графики»

Задачи:

 1. Образовательная: обобщение способов построения и работы с графиками функций у=х² и у=ах²; закрепление умения свободно владеть основными понятиями данной темы; формирование  навыков использования полученных ранее знаний на практике;

2. Воспитательная: формирование навыков самоконтроля и взаимоконтроля; воспитание аккуратности при выполнении заданий;

3. Развивающая: развитие логического мышления, сообразительности, наблюдательности, внимания.

Оборудование: экран, компьютер, мультимедийный проектор, карточки, записи примеров на доске, учебник алгебры под редакцией А.Г.Мордковича.

Тип урока: урок-смотр знаний.

Используемые технологии: ИКТ, проблемное обучение, здоровьесберегающие, работа в парах, игровые.

Предварительная подготовка к уроку: учащиеся должны знать следующие темы: «Функция у=х²», «Функция у=ах²», уметь работать с графиками таких функций.

Ход урока:

1.       Организационный момент (1-2м)

(Приветствие, сообщение темы и целей урока, запись темы в тетрадь).

2.     Устная работа (слайд 1) (3-4м)

 (Цель: развитие логического мышления, внимательности, наблюдательности,  воспитание чувства прекрасного, постановка проблемы).

-Ребята, посмотрите на слайд и отгадайте загадку. Картинки будут вашими помощниками. Будьте внимательны и наблюдательны!

-Ребята, о каком графике    говорится в загадке? Контуры какого графика напоминают  картинки? (Парабола).

-Графиком какой функции является парабола? (у=х²)

3.Повторение. Работа по готовым слайдам (4-5м)

(Цель: повторение свойств функции у=х², отработка умений учащихся работать с графиком, умение  читать график, находить решение уравнения)  2 слайд

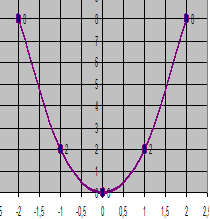
           1.Определите вершину параболы. (0;0)

                                        2. На каком промежутке функция возрастает? ()

                                             3. На каком промежутке функция убывает?

                                            4.Что в данном графике является осью симметрии

                                                             параболы? (ось ординат)

                                            5.Какой функцией задан график?(у=2х²)

3 слайд. Реши графически уравнение:  -х²=2х-3

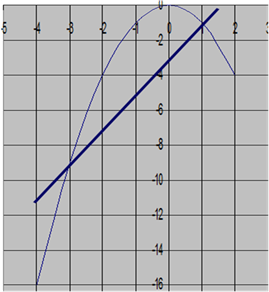
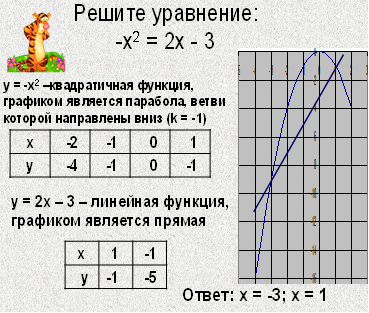
4. Выполнение заданий (15-20 мин) (Цель: применение знаний на практике, воспитание аккуратности при оформлении).

Задания на доске.

1.                                                                                                                                     Не строя графика функции у=х², определите, какие из  перечисленных точек ему принадлежат: А(1;6), В(-2;4), С(-4;16).

Решение:  А(1;6), х=1,у=6

                               у=х², х²=1, следовательно А (1;6) не принадлежит графику у= х².

         и  т.д (В (-2;4), С (-4;16).

2.                                                                                                                                     Определите, является ли функция у=-    или  у=3х²  (на  выбор) убывающей или возрастающей на: а) отрезке[-3; 0]

b) на полуинтервале (-1; 0,5]

Решение: составим таблицу для графика функции у=-

Построим график функции:

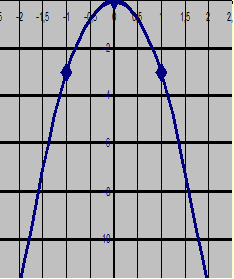1.                                                                                                                                                                                      

2.                                                                                                                                       

Ответ:  на отрезке[-3; 0] функция у=-  возрастает, т.е. является  возрастающей;

на полуинтервале (-1; 0,5]   функция у=-  не  является ни возрастающей,  ни убывающей.

3.                                                                                                         Записать по три функции, где ветви параболы направлены вниз, и где направлены вверх (Примеры: у= -3х², у=-х²,у=-1,5 х²; у=5х², у=0,5х², у=2х²). Из них определить и подчеркнуть разными линиями: функции которые  получаются растяжением вдоль оси ОУ, и функции которые получаются  сжатием вдоль оси ОУ?

5. Физкультминутка (1 мин)

 (Цель: снятие напряжения мышц тела, отдых для глаз, двигательная активность- здоровьесбережение)

-Ребята поиграем, изображая  функции согласно требованиям. Встали из-за парт. Я называю функции, а вы, если ветви параболы направлены вверх, поднимает руки вверх, если ветви направлены вниз -опускаете руки вниз, а если графиком является не парабола, то поворачивает туловище вправо-влево, руки вниз.

Функции: у=х² ,у=- х², у=3х, у=4х² , у=-5х, у=0,5х² ,  у=-3х, у=2х², у=-6 х², у= 12х-3.

6. Самостоятельная работа (7 мин)  Работа в парах по карточкам

(Цель: контроль умения правильно определять координаты точек, через которые проходит парабола, и зеркально отражать их относительно оси ординат, формирование умения работать в парах, воспитание чувства ответственности)

Ребята, сейчас вы работаете самостоятельно в парах по карточкам: 1 Задание -заполнить пропуски. 2 Задание- нужно дорисовать графики из заданных промежутков, не составляя таблицы. Если вопросов нет, приступили к работе.

Карточка:

1.                                                                                                          Заполните пропуски в предложениях:

-график функции у =3 х² получается … (растяжением) графика функции у= х² от оси Ох вдоль оси Оу в 3 раза;

- график функции у=0,5 х² получается … (сжатием) графика функции у= х² от оси Ох вдоль  оси Оу в 2 раза.

- при а, ветви параболы направлены …( вверх)

-при а, ветви параболы направлены … (вниз).

    2.  На карточке  изображены части графиков функций:     у= х² на  ;    у= -2х² на  ;

  у= -0,5 х² на. Необходимо, не составляя таблицы значений, дорисовать графики.

Решение: так как   графики функций у= х² и у=а х²   симметричны относительно оси ординат, то можно дорисовать графики, зеркально отражая значения координат парабол относительно оси ОУ.

3.Построить график функции у= 2х²

7. Проверка самостоятельной  работы по правильным ответам на слайдах (2 мин)  

 Ребята , внимание на слайды-здесь даны ответы к самостоятельной работе, проверьте у себя работы и исправьте ошибки (оценка «5»  за правильно выполненные задания).

8. Итоги, домашнее задание (3-4 мин)

-Когда значение функции у=а х² равно нулю? (при х=0)

-Когда функция у=а х² принимает только отрицательные значения? (при а<0).

-Относительно какой оси симметрична парабола у=а х²? (оси ординат).

-Когда функция у=а х² принимает только положительные значения? (при а>0)

Домашнее задание: №17.12 (в, г), №17.13 (в, г), №17.14  стр. 98-99. Учебник алгебра   под  редакцией   А.Г. Мордковича. Создать по желанию иллюстрацию из графиков   параболы.