В помощь учителю на уроках русского языка

Тема 1: Сложение и вычитание
в пределах 100

Урок 1
Числа 10, 20, 30, … , 100

Цели урока: познакомить учащихся с чтением и записью двузначных чисел, которые оканчиваются нулем; закреплять навыки решения задач; развивать логическое и пространственное мышление; воспитывать интерес к изучению математики.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Улицы Цветочного города проходят по сторонам большого и маленького треугольников. Сколько маршрутов связывают пункты А и В этого города?

2. Назовите сначала однозначные числа, а затем двузначные: 9, 11, 7, 20, 1, 90, 5, 4, 8.

– Какие цифры использованы для записи этих чисел?

– Сколько разных цифр?

3. Заполните таблицу:

4. Сравните тексты задач. Чем они похожи? Чем отличаются? Можно ли утверждать, что решения этих задач будут одинаковыми?

1) Возле дома росло 7 яблонь и 3 вишни. Сколько фруктовых деревьев росло возле дома?

2) Возле дома росло 7 яблонь, 3 вишни и 2 берёзы. Сколько фруктовых деревьев росло возле дома?

· На какие из вопросов вы сможете ответить, пользуясь условием второй задачи:

1. На сколько больше было яблонь, чем вишен?

2. На сколько меньше было берёз, чем яблонь?

3. Сколько всего деревьев росло возле дома?

4. Сколько ёлок росло возле дома?

III. Сообщение темы урока.

– Рассмотрите ряды чисел, записанные на доске:

а) 15, 30, 18, 12, 14;

б) 17, 13, 19, 40, 14.

– Назовите в каждом ряду «лишнее» число.

– Объясните, как вы рассуждали.

– Чем похожи числа 30 и 40?

– Сегодня на уроке мы научимся читать и записывать двузначные числа, которые оканчиваются нулем.

IV. Работа по теме урока.

1. Знакомство с новым материалом.

– Вы уже умеете читать и записывать числа от 0 до 20. Сегодня мы познакомимся с некоторыми двузначными числами, которые больше 20.

Один десяток называют словом «десять». Название числа 20 образуется из двух слов: «два» и «дцать». Слово «дцать» – означает «десять». Два десятка – двадцать, три десятка – тридцать, четыре десятка – сорок, пять десятков – пятьдесят, шесть десятков – шестьдесят, семь десятков – семьдесят, восемь десятков – восемьдесят, девять десятков – девяносто, десять десятков – сто.

Вы, наверное, заметили, что названия всех вышеперечисленных чисел, кроме трех (сорок, девяносто и сто), образуются одинаково: сначала называется число десятков, а затем добавляется слово «дцать». Названия чисел «сорок», «девяносто» и «сто» нужно просто запомнить. Число «сто» часто называют и другим словом – сотня.

Давайте прочитаем записи (буква «д» означает «десяток»).

Я начинаю: 5 д. – пятьдесят,

    6 д. – шестьдесят,

    2 д. – …, 8 д. – …, 7 д. – …, 4 д. – …, 9 д. – …, 10 д. – … .

– Как же эти числа записать цифрами? А так: букву «д» заменим цифрой «нуль». Получаются следующие записи (учитель демонстрирует карточки, учащиеся называют число и записывают его на доске с помощью цифр).

2. Первичное закрепление материала. Работа с учебником.

Задание № 1 (с. 4).

– Прочитайте текст на с. 4.

– Давайте запомним, как читаются и записываются самые «трудные» числа. Посмотрите на первый рисунок. Прочитайте, что написано на карточке, которую держит гусеница.

– Рассмотрите карточку, которую держит журавль. Прочитайте число.

– Прочитайте число, которое держит цыпленок.

Задание № 2 (с. 5).

– Очень часто в жизни предметы приходится считать десятками (если предметов много).

– Какие предметы считают десятками? (Яйца, пуговицы.)

– Рассмотрите рисунки, изображенные на с. 5. Что интересного вы заметили? (Предметы нарисованы группами: морковка, редиска, луковицы связаны в пучки по 10 штук; краски, карандаши, яйца упакованы в коробки по 10 штук; пуговицы прикреплены на картонках по 10 штук.)

– Пересчитайте предметы в каждой группе.

– Какой способ счета вы выбрали? (Счет лучше вести не по одному предмету, а сразу десятками: 1 дес., 2 дес., 3 дес. и т. д. Считаем морковку: один десяток, два десятка. Морковок двадцать.)

Задание № 3 (с. 5).

Задание выполняется с использованием карточек с цифрами. Выкладывание чисел    у учащихся не вызывает затруднений.

– Следующее число – восемьдесят. Это восемь десятков. Какие карточки нам понадобятся? (Карточки с цифрами 8 и 0.)

На доске:  

Задание № 4 (с. 6).

Учащиеся работают с калькулятором: последовательно вводят числа, при этом все цифры в записи каждого числа набираются по порядку слева направо. Перед вводом нового числа нужно напомнить детям о необходимости использования клавиши сброса, иначе на экране останется предыдущее число.

V. Повторение пройденного материала.

1. Работа с учебником.

Задание № 11 (с. 8).

Задание направлено на проверку знания таблицы сложения и вычитания в пределах 1-го десятка.

Задание № 12 (с. 8).

– Прочитайте условие задачи.

– Какие числа входят в условие задачи?

– Что они обозначают?

– Выделите и прочитайте только условие задачи.

– Прочитайте только вопрос.

– Запишите решение и ответ задачи.

Запись: 3 + 9 = 12 (об.) – всего.

– Измените текст задачи: замените слово «несколько» числом 9.

2. Работа в печатной тетради № 1.

Задание № 1.

Прежде чем учащиеся приступят к выполнению заданий, учитель должен обратить их внимание на образец, который представлен в задании.

VI. Итог урока.

– Что нового узнали на уроке?

– Как записать цифрами числа 2-го десятка, 4-го десятка?

– Чтение каких двузначных «круглых» чисел надо запомнить?

Домашнее задание: № 17 (учебник, с. 9); № 2 (рабочая тетрадь).

 

Урок 2
Числа 10, 20, 30, …, 100

Цели урока: показать учащимся способ изображения двузначных чисел с помощью цветных палочек; продолжить работу по формированию навыка чтения двузначных чисел, оканчивающихся нулем; совершенствовать умения составлять и решать задачи; развивать умение анализировать и сравнивать.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Расставьте числа в пустые клетки квадрата так, чтобы по всем направлениям сумма чисел была равна 15.

2. Разгадайте, как связаны числа и рисунки, и запишите верные равенства:

3. Назовите признаки, по которым изменяются фигуры в каждом ряду.

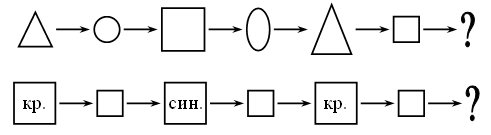
– Выберите фигуру, которой можно продолжить каждый ряд.

4. Решите задачу.

Мальвина загадывала Буратино и Пьеро загадки.

Буратино отгадал 5 загадок, а Пьеро – 12. Кто отгадал загадок больше и на сколько?

– Сколько всего загадок отгадали Буратино и Пьеро?

III. Сообщение темы урока.

– Сегодня на уроке мы продолжим знакомство с чтением и записью чисел вида 10, 20, 30, … , 100.

IV. Работа по теме урока.

Задание № 5 (с. 6).

Это одно из первых заданий, направленных на запоминание последовательности «круглых» чисел в пределах 100.

С целью самопроверки учитель предлагает учащимся открывать карточки с числами в числовом ряду: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100.

Задание № 6 (с. 6).

– Прочитайте числа, записанные в каждом ряду.

– Что их объединяет?

– Разгадайте правило, по которому записан каждый числовой ряд,  и назовите следующие три числа.

Запись:

а) 100, 90, 80, 70, 60, 50. (Каждое следующее число уменьшается на 1 десяток.)

б) 10, 30, 50, 70, 90, 110. (Каждое следующее число увеличивается на 2 десятка.)

Задание № 7 (с. 6).

Учащиеся читают загадки, отгадывают их. Записывают в тетрадь числа из текста: 100, 70, 40.

   

V. Повторение пройденного материала.

1. Работа по учебнику.

Задание № 13.

– Прочитайте задачу.

– Что означают числа 3 и 4?

– Прочитайте вопрос.

– Что сказано о желтых шарах?

– Составьте вопрос со словом «сколько». (Сколько всего шариков купили детям?)

– Какое действие надо выполнить? (3 + 4 = 7.)

Задание № 14.

– Какое действие надо выполнить, чтобы узнать, «на сколько больше (меньше)»? (Вычитание; 12 – 8 = 4.)

Задание № 15.

– Прочитайте текст и рассмотрите иллюстрацию.

– Сформулируйте условие задачи. (У Доктора Айболита было 11 градусников. 3 градусника он поставил больным. Сколько градусников осталось у Айболита?)

– Запишите решение этой задачи. (11 – 3 = 8.)

– Больше или меньше градусников поставил Айболит больным, чем у него было первоначально и чем у него осталось потом?

– Можно ли выяснить на сколько?

– Сформулируйте новые задачи.

– Решите новые задачи.

– Сравните их решения. (Задачи решаются вычитанием.)

2. Работа в печатной тетради № 1.

Задание № 3.

Упражнение выполняется в том случае, если на каждой парте есть хотя бы по одному калькулятору. Вначале надо проверить, все ли дети включили калькуляторы. Далее последовательно вводятся числа, при этом все цифры в записи каждого числа набираются по порядку слева направо. Перед вводом нового числа нужно напомнить детям о необходимости использования клавиши сброса, иначе на экране останется предыдущее число.

VI. Итог урока.

– Что нового узнали на уроке?

– Какие знания необходимы при чтении и записи двузначных чисел, которые оканчиваются нулем?

– Как ответить на вопрос: «На сколько больше (меньше)?»

Домашнее задание: № 16 (учебник, с. 9); № 4 (рабочая тетрадь).

Урок 3
Числа 10, 20, 30, … , 100. Решение задач

Цели урока: совершенствовать навык чтения и записи двузначных чисел, оканчивающихся нулем; закреплять знания о геометрических телах (кубе, пирамиде, шаре); продолжить работу по формированию умений составлять задачи по иллюстрации; развивать пространственное мышление и умение рассуждать.

Ход урока

I. Организационный момент.

II. Устный счёт.

1. Сколько отрезков вы видите на каждом рисунке?

2. Что изменяется? Разгадайте правило.

– Продолжите рисунок.

3. Имя какого сказочного героя здесь зашифровано?

 

4. Решите задачу.

У Доктора Айболита на дне рождения было 12 зверей и 7 птиц. Сколько гостей было на дне рождения Айболита?

5. У кого масса больше – у зайца или у белки?

III. Сообщение темы урока.

– Рассмотрите схему на доске:

– Можно ли по данной схеме составить задачу?

– Составьте задачу.

– Сегодня на уроке будем составлять и решать задачи.

IV. Работа над новым материалом.

Задание № 8 (с. 7).

При решении задачи учащиеся могут рассуждать примерно так: «Три десятка банок – это тридцать банок, значит, во всех коробках тридцать банок».

Можно задать детям дополнительный вопрос: «Сколько коробок заполнили банками с консервами?»

В ходе обсуждения этого вопроса учащиеся должны понять, что ответ зависит не только от того, сколько банок во всех коробках, но и от того, сколько банок в каждой коробке. Если в каждой коробке 10 банок (см. рисунок к задаче), то коробок всего 3.

А если в каждой коробке, например, 6 банок, то, выполнив деление (с помощью фишек), ученики убедятся, что в этом случае коробок будет 5.

Делаем вывод: чтобы ответить на поставленный вопрос, надо знать, сколько банок положили в каждую коробку.

Задание № 9 (с. 7).

Запись: 70 пуговиц – 7 д.

Задание № 10 (с. 7).

– Рассмотрите рисунки на с. 7 учебника.

– Какие числа держит Заяц? А какие – Волк?

– Сравните эти числа. Чем они отличаются?

– Сколько знаков (цифр) в записи чисел у Зайца?

– Сколько знаков (цифр) в записи чисел у Волка?

– Объясните, какие числа называют однозначными, а какие – двузначными.

– Кто держит однозначные числа? (Заяц.)

– Как называются числа, которые держит Волк? (Двузначные.)

V. Повторение пройденного материала.

1. Работа по учебнику.

Задание № 18 (с. 9).

– Что такое «разность» чисел?

– Подберите несколько пар чисел, разность которых равна 6.

Запись:

Задание № 19 (с. 9).

– Прочитайте задание и выполните рисунок к тексту.

Рисунок:

– Сколько семян положили в каждый пакетик? (3.)

– Сколько семян в двух пакетиках? (3 + 3 = 6.)

Задание № 20 (с. 10).

– Какие виды часов изображены здесь? (Ручные, башенные, будильник.)

Так как второклассники умеют определять время только с точностью до часа, то вполне достаточно, если на поставленный вопрос будут даваться следующие ответы:

– Ручные часы показывают больше 4 часов.

– Время на башенных часах больше 12 часов, но меньше 1 часа.

– Будильник показывает время меньше, чем 7 часов.

Подготовленные учащиеся могут дать и более точные ответы.

Задание № 21 (с. 10).

Перед выполнением этого задания учащиеся вспоминают названия геометрических тел, с которыми они познакомились в 1 классе. (Куб, шар, цилиндр, конус, пирамида.)

– Рассмотрите изображенные в учебнике предметы. Какую форму они имеют?

· Форму цилиндра имеют консервная банка и ножка гриба.

· Форму конуса имеют соломенная шляпка и шляпка гриба.

· Форму куба имеет торт.

· Форму пирамиды имеет коробка для подарка.

· Форму шара имеют апельсин и глобус.

Задание № 23 (с. 10).

– Какие фигуры (предметы) являются симметричными? (При мысленном перегибании по оси симметрии получившиеся две части предмета (фигуры) накладываются друг на друга и их контуры совпадают.)

– Какие фигуры на рисунке можно назвать симметричными? (Квадраты.)

– Проверьте свое предположение, перенеся рисунки на кальку.

2. Работа в печатной тетради № 1.

Задание № 6.

– Рассмотрите данную иллюстрацию. Что вы узнали?

(Из рисунка и записи под ним видно, что Мишка надул 6 мыльных пузырей, а Поросенок – на 5 пузырей больше.)

– Какие вопросы можно задать к этому условию? (Сколько пузырей надул Поросенок? Сколько пузырей надули Мишка и Поросенок вместе?)

Далее учитель разбирает с учащимися решение обеих задач. В тетрадь записывают решение простой задачи.

VI. Итог урока.

– Что нового узнали на уроке?

– Какие числа называют однозначными? Двузначными?

– Как можно рационально сосчитать большое количество предметов?

– Какие геометрические тела вы знаете?

– Какие фигуры называют симметричными?

Домашнее задание: № 22 (учебник, с. 10); № 5 (рабочая тетрадь).

 

Справочный материал для учителя

Шар

Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии, не большем данного, от данной точки. Эта точка называется центром шара, а данное расстояние – радиусом шара.

Граница шара называется шаровой поверхностью, или сферой. Таким образом, точками сферы являются все те точки шара, которые удалены от центра на расстояние, равное радиусу.

Любой отрезок, соединяющий центр шара с точкой шаровой поверхности, также называется радиусом.

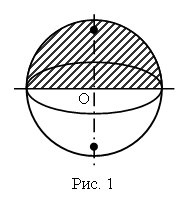
Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром. Концы любого диаметра называются диаметрально противоположными точками шара.

Шар так же, как цилиндр и конус, является телом вращения. Он получается при вращении полукруга вокруг его диаметра как оси (рис. 1).

Многогранник

Многогранником называется тело, ограниченное конечным числом плоскостей. Граница многогранника называется его поверхностью (рис. 2).

Многогранник называется выпуклым, если он лежит по одну сторону от каждой из ограничивающих плоскостей. Общая часть поверхности выпуклого многогранника и ограничивающей его плоскости называется гранью. Стороны граней многогранника называются ребрами, а вершины – вершинами многогранника.

Поясним данное определение на примере знакомого вам куба (рис. 3). Куб есть выпуклый многогранник. Его поверхность состоит из шести квадратов: ABCD, BEFC, ... . Они являются его гранями. Ребрами куба являются стороны этих квадратов АВ, ВС, BE, ... .

Вершинами куба являются вершины квадратов А, В, С, D, Е, ... . У куба шесть граней, двенадцать ребер и восемь вершин.

Призма

Призмой называется многогранник, образованный заключенными между двумя параллельными плоскостями отрезками всех параллельных прямых, которые пересекают плоский многоугольник в одной из плоскостей. Грани призмы, лежащие в этих плоскостях, называются основаниями призмы. Другие грани называются боковыми гранями. Все боковые грани – параллелограммы. Ребра призмы, соединяющие вершины оснований, называются боковыми ребрами. Все боковые ребра призмы параллельны.

Высотой призмы называется расстояние между плоскостями ее оснований. Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю призмы. Диагональным сечением призмы называется сечение плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани. Призма называется прямой, если все боковые грани составляют с основаниями прямые двугранные углы.

Если основание призмы есть параллелограмм, то она называется параллелепипедом. У параллелепипеда все грани – параллелограммы. На рисунке 4а изображен наклонный параллелепипед, а на рисунке 4б – прямой параллелепипед.

Правильные многогранники

Выпуклый многогранник называется правильным, если его грани являются правильными многоугольниками с одним и тем же числом сторон и в каждой вершине многогранника сходится одно и то же число ребер.

Существует пять типов правильных выпуклых многогранников (рис. 5): правильный тетраэдр, куб, октаэдр, додекаэдр, икосаэдр.

У правильного тетраэдра грани – правильные треугольники; в каждой вершине сходится по три ребра. Тетраэдр представляет собой треугольную пирамиду, у которой все ребра равны.

У куба все грани – квадраты; в каждой вершине сходится по три ребра. Куб представляет собой прямоугольный параллелепипед с равными ребрами.

У октаэдра грани – правильные треугольники, но в отличие от тетраэдра в каждой его вершине сходится по четыре ребра.

У додекаэдра грани – правильные пятиугольники. В каждой вершине сходится по три ребра.

У икосаэдра грани – правильные треугольники, но в отличие от тетраэдра и октаэдра в каждой вершине сходится по пять ребер.

 

 

 

 

Урок 4
Двузначные числа и их запись

Цели урока: рассмотреть изображение двузначных чисел с помощью цветных палочек; закреплять навыки сложения и вычитания чисел в пределах 20; совершенствовать навык счёта в пределах 100; развивать логическое мышление и умение анализировать.

Ход урока

I. Организационный момент.

II. Устный счёт.

1. Сколько всего отрезков на чертеже?

2. Являются ли эти квадраты «магическими»?

3. Решите задачу.

Дети были на экскурсии в музее. На первом этаже они осмотрели 6 витрин, а на втором – на 5 витрин больше. Сколько витрин осмотрели дети на втором этаже?

4. Задание на смекалку.

Таня разложила елочные шары в три одинаковые коробки. В одну коробку она положила красные шары, в другую – голубые, а в третью – и те, и другие. Заклеила, и когда стала их надписывать, то перепутала все коробки.

Догадайтесь, какие шары лежат в каждой коробке, если в коробке с надписью «Красные шары» лежат голубые.

III. Сообщение темы урока.

– Сегодня на уроке мы научимся записывать двузначные числа, количество единиц которых не равно нулю.

IV. Знакомство с новым материалом.

Задание № 1 (с. 11).

– Рассмотрите рисунок на с. 11 учебника: Волк и Заяц собирают урожай гороха.

– Сколько горошин в каждом стручке держит Волк? (Десять.)

– А сколько у Волка стручков? (Два стручка, значит, два десятка горошин.)

– Сколько горошин в стручке у Зайца? (Пять горошин, или пять единиц.)

– Сколько всего горошин у Волка и Зайца? (2 десятка и 5 единиц.)

– Прочитайте, что написано в учебнике.

– С такими записями, как 2 д. 5 ед., мы еще не встречались. Сегодня мы научимся читать и записывать такие числа цифрами.

– Прочитайте число 2 д. 5 ед. (два десятка пять единиц) по-другому: сначала назовите число, выраженное первой цифрой и буквой «д», получится «двадцать», а затем число, выраженное второй цифрой, получится «пять». Итак, число 2 д. 5 ед. читается так: «двадцать пять». А как его записать цифрами?

– Посмотрите: на доске составлена запись этого числа с помощью карточек:

Сейчас я уберу буквы, а цифры придвину одна к другой. Получилась запись: 25.

Записи «25» и «2 д. 5 ед.» являются разными обозначениями одного и того же числа – «двадцать пять».

Если переставить цифры, то получится совсем другое число – «52» (пятьдесят два), в нем 5 десятков 2 единицы. Поэтому при записи двузначного числа его цифры располагают в строго определенном порядке: первая цифра слева – это десятки, а вторая – единицы.

В числе «шестьдесят» содержится 6 десятков 0 единиц. Поэтому его записывают так: 60.

Любое двузначное число можно изобразить с помощью цветных палочек. Возьмите из набора одну оранжевую палочку и положите ее перед собой. Поставьте на нее в ряд столько белых палочек, сколько поместится. Сколько белых палочек поместилось на одной оранжевой палочке? (Десять.) Давайте договоримся число десятков в числе обозначать оранжевыми палочками, а число единиц – белыми палочками. Палочки мы будем выкладывать вплотную одна к другой.

– Посмотрите на рисунок в учебнике; скажите, как изображено число 25 с помощью палочек: сколько палочек каждого цвета? Объясните, почему понадобилось именно столько оранжевых и белых палочек.

– Сколько и каких палочек надо взять, чтобы изобразить числа 16, 61, 40, 4? С какой стороны (слева или справа) вы будете выкладывать оранжевые палочки; белые палочки?

Итак, запомним: изображая десятки, выкладываем оранжевые палочки слева; изображая единицы, выкладываем белые палочки слева (вслед за оранжевыми).

Задание № 2 (с. 11).

Учащиеся называют числа по порядку.

а) 31, 32, 33, 34, 35, … , 50 (прямой счет);

б) 80, 79, 78, 77, 76, 75, 74, 73, 72, 71, 70 (обратный счет).

– Как составлен первый числовой ряд? Второй числовой ряд?

Задание № 3 (с. 12).

Задание очень важно с методической точки зрения. В ходе его выполнения дети учатся «выкладывать» числа с помощью цветных палочек, а это умение – одно из ключевых при изучении письменных приемов сложения и вычитания натуральных чисел в пределах 100.

Рассмотрим на примере случая 1, как учащиеся должны рассуждать.

Прочитав фразу, они прежде всего называют числа, которые встретились в этом предложении (три, тринадцать и тридцать один).

Затем последовательно «выкладываем» каждое число.

В числе «три» – три единицы, значит, для «выкладывания» этого числа нужны три белые палочки:

В числе «тринадцать» – один десяток и три единицы, значит, потребуется одна оранжевая палочка и три белые. Сначала кладем оранжевую палочку, а затем белые:

В числе «тридцать один» – три десятка и одна единица, значит, «выложить» это число можно так:

Аналогично ученики рассуждают и при рассмотрении случая 2.

V. Повторение пройденного материала.

1. Работа с учебником.

Задание № 11 (с. 13).

Учащиеся выполняют вычисления, используя знание таблицы сложения и вычитания чисел в пределах 20.

Задание № 12 (с. 13).

– Какое арифметическое действие необходимо выполнить при нахождении значения суммы чисел?

– А какое при нахождении значения разности чисел?

– Значение суммы каких чисел будет равно значению разности этих чисел? (12 + 0 = 12 – 0.)

– Объясните почему.

2. Работа в печатной тетради № 1.

Задание № 7.

Учитель должен обратить внимание учащихся на предложенные образцы.

Запись:

Задание № 8.

Учащиеся работают самостоятельно.

Взаимопроверка в парах.

3. Работа по карточкам.

Задание № 1.

Разгадайте правило, по которому составлены схемы, и вставьте пропущенные числа.

Задание № 2.

Вставьте пропущенные знаки действий, чтобы получились верные равенства.

VI. Итог урока.

– Что нового узнали на уроке?

– Какие числа называют однозначными?

– Какие называют двузначными?

Домашнее задание: № 13, 14 (учебник); № 9, 10 (рабочая тетрадь).

 

 

 

 

 

 

 

 

 

Урок 5
Двузначные числа и их запись

Цели урока: продолжить формирование навыка чтения и записи двузначных чисел; познакомить учащихся с правилами работы на калькуляторе; составить алгоритм набора двузначного числа на калькуляторе; учить выделять симметричные фигуры и строить оси симметрии; совершенствовать вычислительные навыки; развивать умение анализировать и обобщать.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Рассмотрите чертеж и выпишите названия всех треугольников.

2. Отгадайте, какое слово зашифровано.

 

3. Решите задачу.

Кролик разбил свой огород на грядки: 4 грядки для моркови, 7 грядок для капусты и 2 грядки для репы. Сколько грядок на огороде Кролика?

4. Чему равна масса арбуза? Чему равна масса дыни?

 

III. Сообщение темы урока.

– Из чисел 2, 4, и 5 составьте и запишите все возможные двузначные числа.

Запись: 22, 24, 25, 44, 42, 45, 55, 52, 54.

– Прочитайте полученные числа.

– Сегодня на уроке продолжим учиться читать и записывать двузначные числа.

IV. Работа над новым материалом.

Задание № 4 (с. 12).

– Вспомните правила чтения двузначных чисел.

– Прочитайте числа в задании.

Задание № 5 (с. 12).

Учащиеся вводят на калькуляторе данные числа.

– Как включить калькулятор?

– Как правильно набрать на калькуляторе двузначное число?

– Какая кнопка выполняет команду «сброс»?

Задание № 6 (с. 12).

Учащиеся выполняют алгоритм сложения на калькуляторе.

V. Повторение пройденного материала.

1. Работа с учебником.

Задание № 17 (с. 14).

Измерения учащиеся выполняют непосредственно на рисунках в учебнике.

Высота катушки – 3 см.

Длина магнитофонной кассеты – 7 см, ширина – 4 см.

Задание № 18 (с. 14).

– Какие фигуры являются симметричными?

– Рассмотрите таблицу на доске и назовите симметричные фигуры. (Только фигуры 3, 5.)

– Рассмотрите рисунок в учебнике и найдите в нем симметричные фигуры.

Далее учащиеся работают с квадратами, вырезанными из цветной бумаги (квадраты заранее готовятся дома).

– Определите, есть ли оси симметрии у квадрата.

– Если квадрат «перегнуть» по данной прямой, то части, на которые эта прямая разбивает квадрат, совпадут. Эта прямая – ось симметрии квадрата.

– Проведите еще ось симметрии квадрата.

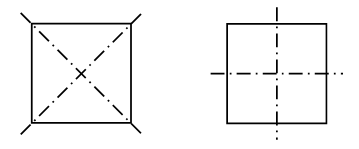
– Сколько осей симметрии у квадрата? Начертите квадрат в тетради и покажите все оси симметрии.

– Проверьте свой ответ на вырезанных квадратах, согнув по этим прямым.

– Какие фигуры в учебнике имеют оси симметрии?

– На рисунке изображены три предмета. У платка треугольной формы одна ось симметрии. У салфетки, имеющей форму квадрата, четыре оси симметрии. Угольник не имеет оси симметрии.

– Почему платок треугольной формы имеет ось симметрии, а угольник (тоже треугольной формы) не имеет оси симметрии? (Платок имеет форму равнобедренного треугольника.)

Задание № 19 (с. 14).

– Прочитайте задачу.

– Что известно? Что требуется узнать?

– Запишите кратко условие задачи и решите ее.

Решение:

6 – 2 = 4 (ст.)

Ответ: 4 столбика.

Задание № 21 (с. 15).

– Прочитайте условие задачи.

– Что известно? Что требуется узнать?

Решение:

15 – 6 = 9 (шт.)

Ответ: на 9 баклажанов купили меньше.

2. Работа в печатной тетради № 1.

Задание № 11.

При выполнении второй части задания учащиеся должны воспользоваться одним из двух правил сравнения натуральных чисел, изученных еще в 1 классе: «Из двух чисел меньше то, которое называют при счете раньше, и больше то, которое называют при счете позже». Это правило автоматически переносится на новую область натуральных чисел (от 20 до 100). Сложность заключается в том, что ряд чисел, из которого надо выбрать большее и меньшее числа, записан в обратном порядке, поэтому первое число в ряду (84) будет наибольшим, а последнее (79) – наименьшим.

Задание № 12.

Учащиеся работают самостоятельно. Далее учитель проводит проверку.

– Докажите, что вы верно провели стрелки.

С этой целью ученики устно называют по порядку все натуральные числа в выбранном промежутке. Если среди этих чисел будет названо число и на номерке, то соответствующая стрелка проведена правильно.

Задание № 13.

Для решения этой задачи в качестве модели (вместо фишек) можно использовать цветные палочки.

По условию задачи папа нашел 3 десятка грибов, а Алеша – 8 грибов. Выложим с помощью цветных палочек эти числа.

Так как в задаче спрашивается, сколько всего грибов принесли домой папа и Алеша, значит, надо сложить (сдвинуть на модели) эти числа:

Получилось число, в котором 3 десятка (3 оранжевые палочки) и 8 единиц (8 белых палочек), – 38. Значит, папа и Алеша принесли домой 38 грибов. В тетради решение задачи записывается так:

Решение:

30 + 8 = 38 (гр.).

Ответ: 38 грибов.

VI. Итог урока.

– Что нового вы узнали на уроке?

– Какие фигуры называют симметричными?

– Что такое ось симметрии?

Домашнее задание: № 18 (учебник); № 14 (рабочая тетрадь).

 

Урок 6
Двузначные числа и их запись

Цели урока: познакомить учащихся с римскими цифрами; совершенствовать вычислительные навыки; продолжить формирование умений строить и читать математические графы; рассмотреть решение задачи разными способами; развивать умение сравнивать и рассуждать.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Сколько всего отрезков на чертеже?

2. Помогите Незнайке найти ошибки.

3. У кого масса меньше – у собаки или у кошки?

4. Решите задачу.

На свой день рождения Мальвина испекла пирожки и положила их на тарелку. После того как все гости взяли по одному пирожку, на тарелке осталось 8 пирожков. Сколько гостей пригласила Мальвина, если на тарелке было 17 пирожков?

III. Сообщение темы урока.

– Сегодня на уроке узнаем, как люди научились записывать числа.

IV. Работа над новым материалом.

– Какие числа называются однозначными? Двузначными?

– Назовите разряды двузначного числа.

Задание № 10 (с. 13).

– Какие двузначные числа можно записать цифрами 0, 2 и 4, если цифры в записи числа не повторяются?

Запись: 20, 40, 24, 42.

– Что такое цифра? Что такое число?

– Сколько цифр вы знаете?

– Сколько чисел в математике? Можете ли вы назвать наибольшее число?

Задание № 11 (с. 13).

– С помощью каких цифр можно записать все возможные двузначные числа?

Запись: 55, 51, 11, 15.

Задание № 16 (с. 14).

Запись: 10, 20, 30, 40, 50, 60, 70, 80, 90.

15, 25, 35, 45, 55, 65, 75, 85, 95.

– Почему количество чисел в этих числовых рядах совпадает?

V. Путешествие в прошлое. Знакомство с римскими цифрами.

Как люди научились записывать числа

– Сегодня мы отправимся в путешествие в Древний Египет, Индию, Вавилон и узнаем, как записывали цифры и числа разные народы. Очень разные и даже забавные были эти «цифры».
В Древнем Египте, например, числа первого десятка записывались соответствующим количеством палочек: ÷ – 1, ÷÷ – 2 и т. д. Десять обозначали в виде подковы –  Чтобы записать число 15, нужно было поставить одну подкову и пять палочек:

В Индии за две тысячи лет до начала нашего летосчисления появился ноль. Его обозначили так же, как и сейчас. Но ведь мы уже привыкли к нему, а тогда это было великим открытием. Назывался он в то время просто кружком. А в Древней Индии кружок – сунья. Арабы перевели это слово как цифр. Не правда ли, напоминает что-то?

Правильно! Цифр – цифра. Так уж получилось, что арабским именем нуля стали называть все остальные знаки. Все они теперь цифры: и 0 – цифра, и 5 – цифра, и 9 – цифра. А само слово ноль возникло позже от латинского nullum – ничто.

После того как был создан алфавит, во многих странах числа стали записывать с помощью букв. В Древней Греции и Древней Руси к буквам добавляли еще специальные знаки, чтобы не путать их с обычными буквами.

Немало различных способов записи чисел было создано людьми. В Древней Руси числа обозначали буквами с особым знаком «~» (титло), который писали над буквой.

Первые девять букв алфавита обозначали единицы, следующие девять букв – десятки, а последние девять букв – сотни. Число десять тысяч называли словом «тьма» (и теперь мы говорим: «народу – тьма тьмущая»).

Современная достаточно простая и удобная десятичная система записи чисел была заимствована европейцами у арабов, которые, в свою очередь, переняли ее у индусов. Поэтому цифры, которыми мы сейчас пользуемся, европейцы называют «арабскими», а арабы – «индийскими». Эта система была введена в Европе примерно в 1120 году английским ученым-путешественником Аделардом. К 1600 году она была принята в большинстве стран мира.

Русские названия чисел тесно связаны с десятичной системой счисления. Например, семнадцать означает «семь на десять», семьдесят – «семь десятков», а семьсот – «семь сотен».

Однако и эта система оказалась очень громоздкой.

Всем с детства знакома римская нумерация. Чаще всего римские цифры встречаются на циферблате в часах:

До сих пор используются римские цифры, которые употреблялись в Древнем Риме уже около 2500 лет тому назад.

I – 1, V – 5, X –10, L – 50, G – 100, D – 500, M – 1000

Остальные числа записываются этими же цифрами с применением сложения и вычитания. Так, например, число XXVII означает 27, так как 10 + 10 + 5 + 1 + 1 = 27.

Если меньшая по значению цифра (I, X, С) стоит перед большей, то ее значение вычитается.

Например: IV означает 4 (5 – 1 = 4), IX означает 9 (10 – 1 = 9). ХС означает 90. Таким образом, число MCMLXXXIX означает 1989, так как:

1000 + (1000 – 100) + 50 + 10 + 10 + 10 + (10 – 1) = 1989.

В настоящее время римские цифры обычно применяются при нумерации глав и разделов книги, месяцев года, для обозначений дат значительных событий, годовщин.

Для вычислений запись чисел с помощью римских цифр неудобна. В этом вы можете убедиться сами, если попробуете выполнить, например, сложение чисел CCXCVII и XLIX или деление числа CCXCVII на число IX.

Большим достижением стало введение нуля, который позволил при записи чисел указывать пропущенный разряд. Способ записи любого числа с использованием всего только десяти цифр 1 2 3 4 5 6 7 8 9 0 был изобретен в Индии. Эта система оказалась настолько простой и удобной, что быстро распространилась по всем странам, а так как распространяли ее именно арабы, а не индусы, то эти цифры мы стали называть арабскими.

VI. Повторение пройденного материала.

1. Работа по учебнику.

Задание № 22 (с. 15).

– Прочитайте текст. Можно ли его назвать задачей? Почему? (Нет вопросов.)

– Придумайте несколько вопросов, чтобы получились разные задачи.

Варианты вопросов:

· Сколько получили бронзовых медалей?

· Сколько всего получили медалей?

· На сколько золотых медалей получили больше, чем серебряных? И т. д.

Далее необходимо разобрать и решить полученные задачи.

Запись:

Задание № 24 (с. 16).

– Прочитайте задание.

– Рассмотрите иллюстрацию. Что вы видите на рисунке?

– Сколько тарелок?

– Сравните число яблок на одной тарелке с числом яблок на другой. Сколько их на каждой тарелке?

– Составьте по рисунку задачу на сложение. (Сколько всего яблок на четырех тарелках, если на каждой лежит по 6 яблок?)

– Составьте по рисунку задачу на вычитание. (Было 24 яблока, съели 6 яблок. Сколько яблок осталось?)

Далее переходим к составлению задачи на умножение, например: мама разложила на 4 тарелках по 6 яблок. Сколько всего яблок разложила мама по тарелкам?

Задача решается с помощью фишек. Ее решение записывается в тетрадь:

Теперь можно переходить к составлению задачи на деление. Здесь могут быть два варианта:

1. Раскладываем 24 яблока на 4 тарелки поровну. Надо найти, сколько яблок оказалось на каждой тарелке.

2. Раскладываем 24 яблока на тарелки по 6 штук на каждую. Надо найти, сколько тарелок потребуется.

И в том и в другом случае задача решается действием деления. Желательно рассмотреть с детьми оба варианта: сначала решить практически эти задачи на фишках, а затем записать решение в тетрадь.

Задание № 26 (с. 16).

– Какую фигуру называют треугольником?

– Сколько треугольников на каждом рисунке?

Задание № 27 (с. 16).

– Какие следующие три числа надо записать в данном числовом ряду?

5, 10, 15, 20, … , … , … .

– Сравните каждые два соседних числа. (Закономерность: каждое следующее число на 5 больше предыдущего, поэтому дальше будут следовать числа: 25, 30, 35.)

Задание № 28 (с. 16).

– Прочитайте условие задачи.

– Мог ли остаться хоть один большой конверт без марки?

– Мог ли остаться хоть один маленький конверт без марки?

– На какие конверты могли наклеить марки? Рассмотрите все варианты.

2. Работа в печатной тетради № 1.

Задание № 17.

Все стрелки графа должны удовлетворять следующим условиям:

1) Выходить из точки, соответствующей числу 40;

2) Быть либо красным (если 40 больше числа, к которому ведет стрелка), либо синим (если 40 меньше числа, к которому ведет стрелка).

Граф должен выглядеть так:

– Прочитайте все полученные высказывания.

Таких высказываний должно быть 6:

1) сорок больше четырех;

2) сорок меньше ста (десяти десятков);

3) сорок больше двадцати;

4) сорок меньше шестидесяти;

5) сорок больше тридцати (трех десятков);

6) сорок больше нуля.

Задание № 16.

Вероятнее всего, учащиеся предложат решать задачу более длинным путем, который естественно вытекает из ее условия:

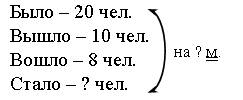
Решение:

1) Сколько пассажиров осталось в автобусе после того, как вышли 10 человек?

20 – 10 = 10 (чел.).

2) Сколько пассажиров стало в автобусе после того, как вошли 8 человек?

10 + 8 = 18 (чел.).

3) На сколько человек уменьшилось число пассажиров автобуса?

20 – 18 = 2 (чел.).

Этот способ решения учитель разбирает с учащимися устно, затем проводит беседу:

– Сколько человек вышло на остановке? (10 чел.)

– А сколько вошло? (8 чел.)

– Уменьшилось или увеличилось число пассажиров автобуса? (Уменьшилось.)

– На сколько человек меньше вошло, чем вышло?

– Является ли ответ на этот вопрос ответом на вопрос задачи?

– Как же решить эту задачу проще?

Решение:

10 – 8 = 2 (чел.).

Ответ: на 2 человека меньше.

– Есть ли в этой задаче лишнее данное? (20 пассажиров было в автобусе.)

Задание № 18.

Учащиеся решают задачу самостоятельно.

Решение:

7 – 5 = 2 (п.).

Ответ: на 2 пчелы стало больше.

– Есть ли в этой задаче лишнее данное? (Нет.)

– Сравните эту задачу с задачей № 16.

VII. Итог урока.

– Что нового узнали на уроке?

– Какие правила чтения математических графов вы знаете?

– Как люди научились записывать числа?

Домашнее задание: № 21, 23 (учебник); № 15 (рабочая тетрадь).

 

 

 

 

Урок 7
Луч и его обозначение

Цели урока: познакомить учащихся с понятием луча как бесконечной фигуры; учить показывать луч с помощью указки; продолжить формирование вычислительных навыков; совершенствовать умение решать задачи; закреплять навыки работы с математическими графами; развивать умение анализировать и обобщать.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Прочитайте числа и назовите «лишнее» число в каждом ряду:

а) 90, 30, 40, 51, 60;

б) 88, 64, 55, 11, 77, 33;

в) 47, 27, 87, 74, 97, 17.

2. Заполните цепочки примеров:

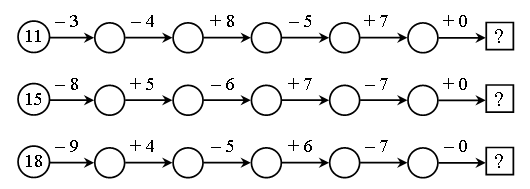
3. Назовите числа по порядку:

а) от 20 до 30;

б) от 46 до 57;

в) от 75 до 84.

4. Как вы думаете, будут ли эти тексты задачами?

– Измените вопрос второго текста так, чтобы он стал задачей. (Сколько всего цветов росло на клумбе?)

– Измените условие так, чтобы текст стал задачей. (На клумбе росло 5 красных тюльпанов и 3 желтых тюльпана.)

– Решите полученные задачи. (5 + 3 = 8.)

III. Сообщение темы урока.

– Рассмотрите геометрические фигуры. Назовите известные вам фигуры.

– Название какой геометрической фигуры вы не знаете?

– Сегодня мы ответим на этот вопрос.

IV. Работа над новым материалом.

– Мы часто слышим и произносим слово «луч». Лучом мы обычно называем полоску яркого света, который идет от светящегося предмета. Это, например, луч фонарика, луч солнца.

Словом «луч» называют и геометрическую фигуру. Это очень интересная фигура: у нее есть начало и нет конца.

А изображают ее так. Отметим на доске точку, приложим к ней линейку и по линейке проведем линию.

Какой бы длинной ни была линейка, весь луч мы все равно не сможем начертить. На рисунке мы изобразили лишь часть луча, которая показывает направление луча.

Луч можно начертить в любом направлении. На рисунке изображено 5 лучей разных направлений:

Чтобы отличать один луч от другого, договоримся обозначать луч двумя буквами латинского алфавита. Писать буквы нужно в строго определенном порядке: первой пишется та буква, которая обозначает начало луча, вторая пишется над или под лучом. Посмотрите на рисунок в учебнике. Луч красного цвета обозначен двумя буквами. Какой буквой обозначено начало луча? (Латинской заглавной буквой А.)

– Прочитаем все вместе запись: «Луч АВ».

– Теперь прочитайте следующие записи, называя при этом начало луча: луч ВС, луч МК, луч ВА, луч ОХ.

Важно научиться правильно показывать луч. Мы будем это делать концом указки или карандаша.

Посмотрите на доску. Прочитайте название луча, который изображен. (МК.)

Смотрите внимательно: я беру указку; нахожу начало луча – точку М; веду указкой по лучу, прохожу нарисованную часть луча; не останавливаясь, веду указкой дальше, пока не кончится доска, веду указкой еще дальше (ведь луч бесконечен!). Можно остановиться, а луч «проходит» стену, «идет» в соседний класс, «выходит» во двор школы и «идет» дальше.

Теперь посмотрите на плакат (подготавливается заранее). На нем изображены три луча. Прочитайте название каждого из них. Называя луч, показывайте его указкой.

Задание № 1 (с. 17).

Учащиеся рассматривают рисунки и читают текст задания.

– Можно ли нарисовать весь луч?

– В каком направлении можно начертить луч?

Задание № 2 (с. 18).

Учащиеся называют каждый луч, читая сначала букву, соответствующую началу луча. (Луч АМ, луч КО, луч DЕ.)

Связывание понятия луча с направлением движения помогает детям лучше осознать бесконечность этой геометрической фигуры.

Задание № 3 (с. 18).

Учащиеся чертят в тетради луч, обозначают его буквами.

– Поставьте в тетради точку. Проведите через нее прямую линию. Сколько получилось лучей? (Два луча: ОА, ОВ.)

– Проведите еще одну прямую линию через эту точку. Сколько теперь лучей? (Четыре луча: ОА, ОВ, ОD, OC.)

– Подумайте: чем луч отличается от прямой линии?

V. Повторение пройденного материала.

1. Работа в печатной тетради № 1.

Задание № 19.

– Назовите номера фигур, которые являются лучами. (1, 3, 6.)

– Как называется фигура под номером 2? (Отрезок.)

– Кто уже знает, как называется фигура под номером 4? (Прямая.) Под номером 5? (Прямоугольник.)

Задание № 20.

Направления движения машин задаются лучами. Начало каждого луча уже изображено на рисунке, поэтому учащимся нужно лишь достроить лучи.

Задание № 21.

Лучей с началом в точке А можно построить сколько угодно.

2. Работа по учебнику.

Задание № 9 (с. 19).

– Прочитайте, какие способы сложения придумал Знайка.

– Найдите результаты сложения такими же способами.

Запись:

После завершения работы над заданием надо обратить внимание учащихся на то, что рассмотренный прием вычисления они могут использовать в дальнейшем для восстановления в памяти забытых табличных случаев сложения и вычитания.

Задание № 10 (с. 19).

– Чем похожи все записи? (Два действия, есть скобки.)

– Какое действие надо выполнить сначала? (Первое действие в скобках.)

– Чем похожи и чем различаются записи в каждом столбике? (Используются одинаковые числа, но выполняются разные арифметические действия.)

– Вычислите результаты действий.

Задание № 12 (с. 20).

Необходимо повторить с учащимися правило чтения высказываний, изображенных с помощью графа:

1) синяя стрелка заменяет слово «меньше», а красная – слово «больше»;

2) в паре первым читается то число, от которого идет стрелка, а вторым – то, к которому идет стрелка;

3) по графу можно прочитать ровно столько высказываний, сколько на нем изображено стрелок.

Далее учащиеся читают высказывания по первому графу:

· Двадцать меньше сорока.

· Сорок меньше шестидесяти.

· Двадцать меньше шестидесяти.

Учащиеся читают высказывания по второму графу:

· Тридцать пять больше шестнадцати.

· Девяносто больше тридцати пяти.

· Девяносто больше семидесяти восьми.

· Девяносто больше шестнадцати.

· Семьдесят восемь больше тридцати пяти.

· Семьдесят восемь больше шестнадцати.

Задание № 14 (с. 20).

Задачу можно решить с помощью фишек.

VI. Итог урока.

– Что нового узнали на уроке?

– Что такое луч?

– Как начертить луч?

– Сколько лучей можно провести через одну точку?

Домашнее задание: № 11, 15 (учебник); № 22 (рабочая тетрадь).

Урок 8
Луч и его обозначение

Цели урока: продолжить знакомство с геометрической фигурой – лучом; научить изображать луч с помощью линейки и обозначать луч буквами; совершенствовать вычислительные навыки и умение решать задачи; развивать логическое и пространственное мышление.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Соедините линией примеры с одинаковыми ответами:

2. Сравните числа первой строки.

– Сравните числа второй строки.

– Сравните пары чисел, записанных друг под другом.

– Сколько разных цифр используется для записи этих чисел?

– Сколько всего чисел записано?

3. Решите задачу.

Для растопки печки брат принес 8 поленьев, а сестра – 5. Отец принес столько поленьев, сколько брат и сестра вместе. Сколько поленьев принес отец?

4. Треугольник разрезали так, как показано на рисунках. Какие фигуры можно составить из полученных частей?

III. Сообщение темы урока.

– Сегодня на уроке будем учиться изображать геометрическую фигуру луч с помощью линейки.

IV. Работа над новым материалом.

– Какую геометрическую фигуру называют лучом?

– Как обозначить луч на чертеже?

– Прочитайте названия лучей, данных на доске.

– Чем они похожи? Чем отличаются?

Задание № 4 (с. 18).

Чертеж:

Задание № 5 (с. 18).

– Рассмотрите чертежи.

– Назовите геометрические фигуры, которые здесь изображены. (Точки, отрезок, лучи.)

– Назовите точки, которые лежат на луче АВ. (Точки А, М, В, Е.)

– Назовите точки, которые не лежат на этом луче. (D, C, F.)

Затруднение у учащихся могут вызвать точки D и Е. Учащиеся знают, что луч – бесконечная фигура, поэтому изобразить полностью любой луч на рисунке невозможно. Точка D расположена за началом луча, следовательно, не может лежать на луче. А вот для выяснения вопроса о том, лежит ли точка Е на луче, удобнее всего воспользоваться линейкой. Если расположить линейку так, как показано на рисунке, то становится видно, что точка Е лежит на луче.

Задание № 6 (с. 18).

Чертежи:

– Волк и Заяц тоже выполнили это задание. Рассмотрите их чертежи. Кто из них прав? Объясните свой ответ.

– Какие ошибки у них допущены?

V. Повторение пройденного материала.

1. Работа в печатной тетради № 1.

Задание № 23.

Направления движения Маши и Миши задаются лучами. Общее начало этих двух лучей изображено на рисунке точкой. Так как Маша и Миша пошли в противоположных направлениях, то для построения сразу обоих лучей удобно линейку расположить так:

Задание № 25.

Скорее всего, дети предложат следующие решения:

Можно дать дополнительное задание, направленное на выявление глубины усвоения материала: «Волк и Заяц тоже выполнили это задание. Рассмотрите чертежи. Справились ли с заданием Волк и Заяц? Свой ответ поясните».

(Чертежи заранее делаются учителем.)

Если у учащихся правильно сформировано представление о луче, то они увидят, что с заданием справился только Заяц.

2. Работа по учебнику.

Задание № 13 (с. 20).

– Вспомните правила построения графа.

Решение:

Задание № 16 (с. 21).

– Прочитайте задачу.

– Что известно? Что требуется узнать?

– Как вы думаете, можно ли изменить условие задачи так, чтобы число 6 называлось только один раз?

Новая формулировка задачи: У Бори 6 простых и столько же цветных карандашей. Сколько карандашей у Бори?

– Запишите решение новой задачи.

Задание № 19 (с. 21).

– Прочитайте условие задачи.

– Что известно? Что требуется узнать?

– Используя цветные палочки, решите эту задачу.

Рассуждение: «По условию задачи Братец Кролик посадил 2 десятка семян моркови и 3 десятка семян редиса. Выложим с помощью цветных палочек эти числа:

Так как в задаче спрашивается, сколько морковок и редисок надеется собрать Братец Кролик, надо сложить (сдвинуть на модели) эти числа:

Получилось число, в котором 5 десятков (5 оранжевых палочек), – это 50. Значит, Братец Кролик надеется собрать 50 морковок и редисок».

В тетради запишем решение задачи:

20 + 30 = 50 (к.).

Ответ: 50 корнеплодов.

– Прочитайте еще раз вопрос задачи.

– Как вы думаете, почему в вопросе задачи используется слово «надеется»?

– Можем ли мы точно утверждать, что Братец Кролик осенью соберет ровно 50 морковок и редисок? Почему?

– Скорее всего, он соберет меньше 50 морковок и редисок или ровно 50?

– Можем ли мы точно утверждать, что Братец Кролик не соберет больше 50 морковок и редисок. Почему?

Справочный материал для учителя

Понятие числового луча вводится после того, как дети освоят чтение и запись двузначных чисел. С помощью числового луча учащиеся осваивают еще один способ сравнения двузначных чисел: чем левее точка расположена на числовом луче, тем ее координата меньше; чем правее, тем ее координата больше.

Числовой луч в математике часто называют координатным лучом. Эти термины являются синонимами. Во 2 классе в активный словарь учащихся вводятся термины: числовой луч, начало луча, единичный отрезок, координата точки (без определений), а также используются обозначения числового луча и координаты точки.

Дети должны понять, что единичный отрезок – это отрезок, длина которого равна условно выбранной единице, начало луча обозначается точкой О, а сам числовой луч – буквами ОХ (читается: луч О – икс); координата точки записывается числом, заключенным в скобки; например, запись А(3) читается так: «Точка А с координатой три, или координата точки А равна трем. Координата точки О считается равной нулю, координата любой точки, отмеченной на луче, – это ее расстояние в единичных отрезках от начала луча (точки О)».

Луч обозначают двумя буквами латинского алфавита, записывая их в строго определенном порядке: первой пишут букву, обозначающую начало луча. Так как у луча нет конца, то вторая буква не обозначает никакой точки луча и ее пишут над или под лучом в любом месте.

Например, на рисунке изображен луч СМ, точка С – начало луча.

Точка X лежит на луче АВ, а точка Y на нем не лежит. В этом легко убедиться, приложив линейку к лучу АВ.

Многоугольником называют часть плоскости, ограниченную замкнутой ломаной линией, состоящей из конечного числа отрезков, вместе с этой ломаной. Отрезки ломаной называют сторонами многоугольника.

На рисунке изображен многоугольник МАВКСЕ. Читать обозначение многоугольника можно, начиная с любой его вершины и в любом направлении.

VI. Итог урока.

– Что нового узнали на уроке?

– Назовите признаки луча.

Домашнее задание: № 17, 18 (учебник); № 24 (рабочая тетрадь).

 

 

 

 

 

 

 

 

 

 

 

Урок 9
Луч и его обозначение

Цели урока: продолжить формирование навыка изображения луча с помощью линейки и обозначения луча буквами; сравнить геометрические фигуры луч и отрезок; совершенствовать навыки решения задач разными способами; рассмотреть объемные тела: куб, цилиндр, конус; развивать умение сравнивать и рассуждать.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Сколько всего отрезков на чертеже?

2. Разгадайте закономерность и заполните пустые «окошки».

3. Решите задачу.

Фокусник достал из волшебной шляпы 3 голубей, 7 сорок и 2 попугайчиков. Сколько птиц вытащил фокусник из волшебной шляпы?

4. Нарисуйте девятую фигуру, используя существующую закономерность.

III. Сообщение темы урока.

– Рассмотрите чертежи на доске:

– Какое изображение будет «лишним»? Почему?

– Как называется первая фигура? (Отрезок.)

– Как называется последняя фигура? (Луч.)

– Сегодня на уроке проведем сравнение этих фигур.

IV. Работа над новым материалом.

Задание № 7 (с. 19).

– Рассмотрите чертежи.

– Что объединяет все фигуры? (Это геометрические фигуры.)

– Найдите на рисунке лучи и назовите их. (CD, OE.)

– Что такое луч?

– Как правильно прочитать луч?

– Как называются остальные фигуры на рисунке? (Отрезки.)

– Что такое отрезок?

– Чем отличается луч от отрезка?

Задание № 8 (с. 19).

Чертежи:

а) отрезок лежит на луче:

б) отрезок пересекает луч:

в) отрезок не пересекает луч:

V. Повторение пройденного материала.

1. Работа по учебнику.

Задание № 20 (с. 22).

– Прочитайте условие задачи.

– Что известно в задаче? Что надо узнать?

– Запишите кратко условие задачи и решите ее.

Запись:

Было – 15 д.

Ушли – ? д., 5 д. и 3 д.

Осталось – ? д.

Решение:

Задание № 22 (с. 22).

– Сколько в коробке было цветных карандашей?

– Сколько простых?

– Сколько взяли из коробки карандашей?

– Какие же могли быть эти карандаши?

Учащиеся заполняют таблицу:

Задание № 23 (с. 22).

Решение:

Чтобы распилить на 4 части, надо сделать 3 распила.

Чтобы распилить на 6 частей, надо сделать 5 распилов.

2. Работа в печатной тетради № 1.

Задание № 27.

– Прочитайте текст.

– Является ли этот текст задачей? Почему?

– Какие вопросы можно поставить к этому условию?

Варианты вопросов:

· Сколько цветных снимков сделал фотограф?

· Сколько всего снимков сделал фотограф?

Далее устно разбирается план решения обеих задач.

В тетрадь учащиеся записывают решение своей задачи.

Задание № 28.

– Из каких чисел состоит данный ряд? (Только из «круглых» чисел.)

– Вставьте пропущенные числа. (30, 60, 70, 90.)

Наименьшим в этом ряду является число 10 (его первым называют при счете, следовательно, именно это число надо обвести синим карандашом), а наибольшим – 100 (его последним называют при счете, следовательно, именно это число надо обвести красным карандашом).

Задание № 29.

– Прочитайте задачу.

– Какие цветы у Вали? (Гвоздики.)

– Сколько у нее гвоздик? (7 гвоздик.)

– Какие цветы у ее брата? (Розы.)

– Что сказано о розах в условии задачи? («Столько же роз».)

– Сколько же роз у брата?

Далее учащиеся заполняют таблицу:

Решают задачу учащиеся самостоятельно.

3. Работа по карточкам.

– Рассмотрите чертежи. Что объединяет эти фигуры? (Это объемные фигуры, геометрические тела.)

– Как они называются? (Цилиндр, конус, куб.)

– Какими линиями на чертеже показывают невидимые элементы геометрических тел? (Штриховой линией.)

Для того чтобы учащимся легче было справиться с заданием, учитель может поставить перед ними модели цилиндра, конуса и куба. Непосредственно сравнивая модель каждой фигуры с ее изображением, учащиеся выделяют видимые и невидимые элементы каждого объемного тела и отражают свои наблюдения на чертеже.

VI. Итог урока.

– Что нового узнали на уроке?

– Чем отличается луч от отрезка?

– Назовите геометрические тела.

– Как на чертеже геометрических тел показать невидимые линии?

Домашнее задание: № 21 (учебник); № 26 (рабочая тетрадь).

 

Справочный материал для учителя

Пирамида

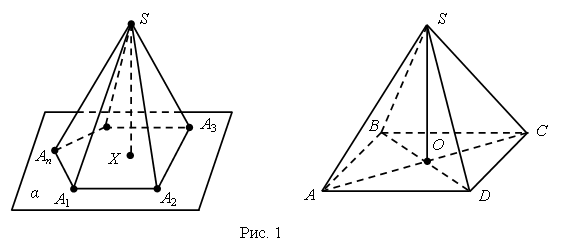
Пирамидой называется многогранник, образованный всеми отрезками, соединяющими данную точку – вершину пирамиды – с точками плоского многоугольника – основания пирамиды. Поверхность пирамиды состоит из основания и боковых граней. Каждая боковая грань – треугольник. Одной из его вершин является вершина пирамиды, а противолежащей ей стороной – сторона основания пирамиды. Боковыми ребрами пирамиды называются ребра, соединяющие вершину пирамиды с вершинами основания. Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания.

На рисунке 1 изображена пирамида. Ее основанием является многоугольник А₁А₂ ... А_n, вершина пирамиды – S, боковые ребра – SA₁, SA₂, … , SA_n, высота пирамиды – SX. Пирамида называется п-угольной, если в ее основании лежит п-угольник. Треугольная пирамида называется также тетраэдром.

Цилиндр

Цилиндром (точнее круговым цилиндром) называется тело, образованное заключенными между двумя параллельными плоскостями отрезками всех параллельных прямых, пересекающих круг в одной из плоскостей. Отрезки с одним концом на окружности этого круга называются образующими цилиндра.

Поверхность цилиндра состоит из оснований цилиндра – двух равных кругов, лежащих в параллельных плоскостях, и боковой поверхности.

Цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований. В дальнейшем мы будем рассматривать только прямой цилиндр, называя его для краткости просто цилиндром.

На рисунке 2 изображен прямой цилиндр. Он образован отрезками XX' параллельных прямых, заключенными между параллельными плоскостями α и α'. Его основаниями являются круги К и К' в этих плоскостях.

Прямой цилиндр можно рассматривать как тело, полученное при вращении прямоугольника вокруг его стороны как оси (рис. 3).

Радиусом цилиндра называется радиус его основания. Высотой цилиндра называется расстояние между плоскостями оснований. Осью цилиндра называется прямая, проходящая через центры оснований. Она параллельна образующим. Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением. Плоскость, проходящая через образующую цилиндра и перпендикулярная осевому сечению, проведенному через эту образующую, называется касательной плоскостью цилиндра.

Конус

Конусом (точнее  круговым конусом) называется тело, образованное всеми отрезками, соединяющими данную точку – вершину конуса – с точками некоторого круга – основания конуса.

Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса. Поверхность конуса состоит из основания и боковой поверхности.

Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания. В дальнейшем мы будем рассматривать только прямой конус, называя его для краткости просто конусом.

На рисунке 4 изображен прямой конус. Его вершиной является точка S, а основанием – круг К в плоскости α. Конус образован всеми отрезками SX, соединяющими вершину S с точками X основания.

Прямой конус можно рассматривать как тело, полученное при вращении прямоугольного треугольника вокруг его катета как оси (рис. 5).

Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. У прямого конуса основание высоты совпадает с центром основания. Осью прямого конуса называется прямая, содержащая его высоту. Сечение конуса плоскостью, проходящей через его ось, называется осевым сечением. Плоскость, проходящая через образующую конуса и перпендикулярная осевому сечению, проведенному через эту образующую, называется касательной плоскостью конуса.

Урок 10
Числовой луч

Цели урока: познакомить учащихся с понятием «числовой луч»; ввести понятие о единичном отрезке на числовом луче; совершенствовать навыки составления и решения задач; продолжить работу с математическими графами; развивать логическое мышление и умение рассуждать.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Найдите примеры с ответом 12.

Запись:

2. В каждой строке вместо точек вставьте недостающие фигуры, сохранив порядок их чередования.

3. Из 9 счетных палочек составьте 5 треугольников. Сверьте с образцом.

III. Сообщение темы урока.

– Рассмотрите рисунок на доске.

– Как называются эти геометрические фигуры?

– Название какой фигуры вы не знаете?

– Сегодня на уроке мы научимся строить эту фигуру и узнаем, как ее называют.

IV. Работа над новым материалом.

На прошлых уроках вы познакомились с лучом, научились его изображать, обозначать буквами, читать обозначения. Посмотрите, какой луч изображен на доске, прочитайте его обозначение.

Возьмем линейку со шкалой. Представим себе, что наша линейка, как и луч, бесконечна. Наложим шкалу линейки на луч ОХ так, чтобы начало шкалы 0 (нуль) совместилось с началом луча – точкой О, а шкала с числами расположилась по лучу ОХ:

Упростим рисунок: снимем изображение линейки и миллиметровые деления, оставив лишь числа 0, 1, 2, 3, ...

Получим луч, который называют числовым лучом. На числовом луче обычно рисуют стрелку (справа). Отрезок от 0 до 1 называют единичным отрезком. Единичный отрезок может быть любой длины.

Числовой луч

Задание № 1 (с. 23).

– Рассмотрите числовой луч, изображенный в учебнике. Что вы видите?

– Где растет цветок? (В точке О.)

– Точку О называют началом числового луча.

– Какой жук сидит дальше от цветка? (Красный жук сидит в точке 1, а синий в точке 3, т. е. синий жук сидит на расстоянии трех единичных отрезков от начала луча. Значит, синий жук сидит дальше от цветка.)

– Что находится в точке 5? (Большой камень.)

Задание № 2 (с. 23).

Учащиеся работают с линейкой.

– Положите перед собой линейку. Рассмотрите ее шкалу.

– Покажите штрих с числом, которое обозначает начало отсчета. (Точка 0.)

– Какое самое большое число написано на шкале линейки?

– Покажите отрезок шкалы от 0 до 1, от 1 до 2, от 2 до 3 и так далее до конца шкалы.

Задание № 3 (с. 23).

– Что изображено в учебнике?

– Прочитайте название луча. (ОX.)

– Какой буквой обозначено начало луча (начало отсчета)?

– Измерьте длину отрезков между двумя любыми соседними штрихами. (1 см.)

– Сравните длины этих отрезков. (Они равны.)

– Прочитайте определение, данное в книге (с. 24).

V. Повторение пройденного материала.

1. Работа в печатной тетради № 1.

Задание № 38.

– Что изображено на рисунке? (Граф отношений «меньше» и граф отношений «больше».)

– Какие правила помогут вам прочитать данные высказывания о числах?

– Прочитайте все высказывания о числах на первом графе.

· Число 21 меньше числа 65.

· Число 65 меньше числа 70.

– Каких стрелок не хватает? Изобразите их и прочитайте высказывания.

– Так как на графе точками отмечены три числа, то каждое из этих чисел должно соединяться синей стрелкой с каждым из двух других. Значит, появляется третье высказывание: число 21 меньше 70.

– Рассмотрите второй граф. Каких стрелок не хватает?

Читаем высказывания:

Задание № 40.

– Рассмотрите данные иллюстрации.

– Что вы узнали по ним?

– Какие задачи можно составить к этим рисункам?

Устно надо разобрать план решения всех составленных задач, но в тетрадь каждый ученик записывает решение той задачи, которую он составил сам.

Варианты составленных задач:

· Мама и сын отдыхали в деревне у бабушки с 3 июня по 9 июня. Сколько дней они отдыхали в деревне?

· Миша и мама отдыхали на море с 10 июня по 15 июня. Сколько дней они были на море?

· Мама и сын сначала отдыхали в деревне, с 3 июня по 9 июня, а потом – на море, с 10 июня по 15 июня. Сколько всего дней они были и в деревне, и на море?

– Где и на сколько дней больше отдыхали мама с сыном?

2. Работа с учебником.

Задание № 10 (с. 26).

Учащиеся записывают выражения с помощью арифметических действий и находят их значения.

Задание № 11 (с. 26).

– Что означают выражения «на 5 больше»?

– «На 5 меньше»? Какие действия надо выполнить?

– Устно ответьте на вопросы.

Задание № 14 (с. 27).

Задание позволяет проверить знание табличных случаев сложения и вычитания и уровень развития логического мышления детей. В первой части задания требуется назвать все возможные варианты решения. Необходимо сказать учащимся, что если они будут хаотично перечислять пары чисел, то могут пропустить какой-нибудь вариант. Нужно прежде всего придумать правило перебора решений, которое исключит вероятность пропуска той или иной пары. Например, будем перебирать по порядку (начиная с наименьшего) возможные варианты первого слагаемого и находить (исходя из условия) второе слагаемое.

– Прочитайте задание. Что известно?

– Сколько вариантов ответа имеет эта задача?

– Как называются числа при сложении?

Учащиеся заполняют таблицу:

Последние 5 решений повторяют первые пять решений, так как слагаемые в суммах одни и те же, но переставлены местами. Значит, в ответе указываем следующие возможные варианты пар: 0 и 9; 1 и 8; 2 и 7; 3 и 6; 4 и 5.

– Прочитайте второе задание.

– Можно ли перечислить все пары чисел, в результате вычитания которых получится 7? (Указать все такие пары невозможно.)

– Как называются числа при вычитании?

Далее учащиеся заполняют таблицу:

VI. Итог урока.

– Что нового узнали на уроке?

– Что такое числовой луч?

– Как обозначают начало луча?

– Что называют единичным отрезком?

Домашнее задание: № 12, 13 (учебник); № 38, 40 (рабочая тетрадь).

Урок 11
Числовой луч

Цели урока: продолжить работу с числовым лучом; ввести понятие «координата точки на луче»; формировать умение строить числовой луч с заданным единичным отрезком; совершенствовать вычислительные навыки; рассмотреть решение задач разными способами; развивать логическое мышление и внимание.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Игра «Веселый счет».

2. Поставьте знак «+» или «–» так, чтобы равенства были верными.

3. Сравните тексты задач. Чем они похожи? Чем отличаются? Решите задачи.

III. Сообщение темы урока.

– Прочитайте данные на доске записи:

– Какие у вас возникли затруднения?

– Сегодня на уроке мы узнаем, что обозначает запись О(3).

IV. Работа над новым материалом.

Задание № 5 (с. 24).

– Что изображено на рисунке?

– Что называют числовым лучом?

– Прочитайте его название. (ОВ.)

– Какие числа соответствуют точкам М, К, А, В? (М – число 2, К – число 5, А – число 6, В – число 9.)

– Как же называются эти числа?

– Итак, координата – это число. Давайте рассмотрим таблицу в учебнике на с. 25. Точка О, ее координата – нуль. Запись О(0) читают так: «Точка О с координатой нуль» или «Точка О имеет координату нуль».

– Прочитайте таблицу до конца.

– Прочитайте записи в таблице: М(2) и А(6).

– Запишите в тетради координаты остальных точек.

Запись: К(5), В(9).

– А теперь научимся изображать числовой луч. Необходимо помнить о том, что числовой луч всегда чертят строго горизонтально в направлении слева направо. Направление надо указывать стрелкой.

Задание № 4 (с. 24).

– Итак, проводим горизонтально луч, обозначим его буквами ОX, указываем направление стрелкой, под точкой О напишем число 0 (нуль).

Далее выбираем единичный отрезок (2 см) и откладываем на луче единичный отрезок. Расставим точки.

– Рассмотрите числовой луч на с. 24.

– Числа можно сравнивать с помощью числового луча. Сравните длины отрезков ОА и ОВ на числовом луче ОX. (Длина отрезка ОА равна 5 единичным отрезкам, а длина отрезка ОВ равна 7 единичным отрезкам. На луче точка А лежит левее точки В, отрезок ОА меньше отрезка ОВ, т. е. 5 меньше 7.)

Задание № 6 (с. 25).

– Рассмотрите рисунок. Прочитайте координаты точек, где сидят улитки. (Точка М с координатой 2; точка К с координатой 6; точка В с координатой 8; точка С с координатой 11.)

– Какая точка находится левее: М(2) или В(8)?

– Какая точка имеет наибольшую координату?

V. Повторение пройденного материала.

1. Работа в печатной тетради № 1.

Задание № 31.

Учитель должен обратить внимание учащихся на то, что единичный отрезок равен 2 клеткам (или 1 см). Значит, чтобы отметить точку С с координатой 3, надо от начала луча отсчитать 3 раза по 2 клетки:

Чертеж:

Задание № 33.

– Рассмотрите верхний числовой луч. Что вы можете о нем сказать? (От начала луча отложены равные по длине отрезки, причем единичный отрезок содержит в себе два таких отрезка.)

– Сколько единичных отрезков укладывается от начала луча до точки А? (6 единичных отрезков, значит, координата точки А равна 6.)

– До точки В? (В(8).)

– До точки С? (С(12).)

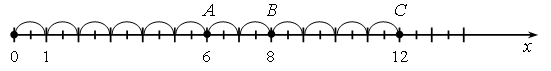
– Рассмотрите нижний числовой луч. Что вы можете о нем сказать? (Здесь изображена часть числового луча, нет точки 0, т. е. начала луча. И не указан единичный отрезок.)

– Как можно восстановить единичный отрезок? (На этом числовом луче отмечены точки Е(45) и А(48). Отрезок между этими точками содержит три единичных отрезка. Разделим длину отрезка ЕА на 3, получим единичный отрезок.)

Чертеж:

2. Работа по учебнику.

Задание № 15 (с. 27).

– Рассмотрите чертеж. Что на нем изображено?

– На какие отрезки разбивает отрезок АВ точка М?

– На какие отрезки разбивает отрезок АВ точка С?

– Сколько всего отрезков на чертеже? (Всего шесть отрезков: АВ, АМ, АС, ВС, ВМ, МС.)

– Из суммы длин каких трех отрезков складывается длина отрезка АВ?

– Длины каких отрезков нам известны?

– Длину какого отрезка надо найти?

– Запишите решение этой задачи.

Решение:

Задание № 16 (с. 27).

– Какое отношение изображено на первом графе? (Отношение «меньше».)

– Прочитайте все высказывания о числах на этом графе. (50 меньше 98; 34 меньше 50; 34 меньше 98; 34 меньше 41; 41 меньше 50; 41 меньше 90.)

– Какое отношение показано на втором графе? (Отношение «больше».)

– Прочитайте все высказывания о числах на этом графе. (Учащиеся должны прочитать шесть высказываний, так как здесь три стрелки и три петли: 78 больше 65; 96 больше 65; 96 больше 78; 78 равно 78; 65 равно 65; 96 равно 96.)

Задание № 19 (с. 28).

– Прочитайте задачу.

– Что известно в задаче? Что надо узнать?

– Запишите кратко условие задачи.

– Какое арифметическое действие надо выбрать, чтобы ответить на вопрос «на сколько меньше»?

– Запишите решение этой задачи.

Задание № 20 (с. 28).

– Прочитайте задачу.

– Сколько грибов нашла Таня? (9 грибов.)

– Что сказано про количество грибов у Лиды? (На 5 грибов меньше, чем Таня.)

– Прочитайте, что требуется узнать.

– Запишите кратко условие задачи и решите ее.

Решение:

1) 9 – 5 = 4 (гр.) – нашла Лида.

2) 9 + 4 = 13 (гр.) – всего.

Ответ: 13 грибов.

VI. Итог урока.

– Что нового узнали на уроке?

– Что называют координатой?

– Как можно сравнивать числа, используя числовой луч?

Домашнее задание: № 17, 18 (учебник); № 31, 33 (рабочая тетрадь).

Урок 12
Числовой луч

Цели урока: закрепить умение чертить числовой луч, выбирать единичный отрезок, отмечать точки с заданными координатами; совершенствовать навык сравнения чисел с использованием числового луча; рассмотреть способы восстановления числового луча; совершенствовать вычислительные навыки; развивать внимание и память.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Какие фигуры были использованы при изображении домика?

2. Расставьте числа 1, 2, 3, 4, 5, 6 так, чтобы сумма чисел вдоль каждой стороны треугольника равнялась 9.

3. Решите задачу.

Оля, Катя и Оксана пошли в кино в платьях разного цвета: желтом, синем и розовом. Оля была не в желтом, Катя – не в желтом и не в розовом. В платье какого цвета была каждая из девочек?

4. Дорисуйте пропущенную фигуру:

III. Сообщение темы урока.

– Сегодня мы будем восстанавливать числовой луч, у которого не отмечен единичный отрезок.

IV. Работа над новым материалом.

Задание № 7 (с. 25).

– Что изображено на чертеже?

– Что называют числовым лучом?

– Чему равен единичный отрезок?

– Что называют координатой точки?

– Определите, какая точка имеет координату 5, 9, 11? (А(5); Е(9); К(11).)

Задание № 8 (с. 25).

Перед выполнением задания учитель просит учащихся внимательно рассмотреть числовой луч. На рисунке изображена та его «часть», на которую не попало начало луча, и, кроме того, не указан единичный отрезок. Чтобы выполнить задание, надо прежде всего выяснить, каков единичный отрезок. Ясно, что между точками (30) и В(31) ровно 1 единичный отрезок. Видно, что между точками А(25) и В(31) 6 таких единичных отрезков, поэтому координаты точек, отмеченных на луче между этими точками, соответственно, 26, 27, 28, 29 и 30.

Задание № 9 (с. 25).

Сложность задания в том, что выполнять его надо без опоры на наглядность, то есть у учащихся не должен быть перед глазами числовой луч с отмеченными на нем точками А, В, С, М и Е. Пользоваться надо правилом сравнения чисел с помощью числового луча.

– Сравните координаты точек, отмеченных Юрой на числовом луче.

– Какая из координат является наименьшей?

– Как расположена на числовом луче точка с этой координатой по отношению к остальным точкам?

– Какая из координат является наибольшей?

– Назовите слева направо все отмеченные на числовом луче точки.

– Какая из точек ближе всех к точке В?

V. Повторение пройденного материала.

1. Работа в печатной тетради № 1.

Задание № 35.

Задание состоит из двух частей. Сначала надо попросить учащихся внимательно рассмотреть все три числовых луча и выбрать тот, на котором можно отметить точки с заданными координатами. Дети должны понимать, что теоретически на любом числовом луче можно отметить точки с любыми координатами, но практически это можно выполнить, лишь изобразив подходящую часть луча. С этой точки зрения среди представленных числовых лучей, безусловно, единственно удобным является нижний луч. Далее можно переходить к выполнению второй части задания. Предложите детям самостоятельно отметить точки с координатами 38, 40 и 44.

Задание № 36.

Между точками с координатами 60 и 61 один единичный отрезок. Если мы будем двигаться влево от точки (60) и последовательно откладывать единичные отрезки, то координаты отмеченных там точек будут таковы: 59, 58 и 57. Двигаясь вправо от точки (61) и также последовательно откладывая единичные отрезки, мы получим такие координаты оставшихся отмеченных точек:

– Что надо определить, прежде чем выполнить построения? (Надо определить единичный отрезок.)

– Сравните единичные отрезки данных числовых лучей.

Задание № 37.

Учащиеся работают самостоятельно.

2. Работа по учебнику.

Задание № 21 (с. 28).

– Прочитайте задачу.

– Что известно в задаче?

– Прочитайте, что требуется найти.

– Все ли числа, необходимые для решения задачи, есть в условии?

– Каким действием можно вычислить возраст кошки Мурки?

– Какие преобразования необходимо выполнить? (1 год = 12 месяцев.)

Решение: 12 – 5 = 7 (м.) – кошке Мурке.

– Изменится ли ответ задачи, если вместо числа 5 в условии будет число 2? (12 – 2 = 10 (м.).)

– Можно ли будет решить задачу, если в условии число 5 заменить числом 14? (Нельзя, так как 12 < 14.)

– Как изменится решение задачи, если слово «моложе» заменить словом «старше»? (Необходимо выполнить сложение.)

Задание № 22 (с. 28).

Учащиеся работают с фишками.

Задание № 23 (с. 29).

Учащиеся записывают выражение к задаче и находят его значение, используя фишки.

Задание № 26 (с. 29).

– Прочитайте задание.

– Что известно про число? (Число меньше 20, значит, в нем будет 1 десяток. А так как единиц на 6 больше, чем десятков, следовательно, 1 + 6 = 7 (ед.). Задуманное число – 17.)

VI. Итог урока.

– Что нового узнали на уроке?

– Как сравнить числа, используя числовой луч?

Домашнее задание: № 24, 25 (учебник).

 

 

 

 

 

 

 

 

 

 

 

Урок 13
Метр. Соотношения между единицами длины

Цели урока: рассмотреть измерения длин и расстояний с помощью измерительных инструментов: линейки, метровой линейки, рулетки; учить сравнивать величины, выраженные в единицах длины; совершенствовать умения решать задачи; развивать внимание и логическое мышление.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Отгадайте, имя какого сказочного героя здесь зашифровано.

 

2. Анализ задач.

Какую из этих задач вы можете решить, а какую – нет? Почему?

а) Таня полила шесть грядок огурцов.

Сколько грядок ей осталось полить?

б) На шахматной доске 20 фигур. Из них 13 черных, остальные – белые. Сколько белых фигур на шахматной доске?

3. Сколькими способами можно прочитать слово «маршрут»?

4. Маша, Оля и Настя заняли призовые места в соревнованиях на коньках. Маша не заняла ни первое, ни второе место. Оля не пришла первой. Какое место заняла каждая из девочек?

III. Сообщение темы урока.

– Мы с вами умеем измерять длины небольших предметов с помощью обычной линейки, получая результаты в сантиметрах. А как быть, если нам надо пойти в магазин и купить отрез ткани на пальто? Неужели продавец будет отмерять ткань такой линеечкой, как наша? Ни один продавец такой линейкой не пользуется, так как в сантиметрах длину большого куска ткани отмерять очень неудобно. Продавцы всегда используют деревянную линейку, которая называется портновским метром.

– Сегодня на уроке мы познакомимся с крупной единицей измерения – метром.

IV. Изучение нового материала.

Метр – это более крупная, чем сантиметр и даже дециметр, единица длины. В метрах измеряют, например, длину куска ткани или обоев, длину и ширину комнаты. При этом, например, для измерения длины комнаты используют рулетку – длинную ленту, свернутую в рулон, на которую нанесена шкала. Рулетки бывают разной длины – метровые, двухметровые, трехметровые, пятиметровые, двадцатиметровые и другие.

– Назовите известные вам единицы измерения длины в порядке их увеличения.

– Как обозначаются сантиметр и дециметр? (См и дм, при этом обозначения записываются без точек в конце.)

– Метр обозначается буквой м (без точки).

– Прочитайте записи на доске:

4 м, 45 м, 4 м 8 дм, 42 м 8 дм 9 см.

– Рассмотрите рисунок в учебнике (с. 30). Какие инструменты для измерения длины здесь изображены? (Ученическая линейка, классная метровая линейка, рулетка.)

– Что вы будете измерять каждым инструментом?

– Прочитайте вслух текст на с. 30.

Задание № 1 (с. 31).

Используя классную метровую линейку, учащиеся заполняют пропуски в таблице соотношений между единицами длины.

Задание № 2 (с. 31).

Учащиеся вслух читают записи.

Задание № 3 (с. 31).

Необходимо закончить фразы, вставив пропущенные единицы длины.

Учащиеся работают самостоятельно. Затем учитель организует проверку.

· Высота дерева 2 м.

· Спортсмены пробежали дистанцию 100 м.

· Длина спички 4 см.

· Школьники приняли участие в заплыве на 50 м.

Задание способствует формированию у учащихся реальных представлений о единицах длины. Поэтому учащиеся не только должны закончить предложение, но и объяснить, почему они выбрали именно эту единицу длины и можно ли ее заменить на какую-нибудь другую.

Задание № 4 (с. 31).

Под руководством учителя дети измеряют свой рост, длину своего шага и записывают в тетрадь результаты измерений.

V. Повторение пройденного материала.

1. Работа в печатной тетради № 1.

Задание № 42.

Так как учащиеся еще незнакомы с символами «>» и «<», то оформить решение они должны так:

Запись: 10 см  меньше  1 м;

                          49 дм  меньше  5 м;

                          80 см  больше  7 дм;

                          5 дм  меньше  60 см.

Задание № 43.

Длина ручки  см. Это  дм  см.

2. Работа по учебнику.

Задание № 10 (с. 32).

Учитель проводит игру «Соревнование».

– Сколько вам удастся решить примеров за одну минуту?

Через минуту учитель определяет победителя игры.

Задание № 13 (с. 33).

– Дополните текст, придумайте вопрос так, чтобы получилась задача.

Для того чтобы предложенный текст превратился в задачу, в случаях 1 и 2 детям необходимо придумать только вопрос. Например, в случае 1 вопросы могут быть такими: «Сколько ключей осталось в связке?», «На сколько меньше ключей отцепили, чем было в связке первоначально?», «На сколько больше ключей осталось в связке, чем отцепили?». Случай 3 принципиально отличается от предыдущих тем, что здесь уже недостаточно придумать только вопрос. Необходимо дополнить и условие, поэтому учащимся предоставляются большие возможности для фантазии. Желательно выслушать и разобрать как можно больше вариантов задач, предложенных детьми, и провести их сравнительный анализ.

Задание № 12 (с. 33).

– Прочитайте задачу.

– Что известно? Что требуется узнать?

– Запишите кратко условие задачи.

Запись:

– Решите задачу по действиям.

VI. Итог урока.

– Что нового узнали на уроке?

– Назовите крупную единицу длины.

– Какие инструменты используют для измерения длины?

Домашнее задание: № 9, 11 (учебник); № 41, 44 (рабочая тетрадь).

Урок 14
Метр. Соотношения между единицами длины

Цели урока: рассмотреть соотношения между единицами длины – метром, дециметром и сантиметром; познакомить учащихся с единицами длины на Руси; совершенствовать вычислительные навыки; формировать навыки решения задач разными способами; развивать умение анализировать.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Решите задачу.

От дома до колодца 20 метров. Сколько метров надо пройти, чтобы принести ведро воды? А кружку воды?

2. Найдите примеры с ответом 13.

3. Решите задачу.

Винни-Пух решил навестить ослика Иа. От дома до моста он прошел 20 метров, по мосту – 10 метров и от моста до домика Иа – еще 10 метров. Какова длина пути, который должен пройти Винни-Пух, чтобы навестить ослика Иа и вернуться домой?

4. Какова масса каждого мешка с мукой?

III. Сообщение темы урока.

– Сегодня мы продолжим работу с единицами длины. Будем решать задачи на определение длины предметов.

IV. Работа над новым материалом.

1. Практическая работа.

– Измерьте длину своей парты. Сколько получилось сантиметров?

– Сколько дециметров?

– Покажите на рулетке отрезок 10 дм.

– Как называется эта единица длины? (1 метр.)

– Как можно начертить отрезок длиной 12 дм?

Варианты выполнения задания:

I вариант – можно отложить 1 дециметр двенадцать раз;

II вариант – можно отложить 1 метр и еще 2 дециметра (так как 12 дм = 1 м 2 дм).

– Какой вариант более рациональный?

2. Работа по учебнику.

Задание № 5 (с. 31).

– Прочитайте задание. Можно ли этот текст назвать задачей?

– Придумайте вопрос задачи.

Варианты вопросов:

· Какова длина всей ленты? (5 + 4 = 9.)

· На сколько метров один кусок длиннее (короче) другого? (5 – 4 = 1.)

Учащиеся объясняют план решения каждой задачи.

Задание № 6 (с. 31).

Это задание развивает глазомер учащихся. На первый взгляд кажется, что жуки находятся на одинаковом расстоянии от финиша. Но это впечатление обманчиво. Выполнив измерения, учащиеся убеждаются, что жук под № 2 ближе к финишу, чем другой участник соревнования.

Задание № 7 (с. 32).

– Прочитайте условие задачи. Что вам известно?

– Какой вопрос можно поставить к данному условию?

Вопросы:

· Чему равна ширина комнаты?

· Чему равен периметр этой комнаты?

Решение:

1) 5 – 2 = 3 (м) – ширина.

2) 5 + 5 + 4 + 4 = 18 (м) – периметр комнаты.

Ответ: 18 м.

Задание № 8 (с. 32).

Сначала лучше разобрать случай 2, так как выполнить это задание можно с опорой на модели. Попросите учащихся положить перед собой оранжевую и белую палочки. Длина оранжевой палочки – 10 см, или 1 дм, а белой – 1 см. Скажите детям, что роль рейки у нас будет играть оранжевая палочка, так как ее длина – 1 дм. Выложим вдоль оранжевой палочки белые палочки. Их получится ровно 10.

5 раз по 2 белые палочки

Так как длина каждой белой палочки – 1 см, то видно, что в оранжевой палочке укладывается 5 раз по 2 см. Следовательно, чтобы получить 1 дм, надо от рейки отмерить 5 раз по 2 см.

Теперь можно переходить к случаю 1. Предложите детям выполнить это задание самостоятельно. Но для того чтобы ученики могли действовать по аналогии со случаем 2, предварительно вспомните с ними, что 1 м – это 10 дм, а 20 см – это 2 дм.

V. Повторение пройденного материала.

1. Работа по учебнику.

Задание № 15 (с. 34).

– Прочитайте задачу.

– Что вам известно? Что требуется узнать?

– Сможете ли вы решить эту задачу? (Это задача с недостающими данными.)

– Как надо изменить условие этой задачи, чтобы она имела решение? (Надо указать либо число подосиновиков, либо число подберезовиков, найденных в лесу.)

– Можно ли выбрать любое число подосиновиков или подберезовиков? (Так как число подберезовиков на 8 больше, чем подосиновиков, то число подосиновиков мы можем выбрать произвольно, а вот число подберезовиков должно быть обязательно больше 8.)

– Верно, если число подберезовиков равно 8, то тогда получается, что подосиновиков не нашли совсем (8 – 8 = 0), а это не соответствует условию задачи. Если же число подберезовиков меньше 8, например 6, то получается, что задача не имеет решения, так как невозможно вычислить число подосиновиков (6 – 8 = ?).

– Придумайте недостающее данное и решите задачу самостоятельно.

2. Путешествие в прошлое.

Как появились меры длины. Как измеряли на Руси

– Нельзя представить себе жизнь человека, не производящего измерений: это и портные, и механики, и обыкновенные школьники. Сегодня мы все знакомы с линейкой, метром. А что же существовало до того, как все это изобрели? Первыми измерительными приборами были части тела: пальцы рук, ладонь, ступня. Так, у древних египтян основной мерой длины служил локоть (расстояние от конца пальцев до согнутого локтя). Он делился на семь ладоней, а ладонь на четыре пальца.

(Учитель показывает, как измеряют локтем длину ленты, а затем предлагает проделать это двум-трем ученикам. Количество локтей получилось разное.)

– Чтобы измерения были более точными и не зависели от роста людей, в Древнем Египте придумали образцовые меры: локоть, ладонь, палец. Теперь было уже неважно, какой длины локоть или ладонь у человека, он измерял не своим, а общим локтем, т. е. условной палочкой. В Англии также существовали единицы длины, связанные с частями тела человека: дюйм (2,54 см) в переводе с голландского означает «большой палец»; фут (30 см 48 мм, или 12 дюймов) в переводе с английского – «нога»; ярд – это расстояние от носа короля Генриха I до конца среднего пальца его вытянутой руки.

Многие народы измеряли длину шагами, двойными шагами, тростями. Очень большие расстояния измерялись переходами, привалами или даже днями.

В Японии существовала мера, называемая лошадиным башмаком. Она была равна пути, в течение которого изнашивалась соломенная подошва, привязанная к копытам лошади.

У многих народов расстояние определялось длительностью полета стрелы или пушечного ядра. До сегодняшнего дня сохранилось выражение «не подпустить на пушечный выстрел».

– А кто знает, какие меры длины использовали издавна на Руси? (Сажень (маховая, косая), верста, локоть, аршин.) О локте мы уже говорили. Маховая сажень (1,76 м) – расстояние между раскинутыми в стороны руками. Косая сажень (2,48 м) – расстояние от каблука правой ноги до кончиков пальцев вытянутой вверх левой руки. Слово аршин пришло с Востока. Приезжие купцы торговали невиданными тканями: китайским шелком, индийской парчой, бархатом, которые отмеряли аршинами (с персидского – «локоть»). Он равен 71 см.

Учитель может предложить следующие вопросы-задания:

1. Измерить длину парты в локтях, ладонях.

2. Какого роста была Дюймовочка?

3. Каков был рост человека, про которого говорят «от горшка два вершка»?

4. 7 футов под килем – это сколько метров?

Для выполнения этого задания удобно пользоваться следующей таблицей:

Задание № 18 (с. 35).

– Прочитайте старинную задачу.

– Что вам известно? Что требуется узнать?

– Какую новую единицу длины содержит эта задача? (Аршин.)

I способ:

1) 6 + 2 = 8 (аршин) – высота 1-й березы.

2) 8 + 2 = 10 (аршин) – высота 2-й березы.

II способ:

1) 2 + 2 = 4 (аршина) – выше 2-я береза, чем изба.

2) 6 + 4 = 10 (аршин) – высота 2-й березы.

Ответ: 10 аршин.

3. Фронтальная работа.

– Рассмотрите чертеж. Как называется данное геометрическое тело? (Пирамида.)

Учитель демонстрирует модель пирамиды.

– Сравните данную модель пирамиды с ее чертежом в тетради.

– Сколько всего граней у пирамиды? (Пять.)

– Сколько граней вы видите на модели? (Две.)

– Какие это грани? (Боковые.)

– Сколько невидимых граней на модели? (Три.)

– Какие это грани? (Две боковые грани и одна нижняя, т. е. основание.)

– Сколько граней нужно раскрасить на чертеже? (Три.)

После этого учитель предлагает раскрасить невидимые грани пирамиды на чертеже. (Раскрашенным окажется весь чертеж.)

4. Работа в печатной тетради № 1.

Задание № 47.

– Какие числа ввели в «машину»?

Учащиеся. В «машину» ввели неизвестное число. Машина прибавила к нему 7. Вышло из «машины» число 13. К неизвестному числу стрелка не идет. Изображаем «машину», обратную данной:  –7.

Идем по стрелке: 13 – 7. Выполняем вычисление.

Получаем 6. Значит, неизвестное число 6. Записываем его в «окошко».

Выполняем проверку. Идем по верхней стрелке: 6 + 7 = 13 (верно).

VI. Итог урока.

– Что нового узнали на уроке?

– Назовите старинные русские единицы длины.

– Назовите признаки пирамиды.

Домашнее задание: № 14, 16 (учебник); № 46, 49, 51 (рабочая тетрадь).

Урок 15
Многоугольник и его элементы

Цели урока: ввести понятие «многоугольник»; научить находить и показывать вершины, стороны и углы многоугольника; рассмотреть обозначение многоугольника латинскими буквами; совершенствовать навыки решения задач; развивать внимание и пространственное мышление.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Имя какого сказочного героя здесь зашифровано?

 

2. Нарисуйте недостающую фигуру, чтобы в каждом ряду были фигуры разной формы.

3. Сравните тексты задач. Чем они похожи? Чем отличаются?

– Можно ли утверждать, что решения этих задач одинаковы?

III. Сообщение темы урока.

– Рассмотрите чертежи на доске:

– Какую закономерность вы обнаружили? (У каждой следующей фигуры увеличивается количество углов и сторон на 1.)

– Название каких фигур вы знаете?

– Какие затруднения у вас возникли?

– Как можно назвать все эти фигуры одним словом?

– Об этом мы и будем говорить сегодня на уроке.

IV. Изучение нового материала.

– Вы уже умеете различать и изображать на бумаге такие фигуры, как треугольник, четырехугольник, пятиугольник. Такие фигуры обычно называют многоугольниками.

Задание № 1 (с. 36).

– Посмотрите на рисунок на с. 36 учебника. В верхней его части нарисовано печенье в форме многоугольников. Сколько углов имеет каждая из этих фигур?

– Теперь рассмотрим желтый многоугольник, нарисованный в рамке. Сколько в нем углов?

– Какой фигурой является каждая сторона многоугольника? (Отрезком.)

– Сколько сторон у желтого многоугольника?

– Какой фигурой является вершина многоугольника? (Точкой.)

– Сколько вершин имеет желтый многоугольник? (Пять.)

Вывод: в желтом многоугольнике 5 углов, 5 сторон и 5 вершин.

Аналогично анализируется количество углов, сторон и вершин в зеленом и красном многоугольниках.

– Что вы можете сказать о количестве углов, сторон и вершин в каждом многоугольнике?

Вывод: в любом многоугольнике углов, сторон и вершин поровну.

– Сколько же углов в семиугольнике? (7.)

– Сколько вершин в десятиугольнике? (10.)

– Сколько сторон в пятнадцатиугольнике? (15.)

Далее учитель демонстрирует заранее подготовленный плакат с изображенным на нем четырнадцатиугольником.

– Как определить название этого многоугольника? Что проще всего сосчитать? (Вершины.)

Справочный материал для учителя

Многоугольники

Ломаная называется замкнутой, если у нее концы совпадают. Простая замкнутая ломаная называется многоугольником, если ее соседние звенья не лежат на одной прямой (рис. 1). Вершины ломаной называются вершинами многоугольника, а звенья ломаной – сторонами многоугольника. Отрезки, соединяющие не соседние вершины многоугольника, называются диагоналями. Многоугольник с п вершинами, а значит и с п сторонами, называется п-угольником.

Плоским многоугольником или многоугольной областью называется конечная часть плоскости, ограниченная многоугольником (рис. 2).

Многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой, содержащей его сторону. При этом сама прямая считается принадлежащей полуплоскости.

На рисунке 3 а изображен выпуклый многоугольник, а на рисунке 3 б – невыпуклый. Углом выпуклого многоугольника при данной вершине называется угол, образованный его сторонами, сходящимися в этой вершине.

Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.

Точки называются вершинами треугольника, а отрезки – его сторонами. На рисунке 4 вы видите треугольник с вершинами А, В, С и сторонами АВ, ВС, АС. Треугольник обозначается указанием его вершин.

Четырехугольником называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться. Данные точки называются вершинами четырехугольника, а соединяющие их отрезки – сторонами четырехугольника. На рисунке 5 представлены три фигуры, каждая из которых состоит из четырех точек А, В, С, D и четырех последовательно соединяющих их отрезков АВ, ВС, CD и AD. Четырехугольником является только третья фигура: у первой фигуры точки А, В, С лежат на одной прямой, а у второй – отрезки ВС и AD пересекаются.

Вершины четырехугольника называются соседними, если они являются концами одной из его сторон. Вершины, не являющиеся соседними, называются противолежащими. Отрезки, соединяющие противолежащие вершины четырехугольника, называются диагоналями. У четырехугольника на рисунке 6 диагоналями являются отрезки АС и BD.

Стороны четырехугольника, исходящие из одной вершины, называются соседними сторонами.

Стороны, не имеющие общего конца, называются противолежащими сторонами. У четырехугольника на рисунке 6 противолежащими являются стороны АВ и СD, BC и AD.

Фронтальная работа. (Чертежи выполнены на доске заранее.)

– Сосчитайте вершины многоугольника. Как он называется? (Четырнадцатиугольник.)

– А теперь попробуйте ответить на более сложные вопросы: бывают ли одноугольники? А двуугольники? Какой из многоугольников имеет наименьшее число углов? Как называется многоугольник, у которого 100 вершин?

– Давайте научимся показывать элементы многоугольника: вершины, стороны и углы. Рассмотрим рисунок. (Сделайте его заранее на доске.)

– Вершины – это точки. (Указкой покажите каждую вершину треугольника.) Теперь покажем стороны. Сторона многоугольника – это какая фигура? (Отрезок.) Показываем стороны как отрезки. (Конец указки движется от вершины, далее по отрезку до другой вершины.) Углы будем показывать вращением указки. Один конец указки должен находиться в вершине треугольника, сама указка – вдоль стороны, выходящей из этой вершины. Далее, не отрывая конца указки от вершины угла, двигаем указку по направлению к другой стороне, пока указка не совместится с этой стороной. Угол можно показать и дугой. (Продемонстрируйте учащимся, как правильно это сделать, и предложите им самостоятельно показать дугами каждый угол треугольника.)

– Вершины треугольника обозначают буквами. Читать обозначение можно разными способами, начиная с любой вершины, например: треугольник АВС, АСВ, ВСА, ВАС, САВ, СВА.

Задание № 2 (с. 37).

– Что изображено на рисунке? (Многоугольники.)

– Как называются данные многоугольники? (Треугольник, пятиугольник.)

– Какими геометрическими фигурами являются вершины и стороны многоугольника? (Это точки и отрезки.)

– Как принято обозначать точки на чертеже? (Прописной буквой латинского алфавита.)

– А отрезки? (Двумя прописными буквами латинского алфавита.)

– Назовите вершины треугольника. (О, М, К.)

– Назовите стороны треугольника. (МО, МК, ОК.)

– Сколько вершин и сколько сторон у этой фигуры?

Аналогично учащиеся называют вершины и стороны пятиугольника.

Задание № 3 (с. 37).

Учащиеся вспоминают, что в любом многоугольнике число сторон, углов и вершин одинаково, причем многоугольник называется в соответствии с числом его сторон, углов и вершин.

Так, в треугольнике по 3 стороны, вершины и угла, поэтому, для того чтобы сложить треугольник, потребуется 3 палочки.

Аналогично учащиеся рассуждают при анализе четырехугольника и пятиугольника.

V. Повторение пройденного материала.

1. Работа в печатной тетради № 1.

Задание № 50.

Учащиеся раскрашивают третью слева фигуру в верхнем ряду и все фигуры – в нижнем.

– Как называется каждый из раскрашенных многоугольников?

– Какие еще известные вам фигуры изображены на чертеже?

Задание № 51.

– Какими геометрическими фигурами являются вершины и стороны многоугольника? (Это точки и отрезки.)

– Каким карандашом мы должны раскрасить вершины? (Красным.)

– Каким карандашом мы раскрасим стороны? (Синим.)

– Как называются все многоугольники на чертеже? (Это четырехугольники.)

– Сколько в четырехугольнике вершин? (Четыре.)

– Сколько в нем сторон? (Четыре.)

– Какой вывод вы можете сделать? (В каждом многоугольнике надо раскрасить красным цветом четыре точки – его вершины, а синим карандашом четыре отрезка – его стороны.)

2. Работа по учебнику.

Задание № 8 (с. 38).

– Что такое «сумма»?

– Что называют «разностью»?

Далее учащиеся называют суммы и разности чисел, указанных в задании.

Задание № 9 (с. 38).

– Что обозначает выражение «увеличить на…», «уменьшить на…»?

Далее учащиеся записывают сложные выражения:

(4 + 3) + 2

(15 – 9) – 5

(6 + 4) + 7

(11 – 5) – 4

(12 – 8) + 8.

– Определите порядок выполнения действий и найдите значение каждого выражения.

Задание № 10 (с. 38).

– Прочитайте задачу.

– Что вам известно? Что требуется узнать?

– Запишите кратко условие и решите эту задачу.

Решение:

8 + 7 = 15 (игр.) – у Сережи.

Ответ: 15 игрушек.

– Как изменить условие задачи, чтобы она решалась вычитанием? (На 7 игрушек меньше.)

– Как изменить вопрос задачи, чтобы в ее решении было два действия? (Сколько игрушек всего?)

Задание № 13 (с. 39).

Учащиеся работают в парах, на калькуляторе набирают данные числа.

VI. Итог урока.

– Что нового узнали на уроке?

– Какие фигуры называют многоугольником?

– Как определить название многоугольника?

– Как обозначают многоугольники на чертеже?

Домашнее задание: № 7, 11 (учебник); № 53, 54, 56 (рабочая тетрадь).

Урок 16
Многоугольник и его элементы

Цели урока: учить определять количество углов в многоугольнике; обозначать латинскими буквами многоугольники; продолжить формирование навыков показывать вершины, стороны и углы в многоугольнике; совершенствовать навык решения задач; развивать умение сравнивать и обобщать.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Разгадайте правило, по которому составлена таблица, и заполните пустые клетки:

2. Вставьте пропущенные числа:

77, 78, 79, , 81, , 

37, 47, 57, , , 87, 

94, 84, 74, , , , 34

89, 87, 85, , , 79

3. Из 9 счетных палочек составьте 4 равных треугольника. Сверьте с образцами.

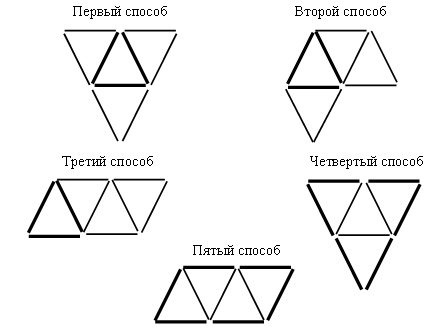
III. Сообщение темы урока.

– Рассмотрите фигуры, изображенные на доске.

– Как называются эти фигуры? (Многоугольники.)

– Назовите номер «лишнего» многоугольника. (3.)

– Как называется этот многоугольник? Об этом мы узнаем сегодня на уроке.

IV. Изучение нового материала.

1. Работа по учебнику.

Задание № 4 (с. 37).

– Рассмотрите рисунок.

– Как определить название многоугольника?

– Как называется первая фигура? (Четырехугольник.)

– Как называется вторая фигура? (Шестиугольник.)

– Покажите каждый угол многоугольника.

– Покажите все стороны четырехугольника.

– Покажите все вершины шестиугольника.

Справочный материал для учителя

Вершины многоугольника ученик показывает, касаясь каждой из них концом указки или карандаша; стороны – как отрезки, то есть ведя указкой по каждой стороне.

Первое время лучше показывать каждый угол многоугольника вращением указки (карандаша) следующим образом: один конец указки помещается в вершине многоугольника, например  в точке А, а сама указка располагается вдоль одной из сторон, выходящей из этой вершины. Не отрывая конца указки от вершины угла, двигаем указку в плоскости доски по направлению к другой стороне многоугольника до совмещения с ней.

Такой способ показа угла облегчит в дальнейшем формирование представлений учащихся о видах углов (прямой, острый, тупой, развернутый), сравнении углов.

В дальнейшем это учебное действие можно упростить: угол будем показывать дугой.

– Чем похожи многоугольники из задания № 4?

– Эти многоугольники называются невыпуклыми.

Многоугольники бывают выпуклые и невыпуклые.

Многоугольник называется выпуклым, если он весь лежит по одну сторону от прямой, которой принадлежит какая-либо его сторона. Если это условие не выполняется, то многоугольник называется невыпуклым.

Задание № 5 (с. 37).

– Рассмотрите рисунок.

– Можно ли назвать этот многоугольник пятиугольником? Почему? (Чтобы выяснить, как называется этот многоугольник, можно пересчитать число его сторон. Их 7. Значит, это семиугольник. В нем не только 7 сторон, но и по 7 вершин и углов.)

Задание № 6 (с. 37).

Учащиеся строят в тетради треугольник и четырехугольник.

2. Работа в печатной тетради № 1.

Задание № 52.

Учащиеся должны зачеркнуть слова «треугольник» и «пятиугольник», так как фигуру на чертеже можно назвать и многоугольником, и четырехугольником, и квадратом.

V. Повторение пройденного материала.

1. Работа с учебником.

Задание № 16 (с. 39).

– Прочитайте задачу.

– Что вам известно? Что требуется узнать?

– Запишите кратко условие задачи.

Запись: Было – 5 ог. и 4 п.

   Порезали – 3 ов.

   Осталось – ? ов.

– Прочитайте, как Миша собирается решить задачу. (Выражением.)

– Верна ли его запись?

– Объясните, что обозначает выражение: 

– Запишите решение задачи по действиям.

Решение:

1) 5 + 4 = 9 (ов.) – было.

2) 9 – 3 = 6 (ов.) – осталось.

– Сравните свою запись с записью Миши.

– Запишите решение задачи уравнением.

2. Фронтальная работа.

– Рассмотрите каждый рисунок. Покажите отрезки АВ и CD. Есть ли у этих отрезков общая часть? Какой фигурой она является?

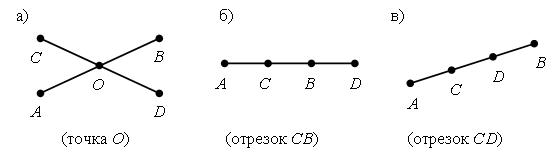
Задание № 14 (с. 39).

Учащиеся работают в парах.

3. Работа в печатной тетради № 1.

Задание № 55.

Так как учащиеся еще незнакомы со знаками «>» и «<» , то оформить решение они должны так:

70 см равно 7 дм;

4 м меньше 51 дм;

95 см меньше 1 м;

6 дм 1 см больше 49 см.

Задание № 56.

Решение: нужно выбрать такую часть числового луча, на которой удобно отметить точки с заданными координатами, например так:

VI. Итог урока.

– Что нового узнали на уроке?

– Как определить название многоугольника?

– Какие многоугольники называют выпуклыми? Невыпуклыми?

– Как обозначить многоугольник на чертеже?

Домашнее задание: № 18 (учебник).

Урок 17
Сложение и вычитание вида 26 ± 2, 26 ± 10

Цели урока: познакомить учащихся с правилами поразрядного сложения и вычитания чисел в пределах 100; рассмотреть практическое выполнение действий с помощью цветных палочек; совершенствовать вычислительные навыки; практическим путем находить значение умножения и деления; развивать внимание и логическое мышление.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Вставьте числа в пустые клетки квадрата так, чтобы сумма по всем направлениям была одинаковой.

2. На каком рисунке больше треугольников – на левом или на правом?

3. Решите задачу.

Вова ищет друзей, которые спрятались от него. Вдруг он заметил, что из-под забора видны 8 ног. Сколько детей стоит за забором?

4. Игра «Парашютисты».

– Куда должен приземлиться каждый из парашютов?

5. Винни-Пух толще Кролика, Кролик толще Пятачка. Кто тоньше всех?

III. Сообщение темы урока.

– Рассмотрите выражения, записанные на доске:

– Значения каких выражений вы не сможете еще вычислить?

– Сегодня мы узнаем, как выполнить сложение и вычитание вида 26 ± 2 и 26 ± 10.

IV. Изучение нового материала.

В учебнике показано, как с помощью цветных палочек познакомить второклассников с правилами поразрядного сложения и вычитания чисел в пределах 100. Оранжевая палочка обозначает десяток, а белая – единицу. Необходимо построить работу таким образом, чтобы при рассмотрении каждого примера дети, выкладывая палочки, повторяли способы действия Волка и Зайца. При этом школьники могут работать в парах.

Задание № 1 (с. 40).

Пример 1. Учитель ставит перед детьми учебную задачу: используя цветные палочки, найти способ сложения чисел 26 и 2.

– Рассмотрите первый рисунок на с. 40 учебника и выскажите свои предположения. (В числе 26 – два десятка и шесть единиц, поэтому Волк составил «поезд» из 2 оранжевых и 6 белых «вагонов».)

– Составьте такой же «поезд» из своих палочек.

– Объясните, что делает Заяц. (Заяц прицепляет к белым «вагонам» еще 2 белых «вагона», так как надо прибавить 2 единицы.)

– Выполните это действие на своих палочках.

– Что у вас получилось? (Получился «поезд», в котором 2 оранжевых и 8 белых «вагонов» (6 + 2 = 8.)

– Какое число обозначает этот поезд? (Он обозначает число 28.)

Учащиеся подводят итог: сумма 26 и 2 есть число, в котором 2 десятка, а единиц 6 и 2, всего 8. Значит, 26 + 2 = 28.

Пример 2. Постановка задачи: необходимо вычесть 2 из 26, используя цветные палочки.

Снова составим «поезд» из 2 оранжевых и 6 белых «вагонов». По рисунку видно, что, вычитая 2, Волк предложил отцепить 2 белых «вагона». Получился «поезд», в котором 2 оранжевых и 4 белых «вагона» (6 – 2 = 4). Он обозначает число 24.

Итак, разность 26 и 2 есть число, в котором 2 десятка, а единиц 6 без 2, то есть 4. Значит, 26 – 2 = 24.

Пример 3. Постановка задачи: сложить 26 и 10. Рассматриваем рисунок: Волк составил «поезд» из 2 оранжевых и 6 белых «вагонов». Так как 10 – это один десяток, то Заяц к оранжевым «вагонам» прицепляет еще 1 оранжевый «вагон». Получился «поезд», в котором 3 оранжевых (2 + 1 = 3) и 6 белых (6 + 0 = 6) «вагонов». Он обозначает число 36. Значит, 26 + 10 = 36.

Пример 4. Постановка задачи: вычесть 10 из 26. Составим «поезд» из 2 оранжевых и 6 белых «вагонов». Отцепим от оранжевых «вагонов» один. Получился «поезд», в котором 1 оранжевый (2 – 1 = 1) и 6 белых (6 – 0 = 6) «вагонов». Он обозначает число 16. Значит, 26 – 10 = 16.

В заключение учитель просит сформировать правило: как же, не используя цветные палочки, можно складывать и вычитать двузначные числа.

– Прочитайте правила, приведенные на с. 41 учебника.

Задание № 2 (с. 41).

Учащиеся работают в парах; используя цветные палочки, они выполняют сложение и вычитание двузначных чисел.

Задание № 3 (с. 41).

Выполнить это задание учащиеся должны уже без цветных палочек, руководствуясь правилами, сформулированными при объяснении нового материала.

Рассмотрим способы рассуждения на примерах.

1) 29 – 8.

При вычитании чисел из единиц вычитают единицы, а из десятков – десятки. В числе 29 – девять единиц, а в числе 8 – восемь единиц. Вычитаем: 9 – 8 = 1. Значит, в результате получится одна единица. В числе 29 – два десятка, а в числе 8 – нуль десятков. Значит, в результате будет два десятка.

Следовательно, 29 – 8 = 21.

2) 20 + 1.

При сложении чисел единицы складываются с единицами, а десятки – с десятками.

В числе 20 – нуль единиц, а в числе 1 – одна единица. Складываем: 0 + 1 = 1. Значит, в результате будет одна единица.

В числе 20 – два десятка, а в числе 1 – нуль десятков. Значит, в результате будет два десятка.

Следовательно, 20 + 1 = 21.

Аналогично дети рассуждают в остальных случаях.

V. Повторение пройденного материала.

1. Работа по учебнику.

Задание № 11 (с. 43).

Запись: 13, 31, 49, 66, 90, 100;

100, 90, 66, 49, 31, 13.

Задание № 12 (с. 43).

– Какое действие необходимо выполнить, чтобы ответить на вопрос «на 3 больше, чем 8»?

– Как вычислить число, которое меньше числа 10 на 6?

Задание № 13 (с. 44).

– Прочитайте первую задачу.

– Что известно? Что необходимо узнать?

– Используя фишки, решите эту задачу.

– Прочитайте вторую задачу.

– Сравните эту задачу с первой. Чем они отличаются?

– Что известно в задаче? Что требуется узнать?

– Используя фишки, решите задачу.

2. Работа в печатной тетради № 1.

Задание № 59.

Если учащиеся будут испытывать затруднения в выполнении этого задания, то учитель может подсказать, что, для того чтобы правильно подобрать знак в каждом конкретном случае, нужно сравнить первый компонент действия с результатом.

После выполнения этого задания учитель проводит устную проверку.

Справочный материал для учителя

История возникновения знаков плюс (+) и минус (–)

– Вы когда-нибудь задумывались над тем, откуда в наших тетрадях и учебниках появились такие необходимые и в то же время простые знаки «+» и «–»? Оказывается, их история уходит в глубокую древность. Обычно виноторговец черточками отмечал, сколько мер вина он уже продал. Так, уменьшение количества стало обозначаться знаком «–», который позже назвали минусом. Приливая в бочку новые запасы, торговец перечеркивал столько расходных черточек, сколько мер он восстановил. Так, возможно, появился знак «+», обозначающий прибавление, увеличение.

Иногда исторические факты со временем искажаются и не всегда бывают достоверными, поэтому многие ученые считают, что происхождение этих знаков имеет совсем другие корни. Давайте познакомимся и с другим мнением.

Раньше, когда знаки плюс и минус не были известны древним математикам, сумму чисел записывали так: 1 и 2 или на латинском 1 et 2. Для краткости стали писать 1 t 2, а потом 1 + 2.

VI. Итог урока.

– Что нового узнали на уроке?

– Какое действие необходимо выполнить, чтобы ответить на вопрос: «На сколько больше?»

Домашнее задание: № 14 (учебник); № 58 (рабочая тетрадь).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                                        Урок 18
Сложение и вычитание вида 26 ± 2, 26 ± 10

Цели урока: продолжить формирование умений выполнять приемы сложения и вычитания двузначных чисел, основанные на поразрядном сложении и вычитании; совершенствовать навыки решения задач; развивать умение анализировать и обобщать.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Из каких фигур построен дом?

2. Прочитайте поговорку.

О т в е т: Не в свои сани не садись.

3. Расшифруйте слово.

 

4. Поставьте знаки действий «+» и «–» между числами так, чтобы получилось верное равенство.

5 … 4 … 3 … 2 … 1 = 1

О т в е т: 5 – 4 + 3 – 2 – 1 = 1.

5. Решите задачу.

В коробке 3 желтых и 3 красных шарика. Мальчик взял 4 шарика. Сколько шариков каждого цвета может быть у мальчика? Найдите все ответы.

– Сколько шариков осталось в коробке?

III. Сообщение темы урока. Работа над новым материалом.

– Сегодня мы продолжим работу по сложению и вычитанию двузначных чисел.

Задание № 4 (с. 41).

– Рассмотрите данные выражения. Что их объединяет? (В каждом выражении по 2 арифметических действия и есть скобки.)

– Какое действие надо выполнять первым? (В скобках.)

– Какие правила сложения и вычитания двузначных чисел вы знаете? (Действия (сложение и вычитание) надо выполнять поразрядно.)

Запись:

Задание № 5 (с. 42).

Учащиеся, не выполняя вычислений, определяют, что больше:

а) 46 + 2 больше 46 – 2, так как сложение двух чисел всегда больше разности этих же чисел;

б) 53 + 4 меньше 6 + 53, так как в данных суммах, используя закон перестановки слагаемых, выясняем, что первое слагаемое одно и то же число – 53. Значит, значение суммы зависит от второго слагаемого: в первом выражении второе слагаемое меньше, чем второе слагаемое во втором выражении (4 < 6), поэтому значение первой суммы меньше значения второй суммы;

в) 90 – 60 больше 80 – 60, так как вычитаемые равны, то значение разности больше в том выражении, где больше уменьшаемое (90 > 80);

г) 37 – 5 больше 37 – 6, так как уменьшаемые равны, то значение разности больше в том выражении, где меньше вычитаемое (5 < 6).

– Выполните сложение и вычитание данных чисел и проверьте свои рассуждения.

Задание № 6 (с. 42).

– Прочитайте текст. Можно ли его назвать задачей?

– Прочитайте только условие.

– Прочитайте вопрос задачи.

– Сформулируйте вопрос задачи со словом «сколько». (Сколько килограммов весят яблоки в этом ящике?)

– Запишите решение этой задачи.

Всего: 23 кг.

Ящик – 1 кг.

Яблоки – ? кг.

Решение:

23 – 1 = 22 (кг) – масса яблок.

Ответ: 22 кг.

V. Повторение пройденного материала.

1. Работа по учебнику.

Задание № 15 (с. 44).

– Прочитайте задачу.

– Что известно в задаче? Что требуется узнать?

– Запишите кратко условие задачи.

Запись:

– Что обозначает слово «цена»? (Стоимость одного предмета.)

– Что обозначает слово «стоимость»? (Выраженная в деньгах ценность чего-либо.)

– Запишите решение этой задачи. (8 + 9 = 17.)

– Измените вопрос задачи так, чтобы она решалась вычитанием. (На сколько рублей дороже второй карандаш?)

 

Справочный материал для учителя

Денежная система в Древней Руси

Торговать люди умели с древнейших времен, но вот деньги появились не так давно. В Древней Руси, когда городами правили князья, появились необычные деньги: не монеты, а слитки из серебра и золота. Слиток из плохого серебра был самой мелкой монеткой и назывался гривна. Слиток из качественного серебра был более ценной деньгой, и называли его серебряный. Ну а золотой слиток ценился выше всех, его так и называли – золотой. Вы понимаете, что ходить за покупками с тяжелым слитком неудобно. Да к тому же, если товара нужно было немного, то, имея такой небольшой ассортимент денег, невозможно было дать сдачу покупателю. Тогда люди додумались делить гривну на несколько частей и стали рубить слитки. Так появился рубль, которым мы называем наши деньги и сейчас. Еще одна денежная единица, копейка, пришла к нам из древности: так назвали монету, на которой был изображен всадник с копьем. Отсюда и копейка. Были еще и другие монеты: деньга (полкопейки), алтын (3 копейки), пятак (5 копеек), гривенник (10 копеек), полтинник (50 копеек).

Задание № 16 (с. 44).

– Прочитайте задачу.

– Что вам известно? Что требуется узнать?

При затруднении учитель может предложить учащимся выполнить схему к этой задаче.

2. Работа в печатной тетради № 1.

Задание № 61.

Перед выполнением задания учитель предлагает учащимся вспомнить, что если в примере есть действие в скобках, то именно оно выполняется первым.

Ошибки допущены в следующих случаях:

(68 + 20) + 1 =   (89.)

(73 + 2) – 50 =   (25.)

(39 – 5) – 2 =   (32.)

Задание № 60.

Учащиеся заполняют самостоятельно «окошки» в цепочках.

Далее учитель проводит устную проверку, учащиеся читают конечный результат в каждой цепочке вычислений.

VI. Итог урока.

– Что нового узнали на уроке?

– Как выполнить сложение двузначных чисел?

– Как выполнить вычитание двузначных чисел?

– Какие денежные единицы вам известны?

Домашнее задание: № 7 (учебник); № 66 (рабочая тетрадь).

Урок 19
Сложение и вычитание вида 26 ± 2, 26 ± 10.
Решение задач

Цели урока: совершенствовать навыки решения задач; продолжить формирование вычислительных умений вида 26 ± 2, 26 ± 10; развивать умение обобщать.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Сколько на рисунке треугольников? (4.)

Сколько на рисунке четырехугольников? (1.)

Сколько всего фигур? (5.)

2. Расположите в каждой клетке квадрата по одному кружку красного, синего и зеленого цвета так, чтобы в каждом столбце и каждой строке были кружки разного цвета.

3. Соедините линиями примеры с одинаковыми ответами:

4. Какие числа надо зачеркнуть, чтобы среди оставшихся чисел каждое следующее было на 2 больше предыдущего?

0   1   2   3   4   5   6   7   8   9

Ответ:

III. Сообщение темы урока.

– Сегодня мы продолжим выполнять сложение и вычитание двузначных чисел и будем учиться решать и преобразовывать задачи.

IV. Работа над новым материалом.

– Что называют «задачей»?

– Назовите элементы задачи. (Условие, вопрос, решение, ответ.)

– Как называются задачи, в которых данные для ответа на вопрос не используются? (С избыточными, лишними данными.)

– Как называются задачи, решение которых невозможно, так как данных не хватает?

Задание № 8 (с. 42).

– Прочитайте текст. Является ли он задачей? Почему?

– Выделите и прочитайте условие.

– Найдите и прочитайте вопрос.

– Придумайте несколько вопросов к данному условию.

· Сколько наклеек собрала Аня? (30 + 20 = 50.)

· Сколько наклеек собрали все девочки вместе? (50 + 50 = 100.)

· На сколько меньше наклеек собрала Оля, чем Маша?

(30 – 20 = 10.)

· На сколько больше наклеек собрала Аня, чем Маша?

(50 – 30 = 20.)

Учащиеся объясняют план решения всех составленных задач.

Анализ решения задачи: «Маша собрала 30 наклеек для журнала, Оля – 20 наклеек, а Аня – столько, сколько Маша и Оля вместе. На сколько больше наклеек собрала Аня, чем Маша?»

– Можно ли решить эту задачу, не выполняя вычислений? (Если у Ани столько же наклеек, сколько у Маши и Оли вместе, то у Ани наклеек больше, чем у Маши, на число Олиных наклеек, то есть на 20.)

Схема:

Задание № 9 (с. 42).

– Прочитайте текст. Является ли он задачей?

– Что известно в задаче?

– Что требуется узнать?

– Какие данные для ответа на вопрос не используются? (30 ягод земляники.)

– Измените вопрос задачи так, чтобы использовались все данные в задаче.

Вопросы:

· Сколько всего грибов и ягод нашла Ира?

· На сколько меньше грибов, чем ягод, принесла Ира?

Далее учитель предлагает решить все полученные новые задачи:

Решение:

1) 22 + 4 + 30 = 56 (шт.) – грибы и ягоды.

2) 22 + 4 = 26 (шт.) – принесла грибов.

3) 30 – 26 = 4 (шт.) – больше ягод, чем грибов.

О т в е т: 56 шт., на 4 ягоды больше.

V. Повторение пройденного материала.

1. Работа в печатной тетради № 1.

Задание № 62.

– Прочитайте условие задачи.

– Что известно? Что требуется узнать?

– Запишите кратко условие этой задачи.

Решение:

1) 20 + 27 = 47 (р.) – застеклили 1-й и 2-й стекольщики.

2) 47 – 5 = 42 (р.) – застеклил 3-й стекольщик.

Учитель может предложить учащимся решить данную задачу другим способом либо объяснить решение:

2. Работа по карточкам.

Карточка 1.

– Рассмотрите чертежи. Какие геометрические фигуры здесь изображены? (Точки, отрезки, луч.)

– Назовите отрезки, которые лежат на луче АВ. (АК, КМ, АМ.)

– Назовите отрезки, которые не лежат на луче АВ. (XY, CD.)

– Назовите отрезки, которые пересекают луч АВ. (Отрезок CD.)

Если в последнем вопросе возникают затруднения у учащихся, то учитель проводит беседу.

– Какую фигуру называют «лучом»? Есть ли у луча начало и конец? (Нет конца, луч – это бесконечная фигура.)

– Значит, луч АВ можно продлить.

Для проверки учащиеся используют линейку.

Карточка 2.

– Закрасьте: восьмиугольники – зеленым, семиугольники – коричневым, шестиугольники – красным, четырехугольники – желтым, треугольники – голубым.

3. Работа по учебнику.

Задание № 17 (с. 44).

– Рассмотрите многоугольники.

– Объясните, по какому правилу они распределены в группы. (По количеству углов, сторон и вершин: треугольники, четырехугольники, пятиугольники.)

VI. Итог урока.

– Что нового узнали на уроке?

– Назовите признаки многоугольника.

Домашнее задание: № 66 (рабочая тетрадь).

Урок 20
Сложение и вычитание вида 26 ± 2, 26 ± 10

Цели урока: совершенствовать вычислительные навыки сложения и вычитания, основанные на знании разрядов двузначных чисел; закреплять навыки составления и чтения математических граф; развивать логическое мышление и внимание.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Найдите значения выражений:

5 + 2 + 3 – 6 + 5 – 1 – 3 + 5 – 1

9 – 2 – 6 + 8 – 7 + 8 – 6 + 4 + 2

50 + 20 + 30 – 60 + 50 – 10 – 30 + 50 – 10

90 – 20 – 60 + 80 – 70 + 80 – 60 + 40 + 20

2. Из 7 счетных палочек составьте 3 равных треугольника. Сравните с образцами.

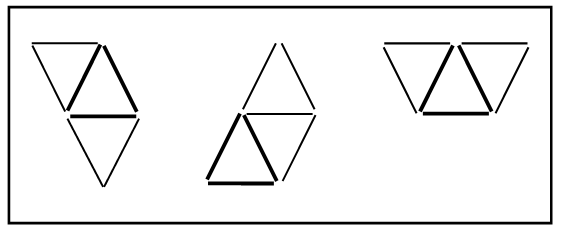
3. Прочитайте условие задачи:

У зайчика было 19 морковок. Он съел 5 морковок утром, а в обед еще 4.

– Подумайте, на какие вопросы вы сможете ответить, пользуясь этим условием:

а) Сколько всего морковок съел зайчик?

б) На сколько больше морковок зайчик съел утром, чем в обед?

в) На сколько меньше морковок зайчик съел в обед, чем утром?

г) Сколько яблок съел зайчик?

д) Сколько морковок у зайчика осталось?

III. Сообщение темы урока.

– Сегодня на уроке узнаем, как выполнять вычисления в примерах вида 26 ± 2, 26 ± 10.

IV. Работа по теме урока.

1. Работа по учебнику.

Задание № 10 (с. 43).

– Прочитайте задачу.

– Что известно? Что требуется узнать?

– Рассмотрите чертеж к задаче.

– Чему равна длина бассейна? (30 + 20 = 50 м.)

– Прочитайте задание под схемой.

– Как называются эти виды задач? (Это обратные задачи.)

– Выполните чертеж к новой задаче и решите ее.

Решение:

50 – 30 = 20 (м) – проплыл второй пловец.

О т в е т: 20 м.

– Сколько всего обратных задач можно составить к данной задаче?

Задание № 19 (с. 45).

Для того чтобы учащимся было проще найти ключ к шифру, можно посоветовать им воспользоваться часами. Соотнеся числа на циферблате обычных часов с буквами на нарисованном циферблате, ученики смогут расшифровать пословицу «Дело мастера боится».

Справочный материал для учителя

Из истории часов

Хозяйственная деятельность человека требовала умения определять точное время. Сначала своеобразными часами было солнце. Так как Земля вращается вокруг своей оси, то кажется, что солнце движется по небосводу. Если вы наблюдательны, то наверняка замечали, что утром солнце «встает» с одной стороны горизонта, а «садится» на противоположной. В полдень же оно находится в самой высокой точке. А замечали ли вы, как при этом «движется» тень от предметов? Греки заметили это несколько тысяч лет тому назад и изобрели солнечные часы, которые достаточно точно показывали время, но были хороши только днем в ясную погоду.

Чтобы определять время ночью, люди использовали звездные часы. Ученые заметили, что все небесные тела кажутся движущимися из-за вращения Земли, и только одна-единственная яркая звезда остается неподвижной. Эта звезда называется Полярной. По положению созвездий относительно этой Полярной звезды и определялось ночное время.

Основная сложность в этих природных часах состояла в том, что по ним невозможно было засекать минуты и секунды. Так появились водяные и песочные часы, с помощью которых можно было измерять 1, 3, 5, 10... минут. До сих пор в языке сохранились такие выражения: «Ваше время истекло», «Время быстро течет». И только сравнительно недавно появились современные механические, а потом и электронные часы.

Задание № 20 (с. 45).

Учащиеся решают ребусы:

 –  = 1 (10 – 9 = 1)

 –  = 1 (100 – 99 = 1)

2. Работа в печатной тетради № 1.

Задание № 63.

Так как учащиеся незнакомы со знаками > и <, то первую часть задания они должны оформить так:

72 больше 10,

5 меньше 48.

– Прочитайте вторую часть задания.

– Как узнать, на сколько одно число больше другого? (Чтобы узнать, на сколько одно число больше или меньше другого, надо из большего числа вычесть меньшее.)

В первой паре чисел 72 больше 10. Находим разность:
72 – 10 = 62. Следовательно, 72 больше 10 на 62.

Во второй паре чисел 5 меньше 48. Значит, 48 больше 5. Находим разность: 48 – 5 = 43. Следовательно, 48 больше 5 на 43.

Задание № 65.

Для каждой тройки чисел можно изобразить как граф отношения «больше», так и граф отношения «меньше».

Вы можете предложить детям самостоятельно выбрать отношение, граф которого они будут строить, либо сами задать это отношение для каждой тройки чисел.

Возможны следующие варианты:

Отношение «больше».

Отношение «меньше».

V. Самостоятельная работа по теме «Сложение и вычитание вида 26 ± 2, 26 ± 10».

№ 1. Какие двузначные числа можно записать цифрами 3, 2, 4, 5?

№ 2. Чем похожи выражения в каждом столбике? Объясните, как вы будете вычислять значения сумм:

№ 3. Запишите задачи.

В первых классах 78 ребят. Из них 40 изучают английский язык, остальные – немецкий. Сколько ребят изучает немецкий язык?

VI. Итог урока.

– Что нового узнали на уроке?

Урок 21
Запись сложения столбиком

Цели урока: составить алгоритм сложения двузначных чисел в столбик; совершенствовать навыки решения задач; развивать внимание и память.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Сколько треугольников вы видите на каждом чертеже?

2. Игра-соревнование.

– Сколько клеток вы заполните за три минуты?

3. Задача.

Подберите условие к данному вопросу и решите задачу.

Сколько всего детей занимается в студии?

а) В студии 30 детей, из них 16 мальчиков.

б) В студии мальчики и девочки. Мальчиков на 7 меньше, чем девочек.

в) В студии 8 мальчиков и 20 девочек.

г) В студии 8 мальчиков, а девочек на 2 больше.

д) В студии занимаются 8 мальчиков, а девочек на 2 меньше.

III. Сообщение темы урока.

– Рассмотрите математические записи на доске:

20 + 5 = ?    25 + 12 = ?     

– Какие записи сложения вам незнакомы? Сегодня мы научимся выполнять сложение двузначных чисел в столбик.

IV. Изучение нового материала.

Задание № 1 (с. 46).

Рассмотрите, используя цветные палочки, пример сложения чисел 23 и 12. Для этого составляются два «поезда», обозначающие числа 23 и 12, затем к первому «поезду» прицепляются слева 1 оранжевый «вагон», а справа – 2 белых «вагона». Получается «поезд», в котором 3 оранжевых и 5 белых «вагонов». Этот «поезд» обозначает число 35.

– Сформулируйте правило сложения двузначных чисел. (Правило поразрядного сложения: единицы складываем с единицами, десятки с десятками.)

– Подходит ли это правило для случаев вида 23 + 12? (Да.)

– При сложении  удобно записывать одно под другим (десятки под десятками, а единицы под единицами). Тогда становится видно, какие разрядные единицы нужно складывать. Такой способ называют «записью столбиком».

– Рассмотрите образцы сложения двузначных чисел в столбик на с. 46.

– Напишем первое число – 23 и подпишем под ним второе число – 12 так, чтобы десятки были под десятками, а единицы – под единицами. Складываем сначала единицы, а потом десятки: 3 и 2 – это 5 (единиц), 2 и 1 –
это 3 (десятка). Получается число 35.

Рассматривая сложение 46 и 3, обратите внимание на второе слагаемое; в числе 3 содержится 0 десятков 3 единицы, поэтому в сумме получается 4 десятка (4 десятка и 0 десятков – это 4 десятка) и 9 единиц.

Такие же пояснения рекомендуем дать и в случае сложения 3 и 46.

 

Памятка

Алгоритм сложения в столбик.

1. Записываем первое слагаемое.

2. Записываем второе слагаемое: единицы под единицами; десятки под десятками.

3. Складываем единицы.

4. Складываем десятки.

5. Читаем ответ.

Задание № 2 (с. 47).

Учащиеся работают в парах. Используя цветные палочки, они выполняют сложение двузначных чисел.

Задание № 2 (с. 47).

Учащиеся работают в паре. Используя цветные палочки, дети находят результат сложения.

30 + 16

ор.

ор.

ор.

30.

 

ор.

б.

б.

б.

б.

б.

б.

16.

О т в е т:

ор.

ор.

ор.

ор.

б.

б.

б.

б.

б.

б.

46.

Задание № 3 (с. 47).

– Что обозначает в записи любого числа последняя цифра? (Число единиц.)

– Если надо определить, сколько единиц получится в результате сложения двух чисел, обязательно ли нам вычислять сумму этих чисел? (Нет.)

– Достаточно найти сумму чего? (Сумму единиц первого и второго чисел.)

Далее учащиеся устно выполняют вычисления.

Например, 32 + 40.

Вычисляют: «К 32 прибавить 40. В числе 32 – две единицы, а в числе 40 – нуль единиц. Находим сумму единиц: 2 + 0 = 2. Значит, сумма чисел 32 и 40 оканчивается цифрой 2».

V. Повторение пройденного материала.

1. Работа в печатной тетради № 1.

Задание № 67.

Учащиеся выполняют сложение двузначных чисел с объяснением, комментированием.

Задание № 68.

– Что обозначает запись 3 д.? (3 десятка.)

– Выполните сложение и запишите цифрами результаты сложения.

Учащиеся работают самостоятельно. Учитель проводит проверку.

2. Работа по учебнику.

Задание № 10 (с. 48).

Учащиеся выполняют вычисления устно, на основе правил поразрядного сложения и вычитания чисел. Записывают  вычисления  в строчку.

Задание № 11 (с. 48).

– Прочитайте текст. Можно ли его назвать задачей? Почему?

– Что вам известно? Что требуется узнать?

– Все ли данные понадобятся для решения этой задачи?

– Прочитайте остальные вопросы.

– Запишите кратко условие этой задачи.

Запись: Написал – ? к., 7 порт. и 9 пейз.

   Отправил – ? к., 4 порт. и 5 пейз.

 

Решение:

1) 7 + 9 = 16 (к.) – всего нарисовал.

2) 4 + 5 = 9 (к.) – всего отправил.

3) 7 – 4 = 3 (к.) – осталось портретов.

4) 9 – 5 = 4 (к.) – осталось пейзажей.

5) 4 – 3 = 1 (к.) – меньше осталось портретов.

VI. Итог урока.

– Что нового узнали на уроке?

– Как выполнить сложение двузначных чисел столбиком?

Домашнее задание: № 9 (учебник).

Урок 22
Запись сложения столбиком

Цели урока: составить алгоритм сложения двузначных чисел столбиком; совершенствовать навыки решения задач; развивать внимание и память.

Ход урока

I. Организационный момент.

II. Устный счет.

1. По какому признаку фигуры разбиты на две группы?

2. Разгадайте правило, по которому составлен первый столбик выражений. Составьте по этому же правилу выражения для других столбиков и найдите их значения:

3. Сравните тексты задач. Чем они похожи? Чем отличаются?

а) Миша сделал 15 флажков, а Коля на 5 флажков меньше. Сколько флажков сделал Коля?

б) Миша сделал 15 флажков, а Коля на 5 флажков больше. Сколько флажков сделал Коля?

– Правильно ли решены задачи? Какое равенство является решением одной и другой задачи?

4. Рассмотрите карточки с фишками.

а) Найдите рисунок, которому соответствует выражение 

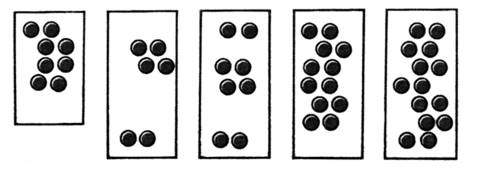
б) Запишите выражения, которые соответствуют каждому рисунку, и вычислите их значения.

III. Сообщение темы урока.

– Сегодня на уроке будем выполнять сложение чисел в столбик и выделять симметричные фигуры на чертеже.

IV. Работа над темой урока.

Задание № 4 (с. 47).

– Объясните, как выполнить сложение чисел в столбик. Какие знания вам для этого нужны?

– Вычислите, выполняя записи в столбик.

Вычисления учащиеся проводят с комментированием рассуждений.

Задание № 5 (с. 47).

– Что означает выражение «увеличь на 5 число»? (Надо выполнить сложение.)

– Вычисления запишите столбиком.

– Что объединяет данные записи? (Это сложение двузначного и однозначного числа.)

Задание № 8 (с. 47).

– Прочитайте задачу.

– Что вам известно? Что требуется узнать?

– Как узнать, сколько испекли пирожных?

– Выполните сложение в столбик.

– Сколько пирожных положили на каждый поднос?

Используя фишки, учащиеся находят ответ на вопрос.

V. Повторение пройденного материала.

1. Работа с печатной тетрадью № 1.

Задание № 69.

Учащиеся решают математические ребусы.

– Объясните, как вы рассуждали.

Цифра 6 – это сумма единиц. Так как в первом числе 5 единиц, то во втором их должно быть: 6 – 5 = 1.

Цифра 9 – это сумма десятков. Так как во втором числе десятков нуль, то в первом числе их должно быть 9.

Подставляем пропущенные цифры и получаем запись:

Далее учащиеся устно выполняют проверку (95 + 1 = 96).

Задание № 73.

Чертеж:

Учащиеся отмечают точку О, симметричную точке D, красным цветом и точку N, симметричную точке К, синим цветом.

– Что такое ось симметрии?

2. Работа по учебнику.

Задание № 12 (с. 48).

– Прочитайте задание.

– На сколько Петя уменьшил число? (25 –  = 20, значит, число уменьшил на 5 единиц.)

Задание № 13 (с. 48).

– Рассмотрите чертеж. Что здесь изображено?

– На рисунке изображена часть числового луча, на которую начало луча не попало.

– Как можно восстановить единичный отрезок? (Между точками 4 и 6 единичный отрезок должен укладываться два раза, следовательно, он равен 3 клеткам.)

– Назовите координаты точек А и В. (Точка А расположена правее точки (6) и на расстоянии одного единичного отрезка от нее, поэтому координата точки А – число 7 (6 + 1 = 7). Точка В тоже расположена правее точки (6), но уже на расстоянии трех единичных отрезков от нее, поэтому координата точки В – число 9 (6 + 3 = 9).)

VI. Итог урока.

– Что нового узнали на уроке?

– Как выполнить сложение чисел в столбик?

– Что называют числовым лучом? Координатой?

– Что такое ось симметрии?

Домашнее задание: № 14 (учебник); № 72 (рабочая тетрадь).

Задание № 14 (с. 49).

Урок 23
Запись сложения столбиком

Цели урока: совершенствовать навыки решения задач; продолжить формирование умений выполнять сложение чисел столбиком; закреплять знания о многоугольниках; развивать логическое мышление и умение анализировать.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Пирог прямоугольной формы разделите двумя разрезами на 4 части так, чтобы две из них были треугольной формы, а две – четырехугольной.

2. Решите задачу.

Синеглазка встречала гостей. Незнайка пришел раньше Доктора Пилюлькина, а Торопыжка раньше Незнайки. Кто пришел раньше всех?

О т в е т: Торопыжка.

3. Вставьте в свободные клетки числа так, чтобы суммы по всем направлениям были равны.

4. Найдите «лишний» столбик.

5. Какая фигура «лишняя»?

III. Сообщение темы урока.

– Сегодня на уроке мы продолжим изучение темы «Запись сложения столбиком».

IV. Работа над новым материалом.

– Рассмотрите записи и найдите в них ошибки:

Задание № 6 (с. 47).

– Что обозначают выражения:

· «сумма чисел» (сложение);

· «уменьши на 10» (вычитание);

· «разность чисел» (вычитание);

· «увеличена на 42» (сложение).

Далее учащиеся читают задание и записывают выражения.

– Как выполнить действия в выражениях со скобками?

– Найдите значения этих выражений.

Задание № 7 (с. 48).

– Прочитайте задачу.

– Что известно? Что требуется узнать?

– Запишите кратко условие задачи.

Решение:

Ответ: 55 плащей, 59 курток.

V. Повторение пройденного материала.

1. Работа по учебнику.

Задание № 15 (с. 49).

Это задание учащиеся должны выполнять с опорой на свойство многоугольника: «В любом многоугольнике углов, сторон и вершин поровну».

Рассуждать дети могут примерно так:

1) в многоугольнике – 4 угла, следовательно, это четырехугольник;

2) в многоугольнике – 9 вершин, значит, в нем – 9 углов, следовательно, это девятиугольник;

3) в многоугольнике – 12 сторон, значит, в нем – 12 углов, следовательно, это двенадцатиугольник.

Задание № 16 (с. 49).

Так как это одна из первых задач, где учащимся для решения предлагается воспользоваться способом составления выражения, то можно сначала решить эту задачу по действиям, а потом соотнести это решение с предлагаемой в учебнике схемой.

– Прочитайте текст. Можно ли его назвать задачей?

– Прочитайте только условие.

– Что неизвестно? Прочитайте вопрос.

– Запишите кратко условие задачи.

Запись: Приготовили – 50 с. и 40 с.

   Проросло – 30 с.

   Осталось – ? с.

Решение: 1) 50 + 40 = 90 (с.) – приготовили.

   2) 90 – 30 = 60 (с.) – осталось.

О т в е т: 60 саженцев.

Выражение: (50 + 40) – 30 = 60.

2. Работа в печатной тетради № 1.

Задание № 70.

Решение этой задачи позволяет познакомить учащихся со способом нахождения суммы трех слагаемых в столбик.

– Прочитайте задание.

– Сколько денег у каждого?

При ответе на вопрос: «Сколько денег у Юли?» – решение можно записать так:

Обратите внимание детей на то, что для ответа на вопрос: «На сколько денег у Юли меньше, чем у Вити?» – нет необходимости выполнять вычисления. Так как у Вити те же монеты, что и у Юли, да еще 1 копейка, значит, у него на 1 копейку больше, чем у Юли. А у Юли, соответственно, на 1 копейку меньше.

О т в е т: У Юли 65 к.; у Вити 66 к.; на 1 к. меньше.

Задание № 74.

Для того чтобы заполнить пропуски, учащиеся должны уловить закономерность: во-первых, все числа – «круглые», а во-вторых, каждое следующее число на 10 меньше предыдущего. Получим ряд: 100, 90, 80, 70, 60, 50, 40, 30, 20, 10. Особое внимание нужно уделить выполнению следующих двух заданий:

1) Сначала предлагается обвести два любых числа, которые меньше 70.

Предложите детям выполнить это задание самостоятельно.

Вариантов решения может быть несколько, например: 60 и 50, 20 и 10, 40 и 20 и т. д.

Можно задать дополнительный вопрос: «А сколько вариантов решения имеет эта задача?» Сразу же предупредите учеников: «Чтобы не ошибиться в ответе, нужно придумать такой способ перебора вариантов, пользуясь которым мы не пропустим ни одного из решений».

Вот один из таких способов: «Берем ближайшее к 70 меньшее число (60) и для него по порядку подбираем возможные пары: 60 и 50, 60 и 40, 60 и 30, 60 и 20, 60 и 10 (5 вариантов). Далее берем следующее число – 50 и действуем так же: 50 и 40, 50 и 30, 50 и 20, 50 и 10 (4 варианта)».

И так далее:

40 и 30, 40 и 20, 40 и 10 (3 варианта).

30 и 20, 30 и 10 (2 варианта).

20 и 10 (1 вариант).

Всего 15 вариантов: 5 + 4 + 3 + 2 + 1 = 15.

2) Далее предлагается обвести все числа, которые больше 80. (Здесь единственное решение: 100 и 90.)

VI. Итог урока.

– Что нового узнали на уроке?

– Как выполнить сложение трех чисел в столбик?

Домашнее задание: № 17 (учебник). (О т в е т: отрезок.); № 71 (рабочая тетрадь).

 Урок 24
Запись вычитания столбиком

Цели урока: познакомить учащихся с записью вычитания двузначных чисел в столбик; совершенствовать вычислительные навыки; продолжить формирование умений определять название многоугольника; развивать внимание и пространственное мышление.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Вставьте пропущенный арифметический знак и число:

2. Что сделали с кубиком?

3. Выберите в каждом столбике выражение, значение которого будет наибольшим. Проверьте себя!

4. Решите задачу.

Таня спросила Олю: «Сколько лет твоей сестре?»

«А вот догадайся сама, – ответила Оля. – Если к наибольшему однозначному числу прибавить наименьшее двузначное, то узнаешь возраст моей сестры».

– Сколько лет Олиной сестре?

III. Сообщение темы урока.

– Рассмотрите математические записи на доске:

28 – 5 = ?      38 – 10 = ?    

– Какие записи вам незнакомы? Сегодня на уроке мы узнаем, как выполнять вычитание двузначных чисел в столбик.

IV. Работа над новым материалом.

Задание № 1 (с. 50).

– Рассмотрите рисунок в учебнике и объясните, используя цветные палочки, способ вычитания 13 из 27.

– Сколько и каких палочек потребовалось Волку и Зайцу для составления «поезда», обозначающего число 27? (Два оранжевых «вагона» и семь белых.)

– Какие «вагоны» они отцепили и почему? (Один оранжевый «вагон» и три белых.)

– Как же получили число 14? (Число 14 можно получить, если из 7 единиц вычесть 3 единицы, а из 2 десятков – 1 десяток.)

– Рассмотрите первый случай записи вычитания в столбик.

– Как подписаны числа одно под другим?

– По какому правилу выполняется вычитание?

Далее учащиеся рассматривают и объясняют вычитание чисел в столбик аналогично.

Памятка

Вычитание чисел в столбик.

1. Записываем уменьшаемое.

2. Записываем вычитаемое на второй строчке (единицы под единицами, десятки под десятками).

3. Вычитаем единицы.

4. Вычитаем десятки.

5. Читаем ответ.

Задание № 2 (с. 51).

Учащиеся работают в парах. Используя цветные палочки, они находят результат вычитания.

Задание № 3 (с. 51).

Учащиеся выполняют вычитание двузначных чисел в столбик с комментированием.

V. Повторение пройденного материала.

1. Работа в печатной тетради № 1.

Задание № 76.

– Что обозначает последняя цифра в записи каждого числа? (Количество единиц.)

– Как вы думаете, нужно ли выполнять вычитание чисел полностью?

– Что необходимо вычислить? (Только разность единиц.)

1. Из 36 вычесть 2. В числе 36 шесть единиц, а в числе 2 две единицы. Находим разность единиц: 6 – 2 = 4. Значит, разность чисел 36 и 2 оканчивается цифрой 4. Этот пример подчеркивать не надо.

2. Из 56 вычесть 30. В числе 56 шесть единиц, а в числе 30 нуль единиц. Находим разность единиц: 6 – 0 = 6. Значит, разность чисел 56 и 30 оканчивается цифрой 6. Подчеркиваю этот пример. (И так далее.)

2. Работа по учебнику.

Задание № 15 (с. 53).

Учащиеся работают самостоятельно.

I вариант – 1-й столбик;

II вариант – 2-й столбик.

Взаимопроверка в парах.

Задание № 16 (с. 53).

– Какую фигуру называют пятиугольником?

– Рассмотрите данный чертеж. Есть ли здесь пятиугольник?

а) Задание имеет два решения:

б) Задание имеет одно решение:

Задание № 17 (с. 53).

– Закончите фразы и объясните, почему вы выбрали именно эту единицу длины.

Правильные ответы:

Длина комнаты – 3 метра.

Высота стакана – 11 сантиметров.

Ширина тетради – 2 дециметра.

Последние два задания направлены на усвоение изученных зависимостей между единицами длины.

                 1 м = 100 см

                 1 м = 10 дм

VI. Итог урока.

– Что нового узнали на уроке?

– Как выполнить вычитание двузначных чисел в столбик?

– Какие единицы длины вы знаете?

– Какой многоугольник называют пятиугольником?

Домашнее задание: № 11, № 12, 3-й столбик (учебник); № 75 (рабочая тетрадь).

Урок 25
Запись вычитания столбиком.
Решение задач

Цели урока: продолжить формирование умений выполнять вычитание двузначных чисел в столбик; совершенствовать навыки решения и преобразования задач; развивать умение анализировать и рассуждать.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Рассмотрите фигуры в каждом ряду и найдите «лишнюю».

2. Решите задачу.

Миша, Олег и Саша играют в песочнице. У них три машины: подъемный кран, бортовой «КамАЗ» и самосвал «ЗИЛ». Миша не приносил подъемный кран и самосвал «ЗИЛ». Олег не приносил самосвал «ЗИЛ». Какую машину принес каждый мальчик?

Миша – бортовой «КамАЗ».

Олег – подъемный кран.

Саша – самосвал «ЗИЛ».

3. Рассмотрите рисунок.

– Сколько горошин может быть в каждом стручке?

4. В какой фигуре кубиков больше?

III. Сообщение темы урока.

– Сегодня на уроке будем выполнять вычитание двузначных чисел в столбик.

IV. Работа над новым материалом.

– Рассмотрите математические записи на доске:

– Какие ошибки допущены?

Задание № 4 (с. 51).

– Чем похожи все выражения? (В каждом выражении есть скобки, надо выполнить два действия.)

– Какое действие надо выполнять первым? (В скобках.)

– Сформулируйте правила сложения и вычитания двузначных чисел.

Запись:

                 и т. д.

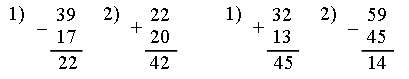
Задание № 5 (с. 51).

– Что значит выражение «уменьшить на 23»? (Выполнить вычитание.)

Учащиеся записывают вычитание двузначных чисел в столбик и выполняют проверку действием сложения столбиком.

Запись:                        Проверка:  

Задание № 6 (с. 51).

– Объясните, что значит выражение «на сколько больше...». (Чтобы узнать, на сколько одно число больше или меньше другого, надо из большего числа вычесть меньшее.)

Далее учащиеся выполняют вычитание чисел столбиком и в строчку:

V. Повторение пройденного материала.

1. Работа в печатной тетради № 1.

Задание № 79.

Учитель демонстрирует перед учащимися различные модели геометрических тел: куб, шар, конус, цилиндр.

– Найдите геометрическое тело, которое имеет такую же форму, что и шкатулка. (Это куб.)

– Рассмотрите модель куба.

– Покажите грани куба. Какую форму имеет каждая грань? (Форму квадрата.)

– Сколько всего граней? (Шесть.)

– Покажите верхнюю, нижнюю и переднюю грань.

– Покажите стороны нижней грани. Сколько их? (Четыре.)

– Покажите вершины верхней грани. Сколько их? (Четыре.)

Далее учащиеся выполняют задание в тетради.

2. Работа по учебнику.

Задание № 19 (с. 54).

– Прочитайте задачу.

– Что известно? Что требуется узнать?

– Запишите кратко условие задачи и решите ее.

Решение:

5 – 2 = 3 (чел.) – осталось.

Ответ: 3 человек.

– Почему задачу решали вычитанием? («Осталось на 2 меньше».)

– Измените условие задачи так, чтобы для ее решения надо было выполнить сложение. (Слово «меньше» заменить словом «больше».)

– Запишите кратко условие задачи и решите ее.

Решение:

5 + 2 = 7 (чел.) – осталось.

Ответ: 7 чел.

– Сравните эти задачи.

– Как надо изменить вопрос задачи, чтобы она решалась в два действия? (Вопрос: «Сколько человек было в аптеке первоначально?»)

– Решите новую задачу.

Задание № 20 (с. 54).

Задание направлено на развитие глазомера учащихся. На первый взгляд кажется, что футляр вполне подходит для очков как по ширине, так и по длине. Выполнив измерения, учащиеся убедятся, что футляр не подходит по длине.

Длина футляра – 5 см, длина очков – больше 5 см.

VI. Итог урока.

– Что нового узнали на уроке?

– Какое геометрическое тело называют кубом?

– Как выполнить сложение и вычитание двузначных чисел?

Домашнее задание: № 15 (учебник); № 80, 81 (рабочая тетрадь).

Урок 26
Запись вычитания столбиком

Цели урока: совершенствовать вычислительные навыки; продолжить формирование умений решать составные задачи; вести подготовку к решению уравнений; развивать внимание и логическое мышление.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Догадайтесь, по какому правилу составлены ряды чисел:

а) 3, 8, 38, 4, 7, 47, 5, 6, 56, …

б) 3, 5, 53, 4, 6, 64, 5, 7, 75, …

в) 35, 38, 41, 44, 47, 50, …

2. Вставьте в «окошки» числа, чтобы получились верные равенства:

3. Задача.

Слон может прожить 60 лет, а лошадь – 20. На сколько лет дольше живут слоны?

4. Какой путь самый короткий?

III. Сообщение темы урока.

– Сегодня на уроке мы будем решать задачи и примеры на сложение и вычитание двузначных чисел, используя запись в столбик.

IV. Работа над новым материалом.

Задание № 7 (с. 51).

– Прочитайте задачу.

– Что известно в задаче? Что требуется узнать?

– Запишите кратко условие задачи и решите ее.

Запись: Было – 65 р.

   Потратила – 42 р.

   Осталось – ? р.

Решение:

Ответ: 23 рубля; 84 рубля.

Задания № 8, 10 (с. 51–52).

Способы рассуждений, рассматриваемые в этом задании, будут в дальнейшем основными при решении уравнений вида:  24 + х = 36 и 49 – х = 16. Поэтому надо не спеша и обстоятельно со всем классом прочитать текст учебника и в нем разобраться.

Для закрепления можно предложить аналогичные упражнения, например:

1. Какое число «машина» прибавила?

2. Какое число «машина» вычла?

Задание № 12 (с. 52).

– Прочитайте текст. Можно ли его назвать задачей?

– Прочитайте условие.

– Найдите и прочитайте вопрос.

– Запишите кратко условие задачи и решите ее.

Решение:

О т в  е т: 33 года, 21 год.

– Почему решали задачу вычитанием?

Задание № 13 (с. 52).

– Прочитайте задачу.

– Что известно? Что требуется узнать?

– Запишите кратко условие задачи.

Запись: Всего – 95 уч.

   В кино – 30 уч.

   В музей – 23 уч.

   В театр – ? уч.

– Решите задачу двумя способами по действиям.

I способ.

1) 95 – 30 = 65 (уч.) – второклассников пошли на экскурсию и в театр;

2) 65 – 23 = 42 (уч.) – второклассника поехали в театр.

II способ.

1) 30 + 23 = 53 (уч.) – второклассника пошли в кино и в музей;

2) 95 – 53 = 42 (уч.) – второклассника поехали в театр.

О т в е т: 42 уч.

Вместе с тем дети уже знакомились с новой для них формой записи решения – выражением, поэтому можно поставить перед ними дополнительное условие: использовать в качестве формы записи выражение. При этом слабым ученикам предложите в помощь следующую карточку:

V. Повторение пройденного материала.

1. Работа по учебнику.

Задание № 22 (с. 55).

Это логическая задача. Перед выполнением этого задания учитель проводит с опорой на наглядность решение аналогичной ситуации.

Учитель берет непрозрачный пакет и на глазах детей кладет в него, например, 2 яблока и 3 груши (или любые другие предметы разной формы, которые легко узнать на ощупь).

Далее работа организуется так. Учащимся задаются вопросы:

– Сколько в пакете груш и яблок? (3 груши и 2 яблока.) Давайте подумаем, сколько раз можно вытащить по одному фрукту, чтобы обязательно достать грушу? Смотрите, я вытаскиваю один фрукт. (Рука учителя в пакете.) Обязательно ли это груша? (Нет, так как в пакете не только груши, но и 2 яблока.) (Учитель вытаскивает яблоко.) Действительно, в первый раз я могу вытащить не грушу, а яблоко. Сколько груш и яблок теперь осталось в пакете? (3 груши и 1 яблоко.) Вытаскиваю фрукт второй раз. Как вы думаете, это обязательно груша? (Нет, так как в пакете остались не только груши, но и 1 яблоко.) (Учитель опять вытаскивает яблоко.) Второй раз я снова могу вытащить яблоко. Сколько груш и яблок осталось в пакете? (3 груши и ни одного яблока.) Буду вытаскивать в третий раз. Как вы считаете, это обязательно груша? (Да, так как в пакете яблок больше нет.)

Делаем вывод: число возможных попыток у нас зависело не от числа груш, а от числа яблок.

Учитель убирает яблоки в пакет. Перед детьми ставится проблема:

– Сколько раз нужно вытащить по одному фрукту, чтобы обязательно достать яблоко? (Ученики быстро сообразят, что число попыток в этом случае зависит не от числа яблок, а уже от числа груш.) (Так как в пакете 3 груши, то мы можем гарантировать, что только в четвертый раз обязательно достанем яблоко.)

Теперь можно переходить к задаче, сформулированной в учебнике. Рассуждение аналогично.

Выводы:

1. Так как конфет «Смородина» – четыре, то надо взять не меньше пяти конфет, чтобы обязательно вытащить «Малину».

2. Так как конфет «Малина» – пять, то надо взять не меньше шести конфет, чтобы обязательно вытащить «Смородину».

2. Работа в печатной тетради № 1.

Задание № 85.

– Прочитайте задачу.

– Что известно? Что требуется узнать?

– Запишите решение задачи по действиям.

Оформить решение задачи в тетради учащиеся должны следующим образом:

Решение:

1) 15 · 3 = 15 + 15 + 15 = 45 (гр.) – нашли.

2) 45 – 25 = (гр.) – пожарили.

Ответ: 20 грибов.

При выполнении первого действия учащиеся используют фишки.

VI. Итог урока.

– Что нового узнали на уроке?

– Как выполнять сложение и вычитание двузначных чисел в столбик?

– Какие единицы длины вы знаете?

Домашнее задание: № 19 (учебник); № 80 (рабочая тетрадь).

Урок 27
Сложение двузначных чисел (общий случай)

Цели урока: рассмотреть общие приемы сложения двузначных чисел; совершенствовать навыки решения задач; развивать умение рассуждать и обобщать.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Чем похожи и чем отличаются друг от друга числа в каждой паре:

2. По какому правилу записан каждый ряд чисел:

а) 90, 60, 70, 40, 50, 20, 30, 0, 10;

б) 10, 30, 20, 40, 30, 50, 40, 60, 50.

3. Найдите значения выражений:

30 + 20 – 40 + 60 – 50 + 20 + 40 =

80 – 30 – 10 + 50 – 70 + 60 – 80 =

90 – 60 + 20 – 40 + 60 + 20 – 50 =

30 + 40 – 60 + 80 – 20 – 60 + 10 =

20 + 70 – 50 + 30 – 60 + 80 – 90 =

4. Сколько отрезков с отмеченными концами можно найти на этом рисунке?

III. Сообщение темы урока.

– Сравните выражения каждого столбика:

– Чем отличаются выражения первого столбика от выражений второго столбика?

– Сегодня на уроке рассмотрим сложение двузначных чисел в пределах 100 с переходом через десяток.

IV. Изучение нового материала.

Подготовительные задания:

1) Назовите число, которое на 1 больше каждого из чисел:

6, 4, 8, 7, 0, 2, 9, 1, 5, 3.

2) Число 6 можно записать так: . Какое число означает каждая из записей: ?

Примечание.

Очень важно выработать у учащихся умение воспринимать подобные записи. Например,   как запись числа 6, являющегося суммой 5 и 1. Во-первых, это предупредит весьма распространенную ошибку, допускаемую детьми: в тех случаях, когда при сложении единиц в результате получается число, большее 10, они, сложив десятки, забывают прибавлять к ним еще 1 десяток. Во-вторых, представляется возможность сократить число шагов алгоритма сложения, что тоже немаловажно для выработки скорости вычислений.

Задание № 1 (с. 56).

– Рассмотрите рисунок на с. 56 и объясните, как Волк и Заяц выполняли сложение вида 27 + 15.

Один из учащихся рассказывает, что и как выполняют Волк и Заяц, а остальные дети работают параллельно, используя наборы оранжевых и белых палочек.

Задача: найти сумму 27 и 15.

Волк и Заяц составили «поезд» из 2 оранжевых и 7 белых «вагонов» и «поезд» из 1 оранжевого и 5 белых «вагонов». Затем к первому «поезду» они прицепляют слева один оранжевый, а справа – 5 белых «вагонов» из второго «поезда». Получился новый «поезд», в котором 3 оранжевых и 12 белых «вагонов». Но 12 – это 1 десяток и 2 единицы. Поэтому Волк и Заяц десяток белых «вагонов» заменили одним оранжевым «вагоном».

Длина «поезда» не изменилась. Получилось 4 оранжевых и 2 белых «вагона». Поезд обозначает число 42. Значит, сумма 27 и 15 равна 42.

Далее переходите к рассмотрению записи сложения этих чисел столбиком.

7 + 5 – двенадцать: 1 десяток (пишем маленькую цифру 1 над цифрой 2) и 2 единицы (пишем 2 под 5), 3 + 1 – четыре (пишем 4 под 1). Получается 42. В дальнейшем можно сократить рассуждение, сделать его более лаконичным.

Рассмотрите со всем классом следующие примеры:

Пример 1: сложить 64 и 29.

Объяснение: 4 + 9 – тринадцать: 1 десяток 3 единицы, 7 + 2 – девять. Сумма 93.

Пример 2: сложить 75 и 6.

Объяснение: 5 + 6 – одиннадцать: 1 десяток 1 единица, 8 + 0 – восемь. Сумма 81.

Пример 3: сложить 4 и 58.

Объяснение: 4 + 8 – двенадцать: 1 десяток 2 единицы, 1 + 5 – шесть. Сумма 62.

Задание № 2 (с. 57).

Учащиеся работают в парах. Используя цветные палочки, они находят значение сумм с переходом через десяток.

Задание № 3 (с. 57).

Учащиеся выполняют задание с комментированием у доски, записывая сложение чисел в столбик.

V. Повторение пройденного материала.

1. Работа в печатной тетради № 1.

Задание № 85.

Если у учащихся нет возможности воспользоваться калькулятором, то выполнить проверку они смогут с помощью цветных палочек, что подготовит второклассников к изучению следующей темы.

Рассмотрим первый пример. Дети письменно выполняют вычисления и заполняют окошко.

2. Работа по учебнику.

Задание № 10 (с. 58).

– Прочитайте текст. Является ли он задачей? Почему?

– Что известно в задаче? Что требуется узнать?

– Все ли необходимые данные есть в тексте?

– Какие данные для решения задачи нужно взять из рисунка?

– Рассмотрите рисунок. Выполните схему к условию задачи.

Решение:

49 – 45 = 4 (см).

Ответ: 4 см.

Задание № 11 (с. 58).

– Прочитайте задание.

– Какая команда одержала победу? (Команда «Вымпел».)

– Сколько очков составила разница в счете? Какое действие необходимо выполнить? (Вычитание, так как узнаем, на сколько больше очков у одной команды, чем у другой.)

Запись:

Задание № 12 (с. 58).

– Рассмотрите рисунок. Какое действие надо выполнить, чтобы найти высоту второго этажа?

Запись: 4 м 69 см – 2 м 35 см = 2 м 34 см.

VI. Итог урока.

– Что нового узнали на уроке?

– Как выполнить сложение чисел с переходом через десяток?

– Что означает запись: ?

Домашнее задание: № 8, 9 (учебник); № 83, 84 (рабочая тетрадь).

Урок 28
Сложение двузначных чисел (общий случай)

Цели урока: совершенствовать вычислительные навыки; продолжить формирование умений составлять задачи по иллюстрации и решать их; закреплять знания о многоугольниках; развивать умения анализировать и сравнивать.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Работа с калькулятором.

– Наберите на калькуляторе любое двузначное число.

– Подумайте, на сколько можно его увеличить, чтобы изменялась только цифра, обозначающая десятки, а цифра, обозначающая единицы, не изменялась? Проверьте свои предположения на различных числах.

2. Задача.

– Чем похожи тексты задач? Чем отличаются? Какую задачу вы можете решить? Какую – нет?

– Почему?

– Решите вторую задачу.

3. Какие числа нужно вставить в «окошки», чтобы получились верные равенства:

4. Сколько здесь треугольников?

О т в е т: ∆АВС, ∆АВЕ, ∆ВСЕ, ∆ACD, ∆ADE, ∆CDE, ∆BCD, ∆ABD.

III. Сообщение темы урока.

– Сегодня мы продолжим закреплять навыки сложения двузначных чисел с переходом через десяток.

IV. Работа над темой урока.

Задание № 4 (с. 57).

– Прочитайте математические записи, используя выражения: «сумма чисел», «разность чисел», «уменьшить на», «увеличить на».

– Чем похожи все выражения? (В них есть скобки.)

– Какое действие выполняется первым в выражении со скобками?

– Проверьте, верно ли выполнены вычисления.

Запись:

(27 + 45) + 8 = 80        96 – (13 + 57) = 36    и т. д.

Задание № 5 (с. 57).

– Что необходимо знать, чтобы установить стоимость покупки?

– Все ли необходимые данные для этого содержатся в тексте?

– Запишите кратко условие задачи и решите ее по действиям.

Запись:

V. Повторение пройденного материала.

1. Работа по учебнику.

Задание № 15 (с. 60).

– Прочитайте задачи.

– Сравните условия и вопросы задач. (Вопрос одинаков, а условия разные.)

– Что известно в каждой задаче?

– Что требуется найти?

– Каким действием решается каждая задача?

– Достаточно ли данных для решения каждой задачи? (Вторая задача с недостающими данными.)

– Запишите кратко условия данных задач.

Задача 1.

Задача 2.

– Какими данными нужно дополнить условие второй задачи? («Марок купил на 4 больше, чем значков».)

Далее учащиеся работают самостоятельно.

Задание № 16 (с. 60).

Последовательность чисел составлена по принципу: из первого числа вычитается 5, а затем к полученному числу прибавляется 10. И так далее:

Следующее число: 25 – 5 = 20.

Задание № 17 (с. 60).

– Рассмотрите данные на рисунке фигуры. Как их можно назвать? (Это все многоугольники.)

– Какие фигуры называют многоугольниками?

– Как определить название многоугольника? (По количеству в нем углов, вершин, сторон.)

– Какие многоугольники называют четырехугольниками?

– Назовите номера всех четырехугольников. (1, 3, 4.)

– Какой четырехугольник является «лишним»? (3, так как это невыпуклый четырехугольник.)

– Назовите признаки выпуклых многоугольников.

Задание № 18 (с. 60).

– Рассмотрите данные фигуры.

– Что их объединяет? (Это многоугольники.)

– На какие две группы можно разбить данные многоугольники? Укажите признак каждой группы.

I группа (1, 2) – выпуклые многоугольники;

II группа (3, 4) – невыпуклые многоугольники.

– Какие из данных фигур являются пятиугольниками? (3.)

2. Работа в печатной тетради № 1.

Задание № 87.

Рассмотрим, как должны рассуждать учащиеся.

Сумма единиц складываемых чисел равна 9. Так как во втором числе 7 единиц, то в первом их должно быть: 9 – 7 = 2. Сумма десятков тоже равна 9.

Так как в первом числе 6 десятков, то во втором их должно быть: 9 – 6 = 3.

Подставляем вместо точек найденные цифры. Далее устно выполняется проверка.

Задание № 88.

Учащиеся выбирают правильный ответ – «нет».

Далее учитель проводит дополнительную работу с текстом задачи.

– Кого больше в стаде: коров или быков? (Коров.)

– А как узнать, на сколько больше коров? Выполните вычисления устно. (Из 24 вычесть 3, получится 21.)

– А на сколько меньше быков, чем коров? (На 21.)

– Можно ли узнать, сколько всего коров и быков в стаде? Как это сделать? (24 + 3 = 27.)

– Пусть в стаде 2 теленка. Можно ли теперь ответить на вопрос задачи?

– Как проще всего решить задачу? (27 + 2 = 29.)

VI. Итог урока.

– Что нового узнали на уроке?

– Какую фигуру называют многоугольником?

– Как определить название многоугольника?

Домашнее задание: № 13, 14 (учебник); № 86 (рабочая тетрадь).

Урок 29
Сложение двузначных чисел (общий случай)

Цели урока: закреплять знания учащихся о симметричных фигурах, о многоугольниках; совершенствовать частные и общие приемы сложения двузначных чисел; рассмотреть способы преобразования задач; развивать внимание и память.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Задачи.

– Сравните тексты задач.

– Чем они похожи?

– Чем они отличаются?

– Как можно дополнить условие каждой задачи, чтобы ответить на поставленный вопрос?

2. Маша и Катя стреляли из лука. Кто из них оказался победителем после трех попыток?

Кто набрал очков больше и на сколько?

3. Чему равна масса арбуза? Чему равна масса дыни?

4. Найдите признак, по которому данные фигуры можно разбить на две группы.

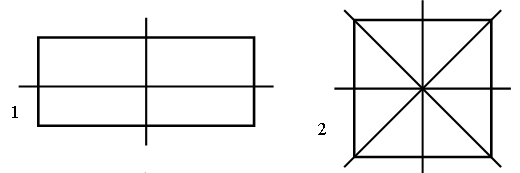
I группа (1, 4, 6) – фигуры, которые имеют две оси симметрии;

II группа (2, 3, 5) – фигуры, которые имеют более двух осей симметрии.

– Что такое ось симметрии?

– Какие фигуры называют симметричными?

III. Сообщение темы урока.

– Сегодня мы продолжим закреплять навыки двузначных чисел.

IV. Работа по теме урока.

1. Работа по учебнику.

Задание № 6 (с. 57).

– Прочитайте текст. Можно ли его назвать задачей? Почему?

– Что известно в задаче?

– Что требуется узнать?

– Запишите кратко условие задачи и решите ее.

Запись: Было – ? кн.

   Взяли – 8 кн.

   Осталось – 12 кн.

Решение:

12 + 8 = 20 (кн.) – было.

О т в е т: 20 книг.

– Измените вопрос задачи так, чтобы она решалась вычитанием. («На сколько больше книг осталось на полке, чем взяли?» 12 – 8 = 4 (кн.).)

Задание № 7 (с. 57).

– Прочитайте условие задачи.

– Что известно? Что требуется узнать?

– Запишите кратко условие задачи и решите ее разными способами.

Запись: Было – 15 в. и 28 в.

   Отцепили – 3 в.

   Стало – ? в.

   Решение:

Задание № 19 (с. 61).

– Рассмотрите чертеж. Что на нем изображено?

– Что называют числовым лучом?

– Прочитайте задание к чертежу.

Учащиеся должны рассуждать примерно так: «Координата точки А – число 15, значит, эта точка расположена на расстоянии 15 единиц от начала числового луча. Координата точки В – число 9, значит, эта точка расположена на расстоянии 9 единиц от начала числового луча. Найдем, на сколько единиц дальше от начала числового луча находится точка А, чем точка В: 15 – 9 = 6. Ответ: на 6 единиц».

Задание № 21 (с. 61).

– Прочитайте задание и выполните схематичный рисунок.

2. Работа в печатной тетради № 1.

Задание № 90.

Учащиеся проводят ось симметрии в каждой фигуре.

V. Самостоятельная работа.

I вариант.

№ 1. Запишите числа с помощью цифр.

№ 2. Решите примеры.

№ 3. Решите задачу.

Миша и Маша собрали 86 кг яблок. Миша собрал 51 кг яблок. Сколько килограммов яблок собрала Маша?

№ 4. Укажите номера пятиугольников.

II вариант.

№ 1. Запишите числа с помощью цифр.

№ 2. Решите примеры.

№ 3. Решите задачу.

С двух участков собрали 74 ведра картофеля. С одного участка собрали 43 ведра картофеля. Сколько ведер картофеля собрали с другого участка?

№ 4. Укажите номера четырехугольников.

VI. Итог урока.

– Что нового узнали на уроке?

– Какие фигуры называют симметричными?

– Что такое числовой луч?

Домашнее задание: № 20, 22 (учебник); № 89 (рабочая тетрадь).

Урок 30
Вычитание двузначных чисел
(общий случай)

Цели урока: рассмотреть вычитание двузначных чисел с переходом в другой разряд; совершенствовать вычислительные навыки; продолжить формирование умений составлять и преобразовывать задачи; вести подготовительную работу к изучению уравнений; развивать умение анализировать и рассуждать.

Ход урока

I. Организационный момент.

II. Устный счет.

Вставьте в «окошки» однозначные числа, чтобы получились верные равенства:

2. Покажите отрезками рост каждой девочки, если Ира и Лена одинакового роста, Лена выше Оли, а Таня выше Иры. Напишите, кто выше всех: Таня или Оля. _____________

          Таня    Ира    Лена    Оля

3. Рассмотрите рисунок. Не нарушая закономерности, дорисуйте недостающий флажок.

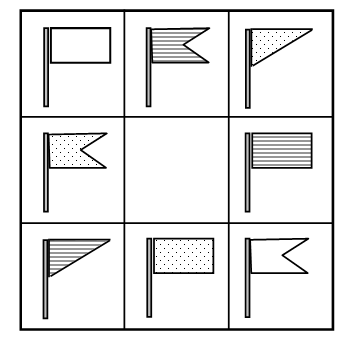
4. Рассмотрите внимательно рисунки. Чем они похожи? Чем отличаются?

Подберите к рисункам числовые выражения и объясните, что обозначает каждое число в этих выражениях.

– Чем похожи выражения верхнего и среднего ряда? Чем похожи выражения нижнего ряда?

– Найдите значение каждого выражения.

III. Сообщение темы урока.

– Рассмотрите математические записи на доске:

– Чем отличаются выражения каждого столбика?

– Сегодня на уроке мы рассмотрим прием поразрядного вычитания в случае, когда в разряде единиц уменьшаемого их меньше, чем в разряде единиц вычитаемого.

IV. Изучение нового материала.

Перед рассмотрением общего случая вычитания двузначных чисел учитель предлагает подготовительные упражнения:

1. Назовите разность:  12 и 5        11 и 4

       17 и 8        13 и 7

       10 и 8        12 и 6

2. Назовите число на 1 меньше, чем каждое из чисел: 8, 4, 9, 6, 5, 1, 3, 2, 7.

3. Число 5 можно записать так: .

Какое число означает каждая из записей: ?

Задание № 1 (с. 62).

– Рассмотрите рисунок и объясните, как выполняли вычитание 52 – 37 Волк и Заяц, используя цветные палочки.

Итак, действуем, как раньше. Составим «поезд» из 5 оранжевых и 2 белых «вагонов»:

От него нужно отцепить 3 оранжевых и 7 белых «вагонов». Но у нас всего 2 белых «вагона». Поэтому возьмем один оранжевый «вагон» (лучше примыкающий к белым) и заменим его 10 белыми «вагонами». Теперь у нас получился поезд, состоящий из 4 оранжевых и 12 белых «вагонов»: число 52 будет выглядеть так:

От 12 белых «вагонов» отцепляем 7, остается 5 белых «вагонов», а от 4 оранжевых отцепляем 3:

Остается «поезд», состоящий из 1 оранжевого «вагона» и 5 белых «вагонов». Он обозначает число 15.

Данная форма записи особенно эффективна на первоначальном этапе освоения детьми алгоритма вычитания. Когда второклассники приобретут необходимые навыки вычитания, можно будет перейти к общепринятой записи.

На с. 62 учебника приведены примеры на вычитание, записанные столбиком. Рассмотрите их со всем классом подробно, не торопясь, с необходимыми комментариями, привлекая учащихся к объяснению шагов алгоритма. Приведем образцы рассуждений.

Пример 1.

О б ъ я с н е н и е: 2 меньше 7. Из 5 десятков возьмем 1 десяток (ставим над 5 точку). В десятке – 10 единиц (запишем 10 над 2). 12 без 7 – это 5 (пишем 5 под 7), 4 без 3 – это 1 (пишем 1 под 3). Разность – 15.

Пример 2.

О б ъ я с н е н и е: 7 меньше 8. Берем 1 десяток. 17 без 8 – это 9, 4 без 4 – это 0. Впереди 9 единиц нуль не пишем. Разность – 9.

Пример 3.

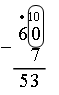
О б ъ я с н е н и е: 0 меньше 7. Берем 1 десяток. 10 без 7 – это 3, 5 без 0 – это 5. Разность – 53.

Задание № 2 (с. 63).

Учащиеся выполняют вычитание столбиком на доске, комментируя каждое действие.

Задание № 3 (с. 63).

– Что означают выражения «на сколько больше», «на сколько меньше»?

– Какое действие необходимо выполнить?

– Выполните вычитание чисел, записывая решение в столбик.

V. Повторение пройденного материала.

1. Работа по учебнику.

Задание № 14 (с. 65).

– Прочитайте условие задачи.

– Что известно?

– Что требуется узнать?

– Что необходимо сделать, чтобы ответить на вопрос задания? (Сравним длины сторон ковра с длиной и шириной комнаты. Длина комнаты больше, а ширина меньше длины стороны ковра:

5 м больше 4 м,

3 м 50 см меньше 4 м.

Поэтому ковер уложится вдоль длинной стены комнаты и не уложится вдоль короткой. Значит, ковер не подойдет для этой комнаты.)

Задание № 16 (с. 65).

– Прочитайте текст. Является ли он задачей? Объясните  почему.

– Что известно в задаче?

– Что требуется узнать?

– Сколько скамеек поставили в парке? (15 + 9 = 24.)

– Что необходимо изменить в задаче, чтобы она решалась в два действия? (Изменить надо условие, а не вопрос.)

– Предложите несколько вариантов новых задач.

· В парке поставили 12 синих скамеек, а зеленых – на 6 больше. Сколько скамеек поставили в парке?

Решение: 1) 12 + 6 = 18 (ск.) – зеленых.

   2) 12 + 18 = 30 (ск.) – всего.

О т в е т: 30 скамеек.

· В парке поставили 15 синих скамеек, а зеленых на 6 скамеек меньше. Сколько всего скамеек поставили в парке?

 

Решение: 1) 15 – 6 = 9 (ск.) – зеленых.

  2) 15 + 9 = 24 (ск.) – всего.

О т в е т: 24 скамейки.

· В парке поставили 15 синих, 9 зеленых и 14 желтых скамеек. Сколько скамеек поставили в парке?

Решение: 1) 15 + 9 = 24 (ск.) – синих и зеленых.

  2) 24 + 14 = 38 (ск.) – всего.

О т в е т: 38 скамеек.

2. Работа в печатной тетради № 1.

Задание № 89.

Рассмотрим на примере, как учащиеся должны рассуждать при выполнении этого задания.

В «машину» ввели неизвестное число. «Машина» вычла из него 19. Из «машины» вышло число 64. К неизвестному числу стрелка не идет. Изображаем «машину», обратную данной: «+ 19»:

Идем по стрелке: 64 + 19. Выполняем вычисления:

Получили 83. Значит, неизвестное число 83. Записываем его:

Выполним проверку. Идем по верхней стрелке:

Значит, неизвестное число нашли верно.

VI. Итог урока.

– Что нового узнали на уроке?

– Что означают записи: ?

Домашнее задание: № 4, 15 (учебник); № 91 (рабочая тетрадь).

Урок 31
Вычитание двузначных чисел (общий случай)

Цели урока: продолжить работу по формированию навыка выполнения вычитания двузначных чисел с переходом в другой разряд; совершенствовать навыки решения задач; закреплять знания о свойствах многоугольника и умения чертить многоугольник с известными длинами сторон; развивать умение анализировать и обобщать.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Заполните таблицу.

2. Задача.

Корзинка с фруктами весит 11 кг, а фрукты весят на 10 кг больше корзинки. Сколько весит корзинка?

3. По какому правилу составлена каждая строка таблицы? Запишите числа в пустые клетки:

4. Сколько треугольников на каждом чертеже?

III. Сообщение темы урока.

– Решите ребусы:

 – 2 = 98

 – 1 = 99

– Как выполнить вычитание любого трехзначного числа из 100? Об этом вы узнаете сегодня на уроке.

IV. Работа по теме урока.

– Рассмотрите запись:

– Объясните, как выполнено вычитание.

О б ъ я с н е н и е (полное): 0 меньше 6, поэтому нужно взять 1 десяток. Но в разряде десятков их 0, поэтому берем 1 сотню (ставим точку над 1). В сотне 10 десятков (пишем 10 над первым нулем слева). Теперь из 10 десятков возьмем 1 десяток (ставим точку над 10 и пишем 10 над 0 справа). 10 без 6 – это 4 (пишем 4 под 6), 9 без 7 – это 2 (пишем 2 под 7). Сотен не осталось. Разность – 24.

О б ъ я с н е н и е (краткое): в разрядах единиц и десятков стоят нули. Берем 1 сотню. В сотне 10 десятков. Берем 1 десяток. 10 без 6 – это 4, 9 без 7 – это 2. Разность – 24.

Задание № 6 (с. 63).

– Какое число надо подставить в окошко в выражениях первого столбика, чтобы получилась верная запись? Какое действие необходимо выполнить? (В первом столбике ищем вычитаемое, поэтому из уменьшаемого надо вычесть значение разности.)

Запись:                100 –  = 19          58 –  = 39

                   100 – 81 = 19          58 – 19 = 39

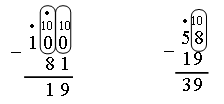
– Сравните выражения второго столбика. Чем они похожи? (Надо найти второе слагаемое.)

– Как найти неизвестное слагаемое? (Надо из суммы вычесть известное слагаемое.)

Запись:                  43 +  = 60          8 +  = 31

                    43 + 17 = 60          8 + 23 = 31

Задание № 5 (с. 63).

– Сравните все выражения. Чем они похожи? (В каждом есть скобки.)

– В каком порядке надо выполнять действия в выражениях со скобками?

– Вычислите их значения.

(95 – 28) + 17 = 84            (50 – 18) – 23 = 9    И т. д.

Задание № 7 (с. 63).

– Прочитайте текст. Можно ли его назвать задачей? Почему?

– Рассмотрите рисунок и решите задачу.

Решение:

О т в е т: 48 м.

– Выполните проверку решения.

– Больше или меньше метров осталось пробежать спортсмену, чем он уже пробежал? (Меньше.)

– На сколько метров меньше?

Задание № 8 (с. 64).

– Прочитайте текст. Является ли он задачей? Почему?

– Что известно?

– Что надо узнать?

– Выполните чертеж к этому заданию.

Решение:

О т в е т: 58 м.

V. Повторение пройденного материала.

1. Работа по учебнику.

Задание № 17 (с. 66).

Учащиеся составляют граф:

Опираясь на граф, учащиеся легко составляют и читают высказывания со словом «больше».

· 70 больше 38;

· 70 больше 64;

· 64 больше 38.

2. Работа в печатной тетради № 1.

Задание № 96.

Построить пятиугольник учащиеся могут различными способами, причем от способа построения зависят и длины сторон.

VI. Итог урока.

– Что нового вы узнали на уроке?

– Какие правила составления граф вы знаете?

– Как найти неизвестное слагаемое? Уменьшаемое?

Домашнее задание: № 10 (учебник); № 92 (рабочая тетрадь).

Урок 32
Вычитание двузначных чисел (общий случай)

Цели урока: совершенствовать навыки вычитания двузначных чисел (общий случай), умения решать задачи разными способами; продолжить формирование умений выделять симметричные фигуры; закреплять знания об объемных фигурах (конусе, цилиндре); развивать внимание и пространственное мышление.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Задачи.

– Прочитайте и сравните задачи.

Подумайте, в какой задаче вы можете ответить на вопрос, а в какой – нет и почему?

2. Игра-соревнование.

Проверьте себя. Сколько клеток вы можете заполнить за 1 минуту?

3. В равенстве из спичек допущена ошибка. Переложите спичку так, чтобы равенство стало верным.

О т в е т:

4. Работа на фланелеграфе.

– Сравните данные фигуры. Являются ли они симметричными?

– Сложите из них квадрат и прямоугольник.

– Сколько осей симметрии имеет прямоугольник?

– Сколько осей симметрии имеет квадрат?

III. Сообщение темы урока.

– Сегодня мы продолжим закреплять навыки вычитания двузначных чисел.

IV. Работа по теме урока.

Задание № 9 (с. 64).

– Рассмотрите рисунки в учебнике. Составьте условие задачи по данным иллюстрациям.

– Прочитайте данные выше вопросы.

– Запишите кратко условие задачи.

Запись:

Решение:

1) 35 – 17 = 18 (шт.) – меньше красных роз, чем белых.

2) 43 – 35 = 8 (шт.) – больше желтых роз, чем белых.

3) 17 + 35 = 52 (шт.) – красных и белых.

4) 35 + 43 = 78 (шт.) – белых и желтых.

5) 52 + 43 = 95 (шт.) – роз всего.

Задание № 12 (с. 65).

– Прочитайте текст. Является ли он задачей? Почему?

– Что известно в задаче?

– Что требуется найти?

– Запишите кратко условие задачи.

Посадили – 7 к. и 18 к.

Миша – 6 к.

Папа – ? к.

Решение:

I способ:

1) 7 + 18 = 25 (к.) – посадили.

2) 25 – 6 = 19 (к.) – посадил папа.

II способ:

1) 7 – 6 = 1 (к.)

2) 18 + 1 = 19 (к.)

III способ:

1) 18 – 6 = 12 (к.)

2) 12 + 7 = 19 (к.)

О т в е т: 19 кустов.

Задание № 13 (с. 65).

– Сравните выражения в первом и втором столбике. Чем они похожи? (Первое слагаемое – 15, а второе слагаемое увеличивается на 10.)

– Как изменяются результаты в этих столбиках? (Значения сумм увеличивается на 10.)

– Проверьте свои высказывания, выполнив сложение.

– Сравните выражения в третьем и четвертом столбиках. Чем они похожи? (Уменьшаемое – одинаковое число – 50.)

– Чем они отличаются? (Вычитаемое увеличивается на 5 в каждом следующем выражении.)

– Как изменяются результаты в этих выражениях? (Значение разности уменьшается на 5 единиц.)

– Проверьте свои высказывания, выполнив вычитание в столбик.

V. Повторение пройденного материала.

1. Фронтальная работа.

Учитель демонстрирует на предметном столе модели геометрических тел: куб, параллелограмм, половина цилиндра, конус.

– Что объединяет эти модели? (Это все объемные тела.)

– Название каких фигур вы знаете?

– Подберите такие фигуры, из которых можно составить конус, цилиндр.

2. Работа по учебнику.

Задание № 18 (с. 66).

– Какие фигуры называют симметричными?

– Рассмотрите рисунки и назовите пары симметричных вершин и сторон многоугольников.

Рисунок а): точка М симметрична точке В;

    точка С симметрична точке D;

    точка A симметрична точке K;

    сторона МА симметрична ВК;

    сторона МС симметрична ВD;

    сторона CА симметрична DК.

Аналогично проводится работа с рисунком б).

Задание № 19 (с. 66).

– Прочитайте задачу.

– Что известно?

– Что требуется найти?

Решение:

1. Сколько было бы ребят, если бы мальчиков было столько, сколько девочек?

12 – 4 = 8 (чел.)

I способ: 12 – 4 = 8 (чел.)

    или

II способ: 4 + 4 = 8 (чел.)

О т в е т: 8 мальчиков.

2. Работа в печатной тетради № 1.

Задание № 94.

– Как узнать, «на сколько больше»?

VI. Итог урока.

– Что нового узнали на уроке?

– Какие фигуры называются симметричными?

– Назовите признаки конуса и цилиндра.

Домашнее задание: № 11 (учебник); № 93 (рабочая тетрадь).

Урок 33
Периметр многоугольника

Цели урока: ввести термин «периметр»; рассмотреть способ вычисления периметров любых многоугольников; совершенствовать вычислительные навыки; продолжить формирование умений решать задачи; развивать глазомер, внимание.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Начертите такую фигуру, не отрывая карандаша от бумаги. Проводить линию карандашом можно только один раз.

– Сколько треугольников на рисунке? (5.)

– Сколько четырехугольников? (6.)

2. Решите примеры.

50 + 20 – 30 + 10 – 20 = 

90 – 20 – 20 + 3 – 4 = 

60 – 30 + 50 – 70 + 20 = 

20 + 70 – 10 – 50 + 0 = 

3. Задача.

Мама купила 5 кг огурцов, 2 кг свёклы и помидоры. Сколько килограммов помидоров купила мама, если масса всех овощей 12 кг?

– Подумайте: какая схема соответствует задаче?

– Что обозначают выражения, записанные по условию задачи:

– Какие действия нужно выполнить, чтобы ответить на вопрос задачи? Решите задачу по действиям.

– Разгадайте, что обозначают равенства:

III. Сообщение темы урока.

– Рассмотрите данные на доске фигуры:

– Что объединяет эти фигуры? (Это многоугольники.)

– Как они называются? (Четырехугольники.)

– Прочитайте записанные на доске задания:

· измерьте стороны четырехугольника под номером 3;

· найдите периметр этого треугольника.

– Какие трудности у вас возникли?

– Сегодня на уроке мы узнаем, что называют периметром и как найти периметр многоугольника.

IV. Работа по теме урока.

Учитель приглашает к доске учащихся по очереди.

– Покажите указкой границу каждого данного на доске многоугольника.

При этом учащиеся должны вести указкой по сторонам многоугольника так, чтобы линия, которую пишет конец указки, представляла бы замкнутую ломаную.

– Длина ломаной линии каждого многоугольника является периметром соответствующего многоугольника.

Справочный материал для учителя

Понятие «периметр многоугольника» не является сложным для учащихся; для многих детей основная трудность состоит в запоминании термина «периметр» и правильном его использовании. Обратим внимание на весьма распространенную терминологическую ошибку, которую допускают не только дети, но и взрослые. Часто мы слышим, как говорят: «Пройдя по периметру двора...» или: «По всему периметру участка посадили кусты смородины». Даже учителя иногда предлагают учащимся «показать» указкой периметр треугольника, «раскрасить» периметр квадрата цветным карандашом. Но периметр – это величина; по ней нельзя пройти, что-то на ней посадить или показать указкой. Периметр можно лишь вычислить, складывая длины всех сторон многоугольника.

Задание № 1 (с. 67).

Постановка задачи: на плане изображен дачный участок, размеры которого указаны. Этот участок надо огородить забором. Какой длины должен быть забор?

– Рассмотрите предложенный в учебнике способ решения.

– Вычислите длину забора другим способом.

Запись:

12 + 15 + 20 + 12 = 59 (м)

20 + 12 + 12 + 15 = 59 (м)  и т. д.

Далее учитель вводит термин «периметр»:

– Сумму длин всех сторон многоугольника называют периметром.

– Прочитайте определение периметра в учебнике на с. 67.

Учитель записывает слово «периметр» на доске. Учащиеся по очереди читают это слово, затем записывают его в тетрадь.

Задание № 2 (с. 67).

– Рассмотрите чертеж. Подсчитайте, сколько сторон клеток содержит каждая сторона четырехугольника. (Две стороны содержат по 5 сторон клеток, а две другие – по 2.)

– Какова по условию длина стороны клетки? (1 см.)

– Значит, чему равны длины сторон четырехугольника? (5 см, 5 см, 2 см, 2 см.)

– Вычислите периметр этого многоугольника.

Запись: 5 + 5 + 2 + 2 = 14 (см).

  О т в е т: 14 см.

Задание № 3 (с. 68).

Учащиеся читают задание и выполняют вычисления.

Запись: 5 + 5 + 5 + 5 = 20 (см).

  О т в е т: 20 см.

– Сколько сторон у данного многоугольника? Как вы узнали? (4 стороны, так как это четырехугольник.)

– Что такое периметр?

V. Повторение пройденного материала.

1. Работа по учебнику.

Задание № 7 (с. 69).

– Рассмотрите прием вычисления, который придумал Петя. Объясните его. (6 + 9. Можно второе слагаемое дополнить до «круглого» десятка, т. е. увеличить на 1. Найти значение суммы 6 + 10, а затем вычесть 1.)

– Используя этот прием, решите следующие примеры.

Задание № 9 (с. 69).

Учащиеся работают самостоятельно по вариантам:

I вариант: 1-й столбик.

II вариант: 2-й столбик.

Задание № 11 (с. 69).

– Прочитайте текст. Является ли он задачей? Почему?

– Что известно в задаче?

– Что требуется узнать?

– Запишите кратко условие задачи.

Запись: Было – 25 м.

   Заняли – 17 м.

   Осталось – ? м.

Решение:

25 – 17 = 8 (м.) – осталось.

Ответ: 8 мест.

2. Работа в печатной тетради № 1.

Задание № 100.

Учащиеся должны выполнить задание по образцу. Важно, чтобы дети не просто механически записали вычисления, но обязательно убедились в их правильности.

Запись:

VI. Итог урока.

– Что нового узнали на уроке?

– Что такое периметр?

– Как вычислить периметр?

Домашнее задание: № 8, 9, 2-й столбик (учебник); № 101 (рабочая тетрадь).

Урок 34
Периметр многоугольника

Цели урока: продолжить формирование умений вычислять периметр любого многоугольника; рассмотреть запись сложения и вычитания величин измерения длины в столбик; совершенствовать навыки решения задач геометрического содержания; развивать умение анализировать и выделять существенные признаки.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Начертите такой домик, не отрывая карандаша от бумаги. Проводить линию карандашом можно только один раз. Сколько получилось треугольников?

О т в е т: 9 треугольников.

2. Решите задачу.

В класс вошли три подруги: Маша, Оля и Рита. В каком порядке они могли войти в класс?

Решение:  М, О, Р

   М, Р, О

   Р, М, О

   Р, О, М

   О, М, Р

   О, Р, М

3. Расшифруйте слово.

 

4. Решите задачу.

Ребята собирали для поделок желуди и шишки. Катя нашла 15 шишек и 32 желудя, Юля – 24 шишки и 17 желудей.

– На какие вопросы вы ответите, выполнив действия:

– Подумайте, сколько нужно выполнить действий, чтобы ответить на вопрос: «Сколько желудей и шишек собрали Катя и Юля?»

– Используйте калькулятор для вычислений.

III. Сообщение темы урока.

– Сегодня на уроке мы будем решать задачи на нахождение периметра многоугольника.

IV. Изучение нового материала.

1. Работа по учебнику.

Задание № 4 (с. 68).

– Прочитайте задачу.

– Что известно в задаче?

– Что требуется узнать?

– Как вычислить периметр многоугольника?

– Можно сразу вычислить периметр? Что еще надо узнать?

– Запишите кратко условие задачи и решите ее по действиям.

Решение:

1) 15 – 5 = 10 (см) – длина третьей стороны.

2) 12 + 15 + 10 = 37 (см) – периметр.

О т в е т: 37 см.

Задание № 5 (с. 68).

– Прочитайте задачу.

– Что вам известно?

– Что надо узнать? Как иначе можно сформулировать данный вопрос? (Найдите периметр четырехугольника.)

– Можно сразу вычислить периметр этого многоугольника?

Запись: 15 + 15 + 15 + 15 = 60 (см).

О т в е т: 60 см.

2. Работа в печатной тетради № 1.

Задание № 99.

– Рассмотрите чертеж. Как называется эта фигура?

– Что известно? (Длина первой, второй и третьей сторон четырехугольника и периметр.)

– Что требуется узнать? (Длину четвертой стороны.)

Решение задачи рекомендуется оформить следующим образом:

О т в е т: 28 м 3 дм.

V. Повторение пройденного материала.

1. Работа по учебнику.

Задание № 10 (с. 69).

Учащиеся выполняют вычисления:

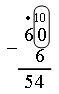
Задание № 13 (с. 70).

– Прочитайте задачу.

– Что известно? Что требуется узнать?

Учащиеся выполняют схему к условию.

Используя фишки, учащиеся решают задачу.

Задание № 15 (с. 70).

Учащиеся выполняют вычисления столбиком.

Если в случаях 2 и 4 у учащихся возникнут трудности в выборе арифметического действия, то ситуацию, представленную в задании, можно проиллюстрировать графической схемой:

Задание № 17 (с. 71).

Задание направлено на развитие внимания учащихся. На чертеже изображено 7 кругов.

VI. Путешествие в прошлое.

Учащиеся читают текст на с. 71.

– Перед тем как читать зашифрованное высказывание Галилея, надо найти ключ к шифру. А сделать это можно, разобравшись в таблице после текста. (Шифр: каждому многоугольнику определенной формы и цвета соответствует определенная буква.)

Слова великого ученого: Язык природы есть язык математики.

Справочный материал для учителя

Галилео Галилей (1564–1642)

Галилео Галилей – великий итальянский физик, математик, инженер и астроном, один из основателей современного естествознания. Еще подростком познакомился Галилей с трудами древнегреческих ученых – Аристотеля, Архимеда, Евклида – и в 20 лет, оставив медицину, которую изучал и Пизанском университете, погрузился в занятия физикой и астрономией. Галилей был профессором математики и физики в крупнейших итальянских университетах. Его научная деятельность и огромной важности открытия оказали решающее влияние на развитие механики, оптики, астрономии. Он создал раздел науки о движении – кинематику, законы которой вывел из точных экспериментов; сформулировал некоторые принципы классической механики; развил законы статики; заложил основы небесной механики.

Открытия Галилея в астрономии буквально потрясли современников. Они стали первыми неопровержимыми доказательствами правильности гелиоцентрической теории Коперника, которую Галилей страстно защищал и пропагандировал, несмотря на жестокие гонения со стороны церкви. При наблюдении неба Галилей использовал совершенно новый инструмент – телескоп, который построил сам на основе только что изобретенной тогда (1609) в Голландии зрительной трубы. Увеличение своих телескопов Галилей довел от 3-кратного до 32-кратного.

Галилей обнаружил фазы у Венеры и открыл четыре спутника Юпитера (их называют галилеевскими). Наблюдая Луну, Галилей обнаружил, что на ней есть горы, долины, глубокие пропасти, т. е. поверхность Луны по своему рельефу похожа на поверхность Земли. Телескоп Галилея впервые разложил на звезды некоторые туманные пятна на небе. Так, сплошное сияние Млечного Пути оказалось гигантским скоплением звезд. Вообще, при телескопических наблюдениях стало видно громадное количество звезд и впервые была постигнута их колоссальная удаленность. Галилею принадлежит открытие ярких пятен – флоккулов на Солнце, перемещение которых подтвердило незадолго до того обнаруженное вращение этого светила. Все наблюдения Галилей описал в небольшой работе «Звездный вестник». Убедившись в справедливости системы Коперника, Галилей посвятил ей свое основное астрономическое сочинение «Диалог о двух главнейших системах мира – птолемеевой и коперниковой» (1632). Оно было резко осуждено церковью (система Коперника с 1616 г. находилась под запретом). Престарелого ученого принудили к публичному покаянию, и последние годы жизни он провел под домашним арестом и надзором инквизиции. «Диалог» Галилея вошел и историю естествознания как символ гражданского мужества ученого и как яркая демонстрация торжества учения Коперника о Вселенной.

VII. Итог урока.

– Что нового узнали на уроке?

– Как вычислить периметр треугольника?

– Как вычислить длину стороны треугольника, если известны периметр и две другие стороны?

Домашнее задание: № 12 (учебник); № 98 (рабочая тетрадь).

Урок 35
Периметр многоугольника

Цели урока: совершенствовать навыки решения задач на вычисление периметров любых многоугольников; продолжить формирование вычислительных навыков; закреплять навыки измерения длин сторон многоугольников и построение многоугольника с помощью линейки; развивать логическое мышление и внимание.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Сколько треугольников изображено на рисунке?

Ответ: 5.

2. Заполните фишки.

3. Решите задачу.

Стоят 6 стаканов в ряд, первые 3 из них с водой.

Как переставить 2 стакана так, чтобы пустой стакан и стакан с водой чередовались?

4. Рассмотрите чертежи.

– Догадайтесь, по какому признаку можно разбить эти фигуры на группы.

III. Сообщение темы урока.

– Сегодня мы продолжим закреплять навыки вычислений периметра многоугольника.

IV. Работа по теме урока.

1. Работа по учебнику.

Задание № 6 (с. 68).

– Рассмотрите чертеж. Какие фигуры здесь изображены?

– Что такое многоугольник?

– Как определить название каждого многоугольника? (Посчитать количество углов, вершин или сторон.)

– Как называются данные многоугольники?

– Что такое периметр многоугольника?

– Что надо знать, чтобы вычислить периметр?

– Выполните необходимые измерения и вычислите периметр многоугольников.

Задание № 14 (с. 70).

– Прочитайте задачу.

– Что известно в задаче?

– Что требуется узнать?

Учащиеся выполняют схему к данной задаче.

Решение:

I способ.

1) Сколько ведер воды наливается за 2 часа через верхний кран?

12 + 12 = 24 (в.).

2) Сколько ведер воды выливается за 2 часа через нижний кран?

8 + 8 = 16 (в.).

3) Сколько ведер воды останется в баке?

24 – 16 = 8 (в.).

II способ.

1) 12 – 8 = 4 (в.) – воды остается в баке за час.

2) 4 + 4 = 8 (в.) – воды остается в баке за 2 часа.

Ответ: 8 ведер.

Задание № 16 (с. 70).

Учащиеся восстанавливают примеры:

2. Работа в печатной тетради № 1.

Задание № 102.

При выполнении задания лучше всего искать не каждую отдельную цифру числа, а все неизвестное число. Рассмотрим случай:

Изобразим «машину»:

В «машину» ввели число 60, «машина» вычла из него какое-то число. Вышло число 25. Сколько вычла «машина»? Из «машины» вышло число, меньшее 60. На сколько? На столько, сколько вычла «машина». Как это узнать? Нужно из большего числа (60) вычесть меньшее (25):

Значит, неизвестное число – 35.

Далее выполняем проверку. Если нет калькулятора, проверку можно сделать так:

Аналогично можно рассуждать в остальных случаях.

Задание № 104.

Задание является подготовительным к теме «Взаимное расположение фигур на плоскости».

Воспользовавшись линейкой, учащиеся убеждаются, что луч пересекает стороны пятиугольника в двух точках – А и В.

V. Самостоятельная работа по карточкам.

Найдите периметр каждой фигуры.

VI. Итог урока.

– Что нового узнали на уроке?

Домашнее задание: № 105 (рабочая тетрадь).

Урок 36
Окружность, ее центр и радиус

Цели урока: познакомить учащихся с понятием «окружность»; ввести термины «центр окружности», «радиус окружности»; рассмотреть построение окружности с помощью циркуля; совершенствовать вычислительные навыки; развивать логическое мышление и внимание.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Рассмотрите фигуры. Определите, чем каждая следующая отличается от предыдущей. Нарисуйте четвертую фигуру, не нарушая закономерности.

2. В каждой из трех ваз стояли цветы: или колокольчики, или васильки, или ромашки. В первой вазе не было ромашек, во второй не было ни ромашек, ни васильков. Какие цветы стояли в каждой вазе?

 

3. Расшифруйте слово.

 

4. Сколько четырехугольников на чертеже?

Ответ: 6.

III. Сообщение темы урока.

– Рассмотрите фигуры, данные на доске:

– Найдите «лишнюю» фигуру. (Номер 2.)

– Как она называется?

– Сегодня на уроке мы познакомимся с новым понятием «окружность».

IV. Изучение нового материала.

Несмотря на то что определение окружности учащимся не дается, необходимо познакомить их со свойством точек окружности.

Подготовительное упражнение.

Учитель отмечает на доске какую-нибудь точку и обозначает ее буквой О (учащиеся выполняют то же самое в своих тетрадях). Далее учитель отмечает сначала одну, затем другую, третью, четвертую точки, каждая из которых находится на расстоянии 2 см от точки О. При этом можно использовать линейку или циркуль.

В результате получится такой чертеж:

– Можно отметить еще очень много точек, каждая из которых находится на расстоянии 2 см от точки О. Давайте представим себе, что нам удалось отметить все такие точки. Все точки, находящиеся на расстоянии 2 см от точки О, образуют фигуру, которую называют словом «окружность». Чтобы изобразить окружность, не нужно отмечать все точки, для этого нам понадобится циркуль. Посмотрите, как нужно правильно им пользоваться.

Отмечаем точку О; она будет центром окружности. Берем циркуль и немного разводим в стороны концы его ножек (не обязательно на 2 см, можно взять любое расстояние). Держа циркуль правой рукой (покажите), ставим в точку О ножку циркуля с иглой. Чуть отклоняя циркуль, поворачиваем ножку с карандашом вокруг точки О, касаясь карандашом доски. Получается окружность.

Теперь вы сами попробуйте начертить окружность в тетрадях. Отмечайте центр окружности. Далее берите циркуль. Проводя окружность, придерживайте тетрадь левой рукой. Окружность чертить трудно, поэтому придется потренироваться. Изобразите несколько окружностей.

– Рассмотрите чертеж на доске.

– На какие две группы можно разделить фигуры на рисунке?

– Запишите номера и общее название фигур каждой группы.

I группа – это линии (2, 4, 5, 6);

II группа – это фигуры (1, 3, 7, 8).

– Разделите эти же фигуры на 2 группы по другому признаку. Запишите номера фигур новых групп и объясните, в чем сходство фигур каждой группы.

I группа – это линии, которые являются границей круга, т. е. окружности (2).

II группа – это линии, которые являются границей овала (4, 5, 6).

III группа – фигуры, которые являются кругами (3, 7).

IV группа – фигуры, которые являются овалами (1, 8).

– Рассмотрите рисунок. Что здесь изображено? (Рис. а – круг, рис. б – окружность.)

– Каким инструментом удобно чертить окружность?

– Как называется точка О? (Центр окружности.)

– Отметьте любую точку на окружности. Соедините отрезком центр окружности с этой точкой. Этот отрезок называют радиусом.

– Постройте еще несколько радиусов этой окружности.

– Назовите радиусы на чертеже. (ОА, ОВ, ОС, OD, ОЕ.)

– Сколько радиусов можно провести в одной и той же окружности?

– Измерьте длину каждого радиуса. Почему все радиусы окружности имеют одну и ту же длину?

Задание № 1 (с. 72).

– Какие предметы похожи на окружность? (Обруч, колесо, солнце и т. д.)

– Рассмотрите чертеж (с. 72 учебника).

– Покажите концом указки окружность (конец указки должен скользить по окружности).

– Покажите центр окружности. (Это точка.)

– Покажите радиус окружности. (Это отрезок.)

– Рассмотрите правую часть чертежа. Что здесь изображено? (Способ построения окружности с длиной радиуса 4 см.)

– Расскажите о порядке работы.

– Выполните данное построение окружности на доске и в тетрадях.

Задание № 2 (с. 72).

Используя циркуль, учащиеся строят в тетради три разные окружности.

– Отметьте центр каждой окружности.

– Укажите длину радиуса.

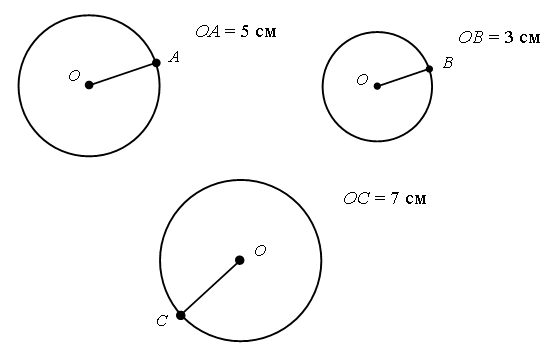
Задание № 3 (с. 72).

Перед выполнением задания необходимо обсудить с учащимися план построения окружности.

1. Отметить произвольную точку О – центр окружности.

2. Установить расстояние между ножками циркуля, равное 5 см, то есть длине радиуса окружности.

3. Выполнить построение окружности.

Задание № 4 (с. 72).

Учащиеся строят окружность и проводят в ней три радиуса.

– Сколько еще радиусов можно провести для этой окружности?

Справочный материал для учителя

В математике окружность определяют по-разному. С теоретико-множественной точки зрения окружность – это множество точек, находящихся на одном и том же расстоянии от одной точки, называемой центром окружности. При этом центр окружности самой окружности не принадлежит.

Определение.

Окружностью называется фигура, которая состоит из всех точек плоскости, равноудаленных от данной точки. Эта точка называется центром окружности.

Расстояние от точек окружности до ее центра называется радиусом окружности.

Радиусом называется также любой отрезок, соединяющий точку окружности с ее центром (рис. 1).

Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр, называется диаметром.

На рисунке 1 ВС – хорда, AD – диаметр.

V. Повторение пройденного материала.

1. Работа по учебнику.

Задание № 9 (с. 73).

– Рассмотрите математические записи. Чем они похожи? (Есть скобки.)

– Каков порядок выполнения арифметических действий в выражениях со скобками?

– Вычислите их значение.

Запись: (80 – 7) + 13 = 86        52 – (6 + 18) = 28    и т. д.

Задание № 11 (с. 74).

– Какую фигуру называют треугольником?

– Что известно в задаче?

– Что требуется узнать?

– Как вычислить периметр многоугольника?

Запись:

Ответ: 11 дм 4 см.

2. Работа в печатной тетради № 1.

Задание № 116.

– Рассмотрите рисунок. Что здесь изображено?

– Составьте по данному рисунку задачу.

Задание можно использовать для тренировки в записи решения задачи выражением. При этом слабым детям можно предложить в помощь следующую карточку:

3. Самостоятельная (практическая) работа по теме:

Окружность

Карточка А

Проведите окружность с центром в точке О так, чтобы она проходила:

а) через точку А, и закрасьте круг радиусом ОА;

б) через точку К, и закрасьте круг радиусом ОК;

в) через точку С, и закрасьте круг радиусом ОС.

Карточка В

Отметьте красным цветом точки, которые находятся на окружности с центром в точке О.

Карточка С

Отметьте синим цветом точки пересечения:

а) двух окружностей;

б) окружности и прямой;

в) окружности и ломаной;

г) окружности и кривой.

Карточка D

Проведите окружность, радиус которой:

VI. Итог урока.

– Что нового узнали на уроке?

– Что такое окружность?

– Что называют центром окружности?

Урок 37
Окружность, ее центр и радиус.
окружность и круг

Цели урока: рассмотреть и сравнить признаки окружности и круга; продолжить формирование умений измерять длину радиуса окружности, строить окружность с помощью циркуля; совершенствовать навыки решения задач; развивать внимание и пространственное мышление.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Рассмотрите фигуры. Определите, чем каждая следующая отличается от предыдущей. Нарисуйте четвертую фигуру, не нарушая закономерности.

2. Решите задачу.

На велогонках стартовали 70 спортсменов. На первом этапе с трассы сошли 4 велосипедиста, на втором – 6.

– Сколько спортсменов пришло к финишу?

– Выберите выражение, которое является решением задачи:

3. Вставьте знаки арифметических действий, чтобы получились верные равенства:

4. Анализ чертежа.

– На какие две группы можно разделить фигуры на рисунке?

– Запишите номера и общее название фигур каждой группы.

– Сравните свои группы с такими:

I группа – фигуры 1, 3, 8;

II группа – фигуры 2, 4, 5, 6, 7.

– Они похожи? По какому признаку выделены эти группы?

III. Сообщение темы урока.

– Рассмотрите данный на доске чертеж:

– Чем похожи и чем отличаются рисунки слева и справа?

– Сегодня на уроке мы узнаем, чем отличается окружность от круга.

IV. Изучение нового материала.

Задание № 6 (с. 78).

– Рассмотрите рисунок в учебнике.

– Назовите, что имеет в очках форму окружности, а что – круга. (Стекло – это круг, а оправа – окружность.)

– В этом и состоит различие между кругом и окружностью.

– Начертите в тетради какой-нибудь круг. В отличие от окружности круг нужно закрасить.

– Отметьте центр этого круга и радиус.

Задание № 7 (с. 73).

Две разные окружности могут иметь один и тот же радиус лишь в том случае, если их центры – различные точки. (После устного обсуждения задания попросите учащихся в тетрадях построить две разные окружности с одним и тем же радиусом.)

Задание № 8 (с. 73).

Задание направлено на развитие внимания учащихся.

На первом чертеже изображено 6 окружностей, на втором чертеже – 10 окружностей.

Задание № 5 (с. 73).

Чертеж:

V. Повторение пройденного материала.

1. Работа в печатной тетради № 1.

Задание № 106.

Среди данных фигур только фигура № 3 является окружностью. По ходу выполнения задания обратите внимание учащихся на фигуру № 1 (круг). Попросите детей сравнить круг и окружность. Выясните, чем они похожи и чем отличаются.

Задание № 107.

Учащиеся объясняют, что при построении радиуса надо сначала выбрать произвольную точку на окружности. Соединив центр окружности и выбранную точку отрезком, мы получим радиус.

Затем можно переходить к измерению длины радиуса (длины построенного отрезка). Она равна 2 см.

Задание № 108.

Так как в условии не указана длина радиуса, то ее мы можем выбрать произвольно. Значит, окружностей с центром в точке Р можно построить сколько угодно.

Чертеж:

– Сколько окружностей у вас получилось?

Задание № 110.

Если у слабоуспевающих учащихся возникнут трудности при построении окружности, предложите им воспользоваться карточкой-помощницей.

Учитель должен обратить внимание учащихся на то, что для измерения длины радиуса построенной окружности необязательно его строить. Достаточно измерить расстояние между точками В и С. Исходя из условия задания, можно построить единственную окружность, так как задан не только центр (В), но и радиус (ВС).

2. Работа по учебнику.

Задание № 15 (с. 75).

– Прочитайте текст. Является ли он задачей?

– Что известно в задаче?

– Что требуется узнать?

При решении этой задачи учащиеся могут рассуждать следующим образом: «На каждой полке 15 книг, следовательно, на двух полках вместе: 15 + 15 = 30 (книг). Всего с двух полок сняли столько книг, сколько было на первой полке, то есть 15 книг, следовательно, на полках осталось: 30 – 15 = 15 (книг)».

VI. Итог урока.

– Что нового узнали на уроке?

– Чем отличаются окружность и круг?

Справочный материал для учителя

Кругом называется фигура, состоящая из всех точек плоскости, расстояние от которых до данной точки не больше данного. Эта точка называется центром круга, а данное расстояние – радиусом круга. Границей круга является окружность с теми же центром и радиусом.

Домашнее задание: № 13 (учебник); № 109 (рабочая тетрадь).

Урок 38
Окружность, ее центр и радиус.
Окружность и круг

Цели урока: продолжить формирование умений строить окружности с помощью циркуля; совершенствовать навыки решения задач с величинами «цена», «количество», «стоимость»; вести подготовительную работу по выделению среди четырехугольников группы прямоугольников; развивать логическое мышление и умение обобщать.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Рассмотрите фигуры. Определите, чем каждая следующая отличается от предыдущей. Нарисуйте четвертую фигуру, не нарушая закономерности.

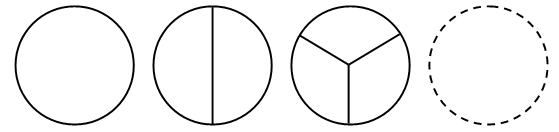
2. Решите задачу.

Витя и Дима играют в бадминтон. Первая партия закончилась со счетом 11 : 5 в пользу Вити. Вторая партия – со счетом 11 : 7 в пользу Димы.

а) Кто набрал очков больше?

б) На сколько у одного мальчика очков больше, чем у другого?

– Подумайте, на какой из этих вопросов можно ответить, не выполняя арифметического действия.

3. Вставьте знаки арифметических действий, чтобы получились верные равенства.

III. Сообщение темы урока.

– Рассмотрите рисунки на доске.

– Чем похожи и чем отличаются рисунки слева и справа?

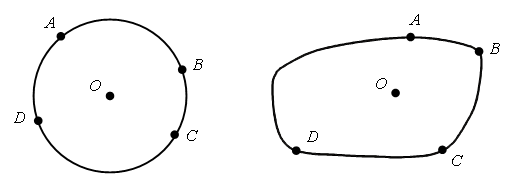
Учащиеся. Слева и справа нарисованы замкнутые кривые линии. На каждой из них отмечены 4 точки. Точка О находится внутри замкнутой линии на левом и на правом рисунках.

– Вы назвали признаки, по которым рисунки похожи. А чем они отличаются?

Учащиеся. На левом рисунке все точки, которые отмечены на замкнутой кривой, находятся на одинаковом расстоянии от точки О, а на правом рисунке это условие не выполняется.

– Поставьте на одной и на другой линии слева еще 4 любые точки. На каком расстоянии от точки О они будут находиться?

Замкнутая кривая слева – окружность.

Точка О – центр окружности.

– С помощью какого инструмента можно провести окружность?

– Сегодня на уроке будем закреплять умение строить окружности.

IV. Работа по теме урока.

1. Работа по учебнику.

Задание № 12 (с. 74).

– Рассмотрите чертеж. Что здесь изображено? (Многоугольник, четырехугольник, прямоугольник, квадрат.)

– Назовите более точное название этой фигуры. (Квадрат.)

– Укажите свойства квадрата.

– Сравните с помощью циркуля длины сторон квадрата. Какой вывод можно сделать?

– Сколько измерений надо выполнить, чтобы найти периметр квадрата? (Одно измерение.)

– Как вычислить периметр многоугольника?

– Найдите периметр квадрата.

Задание № 14 (с. 74).

– Рассмотрите рисунок. Что вы узнали?

– Прочитайте текст задания. Что требуется узнать?

– Запишите условие задачи в таблицу.

Было – 50 рублей.

Решение:

1. Сколько стоят 2 плитки шоколада?

18 + 18 = 36 (р.).

2. Сколько стоят пачка печенья и шоколадка?

12 + 18 = 30 (р.).

3. Сколько стоят пачка вафель, пачка печенья и плитка шоколада?

10 + 12 + 18 = 40 (р.).

4. Сколько стоят 3 пачки печенья?

12 + 12 + 12 = 36 (р.).

5. Сколько стоят 2 пачки вафель, шоколадка и пачка печенья?

10 + 10 + 18 + 12 = 50 (р.).

Задание № 16 (с. 75).

– Прочитайте задание. Выполните рисунок к условию.

– Остался ли в коробке хотя бы один красный шар? (Да.)

– Мог ли остаться в коробке хотя бы один зеленый шар? (Мог остаться, если бы взяли все красные шары или два красных и один зеленый.)

V. Самостоятельная работа по теме «Окружность, ее центр и радиус».

Задание № 1.

– Выберите рисунок, на котором все точки линии находятся на одинаковом расстоянии от точки О.

– Как называется такая линия?

Задание № 2.

– Рассмотрите рисунки.

– Как получили такие красивые узоры?

– Попробуйте начертить такие же узоры.

– Придумайте свои узоры из окружностей.

Задание № 3.

– Измерьте длину радиусов каждой окружности:

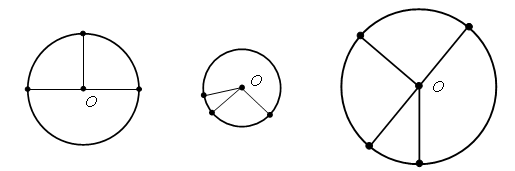
– Что о них можно сказать? (Радиусы одной окружности равны между собой.)

– Начертите несколько своих окружностей и проведите в каждой несколько радиусов. Радиусы каждой из них равны?

– Вы согласны, что все точки окружности находятся на одинаковом расстоянии от ее центра? Объясните свой ответ.

Задание № 4.

Можно ли провести окружность с центром в точке О так, чтобы она проходила через точки А, В, С, D?

Задание № 5.

Какие точки лежат на окружностях:

а) с центром в точке О и с центром в точке М?

б) с центром в точке М и с центром в точке К?

VI. Итог урока.

– Рассмотрите рисунок 1 на доске.

– Что на нем изображено?

– Как называется отрезок ОА?

– Подумайте, есть ли на рисунке другие радиусы этой окружности?

– Назовите их. (ОВ, OD, OC, OK.)

– Что же такое радиус? (Радиус – это отрезок, который соединяет центр окружности с точкой окружности.)

– Рассмотрите второй рисунок на доске.

– Назовите имена линий, которые не являются радиусами. (СВ, OY, OX, OК, РК.)

– Начертите окружность с радиусом 4 см. Проведите в ней красным цветом 3 радиуса, синим столько же отрезков, которые не являются радиусами.

Домашнее задание: № 113 (рабочая тетрадь).

Урок 39
Взаимное расположение фигур на плоскости

Цели урока: показать учащимся на примерах различные случаи возможного расположения фигур на плоскости: фигуры накладываются одна на другую (пересекаются), расположены отдельно одна от другой (не пересекаются); ввести понятие о пересекающихся и непересекающихся фигурах; совершенствовать вычислительные навыки; развивать умение сравнивать и рассуждать.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Сколько четырехугольников изображено на чертеже?

Ответ: 5.

2. Какие числа должны стоять в пустых клетках такого треугольника?

3. Решите задачу.

В круглом аквариуме 20 рыбок, а в прямоугольном – 6. На сколько в прямоугольном аквариуме меньше рыбок, чем в круглом?

4. Вычислите массы и покажите отношения: синим – «Я легче тебя», зеленым – «Наши массы равны», красным – «Я не легче тебя».

– На сколько свинья тяжелее кота?

III. Сообщение темы урока.

– Рассмотрите чертеж на доске:

– Какие фигуры здесь изображены?

– Укажите признаки окружности, треугольника, четырехугольника.

– Какая фигура лежит сверху?

– Какие трудности у вас возникли?

– Сегодня на уроке мы рассмотрим взаимное расположение фигур на плоскости.

IV. Изучение нового материала.

Учащиеся выполняют задание по карточке.

· Отметьте красным карандашом точку, которая расположена вне круга, но внутри квадрата.

· Отметьте синим карандашом точку, которая расположена вне круга и вне квадрата.

· Отметьте зеленым карандашом точку, которая расположена внутри круга, но вне квадрата.

· Отметьте желтым карандашом точку, которая расположена и внутри круга и внутри квадрата.

 Далее учитель проводит практическую работу, в которой используются заранее вырезанные из бумаги многоугольники и круги.

 Учитель показывает, как могут располагаться две фигуры на плоскости, например, треугольник и четырехугольник, четырехугольник и круг (пересекаться и не пересекаться).

Задание № 1 (с. 76).

– Рассмотрите рисунок. Что здесь изображено? (Луч CD, луч ОМ и синяя линия АВ.)

– Что такое луч? Назовите признаки луча.

– Какая из машин пересечет шоссе АВ?

При выполнении задания учащиеся должны опираться на тот факт, что луч – бесконечная фигура. По рисунку видно, что луч CD не пересекает линию АВ, значит, красная машина, двигающаяся в направлении этого луча, не пересечет шоссе.

А луч ОМ пересекает линию АВ, значит, желтая машина, двигающаяся в направлении этого луча, пересечет шоссе.

Задание № 2 (с. 76).

Учащимся будет проще выполнить задание, если одну из моделей они вырежут из прозрачной бумаги.

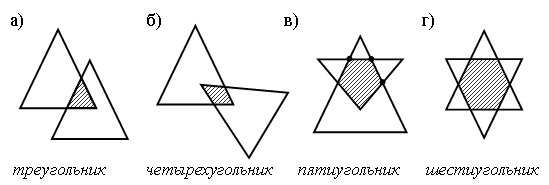
Задание № 3 (с. 77).

– Рассмотрите чертеж.

– Какие фигуры являются пересечением треугольника и четырехугольника?

V. Повторение пройденного материала.

1. Работа по учебнику.

Задание № 7 (с. 78).

Учащиеся записывают условие, используя «окошки».

– Какие знания помогли вам выполнить это задание?

Задание № 10 (с. 78).

– Прочитайте задачу.

– Что известно в задаче? Что требуется узнать?

– Запишите кратко условие задачи и решите ее.

Решение: 5 + 5 + 5 + 5 + 10 + 10 = 40 (коп.)

Ответ: 40 копеек.

Задание № 11 (с. 78).

– Прочитайте текст. Является ли он задачей? Почему?

– Что известно в задаче? Что требуется узнать?

– Запишите кратко условие задачи в таблице.

Решение:

1) 15 + 15 = 30 (р.) – стоят 2 бутылки молока.

2) 30 + 36 = 66 (р.) – стоимость всей покупки.

Ответ: 66 рублей.

2. Работа в печатной тетради № 1.

Задание № 114.

Вспомните с учащимися, что луч (в отличие от отрезка) – бесконечная фигура, поэтому, для того чтобы ответить на вопрос задания в отношении каждого из лучей, надо сначала правильно показать этот луч на чертеже.

Выполняя задание, дети должны прийти к выводу, что окружность пересекают лучи CD, FN и отрезок КМ.

Справочный материал для учителя

Учащимся предлагаются задания, в которых представлены разнообразные случаи расположения многоугольников, окружностей, отрезков, лучей; при этом фигуры могут пересекаться либо не пересекаться. Интересны примеры взаимного расположения двух окружностей:

а) окружности пересекаются в двух точках;

б) касаются одна другой (два случая – внутреннее и внешнее касание);

в) расположены концентрически (имеют общий центр).

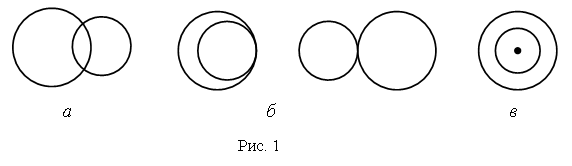
Прямая, проходящая через точку окружности перпендикулярно к радиусу, проведенному в эту точку, называется касательной. При этом данная точка окружности называется точкой касания. На рисунке 2 прямая а проведена через точку окружности А перпендикулярно к радиусу ОА. Прямая а является касательной к окружности. Точка А является точкой касания. Можно сказать также, что окружность касается прямой а в точке А.

Говорят, что две окружности, имеющие общую точку, касаются в этой точке, если они имеют в этой точке общую касательную (рис. 3). Касание окружностей называется внутренним, если центры окружностей лежат по одну сторону от их общей касательной (рис. 3,а). Касание окружностей называется внешним, если центры окружностей лежат по разные стороны от их общей касательной (рис. 3,б).

VI. Итог урока.

– Что нового узнали на уроке?

– Назовите признаки окружности.

Домашнее задание: № 8, 9 (учебник).

Урок 40
Взаимное расположение фигур на плоскости

Цели урока: рассмотреть случаи взаимного расположения двух окружностей; совершенствовать навыки решения практических задач; продолжить подготовительную работу по введению умножения и деления; развивать внимание и логическое мышление.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Сколько треугольников изображено на рисунке?

Ответ: 6.

2. Решите задачу.

Вдоль прямого участка забора растет 5 деревьев. Расстояние между соседними деревьями равно 2 метрам. Чему равно расстояние между крайними деревьями?

3. Вставьте пропущенный знак действия и число.

4. Определите массу зверят в килограммах. Напишите выражения для определения массы и найдите их значения.

Покажите стрелочкой  ↷, в каком порядке вы рассматривали весы.

Жираф – 12 кг;

Слон – 20 кг;

Бегемот – 25 кг;

Лев – 12 кг.

III. Сообщение темы урока.

– Сегодня на уроке мы рассмотрим случаи пересечения двух окружностей.

IV. Изучение нового материала.

Задание № 4 (с. 77).

– Рассмотрите чертеж. Какие фигуры здесь изображены?

– Есть ли среди них бесконечные фигуры? (Луч.)

– Какие фигуры пересекаются? Что является их общей частью?

– Какие фигуры не пересекаются?

Задание № 5 (с. 77).

Слабоуспевающим ученикам можно предложить выполнить задание с помощью моделей.

Возможны два принципиально различных варианта решения.

1. Четырехугольники имеют какую-нибудь одну общую сторону.

2. Общей у четырехугольников является только часть одной из сторон.

Учитель рассматривает с классом оба варианта.

Задание № 6 (с. 77).

Интерес представляет случай расположения двух окружностей, пересекающихся в двух точках. Дети уже подготовлены к тому, чтобы понять, почему пересечением этих окружностей являются именно точки, а не какие-нибудь другие фигуры. Полезно задать учащимся этот вопрос и выслушать их ответы. Не следует ожидать от второклассников идеально правильного ответа. Важно, чтобы дети поняли, что так как любую окружность можно представить состоящей из точек, то общей частью (пересечением) окружностей являются точки.

V. Повторение пройденного материала.

1. Работа по учебнику.

Задание № 12 (с. 78).

– Рассмотрите выражения.

– Чем они похожи? Чем отличаются?

– Как выполнить арифметические действия в выражениях со скобками?

– Вычислите их значения.

Запись: (90 – 45) + 45 = 90         90 – (45 + 15) = 30   и т. д.

Задание № 13 (с. 78).

– Прочитайте условие задачи. Что известно?

– Запишите кратко условие задачи.

– Сформулируйте вопрос и решите задачу.

К условию, данному в задании, можно придумать много различных вопросов. Например: сколько серебряных монет было в кладе? Сколько медных монет было в кладе? Сколько всего было монет? На сколько медных монет было меньше, чем золотых? Сколько всего было золотых и серебряных монет? На сколько золотых и серебряных монет было больше, чем медных?

Разберите как можно больше вариантов задач. А завершить работу следует сравнением всех рассмотренных задач и способов их решения.

Задание № 16 (с. 79).

Задание следует рассматривать как подготовительное к изучению ряда последующих тем, посвященных табличным случаям умножения и деления.

Напомните учащимся известные им способы выполнения умножения.

Первый способ – пересчет элементов прямоугольной таблицы, составленной из фишек.

Например, 3 умножить на 2 – это 2 раза по 3.

Второй способ – использование действия сложения.

Например, 5 умножить на 4 – значит, число 5 повторить слагаемым 4 раза, то есть:

5 + 5 = 10,

10 + 5 = 15,

15 + 5 = 20.

Следовательно, 5 · 4 = 20.

Задание № 14 (с. 79).

Задание выполняется с помощью портновского метра. Необходимо продемонстрировать ученикам, как правильно производить измерения.

2. Работа в печатной тетради № 1.

Задание № 116.

Наиболее сложный из всех случаев – № 3. Некоторым учащимся может показаться, что общей частью двух касающихся окружностей является дуга или отрезок, поэтому необходимо обратить внимание учащихся на то, что пересечением двух окружностей в данном случае является точка.

А – точка пересечения окружностей.

В первом случае две точки пересечения – В и С.

Во втором случае окружности пересекаются – имеют общий центр.

Задание № 117.

Выполняя задание, учащиеся наверняка столкнутся с ситуацией, когда длину того или иного пальца невозможно указать только в сантиметрах. А с более мелкой единицей длины (миллиметром) они еще не знакомы. Учитель советует использовать в этом случае слова «примерно», «около», «больше … , но меньше  … », которые указывают на приближенные значения полученного результата.

VI. Итог урока.

– Что нового узнали на уроке?

– Назовите признаки окружности.

– Назовите признаки многоугольника.

Домашнее задание: № 15 (учебник); № 118 (рабочая тетрадь).

Урок 41
Контрольная работа по теме «Сложение
и вычитание чисел в пределах 100»

Цели урока: проверить вычислительные навыки сложения и вычитания чисел в пределах 100; умение находить периметр любого многоугольника; умение строить окружность с помощью циркуля; умение решать составные задачи.

I вариант

1. Запишите цифрами:

2. Выполните действия:

3. У Тамары было 100 р. Она купила пачку чая за 35 р. и батон хлеба за 18 р. Сколько денег у нее осталось?

4. Вставьте пропущенные числа так, чтобы равенства были верными:

5. Вычислите периметр многоугольника.

6. Постройте первую окружность с радиусом 4 см, а другую – с радиусом на 2 см больше. Отметьте точкой О центр окружности.

II вариант

1. Запишите цифрами:

2. Выполните действия:

3. В ларьке было 100 кг капусты. Продали 54 кг капусты, а привезли еще 45 кг. Сколько килограммов капусты стало в ларьке?

4. Вставьте пропущенные числа так, чтобы равенства были верными:

5. Вычислите периметр многоугольника.

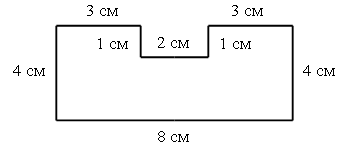
6. Постройте первую окружность с радиусом 5 см, а другую – с радиусом на 1 см меньше. Отметьте точкой О центр окружности.

Урок 42
Работа над ошибками. Решение задач

Цели урока: провести анализ выполненной контрольной работы; совершенствовать умение решать задачи; развивать умение рассуждать.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Геометрическое задание.

                       Часто знает и дошкольник,

                       Что такое треугольник.

                       А уж вам-то как не знать?

                       Но совсем другое дело –

                       Быстро, точно и умело

                       Треугольники считать.

                       Например, в фигуре этой

                       Сколько разных? Рассмотри!

                       Все внимательно исследуй

                       И по краю, и внутри.

– Сосчитайте, сколько треугольников.

2. Задача на смекалку.

Из 25 учеников в классе 17 изучают английский язык, а 15 – французский. Сколько детей изучают оба языка?

Комментарий. Желательно иллюстрировать решение схемой, в которой круг слева означает детей, изучающих английский язык, а круг справа – французский. В пересечении кругов – дети, изучающие оба языка.

Схема дополняется в процессе решения задачи.

– Сколько ребят не изучают французский язык (изучают только английский)? (25 – 15 = 10.)

– Сколько человек изучают только французский язык (не изучают английский)? (25 – 17 = 8.)

– Сколько человек изучают только один язык? (10 + 8 = 18.)

– Сколько человек изучают оба языка? (25 – 18 = 7.)

III. Сообщение результатов выполнения контрольной работы.

IV. Работа над ошибками.

V. Самостоятельная работа по карточкам.

Карточка А

Сколько квадратов:

а) внутри большого круга;

б) внутри маленького круга;

в) вне маленького круга;

г) вне большого круга?

Карточка В

а) Прочитайте условие задачи.

На трех тарелках лежали груши, по 7 штук на каждой. С каждой тарелки взяли по 4 груши.

б) Используя данное условие, ответьте на вопросы, соединив каждый из них с соответствующим выражением:

Карточка С

а) Прочитайте условие задачи.

Саша поймал 5 лещей, а папа – в 3 раза больше. Дедушка поймал на 2 леща меньше, чем папа.

б) Отметьте на каждой схеме отрезки, обозначающие лещей, которых поймал Саша, буквой С, которых поймал папа  – буквой П, которых поймал дедушка  – буквой Д.

в) Ответьте на вопросы, выполнив арифметические действия:

1. Сколько лещей поймал папа?

_________________________________________________

2. Сколько лещей поймал дедушка?

_________________________________________________

3. На сколько больше лещей поймал папа, чем Саша?

_________________________________________________

4. На сколько меньше лещей поймал Саша, чем дедушка?

_________________________________________________

5. Сколько лещей поймали Саша и папа?

_________________________________________________

6. Сколько всего лещей поймали Саша, папа и дедушка?

_________________________________________________

VI. Итог урока.

 

Урок 43
Умножение и деление на 2

Цели урока: составить таблицу умножения двух и на два; совершенствовать навыки решения задач; развивать умение анализировать и сравнивать.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Сколько на чертеже треугольников? (6.)

 Сколько на чертеже четырехугольников? (3.)

2. Решите задачу.

Для записи чисел в математике используют 10 знаков, которые называют цифрами. Для записи слов в русском языке используют 33 знака, которые называют буквами.

– На сколько больше в русском языке букв, чем в математике цифр?

3. Что вы можете сказать о массе каждого предмета?

– Узнайте массу каждого предмета.

Ананас – весит меньше 6 кг (10 – 2 – 2 = 6).

Арбуз – тяжелее 15 кг (10 + 10 – 5 = 15).

Тыква – 15 кг (10 + 5 = 15).

Баклажан – весит меньше 2 кг.

III. Сообщение темы урока.

– Рассмотрите данные на доске записи:

– Какие примеры связаны друг с другом?

– Можете ли вы сразу сказать, чему равно значение данных примеров?

– Сегодня на уроке мы начнем изучать таблицу умножения и деления, составим таблицу умножения на 2.

IV. Изучение нового материала.

Задание № 1 (с. 80).

Постановка задачи: Волк и Заяц испекли пирожные и разложили их по 2 на 8 блюдцах. Нужно сосчитать, сколько пирожных на всех этих блюдцах.

Предлагаем возможный вариант беседы учителя и учащихся:

– Как Волк предложил решить эту задачу? Кто сможет объяснить?

– Волк предлагает складывать числа по порядку, каждый раз прибавляя 2 и вычисляя сумму.

– Петя, прочитай вслух все записи, которые сделал Волк. Сколько же пирожных на всех блюдцах?

– Шестнадцать: 14 + 2 = 16.

– Посмотрите, как много записей сделал Волк, чтобы решить такую простую задачу. Как решить задачу, выполняя лишь одно действие?

– Можно использовать умножение: 2 · 8.

– Посмотрите на плакат, который держит Заяц. На нем записана таблица умножения числа 2. Достаточно только найти нужную строку, и сразу получите ответ. Найдите строку, обведенную красной рамкой. Что там написано?

– Два умножить на восемь равно шестнадцати.

– Если запомнить результаты умножения числа 2, то ответ к любой такой задаче можно дать сразу, ничего не пересчитывая.

Задание № 2 (с. 81).

– Рассмотрите рисунки и объясните, как сделаны эти записи.

Ответ: два взяли 3 раза, получили 6 кружков.

Задание № 3 (с. 81).

Учащиеся используют фишки.

В математике во всех случаях умножения с нулем (2 · 0, 3 · 0, ... , 9 · 0) результат считают равным нулю по определению. Однако младшим школьникам эти случаи лучше проиллюстрировать с помощью фишек аналогично общему случаю умножения чисел.

Напомним способ действия. Чтобы умножить 3 на 4, мы раскладываем фишки в 4 ряда по 3 штуки. В данном случае, выполняя умножение 2 · 0, надо выложить фишки в 0 рядов по 2 штуки. Каждый ученик понимает, что всего будет 0 фишек, то есть 2 · 0 = 0.

Задание № 4 (с. 81).

Учащиеся с помощью фишек проверяют табличные случаи умножения.

Задание № 5 (с. 81).

Учащиеся сравнивают устно результаты умножения, используя калькулятор. Если нет возможности выполнить задание с помощью калькулятора, можно использовать фишки.

Вывод: значения умножений вида 2 · 6 и 6 · 2 равны.

Задание № 7 (с. 81).

Учащиеся работают самостоятельно.

V. Повторение пройденного материала.

1. Работа по учебнику.

Задание № 23 (с. 84).

– Прочитайте вопрос. Что требуется узнать?

– Рассмотрите рисунки. Что вам известно?

– Какую задачу вы можете составить?

Это пример задачи с несколькими вариантами ответа. Учащимся надо объяснить, что любую задачу можно считать решенной только в том случае, если даны все возможные варианты ответов.

В данном случае они следующие:

1) Мишка, так как 40 р. меньше 50 р.

2) Книга, так как 15 р. меньше 50 р.

3) Видеокассета, так как 30 р. меньше 50 р.

4) Книга и видеокассета, так как 45 р. (15 р. + 30 р.) меньше 50 р.

Учитель разбирает задачу с классом во время устной фронтальной работы.

2. Работа в печатной тетради № 1.

Задание № 130.

На чертеже пять треугольников – AED, DEB, DBC, ABD и ABC и один четырехугольник – DEBC.

Если у учащихся возникнут затруднения, то можно для наглядности воспользоваться демонстрационной моделью, составленной из моделей трех треугольников той же формы, что и треугольники AED, DEB и DBC, и расположенных по отношению друг к другу так же, как и на чертеже, данном в тетради.

Задание № 131.

В результате выполнения задания учащиеся должны получить такой квадрат.

VII. Итог урока.

– Что нового узнали на уроке?

Домашнее задание: № 6, 21 (учебник); № 120 (рабочая тетрадь).

Урок 44
Умножение и деление на 2

Цели урока: составить таблицу деления на 2, используя знания таблицы умножения на 2; вести подготовительную работу к введению понятия площади фигуры (пересчитывание квадратов, на которые разделена фигура, с использованием таблицы умножения); совершенствовать навыки решения задач; развивать глазомер и внимание.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Задача.

В коробке на 4 карандаша больше, чем в пенале. На сколько в пенале карандашей меньше, чем в коробке? Сколько карандашей в коробке?

– На какой вопрос вы можете ответить, а на какой – нет? Почему?

– Подумайте: как дополнить условие задачи, чтобы ответить на оба вопроса?

2. Фронтальная работа.

– Запишите числа в порядке убывания:

70, 55, 40, 50, 60, 45, 65, 35.

– По какому признаку можно разбить числа на две группы? Найдите разность самого большого и самого маленького числа в этом ряду. Увеличьте каждое число на 5 единиц.

– Запишите равенства.

– На какие две группы можно разбить эти равенства?

3. Какая фигура «лишняя»?

III. Сообщение темы урока.

– Рассмотрите рисунок на доске:

– Используя данный рисунок, запишите выражение по схеме:  :  = .

– Сегодня на уроке мы составим таблицу деления на 2.

IV. Изучение нового материала.

Составление таблицы деления на 2.

Учащиеся вставляют числа в «окошки» примера на умножение и составляют пример на деление по образцу.

– Как связаны между собой примеры на деление и умножение?

– Рассмотрите таблицу деления и умножения на 2 на с. 82 учебника. Расскажите, как она составлена.

Задание № 13 (с. 82).

Используя таблицу умножения на 2, учащиеся выполняют деление на 2.

Задание № 8 (с. 82).

– Прочитайте задачу.

– Что известно в задаче? Что требуется узнать?

– Выполните рисунок и запишите решение задачи.

Задание № 9 (с. 82).

– Прочитайте текст. Можно ли его назвать задачей?

– Что известно? Что требуется узнать?

– Запишите кратко условие задачи и решите ее.

Запись: Было – 40 л.

   Взяли – ? л., 2 раза по 9 л.

   Осталось – ? л.

Решение: 1) 9 · 2 = 18 (л) – взяли.

   2) 40 – 18 = 22 (л) – осталось.

Ответ: 22 литра.

Задание № 10 (с. 82).

– Прочитайте задачу. Самостоятельно решите ее, выполнив рисунок к условию.

Запись:

Решение:  1) 2 · 5 = 10 (ч.)

   2) 10 + 3 = 13 (ч.)

Ответ: 13 ч.

Задание № 12 (с. 82).

(Данное задание носит пропедевтический характер, т. е. предваряет введение понятия площади.)

– Рассмотрите рисунок. Что на нем изображено?

– Как называются данные фигуры?

– На сколько квадратов разделен каждый четырехугольник? Посчитайте разными способами.

– Какие способы более удобны?

V. Повторение пройденного материала.

1. Работа по учебнику.

Задание № 24 (с. 85).

Очень важно побудить учащихся перебирать возможные варианты костюма не хаотично, а по определенному плану.

Рассуждаем так: с первой юбкой можно составить три варианта костюма (если брать по очереди каждую из блузок). И со второй юбкой – три варианта. Следовательно, всего можно составить: 3 + 3 = 6 различных вариантов костюма.

2. Работа в печатной тетради № 1.

Задание № 123.

– Прочитайте задачу.

– Что известно? Что требуется узнать?

Решая эту задачу, учащиеся вспоминают практические способы выполнения действия деления. В тетради учащиеся рисуют стаканы замкнутой линией.

Далее, пересчитав «стаканы», учащиеся делают вывод, что их потребовалось шесть.

Запись: 12 : 2 = 6 (ст.).

   Ответ: 6 ст.

Задание № 124.

На каждое блюдо «кладем» по очереди по одному пирожному, пока не разложим все шесть.

– Сколько пирожных получилось на каждом блюдце? (По три.)

При выполнении этой части задания слабоуспевающие дети могут пользоваться фишками.

Решение: 6 : 2 = 3 (п.).

Ответ: 3 п.

VI. Итог урока.

– Что нового узнали на уроке?

– Как связаны между собой умножение и деление?

Домашнее задание: № 22 (учебник); № 121, 122 (рабочая тетрадь).

Урок 45
Умножение и деление на 2. Половина числа

Цели урока: ввести понятие «половина числа»; показать способ нахождения доли числа действием деления; совершенствовать навыки решения составных задач; продолжить формирование умений по решению практических задач о взаимном расположении фигур на плоскости; развивать умение рассуждать и обобщать.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Сколько фигур на чертеже?

– Четырехугольников? (5.)

– Треугольников? (4.)

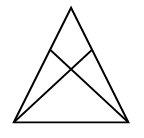
2. Заполните цепочку:

3. Решите задачу.

Лена прыгнула через скакалку 25 раз, Маша – 35 раз, Таня – 30. На сколько больше прыжков сделала Маша, чем Таня? На сколько меньше прыжков сделала Лена, чем Маша?

Что обозначают выражения, записанные по условию задачи?

III. Сообщение темы урока.

– Рассмотрите чертеж:

– Как называется эта фигура?

– Сколько клеток содержит этот четырехугольник?

– Закрасьте половину этой фигуры. Сколько клеток будет в половине данного четырехугольника?

– Сегодня на уроке мы узнаем, как найти половину числа.

IV. Изучение нового материала.

При объяснении учащимся понятия «половина числа» учитель опирается на рисунок на с. 83 учебника. Учащиеся выполняют практическую работу (используют фишки).

– Разделим 6 на 2. Выполним это с помощью фишек.

Ученик выходит к доске, отсчитывает 6 красных фишек и раскладывает их в 2 кучки: сначала по одной, потом еще по одной и так, пока не будут разложены все фишки.

– Сколько фишек получилось в каждой из 2 кучек?

– Рассмотрите рисунок с фишками на с. 83 учебника.

– Шесть мы разделили на две части поровну: в одной 3 фишки и в другой – 3 фишки. Разделить число на 2 – это значит найти его половину. А если нужно найти половину числа 10, что вы будете с этим числом делать? (Разделим 10 на 2.)

Далее учащиеся читают правило в учебнике на с. 83.

Задание № 19 (с. 84).

– Прочитайте задание. Что значит «половину всех марок он подарил»?

Решение:

10 : 2 = 5 (м.).

Ответ: 10 м.

Задание № 17 (с. 83).

– Прочитайте задачу.

– Что известно? Что требуется узнать?

– Запишите кратко условие задачи.

Запись: 1 б. – 2 л. с.

   6 б. – ? л. с.

   Хватит ли – 8 л. с.

Решение: 1) 2 · 6 = 12 (л. с.) потребуется.

   2) 8 меньше 12.

Ответ: 8 ломтиков сыра не хватит.

Задание № 18 (с. 83).

– Прочитайте данные задачи. Решите только задачу на деление.

Учащиеся работают самостоятельно.

Вторая задача:

Решение: 4 : 2 = 2 (л.).

Ответ: 2 л.

V. Повторение пройденного материала.

1. Работа по учебнику.

Задание № 25 (с. 85).

– Рассмотрите чертежи. Какие фигуры изображены?

– Имеют ли эти фигуры общую часть, пересекаются ли они?

– Какая фигура является пересечением треугольника и четырехугольника?

– Выполните рисунок, на котором пересечением треугольника и четырехугольника будет являться пятиугольник.

Задание № 26 (с. 85).

Чертежи:

Точка А – общая часть двух отрезков.

Задание № 27 (с. 85).

Чертежи:

– Что такое окружность?

– Какую фигуру называют лучом?

Задание № 28 (с. 85).

– Какие фигуры называют симметричными?

– Что такое ось симметрии?

– Рассмотрите чертеж. Являются ли данные отрезки симметричными?

После того как учащиеся ответят на вопрос задачи, учитель предлагает им проверить себя с помощью зеркала.

– Установите вертикально на ось симметрии зеркало и сравните изображение в зеркале с чертежом, а затем сделайте вывод.

2. Работа в печатной тетради № 1.

Задание № 126.

После того как учащиеся выберут и выпишут из ряда чисел от 0 до 19 те из них, которые делятся на 2, целесообразно сравнить первоначальный ряд чисел и полученный. При этом обратите внимание детей на тот факт, что числа, которые делятся на 2, расположены через одно.

Можно проверить эту закономерность на нескольких последующих числах натурального ряда, например с помощью калькулятора.

Задание № 129.

Проще всего найти числа в последних двух «окошках». Для этого нужно лишь последовательно выполнить вычисления: 20 + 32 = 52, 52 – 52 = 0.

Вписываем полученные результаты:

Заполнение же оставшихся двух «окошек» невозможно без построения обратных «машин»:

Двигаясь по нижним стрелкам, выполняем вычисления:  20 + 17 = 37, 37 – 24 = 13. Затем вписываем результаты в «окошки». В итоге в тетрадях получится запись:

VI. Итог урока.

– Что нового узнали на уроке?

– Как найти половину числа?

– Назовите признаки окружности, треугольника, четырехугольника.

Домашнее задание: № 14, 20 (учебник); № 125, 127, 128 (рабочая тетрадь).

Урок 46
Умножение трех и на 3

Цели урока: составить таблицу умножения трех и на 3; совершенствовать вычислительные навыки; закреплять умения решать задачи с величинами «цена», «количество», «стоимость»; продолжить формирование умений проводить ось симметрии в геометрических фигурах; развивать практические навыки построения геометрических фигур.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Сколько четырехугольников изображено на чертеже?

Ответ: 8.

2. Найдите в каждом ряду «лишнее» число.

40, 8, 90, 16, 20;

50, 70, 14, 20, 90;

7, 5, 3, 9, 15, 6.

3. Решите задачу.

На аэродроме было 75 самолетов. Сколько самолетов осталось?

– Выберите данные, которыми можно дополнить условие задачи, чтобы ответить на поставленный в ней вопрос:

а) Утром прилетело 10 самолетов, а вечером улетело 30.

б) Улетело на 20 самолетов больше, чем было.

в) Улетело сначала 30 самолетов, а потом 20.

4. Расшифруйте слово.

 

III. Сообщение темы урока.

– Рассмотрите рисунок на доске:

– Объясните, что обозначают выражения, используя данный рисунок.

– Какое выражение более удобно в записи?

– Сегодня на уроке составим таблицу умножения на 3.

IV. Изучение нового материала.

Задание № 1 (с. 86).

– Рассмотрите иллюстрацию на с. 86. Сколько столовых приборов получил каждый гость? (По три прибора.)

– Сколько гостей должны прийти?

– Сколько же понадобилось столовых приборов?

– Как решил эту задачу Волк? (3 + 3 + 3 + 3 + 3 = 15.)

– Как решил задачу Заяц? (3 · 5 = 15.)

– Кто из них решил эту задачу быстрее? Почему?

Далее учащиеся составляют и записывают в тетрадь таблицу умножения трех.

Задание № 2 (с. 87).

Используя карточку-помощницу, фишки, учащиеся находят значение произведений.

Задание № 3 (с. 87).

Учащиеся сравнивают значения произведений, используя калькулятор.

3 · 8 равно 8 · 3, так как 3 · 8 = 24 и 8 · 3 = 24;

3 · 6 равно 6 · 3, так как 3 · 6 = 18 и 6 · 3 = 18.

Вывод: от перестановки множителей значение произведения не изменяется.

Задание № 4 (с. 87).

Используя цветные фишки, учащиеся находят значение произведений:

3 · 0 = 0

0 · 3 = 0

Вывод: если любое число умножить на нуль или нуль умножить на любое число, значение произведения равно нулю.

Задание № 8 (с. 87).

– Прочитайте задание.

– Что известно в задаче? Что надо узнать?

– Выполните рисунок и ответьте на вопрос.

Решение:  6 + 6 + 6 = 18 (м).

   6 · 3 = 18 (м).

Ответ: 18 метров.

Задание № 9 (с. 88).

– Прочитайте задачу.

– Что известно? Что требуется узнать?

– Составьте таблицу по условию задачи.

Решение:

1) 3 · 3 = 9 (р.) – стоимость 3 пакетиков.

2) 3 · 5 = 15 (р.) – стоимость 5 пакетиков.

3) 3 · 7 = 21 (р.) – стоимость 7 пакетиков.

4) 3 · 9 = 27 (р.) – стоимость 9 пакетиков.

V. Повторение пройденного материала.

1. Работа по учебнику.

Задание № 28 (с. 91).

– Какой многоугольник называется семиугольником? Назовите его признаки.

– Как построить семиугольник? (При построении многоугольника сначала отмечают его вершины (точки), а затем по линейке проводят стороны (отрезки).)

Задание № 29 (с. 91).

– Какая линия называется окружностью?

– Что такое радиус?

– Как построить окружность с заданным радиусом?

– Чему равен радиус второй окружности? (6 – 2 = 4 (см).)

Чертеж:

– Назовите точки пересечения данных окружностей. (Центр О.)

Задание № 30 (с. 91).

– Какие фигуры называются симметричными?

– Симметричны ли цветочки относительно линии сгиба?

– Проверьте свой ответ с помощью зеркала, которое нужно установить вертикально на линии сгиба каждого из платочков.

2. Работа в печатной тетради № 1.

Задание № 142.

– Рассмотрите чертеж. Что здесь изображено?

– Что такое числовой луч?

– Что называют координатой?

– Какую координату имеет точка А?

– Как отметить точку В?

– Как отметить точку С?

Решение:

Точка В расположена правее точки А и на расстоянии четырех единичных отрезков от нее. Следовательно, точка С должна быть левее точки А и находиться на расстоянии четырех единичных отрезков от нее.

Задание № 143.

– Чем окружность отличается от круга?

– Рассмотрите чертеж. Как расположены круг и окружность? Есть ли у них общая часть? (Общей частью окружности и круга является дуга окружности АВ.)

Справочный материал для учителя

Числа 3 и 7

– Какую цифру вы любите больше всего? Семерку? А может, единицу? Вас удивляет такой вопрос: как можно любить или не любить какие-то цифры или числа? Однако не все так думают. У некоторых людей есть числа «хорошие» и «плохие». Например, числа 3 и 7 издревле считаются хорошими. Так уж сложилась их история. Сейчас мы можем легко сосчитать все карандаши в пенале, стулья на кухне. А в далекие времена человеку с трудом удавалось досчитать до двух. И каждый раз за двойкой начиналось что-то неизведанное, загадочное. Считали так: «один», «два», «много». Поэтому число 3, которое при счете должно было идти за числом 2, обозначало «все».

Долгое время у многих народов пределом счета была именно тройка. Так, число 3 стало излюбленным в мифах и сказках. Поэтому в сказках 3 медведя, 3 богатыря, 3 брата, 3 сестры и т. д.

Особым почетом в древности была окружена семерка. Отголоски почитания этого числа дошли до наших дней. Вспомните пословицы русского народа: «Семь бед – один ответ», «Семеро одного не ждут». Наша неделя состоит из семи дней. Древние заметили, что 7 нельзя поделить на равные части. Вот и назвали 7 – «не деля».

VI. Итог урока.

– Что нового узнали на уроке?

– Какую помощь оказывает знание таблицы умножения на 3?

Домашнее задание: № 6, 7 (учебник); № 132, 133, 134 (рабочая тетрадь).

Урок 47
Умножение и деление на 3

Цели урока: составить таблицу деления на 3; совершенствовать навыки решения задач с использованием действий умножения и деления; развивать умение анализировать и обобщать.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Сколько треугольников изображено на чертеже? (12.)

 Сколько четырехугольников? (4.)

2. Прочитайте цифры:

7, 20, 17, 12, 10, 19, 5, 6, 2, 60.

– Назовите цифры, с помощью которых написаны эти числа.

– Назовите однозначные числа.

– Назовите двузначные числа.

– Назовите «круглые» числа.

– Расположите все числа в порядке убывания.

3. Решите задачу.

На первую машину погрузили половину всех шкафов, а на вторую – оставшиеся 5. Сколько всего было шкафов?

4. Рассмотрите иллюстрации.

На каждых весах раскрасьте более легкую игрушку.

III. Сообщение темы урока.

– Сегодня на уроке мы составим таблицу деления на 3.

IV. Работа по теме урока.

Используя фишки и опираясь на таблицу умножения трех и на 3, учащиеся составляют таблицу деления на 3.

Далее учащиеся сравнивают свою таблицу с таблицей деления на 3 на с. 88 учебника.

Задание № 13 (с. 88).

Используя таблицу умножения на 3, учащиеся выполняют деление. Это задание учит детей использовать способ подбора по таблице умножения.

Задание № 15 (с. 89).

Задание выполняется фронтально.

Запись: 0 · 3 = 0.

   0 : 3 = 0.

Задание № 16 (с. 89).

– Прочитайте текст. Является ли он задачей?

– Что известно? Что требуется узнать?

– Выполните рисунок и решите задачу.

Задание № 18 (с. 89).

– Что известно? Что требуется узнать?

Решение:

12 : 3 = 4 (окна) – всего.

Ответ: 4 окна.

Задание № 20 (с. 89).

– Прочитайте текст. Является ли он задачей? Почему?

– Что известно? Что требуется узнать?

– Есть ли в задаче «лишние» данные? Какие? (За два дня.)

Учитель предлагает задачу:

– Каждый из 3 школьников делал для детского сада по 4 лопатки в день. Сколько всего лопаток сделали школьники за 2 дня?

– Сравните условия и вопросы обеих задач.

– Объясните, чем отличаются их решения.

– Запишите решение второй задачи.

Решение: 1) 4 · 3 = 12 (л.) – делают 3 школьника за 1 день.

   2) 12 + 12 = 24 (л.) – за 2 дня.

Ответ: 24 лопатки.

Задание № 10 (с. 88).

– Запишите кратко условие задачи.

Решение: 1) 8 · 3 = 24 (к.) – смородины.

   2) 24 + 18 = 42 (к.) – всего.

Ответ: 42 куста.

V. Повторение пройденного материала.

1. Работа в печатной тетради № 1.

Задание № 136.

«Связывать» морковку в пучки ученики должны непосредственно на рисунке в тетради. При этом каждый пучок можно заменить замкнутой линией.

Пересчитав «пучки», дети делают вывод: «Получилось пять пучков». Далее можно переходить к записи решения с помощью арифметического действия:

15 : 3 = 5 (п.)

Ответ: 5 пучков.

Задание № 141.

– Прочитайте задачу.

– Что известно? Что требуется узнать?

– Запишите решение задачи по действиям.

Решение: 1) 9 + 9 = 9 · 2 = 18 (л) – было.

   2) 15 л < 18 л.

Значит, 18 л молока не поместится в 15-литровый бидон.

2. Работа по учебнику.

Задание № 37 (с. 92).

– Прочитайте задачу.

– Что известно? Что требуется узнать?

– Что значит «половина цветов в букете»?

– Рассмотрите карточку-помощницу. Как ответить на вопрос задачи?

Решение: 7 · 2 = 14 (цв.) – всего.

Задание № 38 (с. 93).

Учащиеся должны сообразить, что до того, как выполнять вычисления, надо длину отрезка представить в сантиметрах. Поэтому запись решения задачи будет выглядеть так:

Решение: 1) 1 дм 8 см = 18 см,

   2) 18 : 2 = 9.

Ответ: 9 см.

VI. Итог урока.

– Что нового узнали на уроке?

– Как связано деление с умножением?

Домашнее задание: № 32, 36 (учебник); № 135, 137 (рабочая тетрадь).

Урок 48
Умножение и деление на 3. Треть числа

Цели урока: ввести понятие «треть числа»; учить находить треть числа действием деления; продолжить формирование умений решать задачи умножением и делением; вести подготовительную работу по знакомству с уравнениями; развивать умение сравнивать и рассуждать.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Решите задачу.

В коробке на 4 карандаша больше, чем в пенале. Сколько карандашей в пенале? Почему вы не можете решить эту задачу? Выберите данные, которыми можно дополнить условие этой задачи, чтобы ответить на ее вопрос, выполнив сложение:

а) в пенале 7 карандашей;

б) в пенале на 6 карандашей меньше;

в) в коробке 9 карандашей;

г) всего в коробке и в пенале 14 карандашей.

2. Рассмотрите карточки с фишками.

Прочитайте записанные под рисунками выражения и догадайтесь, что обозначают в каждом произведении первый и второй множители:

3. Найдите в каждом столбике «лишнее» выражение:

– Вычислите его значение.

III. Сообщение темы урока.

– Рассмотрите рисунки на доске.

– Чем они похожи? Чем отличаются?

– Как найти половину числа?

– Сегодня на уроке мы узнаем, как вычислить третью часть числа.

IV. Изучение нового материала.

Учащиеся выполняют действия с фишками: надо 6 разделить на 3.

– Если число разделить на 3, то можно найти его часть – треть числа. Чему равна треть числа 6?

Задание № 21 (с. 90).

– Прочитайте задачу.

– Что известно? Что требуется узнать?

– Как узнать треть числа? (Надо разделить на 3.)

Решение: 27 : 3 = 9 (гр.) – подосиновики.

Задание № 23 (с. 90).

– Прочитайте текст. Можно ли его назвать задачей?

– Что известно? Что требуется узнать?

Слабоуспевающим детям учитель может помочь схемой:

Решение: 1) 18 : 3 = 6 (ст.) – черной смородины.

   2) 6 + 9 = 15 (ст.) – черной и белой смородины.

   3) 18 – 15 = 3 (ст.) – красной смородины.

Ответ: 3 стакана.

Задание № 24 (с. 90).

– Прочитайте задачу.

– Что известно? Что требуется узнать?

Если возникают трудности, учитель предлагает схему-помощницу:

Решение: 1) 27 – 9 = 18 (м) длина второй веревки.

   2) 18 : 3 = 6 (м) – длина каждой части.

Ответ: 6 метров.

V. Повторение пройденного материала.

1. Работа по учебнику.

Задание № 40 (с. 93).

Задание направлено на закрепление способов рассуждений, изложенных ранее, и предваряет введение приемов решения уравнений вида 15 + x = 20, 40 – y = 30.

Решение:

Задание № 41 (с. 93).

– Что известно в задаче? Что требуется узнать?

– Запишите кратко условие задачи.

Решение:

12 – 7 = 5 (шт.) – продали паласов.

– Объясните, что значит выражение «в универмаге продали 12 ковров, что оказалось на 7 больше, чем продали паласов». (Значит, паласов продали на 7 меньше.)

– Измените текст задачи так, чтобы вместо слова «больше» было слово «меньше». Решите новую задачу.

Задание № 42 (с. 93).

Учащиеся могут выполнить схему:

Ответ: 3 дм.

2. Работа в печатной тетради № 1.

Задание № 139.

– Используя знания таблицы умножения и деления на 3, учащиеся заполняют таблицу.

VI. Итог урока.

– Что нового узнали на уроке?

– Как вычислить третью часть числа?

Домашнее задание: № 22, 25 (учебник); № 138 (рабочая тетрадь).

Урок 49
Умножение четырех и на 4

Цели урока: составить таблицу умножения четырех и умножения на 4; совершенствовать вычислительные навыки; продолжить формирование умений решать задачи разными способами; развивать внимание и логическое мышление.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Решите задачу.

Ребята поехали на экскурсию в двух автобусах.

В первый автобус сели 26 ребят, из них 16 мальчиков. Во второй автобус сели 29 ребят, из них 9 девочек.

– Подумайте: на какие вопросы вы ответите, выполнив действия:

– На какие еще вопросы вы можете ответить, пользуясь данным условием?

2. Значения каких выражений будут меньше, чем число 50? Найдите значения выражений:

3. Соедините 4 точки так, чтобы получился четырехугольник:

4. Подчеркните «лишнее» слово:

а) слагаемое, сумма, вычитаемое;

б) круг, треугольник, квадрат;

в) плюс, число, минус;

г) длина, масса, циркуль.

III. Сообщение темы урока.

– Рассмотрите математические записи.

– Чем они похожи? Чем отличаются?

– Сегодня на уроке мы составим таблицу умножения четырех и на 4.

IV. Изучение нового материала.

Задание № 1 (с. 94).

– Рассмотрите рисунок в учебнике. Сколько машин отремонтировали Волк и Заяц?

– Сколько колес у каждой машины?

– Сколько колес у всех машин?

– Объясните, как решали задачу Волк и Заяц.

– Кто из них быстрее посчитал? (Заяц, так как использовал умножение.)

Далее, используя фишки, учащиеся составляют таблицу умножения четырех.

Задание № 2 (с. 95).

Учитель проводит фронтальную работу с классом.

  

Число 4 надо взять 6 раз. Разложим фишки по 4 в 6 рядов и т. д.

Задание № 4 (с. 95).

Используя калькулятор, учащиеся сравнивают результаты умножения.

4 · 8 равно 8 · 4, так как 4 · 8 = 32 и 8 · 4 = 32;

4 · 6 равно 6 · 4, так как 4 · 6 = 24 и 6 · 4 = 24.

Вывод: при перестановке множителей результат умножения не изменяется.

Задание № 5 (с. 95).

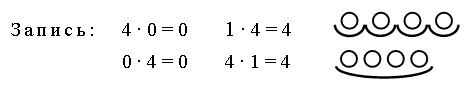
Вывод: если нуль умножить на любое число или любое число умножить на нуль, то в результате умножения получим нуль.

Если единицу умножить на какое-нибудь число или это число умножить на единицу, то получим это же число.

Запись в общем виде:  а · 0 = 0 · а = 0;

        1 · а = а · 1 = 1.

Задание № 7 (с. 95).

– Как называются данные фигуры?

– Какие фигуры называются многоугольниками?

– Определите название каждого многоугольника.

– На сколько квадратов разделена каждая фигура?

– Посчитайте их число разными способами.

– Каким способом считать удобнее?

Задание № 10 (с. 96).

– Прочитайте текст. Является ли он задачей?

– Что известно в задаче? Что требуется узнать?

– Запишите решение задачи по действиям.

Решение:

1. Сколько бутылок с водой в ящике?

6 · 4 = 24 (б.).

2. Сколько бутылок в двух таких ящиках?

24 + 24 = 48 (б.).

3. Сколько бутылок в трех ящиках?

48 + 24 = 72 (б.).

V. Повторение пройденного материала.

1. Работа по учебнику.

Задание № 32 (с. 100).

При разборе данного задания учитель использует карточку-помощницу. С опорой на «машину» дети легко находят способ решения задачи.

12 : 3 = 4.

Ответ: 4.

Задание № 33 (с. 100).

5 · 3 = 15.

Ответ: 15.

– Что значит «треть числа»?

Задание № 35 (с. 100).

– Прочитайте задачу.

– Что известно? Что требуется узнать?

– Запишите кратко условие задачи и решите ее.

Запись: Черной – 12 к.

   Красной – ? к.

   Всего: – 20 к.

Решение:

20 – 12 = 8 (к.) – посадили красной смородины.

Ответ: 8 кустов.

2. Работа в печатной тетради № 1.

Задание № 148.

Запись:	4 · 7 = 28	6 · 4 = 24
	7 · 4 = 28	4 · 6 = 24
	28 : 7 = 4	24 : 6 = 4
	28 : 4 = 7	24 : 4 = 6

VI. Итог урока.

– Что нового узнали на уроке?

– Что значит число умножить на 0?

– Что значит число умножить на единицу?

Домашнее задание: № 6, 8, 9 (учебник); № 144–146 (рабочая тетрадь).

Урок 50
Умножение и деление на 4

Цели урока: составить таблицу деления на 4, используя таблицу умножения; познакомить учащихся с историей возникновения календаря; совершенствовать умения решать задачи, выполняя действия деление и умножение; развивать умение анализировать и рассуждать.

Ход урока

I. Организационный момент.

II. Устный счет.

1. По какому признаку можно разбить данные выражения на 2 группы? Найдите значения выражений:

 

2. Решите задачу.

От проволоки длиной 15 дм отрезали сначала 2 дм, а потом еще 4 дм.

– Подумайте, на какие вопросы можно ответить, пользуясь этим условием:

а) Сколько всего дециметров проволоки отрезали?

б) На сколько дециметров меньше отрезали в первый раз, чем во второй?

в) На сколько дециметров проволока стала короче?

г) Сколько дециметров проволоки осталось?

3. Рассмотрите рисунок.

– Что здесь изображено?

– Что обозначают данные выражения и как они связаны с рисунком?

– Найдите значения всех произведений.

III. Сообщение темы урока.

– Рассмотрите рисунок на доске.

– Составьте по рисункам примеры вида:

 ·  = 

 : 4 = 

– Сегодня на уроке мы составим таблицу деления на 4.

IV. Изучение нового материала.

Задание № 13 (с. 96).

– Сколько дней в одной неделе?

– Сколько дней в феврале, если в этом месяце 4 недели?

Запись: 7 · 4 = 28 (дн.).

– К данной задаче составьте обратную задачу.

Задача. В феврале 28 дней. Сколько недель в феврале?

– Какое действие поможет вам решить эту задачу? (Деление.)

Используя фишки, учащиеся решают обратную задачу.

При решении этой задачи учитель может сообщить про високосный год, когда в феврале – 29 дней.

Справочный материал для учителя

История возникновения названий месяцев года

– Названия месяцев и их продолжительность ведут свое начало из Рима. Первым у римлян считался месяц, название которого произошло от имени бога войны Марса. Догадайтесь, что это за месяц.  (Март.) Рим славился своими мифами и легендами, поэтому многие вещи и предметы называли в честь вымышленных героев. Так, божество Янус дало название январю. Другие месяцы стали называться от своих порядковых номеров. Были и такие месяцы, которые называли именами правителей государств: Юлий Цезарь (июль), император Август (август).

Но не только римляне были такими изобретательными. Многие старинные славяно-русские названия месяцев года существуют и по сей день в некоторых языках. В основном все они произошли от названий сельскохозяйственных работ или природных явлений каждого месяца:

январь – сечень (сечь, рубить дрова);

февраль – сухень или лютень (лютый, холодный ветер высушивал деревья);

март – березень (сожжение деревьев до золы для удобрения почвы);

апрель – квитень (цветение растений);

май – травень (появление травы);

июнь – червень (пробуждение насекомых);

июль – липень (цветение липы);

август – жнивень или серпень (пора жатвы);

сентябрь – вересень (вересеня – жатва);

октябрь – жовтень;

ноябрь – листопад;

декабрь – снежинь или грудень (груда – замерзший ком земли).

Далее учащиеся решают примеры на умножение четырех и, опираясь на них, составляют таблицу деления на 4.

Запись на доске:

Задание № 14 (с. 97).

Используя таблицу умножения на 4, учащиеся выполняют деление.

Задание № 17 (с. 97).

– Прочитайте обе задачи. Сравните их.

– Запишите решение каждой задачи.

Задача а).

20 : 4 = 5 (к.) – получилось.

Ответ: 5 к.

Задача б).

20 : 4 = 5 (ф.) – в одной кучке.

Ответ: 5 ф.

– Сравните решения и ответы этих задач. В чем они сходны? В чем различаются?

V. Повторение пройденного материала.

1. Работа по учебнику.

Задание № 11 (с. 96).

– Прочитайте задачу.

– Что известно? Что требуется узнать?

– Запишите кратко условие задачи и решите ее по действиям.

Решение: 1) 8 · 4 = 32 (п.) – с 4 кустов.

   2) 6 · 3 = 18 (п.) – с 3 кустов.

   3) 32 + 18 = 50 (п.) – всего.

Ответ: 50 п.

Задание № 20 (с. 98).

– Прочитайте условие задачи.

– Что вам известно? Что требуется найти?

Запись: 24 : 4 = 6 (ш.).

   28 : 4 = 7 (ш.).

   36 : 4 = 9 (ш.).

Задание № 21 (с. 98).

– Прочитайте текст. Является ли он задачей? Почему?

– Что известно? Что неизвестно?

– Запишите кратко условие задачи в таблицу.

Решение: 1) 4 : 1 = 4 (б.) – было литровых.

   2) 15 : 3 = 5 (б.) – было трехлитровых.

   3) 5 + 4 = 9 (б.) – всего.

Ответ: 9 банок.

2. Работа в печатной тетради № 1.

Задание № 149.

– Прочитайте условие задачи.

– Что известно? Что требуется узнать?

При необходимости учитель предлагает учащимся заполнить таблицу.

Ответ: масса одинакова: 2 · 4 = 4 · 2.

Задание № 158.

– Изобразите тропинки, ведущие от домиков поросят к их огородам, так, чтобы они пересекались.

– Изобразите тропинки так, чтобы они не пересекались.

Чертеж:

VI. Итог урока.

– Что нового узнали на уроке?

– Как связано деление с умножением?

Домашнее задание: № 18, 19 (учебник); № 150 (рабочая тетрадь).

Урок 51
Умножение и деление на 4. Четверть числа

Цели урока: ввести понятие «четверть числа»; рассмотреть способ нахождения четвертой части числа; совершенствовать навыки составления и преобразования задач; развивать умение анализировать и сравнивать.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Решите задачу.

Отец и сын возвращаются из магазина. Отец несет 3 кг картофеля, 4 кг капусты и 5 кг лука. Сын несет 2 кг моркови, 3 кг свеклы и 1 кг репы. Чей груз тяжелее и на сколько? Что обозначают выражения, составленные по условию задачи:

2. Вставьте числа в «окошки», чтобы получились верные равенства:

3. Что обозначают выражения, записанные под каждой картинкой?

– Прочитайте выражения по-разному.

4. Сколько треугольников на чертеже?

Ответ: 10 треугольников.

III. Сообщение темы урока.

– Рассмотрите чертеж на доске:

– Найдите половину этого отрезка. (12 : 2 = 6 (дм).)

– Чему равна треть этого отрезка? (12 : 3 = 4 (дм).)

– Можно ли узнать, чему равна четверть этого отрезка?

– Сегодня на уроке мы узнаем, как найти четверть любого числа.

IV. Изучение нового материала.

Учащиеся работают с фишками.

– Разложите 24 фишки на 4 полочки поровну. Сколько фишек будет на каждой полочке?

– На каждой одной полочке находится четвертая часть числа 24 или четверть этого числа.

– Чему равна четверть числа 24?

– Как найти четверть какого-нибудь числа?

Далее учащиеся читают правило на с. 98 учебника.

 

Задание № 22 (с. 98).

– Что известно? Что надо узнать?

– Как найти четвертую часть числа?

Запись: 28 : 4 = 7 (дн.).

Задание № 23 (с. 98).

– Прочитайте текст. Является ли он задачей?

– Что известно? Что надо узнать?

– Запишите кратко условие задачи.

      Сыр – ? р.

Решение: 1) 32 : 4 = 8 (р.) – цена хлеба.

   2) 32 – 8 = 24 (р.) – стоит сыр.

Ответ: 8 рублей, 24 рубля.

Задание № 24 (с. 98).

Учащиеся при затруднении могут выполнить схему к данному условию задачи.

Решение: 4 · 2 = 8 (ч.).

Ответ: 8 частей.

Задание № 27 (с. 99).

Используя иллюстрацию «машины», учащиеся находят способ решения задачи.

9 · 4 = 36.

Проверка: 36 : 4 = 9.

Ответ: 36.

Задание № 28 (с. 99).

Методом подбора числа учащиеся находят ответ.

Учитель на доске записывает условие задания:

Ответ: 12.

V. Повторение пройденного материала.

1. Работа по учебнику.

Задание № 39 (с. 101).

– Рассмотрите рисунок. Что вам известно? (В тарелке – 5 морковок, у Зайца – 6 морковок.)

– Составьте задачу по рисунку так, чтобы она решалась в одно действие.

· Сколько всего морковок?

6 + 5 = 11 (м.).

· Сколько морковок у Зайца, если в тарелке их 5, а всего морковок 11?

11 – 5 = 6 (м.).

· Сколько морковок в тарелке?

11 – 6 = 5 (м.).

· На сколько больше (меньше) морковок у Зайца, чем лежит в тарелке?

6 – 5 = 1 (м.).

– Составьте задачу, которая решается двумя действиями.

· На тарелке лежало 5 морковок. Зайка еще принес в двух лапах по 3 морковки. Сколько морковок стало всего?

Решение: 1) 3 · 2 = 6 (м.) – у Зайца.

   2) 6 + 5 = 11 (м.) – всего.

Ответ: 11 морковок.

Задание № 40 (с. 101).

– Рассмотрите схему и составьте по ней задачу.

· В первой корзине лежит 9 кг яблок, а в другой – на 2 кг больше. Сколько килограммов яблок в двух корзинах?

Решение: 1) 9 + 2 = 11 (кг) – во 2-й корзине.

   2) 9 + 11 = 20 (кг) – всего.

Ответ: 20 килограммов.

– Измените условие задачи так, чтобы первым действием было вычитание.

– Измените условие задачи так, чтобы она решалась в одно действие.

Задание № 41 (с. 101).

Составьте задачу по рисунку, которая решается делением.

· Десять бананов разложили на 5 равных кучек. Сколько бананов в каждой кучке?

10 : 5 = 2 (б.).

· Десять бананов раздали детям, по 2 банана каждому. Сколько детей получили бананы?

10 : 2 = 5 (б.).

2. Работа в печатной тетради № 1.

Задание № 151.

– Как найти четверть числа?

– Как найти половину числа?

– Как вы думаете, что будет больше: четверть или половина числа? (Половина числа больше, чем его четверть.)

– Выполните вычисления и проверьте свое предположение.

Задание № 154.

– Прочитайте задачу.

– Что значит «столько же»? (6.)

 – Что значит «полстолько же»? (Это 3 пирожка, так как 6 : 2 = 3.)

– Сколько всего пирожков испекла бабушка?

Решение: 6 + 6 + 6 : 2 = 15 (п.).

Ответ: 15 пирожков.

VI. Итог урока.

– Что нового узнали на уроке?

– Можно ли сравнивать доли числа?

Домашнее задание: № 36, 37, 42 (учебник); № 153 (рабочая тетрадь).

Урок 52
Умножение пяти и на 5

Цели урока: составить таблицу умножения пяти и умножения на 5; вести подготовку к введению понятия площади фигуры; рассмотреть особые случаи умножения на 1 и на 0; совершенствовать навыки решения составных задач; продолжить формирование умений выделять симметричные фигуры и проводить ось симметрии; развивать внимание и логическое мышление.

Ход урока

I. Организационный момент.

II. Устный счет.

1. Разгадайте правило, по которому составлены схемы, и вставьте пропущенные числа:

2. Стрелки показывают отношения «Я больше тебя».

Напишите числа.

3. Задача.

Мама Енотиха сварила раков и разделила их поровну – Крошке Еноту и себе. «Мне столько не съесть», – сказал Крошка Енот и отдал 7 раков Маме. На сколько меньше раков стало у Крошки Енота, чем у Мамы?

4. Сколько на чертеже:

квадратов ?

прямоугольников ?

четырехугольников ?

III. Сообщение темы урока.

– Рассмотрите рисунок.

– Какие выражения можно составить по этому рисунку?

– Как быстро узнать количество цветов?

– Сегодня на уроке мы составим таблицу умножения на 5.

IV. Изучение нового материала.

Задание № 1 (с. 4).

– Рассмотрите иллюстрацию в учебнике.

– Сколько всего здесь рублей?

– Как решил задачу Волк? (Прибавлял по 5.)

– Как решил задачу Заяц? (Составил таблицу умножения на 5.)

– Кто из них справился быстрее с заданием? Почему?

Далее учащиеся под руководством учителя составляют таблицу умножения на 5.

Задание № 2 (с. 5).

– Объясните, как найти результаты умножения чисел, используя рисунок?

5 · 2 = 10

5 · 5 = 25

Задание № 3 (с. 5).

Учащиеся вычисляют, используя таблицу умножения.

Задание № 4 (с. 5).

Запись:

Вывод: от перестановки множителей значение произведений не изменяется.

Задание № 5 (с. 5).

Запись: 5 · 0 = 0.

   0 · 5 = 0.

Вывод:

· При умножении какого-нибудь числа на нуль получаем нуль.

· При умножении нуля на какое-нибудь число получаем нуль.

Задание № 7 (с. 5).

– Рассмотрите рисунок в учебнике.

– Как называются данные фигуры?

– На сколько квадратов разделена каждая фигура?

– Решите задачу разными способами.

Запись:

I способ:  5 + 5 + 2 + 2 = 14 (кв.).

II способ:  3 + 3 + 4 + 4 = 14 (кв.).

III способ:  5 · 2 + 2 · 2 = 14 (кв.).

– Какой способ более рациональный?

I способ:  5 + 5 + 5 + 2 = 17 (кв.).

II способ:  3 + 3 + 5 + 3 + 3 = 17 (кв.).

III способ:  5 · 3 + 2 = 17 (кв.).

– Какой способ более рациональный?

V. Повторение пройденного материала.

1. Работа по учебнику.

Задание № 30 (с. 11).

– Как найти треть числа? (Разделить на 3.)

Запись: 18 : 3 = 6.

   27 : 3 = 9.

   21 : 3 = 7.

Задание № 32 (с. 11).

– Сравните данные выражения. Чем они похожи? (Есть скобки.)

– Как найти значение выражений со скобками?

Запись:            

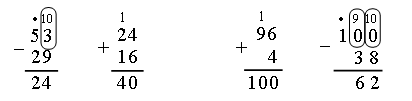
Задание № 33 (с. 11).

Учащиеся работают устно, используя карточку-помощницу:

Задание № 34 (с. 11).

Учащиеся работают устно, используя карточку-помощницу:

2. Работа в печатной тетради № 2.

Задание № 13.

– Прочитайте задачу.

– Что известно? Что требуется узнать?

– Рассмотрите решение Кости и Коли. Кто из мальчиков правильно решил задачу?

Запись:                                            Решение:

             7 – 3 = 4 (м) – высота ели.

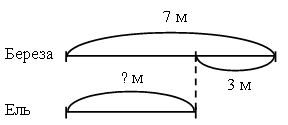
Ответ: 4 метра.

Задание № 15.

Учащиеся проводят оси симметрии, используя прозрачную линейку или от руки.

После того как учащиеся выполнили задание, учитель предлагает им проверить свою работу с помощью зеркала, которое нужно разместить вертикально (ребром) на проведенных осях симметрии.

– Нарисуйте ось симметрии пятиконечной звезды так, чтобы точка А была симметрична точке В относительно этой прямой. Отметьте ее красным цветом. Нарисуйте еще четыре оси симметрии этой звезды.

VI. Итог урока.

– Что нового узнали на уроке?

– Какие фигуры называют симметричными?

– Что такое ось симметрии?

– Что значит запись: «2 · 5»?

Домашнее задание: № 6, 31 (учебник); № 14 (рабочая тетрадь № 2).