Варианты заданий по математике для подготовки к экзамену в форме ГВЭ

Муниципальное бюджетное общеобразовательное учреждение

«Средняя общеобразовательная школа № 2»

 

 

 

 

 

 

 

 

 

Варианты заданий по математике для подготовки к экзамену в форме ГВЭ

 

 

Сборник вариантов

 

 

 

 

 

Выполнила: Лужных Ирина Викторовна

учитель математики

 

 

 

Ленинск-Кузнецкий

2021

Содержание

 

Введение………………………………………………………………………..….3

§1. Структура и содержание экзаменационной работы…….……...…………...4

§2. Система и критерии оценивания экзаменационной работы ………..….…..5

§3. Варианты заданий экзаменационной работы.……........................................6

Ответы………………………………………………………………………...….19

Литература………………………………………………………………….……21

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Введение

Данное пособие предназначено для подготовки к ГВЭ по математике базового уровня. Задания относятся к первой и второй частям, за которые можно получить оценку, рассмотрена структура и содержание экзаменационной работы, отвечающие всем критериям, предъявляемым к ней. В данном сборнике представлены 4 варианта для сдачи экзамена в форме ГВЭ.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

§1.  Структура и содержание экзаменационной работы.

     Каждый вариант экзаменационной работы содержит 12 заданий, из них 10 заданий с кратким ответом, в которых необходимо записать ответ в виде целого числа, конечной десятичной дроби или последовательности цифр, и 2 задания с развёрнутым ответом. На выполнение работы по математике отводится 3 часа 55 минут (235 минут).  Задания 1–10 с кратким ответом группируются исходя из тематической принадлежности заданий: алгебра, уравнения и неравенства, функции, начала математического анализа, геометрия (планиметрия и стереометрия). Задания 11 и 12 с развёрнутым ответом предполагают составляются на повышенном уровне, необходимом для применения математики в профессиональной деятельности.

Распределение заданий по основным содержательным разделам (темам) курса математики

Содержательные разделы	Количество заданий
Алгебра	5
Уравнения и неравенства	2
Функции	1
Начала математического анализа	1
Геометрия	3
Итого	12

 

 

 

 

 

 

 

 

 

 

 

 

 

§2. Система и критерии оценивания экзаменационной работы

    Каждое из заданий 1–10 считается выполненным верно, если экзаменуемый дал верный ответ в виде целого числа, конечной десятичной дроби или последовательности цифр. Ответ на каждое верно выполненное задание оценивается 1 баллом.

Количество баллов, выставляемых за выполнение заданий 11 и 12, зависит от полноты решения и правильности ответа. Общие требования к выполнению заданий с развёрнутым ответом: решение должно быть математически грамотным, полным, в частности все возможные случаи должны быть рассмотрены. Методы решения, формы его записи и формы записи ответа могут быть разными. За решение, в котором обоснованно получен правильный ответ, выставляется максимальное количество баллов. Правильный ответ при отсутствии текста решения оценивается в 0 баллов.

 

Содержание критерия	Баллы
Обоснованно получены верные ответы в обоих пунктах	2
Обоснованно получен верный ответ в пункте а  ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов – пункта а и пункта б	1
Решение не соответствует ни одному из критериев, перечисленных выше	0
Максимальный балл	2

 

 

Содержание критерия	Баллы
Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б	2
Имеется верное доказательство утверждения пункта а ИЛИ обоснованно получен верный ответ в пункте б	1
Решение не соответствует ни одному из критериев, перечисленных выше	0
Максимальный балл	2

§3 Варианты заданий экзаменационной работы.

Вариант 1

Часть 1

Ответами к заданиям 1–10 являются целое число, конечная десятичная дробь или последовательность цифр. Запишите ответ в поле ответа в тексте работы, затем перенесите в  БЛАНК  ОТВЕТОВ  справа  от  номера соответствующего задания. Единицы измерений писать не нужно.

 

1.       В летнем лагере 249 детей и 28 воспитателей. В одном автобусе можно перевозить не более 45 пассажиров.  Какое наименьшее количество таких автобусов понадобится, чтобы за один раз перевезти всех из лагеря в город?

Ответ: ___________________________

2.       Пачка сливочного масла стоит 50 рублей. Пенсионерам магазин делает скидку 10%. Сколько рублей стоит пачка масла для пенсионера?

Ответ: ___________________________

3.       Решите уравнение x² =− 2x + 24. Если уравнение имеет более одного корня, в ответе укажите больший из них.

Ответ: ___________________________

4.       Фабрика выпускает сумки. В среднем из 150 сумок 3 сумки имеют скрытый дефект. Найдите вероятность того, что случайно выбранная сумка окажется без дефектов.

Ответ: ___________________________

5.       На рисунке жирными точками показан курс евро, установленный Центробанком РФ, во все рабочие дни в январе 2007 года. По горизонтали указываются числа месяца, по вертикали — цена евро в рублях. Для наглядности жирные точки на рисунке соединены линиями. Определите по рисунку наибольший курс евро в рублях в период с 16 по 27 января. 

 

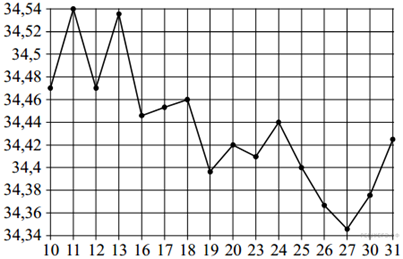
Ответ: ___________________________.

 

6.       Каждому   из   четырёх   неравенств   в   левом   столбце   соответствует   одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.

 

НЕРАВЕНСТВА                                                  РЕШЕНИЯ

А)  Б)  В)  Г)

1)  2)  3)  4)

 

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

Ответ: 

A	Б	В	Г

 

7.       В треугольнике ABC угол C равен 90°, AB = 25, AC = 24. Найдите cosB.

 

Ответ: ___________________________.

 

8.       В бак, имеющий форму прямой призмы, налито 5 л воды. После полного погружения в воду детали уровень воды в баке поднялся в 1,4 раза. Найдите объём детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров.

                                                                                     

Ответ: ___________________________.

 

9.       На рисунке изображён график дифференцируемой функции y = f(x). На оси абсцисс отмечены девять точек: x₁, x₂, x₃, ..., x₉. Среди этих точек найдите все точки, в которых производная функции f(x) отрицательна. В ответе укажите количество найденных точек.   

           Ответ: ___________________________

10.    Из городов А и В навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в город В на 2 часа раньше, чем велосипедист приехал в город А, а встретились они через 1 час 20 минут после выезда. Сколько часов затратил на путь из города В в город А велосипедист?

           Ответ: ___________________________.

 

Не забудьте перенести все ответы в БЛАНК ОТВЕТОВ в соответствии с инструкцией по выполнению работ

 

Часть 2

Для записи решений и ответов  на  задания  11  и  12  используйте  БЛАНК ОТВЕТОВ. Запишите сначала номер выполняемого задания (11 или 12), а затем полное обоснованное решение и ответ.  Ответы записывайте  чётко  и разборчиво

 

11.   а) Решите уравнение 

       б) Найдите корни этого уравнения, принадлежащие промежутку 

12.   Все рёбра правильной треугольной призмы ABCA1B1C1 имеют длину 6. Точки M и N — середины рёбер AA1 и A1C1 соответственно.

      а) Докажите, что прямые BM и MN перпендикулярны.

 б) Найдите угол между плоскостями BMN и ABB1.

 

Вариант 2

Часть 1

Ответами к заданиям 1–10 являются целое число, конечная десятичная дробь или последовательность цифр. Запишите ответ в поле ответа в тексте работы, затем перенесите в  БЛАНК  ОТВЕТОВ  справа  от  номера соответствующего задания. Единицы измерений писать не нужно.

 

1.       Килограмм орехов стоит 75 рублей. Маша купила 4 кг 400 г орехов. Сколько рублей сдачи она должна получить с 350 рублей?

Ответ: ___________________________

2.       Флакон шампуня стоит 160 рублей. Какое наибольшее число флаконов можно купить на 1000 рублей во время распродажи, когда скидка составляет 25%? 

Ответ: ___________________________

3.       Решите уравнение   .

Ответ: ___________________________

4.       На экзамен вынесено 60 вопросов, Андрей не выучил 3 из них. Найдите вероятность того, что ему попадется выученный вопрос.

Ответ: ___________________________

5.       На рисунке жирными точками показана цена золота на момент закрытия биржевых торгов во все рабочие дни с 5 по 28 марта 1996 года. По горизонтали указываются числа месяца, по вертикали — цена унции золота в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа цена золота на момент закрытия торгов была наименьшей за данный период.

 

Ответ: ___________________________.

 

6.       Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.

 

НЕРАВЕНСТВА		РЕШЕНИЯ
А)  Б)  В)  Г)		1)  2)  3)  4)

 

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

Ответ: 

A	Б	В	Г

 

7.       Диагональ параллелограмма образует с двумя его сторонами углы  и  Найдите больший угол параллелограмма. Ответ дайте в градусах.

Ответ: ___________________________.

 

8.       Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).                                                                                                                                                

Ответ: ___________________________.

 

9.       На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) вточке x₀.                                                               

           Ответ: ___________________________

10.    Из городов  и , расстояние между которыми равно 330 км, навстречу друг другу одновременно выехали два автомобиля и встретились через 3 часа на расстоянии 180 км от города  Найдите скорость автомобиля, выехавшего из города  Ответ дайте в км/ч.

           Ответ: ___________________________.

 

Не забудьте перенести все ответы в БЛАНК ОТВЕТОВ в соответствии с инструкцией по выполнению работ

 

Часть 2

Для записи решений и ответов на  задания  11  и  12  используйте  БЛАНК ОТВЕТОВ. Запишите сначала номер выполняемого задания (11 или 12), а затем полное обоснованное решение и ответ.  Ответы записывайте  чётко  и разборчиво

 

11.   а) Решите уравнение 

     б) Укажите корни, принадлежащие отрезку 

12.   Все рёбра правильной треугольной призмы ABCA1B1C1 имеют длину 6. Точки M и N — середины рёбер AA1 и A1C1 соответственно.

      а) Докажите, что прямые BM и MN перпендикулярны.

 б) Найдите угол между плоскостями BMN и ABB1.

 

 

Вариант 3

Часть 1

Ответами к заданиям 1–10 являются целое число, конечная десятичная дробь или последовательность цифр. Запишите ответ в поле ответа в тексте работы, затем перенесите в  БЛАНК  ОТВЕТОВ  справа  от  номера соответствующего задания. Единицы измерений писать не нужно.

 

1.       На автозаправке клиент отдал кассиру 1000 рублей и залил в бак 28 литров бензина по цене 28 руб. 50 коп. за литр. Сколько рублей сдачи он должен получить у кассира?

Ответ: ___________________________

2.       Мобильный телефон стоил 3500 рублей. Через некоторое время цену на эту модель снизили до 2800 рублей. На сколько процентов была снижена цена?

Ответ: ___________________________

3.         Решите уравнение   

Ответ: ___________________________

4.       В сборнике билетов по химии всего 50 билетов, в 14 из них встречается вопрос по теме "Соли". Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по теме "Соли".

Ответ: ___________________________

5.         Когда самолёт находится в горизонтальном полёте, подъёмная сила, действующая на крылья, зависит от скорости движения. На рисунке изображена эта зависимость для некоторого самолёта. На оси абсцисс откладывается скорость (в километрах в час), на оси ординат — сила (в тоннах силы). Определите по рисунку, чему равна подъёмная сила (в тоннах силы) при скорости 200 км/ч.

 

Ответ: ___________________________.

 

6.       Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.

НЕРАВЕНСТВА		РЕШЕНИЯ
А)  Б)  В)  Г)		1) 1 < x < 2 2) x > 1 3) x > 2 4) x < 1

Впишите в приведённую в ответе таблицу под каждой буквой соответствующий решению номер.

А	Б	В	Г

 

 

7.      .

Найдите площадь четырёхугольника, изображённого на клетчатой бумаге с размером клетки 1х1.

 

Ответ: ___________________________.

 

 

8.      

План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м × 1 м. Найдите площадь участка, изображённого на плане. Ответ дайте в квадратных метрах.

Ответ: ___________________________.

 

9.        

На рисунке изображен график функции y = f(x), определенной на интервале (−6; 8). Определите количество целых точек, в которых производная функции положительна.

 

Ответ: ___________________________.

10.   Моторная лодка в 10:00 вышла из пункта А в пункт В, расположенный в 30 км от А. Пробыв в пункте В 2 часа 30 минут, лодка отправилась назад и вернулась в пункт А в 18:00 того же дня. Определите (в км/ч) собственную скорость лодки, если известно, что скорость течения реки 1 км/ч.

Ответ: ___________________________.

 

Не забудьте перенести все ответы в БЛАНК ОТВЕТОВ в соответствии с инструкцией по выполнению работ

 

Часть 2

Для записи решений и ответов  на  задания  11  и  12  используйте  БЛАНК ОТВЕТОВ. Запишите сначала номер выполняемого задания (11 или 12), а затем полное обоснованное решение и ответ.  Ответы записывайте  чётко  и разборчиво

 

11.   а) Решите уравнение 

     б) Найдите все корни этого уравнения, принадлежащие отрезку 

                                                                       

12.   На В основании прямой призмы ABCA₁B₁C₁ лежит равнобедренный прямоугольный треугольник ABC с гипотенузой AB, равной  Высота призмы равна 6.

     а) Докажите, что плоскость, содержащая прямую AC₁ и параллельная   прямой CB₁ проходит через середину ребра A₁B₁.

б) Найдите угол между прямыми AC₁ и CB₁.

 

Вариант 4

Часть 1

Ответами к заданиям 1–10 являются целое число, конечная десятичная дробь или последовательность цифр. Запишите ответ в поле ответа в тексте работы, затем перенесите в  БЛАНК  ОТВЕТОВ  справа  от  номера соответствующего задания. Единицы измерений писать не нужно.

 

1.       На день рождения полагается дарить букет из нечетного числа цветов. Тюльпаны стоят 30 рублей за штуку. У Вани есть 500 рублей. Из какого наибольшего числа тюльпанов он может купить букет Маше на день рождения?

Ответ: ___________________________

2.       Налог на доходы составляет 13% от заработной платы. Заработная плата Ивана Кузьмича равна 12 500 рублей. Сколько рублей он получит после вычета налога на доходы?

Ответ: ___________________________

3.         Решите уравнение   

Ответ: ___________________________

4.       На конференцию приехали 6 учёных из Швейцарии, 3 из Болгарии и 6 из Австрии. Каждый из них делает на конференции один доклад. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что третьим окажется доклад учёного из Болгарии."

Ответ: ___________________________

5.       На диаграмме показана среднемесячная температура воздуха в Санкт-Петербурге за каждый месяц 1999 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме, на сколько градусов Цельсия февраль был в среднем холоднее июля.

      

6.       На координатной прямой точками отмечены числа a, b, c, d и m. Установите соответствие между указанными точками и числами из правого столбца.

 

ТОЧКИ		ЧИСЛА
		1)  2)  3)  4)

 

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

a	b	c	d

7.        На клетчатой бумаге с размером клетки   изображён круг. Найдите площадь закрашенного сектора. Ответ дайте в квадратных сантиметрах.

 

Ответ: ___________________________.

 

8.       От столба высотой 12 м к дому натянут провод, который крепится на высоте 4 м от земли (см. рисунок). Расстояние от дома до столба 15 м. Найдите длину провода. Ответ дайте в метрах.

 

Ответ: ___________________________.

 

9.       На рисунке изображен график производной функции f(x), определенной на интервале (−16; 4). Найдите количество точек экстремума функции f(x) на отрезке [−14; 2].

 

 

 

Ответ: ___________________________.

 

 

10.    Каждый из двух рабочих одинаковой квалификации может выполнить заказ за 8 часов. Через 4 часа после того, как один из них приступил к выполнению заказа, к нему присоединился второй рабочий, и работу над заказом они довели до конца уже вместе. Сколько часов потребовалось на выполнение всего заказа?

 

Ответ: ___________________________.

 

 

Не забудьте перенести все ответы в БЛАНК ОТВЕТОВ в соответствии с инструкцией по выполнению работ

 

Часть 2

Для записи решений и ответов  на  задания  11  и  12  используйте  БЛАНК ОТВЕТОВ. Запишите сначала номер выполняемого задания (11 или 12), а затем полное обоснованное решение и ответ.  Ответы записывайте  чётко  и разборчиво

 

11.   а) Решите уравнение 

     б) Найдите все корни этого уравнения, принадлежащие отрезку 

 

12. В правильной треугольной пирамиде SABC с основанием ABC боковое ребро равно 7, а сторона основания равна 6. На продолжении ребра SA за точку A отмечена точка P, а на продолжении ребра SB за точку B — точка Q, причём AP = BQ = SA.

а) Докажите, что прямые PQ и SC перпендикулярны друг другу.

б) Найдите угол между плоскостями ABC и CPQ.

 

 

 

 

 

 

 

 

 

 

 

 

 

Ответы

№		Варианта
		1	2
Задания	1	7	330
	2	45	8
	3	4	-1
	4	0,98	0,98
	5	34,46	6
	6	1342	2341
	7	0,28	120
	8	2000	78
	9	2	0,25
	10	4	50
	11	а)  б)	а)  б)
	12	б)	б)

 

 

 

 

 

№		Варианта
		3	4
Задания	1	202	15
	2	20	10875
	3	-11	-0,5
	4	0,28	0,2
	5	1	28
	6	4231	3142
	7	22,5	0,75
	8	8	17
	9	4	4
	10	11	6
	11	а)   б)	а) б)
	12	или

 

 

 

 

 

 

Литература.

1.     Математика. Подготовка к ЕГЭ 2021. Базовый уровень. 40 тренировочных вариантов по демоверсии 2020 года: учебно-методическое пособие / под редакцией Ф.Ф. Лысенко, С.Ю. Кулабухова.- Ростов-на-Дону: Легион, 2019. – 416с. – (ЕГЭ)

2.     Алгебра: 9 класс: учебник для учащихся общеобразовательных организаций / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир.- М. : Вентана-Граф, 2018. – 304 с. : ил.

3.     ЕГЭ. Математика. Базовыйый уровень: типовые экзаменационные варианты: 36 вариантов / под редакцией И.В. Ященко. – М.:  Издательство «Национальное образование», 2019. – 256с. – (ЕГЭ. ФКР – школе)

4.     Решу ЕГЭ Дмитрий Гущин.

https://math11_100-gve.sdamgia.ru/

5.     ЕГЭ. Математика. Профильный уровень: типовые экзаменационные варианты : 36 вариантов / под редакцией И.В. Ященко. – М.:  Издательство «Национальное образование», 2020. – 256с. – (ЕГЭ. ФКР – школе)