
Магические квадраты

Ло шу-единственный нормальный магический квадрат 3*3.Был известен даже
В Древнем Китае.
Первое изображение на черепаховом панцире датируется с 2200г.до.н.э  Магический
квадрат 3-го порядка из 9-ти первых натуральных чисел (известный в Китае как
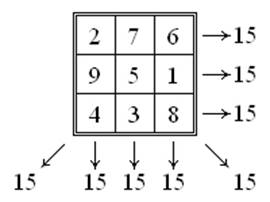
талисман Ло-шу) представляется следующей матрицей 3x3 (рис.2):
Магический
квадрат 3-го порядка из 9-ти первых натуральных чисел (известный в Китае как
талисман Ло-шу) представляется следующей матрицей 3x3 (рис.2):
В 13 в. математик Ян Хуэй занялся проблемой методов построения магических квадратов. Его исследования были потом продолжены другими китайскими математиками. Ян Хуэй рассматривал магические квадраты не только третьего, но и больших порядков. Некоторые из его квадратов были достаточно сложны, однако он всегда давал правила для их построения. Он сумел построить магический квадрат шестого порядка, причем последний оказался почти ассоциативным (в нем только две пары центрально противолежащих чисел не дают сумму 37)[4]
МАГИЧЕСКИЙ КВАДРАТ, квадратная таблица из целых чисел, в которой суммы чисел вдоль любой строки, любого столбца и любой из двух главных диагоналей равны одному и тому же числу.
Магическим квадратам приписывали различные мистические свойства. В 16 в. Корнелий Генрих Агриппа построил квадраты 3-го, 4-го, 5-го, 6-го, 7-го, 8-го и 9-го порядков, которые были связаны с астрологией 7-ми планет. Бытовало поверье, что выгравированный на серебре магический квадрат защищает от чумы. Даже сегодня среди атрибутов европейских прорицателей можно увидеть магические квадраты.




 один из магических квадратов!
один из магических квадратов!
Полного описания всех возможных магических квадратов не получено и до сего времени. Магических квадратов 2х2 не существует. Существует единственный магический квадрат 3х3 ,так как остальные магические квадраты 3х3 получаются из него либо поворотом вокруг центра, либо отражением относительно одной из его осей симметрии.
Расположить натуральные числа от 1 до 9 в магический квадрат 3х3 можно 8 различными способами:
|
4 |
9 |
2 |
|
3 |
5 |
7 |
|
8 |
1 |
6 |
9+5+1
9+4+2
8+6+2
8+5+2
8+4+3
7+6+2
7+5+3
6+5+4
Великий ученый Пифагор, основавший религиозно – философское учение, провозгласившее количественные отношения основой сущности вещей, считал, что сущность человека заключается тоже в числе – дате рождения. Поэтому с помощью магического квадрата Пифагора можно познать характер человека, степень отпущенного здоровья и его потенциальные возможности, раскрыть достоинства и недостатки и тем самым выявить, что следует предпринять для его совершенствования.
Для того, чтобы понять, что такое магический квадрат Пифагора и как подсчитываются его показатели, сделаю его расчет на своем примере. А чтобы убедиться, что результаты подсчета действительно соответствуют реальному характеру той или иной личности, вначале я проверю его на себе. Для этого я буду делать расчет по своей дате рождения. Итак, моя дата рождения 20.08.1986. Сложим цифры дня, месяца и года рождения (без учета нулей): 2+8+1+9+8+6=34. Далее складываем цифры результата: 3+4=7. Затем из первой суммы вычитаем удвоенную первую цифру дня рождения: 34-4=30. И вновь складываем цифры последнего числа:
3+0=3. Осталось сделать последние сложения – 1-й и 3-й и 2-й и 4-й сумм: 34+30=64, 7+3=10. Получили числа 20.08.1986,34,7,30, 64,10.
и составляем магический квадрат так, чтобы все единицы этих чисел вошли в ячейку 1, все двойки – в ячейку 2 и т. д. Нули при этом во внимание не принимаются. В результате мой квадрат будет выглядеть следующим образом:
|
44 |
9 |
2 |
|
33 |
- |
7 |
|
88 |
11 |
66 |
Ячейки квадрата означают следующее:
Ячейка 1 – целеустремленность, воля, упорство, эгоизм.
1 – законченные эгоисты, стремятся из любого положения извлечь максимальную выгоду.
11 – характер, близкий к эгоистическому.
111 – «золотая середина». Характер спокойный, покладистый, коммуникабельный.
1111 – люди сильного характера, волевые. Мужчины с таким характером подходят на роль военных – профессионалов, а женщины держат свою семью в кулаке.
11111 – диктатор, самодур.
111111 – человек жестокий, способный совершить невозможное; нередко попадает под влияние какой – то идеи.
Не смотря на то, что математиков интересовали в основном магические квадраты наибольшее применение в науке и технике нашли латинские квадраты.
Латинским квадратом называется квадрат nхn клеток, в которых написаны числа 1, 2,…, n, притом так, что в каждой строке и каждом столбце встречаются все эти числа по одному разу. На рис.3 изображены два таких квадрата 4х4. Они обладают интересной особенностью: если один квадрат наложить на другой, то все пары получившихся чисел оказываются различными. Такие пары латинских квадратов называются ортогональными.
|
1 |
2 |
3 |
4 |
|
2 |
1 |
4 |
3 |
|
3 |
4 |
1 |
2 |
|
4 |
3 |
2 |
1 |
1. Магические квадраты
Впервые
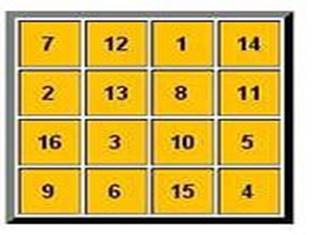
это сделал немецкий художник Альбрехт Дюрер (1441-1528г.г.), выпустивший в 1514
году гравюру «Меланхолия», на которой в правом верхнем углу есть изображение
магического квадрата четвертого порядка. Причем, два числа в середине нижней
строки указывают
 в этом квадрате будит всё ровно
одному числу 15
в этом квадрате будит всё ровно
одному числу 15
 Пифагор
Пифагор
Магические квадраты.
Магический квадрат второго порядка не существует. В этом легко убедиться испытанием. Учитывая симметрию квадрата, абсолютно безразлично, в какой из четырех углов мы поставим 1, допустим в левый нижний угол. В расположении чисел по одной диагонали возможны три варианта
.
История появления магических квадратов.
Магический квадрат - квадратная таблица из целых чисел, в которой суммы чисел вдоль любой строки, любого столбца и любой из двух главных диагоналей равны одному и тому же числу.
Страна, в которой был впервые придуман магический квадрат, точно неизвестна, неизвестен век, даже тысячелетие нельзя установить точно. Первые упоминания о магических квадратах были у древних китайцев. И, вероятно, самым старым из дошедших до нас магических квадратов является таблица Ло Шу. Она имеет размер 3*3 и заполнена натуральными числами от 1 до 9. В этом магическом квадрате сумма чисел в каждой строке, столбце и диагонали равна 15. Согласно одной из легенд прообразом Ло Шу стал узор из связанных черных и белых точек, украшавший панцирь огромной священной черепахи, всплывшей из вод реки Хуанхэ.
 Из Китая магические квадраты
распространились сначала в Индию, а затем и в другие страны. В начале XVI
века знаменитый немецкий художник Альбрехт Дюрер увековечил магический
квадрат в искусстве, изобразив его на гравюре «Меланхолия». Дата создания
гравюры (1514 год) указана числами, стоящими в двух центральных клетках нижней
строки.
Из Китая магические квадраты
распространились сначала в Индию, а затем и в другие страны. В начале XVI
века знаменитый немецкий художник Альбрехт Дюрер увековечил магический
квадрат в искусстве, изобразив его на гравюре «Меланхолия». Дата создания
гравюры (1514 год) указана числами, стоящими в двух центральных клетках нижней
строки.
Виды магических квадратов и способы их заполнения.
В ходе своей работы, я пришла к выводу, что магических квадратов 2*2 не существует. Квадрат размером 2*2 должен был бы состоять из чисел 1,2,3,4, а его постоянная была бы равна 5. У такого квадрата по две строки, столбца и диагонали. Чтобы квадрат стал магическим, надо представить число 5 в виде суммы двух данных чисел шестью различными способами, но это сделать не возможно! Ведь таких комбинаций всего две: 1+ 4 и 2+3. Как ни расставляй числа в клетках таблицы, их сумма будет равна 5 либо в каждой строке, либо в обоих столбцах, либо по диагоналям, но никак не одновременно.
Существует единственный магический квадрат 3*3, так как остальные магические квадраты 3*3 получаются из него либо перестановкой строк или столбцов либо путем поворота исходного квадрата на 900 или на 1800
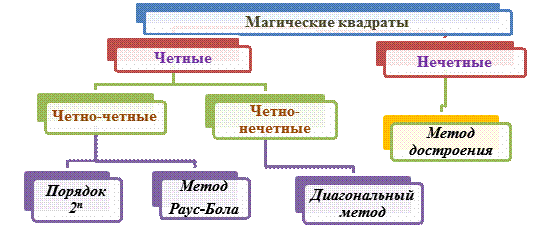
Общий метод построения квадратов неизвестен. Правила построения магических квадратов делятся на три категории в зависимости от того, каков порядок квадрата. Квадраты могут быть:
- нечетными, то есть состоять из нечетного числа клеток,
- четно-четные, то есть порядок равен удвоенному четному;
- четно-нечетные, то есть порядок равен удвоенному нечетному.
Актуальность: умение составлять магические
квадраты помогает в решении различных головоломок и олимпиадных задач по данной
теме, а так же повышает интерес учащихся к изучению математики. 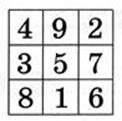
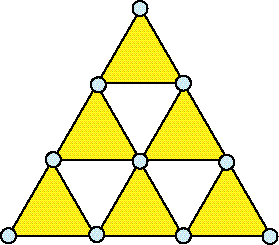
Пифагорейцы представляли Монаду фигурой, состоящей из десяти точек - узлов. Эти десять узлов, называемые пифагорейцами тетрактисом, образуют девять равносторонних треугольников, как бы олицетворяющих полноту всемирной пустоты и Животворящий крест (рис. 1).
Именно Монада стала стартовой точкой в изучении магических фигур.
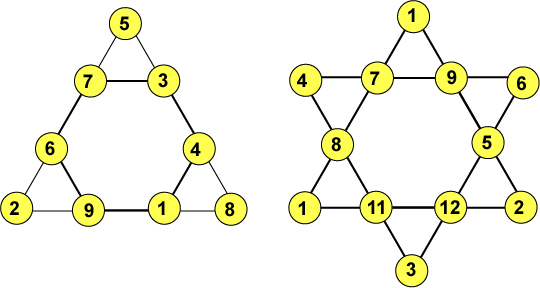
Баше де Мезириак описал простой графический способ построении квадратов нечетного порядка. Последний не раз переоткрывался и, вероятно, был изобретен еще в древности. Отметим, что в XVI-XV1I вв. составлением магических квадратов занимались с таким же увлечением, с каким сегодня придумывают и разгадывают кроссворды. Любопытно, что именно в одной из книг Баше магические квадраты впервые предстали как математическая забава.

 всё ровно 15
всё ровно 15
В наше время магические квадраты продолжают привлекать к себе внимание не только специалистов, но и любителей математических игр и развлечений. За последнее столетие значительно возросло число книг по занимательной математике, в которых содержатся головоломки и задачи, связанные с необычными квадратами. Для их успешного решения требуются не столько специальные знания, сколько смекалка и умение подмечать числовые закономерности. Решение таких задач не только доставит удовольствие тем, кто интересуется математикой, но и послужит прекрасной гимнастикой для ума!!!!!!!!
Спасибо за просмотр!
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.