Внеклассное мероприятие «Занимательные системы счисления»

Внеклассное мероприятие «Занимательные системы счисления»

 

О.М. Давыдова,

преподаватель ГБПОУ АО «Каргопольский педколледж»

 

1. Орг. момент (размещение студентов, подготовка к занятию)

 

2. Верите ли вы, что

- система счисления которой мы пользуемся называется десятичной? (да)

- 3211,  3121 это запись одного и того же числа?

- в наши дни используется двенадцатеричная система счисления? (Да)  (Год состоит из 12 месяцев, половина суток из 12 часов. В русском языке счет часто идет дюжинами, английский фунт состоит из 12 шиллингов, сервизы, салфетки, столовые приборы продают наборами по 6 и 12 штук.)

- мой возраст –  выражается числом10001?  (да, в двоичной системе)

- это запись некоторого числа – _# ҃в  ҃к   (это запись числа 2020)

- арабские цифры изобрели арабы? (Нет, их придумали в Индии, но в Европу эти цифры попали от арабов)

 

Итак,  речь сегодня пойдет о системах счисления

Многие тысячи лет назад наши далекие предки жили небольшими племенами. Первобытные люди не знали счета. Современному человеку трудно представить себе математику без обозначений чисел и арифметических действий.

Но ведь когда-то же этих обозначений не существовало. А тогда откуда они взялись? И почему именно такие, а не другие? И вообще много ли их существовало? Ни для кого не секрет, что всюду и повсеместно каждое мгновение наша жизнь наполнена цифрами и числами: день недели, год и дата рождения, номер автомобиля, магазинный ценник, штрих-код на книжной обложке, сколько дней осталось до каникул.

 

Люди приручили животных, на земле появились первые скотоводы, земледельцы. Людям приходилось всё чаще сталкиваться с большими числами. Нужно было придумать, как их записывать.

Первым способом «записи» чисел были зарубки на палке. Глиняные шарики и другие фигурки. Однако таким способом большое число не запишешь, да и читать трудно и долго. Около пяти тысяч лет назад у разных народов (в Вавилоне, Египте, Китае) появился новый способ записи чисел с помощью особых знаков - цифр.

 

3. Информация о системах счисления

 

С развитием человечества появились различные системы счисления

Система счисления - это метод записи числа при помощи указанного набора специальных знаков (цифр).

Система счисления:

 

• даёт представление множества чисел (целых и/или вещественных);

• даёт каждому числу уникальное представление (либо, хотя бы, стандартное представление);

• отображает алгебраическую и арифметическую структуру числа.

Отдельная позиция в отображении числа называется  разряд, значит, номер позиции - номер разряда.

Системы счисления делятся на позиционные и непозиционные. В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее позиции в числе. Например 257  и 725 совершенно разные числа, хотя записаны о с помощью одних и тех же цифр.

 

Существуют такие позиционные системы как

Пятеричная система была распространена у некоторых африканских  племен.

Десятичная система оказалась общепринятой по причине того, что десять пальцев рук - это самый первый аппарат для счета, которым человек пользовался с доисторических времен. По пальцам удобно считать от 1 до 10. Сосчитав до 10, естественно принять само число 10 за новую, более крупную единицу – единицу следующего разряда и т.д. Именно счет по пальцам рук положил начало той системе, которая кажется нам самой привычной.

Десятичная система счисления представляет собой систему, в которой, каждое целое положительное число представляется в виде суммы различных степеней числа 10 с коэффициентами, которые могут принимать значения от 0 до 9 включительно. Например, запись числа 3 756 означает, что рассматриваемое число содержит 6 единиц, 5 десятков, 7 сотен и 3 тысячи.

Десятичная система счисления не сразу заняла господствующее положение. В разные исторические периоды разные народы мира пользовались другими система счисления.

Двенадцатеричная система.

Широкое распространение имела двенадцатеричная система счисления. Ее происхождение тоже связано со счетом пальцев рук. Так как четыре пальца руки (кроме большого) имеют 12 фаланг, то по этим фалангам, перебирая их по очереди большим пальцем, и ведут счет от 1 до 12. Потом 12 принимается за единицу следующего разряда и т.д. Остатки двенадцатеричной системы сохранились до наших дней: вместо «двенадцать» говорят «дюжина». Многие предметы часто считают именно дюжинами (вилки, тарелки, ножи, носовые платки). А также число месяцев в году - 12. Остатки двенадцатеричной системы счисления имеются у англичан, например, в системе мер 1 фут = 12 дюймам или в денежной системе 1 шиллинг = 12 пенсам.

С математической точки зрения, двенадцатеричная система имела некоторые преимущества перед десятичной, потому что число 12 делится на 2, 3, 4, 6 и 12, а число 10 только на 2, 5 и 10. А больший запас делителей у числа, служащего основанием системы счисления создает удобства в ее использовании.

Двадцатеричная система.

У ацтеков и майя - народов, населявших в течении многих столетий обширные области американского континента и создавших там высокую культуру – была принята двадцатеричная система. Она же была принята у кельтов, населявших Западную Европу, начиная со второго тысячелетия до нашей эры. Следы двадцатеричной системы кельтов сохранились и в современном французском языке, например, «восемьдесят» по-французски будет как «четырежды двадцать». Число 20 встречалось и во французской денежной системе: франк делится на 20 су.

Шестидесятеричная система.

В древнем Вавилоне существовала сложная шестидесятеричная система. Мнения историков по поводу происхождения данной системы расходятся. Но не смотря на недоказанность гипотез возникновения шестидесятеричной системы, сам факт её существования и широкого распространения в древнем Вавилоне установлен. Эта система сохранилась до наших дней, например, в часе 60 минут, а в минуте 60 секунд или в системе измерения углов: градус = 60 минутам, минута = 60 секундам.

 

Двоичная система счисления

В двоичной системе счисления основание равно двум. В этой системе счисления используются всего два знака, две цифры – «0» и «1».

Чтобы научиться понимать числа в двоичной системе счисления, сначала рассмотрим, как формируются числа в привычной для нас десятичной системе счисления.

В десятичной системе счисления мы располагаем десятью знаками-цифрами от 0 до 9. Когда счет достигает 9, то вводится новый разряд (десятки), а единицы обнуляются и счет начинается снова. После 19 разряд десятков увеличивается на 1, а единицы снова обнуляются. И так далее. Когда десятки доходят до 9, то появляется третий разряд – сотни.

Двоичная система счисления аналогична десятичной за исключением того, что в формировании числа участвуют всего лишь две цифры: 0 и 1. Как только разряд достигает своего предела, т.е. единицы, появляется новый разряд, а старый обнуляется¹.

Таблица 1. Соответствие десятичных и двоичных чисел

Десятичное число	Двоичное число	Десятичное число	Двоичное число
0	0	11	1011
1	1	12	1100
2	10	13	1101
3	11	14	1110
4	100	15	1111
5	101	16	10000
6	110	17	10001
7	111	18	10010
8	1000	19	10011
9	1001	20	10100
10	1010

 

Таблица 2. Таблица степеней основания 2

10	9	8	7	6	5	4	3	2	1	0
1024	512	256	128	64	32	16	8	4	2	1

 

Перевод чисел из двоичной системы счисления в десятичную

В двоичной системе счисления длины чисел с увеличением значения растут быстрыми темпами. Как определить, что значит вот это: 10001001? Непривычный к такой форме записи чисел человеческий мозг обычно не может понять сколько это. Необходимо уметь переводить двоичные числа в десятичные².

В десятичной системе счисления любое число можно представить в форме суммы единиц, десяток, сотен и т.д.

пример:

1365 = 1000 + 300 + 60 + 5 или

1365 = 1 * 10³ + 3 * 10² + 6 * 10¹ + 5 * 10⁰

Если посмотреть на эту запись внимательно мы увидим здесь цифры 1, 3, 6 и 5 - это набор цифр из которых состоит число 1365. Все эти цифры поочередно умножаются на десять возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы.

Аналогично можно разложить и любое двоичное число, только основание здесь будет 2.

Пример:

10110001 = 1*2⁷ + 0*2⁶ + 1*2⁵ + 1*2⁴ + 0*2³ + 0*2² + 0*2¹ + 1*2⁰

Посчитав сумму составляющих, мы получим десятичное число, соответствующее 10110001

 

Римская нумерация

 

Среди множества цифр, которые существовали в разные времена у разных народов, только одни используется до сих пор. Это римские цифры. Более двух тысяч лет назад появилась римская нумерация, т. е. в Древнем Риме числа записывали при помощи букв латинского алфавита.

Система эта довольно проста и основывается на применении 7 букв латинского алфавита:

·                     1         I 

·                     5        V 

·                     10      X 

·                     50       L 

·                     100    C 

·                     500    D 

·                     1000  M

Правила записи чисел римскими цифрами:

·                     Сначала пишутся тысячи и сотни, а затем - десятки и единицы.

·                     Если большая цифра стоит перед меньшей, то они складываются (принцип сложения), если же меньшая - перед большей, то меньшая вычитается из большей (принцип вычитания).

Для легкого запоминания буквенных обозначений цифр в порядке убывания используют мнемоническое правило:

Mы Dарим Cочные Lимоны, Xватит Vсем Iх,

что соответствует M,D,C,L,X,V,I.

Для правильной записи больших чисел римскими цифрами необходимо сначала записать число тысяч, затем сотен, затем десятков и, наконец, единиц. Например, число 283 записывается как CCLXXXIII, то есть 100+100+50+30+3=283. Здесь цифра, изображающая сотню, повторена два раза, а цифры, изображающие соответственно десяток и единицу, повторены по три раза. А число 1988 как MCMLXXXVIII. (5)

На данный момент не существует единой теории происхождения римских цифр. Одна из самых популярных гипотез гласит, что римские цифры произошли от системы счета, которая использует вместо цифры штрихи-зарубки. Таким образом, цифра «I» - это не латинская или более древняя буква «и», а насечка, напоминающая форму этой буквы. Каждую пятую насечку обозначали скосом – V, а десятую перечеркивали – Х. 

Единица - I - это отображение пальца. Пятерка - V - это отображение ладони с сомкнутыми вместе четырьмя пальцами и оттопыренным большим пальцем.

Десятка - Х - это соединенные основаниями две ладони, обозначающие две пятерки.

Римская (буквенная) система нумерации появилась примерно в 500 году до нашей эры. Просуществовала она много столетий, прежде чем в средние века была заменена на привычную нам систему, взятую у арабов.

В настоящее время римская нумерация применяется для обозначения знаменательных дат, разделов разного рода книг, для обозначения порядкового номер монарха, Маркировка циферблатов часов «под старину»  и т.д.

В части Европы, в особенности в Литве, нередко можно встретить обозначение римскими цифрами дней недели (I – понедельник и так далее). В Голландии римскими цифрами иногда обозначают этажи. А в Италии ими отмечают 100-метровые отрезки пути, отмечая, в то же время, арабскими цифрами каждый километр.

 

Система записи чисел кириллицей

В древности широко распространенными были системы, в которых числа обозначалась буквами алфавита. К таковым относилась и греческая алфавитная система, называемая также ионической. К славянским племенам она пришла вместе с христианством и письменностью. Первыми ей начали пользоваться южные славяне, затем — восточные.

Создана славянская нумерация была греческими монахами Кириллом и Мефодием в IX веке по образцу греческой. До сих пор такая форма записи чисел используется в православных церковных книгах.

Чтобы показать, что букву в данном контексте следует воспринимать как число, над ней писали специальный значок — титло, представляющий собой волнистую линию. Букве «аз» соответствовала, как вы, наверное, догадались, единица. Последней буквой в алфавите, имевшей числовое значение, была «цы». С ее помощью записывали число 900. Таким образом можно было легко записать любое целое число от 1 до 999.

Тысячи записывались теми же буквами с титлом, что и 1, 2, …, 9, но слева внизу изображался еще один знак — наклонная линия, которая пересекается двумя черточками. Десятки тысяч отмечались тоже первыми буквами алфавита, но без титла, а сами буквы брались в кружок. Для изображения сотен тысяч кружок составлялся из точек, а для миллионов — из черточек.

Записанные таким способом числа имели свои названия. Десять тысяч называли тьмой, сто тысяч — легионом, а миллион — леодром.

Описанная здесь нумерация называлась «малое число», или «малый счет» . Кроме нее, существовал еще и «большой счет» («большое число», «великое число»).

 

4. Математическая игра

Для проведения игры нам потребуется 2 чел, которые будут членами жюри и две команда. Проведем жеребьевку.

Придумайте название своей команде

 

1). Конкурс “Веселый художник” . По два человека от каждой команды – 10 минут. Жюри попрошу засечь время выполнения.

В данном конкурсе каждой команде выдается листок с заданием. Необходимо выполнить перевод координат из двоичной системы счисления в десятичную и отметить точку на координатной плоскости. Правильно сделав перевод и соединив последовательно все точки, вы получите рисунок.

Жюри оценивает конкурс по 5-бальной системе.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

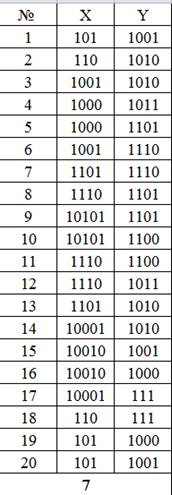
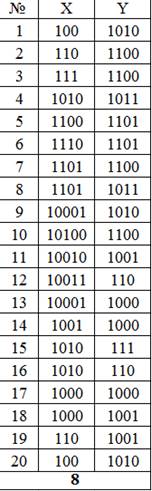
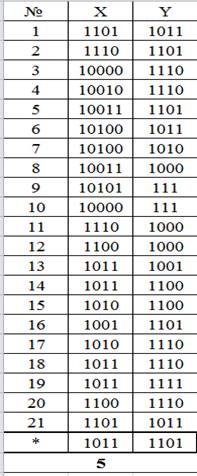
5 – улитка, 7 – танк,

2)«Интересный счёт».

 

Задача.

В старину на Руси широко применяли систему счисления, отдаленно напоминающую римскую. С ее помощью сборщики податей заполняли квитанции об уплате податей.

Для записи чисел употреблялись следующие знаки:

R - 1000 рублей

® - 100 рублей

¨ - 10 рублей

O - 1 рубль

|- 1 копейка

а) Какую сумму денег вы должны были  бы заплатить сборщику податей, если получили бы следующую квитанцию:

Вариант для  команды 1:

«Квитанция об уплате подати за движение по дороге.

Сумма: R®®®R¨OOOO|||||||||»

 

 

Вариант для  команды 2:

«Квитанция об уплате подати за пользование солью.

Сумма: R®®||||¨OOO®¨OO|||»

«Я окончил курс университета 44 лет от роду. Спустя год, 100-летним молодым человеком, я женился на 34-летней девушке. Незначительная разница в возрасте - всего 11 лет - способствовала тому, что мы жили общими интересами и мечтами. Спустя немного лет у меня была уже и немаленькая семья из 10 детей».

Чем объяснить странные противоречия в числах этого отрывка? Восстановите их истинный смысл. Жюри: время пошло.

Ответ: недесятичная система счисления - вот единственная причина кажущейся противоречивости приведенных чисел. Основание этой системы определяется фразой: «спустя год (после 44 лет), 100-летним молодым человеком…». Если от прибавления одной единицы число 44 преобразуется в 100, то, значит, цифра 4 - наибольшая в этой системе (как 9 - в десятичной), а, следовательно, основанием системы является 5. Т. е. все числа в автобиографии записаны в пятеричной системе счисления.

44 - 24, 100 -25, 34 - 19, 11 -6, 10 -5

О чем идет речь в стихотворении?

Наша умница Мальвина
Опекает Буратино
И купила для него,
Что ему нужней всего:
10 (2) обложки, 11 (3) линейки
И на 111 (7) рублей наклейки.
На обложках – Бармалей,
Цена каждой – 101 (5) рублей.
На линейки, что купила,
101010 (42) рубля хватило.
Сколько стоили покупки?
На раздумье – полминутки.

 

СТРАННАЯ ДЕВОЧКА

Ей было тысяча сто лет.

Она в сто первый класс ходила,

В портфеле по сто книг носила -

Всё это правда, а не бред.

Когда пыля десятком ног,

Она шагала по дороге,

За ней всегда бежал щенок

С одним хвостом, зато стоногий.

Она ловила каждый звук

Своими десятью ушами,

И десять загорелых рук

Портфель и поводок держали.

И десять тёмно-синих глаз

Рассматривали мир привычно…

Но станет всё совсем обычным,

Когда поймёте наш рассказ.(А. Стариков)

 

ОБЫЧНАЯ ДЕВОЧКА
Ей было двенадцать лет.
Она в пятый класс ходила,
В портфеле по четыре книги носила -
Всё это правда, а не бред.
Когда пыля двумя ногами,
Она шагала по дороге,
За ней всегда бежал щенок
С одним хвостом, зато четырехногий.
Она ловила каждый звук
Своими двумя ушами,
И двое загорелых рук
Портфель и поводок держали.
И двое тёмно-синих глаз
Рассматривали мир привычно…
И стало всё совсем обычным,
Когда вы поняли рассказ.

 

3. Числовой кроссворд

 

4. Блицопрос

1.                  Какой счётный прибор после появления калькуляторов стали в шутку называть “деревянным калькулятором”? (Счёты).

2.                  Число 14263 может быть записано в пятеричной системе счисления? (Нет)

3.                  Из каких цифр состоит алфавит двоичного кода? (0 и 1)

4.                  Первым вычислительным инструментом у человека были – (пальцы).

5.                  Римская система счисления является – (непозиционной).

6.                  Какое число записано LXXV ? (75)

7.                  7+1 в восьмеричной системе счисления – (10)

 

Подведение итогов игры. Вручение грамот