Интерполяционный многочлен в форме Ньютона.
Если интерполируемая функция задана таблицей с
равноотстоящими значениями аргумента с фиксированным шагом h=xi+1–xi, i=
, то для таких таблиц построение интерполяционного
многочлена во многом упрощается.
(1)
|
x |
x0 |
… |
xi |
… |
xn |
|
f(x) |
y0 |
… |
yi |
… |
yn |
Пусть искомая функция f(x) задана таблицей (1) с постоянным шагом. Тогда
разности вида Dyi=yi+1–yi , i=
(между значениями функций соседних узлов
интерполяции) называются конечными разностями первого порядка.
Разность конечных разностей первого порядка называется конечной разностью второго порядка. D2yi =Dyi+1–Dyi=(yi+2 – yi+1)–(yi+1 – yi)= yi+2 –2 yi+1+ yi
Аналогично найдем конечные разности третьего порядка:
D3yi=D2yi+1–D2yi =(yi+3–2 yi+2+yi+1)–(yi+2–2 yi+1+yi) =yi+3–3 yi+2+3 yi+1–yi
и т.д. Методом математической индукции можно доказать, что
Dkyi =yi+к –k yi+k–1+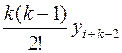 
–…+(–1)kyi.
Можно составить таблицу конечных разностей.
|
x |
y |
Dy |
D2y |
D3y |
… |
|
x0 |
y0 |
Dy0 |
D2y0 |
D3y0 |
|
|
x1 |
y1 |
Dy1 |
D2y1 |
|
|
|
x2 |
y2 |
Dy2 |
|
|
|
|
x3 |
y3 |
|
|
|
|
|
… |
… |
|
|
|
|
Первая интерполяционная формула Ньютона
Пусть функция f(x) представлена таблицей (1) с постоянным шагом и таблицей конечных разностей. Тогда будем искать интерполяционный многочлен в виде
Pn(x)=a0+a1(x–x0)+a2(x–x0)(x–x1)+…+an(x–x0)(x–x1)…(x–xn-1) – многочлен n-ой степени. Необходимо найти коэффициенты a0…an. Их ищут из условия совпадения многочлена Р со значениями функций в узлах.
При х=х0 имеем Р0(х0)=а0=y0; при x=x1 P1(x1)=а0+а1(x1–х0)=y1 =>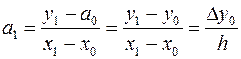 
; при x=x2 y2=P2(x2)=а0+а1(x2–х0)+а2(x2–х0)(x2–х1) =>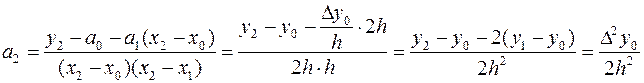 
Аналогично находим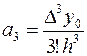 
,…,
ak=
.
Подставим выражения для ai в формулу интерполяционного многочлена n-ой степени:
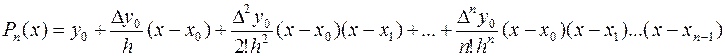
Пусть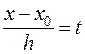
=>х=х0+ht.Тогда
;
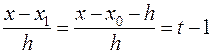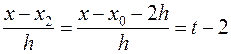
Рn(x)=Pn(x0+ht)=y0+tDy0+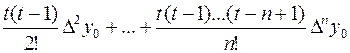
–первая интерполяционная формула Ньютона. Она применяется для
интерполирования в начале отрезка интерполяции, когда 
<<1. Поэтому она называется формулой интерполяции вперёд.
Вторая интерполяционная формула Ньютона
Когда значения аргумента близки к концу отрезка интерполирования, то первую формулу использовать не выгодно. В этом случае применяется формула Ньютона для интерполирования назад. Вторая интерполяционная формула ищется в виде:
Pn(x)=a0+a1(x–xn)+a2(x–xn)(x–xn-1)+…+an(x–xn)(x–xn-1)…(x–x1)
Аналогично
первой ИФН для каждого узла коэффициент ak=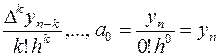
Пустьt=
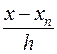.Рn(x)=Pn(xn+ht)=yn+tDyn–1+
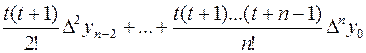– вторая интерполяционная формула Ньютона.
Если количество узлов велико, тогда лучше пользоваться формулами для первой и второй ИФН. Если количество узлов мало и конечные разности считаются в ручную, тогда используют формулу Ньютона по схеме Горнера:
Рn(x)=Pn(x0+ht)=y0+t(Dy0+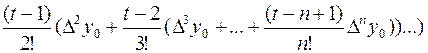 
При n=1 Рn(x)=y0+tDy0 – линейная формула интерполирования.
При n=2 Рn(x)=y0+tDy0+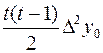
– квадратичная формула интерполирования.
Интерполяционный многочлен в форме
Подставим выражения для a i в формулу интерполяционного многочлена n -ой степени:
© ООО «Знанио»
