Вопрос 41.doc

Системы линейных алгебраических уравнений, нормы; обусловленность задачи решения линейной системы.

Норма – функция f: Rⁿ→R, обозначается , обладает следующими свойствами:

1.        ,,

2.       

3.                       1, 2, 3 – аксиомы нормы.

Чтобы доказать аксиомы нормы докажем неравенство Коши-Буняковского.

В трехмерном пространстве нормой вектора является его длина.

Док-во: рассмотрим ,

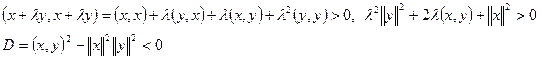
Если извлечь корень из D, то неравенство Коши-Буняковского превращается в строгое неравенство. Равенство возможно в случае, когда один из векторов равен нулю.

Неравенство треугольника.

Извлекая корень, получим неравенство треугольника.

В вычислениях применяются все три вида норм. Они применяются для оценки погрешностей. Применение различных норм неравносильно.

Норма линейного оператора.

Линейный оператор – это отображение Rⁿв R, т. е. A: Rⁿ → R. Ax=y , при

Отождествлять, что матрица соответствует оператору нельзя. Если    (*) – такой оператор называется ограниченным. Операторы, действующие в пространстве Rⁿ  ограничены.

Наименьшая из констант C, для которых для любого x из пространства Rⁿ выполняется условие (*) называется оператором.   (**)  .

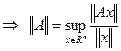Рассмотрим первую норму:

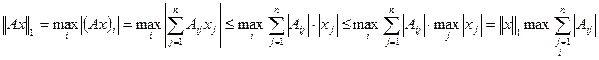
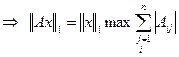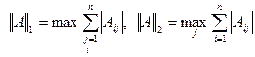Возьмем x=(α,α,α,α,….,α), тогда первая норма x равна α, - это есть норма. Т. е.  С помощью неравенства Коши-Буняковского можно показать, что

Обусловленность задачи решения системы линейных алгебраических уравнений.

Если правая часть линейного уравнения задана с погрешностью, то и в входном параметре будет погрешность, т. е. . Систему линейных уравнений можно записать как  (1). Если , то . Подставим в систему и получим:(2). Вычтем из (2) выражение (1), тогда . Обусловленность любой задачи определяется числом обусловленности. Пусть в какой-то задаче f - совокупность входных параметров, а x – совокупность входных параметров.

  Мы должны получить оценку 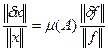, где μ(A) – число обусловленности и . Начнем с правой части. Система имеет решение при любых x следовательно , тогда существует обратная матрица A^-1 и .        (согласно аксиомам норм).

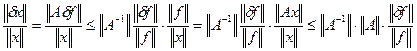. Мы доказали обусловленность для линейной системы.

Если  , тогда . Хотя детерминант мал, но норма оказалась бесконечно большим числом, следовательно μ(A) будет велико. Однако, даже если решение плохо обуславливает систему точным методом, результат может получиться далеким от истинного, значит плохо обусловленные системы надо решать другими методами.

  Рассмотрим систему с диагональным преобладанием Ax=f, , . Тогда справедлива теорема:

Система с диагональным преобладанием всегда совместна. Обратная матрица существует и .

Решение нелинейных уравнений методом Ньютона.

Пусть x* – корень уравнения F(x)=0 на отрезке [a,b] => F(a)=F(b) имеют разные знаки, F’(x) и F’’(x) сохраняют знак на всем интервале. Проведем касательную к кривой y=F(x) в точку A(a, F(a)). Пусть с₁ – точка пересечения касательной с осью Ох. y–F(a)=F’(a)(x–a) – уравнение касательной в точке А. Найдем точки пересечения прямой с Ох – для этого положим в уравнение касательной y=0, x=c₁: –F(a)=F’(a)(c₁–a)=>c₁=a– F(a)/F’(a)  (1) – формула метода касательных (метода Ньютона). Если провести касательную в точку b, тогда c₁=b– F(b)/F’(b) (1)

Условия выбора вершины: для того, чтобы точка пересечения касательной с осью Ох лежала внутри [a,b], касательную надо проводить в том конце отрезка [a,b], где знаки F’(x)  и F’’(x) одинаковы.

Найдя значение c₁ по (1), вычислим F(с₁). Выбираем тот из 2-х отрезков [a,c₁], [c₁,b], где функция F(x) на концах принимает значение разных знаков, и снова применяем формулу (1). В общем случае формула метода Ньютона имеет вид:  c_n+1= c_n – F(c_n )/F’(c_n), n=0,1,…,

c₀=a или c₀=b.