
|
ОДОБРЕНО на заседании цикловой комиссии математических дисциплин и
Протокол №___ от «___» _________ 2017г. Председатель____________ Е.В.Степанец
|
УТВЕРЖДАЮ Зам. директора по учебной работе
___________ Е.Н.Горбанева
«____» _____________ 2017г. |
Вопросы к экзамену
по дисциплине
«ОП.08 Дискретная математика»
для студентов специальности 09.02.01 Компьютерные системы и комплексы
2 курс
Вопросы теоретической части:
Вопросы практической части:
1
Даны отрезки А = [-4; 5], B = [2; 6], C = [5; 10]. Найдите следующее множество и изобразите его
кругами Эйлера: ![]()
2
Даны отрезки А = [-7; 3], B = [1; 5], C = [4; 10]. Найдите следующие множества и изобразите их
кругами Эйлера: ![]() ;
;
3
Даны отрезки А = [-2; 4], B = [2; 6], C = [5; 10]. Найдите следующие множества и изобразите их
кругами Эйлера: ![]() ;
;
4
Выполните действия и определите мощность полученного множества![]()
5
Выполните действия и определите мощность полученного множества ![]()
6
![]()
![]() В=
В=![]()
7
По заданной функции
постройте таблицу истинности, приведите функцию к минимальной ДНФ:
![]()
8
Проверьте, являются ли булевы функции F1 и F2 эквивалентными:
F1 = X → (Y ≡ Z) и F2 = (X → Y) ≡ (X → Z)
9
Проверьте, являются ли булевы функции F1 и F2 эквивалентными:
F1 = X ∙
(Y ≡ Z) и F2 = (XY) ≡ (XZ);
10
Проверьте, являются ли булевы функции F1 и F2 эквивалентными:
F1 = X → (Y Ú
Z) и F2 = (X
→ Y) Ú
(X → Z);
11 Используя законы алгебры логики доказать
справедливость Закона склеивания относительно дизъюнкции и конъюнкции: ![]() и
и ![]() .
.
12 Доказать с помощью таблиц истинности справедливость закона де Моргана относительно операций конъюнкции и дизъюнкции.
13 Проверьте,
являются ли булевы функции F1 и F2 эквивалентными, если ![]() и
и ![]() .
.
14 Проверьте,
являются ли булевы функции F1 и F2 эквивалентными, если ![]() и
и ![]() .
.
15 Вычислите
значение функции F(x1,
x2, x3) при
заданных значениях аргументов
x1 = 0, x2
= 1, x3 = 1 и при x1 = 0, x2
= 0, x3 = 1:
F(x1, x2, x3) = ![]()
16 Докажите
или опровергните: ![]()
17 Построить таблицу истинности для следующей формулы: A & (B Ú ![]() Þ
Þ ![]() )
)
18 Построить таблицы истинности алгебраически для
следующей формулы: A Ú (B Ú ![]() Þ)
Þ)![]()
19 По заданной функции постройте таблицу
истинности, приведите функцию к минимальной ДНФ:
F(x1,x2,x3) = ![]()
20
Вычислите значение функции F(x1, x2,
x3) при заданных
значениях аргументов x1 = 1, x2 = 0,
x3 = 1 и при x1 = 1, x2
= 0, x3 = 1: F(x1,x2,x3) = ![]()
21
Вычислите значение функции F(x1, x2,
x3) при заданных
значениях аргументов x1 = 0, x2 = 0,
x3 = 1 и при x1 = 0, x2
= 1, x3 = 1: F(x1,x2,x3) = ![]()
22
Упростите функцию, приведя ее к минимальной ДНФ: F(x1,x2,x3) = ![]()
23
Упростите функцию, приведя ее к минимальной ДНФ: F(x1,x2,x3) = ![]()
24
Упростите функцию, приведя ее к минимальной ДНФ: F(x1,x2,x3) = ![]()
25 Постройте логическое выражение по заданной таблице истинности, приведите его к минимальной ДНФ алгебраически:
|
26 Постройте логическое выражение по заданной таблице истинности, приведите его к минимальной ДНФ алгебраически:
|
27 Минимизируйте булеву функцию с помощью карт Карно или диаграмм Вейча:
![]()
28
Минимизируйте булеву функцию с помощью карт Карно или диаграмм Вейча:![]()
29 Постройте совершенные ДНФ и соответствующие минимальные формы для булевых функций, заданных таблично, с помощью карт Карно. Постройте соответствующий логический элемент.
|
X1 |
X2 |
X3 |
F |
|
|
0 |
0 |
0 |
1 |
|
|
0 |
0 |
1 |
1 |
|
|
0 |
1 |
0 |
1 |
|
|
0 |
1 |
1 |
0 |
|
|
1 |
0 |
0 |
0 |
|
|
1 |
0 |
1 |
1 |
|
|
1 |
1 |
0 |
1 |
|
|
1 |
1 |
1 |
0 |
|
30 Постройте совершенную ДНФ по таблице истинности и преобразуйте ее в полином Жегалкина:
|
X1 |
X2 |
F |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
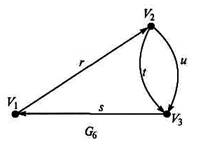
31 Определите по рисунку справа вид графа, степени его вершин. Имеет ли граф висячие вершины?
32 Определите по рисунку слева вид графа и постройте таблицы инцидентности и смежности
|
Преподаватель |
___________________ М. В.Алексеева |
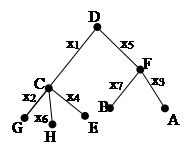
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.