Практическая работа № 32.

Тема: Алгоритмизация.

Наименование: Вспомогательные алгоритмы.

Цель работы: Ознакомить с различными способами записи алгоритма и видами алгоритмов. Научить составлять алгоритмы с использованием вспомогательных алгоритмов.

1. Краткие теоретические сведения.

Сложный алгоритм при разработке можно разбивать на отдельные алгоритмы, которые называются вспомогательными. Каждый вспомогательный алгоритм описывает решение какой-либо подзадачи. Как основной алгоритм, так и вспомогательные могут включать основные алгоритмические структуры: линейную, разветвляющуюся и циклическую.

Вспомогательные алгоритмы используются в следующих случаях:

1) Если одна и та же серия команд используется в нескольких местах алгоритма.

2) При составлении новых алгоритмов могут использоваться ранее составленные.

Обращение к вспомогательному алгоритму в основном алгоритме осуществляется командой вызова вспомогательного алгоритма, которая имеет вид:

<имя вспомогательного алгоритма> (<список фактических параметров>)

Фактические параметры - это информация о том, какие значения нужно передать аргументам вспомогательного алгоритма и каким именам основного алгоритма передать значения результатов вспомогательного алгоритма.

Вспомогательный алгоритм должен:

-   иметь имя, с помощью которого его можно вызвать из основного или другого вспомогательного алгоритма

-   возвращать управление тому алгоритму, из которого был вызван

-   быть относительно небольшим

Основной алгоритм определяет порядок вызова  вспомогательных алгоритмов для решения задачи.

алг  АЛГ 1                            основной алгоритм

нач

         серия команд

         АЛГ 2                           команда вызова вспомогательного алгоритма

         серия команд

кон

алг  АЛГ 2

нач                                         вспомогательный алгоритм

         серия команд

кон

В блок-схеме обращение к вспомогательному алгоритму производится с помощью блока     . Внутри блока записывается имя вспомогательного алгоритма и список фактических параметров.

Пример 1. Составить алгоритм нахождения большего из трех чисел a, b, c, используя в качестве вспомогательного алгоритм поиска наибольшего из двух чисел.

Алгоритм поиска наибольшего из двух чисел (БИД) может быть записан следующим образом.

алг  БИД

арг a,b

рез y

нач  если a>b

то y:=a

иначе y:=a

все

кон

Алгоритм нахождения большего из трех чисел (обозначим его БИТ) можно составить в форме двукратного обращения к алгоритму БИД.

алг  БИТ

арг a,b,с

рез y

нач

БИД(a,b,z)

БИД(z,c,y)

кон

При первом обращении к вспомогательному алгоритму будет определено большее из чисел a,b. Результат обозначен переменной z. При втором обращении будет найдено большее из чисел z и с.

Пример 2. Определить наибольший общий делитель) четырех натуральных чисел (НОДЧ, используя в качестве вспомогательного нахождение НОД двух натуральных чисел:

алг НОД

арг х,у

рез z

нач

пока х¹у

нц

если х>у

то х:=х – у

иначе у:= у – х

все

кц

z:= х

кон

Для нахождения НОД четырех чисел нам придется три раза обращаться к вспомогательному алгоритму НОД.

алг НОДЧ

арг a,b,c,d

рез z

нач

НОД(a,b,z)                                 Находим НОД для двух чисел a, b

НОД(z,c,z)                                  НОД для чисел a, b, c, т.к. z- НОД                                                            чисел a, b

НОД(z,d,z)                                 НОД для четырех чисел

кон

2. Задания.

1. Внимательно изучите теоретический материал.

2. Составить алгоритм и блок-схему решения задачи:

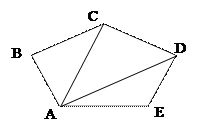
Определить площадь выпуклого пятиугольника ABCDE, если заданы пять его сторон и две диагонали, выходящие из вершины А. Использовать в качестве вспомогательного алгоритм вычисления площади треугольника по формуле Герона:

алг Герон

арг a,b,c

рез S

нач

p:= (a+b+c)/2

S:=

кон

Вопросы:

1. В каких случаях обычно используют вспомогательные алгоритмы?

2. Каким требованиям  должен удовлетворять вспомогательный алгоритм?

3. Какие алгоритмы могут быть использованы в качестве вспомогательного?

3. Оформление отчета:

1. Перепишите определение вспомогательного алгоритма, форму записи команды вызова вспомогательного алгоритма, алгоритмы и блок-схему примера 1, 2 из методического пособия в тетрадь.

2. Выполнить п. 2 задания.

3. Дать ответы на вопросы задания и объяснить их.