Вычисление корней

 

 

 

 

 

 

 

 

 

 

 

 

 

Методическая разработка

практического занятия для студента

Тема: «Вычисление и сравнение корней. Преобразование выражений, содержащих степени »

 

ОУП. 04 «МАТЕМАТИКА»

 

Специальность 34.02.01 «Сестринское дело»

 

 

 

 

 

 

 

 

 

 

 

ТЕМА: «ВЫЧИСЛЕНИЕ И СРАВНЕНИЕ КОРНЕЙ. ПРЕОБРАЗОВАНИЕ ВЫРАЖЕНИЙ, СОДЕРЖАЩИХ СТЕПЕНИ»

1.     Тип занятия: практическое.

2.     Место проведения, продолжительность занятия: учебная аудитория, 90 минут

3.     Цели занятия для студентов: закрепить навыки    выполнения действий по преобразованию алгебраических, рациональных, иррациональных, степенных выражений

4.     Требования к уровню освоения дидактических единиц:

В результате студент должен:

-Знать определение корня и его свойств.

-Знать понятие степени с действительным показателем и ее свойства.

- Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни; для практических расчетов по формулам, включая формулы, содержащие степени, радикалы, используя при необходимости справочные материалы и простейшие вычислительные устройства.

5.     Оснащение занятия: Алимов Ш. А., Колягин Ю. М. «Алгебра  и начала математического анализа», доска, мел, тетради с конспектами, карточки с заданиями для практической работы, карточки со справочным материалом.

6.     Деятельность студентов в ходе занятия

6.1        Выполните следующие задания у доски с целью проверки домашнего задания

Вариант 1

 

1.     Вычислить:

а)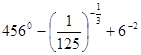

б)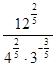

 

в)

 

2. Упростить:

а) 

 

б)

 

6.2        Прослушайте инструктаж по выполнению практической работы, возьмите справочный материал и карточки с заданиями

Инструктаж студентов по выполнению практических заданий

Задания необходимо оформить в тетрадях для практических работ. Выполнить индивидуальную работу по варианту. Вариант содержит необходимый справочный материал.  На выполнение задания отводится 60 минут. В конце работы необходимо написать вывод. В конце занятия необходимо сдать тетради для проверки и оценивания.

Справочный материал

КОРНИ НАТУРАЛЬНОЙ СТЕПЕНИ ИЗ ЧИСЛА, ИХ СВОЙСТВА.

Корень n – степени:  , n -  показатель корня, а – подкоренное выражение

Если n – нечетное число, то выражение  имеет смысл при  а

Если  n – четное число, то выражение  имеет смысл при  

Арифметический корень:

Корень нечетной степени из отрицательного числа:

ОСНОВНЫЕ СВОЙСТВА КОРНЕЙ

1.      Правило извлечения корня из произведения:

 

2.      Правило извлечения корня из дроби:

 

3.      Правило извлечения корня из корня:

 

4.      Правило вынесения множителя из под знака корня:

 

5.      Внесение множителя под знак корня:

,

 

6.      Показатель корня и показатель подкоренного выражения можно умножить на одно и тоже число.

7.      Правило возведения корня в степень.

СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ

=,a – основание степени, n – показатель степени

 

 

Свойства:

1.      При умножении степеней с одинаковыми основаниями показатели складываются, а основание остается неизменным. 

2.      При делении степеней с одинаковыми основаниями показатели вычитаются, а основание остается неизменным. 

3.      При возведении степени в степень показатели перемножаются. 

4.      При возведении в степень произведения двух чисел, каждое число возводят в эту степень, а результаты перемножают.

5.      Если в степень возводят частное двух чисел, то в эту степень возводят числитель и знаменатель, а результат делят друг на друга.

6.      Если

 

СТЕПЕНЬ С ЦЕЛЫМ ПОКАЗАТЕЛЕМ

 

1.     

2.     

3.     

4.      По определению:

 

Свойства:

1.     

2.     

3.     

4.     

5.     

6.      Пусть r рациональное число , тогда

 при r>0                               > при r<0

   7 .Для любого рациональных чисел r и s из неравенства > следует

> при a>1                                             при

6.3        Самостоятельно выполните задания  из практической работы № 2

Тема: «Вычисление и сравнение корней. Преобразования выражений, содержащих степени»

Цель: закрепить навыки    выполнения действий по преобразованию алгебраических, рациональных, иррациональных, степенных выражений

ВАРИАНТ - I

1. Упростите выражение:

2. Найдите значение выражения:

3. Представьте степень с дробным показателем в виде корня

4. Избавиться от корня в знаменателе,

5. Упростить:

;

6. Замените арифметические корни степенями с дробным показателем

, ,

7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня

                                                   

8. Сократите дробь                                                                         

9. Выполните действие

10. Перевести бесконечную периодическую дробь в обыкновенный вид : 0.12(35)

 

ВАРИАНТ - II

1. Упростите выражение:

2. Найдите значение выражения:

3. Представьте степень с дробным показателем в виде корня

4. Избавиться от корня в знаменателе ,

5. Упростить:

;

6. Замените арифметические корни степенями с дробным показателем

, ,

7. Представьте выражение в виде дроби, знаменатель которой не содержит знака корня

                                                      

8. Сократите дробь                                      

9. Выполните действие

10. Перевести бесконечную  периодическую дробь в обыкновенный вид : 0,21(28)

 

Критерии оценивания практической работы.

 

Отметка «5» ставится, если студент:

 работа выполнена полностью;

 в логических рассуждениях и обосновании решения нет пробелов и ошибок;

 в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).

Отметка «4» ставится, если студент:

 работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);

 допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).

Отметка «3» ставится, если студент:

 допущено более одной ошибки или более двух – трех недочетов в выкладках,

чертежах или графиках, но учащийся обладает обязательными умениями по проверяемой теме.

Отметка «2» ставится, если студент:

 допущены существенные ошибки, показавшие, что учащийся не обладает

обязательными умениями по данной теме в полной мере.

 

6.4 Запишите домашнее задание в тетрадь

Подготовиться к практическому занятию № 3, выучить теоретический материал в тетрадях, выполнить задание по варианту

6.4        Рефлексия

Оцените свою деятельность и заполните таблицу

Утверждения	«+» или «-», перечисление ошибок, темы для доработки.
1) У меня сегодня всё получалось, я не допускал ошибок
2) Я допустил ошибки в самостоятельной работе (перечислить ошибки)
3) Я исправил допущенные ошибки в процессе работы над ними
4) Мне необходимо поработать над…