Вычисление площадей с помощью интегралов

Вычисление площадей с помощью интегралов.

По данной теме это третий урок из четырёх.

На первом уроке - изучение нового материала и решение типовых задач на нахождение площадей с помощью интегралов.

На втором уроке - нахождение площадей фигур, состоящих из двух криволинейных трапеций, симметричных фигур.

На третьем  уроке - решение разнообразных задач по теме.

На четвёртом уроке – обобщение, самостоятельная работа.

             Тип урока: урок применения знаний и умений учащихся.

               Цели и задачи урока:

-формировать умение решать задачи на вычисление площадей плоских фигур

с  помощью определенного интеграла;

-отрабатывать навыки вычисления  определенных интегралов;

- развивать  познавательные  интересы  и способности  учащихся;

-развивать умения выделять главное в материале;

-развивать умения логически излагать мысли:

-реализовывать  дифференцированный подход к учащимся;

-воспитывать аккуратность изображения графиков функций и выполнения записей в тетради и на доске.

 Оборудование:

Презентация для данного урока

Мультимедийный проектор

Компьютер.

                  Основные этапы урока:

1) организационный момент;

2) проверка домашнего задания;

3) проверка знаний и умений учащихся для подготовки к решению задач;

4) постановка цели занятия перед учащимися;

5) организация восприятия и осмысления новой информации;

6) первичная проверка понимания;

7) организация усвоения способов деятельности путем воспроизведения информации и упражнений в ее применении;

8) домашнее задание.

ХОД  УРОКА 

1.            Организационный момент-тема, цели, задачи урока (1мин.).

2.            Проверяем домашнее задание (3 мин.).

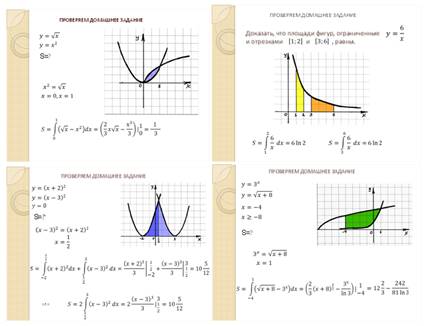
·        Найти площадь фигуры, ограниченной графиками функций

        .

·        Доказать, что площади фигур, ограниченные графиком  функции

       и отрезками   ,  равны.

·               Найти площадь фигуры, ограниченной графиками функций

         и прямой .

·          Найти площадь фигуры, ограниченной графиками функций,                                                  

         при  и  прямой  (слайды 2-5):

3.            Устно фронтально (7 мин.).

·               Как найти площадь выделенной фигуры?

            ,      (слайды 6-11):

4.            Класс самостоятельно выполняет задачи, которые можно решить с помощью одного чертежа  (первый ряд - а), второй ряд - б), третий  ряд - в)) с последующей проверкой (8 мин):

·               Найти площадь фигуры, ограниченной графиками функций:

а)  и осью Ох;

б);

в) и осью Оу (слайды 12-14):

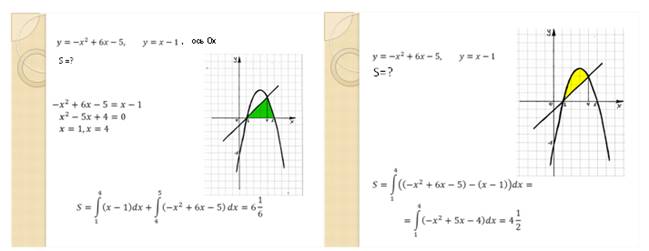
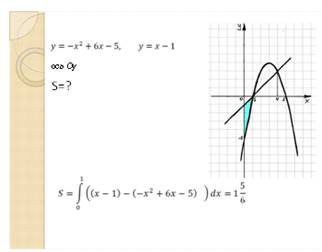
  Убеждаемся, что для успешного решения задач на нахождение площади фигуры необходимо не только верно схематически  изобразить графики функций, ограничивающие фигуру, но и верно выделить искомую фигуру на чертеже.

Одновременно на боковых досках  четыре ученика выполняют индивидуальные задания, которые показывают (3мин.) всему классу:

·               Найти площадь фигуры, ограниченной графиками функций

,    и прямой .

·               Найти площадь фигуры, ограниченной графиками функций

,   и прямыми  ,  .

·        Фигура  ограничена  графиками функции   и

прямыми   .  Прямая делит фигуру

на две части. Равны ли их площади?

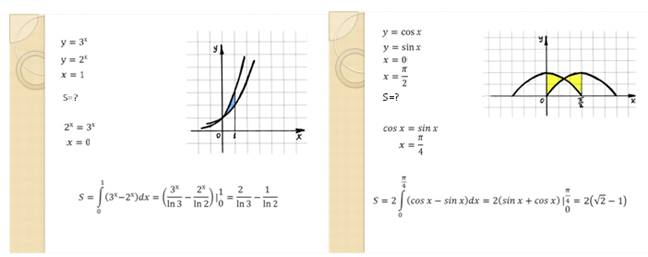
·        Используя геометрическую интерпретацию, вычислите интегралы:  , (слайды 15-18):

5.            Далее на уроке рассматриваем следующую задачу (устно, по готовому решению)  (3мин.):

·               Найти площадь фигуры, ограниченной графиком функции

        , касательной к графику в точке с абсциссой  и осью (слайд 19):

2)      

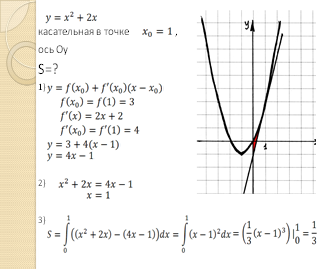
 А дальше вместе решаем (10 мин.):

·        Найти площадь фигуры, ограниченной графиком функции  и касательной, проведённой  к графику функции  в точке с абсциссой  (слайд 20):

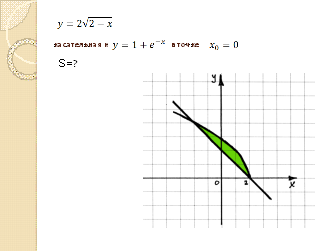
2)

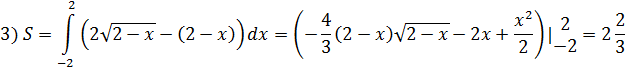
Следующая задача выглядит так (8 мин):

·               Найти площадь фигуры, ограниченной графиками функций:

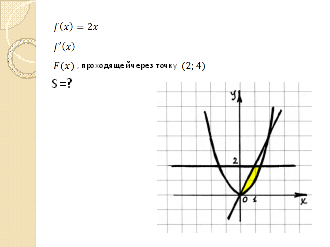     f(x), f(x) и F(x),проходящей через точку (2;4), если f(x)=2x (слайд 21):

                     1)

                    2);   

                     ;   

6.            Дополнительно  предлагаются такие задачи:

·        При каком значении графики функций    и               ограничивают фигуру с площадью 9?

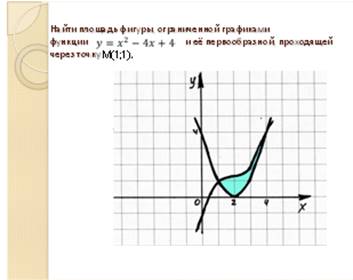
·    Найти площадь фигуры, ограниченной графиком  функций

     и графиком её первообразной, проходящей через точку М (1;1).

     (если понадобится, слайд 22)

7.            Итог урока.  Домашнее задание (2 мин.).

Придумать фигуру, используя известные формулы графиков функций, изобразить

 её и найти площадь полученной  фигуры.

Как пример-слайд 23.