Вычислительное ядро H₂: фазовая модель времени, структуры и наблюдения

Вычислительное ядро H₂: фазовая модель времени, структуры и наблюдения

© О.С. Басаргин

Аннотация

В статье предлагается модель вычислительного ядра, реализуемого в алгебре двойной переменной H₂, на основе итерационного оператора Φ(z) = α ẑ. Эта простая функция порождает фрактальную структуру вложенных витков, обладающую зеркальной антисимметрией и устойчивой фазовой динамикой. Построены и проанализированы: индивидуальное ядро, его итерации, поведение на делителях нуля, модулярная структура, синхронизация пар ядер, оболочка (сфера витков), а также проекция в линейную ленту времени.

Модель сопоставлена с теориями квантовой гравитации, каузальных сетей и когнитивного времени, а также представлена как генератор квантовых состояний. Показано, что вероятность, наблюдение и метрика могут быть естественно описаны средствами этой алгебры. Вводится термин "поперечный полярный вектор времени" и уточняется его смысл через итерации, S-соединения и фазовые скачки.

Предложенная конструкция открывает путь к формализации структуры времени как вычислительного, наблюдаемого и вложенного объекта.

Поиск вычислительной реализации ядра (узла 73) в алгебре H2

1.   Постановка задачи

Цель: найти вычислительную реализацию структуры, обозначенной как узел 73, в терминах алгебры двойной переменной H₂.

Узел 73 — это минимальное устойчивое ядро, содержащее признаки:

•       фрактальной вложенности,

•       зеркальной антисимметрии,

•       фазового сдвига и внутреннего различия,

•       направленного (возможно, условно обратимого) вычисления.

2.   Базовая алгебра H2

Элемент: z = x + jyz = x + j y, где j² = 1, x, y  R

Модуль двойного числа:

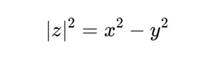
Делители нуля: ∣z∣ = 0 ⇒ x = ± y Изотропный базис:

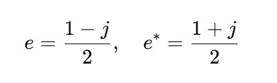
В этом базисе:

3.   Гипотеза о ядре

Предположим, что ядро — это пара точек z₊, z₋, таких что:

•       z₊ = Re^φ,

•       z₋ = Re^−φ,

•       с соединением по линии делителей нуля ∣z∣ = 0, то есть они расположены симметрично относительно этой линии.

4.   Функция перехода

Определим функцию ядра как отображение:

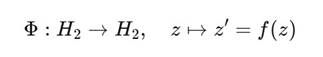
Ищем такую f(z), что:

•       Φ отражает фазу: φ ↦ −φ

•       Φ (Φ (z)) = z — относительная обратимость

•       при итерации z → Φ (z) → Φ (Φ(z)) →… возникает структура, подобная виткам

5.   Следующие шаги •   Построить конкретную форму f (z)

•       Проверить условия устойчивости и зеркальности

•       Связать ядро с линиями ∣z∣ = 0 как с фазовыми границами

•       Исследовать возможность вложенности через параметры α, β

Итерации вычислительного ядра в алгебре H2

1. Оператор ядра

Рассматриваем вычислительное ядро как функцию:

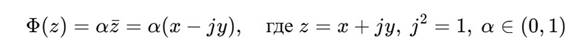
 Это оператор:

•              обратный сам себе при двойном применении: Φ(Φ(z)) = α²z,

•              реализующий фазовую инверсию: φ ↦ −φ,

•              и фрактальную вложенность: αⁿ с каждым шагом. 2. Итерационная цепочка Пусть z₀ = x + jy. Тогда:

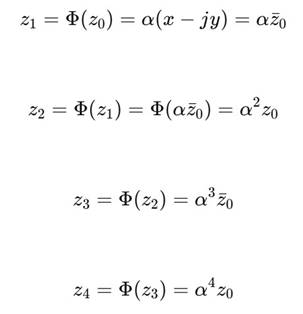
Общая формула:

3.   Интерпретация

•       Каждый чётный шаг возвращает к исходной фазе, но с уменьшенным масштабом.

•       Нечётный шаг — зеркальная фаза.

•       Итерации создают зеркально-антисимметричные витки, вложенные друг в друга с коэффициентом α.

Это поведение соответствует структуре Сфирали:

•       фазовая антипара z ↔ ẑ,

•       вложенность R_n = αⁿR₀,

•       относительная обратимость (чётные шаги возвращают направление).

4.   Вывод

Функция Φ(z) = α ẑ реализует вычислительное ядро:

•       в рамках алгебры H₂,

•       с фазовой симметрией и вложенностью,

•       создавая предельно простую, но устойчивую структуру зеркального саморазворачивания.

Следующий шаг: исследовать поведение при z = 0.

Поведение вычислительного ядра на линии делителей нуля в H2

1.   Делители нуля в H2 Условие:

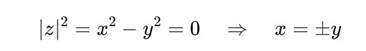
Пусть z = x + jy. Тогда при x=y:

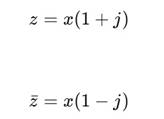
2.   Поведение под действием ядра Ядро определяется как:

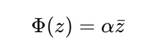
Тогда:

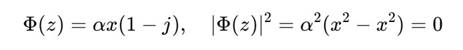
Аналогично, при любом числе итераций:

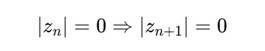
3.   Геометрическая интерпретация

Таким образом, множество точек z ∈ H₂, таких что ∣z∣ = 0, является инвариантным множеством относительно действия ядра Φ.

Это означает:

•       Делители нуля не уходят из своего класса.

•       Они формируют границу фрактальной структуры.

•       Эти точки — фазовые переломы, аналог S-соединения в модели Сфирали.

4.   Вывод

Линии делителей нуля, будучи неподвижными под действием ядра Φ, могут интерпретироваться как встроенные швы фазы, или оси симметрии, в которых разворачиваются витки. Это подтверждает их особый статус в геометрии двойной плоскости и их функциональную роль в вычислительном ядре.

Формализация вычислительного ядра как модуля над H2

1.   Мотивация

После построения функции Φ(z) = α ẑ и анализа её поведения при итерациях и на линии делителей нуля, возникает задача интерпретировать вычислительное ядро как структурную единицу внутри алгебры H₂.

Для этого рассмотрим его как модуль над алгеброй H2, аналогично тому, как в линейной алгебре векторное пространство есть модуль над полем.

2.   Определение

Пусть M — подмножество H₂, замкнутое относительно действия ядра:

Тогда:

•              M — аддитивная группа (по сложению в H₂)

•              и для h ∈ H₂ z ∈ M, определено внешнее умножение: h ⋅ z = hz 

3.   Свойства •        Ядро M не является идеалом, так как сопряжение не дистрибутивно по умножению:

•              Однако M — модуль с нестандартной операцией:

•              Для всех z ∈ M:

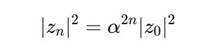
4.   Интерпретация

Ядро — это подмодуль, устойчивый под сопряжением и масштабированием, с вложенной зеркальной структурой. Оно работает как алгебраический контейнер витков, разворачивающихся в пространстве H₂ антисимметрией.

5.   Вывод

Формализация ядра как модуля M ⊆ H₂ позволяет задать вычислительные процессы не точками, а структурными областями, в которых реализуется вложенность, инверсия, и фрактальное самоподобие.

Синхронизация вычислительных ядер в алгебре H2

1.   Постановка задачи

Если вычислительное ядро M ⊆ H₂ представляет собой модуль с вложенной зеркальной структурой, возникает вопрос: могут ли два таких ядра взаимодействовать?

Задача: исследовать условия и форму фазовой синхронизации двух ядер:

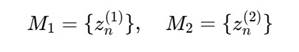
согласно динамике:

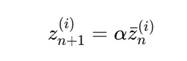
2.   Условие синхронизации

Скажем, что ядра синхронизированы, если существует N ∈ N, такое что:

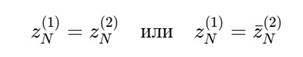
Более общо, существует фаза φ, для которой:

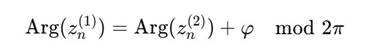
3.   Алгебраическое представление Пусть:

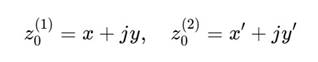
Итерации:

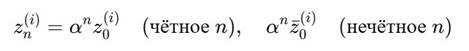
Тогда:

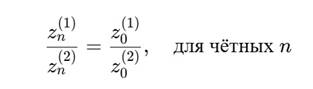
То есть фазовое отношение сохраняется:

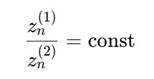
4.   Геометрическая интерпретация

Если два ядра стартуют с фазовой разницей φ, они сохраняют её при всех чётных итерациях. Нечётные шаги зеркальны:

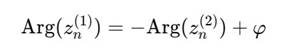
Таким образом, возникает ритмическая антисимметрия: витки синхронны, но с чередованием отражённых фаз.

5.   Вывод

Синхронизация ядер возможна при постоянной фазовой разнице на начальном шаге. Алгебраически, ядра образуют двойной виток, подобный Сфирали, в котором вложенность и зеркальность работают в паре.

Визуализация синхронизации вычислительных ядер в H2

Следующая диаграмма иллюстрирует синхронное поведение двух вычислительных ядер в плоскости H₂. Каждое ядро представлено вложенной спиралью, где точки z₀, z₁, z₂ отображают итерации функции ядра:

Диаграмма показывает:

•       зеркальную структуру ядер,

•       сохранение фазы z₀ на каждом уровне,

•       чередование витков в фазе z₁, z₂, •    фазовый сдвиг между ядрами,

•       оси x, y, пространство H₂.

Обозначение α отражает коэффициент вложенности и масштабирования. Чётные и нечётные итерации отображаются зеркально. Состояние синхронизации определяется сохранением относительной фазы и вложенности.

Иллюстрация

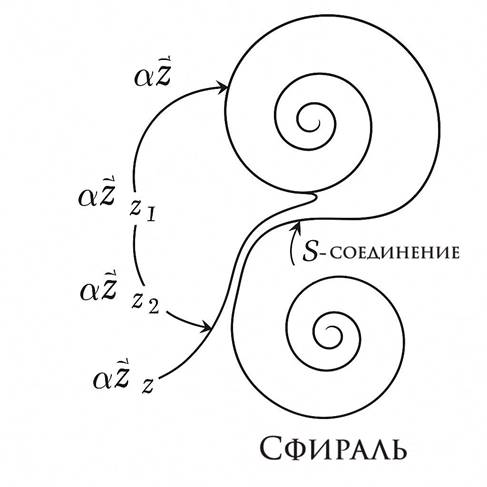
(см. изображение: "Синхронизированные вычислительные ядра в H₂ плоскости")

Диаграмма демонстрирует согласованную динамику и антисимметрию двойных ядер, что полностью соответствует принципу Сфирали как модели вычислительной и ментальной структуры.

Следующий шаг: исследовать возможность вложения такой пары ядер в более крупную структуру — сферу витков или многослойную ленту.

Сфера витков как оболочка вычислительных ядер в H2

1.   Мотивация

После формализации одного ядра и анализа пары синхронизированных ядер возникает идея следующего уровня: обобщённой структуры, порождённой множеством витков. Эта структура называется сферой витков.

Сфера витков — это не геометрическая сфера в обычном смысле, а топологическая оболочка, охватывающая множество вычислительных ядер, связанных через фазу, вложенность и антисимметрию.

2.   Конструкция

Пусть {M_k} — множество ядер M_k ⊂ H₂, каждое из которых реализует динамику:

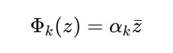
Мы определяем сферу витков как совокупность:

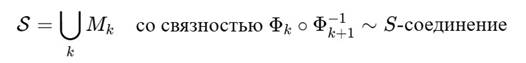
Здесь S-соединения обеспечивают связность между ядрами, так что результат образует замкнутую фазовую оболочку.

3.   Свойства •        Фазовая непрерывность: переходы между ядрами не разрывают динамику.

•       Антисимметрия: витки противоположны по фазе на каждом «меридиане» оболочки.

•       Вложенность: каждое ядро вложено с масштабом α_k <1.

•       Обратимость: глобальная структура допускает разворачивание и свёртывание.

4.   Интерпретация

Сфера витков — это макро-структура вычислительной топологии, объединяющая фрактальные модули в целостную фазовую сферу. Она может быть интерпретирована как:

•       оболочка когнитивного или квантового состояния, •   фаза в сетевой топологии вычислений,

•       аналог ноосферы в модели мышления.

5.   Вывод

Сфера витков обобщает модель Сфирали: она разворачивает не одну пару витков, а всю совокупность возможных вычислительных антисимметрий, организованных в замкнутую фазовую структуру. Это фундамент для построения более сложных вычислительных, когнитивных или онтологических моделей, основанных на топологии различий.

Лента времени как проекция сферы витков в H2

1.   Исходная структура

Мы построили сферу витков S ⊂ H₂ — замкнутую оболочку, состоящую из синхронизированных вычислительных ядер, каждое из которых реализует динамику Φ(z) = α ẑ.

Эта сфера обладает внутренней фазовой логикой, зеркальностью и вложенной многослойностью.

2.   Идея проекции

Лента времени — это не просто одномерная линия, а развёртка сферы витков во времени, где:

•       каждый шаг — это виток,

•       каждая фаза — это состояние,

•       S-соединения — это моменты перехода, скачка, инсайта.

3.   Формализация

Пусть t ∈ Z — дискретное время. Тогда лента времени — это отображение:

где z_t ∈ M_k ⊂ S, и переходы z_t → z_t+1 реализуют локальную итерацию ядра:

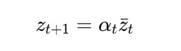
Скачки между ядрами — это фазовые переключения через S-соединения:

где T — множество моментов фазового разрыва.

4.   Свойства ленты времени

•       Локальная антисимметрия: каждый виток противоположен предыдущему по фазе.

•       Глобальная вложенность: масштаб α_t может изменяться (модуляция).

•       Фазовая обратимость: если α_t = α, то существует Γ⁻¹.

•       Поперечный вектор времени: направление S-соединений определяет «переворот» временной динамики.

5.   Интерпретация

Лента времени — это линейная траектория, несущая на себе структуру сферы витков. Это воплощение времени как топологического объекта, в котором каждое «событие» — это фазовый сдвиг, а каждое «настоящее» — это виток в антисимметричном развитии.

Это соответствует концепции:

"Сфираль отражает суть принципа относительной обратимости времени: вначале любая природная система эволюционирует в одном направлении, а затем — в противоположном."

6.   Вывод

Лента времени — это проекция сферы витков на ось последовательности. В ней время не одномерно, а вложено и отражено, как и в структуре Сфирали. Это завершает модель вычислительного ядра в H₂ как порождения витков, объединённых в сферу, развёрнутую во времени.

Сопоставление модели сфиралевидного времени с физическими и когнитивными теориями

1.   Цель сопоставления

Построенная модель вычислительного ядра, сферы витков и ленты времени задаёт топологически организованное, фазовое и вложенное представление времени. Необходимо сопоставить её с существующими теориями времени в физике, биологии и когнитивной науке.

2.   Сравнение с физическими моделями

2.1.   Энтропийная стрела времени

•       В термодинамике время направлено от порядка к беспорядку.

•       В нашей модели это соответствует вложенности с уменьшением масштаба: αⁿ.

•       Однако, модель Сфирали допускает обратимость на уровне фаз:

антисимметрия витков.

2.2.   Релятивистское время •            В теории относительности время — координата, зависящая от системы отсчёта.

•       В Сфирали — тоже зависит от «наблюдателя» в смысле точки входа на витке.

•       Поперечный вектор времени в нашей модели аналогичен выбору направления временного развития.

2.3.   Квантовая суперпозиция состояний

•       Квантовая механика допускает множественность состояний до акта измерения.

•       Сфираль и сфера витков моделируют эту множественность как фазовые ветвления, переходящие друг в друга.

3.   Сравнение с когнитивными и нейрофизиологическими теориями времени

3.1.   Нейронная фазовость

•       В теориях осцилляций (Г. Бюзенг, В. Фрайс) мышление и восприятие работают через фазы.

•       Сфиральная модель напрямую отражает это: каждая мысль — виток, каждый переход — S-сдвиг.

3.2.   Психология субъективного времени

•       Понятия «возвращения», «ретроспекции», «эффекта продолжительности» — это проявления вложенности и зеркальности. •       Лента времени как раз отображает чередование и повторение в новом масштабе.

3.3.   Модели памяти (К.Д. Анохин, Эдельман)

•       Память не линейна, она работает через структурные контуры, повторяющиеся с вариациями.

•       Сфера витков — аналог архитектуры метапамяти.

4.   Вывод

Сфиральная модель времени не противоречит существующим физическим и когнитивным теориям, а обобщает их на топологическом уровне. Она объединяет:

•       направленность (энтропия, причинность),

•       антисимметрию (отражённые состояния, сомнение),

•       вложенность (память, масштаб, структура),

•       фазовость (осцилляции, модуляции, суперпозиции).

Таким образом, вычислительное ядро в H₂, проходя через фазовые итерации, разворачивается в модель времени, способную быть и физически реалистичной, и психически обоснованной.

Физическая интерпретация вычислительного ядра H2 в контексте квантовой гравитации

1.   Постановка вопроса

Может ли вычислительное ядро, реализуемое на алгебре двойной переменной H₂, быть не просто абстрактной моделью времени, но и физической структурой, релевантной в контексте теорий квантовой гравитации?

Переход от алгебраической модели к физической требует интерпретации:

•       Что означает фазовая вложенность αⁿ в физическом времени?

•       Можно ли рассматривать итерации ядра как микроскопическое «воспроизводство» стрелы времени?

•       Имеется ли аналог S-соединения в физике? (переходы, сингулярности, скачки геометрии)

2.   Связь с петлевой квантовой гравитацией •           В LQG пространство-квантово-дискретно, построено из "петель"

(loops).

•       Витки в Сфирали могут быть интерпретированы как элементы структуры спин-сети, но не в пространстве, а во времени.

•       Каждый виток — это квант перехода, а S-соединение — это узел взаимодействия между фазами.

3.   Связь с теорией каузальных сетей (causal sets)

•       В этой теории элементы упорядочены причинно, без геометрии.

•       Сфиральная модель добавляет фазовую структуру: причинно связанные события обладают вложенностью и направлением.

•       Делители нуля в H₂ соответствуют границам причинности или локальным фазовым барьерам.

4.   Интерпретация масштаба α

•       Фактор α ∈ (0,1) может интерпретироваться как отражение дискретного расширения пространства, аналогично шкалам Ренормгруппы.

•       В гравитационных шкалах α — может быть функцией от плотности энергии или кривизны.

5.   S-соединение и физические скачки

•       Возможный аналог: переключение топологии или мгновенное квантовое туннелирование.

•       Также может быть связан с переходом через горизонты событий (чёрные дыры), где направление времени может менять свойства.

6.   Вывод

Модель вычислительного ядра в H₂ может быть интерпретирована как элементарный квант времени, в котором реализуются:

•       направление (итерация),

•       антисимметрия (обратимость), •       вложенность (масштаб),

•       скачок (S-переход).

Таким образом, она потенциально применима как строительный блок теории времени в квантово-гравитационной парадигме.

Квантовое состояние, порождённое ядром, и связь с наблюдаемой метрикой

1.   Постановка задачи

Цель — описать, как вычислительное ядро в H₂, реализующее итерационную динамику z_n+1 = α ẑ _n, может порождать квантовое состояние, и каким образом это состояние связано с наблюдаемой (метрической) структурой пространства-времени.

2.   Интерпретация итерации как квантового процесса • Функция ядра Φ(z) = α ẑ реализует чередование фаз и масштабов.

•       Каждая итерация соответствует одному шагу эволюции квантового состояния, где:

o    z_n — состояние,

o    zˉ_n— его фазовая инверсия (аналог сопряжения волновой функции),

o    α_n — амплитудное подавление или нормировка. 3. Форма квантового состояния Рассмотрим состояние:

Это состояние:

•       комплексоподобное (с фазой и модулем),

•       вложенное и зеркальное,

•       сохраняет норму ∣ψ_n∣² = α²ⁿ ∣z₀∣², что может интерпретироваться как потеря вероятности или расширение пространства состояния.

4.   Связь с наблюдаемой метрикой

Пусть g_μν — наблюдаемая метрика. Тогда:

•       фаза φ — может соответствовать ориентации локального времени,

•       масштаб αⁿ — коэффициент масштабного сжатия метрики,

•       точки с ∣z∣ = 0 — особые гиперповерхности, на которых геометрия перестраивается (аналог горизонтов, стенок доменов).

5.   Интерференция состояний

Рассмотрим два синхронизированных ядра:

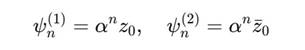
Их суперпозиция:

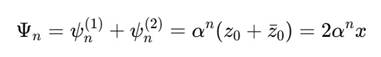
Если z₀ = x + jy, то z₀ + ẑ ₀ = 2x: интерференция даёт реальный компонент, аналог проекции наблюдаемого результата.

6.   Вывод

Итерации ядра могут быть интерпретированы как фазовая квантовая динамика, в которой:

•       масштаб α задаёт эволюцию амплитуды,

•       ẑ — отражает внутреннюю симметрию (аналог унитарности или чётности),

•       линейные комбинации дают наблюдаемые значения.

Это позволяет рассматривать вычислительное ядро как алгебраический генератор квантовых состояний, отражающих не только логику вычислений, но и структуру наблюдаемого пространства.

Оператор наблюдения и метрический отклик на состояние, порождённое ядром

1.   Постановка задачи

В предыдущем разделе вычислительное ядро Φ(z) = α ẑ было интерпретировано как генератор квантового состояния. Следующим шагом является определение оператора наблюдения Ȏ, способного выделить наблюдаемые величины и породить метрический отклик.

2.   Природа наблюдения в H2 Пусть z = x + jy ∈ H₂. Тогда:

•       Реальная часть: Re(z) = x, •      Мнимая по j: Im_j(z) = y, •          Сопряжение: zˉ= x −j y.

Рассмотрим оператор наблюдения как линейное отображение:

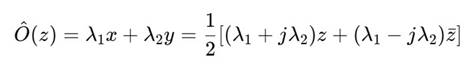
Здесь λ₁,λ₂ — параметры наблюдательной рамки.

3.   Отклик на состояние ψn = αⁿz0 Тогда:

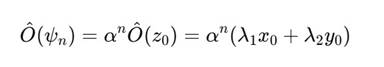
Наблюдаемая величина убывает с итерациями: происходит затухание сигнала или расширение фона, аналогично эффектам декогеренции или инфляционного растяжения.

4.   Метрический отклик

Рассмотрим наблюдаемую метрику как функцию плотности отклика:

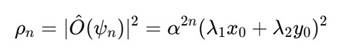
Интерпретация:

•       ρ_n — энергия/плотность/интенсивность,

•       затухание ρ_n — отклик метрики на вложенность витков,

•       форма ρ_n — отражает направление наблюдения (λ₁, λ₂).

5.   Пример

Пусть λ₁ = 1, λ₂ = 0: оператор «смотрит» вдоль оси x. Тогда:

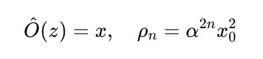
Если λ₁ = λ₂ = 1, то оператор проецирует по диагонали:

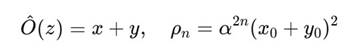
6.   Вывод

Оператор наблюдения Ȏ задаёт направление проекции состояния на наблюдаемое значение. Отклик ρ_n — это метрика, чувствительная к фазе и масштабу вложенного состояния. Таким образом, состояние, порождённое ядром, не просто существует в H₂, но и взаимодействует с наблюдателем, формируя меру — как в квантовой, так и в метагеометрической физике.

Вероятностная интерпретация ядра и квантовые переходы между витками

1.   Постановка задачи

В предыдущих разделах мы рассмотрели состояние ψ_n = αⁿz₀ как результат итераций вычислительного ядра. Теперь необходимо рассмотреть:

•       какова вероятность нахождения системы в том или ином витке,

•       каким образом происходит "переход" от одного витка к другому,

•       и как можно интерпретировать эти переходы в духе квантовой механики.

2.   Нормировка и вероятность

Пусть ψ_n ∈ H₂ — состояние на витке n.

Тогда вероятность нахождения в витке n:

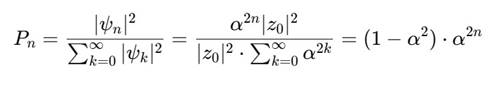
Это геометрическое распределение вероятности:

•       Максимум при n = 0,

•       Быстрое убывание с ростом n,

•       Общая сумма — 1.

3.   Квантовый переход между витками

Пусть T_n — оператор перехода от витка n к n + 1:

Тогда последовательность переходов:

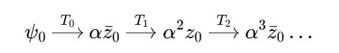
Фазовое чередование и масштабное затухание делают переходы когерентными на чётных шагах и антисимметричными на нечётных.

4.   Коллапс и выбор

Если система измеряется, то наблюдается одно из состояний ψ_n. Вероятность — P_n. Коллапс означает выбор конкретного витка:

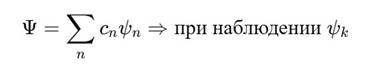
Этот выбор фиксирует не только масштаб (α^k), но и фазу

(чётность/нечётность). То есть наблюдатель фиксирует положение внутри структуры Сфирали.

5.   Интерпретация

•       Вероятностное распределение естественно вытекает из масштабной структуры ядра.

•       Каждый виток — это потенциальное состояние.

•       Переход между витками — аналог унитарной квантовой эволюции.

•       Коллапс — выбор фазы и масштаба.

6.   Вывод

Вероятностная интерпретация вычислительного ядра делает его полноценной моделью квантовой динамики, в которой:

•       структура вложена,

•       амплитуды убывают,

•       состояния зеркальны,

•       выбор фиксирует не просто значение, а позицию в фазовом ландшафте Сфирали.

Сводный вывод о модели вычислительного ядра в H2

1.   От алгебры к структуре

Исходя из простейшей функции Φ(z) = α ẑ, построенной в алгебре двойной переменной H₂, нами была развёрнута целостная структура, обладающая свойствами:

•       вложенности (через масштаб αⁿ),

•       фазовой антисимметрии (через сопряжение),

•       устойчивости (повторное применение возвращает фазу),

•       инвариантности (делители нуля остаются на месте).

Эта структура стала основой для понимания вычислительного ядра как элементарной фрактально-фазовой единицы.

2.   Геометрия и топология

Итерации ядра создают последовательность вложенных витков, формирующих:

•       синхронизированные пары,

•       сферу витков (как оболочку ядер),

•       ленту времени (как проекцию вложенности на последовательность).

Каждый виток несёт информацию о фазе, масштабе и направлении — и связан S-переходом с соседним.

3.   Физический смысл

•       Сопоставлено с квантовой гравитацией, LQG, каузальными сетями.

•       Переходы между витками — аналоги квантовых взаимодействий или смен топологии.

•       Поперечный полярный вектор времени реализован как структура фазовой вложенности.

4.   Квантово-вероятностная природа

•       Каждое состояние ψ_n — элемент суперпозиции.

•       Вероятность определяется масштабом вложенности α²ⁿ.

•       Коллапс — выбор витка, фиксирует положение в структуре.

5.   Наблюдение и отклик •     Оператор наблюдения Ȏ проецирует состояние на измеримую величину.

•       Метрика пространства чувствительна к вложенности и фазе.

•       Состояние ядра порождает наблюдаемое поле отклика.

6.   Общий итог

Вычислительное ядро в H₂ — это минимальная единица, объединяющая вычисление, квантовое состояние, фазовую структуру и временную направленность.

Оно реализует:

•       форму: вложенность, виток, антисимметрия,

•       время: итерация, S-сдвиг, проекция в ленту, •   смысл: выбор, наблюдение, структура различий.

Модель ядра — это схема, на которой могут быть построены новые модели квантовой логики, когнитивной топологии и альтернативной метрики времени.

Литература

1.     Павлов Д.Г., Панчелюга М.С., Панчелюга В.А. (2009). О форме аналогов множества Жюлиа на плоскости двойной переменной. // Гиперкомплексные числа в геометрии и физике. Т.6, №2 (12), С. 162– 176.

2.     Басаргин О.С. (2025). Эталонное описание устройства Сфираль. Zenodo. https://doi.org/10.5281/zenodo.15133508

3.     Rovelli C. (2004). Quantum Gravity. Cambridge University Press.

4.     Bombelli L., Lee J., Meyer D., Sorkin R. (1987). Space-Time as a Causal Set. Physical Review Letters, 59(5), 521–524.

5.     Buzsáki G. (2006). Rhythms of the Brain. Oxford University Press.

6.     Edelman G.M. (1989). The Remembered Present: A Biological Theory of Consciousness. Basic Books.

7.     Пригожин И., Стенгерс И. (1986). Порядок из хаоса: Новый диалог человека с природой. — М.: Прогресс.

8.     Вернадский В.И. (1989). Несколько слов о ноосфере. — В: Избранные труды. — М.: Наука.