Выполнение расчетов с радикалами. Решение иррациональных уравнений

Методическая разработка

практического занятия для студента

Тема: «Решение иррациональных уравнений»

ОУП. 04 «МАТЕМАТИКА»

Специальность 34.02.01 «Сестринское дело»

ТЕМА: «ВЫПОЛНЕНИЕ РАСЧЕТОВ С РАДИКАЛАМИ. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ»

1.     Тип занятия: практическое.

2.     Место проведения, продолжительность занятия: учебная аудитория, 90 минут

3.     Цели занятия для студента: закрепить знания и умения по освоению применения формул при выполнении вычислений и решении иррациональных уравнений

4.     Требования к уровню освоения дидактических единиц:

В результате студент должен:

-Знать определение корня и его свойств.

-Уметь решать иррациональные уравнения

- Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни; для практических расчетов по формулам, включая формулы, содержащие радикалы, используя при необходимости справочные материалы и простейшие вычислительные устройства.

-Уметь правильно пользоваться математической символикой в процессе выполнения заданий.

5.     Оснащение занятия: Алимов Ш. А., Колягин Ю. М. «Алгебра  и начала математического анализа», доска, мел, тетради с конспектами, карточки с заданиями для практической работы, карточки со справочным материалом.

6.     Деятельность студентов в ходе занятия

6.1       Выполните следующие упражнения у доски с целью проверки домашнего задания

6.2       Прослушайте инструктаж по выполнению практической работы, возьмите справочный материал и карточки с заданиями у преподавателя

Инструктаж студентов по выполнению практических заданий

Задания необходимо оформить в тетрадях для практических работ. Выполнить индивидуальную работу по варианту. Вариант содержит необходимый справочный материал.  На выполнение задания отводится 60 минут. В конце работы необходимо написать вывод. В конце занятия необходимо сдать тетради для проверки и оценивания.

Справочный материал

Уравнения, в которых переменная находится под знаком корня, называются иррациональными.

Для решения иррационального уравнения надо левую и правую части уравнения возвести в п-ую степень, равную показателю корня

Алгоритм решения уравнений

1. Решение иррациональных уравнений сводится к переходу от иррационального к рациональному уравнению путем возведения в степень обеих частей уравнения или замены переменной.

2. При возведении обеих частей уравнения в четную степень возможно появление посторонних корней. Поэтому при использовании указанного метода следует проверить все найденные корни подстановкой в исходное уравнение.

3. Иногда удобнее решать иррациональные уравнения, определив область допустимых значений неизвестного и используя равносильные переходы.

Пример

Решение уравнения  = 1 – х методом возведения в квадрат обеих частей уравнения.
             () = (1 – х);

1+ 3х = x² – 2x + 1;

x²– 5x = 0.
Решив это уравнение, находим корни        .

Проверка: если x = 0, то , 1 = 1 – верно;
если х = 5, то , 4 = 4 – неверно.
Ответ:  х = 0.

6.3       Самостоятельно выполните задания из практической работы № 3

Практическая работа № 3

Тема: «Решение иррациональных уравнений»

Цель: закрепить знания и умения по освоению применения формул при выполнении вычислений и решении иррациональных уравнений

Вариант 1

1. Найдите корни уравнения

2. Решите уравнение

3. Найдите корни уравнения

4. Решите уравнение

5. Найдите корни уравнения

6. Решите уравнение

7. Найдите корни уравнения

8. Решите уравнение  

9. Найдите корни уравнения

10. Найти корень уравнения: . Если уравнение имеет более одного корня, укажите меньший из них.

11.Упростить: 

Вариант 2

1. Найдите корни уравнения

2. Решите уравнение

3. Найдите корни уравнения

4. Решите уравнение

5. Найдите корни уравнения

6. Решите уравнение

7. Найдите корни уравнения

8. Решите уравнение 

9. Найдите корни уравнения

10. Найти корень уравнения: . Если уравнение имеет более одного корня, укажите меньший из них.

11.  Упростить:

Критерии оценивания практической работы.

Отметка «5» ставится, если студент:

 работа выполнена полностью;

 в логических рассуждениях и обосновании решения нет пробелов и ошибок;

 в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).

Отметка «4» ставится, если студент:

 работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);

 допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).

Отметка «3» ставится, если студент:

 допущено более одной ошибки или более двух – трех недочетов в выкладках,

чертежах или графиках, но учащийся обладает обязательными умениями по проверяемой теме.

Отметка «2» ставится, если студент:

 допущены существенные ошибки, показавшие, что учащийся не обладает

обязательными умениями по данной теме в полной мере.

6.4 Запишите в тетрадь домашнее задание

Подготовиться к практическому занятию № 4, выучить теоретический материал в тетрадях, выполнить задание по варианту

Вариант 1

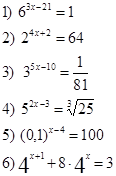
1) 

6.5  Рефлексия

Оцените свою деятельность и заполните таблицу