
Высшая математика
Контрольная работа для заочного отделения
Составитель
Бадика Т.А.
Каменка 2020
ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ПОРЯДОК ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ
К выполнению каждой контрольной работы следует приступать только после изучения соответствующего материала курса по учебнику и решения задач, указанных в каждой теме. Следует также внимательно разобрать решения тех задач, которые приводятся в данном пособии к каждой теме.
При этом следует руководствоваться следующими указаниями:
1. Каждую работу следует выполнять в отдельной тетради в рукописном виде (набранные на компьютере контрольные работы не рассматриваются).
2. На внешней обложке тетради должны быть указаны фамилия и инициалы студентов, полный шифр, номер контрольной работы и дата ее сдачи.
3. Решения всех задач и пояснения к ним должны быть достаточно подробными.
4. При необходимости следует делать соответствующие ссылки на вопросы теории с указанием формул, теорем, выводов, которые используются при решении данной задачи. Все вычисления (в том числе и вспомогательные) необходимо делать полностью.
5. Чертежи и графики должны быть выполнены аккуратно и четко с указанием единиц масштаба, координатных осей и других элементов чертежа.
6. Объяснения к задачам должны соответствовать тем обозначениям, которые даны на чертеже.
7. Для замечаний преподавателя необходимо на каждой странице оставлять поля шириной 4 см.
8. После получения работы (как зачтенной, так и незачтенной) студент должен исправить в ней все отмеченные рецензентом недостатки.
9. В случае незачета студент обязан в кратчайший срок выполнить все требования и представить работу на повторную проверку приложив при этом первоначально выполненную работу.
10. Контрольные работы должны выполняться самостоятельно. Если будет установлено, что та или иная контрольная работа выполнена несамостоятельно, то она не будет зачтена, даже если в этой работе все задачи решены верно.
11. В период экзаменационной сессии студент обязан представить все зачтенные контрольные работы.
12. При необходимости (по требованию преподавателя) студент должен давать на экзамене устные пояснения ко всем или некоторым задачам, содержащимся в этих работах.
13. Номер варианта определяется по двум последним цифрам зачетной книжки. Если предпоследняя цифра 3, 4 или 5, то из неё надо вычесть 3. Если предпоследняя цифра 6, 7 или 8, то из неё надо вычесть 6. Если же предпоследняя цифра 9, то из неё надо вычесть 9. Например, если две последние цифры 56, то вариант 26; если две последние цифры 75, то вариант 15; если две последние цифры 98, то вариант 08.
Задание № 1. Найти значение многочлена ![]() (варианты
№ 1-15) и
(варианты
№ 1-15) и ![]() (варианты № 16 - 30) от матрицы А:
(варианты № 16 - 30) от матрицы А:
№1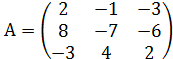
№2 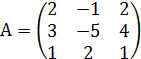
№ 3 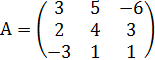
№ 4 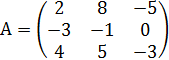
№ 5 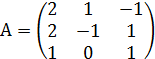
№ 6 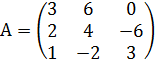
№ 7 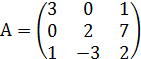
№ 8 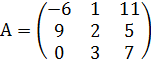
№ 9 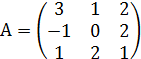
№ 10 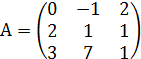
№ 11 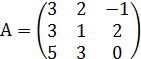
№ 12 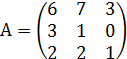
№ 13 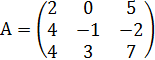
№ 14 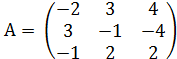
№ 15 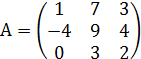
Задание № 2. Проверить на совместимость системы уравнений и в случае совместности решить её:
· По формулам Кремера;
· С помощью обратной матрицы;
· Методом Гаусса.
№ 1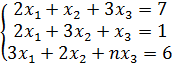
№ 2 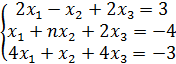
№ 3 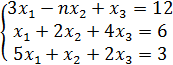
№ 4 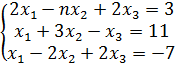
№ 5 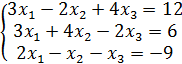
№ 6 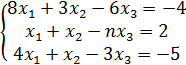
№ 7 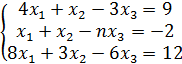
№ 8 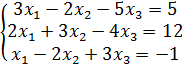
№ 9 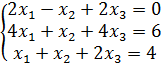
№ 10 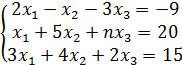
Задание № 3. Вычислить указанные пределы, не используя правило Лопиталя. Варианты:
|
|
|
А) X0 = 1 |
Б) X0 = 2 |
В) X0 = ¥ |
|
|
|
А) X0 = 3 |
Б) X0 = -1 |
В) X0 = ¥ |
|
|
|
А) X0 = 3 |
Б) X0 = 1 |
В) X0 = ¥ |
|
|
|
А) X0 = 2 |
Б) X0 = 1 |
В) X0 = ¥ |
|
|
|
А) X0 = -1 |
Б) X0 = 1 |
В) X0 = ¥ |
|
|
|
А) X0 = -2 |
Б) X0 = 1 |
В) X0 = ¥ |
|
|
|
А) X0 = 1 |
Б) X0 = -1 |
В) X0 = ¥ |
|
|
|
А) X0 = 2 |
Б) X0 = 3 |
В) X0 = ¥ |
|
|
|
А) X0 = 3 |
Б) X0 = -3 |
В) X0 = ¥ |
|
|
|
А) X0 = -3 |
Б) X0 = -2 |
В) X0 = ¥ |
|
|
|
А) X0 = 2 |
Б) X0 = -1 |
В) X0 = ¥ |
|
|
|
А) X0 = -1 |
Б) X0 = 1 |
В) X0 = ¥ |
|
|
|
А) X0 = 2 |
Б) X0 = -2 |
В) X0 = ¥ |
|
|
|
А) X0 = 1 |
Б) X0 = 2 |
В) X0 = ¥ |
|
|
|
А) X0 = -2 |
Б) X0 = -1 |
В) X0 = ¥ |
|
|
|
А) X0 = -1 |
Б) X0 = 1 |
В) X0 = ¥ |
|
|
|
А) X0 = 2 |
Б) X0 = -2 |
В) X0 = ¥ |
|
|
|
А) X0 = 1 |
Б) X0 = 2 |
В) X0 = ¥ |
|
|
|
А) X0 = -2 |
Б) X0 = -1 |
В) X0 = ¥ |
|
|
|
А) X0 = -1 |
Б) X0 = 1 |
В) X0 = ¥ |
|
|
|
А) X0 = 2 |
Б) X0 = -2 |
В) X0 = ¥ |
|
|
|
А) X0 = 1 |
Б) X0 = 2 |
В) X0 = ¥ |
|
|
|
А) X0 = -2 |
Б) X0 = -1 |
В) X0 = ¥ |
|
|
|
А) X0 = -1 |
Б) X0 = 1 |
В) X0 = ¥ |
|
|
|
А) X0 = 2 |
Б) X0 = -2 |
В) X0 = ¥ |
|
|
|
А) X0 = 1 |
Б) X0 = 2 |
В) X0 = ¥ |
|
|
|
А) X0 = -2 |
Б) X0 = -1 |
В) X0 = ¥ |
|
|
|
А) X0 = -1 |
Б) X0 = 1 |
В) X0 = ¥ |
|
|
|
А) X0 = 2 |
Б) X0 = -2 |
В) X0 = ¥ |
|
|
|
А) X0 = 2 |
Б) X0 = 4 |
В) X0 = ¥ |
Задание № 4. Найти производные функций. Варианты:
|
1. |
А) В) |
Б) Г) |
|
2. |
А) В) |
Б) Г) |
|
3. |
А) |
Б) Г) |
|
4. |
А) В) |
Б) Г) |
|
5. |
А) В) |
Б) Г) |
|
6. |
А) |
Б) Г) |
|
7. |
А) В) |
Б) Г) |
|
8. |
А) В) |
Б) Г) |
|
9. |
А) В) |
Б) Г) |
|
10. |
А) |
Б) |
|
11. |
А) Б) |
В) |
|
12. |
А) Б) |
В) |
|
13. |
А) Б) |
В) |
|
14. |
А) Б) |
В) |
|
15. |
А) Б) |
В) Г) |
|
16. |
А) Б) |
В) Г) |
|
17. |
А) Б) |
В) Г) |
|
18. |
А) Б) |
В) Г) |
|
19. |
А) Б) |
В) Г) |
|
20. |
А) Б) |
В) |
|
21. |
А) Б) |
В) |
|
22. |
А) Б) |
В) |
|
23. |
А) Б) |
В) |
|
24. |
А) Б) |
В) |
|
25. |
А) Б) |
В) |
|
26. |
А) Б) |
В) |
|
27. |
А) Б) |
В) |
|
28. |
А) Б) |
В) |
|
29. |
А) Б) |
В) |
|
30. |
А) Б) |
В) |
Задание № 5. Исследовать данную функцию методами дифференциального исчисления и построить ее график.
Варианты:
|
1.
|
2.
|
3.
|
4.
|
5.
|
|
6.
|
7.
|
8.
|
9.
|
10.
|
|
11.
|
12.
|
13.
|
14.
|
15.
|
|
16.
|
17.
|
18.
|
19.
|
20.
|
|
21.
|
22.
|
23.
|
24.
|
25.
|
|
26.
|
27.
|
28.
|
29.
|
30.
|
Задание № . 6 Вычислить неопределенные интегралы. Варианты:
|
1. |
А) |
Б) |
В) |
|
2. |
А) |
Б) |
В) |
|
3. |
А) |
Б) |
В) |
|
4. |
А) |
Б) |
В) |
|
5. |
А) |
Б) |
В) |
|
6. |
А) |
Б) |
В) |
|
7. |
А) |
Б) |
В) |
|
8. |
А) |
Б) |
В) |
|
9. |
А) |
Б) |
В) |
|
10. |
А) |
Б) |
В) |
|
11. |
А) |
Б) |
В) |
|
12. |
А) |
Б) |
В) |
|
13. |
А) |
Б) |
В) |
|
14. |
А) |
Б) |
В) |
|
15. |
А) |
Б) |
В) |
|
16. |
А) |
Б) |
В) |
|
17. |
А) |
Б) |
В) |
|
18. |
А) |
Б) |
В) |
|
19. |
А) |
Б) |
В) |
|
20. |
А) |
Б) |
В) |
|
21. |
А) |
Б) |
В) |
|
22. |
А) |
Б) |
В) |
|
23. |
А) |
Б) |
В) |
|
24. |
А) |
Б) |
В) |
|
25. |
А) |
Б) |
В) |
|
26. |
А) |
Б) |
В) |
|
27. |
А) |
Б) |
В) |
|
28. |
А) |
Б) |
В) |
|
29. |
А) |
Б) |
В) |
|
30. |
А) |
Б) |
В) |
Задание № 7. Вычислить площадь фигуры, ограниченной линиями y=ax2+bx+c и y=mx+n (параметры a, b, c, m, n заданы в таблице). Построить график.
Варианты:
|
№ |
a |
b |
c |
m |
n |
№ |
a |
b |
c |
m |
n |
|
1. |
1 |
-4 |
3 |
1 |
-1 |
16. |
-1 |
1 |
5 |
1 |
1 |
|
2. |
1 |
2 |
0 |
1 |
2 |
17. |
2 |
-4 |
4 |
2 |
0 |
|
3. |
1 |
4 |
3 |
1 |
3 |
18. |
1 |
6 |
-4 |
2 |
8 |
|
4. |
1 |
-6 |
10 |
1 |
0 |
19. |
-1 |
-2 |
5 |
1 |
1 |
|
5. |
1 |
-2 |
1 |
1 |
-1 |
20. |
1 |
-3 |
-1 |
1 |
4 |
|
6. |
1 |
6 |
8 |
1 |
4 |
21. |
-1 |
2 |
-1 |
-1 |
-5 |
|
7. |
1 |
-6 |
13 |
1 |
3 |
22. |
2 |
-5 |
1 |
1 |
1 |
|
8. |
1 |
8 |
15 |
1 |
5 |
23. |
-1 |
1 |
-5 |
1 |
-9 |
|
9. |
1 |
0 |
0 |
1 |
2 |
24. |
-1 |
-1 |
1 |
1 |
-2 |
|
10. |
1 |
0 |
-1 |
1 |
1 |
25. |
1 |
-5 |
-3 |
1 |
-11 |
|
11. |
2 |
4 |
-7 |
1 |
-3 |
26. |
1 |
-3 |
2 |
1 |
-1 |
|
12. |
-1 |
-1 |
1 |
2 |
-1 |
27. |
1 |
-2 |
1 |
2 |
22 |
|
13. |
1 |
-6 |
-2 |
-2 |
18 |
28. |
1 |
-4 |
4 |
2 |
20 |
|
14. |
-1 |
-1 |
8 |
1 |
5 |
29. |
1 |
-2 |
1 |
3 |
-3 |
|
15. |
1 |
-3 |
-4 |
1 |
1 |
30. |
3 |
0 |
1 |
3 |
7 |
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.