XUSUSIY HOSILALI GIPERBOLIK TIPGA TEGISHLI TENGLAMALAR HAQIDA AYRIM MULOHAZALAR

Xikmatulloyev Raxmatullo

Farg’ona Politexnika Instituti akademik litseyi matematika fani  o‘qituvchisi

Annotatsiya. Maqolada xususiy hosilali giperbolik tipga tegishli tenglamalarning paydo bo‘lish tarixi va amaliy tadbiqlari hamda shu yo‘nalishda izlanishlar olib borgan olimlar haqida ma'lumotlar keltirilgan. Tebranish tenglamasi, xususan ipning elastik ko‘ndalang tebranishlarining tenglamasi va yechimlari bayon qilingan. Xususiy hosilali tenglamalar tasnifi keltirilgan va giperbolikka tipga tegishli xususiy hosilali tenglamalar uchun qo‘yiladigan chegaraviy va boshlang‘ich masalalar tahlil qilingan. Tipik misollar oson usullar bilan yechib ko‘rsatilgan. Aralash tipdagi tenglamalar, xususan buzilish chizig‘iga ega giperbolik tenglama haqida fikrlar bayon qilingan va uning yechimi Riman funksiyasi orqali yozilishi ko‘rsatilgan.

Kalit so‘zlar: matematik fizika, osmon mexanikasi, elektromagnit tebranishla, funksiya, elastik ip, kuchlanish, segment, Guk qonuni, tortishish kuchi, perpendikulyar harakat, differentsial tenglama, chiziqli algebra, elliptik tip, statsionar jarayonlar, chegaraviy shartlar, giperbolik tip, parabolik tip, Koshi masalasi.

НЕКОТОРЫЕ ЗАМЕЧАНИЯ ОБ УРАВНЕНИЯХ ГИПЕРБОЛИЧЕСКОГО ТИПА С ЧАСТНЫМИ ПРОИЗВОДНЫМИ

Аннотация. В статье приведены история возникновения и практического применения уравнений гиперболического типа с частными производными, а также сведения об ученых, проводивших исследования в этом направлении. Изложены уравнения колебаний, в частности уравнение и решения упругих поперечных колебаний струны. Дана классификация дифференциальных уравнений частных производных, проанализированы краевыя и начальныя задачи для гиперболического типа. Указаны методы решения типичных примеров простыми способами. Изложены замечания об уравнениях смешанного типа, в частности, гиперболическом уравнении с линией вырождения, и указаны ее решение с помощью функцией Римана.

Ключевые слова: математическая физика, небесная механика, электромагнитные колебания, функция, струна, натяжение, отрезок, закон Гука, гравитация, перпендикулярное движение, дифференциальное уравнение, линейная алгебра, эллиптический тип, гиперболический тип, параболический тип, стационарные процессы, граничные условия, задача Коши.

SOME REMARKS ON EQUATIONS OF THE HYPERBOLIC TYPE WITH PARTICULAR DERIVATIVES

Abstract. The article presents the history of the emergence and practical applications of equations of the hyperbolic type with specific derivatives, as well as information about scientists who conducted research in this direction. The vibration equation, in particular, the equation and solutions of the elastic transverse vibrations of the string are described. The classification of differential equations is given, and the boundary and initial problems for differential equations of the hyperbolic type are analyzed. A number of typical examples are shown in easy ways. The ideas about mixed-type equations, in particular, the hyperbolic equation with a fault line, are

presented, and its solution is shown to be written by the Riemannian function.

Keywords: mathematical physics, celestial mechanics, electromagnetic oscillation, function, elastic thread, tension, segment, Hooke's law, gravity, perpendicular motion, differential equation, linear algebra, elliptic type, stationary processes, boundary conditions, hyperbolic type, parabolic type, Cauchy problem.

KIRISH

Xususiy hosilali differensial tenglamalar nazariyasi ikkita xarakterli xususiyatga ega. Birinchidan, u zamonaviy matematik fizikaning asosiy tadqiqot vositasidir. Ma'lumki, oddiy differentsial tenglamalar nazariyasi XVIII asrda differensial va integral hisoblar paydo bo'lgandan so'ng darhol rivojlana boshladi. Oddiy differensial tenglamalar orqali yangi hisob- kitoblar geometriya va mexanika masalalariga o'tdi. Osmon mexanikasi nafaqat ilgari ma'lum bo'lgan faktlarni tushuntirishga, balki yaratishga ham muvaffaq bo'ldi (masalan, Neptun sayyorasi xususiy hosilali differensial tenglamalar tahlili yordamida kashf etilgan).

Fizikada paydo bo'lgan o'ziga xos tenglamalar shakli ancha keyinroq o'rganila boshlandi. Bu esa XVIII asr o'rtalarida tahlilning yangi tarmog'i - matematik fizikaning tenglamalari paydo bo'lishiga olib keldi. Bu fan Dalamber, Eyler, Bernulli, Furye asarlarida o'z ifodasini topgan. Bu olimlar matematikaning o'ziga xos muammolarini tadqiq qildilar. Fizika va ular tomonidan ishlab chiqilgan g'oyalar va usullar keng sinflarga taalluqli bo'lib chiqdi XIX asrning oxirida xususiy hosilali differensial tenglamalarning umumiy nazariyasini ishlab chiqish uchun asos bo'lib xizmat qilgan. Xususiy hosilali differensial tenglamalar nazariyasining yana bir xususiyati uning matematikaning boshqa sohalari bilan chambarchas bog'liqligidir: funktsional analiz va funksiyalar nazariyasi, topologiya, algebra, kompleks analiz va boshqalar.

TADQIQOT MATERIALLARI VA METODOLOGIYASI

Tebranish tenglamasi Dalamber tomonidan 1747 yilda kiritilgan. Tor tebranishlar tenglamasi uchun Koshi masalasini yechish Dalamber formulasi deb ataladi. Bernulli bu tenglamaning har bir yechimini ta'kidladi va trigonometrik qator bilan ifodalanadi. Eylerning Dalamber va Bernulli bilan torli tebranish tenglamasining yechimlari tabiati bo'yicha tortishuvi matematik fizika va trigonometrik qatorlar nazariyasi rivojiga juda katta hissa qo’shdi.

Funksiyalarni trigonometrik qatorlarga kengaytirish muammosini keying tadqiq etish Furye tomonidan 1822 yilda amalga oshirilgan, u issiqlik tarqalishi muammolari bilan bog’liq. Keyinchalik esa Dirixlening ishlari birinchi bo’lib parchalanish uchun yetarli shartlarni ishlab chiqib, funksiyalarni trigonometrik qatorlarga aylantirdi. Demak, funksiyani trigonometrik qator bilan ifodalash masalasini ko'radigan bo’lsak, birinchi marta matematik fizika masalalarida paydo bo'ldi va zamonaviy to‘plamlar nazariyasi va funksiyalar nazariyasini yaratishda katta hissa qo'shdi. Maxsus o'rganish paytida fizik masalalardan tenglamalar, umumiy usullar ko'pincha yaratilgan bo'lib, ular dastlab keng ko'lamli masalalarga qat'iy matematik asoslanmagan holda qo'llanilgan.

Fizik hodisani o'rganish bilan bog'liq matematik muammoni shakllantirishda, birinchi navbatda uni tavsiflovchi miqdorlar ajratib ko'rsatiladi. Bunday qadriyatlar bilan zinchlik, tezlik, harorat va boshqalar bo'lishi mumkin. Keyin fizik qonunlar tanlanadi va matematik shakllantiriladi, bu hodisa nazariyasining asosi bo'lishi mumkin. Ushbu qonunlar sodda va izchil bo'lishi kerak. Qoidaga ko'ra, bu qonunlar hodisaning asosiy belgilari va fazoning ma'lum bir nuqtasida ularning xususiy hosilalari o'rtasidagi nisbatlar sifatida yozilishi mumkin.

TADQIQOT NATIJALARI

Bunday yozuvning mumkinligi mohiyatiga ko'ra ko'pincha tenglamalarni chiqarishda barcha ma'lum turdagi o'zaro ta'sirlarning joylashishi va avval ba'zi integral saqlanish qonunlaridan (masalan, massa, impuls, energiya va boshqalar) foydalanish qulay va shundan keyingina o'rganilayotgan miqdorlarning yetarli darajada silliqligini nazarda tutgan holda mahalliy tenglamalarga o'tiladi. Mexanikadagi (torlar, novdalar, membranalar va uch o'lchamli hajmlarning tebranishlari bo'yicha), shuningdek fizikadagi (elektromagnit tebranishlar bo'yicha) ko'plab muammolar quyidagi shakldagi tenglamaga olib keladi:

𝜕²𝑢

𝑝 ∗ 𝜕𝑡2 = 𝑑𝑖𝑣(𝑝∇𝑢) − 𝑞𝑢 + 𝐹(𝑥, 𝑡)                                                                        (1)

bu yerda ∇= ( 𝜕 , 𝜕 , 𝜕 ).

𝜕𝑥  𝜕𝑦   𝜕𝑧

No’malum funksiya 𝑢(𝑥, 𝑡) 𝑛 (𝑛 = 1,2,3) fazoviy o’zgaruvchilar 𝑥 = (𝑥₁, 𝑥₂, … , 𝑥_𝑛) va vaqt 𝑡 ga bog’liq. 𝜌, 𝑝, 𝑞 koeffitsientlari muhit xossalari bilan aniqlanadi. 𝐹(𝑥, 𝑡) funksiyasi tashqi bezovtalanishning zichligi.

Torning elastik ko‘ndalang tebranishlarining (1) tenglamasini keltiraylik. egilishga qarshilik qilmaydigan elastik tor string deyiladi (𝑛 = 1). Tor o'zining muvozanat holati atrofida tekislikda (𝑥, 𝑢) ko'ndalang tebranishlarni amalga oshiradi va bu 𝑥 o'qi bilan mos keladi. 𝑢(𝑥, 𝑡) bilan ipning 𝑡 vaqtdagi 𝑥 nuqtadagi muvozanat holatidan chetlanishini belgilaymiz. Demak, 𝑢 =

𝑢(𝑥, 𝑡) da bu 𝑡 vaqtdagi ipning grafigi. Tor egilishga qarshilik ko'rsatmagani uchun uning taranglik kuchi 𝑇⃗→(𝑥, 𝑡) nuqtada 𝑥 ga, 𝑡 vaqt nuqtasi ipga yo'naltiriladi (1-rasm).

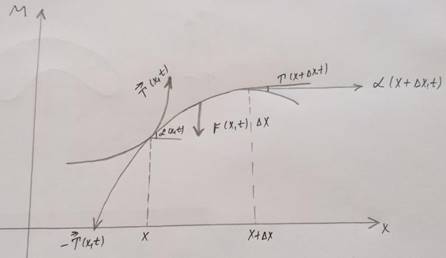
1- rasm

𝑇⃗→(𝑥, 𝑡) kuchlanish kuchini topamiz. Guk qonuniga ko'ra, kuchlanish kuchi ipning nisbiy uzayishiga proportsionaldir. Segmentdagi tor uzunligi [𝑥, 𝑥 + ∆𝑥], quyidagi formula bo'yicha

hisoblanadi: 𝑙 =

^𝑥+∆𝑥 √1 + (𝜕𝑢 (𝑦, 𝑡))²𝑑𝑦 = ∆𝑥 ∙ √1 + (𝜕𝑢 (𝜉, 𝑡))².

∫𝑥

𝜕𝑥

𝜕𝑥

^𝑙 = √1 + (𝜕𝑢 (𝜉, 𝑡)² → √1 + (𝜕𝑢 (𝑥, 𝑡)² , ∆𝑥 → 0.

∆𝑥

𝜕𝑥

𝜕𝑥

2

Bundan kelib chiqadiki, tortish kuchi moduli |𝑇(𝑥, 𝑡)| = 𝑇₀

∙  (1 + (𝜕𝑢 (𝑥, 𝑡))

𝜕𝑥

)^1⁄2 = 𝑇₀ ∙

√1 + 𝑡𝑔²𝛼 bo’ladi. Endi 𝑢 o'qiga taranglik kuchining proyeksiyasini topamiz:

𝑇_𝑢(𝑥, 𝑡) = |𝑇(𝑥, 𝑡)| ∙ 𝑠𝑖𝑛𝛼 = 𝑇₀ ∙ √1 + 𝑡𝑔2𝛼 ∙ 𝑠𝑖𝑛𝛼 = 𝑇₀

𝑠𝑖𝑛𝛼

𝑐𝑜𝑠𝛼

= 𝑇₀ ∙

𝜕𝑢

𝜕𝑥

(𝑥, 𝑡).         (2)

𝐹(𝑥, 𝑡) taʼsir etuvchi tashqi kuchning (maʼlum) zichligini bildirsin, tor 𝑡 vaqtda 𝑥 nuqtada

va 𝑥 o‘qiga perpendikulyar yo‘naltirilgan, tortishish kuchi 𝐹(𝑥, 𝑡) = −𝑔 ∙ 𝜌(𝑥).

Bu yerda 𝜌(𝑥) chiziqlilikni bildiradi. 𝑥 nuqtadagi tor zichligi, ya'ni 𝜌(𝑥)∆𝑥 - tor segmentining  massasi  [𝑥, 𝑥  +  ∆𝑥].  Bu  kesmada  taranglik  kuchlari  𝑇⃗→(𝑥 + ∆𝑥, 𝑡) − 𝑇⃗→(𝑥, 𝑡)  va tashqi  kuch  𝐹→(𝑥, 𝑡)∆𝑥   segmentga  taʼsir  qiladi,  ularning  yigʻindisi  Nyuton  qonuniga  koʻra segmentning massasi va uning tezlanishi teng boʻlishi kerak. 𝑥 o'qidagi kuchlarning proyeksiyasi nolga teng (bu shuni anglatadiki 𝑥 ning har bir nuqtasi 𝑥 o'qiga perpendikulyar harakat qiladi).

Bizning vektorimizning proyeksiyasi 𝑢 o'qiga teng (2): 𝑇 ∙ 𝜕𝑢 (𝑥 + ∆𝑥, 𝑡) − 𝑇 ∙ 𝜕𝑢 (𝑥, 𝑡) −

0    𝜕𝑥                                                     0    𝜕𝑥

𝐹(𝑥, 𝑡) ∙ ∆𝑥 = 𝑝(𝑥) ∙ ∆𝑥 ∙ 𝜕2𝑢 (𝑥, 𝑡).               Natijada,       𝑝(𝑥) ∙ 𝜕2𝑢 (𝑥, 𝑡) = 𝑇

∙ 1   ∙ [𝜕𝑢 (𝑥 + ∆𝑥, 𝑡) −

𝜕𝑥2

𝜕𝑥2

0    ∆𝑥

𝜕𝑥

^𝜕𝑢 (𝑥, 𝑡)] − 𝐹(𝑥, 𝑡). ∆𝑥 → 0 sifatida chegaraga o'tamiz va 𝑢(𝑥, 𝑡) funksiyani ikki marta uzluksiz

𝜕𝑥

deb faraz qilamiz, 𝑥 ga nisbatan differensiallaymiz va 𝑡 ga nisbatan biz tenglamani qaraymiz:

𝜕²𝑢                 𝜕²𝑢

𝑝(𝑥) ∙ 𝜕𝑡2 = 𝑇₀ ∙ 𝜕𝑥2 − 𝐹(𝑥, 𝑡).                                                                 (3)

Bu torning elastik ko‘ndalang tebranishlar tenglamasi deyiladi.

Agar tor doimiy zichlikka ega bo'lsa 𝜌(𝑥) = 𝜌 , u holda tenglama quyidagicha bo'ladi:

𝜕²𝑢

𝜕𝑡²

= 𝛼² ∙

𝜕²𝑢

𝜕𝑥²

+ 𝑓,                                                                                            (4)

bu erda 𝑎 ko'rsatilgan 𝛼² = 𝑇₀/𝜌, 𝑓 = 𝐹/𝜌. (4) Bir o'lchovli to'lqin tenglamasi deb ataladi.

(1) tenglama elastik tayoqning bo’ylama tebranishlarini ham tavsiflaydi (𝑛 = 1):

𝜕²𝑢          𝜕

𝜕𝑢

𝑝(𝑥) ∙ 𝑆(𝑥) ∙ 𝜕𝑡2 = 𝜕𝑥 (𝐸(𝑥)𝑆(𝑥) ∙ 𝜕𝑥) + 𝐹(𝑥, 𝑡)                         (5)

bu yerda 𝑆(𝑥) novda koʻndalang kesimi maydoni, 𝐸(𝑥) 𝑥 nuqtadagi Yang moduli.

Agar membrana zichligi 𝜌 doimiy bo'lsa, tenglama soddalashtiriladi:

𝜕²𝑢

= 𝛼² (

𝜕²𝑢

𝜕²𝑢

+

) + 𝑓(𝑥, 𝑡)                                         (6)

𝜕𝑡²

𝜕𝑥₁²

𝜕𝑥₂²

bunda 𝛼² = 𝑇₀/𝜌, 𝑓 = 𝐹/𝜌. (6) tenglama ikki o'lchovli to'lqin tenglamasi deb ataladi.

Ucho’lchovli to’lqin tenglamasi:

𝜕²𝑢

𝜕𝑡2

= 𝛼² (

𝜕²𝑢

𝜕𝑥12

𝜕²𝑢

+

𝜕𝑥22

𝜕²𝑢

+

𝜕𝑥23

) + 𝑓(𝑥, 𝑡)                                     (7)

elektr   o'tkazmaydigan   muhit       tovushning   o'rtada,   elektromagnit        to'lqinlarning bir xilda tarqalishini tavsiflaydi. To'lqin tenglamalari odatda quyidagi shaklda yoziladi

𝜕²𝑢

𝜕𝑡²

= 𝛼²∆𝑢 + 𝑓(𝑥, 𝑡),                                                                                 (8)

bu erda ∆ −Laplas operatori va u: ∆= ∑^𝑛

𝜕2𝑢  .

𝑖=1 𝜕𝑥12

Haqiqiy hodisalarni differensial tenglamalar yordamida matematik ma'lum bir tavsiflash modellashtirish hisoblanadi. Masalan, Guk qonuni taxminiy, Furye issiqlik uzatish qonuni esa molekulyar strukturani hisobga olgan holda aniqlanishi mumkin. Shuning uchun, tadqiqotdan olingan xulosalar yoki hatto aniq olingan differensial tenglamalarning yechimlari ham

taxminiydir. Masalan, issiqlik tenglamasi issiqlik tarqalishining cheksiz tezligini (hatto nuqta manbasidan ham) bashorat qiladi, bu albatta, absurddir. Shu bilan birga vaqt, bu ta'sir issiqlik tenglamasining matematik nazariyasi juda muvaffaqiyatli qo'llaniladigan muhandislikdagi issiqlik uzatish hisob-kitoblariga juda oz ta'sir qiladi. U xususiy hosilali differensial tenglamalarga tegishli asoslangan va boshqa ko'plab matematik modellarga. Biroq, matematik model asosida olingan xulosalar eksperimental natijalardan sezilarli darajada farq qiladi. Bu modelning nomukammalligini va uni o'rganilayotgan ob'ektning xususiyatlarini aniqroq aks ettiruvchi boshqa qonunlar bilan almashtirish zarurligini ko'rsatadi. Asosiy harakatni tavsiflovchi funksiyalarning silliqligi haqida qo'shimcha taxminlar, parametrlar odatda differensial tenglamalarni olishda, matematikada tabiat qonunlarini yozishda, soddalashtirish uchun qabul qilinadi. Biroq, bu taxminlar har doim ham qulay yoki jismoniy oqlangan emas.

Xususiy hosilali differensial tenglamalar quyidagi shakldagi tenglamadir:

𝐹 (𝑥, 𝑢(𝑥), 𝜕𝑢

𝜕𝑥1

(𝑥), … , 𝜕𝑢

𝜕𝑥𝑛

(𝑥);  𝜕2𝑢

𝜕𝑥𝑘𝑥1

(𝑥), … ) = 0, bu yerda 𝑥 = (𝑥₁

, 𝑥₂

, … , 𝑥_𝑛

) 𝜖 Ω ⊂

𝑅^𝑛, 𝑎 𝑢(𝑥) − noma’lum funksiya.

Differensial tenglamaning tartibi uning hosilalarining maksimal tartibidir. Agar noma'lum funksiyaga va uning barcha xususiy hosilalariga nisbatan chiziqli bo'lsa, xususiy hosilali differensial tenglamalar chiziqli deb ataladi. Agar u barcha yuqori hosilalarga nisbatan chiziqli bo'lsa, u holda kvaziziqli tenglama deyiladi. Misol uchun quyidagi tenglama:

𝜕𝑢

𝜕𝑥₁

𝜕²𝑢

∙

𝜕𝑥₁²

𝜕𝑢  ²

+ (         )

𝜕𝑥₂

𝜕²𝑢

∙

𝜕𝑥₂²

+ 𝑢² = 0

ikkinchi tartibli kvazliziqli tenglamadir.

) 𝜕2𝑢

ikkinchi tartibli chiziqli tenglama,

𝜕2𝑢   2

𝜕2𝑢    2

𝜕𝑥  2 + 𝑎

𝑥₁, 𝑥₂

𝜕𝑥  2  = 2𝑢

(         )

𝜕𝑥12

+ (         )

𝜕𝑥22

= 2𝑢

Quyidagi 2-tartibli chiziqli tenglama

𝜕²𝑢

𝑝 ∙ 𝜕𝑡2 = 𝑑𝑖𝑣(𝑝∇𝑢) − 𝑞 ∙ 𝑢 + 𝐹(𝑥, 𝑡)                                                        (9)

tebranish jarayonlarini tenglamasini tavsiflaydi.

Diffuziya jarayonlarini ushbu

𝜕𝑢

𝑝 ∙

𝜕𝑡

= 𝑑𝑖𝑣(𝑝∇𝑢) − 𝑞 ∙ 𝑢 + 𝐹(𝑥, 𝑡)                                                       (10)

tenglamani tavsiflaydi.

Statsionar jarayonlarni ushbu

−𝑑𝑖𝑣(𝑝∇𝑢) + 𝑞 ∙ 𝑢 = 𝐹(𝑥)                                                                             (11)

tenglama tavsiflaydi.

𝐺 ⊂ 𝑅^𝑛 jarayon sodir bo'ladigan maydon, 𝑆 maydonning chegarasi 𝐺 bo'lsin. Uni bo'lakli silliq sirt deb hisoblaymiz. Demak, 𝐺 − 𝑥 (11) tenglamada argumentning aniqlanish sohasi, ya'ni bu tenglama berilgan soha. (9) va (10) tenglamalar berilgan soha Π_𝑇 = 𝐺 × (0, 𝑇) - balandligi 𝑇, asosi 𝐺 boʻlgan silindr boʻlsin. Uning chegarasi pastki yon yuzadan 𝑆 × [0, 𝑇] va

ikkita asosdan iborat: 𝐺̅ ×  {0} va yuqori

̅𝐺

× {𝑇}. Faraz qilamizki, (9)-(11) tenglamalarda

𝜌, 𝑝, 𝑞 koeffitsientlar 𝑡 vaqtga bog'liq emas (2-rasm).

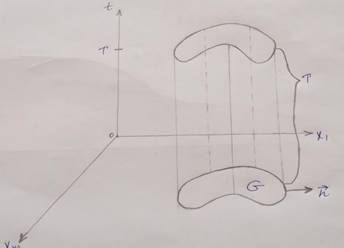
2-                                                                                                                                                     rasm

Keyinchalik, bu miqdorlarning fizik ma'nosiga muvofiq, 𝜌(𝑥) > 0, 𝑝(𝑥) > 0, 𝑞(𝑥) ≥ 0, 𝑥 ∈ 𝐺̅ deb faraz qilamiz. Matematik ma'noga ega deb 𝜌 ∈ 𝐶(𝐺̅), 𝑝 ∈ 𝐶¹(𝐺̅), 𝑞 ∈ 𝐶(𝐺̅) faraz qilishimiz kerak. Bizning tasnifimizga ko’ra, (9) tebranish tenglamasi giperbolik, (10) diffuziya tenglamasi parabolik, (11) tenglama esa elliptik tipda tegishli. Bu tenglamalarning turlarining farqi ular tasvirlaydigan fizik jarayonlar bilan chambarchas bog'liq. U yoki bu fizik jarayonni to‘liq tavsiflash uchun tenglamaga qo‘shimcha ravishda ushbu jarayonning dastlabki holatini va jarayon sodir bo'lgan hududning chegarasida rejimini ham ko‘rsatish kerak. Matematik jihatdan

bu differensial tenglamalar uchun yechimning o'ziga xos emasligi bilan bog'liq. Xususiy hosilali differensial tenglamalar uchun yechim odatda ixtiyoriy funksiyalarga bog'liq.

Masalan, ^𝜕𝑢 (𝑥, 𝑦) = 0 tenglamaning umumiy yechimi (bu yerda 𝐺 = (0, 1) × (0, 1))

𝜕𝑥

𝑢(𝑥, 𝑦) = 𝑓(𝑦) koʻrinishga ega, bu yerda 𝑓(𝑦) funksiya 𝐶¹([0,1]) sinfga tegishli.

Shuning uchun, haqiqiy jismoniy jarayonni tavsiflovchi yechimni ajratib olish uchun, qo'shimcha shartlar belgilanishi kerak. Ushbu qo'shimcha shartlar va chegara shartlari: boshlang'ich shartlar va chegara shartlariga muvofiq vazifa chegaraviy masala deb ataladi.

Differensial tenglamalar uchun chegaraviy masalalarning uch turi mavjud.

a) Giperbolik va parabolik tipdagi tenglamalar uchun Koshi masalasi; b) Elliptik tipdagi tenglamalar uchun chegaraviy masala; c) Giperbolik va parabolik tipdagi tenglamalar uchun aralash masala: ham boshlang‘ich, ham chegaraviy shartlar. Tebranish tenglamasi (12) (giperbolik tip) uchun Koshi masalasi quyidagicha beriladi: {𝑡 > 0} yarim fazoda (12) tenglamani va 𝑡 = +0 da quyidagi boshlang‘ich shartlarni qanoatlantiruvchi

𝑢(𝑥, 0) = 𝑢

𝜕𝑢

(𝑥),            (𝑥, 0) = 𝑢

(𝑥),        𝑥 ∈ 𝑅^𝑛,                                             (12)

0                     𝜕𝑡                        1

𝐶²(t > 0) ∩ C(t ≥ 0) sinfdagi 𝑢(𝑥, 𝑡) funksiyani toping, bunda 𝐹 ∈ 𝐶(𝑡 > 0), 𝑢₀ ∈ 𝐶¹(𝑅^𝑛),

𝑢₁ ∈ 𝐶(𝑅^𝑛).

Diffuziya tenglamasi (10) (parabolik tip) uchun Koshi masalasi quyidagicha qo’yilgan:

{𝑡 > 0} yarim fazoda (10) tenglamani va 𝑡 = +0 da boshlang'ich shart qanoatlantiruvchi

𝑢(𝑥, 0) = 𝑢₀(𝑥),             𝑥 ∈ 𝑅^𝑛                                                                                      (13)

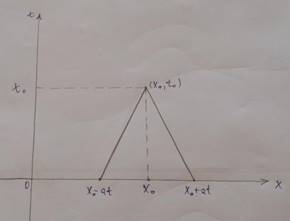
𝐶²(𝑡 > 0) ∩ 𝐶(𝑡 ≥ 0) sinfidagi 𝑢(𝑥, 𝑡) funksiyani toping, bunda 𝐹 ∈ 𝐶(𝑡 > 0), 𝑢₀(𝑥) ∈ 𝐶(𝑅^𝑛). (𝑥, 𝑡)   tekislikdadagi                 (𝑥₀, 𝑡₀) oʻzgarmas nuqta boʻlsin. U holda tor tenglamasi

yechimining shu nuqtadagi qiymati (𝑥 o'qida 𝑥₀ − 𝑎𝑡, 𝑥₀ + 𝑎𝑡 nuqtalar belgilangan)

𝑢(𝑥₀ + 𝑎𝑡, 0) + 𝑢(𝑥₀ − 𝑎𝑡, 0)              1

𝑥0+𝑎𝑡 𝜕𝑢

𝑢(𝑥₀, 𝑡₀) =

+         ∫

2                                      2𝑎     𝑥0−𝑎𝑡

(𝑦, 0)𝑑𝑦.

𝜕𝑡

va ularni (𝑥₀, 𝑡₀) nuqta bilan segmentlar bo'yicha bog'laymiz.

Bu chiziqlar torning erkin tebranish tenglamasining xarakteristikasidir. Dalamber formulasidan nuqtadagi eritmaning qiymati (𝑥₀, 𝑡₀) faqat [𝑥₀ − 𝑎𝑡, 𝑥₀ + 𝑎𝑡] oraliqdagi boshlangʻich funksiyalarning qiymatlariga bogʻliq boʻlib, u (𝑥₀, 𝑡₀) nuqtadan oʻtuvchi xarakteristikalar orqali absissa oʻqidan 𝑥 uzilib qoladi. Bu yechimda tekislikning chegarasi dastlabki ma'lumotlarga bog'liq. Dalamber formulasiga boshqa tomondan yondashamiz. 𝜙(𝑥) va

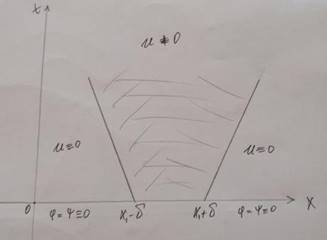
𝜓(𝑥) funksiyalari faqat [𝑥₁ − 𝛿, 𝑥₁ + 𝛿] segmentda noldan farqli bo’lsin.

Savol: {(𝑥, 𝑡), 𝑡 ≥ 0} yarim tekislikning qayerida yechim noldan farq qiladi?

Dalamber formulasidan kelib chiqadiki, yechim 𝑥 − 𝑥₁ − 𝛿 − 𝑎𝑡 = 0 xarakteristikasining o‘ng tomonida va 𝑥 − 𝑥₁ + 𝛿 + 𝑎𝑡 = 0 xarakteristikasining chap tomonida xuddi shunday nolga teng bo‘ladi. Boshqacha aytganda, tebranish xarakteristikalar bo'yicha 𝑎 tezlik bilan tarqaladi. Bu buzilishning tarqalish tezligi chekli ekanligini anglatadi (3-rasm).

(3-rasm)

Tor tenglamasining umumiy yechimining yana bir muhim talqini bor:

𝑢(𝑥, 𝑡) = 𝑓₁(𝑥 − 𝑎𝑡) + 𝑓₂(𝑥 + 𝑎𝑡),

bunda 𝑓₁(𝑥 − 𝑎𝑡) funksiyasi 𝑥 o‘qi bo‘ylab 𝑎 tezlik bilan o‘ngga o‘tadigan to‘lqinni bildiradi.

𝑓₂(𝑥 + 𝑎𝑡) funksiyasi 𝑎 tezlik bilan chapga bir xil harakatlanuvchi to‘lqin. Demak, har qanday yechim turli yo‘nalishlarda 𝑎 tezlik bilan harakatlanuvchi ikki to‘lqin yig‘indisidir (4-rasm).

4-                                                                                                                                                     rasm

Tor tebranishlarining bir jinsli bo'lmagan tenglamasi uchun Koshi masalasini ko'rib chiqamiz. Bizga 𝑓(𝑥, 𝑡) ∈ 𝐶¹ (𝑅 × 𝑅₊) funksiya berilgan

𝜕²𝑢

𝜕𝑡²

𝜕²𝑢

= 𝑎²         + 𝑓(𝑥, 𝑡),        𝑥 ∈ 𝑅, 𝑡 ≥ 0,                                                  (14)

𝜕𝑥²

𝑢(𝑥, 0) = 𝜑(𝑥),

𝜕𝑢

𝜕𝑡

(𝑥, 0) = 𝜓(𝑥),        𝑥 ∈ 𝑅.                               (15)

(1) va (2) masalalarni quyidagi ko’rinishda ifodalab tekshirish mumkin

𝑢(𝑥, 𝑡) = 𝑣(𝑥, 𝑡) + 𝑤(𝑥, 𝑡),                                                                              (16)

bu yerda 𝑣(𝑥, 𝑡) − berilgan 𝜙, 𝜓, 𝑓 ≡ 0 bilan Koshi masalasini (14), (15) yechimi va 𝑤(𝑥, 𝑡) funksiyasi Koshi masalasini (14), (15) ma’lumotlar bilan yechish 𝜙 ≡ 0, 𝜓 ≡ 0, 𝑓(𝑥, 𝑡):

𝜕2𝑤 = 𝑎² 𝜕2𝑤 + 𝑓(𝑥, 𝑡),

𝜕𝑡2                        𝜕𝑥2

𝑤(𝑥, 0) = 0,        𝜕𝑤 (𝑥, 0) = 0.                                                                 (17)

𝜕𝑡

𝑤 (𝑥, 𝑡) funksiya Dalamber formulasi yordamida tuziladi va uning yechimi:

1       𝑡            𝑥+𝑎(𝑡+𝑟)

𝑤(𝑥, 𝑡) =           ∫  [∫                    𝑓(𝜉, 𝑟)𝑑𝜉] 𝑑𝑟.

2𝑎 0

𝑥−𝑎(𝑡−𝑟)

Umumiy to'lqin tenglamasi uchun (18) formulani keyinroq chiqaramiz, ammo hozircha bu formula (17) muammoning yechimini aniqlab berishiga ishonch hosil qilamiz. Darhaqiqat,

𝑤(𝑥, 0) ≡ 0 shartni qanoatlantirilishi aniq. 𝑡 va 𝑥 ga nisbatan xususiy hosilalarni topamiz:

𝜕𝑤

𝜕𝑡

= 0 +

1

2𝑎

𝑡

∫ [𝑎𝑓(𝑥 + 𝑎(𝑡 − 𝑟), 𝑟) + 𝑎𝑓(𝑥 − 𝑎(𝑡 − 𝑟), 𝑟]𝑑𝑟,

0

𝜕²𝑤

𝑎      𝑡

𝜕𝑓

𝜕𝑓

𝜕𝑤

𝜕𝑥

1

= 2𝑎

𝑡

∫ [𝑓(𝑥 + 𝑎(𝑡 − 𝑟), 𝑟) − 𝑓(𝑥 − 𝑎(𝑡 − 𝑟), 𝑟]𝑑𝑟,

0

𝜕²𝑤

1       𝑡

𝜕𝑓

𝜕𝑓

Bulardan kelib chiqib shuni xulosa qilamizki,

𝜕𝑤

𝜕𝑡

(𝑥, 0) = 0,

𝜕²𝑤

𝜕𝑡²

𝜕²𝑤

− 𝑎²          = 𝑓(𝑥, 𝑡).

𝜕𝑥²

Formula (18) biroz sun'iy tuyulishi mumkin, ammo u Dyuamel printsipi yordamida shaffof

asosga ega. 𝑓 ∈ 𝐶¹ bo'lishi sharti bilan bir jinsli bo'lmagan (14), (15) masalani yechish uchun mavjudlik teoremasi isbotlandi. Har doimgidek chiziqli masalalarda o'ziga xoslik 𝑓 ≡ 0 bilan bir jinsli masalani isbotlash uchun yetarli.

Agar   𝑢(𝑥, 𝑦) −      funksiya      ikkita      erkli      o'zgaruvchili      funksiya      bo’lib,

𝑎₁₁, 𝑎₁₂, 𝑎₂₂, 𝑎, 𝑏, 𝑐, 𝑓 − 𝑥, 𝑦 o’zgaruvchili funksiyalar berilganlar bo’lsa, u holda bunday tenglamalar xususiy hosilali differensial tenglamalar deyiladi.

𝑎₁₁𝑢_𝑥𝑥 + 2𝑎₁₂𝑢_𝑥𝑦 + 𝑎₂₂𝑢_𝑦𝑦 + 𝑎𝑢_𝑥 + 𝑏𝑢_𝑦 + 𝑐𝑢 = 𝑓(𝑥, 𝑦),                                  (19)

ikkinchi tartibli chiziqli xususiy hosilali differensial tenglama deyiladi.

Agar 𝑎₁₁, 𝑎₁₂, 𝑎₂₂, 𝑎, 𝑏, 𝑐, 𝑓 − funksiyalar faqat 𝑥 va 𝑦 o'zgaruvchilarga emas, balki 𝑢

funksiyaga ham bog'liq bo'lsa, (1) tenglama kvazichiziqli deb ataladi.

𝑎₁₁𝑑𝑦² − 2𝑎₁₂𝑑𝑥𝑑𝑦 + 𝑎₂₂𝑑𝑥² = 0                                         (20)

yuqoridagi (20) ko’rinishdagi tenglama xarakteristik tenglama deyiladi.

𝜑(𝑥, 𝑦) = 𝐶        tenglama  bilan  tasvirlangan  egri  chiziq,          𝜑 − bu yerda (20) tenglamaning yechimi, (19) tenglamaning xarakteristikasi deyiladi.

E'tibor berish kerakki,

𝜑(𝑥, 𝑦) = 𝐶         →       𝑑𝜑  = 𝜑_𝑥

𝑑𝑥 + 𝜑_𝑦

𝜑_𝑥

𝑦

xarakteristik tenglamani (20) quyidagicha ifodalash ham mumkin:

𝑎₁₁𝜑_𝑥𝑥 + 2𝑎₁₂𝜑_𝑥𝜑_𝑦 + 𝑎₂₂𝜑_𝑦𝑦 = 0.                                                         (21)

𝑎₁₁𝑑𝑦 − (𝑎₁₂ + √𝑎²₁₂ − 𝑎₁₁𝑎₂₂) 𝑑𝑥 = 0,                                               (22)

𝑎₁₁𝑑𝑦 − (𝑎₁₂ − √𝑎²₁₂ − 𝑎₁₁𝑎₂₂) 𝑑𝑥 = 0.                                               (23)

𝜑(𝑥, 𝑦) = 𝐶₁ 𝑣𝑎 𝜓(𝑥, 𝑦) = 𝐶₂ bu tenglamalarning umumiy integrallari haqiqiydir va (1) tenglama xarakteristikasining ikki xil turkumini belgilaydi.

O'zgaruvchilarning shakl almashinishi

𝜉 = 𝜑(𝑥, 𝑦),            𝜂 = 𝜓(𝑥, 𝑦)                                                                      (24)

giperbolik tipdagi tenglamani kanonik shaklga keltiradi:

𝑢_𝜉𝑦 + 𝑎₁𝑢_𝜉 + 𝑏₁𝑢_𝑦 + 𝑐₁𝑢 = 𝑑₁,                                                                   (25)

bu yerda 𝑎₁, 𝑏₁, 𝑐₁𝑑₁ − 𝜉 va 𝜂 funksiyalarning o’zgaruvchilari.

Endi bir nechta tipik misollarni yechib ko’rsatamiz.

Masala 1. Tenglamani xarakteristik tenglamasi va yechimini toping: 𝑎²𝑢_𝑥𝑥 − 𝑢_𝑦𝑦 = 0.

Yechish. Xarakteristik tenglamaning ko’rinishi quyidagicha: 𝑎²𝑑𝑦² − 𝑑𝑥² = 0.

Bu tenglamaning umumiy integrallari tenglik bilan aniqlanadi: 𝑥 = ±𝑎𝑦 + 𝑐𝑜𝑛𝑠𝑡.

O'zgaruvchilarning almashtirsak, 𝜉 = 𝑥 + 𝑎𝑦, 𝜂 = 𝑥 − 𝑎𝑦 ko'rib chiqilgan tenglamani kanonik shaklga keltiramiz: 𝑢_𝜉𝑦 = 0.

Tenglamaning umumiy yechimi quyidagicha bo’ladi:

𝑢(𝜉, 𝜂) = 𝑓₁(𝜉) + 𝑓₂(𝜂), ⇒ 𝑢(𝑥, 𝑦) = 𝑓₁(𝑥 + 𝑎𝑦) + 𝑓₂(𝑥 − 𝑎𝑦) Masala 2. Tenglamani tipini aniqlang: 𝑢_𝑥𝑥 + 2𝑢_𝑥𝑦 − 3𝑢_𝑦𝑦 + 𝑢_𝑥 + 𝑢_𝑦 = 0. Yechish. Bu giperbolik tipdagi tenglamaga kiradi, chunki u

𝑎² − 𝑎₁₁𝑎₂₂ = 1 + 1 ∗ 3 = 4 > 0.

Masala 3. Oldingi misol shartlarida tenglamani kanonik shaklga keltiring.

Yechish. Giperbolik tenglamaning xarakteristik tenglamasi ikkita tenglamaga bo'linadi:

𝑑𝑦 − 3𝑑𝑥 = 0, 𝑑𝑦 + 3𝑑𝑥 = 0.

Ushbu     tenglamalarning      umumiy     integrallari:      3𝑥 − 𝑦 = 𝐶₁, 3𝑥 + 𝑦 = 𝐶₂.           Yangi o’zgaruvchi kiritsak: 𝜉 = 3𝑥 − 𝑦,                 𝜂 = 3𝑥 + 𝑦. U holda:

𝑢_𝑥 = 𝑢_𝜉𝜉_𝑥 + 𝑢_𝑦𝜂_𝑥 = 3𝑢_𝜉 + 3𝑢_𝑦,                   (𝜉_𝑥 = 3,          𝜂_𝑥 = 3),

𝑢_𝑦 = 𝑢_𝑦𝜉_𝑦 + 𝑢_𝑦𝜂_𝑦 = −𝑢_𝜉 + 𝑢_𝑦,                   (𝜉_𝑦 = −1,         𝜂_𝑦 = 1),

𝑢_𝑥𝑥 = 3(𝑢_𝜉 + 𝑢_𝑦)𝜉𝜉_𝑥 + 3(𝑢_𝜉 + 𝑢_𝑦)𝑦𝜂_𝑥 = 9𝑢_𝜉𝜉 + 18𝑢_𝜉𝑦 + 9𝑢_𝑦𝑦𝑢_𝑥𝑦 = 3(𝑢_𝜉 + 𝑢_𝑦)𝜉𝜉_𝑦 + 3(𝑢_𝜉 + 𝑢_𝑦)𝑦𝜂_𝑦 = −3𝑢_𝜉𝜉 + 3𝑢_𝑦𝑦,

𝑢_𝑦𝑦 = (−𝑢_𝜉 + 𝑢_𝑦)_𝜉𝜉_𝑦 + (−𝑢_𝜉 + 𝑢_𝑦)_𝑦𝜂_𝑦 = 𝑢_𝜉𝜉 − 4𝑢_𝜉𝑦 + 𝑢_𝑦𝑦.

Yangi o'zgaruvchili tenglama giperbolik tipdagi kanonik tenglama shaklini oladi:

15u_𝜉𝑦 + 𝑢_𝜉 + 2𝑢_𝑦 = 0.

Xususiy hosilali differensial tenglama tekshirilayotgan sohaning bir qismida elliptik tipga, ikkinchi qismida esa giperbolik tipga tegishli bo’lsa, temglama aralash tipga tegishli deyiladi; bu qismlar o’tish chizig’i (yoki sirti) bilan ajraladi, bu chiziqda tenglama yoki parabolik buziladi, toki aniqlanmagan bo’ladi. Aralash tipdagi tenglama uchun chegaraviy masalani XX asrning 20-yillarida birinchi martta Italiyalik matematik Franchesko Trikomi

𝑦𝑢_𝑥𝑥 + 𝑢_𝑦𝑦 = 0

tenglama uchun qo’ygan va tekshirgan.

Biz bu bobda umumlashgan Trikomi

𝑠𝑖𝑔𝑛𝑦|𝑦|^𝑚𝑢_𝑥𝑥 + 𝑢_𝑦𝑦 = 0 , 𝑚 = 𝑐𝑜𝑛𝑠𝑡 > 0                                             (27) teglamasini o’rganamiz.

Bu tenglama 𝑦 = 0 o’qining ixtiyoriy qismini o’z ichiga olgan sohada aralash tipga

tegishli bo’ladi, ya’ni 𝑦 > 0 yarim tekislikda elliptik, 𝑦 < 0 da giperbolik bo’lib, 𝑦 = 0 da parabolik buziladi. 𝑚 = 0 bo’lganda (1) tenglama 𝑠𝑖𝑔𝑛𝑦𝑢_𝑥𝑥 + 𝑢_𝑦𝑦 = 0 ko’rinishga ega bo’ladi.

Bu tenglamani aralash tipdagi tenglamalarning eng sodda vakili sifatida o’rganishni akdemik M.A.Lavrentev tavsiya qilgan va uning uchun turli masalalarni akademik A.V.Bisadze tekshirgan. Shuning uchun ham bu tenglama Lavrentev – Bisadze tenglamasi deyiladi.

𝑦 < 0 yarim tekislikda (27) tenglama giperbolik tipga tegishli:

−(−𝑦)^𝑚𝑢_𝑥𝑥 + 𝑢_𝑦𝑦 = 0.                                                                                                (28)

Koshi masalasining qo’yilishi. Bizning asosiy maqsadimiz (28) tenglama uchun boshlang’ich shartlar parabolik buzilish chizig’ida berilganda Koshi masalasini o’rganishdir:

(28) tenglamaning 𝑦 < 0 da o’zining ikkinchi tartibgacha hosilalari bilan uzluksiz bo’lgan va

𝑦 = 0 da o’qning biror qismida, masalan, 𝐴(−1,0) 𝐵(1,0) kesmada

lim 𝑢(𝑥, 𝑦) = 𝑟(𝑥),                                                                                                      (29)

𝑦→0

lim

𝜕𝑢

= 𝑣(𝑥).                                                                                                         (30)

𝑦→0 𝜕𝑦

Shartlarni qanoatlantiruvchi 𝑢(𝑥, 𝑦) yechimi topilsin, bu yerda 𝑟(𝑥) va 𝑣(𝑥) – berilgan funksiyalar o’zlarining ikkinchi tartibgacha hosilalari bilan uzluksizdir. (2) tenglama

𝜉 = 𝑥 −

2

𝑚 + 2

(−𝑦)

𝑚+2

2   , 𝜂 = 𝑥 +

2

𝑚 + 2

(−𝑦)

𝑚+2

2                                          (31)

xarakteristik koordinatalarda ushbu

𝜕²𝑢

𝑚               1

𝜕𝑢

𝑚              1

𝜕𝑢

𝜕𝜉𝜕𝜂 − 2(𝑚 + 2) 𝜉 − 𝜂  𝜕𝜉 + 2(𝑚 + 2) 𝜉 − 𝜂 𝜕𝜂 = 0                             (32)

ko’rinishda yoziladi. (6) tenglama Eyler-Darbu tenglamasi deb ataluvchi

𝜕²𝑢

𝛼      𝜕𝑢

𝛽      𝜕𝑢

𝜕𝜉𝜕𝜂 − 𝜉 − 𝜂 𝜕𝜉 + 𝜉 − 𝜂 𝜕𝜂 = 0.                                                                     (33)

tenglamaning xususiy holidir, bu yerda 𝛼, 𝛽 – ixtiyoriy o’zgarmaslar.

(31) almashtirish 𝑦 < 0 da maxsus bo’lmagan almashtirishdir, shu bilan birga (31) 𝑦 < 0

yarim tekislikka 𝜂 > 𝜉 yarim tekislikni mos qo’yadi. 𝑦 = 0 to’g’ri chiziq, ya’ni 𝜂 − 𝜉 = 0, bu

4                        𝑚+2

𝜕𝑢

𝑚  𝜕𝑢

𝜕𝑢

almashtirishning     maxsus    chizig’idir.     Ushbu    −𝜉 =

𝑚

𝑚+2

(−𝑦)

2    ,

𝜕𝑦

= (−𝑦) 2 (

𝜕𝜉

−       ) =

𝜕𝑦

(

)𝑚+2

𝑚

(𝜂 − 𝜉)𝑚+2   (

𝜕𝑢 −

). (3), (4) boshlang’ich shartlar   lim

𝑢(𝜉, 𝜂) = 𝑟(𝜉),

4                                                                 𝜕𝜉

𝜕𝑦

𝑦→𝜉→0

lim

𝑦→𝜉→0

ko’rinishda yoziladi.

𝑚 + 2 (             )

4

   𝑚

𝑚+2

   𝑚

(𝜂 − 𝜉)𝑚+2 (

𝜕𝑢

𝜕𝜉

𝜕𝑢

− 𝜕𝜂

) = 𝑣(𝜉)                          (34)

Bizga ma’lumki, (33) Eyler-Darbu tenglamasini Riman funksiyasi R(𝜉, 𝜂; 𝜉₁, 𝜂₁) ushbu

𝜕²𝑅

𝛼     𝜕𝑅

𝛽      𝜕𝑅

𝛼 + 𝛽

𝜕𝜉𝜕𝜂 + 𝜉 − 𝜂 𝜕𝜉 − 𝜉 − 𝜂 𝜕𝜂 − (𝜉 − 𝜂)² 𝑅 = 0                                     (35)

qo’shma differensial tenglamani qanoatlantiradi va 𝜉 = 𝜉_1, 𝜂 = 𝜂₁ xarakteristikalarda

𝜉 𝛽𝑑𝑡

𝜉 − 𝜂       ^𝛽

𝑅(𝜉, 𝜂

; 𝜉 , 𝜂

) = 𝑒∫𝜉1𝑡−𝑦1  = (            1 )

(36)

1          1

qiymatlarni qabul qiladi.

1

𝜉₁ − 𝜂₁

 𝜉 − 𝜂₁ ^𝛽

𝐹|_𝜉=𝜉1 ,             𝑅(𝜉, 𝜂₁; 𝜉₁, 𝜂₁) = (𝜉

)

− 𝜂₁

𝐹|𝑦=𝑦1 .

Bu tengliklardan (36) ga asosan ko’rinyaptiki, 𝐹|_𝜉=𝜉1 = 𝐹|_𝑦=𝑦1 = 1 bo’lishi kerak. Bir qator hisoblashlardan so’ng, quyidagi tenglamani hosil qilamiz:

𝜎(1 − 𝜎)𝐹_𝜎𝜎 + [1 − (𝑎 + 𝑏 + 1)𝜎]𝐹_𝜎 − 𝛼𝛽𝐹 = 0.                                  (37)

bunda 𝜎 = (𝜉−𝜉1)(𝑦−𝑦1).

(𝜉1−𝑦)(𝜉−𝑦1)

(37) tenglama Gauss tenglamasi bo’lib, uning yechimi gipergeometrik funksiya bo’ladi:

𝐹(𝛼, 𝛽, 1, 𝜎) = 𝐹 (𝛼, 𝛽, 1, (𝜉1−𝜉)(𝑦−𝑦1)). 𝐹|

(𝜉1−𝑦)(𝜉−𝑦1)

𝜉=𝜉1

= 𝐹|

𝑦=𝑦1

= 1 bo’lishidan quyidagi topamiz:

   𝑚

      𝑚

−

𝑚                𝑚

(𝜉1−𝜉)(𝑦−𝑦1)

𝑅(𝜉, 𝜂; 𝜉₁, 𝜂₁) == (𝜉 − 𝜂)𝑚+2[(𝜉 − 𝜂₁)(𝜉₁ − 𝜂)]

2(𝑚+2) ∗ 𝐹 (

,

2𝑚+4

2𝑚+4

, 1,

).

(𝜉1−𝑦)(𝜉−𝑦1)

Yuqorida aytilganidek, 𝜂 − 𝜉 = 0 to’g’ri chiziq (31) almashtirish uchun maxsus chiziqdir, ya’ni bu chiziqda (32) tenglamaning koeffisientlari cheksizlikka intiladi. Shu bilan birga, 𝜉 ≥ 𝜂 + 𝜀 yarim tekislikda, bu yerda 𝜀- ixtiyoriy musbat son, (32) tenglama uchun Koshi masalasi, biz yuqorida ko’rganimizdek, oddiy usul bilan yechiladi, Koshi masalasi, boshlang’ich shartlar 𝑦 = 0 parabolik buzilish chizig’ida berilganda maxsus tekshirishni talab qiladi.

𝐷 orqali 𝜉 = 𝜂 + 𝜀, 𝜀 > 0 chiziqning 𝑄(𝜂₁ + 𝜀, 𝜂₁)𝑄₁(𝜉₁, 𝜉₁ − 𝜀) kesmasi va (32) ning

𝑄𝑃: 𝜂 = 𝜂₁. 𝑄₁𝑃: 𝜉 = 𝜉₁ xarakteristikalari bilan chegaralangan sohani belgilaymiz (5-rasm).

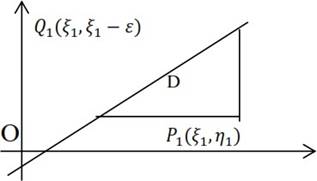5- rasm

(32) tenglama uchun Koshi masalasi yechimi quyidagicha (Салохитдинов М.С. Математик физика тенгламалари, Тошкент, «Ўзбекистон, 448 б.»):

   𝑚    

  Γ (𝑚 + 2)

   2              1

𝑚+2

2                  𝑚+2

 𝑚+4

2 −

𝑢(𝑥, 𝑦) =

     𝑚      2

2𝑚 + 4

∫   𝑟 [𝑥 +                  (−𝑦)

−1                        𝑚 + 2

2    𝑡] (1 − 𝑡 )

2𝑚+4𝑑𝑡 +

𝑚 + 4

   ₂     Γ (𝑚 + 2)            1

2                  𝑚+2

    𝑚

2 −

2𝑚+2

2       𝑚 + 4 2𝑚 + 4

𝑦 ∫   𝜈 [𝑥 +                   (−𝑦)

2    𝑡] (1 − 𝑡 )

2𝑚+4𝑑𝑡

(38)

formula hosil qilamiz. (38) formula Darbu formulasi deyiladi.

MUHOKAMA

Yuqorida aytib o‘tilganidek, oddiy va xususiy hosilali differensial tenglamalar nazariyasining paydo bo‘lishi XVIII asrlarga borib taqaladi. Aksariyat jarayonlarning (fizik, biologik, mexanik, kimyoviy, iqtisodiy, ekologik va shu kabilarning) matematik modellari oddiy va xususiy hosilali differensial tenglamalar [1-16] orqali ifodalanadi.

Mazkur maqolada olib borilgan ilmiy izlanishlar yo’nalishida boshqa mualliflar tomonidan ham bir qator maqolalar [17-53] chop qilingan. Ushbu maqolalarda xususiy hosilali differensial tenglamalar, xususan aralash tipga tegishli tenglamalar o‘rganilgan. Energiya integrali, integrallar nazariyasi, ketma-ket yaqinlashish, prinsipi, singulyar integral tenglamalar nazariyasi, potensiallar nazariyasi, maxsus funksiyalar – Eylerning Gamma va Beta funksiyalari, Riman funksiyasi, gipergeometrik funksiyalar, Arsel teoremasi, Dyuamel va Shauder prinsiplari, Vishik lemmasi, birinchi tartibli xususiy hosilali differensial tenglamalar nazariyasi, chiziqli fazolar, ortogonal funksiyalar va ularni ortonormallashtirish jarayonidan keng foydalanilgan.

XULOSA

Ushbu mavzu va boshqa maxsus fanlarni o‘qitishda interfaol usullarni [54-57] qo‘llash tavsiya qilingan bo‘lib, ularda bir qator uslubiy tavsiyalar berilgan. O‘z navbatida talabalar tomonidan nazariy va amaliy mashg‘ulotlarda ilg‘or pedagogik texnologiyalarni qo‘llash ijobiy baholangan. Chunki interfaol usullar talabalarni ijodiy fikrlashga va izlanishga undaydi. Mavzuni oson tushunishlariga qulaylik tug‘diradi.

REFERENCES

1.        Raupova, M. (2021). Роль математики в биологических науках. Центр научных публикаций (buxdu.Uz), 5(5).

2.        Raupova, M. (2021). Математические модели и законы в биологии. Центр научных публикаций (buxdu.Uz), 5(5).

3.        Расулов Х.Р. О некоторых символах математического анализа // Science and Education, scientific journal, 2:11 (2021), p.66-77.

4.        Расулов Х.Р. О понятие асимптотического разложения и ее некоторые применения // Science and Education, scientific journal, 2:11 (2021),  pp.77-88.

5.        Расулов Х.Р., Раупова М.Х. Яшиева Ф.Ю. Икки жинсли популяция ва унинг математик модели ҳақида // Science and Education, scientific journal, 2:10 (2021), р.81- 96.

6.        Расулов Х.Р., Яшиева Ф.Ю. Икки жинсли популяциянинг динамикаси ҳақида // Scientific progress, 2:1 (2021), р.665-672.

7.        Расулов Х.Р., Камариддинова Ш.Р. Об анализе некоторых невольтерровских динамических систем с непрерывным временем // Наука, техника и образование, 77:2- 2 (2021) с.27-30.

8.        Rasulov X.R., Qamariddinova Sh.R. Ayrim dinamik sistemalarning tahlili haqida // Scientific progress, 2:1 (2021), р.448-454.

9.        Расулов Х.Р., Джуракулова Ф.М. Об одной динамической системе с не-прерывным временем // Наука, техника и образование, 77:2-2 (2021) с. 19-22.

10.    Расулов Х.Р., Ф.М. Джуракулова (2021). Баъзи динамик системаларнинг сонли ечимлари ҳақида // Scientific progress. 2:1, 455-462 бетлар.

11.    Расулов Х.Р., Яшиева Ф.Ю. О некоторых вольтерровских квадратичных стохастических операторах двуполой популяции с непрерывным временем // Наука, техника и образование, 77:2-2 (2021) с.23-26.

12.    Расулов Х.Р., Яшиева Ф.Ю. Об одном квадратично стохастическом операторе с непрерывным временем // «The XXI Century Skills for Professional Activity» International Scientific-Practical Conference, Tashkent, mart 2021 y., p.145-146.

13.    Расулов Х.Р., Камариддинова Ш.Р. Об одной динамической системе с непрерывным временем // «The XXI Century Skills for Professional Activity» International Scientific- Practical Conference, Tashkent, mart 2021 y., p.115-116.

14.    Rasulov Kh.R., Sayfullayeva Sh.Sh. Analysis of Some Boundary Value Problems for Mixed-Type Equations with Two Lines of Degeneracy // Irish Interdisciplinary Journal of Science & Research (IIJSR), 6:2 (2022), p. 8-14. DOI: http://doi.org/10.46759/IIJSR.2022.6202.

15.    Расулов Х.Р., Раупова М.Х. Роль математики в биологических науках // Проблемы педагогики, № 53:2 (2021), с. 7-10.

16.    Расулов Х.Р., Раупова М.Х. Математические модели и законы в биологии // Scientific progress, 2:2 (2021), р.870-879.

17.    Rasulov Kh.R. (2018). On a continuous time F - quadratic dynamical system // Uzbek Mathematical Journal, №4, pp.126-131.

18.    Расулов Х.Р. (1996). Задача Дирихле для квазилинейного уравнения эллиптического типа с двумя линиями вырождения // ДАН Республики Узбекистан, №12, с.12-16.

19.    Исломов Б., Расулов Х.Р. (1997). Существование обобщенных решений краевой задачи для квазилинейного уравнения смешанного типа с двумя линиями вырождения

// ДАН Республики Узбекистан, №7, с.5-9.

20.    Расулов Х.Р., Собиров С.Ж. Задача типа задач Геллерстедта для одного уравнения смешанного типа с двумя линиями вырождения // Scientific progress, 2:1 (2021), р.42- 48.

21.    Расулов Х.Р. Об одной нелокальной задаче для уравнения гиперболического типа // XXX Крымская Осенняя Математическая Школа-симпозиум по спектральным и эволюционным задачам. Сборник материалов международной конференции КРОМШ- 2019, c. 197-199.

22.    Расулов Т.Ҳ., Расулов Х.Р. (2021). Ўзгариши чегараланган функциялар бўлимини ўқитишга доир методик тавсиялар. Scientific progress. 2:1, 559-567 бетлар.

23.    Салохитдинов М.С., Расулов Х.Р. (1996). Задача Коши для одного квазилинейного вырождающегося уравнения гиперболического типа // ДАН Республики Узбекистан,

№4, с.3-7.

24.    Rasulov H. KD problem for a quasilinear equation of an elliptic type with two lines of degeneration // Journal of Global Research in Mathematical Archives. 6:10 (2019), р.35-38.

25.    Расулов Х.Р., Рашидов А.Ш. О существовании обобщенного решения краевой задачи для нелинейного уравнения смешанного типа // Вестник науки и образования, 97:19-1 (2020), С. 6-9.

26.    Расулов Х.Р. и др. О разрешимости задачи Коши для вырождающегося квазилинейного уравнения гиперболического типа // Ученый XXI века. 53:6-1, 2019. С.16-18.

27.    Rasulov, X. (2022). Об одной динамическойсистеме с непрерывным временем. Центр научных публикаций (buxdu.Uz), 22(22).

28.    Rasulov, R. X. R. (2022). Buzilish chizig’iga ega kvazichiziqli elliptik tenglama uchun Dirixle-Neyman masalasi. Центр научных публикаций (buxdu.Uz), 18(18), https://journal.buxdu.uz/index.php/journals_buxdu/article/view/7328.

29.    Rasulov, R. X. R. (2022). Иккита перпендикуляр бузилиш чизиғига эга бўлган аралаш типдаги тенглама учун чегаравий масала ҳақида. Центр научных публикаций (buxdu.Uz), 22(22), https://journal.buxdu.uz/index.php/journals_buxdu/article/view/7996.

30.    Rasulov X.R. Sayfullayeva Sh.Sh. Buzilish chizig’iga ega bo’lgan elliptik tipdagi tenglamalar uchun qo’yiladigan chegaraviy masalalar haqida // Science and Education, scientific journal, 3:3 (2022), р.46-54.

31.    Rasulov X.R., Sayfullayeva Sh.Sh. Ikkita buzilish chizig’iga ega giperbolik tipdagi tenglama uchun Koshi masalasi haqida // «Zamonaviy ta’lim tizimini rivojlantirish va unga qaratilgan kreativ g’oyalar, takliflar va yechimlar», 35-sonli Respublika ilmiy-amaliy on-line konferensiyasi, 2022, 192-195 b.

32.    Rasulov X.R., Sayfullayeva Sh.Sh. Ikkita buzilish chizig'iga ega elliptik tenglama uchun chegaraviy masalaning yechimi haqida // Models and methods for increasing the efficiency of innovative research, Germany, 10 (2022), p. 184-186.

33.    Rasulov X.R., Sayfullayeva Sh.Sh. (2022) Ikkita buzilish chizig’iga ega kvazichiziqli elliptic tenglama uchun chegaraviy masala haqida // Central Asian Academic Journal Of Scientific Research, 2(5), 544-557 b.

34.    Rasulov, R. X. R. (2022). Бузилиш чизиғига эга бўлган квазичизиқли аралаш типдаги тенглама учун Трикоми масаласига ўхшаш чегаравий масала ҳақида Центр научных публикаций (buxdu.Uz), 18(18).

35.    Rasulov, X. (2022). Краевые задачи для квазилинейных уравнений смешанного типа с двумя линиями вырождения. Центр научных публикаций (buxdu.Uz), 8(8), https://journal.buxdu.uz/index.php/journals_buxdu/article/view/5675.

36.    Rasulov, X. (2022). Об одной краевой задаче для нелинейного уравнения эллиптического типа с двумя линиями вырождения. Центр научных публикаций (buxdu.Uz), 18(18), https://journal.buxdu.uz/index.php/journals_buxdu/article/view/7320.

37.    Rasulov, X. (2022). О динамике одной квадратичной динамической системы с непреривным временем. Центр научных публикаций (buxdu.Uz), 18(18).

38.    Rasulov, X. (2022). Об одном краевом задаче для квазилинейного уравнения эллиптического типа с двумя линиями вырождения. Центр научных публикаций (buxdu.Uz), 8(8), https://journal.buxdu.uz/index.php/journals_buxdu/article/view/5674.

39.    Rasulov, X. (2022). Об одной задаче для вырождающеюся квазилинейного уравнения гиперболического тип. Центр научных публикаций (buxdu.Uz), 18(18), https://journal.buxdu.uz/index.php/journals_buxdu/article/view/7319.

40.    Rasulov, R. X. R. (2021). Boundary value problem in a domain with deviation from the characteristics for one nonlinear equation of a mixed type. Центр научных публикаций (buxdu.Uz), 7(7), https://journal.buxdu.uz/index.php/journals_buxdu/article/view/3637.

41.    Rasulov, R. X. R. (2022). Analysis of Some Boundary Value Problems for Mixed-Type Equations with Two Lines of Degeneracy. Центр научных публикаций (buxdu.Uz), 18(18), https://journal.buxdu.uz/index.php/journals_buxdu/article/view/7317.

42.    Rasulov, R. X. R. (2022). Квази чизиқли гиперболик турдаги тенглама учун Коши масаласи. Центр научных публикаций (buxdu.Uz), 18(18).

43.    Rasulov, X. (2021). Краевая задача для одного нелинейного уравнения смешанного типа. Центр научных публикаций (buxdu.Uz), 7(7).

44.    Rasulov, R. X. R. (2021). Гиперболик типдаги тенглама учун Коши масаласи. Центр научных публикаций (buxdu.Uz), 7(7).

45.    Rasulov, R. X. R. (2022). О краевых задачах для уравнений эллиптического типа с линией искажения. Центр научных публикаций (buxdu.Uz), 8(8), https://journal.buxdu.uz/index.php/journals_buxdu/article/view/5677.

46.    Rasulov, R. X. R. (2022). Иккита бузилиш чизиғига эга бўлган аралаш типдаги квазичизиқли тенглама учун Нейман масаласига ўхшаш чегаравий масала ҳақида. Центр научных публикаций (buxdu.Uz), 18(18).

47.    Rasulov, H. (2021). Funksional tenglamalarni yechish bo‘yicha ba’zi uslubiy ko‘rsatmalar. Центр  научных публикаций          (buxdu.Uz),               5(5), https://journal.buxdu.uz/index.php/journals_buxdu/article/view/2507

48.    Rasulov, H. (2021). «Kompleks analiz» fanida mustaqil ta’limni tashkil qilish. Центр научных публикаций (buxdu.Uz),                         5(5), https://journal.buxdu.uz/index.php/journals_buxdu/article/view/2506

49.    Rasulov, H. (2021). Boundary value problem for a quasilinear elliptic equation with two perpendicular line of degeneration. Центр научных публикаций (buxdu.Uz), 5(5), https://journal.buxdu.uz/index.php/journals_buxdu/article/view/2504.

50.    Rasulov, H. (2021). Баъзи динамик системаларнинг сонли ечимлари ҳақида. Центр научных публикаций (buxdu.Uz), 2(2).

51.    Rasulov, H. (2021). Funksiyaning toʻla oʻzgarishini hisoblashdagi asosiy qoidalar. Центр научных публикаций (buxdu.Uz), 6(6).

52.    Rasulov, H. (2021). One dynamic system with continuous time. Центр научных публикаций (buxdu.Uz), 5(5).

53.    Xaydar R. Rasulov. On the solvability of a boundary value problem for a quasilinear equation of mixed type with two degeneration lines // Journal of Physics: Conference Series 2070 012002 (2021), pp.1–11.

54.    Расулов Х.Р., Собиров С.Ж. Модуль қатнашган баъзи тенглама, тенгсизлик ва тенгламалар системаларини ечиш йўллари // Science and Education, scientific journal, 2:9 (2021), р.7-20

55.    Расулов Х.Р., Собиров С.Ж. Айрим рационал тенгламаларни ечишда интерфаол усулларни қўлланилиши ҳақида // Science and Education, scientific journal, 2:10 (2021), р. 586-595

56.    Расулов Х.Р., Собиров С.Ж. Айрим иррационал тенгламаларни ечишда интерфаол усулларни қўлланилиши // Science and Education, scientific journal, 2:10 (2021), р.596- 607.

57.    Расулов Х.Р., Рашидов А.Ш. Организация практического занятия на основе инновационных технологий на уроках математики // Наука, техника и образование, 72:8 (2020) с.29-32.

58.    Скачано с www.znanio.ru