
Поступающим в вузы
![]()
П. Т. ДЫБОВ
В. А. ОСКОЛКОВ
по МАТЕМАТИКЕ
(с указаниями и решениями)
Москва
ОНИКС
Мир и Образование 2006
УДК 51(076.2) ББК 22.1я721
Д87
Дыбов П. Т.
Д87 Задачи по математике (с указаниями и решениями) / П. Т. Дыбов, В. А. Осколков. — М.: ООО «Издательство Оникс»: ООО «Издательство «Мир и Образование», 2006. — 464 с.: ил. — (Поступающим в вузы).
ISBN 5-488-00573-0 (ООО «Издательство Оникс»)
ISBN 5-94666-317-8 (ООО «Издательство «Мир и Образование»)
Книга содержит более 3000 задач по всем разделам школьного курса математики, а также не входящим в программу средней школы, но часто предлагаемым на вступительных экзаменах в вузы. Большинство задач сборника в разные годы предлагалось на вступительных экзаменах по математике в ведущих вузах России и ближнего зарубежья.
В каждом параграфе приводятся необходимые теоретические сведения и примеры решения типовых задач, а также задачи для самостоятельного решения. В конце книги даны ответы и методические указания, а к наиболее трудным задачам — подробные решения.
Сборник предназначен для школьников старших классов, абитуриентов, учителей и преподавателей подготовительных курсов.
УДК 51(076.2)
ББК 22.1я721
ISBN 5-488-00573-0
(ООО «Издательство Оникс»)
ISBN 5-94666-317-8
(ООО «Издательство «Мир и Образование»)
© Дыбов П. Т., Осколков В. А., 2006
© Оформление обложки.
ООО «Издательство Оникс», 2006
Данный сборниê содержит более 3000 задач по всем разделам шêольноãо êурса математиêи. В неãо таêже вêлючены разделы, не входящие в проãрамму средней шêолы, но необходимые при сдаче вступительноãо письменноãо эêзамена по математиêе в университеты, техничесêие и педаãоãичесêие вузы России, а именно в те вузы, êоторые предъявляют высоêие требования ê поступающим.
Большинство задач сборниêа в разные ãоды предлаãалось на вступительных эêзаменах по математиêе в ведущих вузах нашей страны и ближнеãо зарубежья.
Пособие состоит из 11 ãлав, êоторые имеют одинаêовую струêтуру. В êаждом параãрафе приводятся необходимые теоретичесêие сведения и примеры решения типовых задач, а таêже задачи для самостоятельноãо решения, ê êоторым в êонце êниãи даны ответы. Часть из них сопровождается методичесêими уêазаниями, а наиболее трудные — подробными решениями. Сложные задачи иллюстрируются ãрафиêами и чертежами, что способствует развитию у учащихся êаê аналитичесêих, таê и пространственных навыêов.
В êниãе приняты следующие обозначения: задачи, ê êоторым даны решения, отмечены знаêом ; задачи, êоторые сопровождаются методичесêими уêазаниями, — знаêом .
Сборниê предназначен для шêольниêов старших êлассов, учащихся математичесêих и физиêо-математичесêих лицеев. Пособие таêже полезно слушателям и преподавателям подãотовительных êурсов при высших учебных заведениях и абитуриентам, самостоятельно ãотовящимся ê вступительным эêзаменам в вуз.
Авторы
Глава I Алãебраичесêие óравнения и неравенства. Фóнêции одной переменной
![]()
Модóль действительноãо числа. Определение. Модулем (абсолютной величиной) действительноãо числа a называют число, равное:
1) числу a при a > 0; 2) нулю при a = 0;
3) числу –a при a < 0.
Модуль любоãо числа есть число неотрицательное.
Модуль числа a обозначают |a|. С помощью этоãо обозначения модуль действительноãо числа a можно записать следующим образом:
![]() a при a > 0,
a при a > 0,
|a| = 0 при a = 0, –a при a < 0. Таê êаê при a = 0 имеем |a| = 0 = a = –a, то определение модуля действительноãо числа можно таêже записать в одной из следующих форм:
![]()
![]() a при a l 0, или 2) |a| = a–a
припри aa > 0, m 0.
a при a l 0, или 2) |a| = a–a
припри aa > 0, m 0.
1) |a| = –a при a < 0
1. Доêажите справедливость неравенства –|x| m x m |x|.
2. Доêажите, что при a > 0 неравенство |x| < a равносильно двойному неравенству –a < x < a (при a l 0 неравенство |x| m a равносильно двойному неравенству –a m x m a).
3. Доêажите, что для тоãо чтобы число x удовлетворяло неравенству |x| > a, необходимо и достаточно, чтобы оно удовлетворяло одному из двух неравенств: x > a, x < –a.
4. Доêажите, что неравенство |a| < |b|:
а) равносильно неравенству –b < a < b, если b > 0;
б) равносильно неравенству b < a < –b, если b < 0.
5. Доêажите, что |x + y| m |x| + |y|.
6. Доêажите, что |x – y| l |x| – |y|.
7.
![]() Доêажите,
что: а) |xy| = |x| · |y|; б) x-y = ----xy , y −
0.
Доêажите,
что: а) |xy| = |x| · |y|; б) x-y = ----xy , y −
0.
8. Доêажите, что:
а) если a и b имеют одинаêовые знаêи, то
a-b- + -ab- l 2,
причем равенство выполняется лишь при a = b;
б) если a и b имеют разные знаêи, то
a-b- + -ab- m –2,
причем равенство выполняется лишь при a = –b.
Иначе ãоворя, для любых a − 0, b − 0 справедливо неравенство
![]() a-b-
+ a-b-
l 2,
a-b-
+ a-b-
l 2,
причем знаê равенства имеет место лишь при a = äb.
9. Решите уравнение:
а) ax = x2; б) (a – 2)x = a2 – 4; в) (a2 – 9)x = a2 + 27.
10. Решите неравенство:
а) –4x > 5; б) 5x + 6 m 3x – 8; в) ax m 1; ã) ax > 1.
11. Решите систему неравенств:
![]() а)
а) ![]() –3xx
> 1, < 3; б)
–3xx
> 1, < 3; б) ![]() –2xx
< > –1;π,
в)
–2xx
< > –1;π,
в) ![]() x2x
> –1, + 1 m 5; ã) 3xx + + 2 5l < 0. 0,
x2x
> –1, + 1 m 5; ã) 3xx + + 2 5l < 0. 0,
12. Найдите значения x ° N, удовлетворяющие неравенству 5x – 7 < 2x + 8.
Решите уравнение:
13. а) |x – 1| = 3; б) |x + 2| = –1; в) |3 – x| = a; ã) |x – a| = 2.
14. а) |x – 3| = x – 3; б) |x – 3| = 3 – x; в) |x – 3| = x.
15. а) |2x – 1| = |x + 3|; б) |x – a| = |x – 4|.
16. а) |x – 4| + |x + 4| = 9; б) |x – 4| + |x + 4| = 8;
в) |x – 4| – |x + 4| = 8; ã) |x + 4| – |x – 4| = 8.
17. |x – 3| + |x + 2| – |x – 4| = 3.
18. При êаêих значениях a уравнение |2x + 3| + |2x – 3| = = ax + 6 имеет более двух êорней?
Решите неравенство:
19. а) |x| > a; б) |x – 1| > –1; в) |x – 1| > 1.
20. а) |x| < a; б) |x + 2| m –2; в) |x + 2| < 2.
21. а) |2x + 1| > x; б) |2x + 3| m 4x.
22. а) |1 – 3x| – |x + 2| m 2; б) |x + 2| + |x – 3| > 5.
23. Решите систему неравенств:
а) ![]() |2xx| l – 1 > 3; x, б)
|2xx| l – 1 > 3; x, б)
![]() ||xx| +
2| > 1.m –x,
||xx| +
2| > 1.m –x,
24. При êаêом значении a фунêция f(x) = (a – 2)x + 3a – 4, x ° (–×; +×), является: а) четной; б) нечетной?
25. При êаêом значении a фунêция f(x) = (a + 3)x + 5a, x ° (–×; +×), является периодичесêой?
26. Найдите значения k, при êоторых фунêция f(x) = (k – 1)x + + k2 – 3, x ° (–×; +×): а) монотонно возрастает; б) монотонно убывает.
27. Определите значения m, при êоторых фунêция y = (m2 – – 4)x + |m|, x ° (–×; +×), имеет обратную фунêцию. Найдите эту фунêцию.
28. Дана линейная фунêция f(x). Доêажите, что фунêция F(x) = f(f(x)) таêже является линейной.
Уравнение прямой в прямоóãольной системе êоординат на плосêости. Пусть на плосêости задана прямоуãольная система êоординат xOy.
y Тоãда уравнение прямой (рис. 1), не парал-
 лельной оси Oy
(для êратêости будем называть ее наêлонной прямой), имеет вид
y = kx + b, k = tg ϕ,
лельной оси Oy
(для êратêости будем называть ее наêлонной прямой), имеет вид
y = kx + b, k = tg ϕ,
ãде tg ϕ — уãловой êоэффициент прямой, ϕ — уãол между прямой и положительным направ-
Рис. 1 лениемêаемоãо осипрямой Ox, наb — осивеличина Oy; отрезêа, отсеуравнение прямой, параллельной оси Oy и проходящей че-
рез точêу x = x0 на оси Ox, имеет вид
x = x0, или x – x0 = 0;
уравнение прямой, параллельной оси Ox и проходящей че-
рез точêу y = y0 на оси Oy, имеет вид
y = y0, или y – y0 = 0.
Если наêлонные прямые y = kx + b и y = k1x + b1 параллельны, то их уãловые êоэффициенты равны: k = k1. Если же эти наêлонные прямые перпендиêулярны, то их уãловые êоэффициенты связаны соотношением k1 = –1-k .
Уравнение прямой, проходящей через точêу (x0; y0) и имеющей уãловой êоэффициент k, записывают в виде y – y0 = k(x – x0),
а уравнение прямой, проходящей через точêи M1(x1; y1) и M2(x2; y2), — в виде
-----------------xx2−−xx11- = ----------------yy2−−yy11 .
Если фунêция y = f(x) в точêе (x0; y0), ãде y0 = f(x0), имеет êонечную производную f′(x0), то уравнение êасательной ê ãрафиêу фунêции y = f(x) в точêе (x0; y0) записывают в виде y – y0 = f′(x0) (x – x0),
а уравнение нормали (т. е. прямой, перпендиêулярной êасательной) ê ãрафиêу фунêции y = f(x) в этой точêе имеет вид
y – y0 = –f--------------′(1x0-) (x – x0).
Постройте ãрафиê фунêции:
29. а) y = 2x; б) y = –1-3 x.
30. а) y = x – 2; б) y = 3 – x.
31. а) y = 2x – 1; б) y = 1 – 3x.
32. а) y = |x – 1|; б) y = –|x + 2|.
33. а) y = |1 + 2x|; б) y = –|–4x + 2|.
34. y = ||x – 1| – 2|.
35. y = |x + 2| + |x – 3|. 36. y = |2x + 1| – |2x – 2|.
![]()
![]() 37. y = x + ----xx . 38.
y = x + |x – 1| + --------------xx −−
22- .
37. y = x + ----xx . 38.
y = x + |x – 1| + --------------xx −−
22- .
Постройте ãрафиê уравнения:
39. -----------x y+ 1- = –1. 40. |y| + x = –1.
41. |x| + |y| = 2. 42. |y – 3| = |x – 1|.
На плосêости xOy уêажите точêи, удовлетворяющие неравенству:
43. y > x. 44. y < –x.
45. y l |x|. 46. x > |y|.
На плосêости xOy уêажите точêи, удовлетворяющие уравнению:
47. y + |y| – x – |x| = 0. 48. |x + y| + |x – y| = 4.
49. |y|x = x. 50. |x – y| + y = 0.
51. Найдите значение a, при êотором фунêция y непрерывна в точêе x = 0, если
![]() 2x +
1 при x m 0, y = –x + a
при x > 0.
2x +
1 при x m 0, y = –x + a
при x > 0.
Дифференцирование. Если фунêции u(x) и v(x) определены в области D ÷ R и дифференцируемы в этой области, то производную их произведения находят по формуле
(uv)′ = u′v + v′u
в точêах x ° D, а производную их частноãо — по формуле
u-v ′ = u------------------------′vv−2v′u
в точêах x ° D, ãде v(x) − 0.
52. Найдите êритичесêие точêи фунêции:
а) y = |3x + 1|; б) y = |x + 1| + x + 1;
в) y = |x + 1| + |x – 1|; ã) y = |x – 3| – |x + 3|. Найдите интервалы монотонноãо возрастания и убывания фунêции:
53. а) y = 3 – x; б) y = -x1 x + 1.
54. а) y = 2 + |x – 4|; б) y = 3 – |x|.
55. а) y = –(|x + 10| + |x – 10|); б) y = |x – 4| – |x + 5|;
в) y = |x + 4| – |x + 3| + |x + 2| – |x + 1| + |x|.
1. C′ = 0, C = const.
2. (xα)′ = αxα – 1, x > 0, при α ° R; x ° R при α = 2n + 1, n ° Z.
3. (ex)′ = ex. 4. (ax)′ = ax ln a, a > 0, a − 1.
5. (ln |x|)′ = -x1 . 6. (loga |x|)′ = ------------xln1 a- , |x| − 0, a > 0, a − 1.
7. (sin x)′ = cos x. 8. (cos x)′ = –sin x.
9. (tg x)′ = cos---------------12x , x − -2π + πn, n ° Z.
10. (ctg x)′ = –-------------sin12x- , x − πn, n ° Z.
11. ![]() (arcsin
x)′
= , |x| < 1.
(arcsin
x)′
= , |x| < 1.
12. (arccos x)′ = – , |x| < 1.
13. (arctg x)′ = 1--------------+1x2- .
14. (arcctg x)′ = –--------------1 +1x2- .
Если арãумент фунêции, приведенной в таблице, является фунêцией, дифференцируемой в области D ° R, то производные сложных фунêций находят по правилам:
1. (c f(x))′ = c · f′(x), c = const.
2. [(f(x))α]′ = α(f(x))α – 1 · f′(x), f(x) > 0 при α ° R; f(x) ° R при α = 2n + 1, n ° Z.
3. (ef(x))′ = ef(x) · f′(x).
4. (af(x))′ = af(x) · ln a · f′(x), a > 0, a − 1.
5. (ln|f(x)|)′ = -----------ff x′( )( )x- , f(x) − 0.
6. (loga |f(x)|)′ = -------------------f x( )f′( )xlna- , f(x) − 0, a > 0, a − 1.
7. (sin f(x))′ = cos f(x) · f′(x).
8. (cos f(x))′ = –sin f(x) · f′(x).
9. (tg f(x))′ = cos---------------------f′2( )f xx( ) , f(x) − 2-π + πn, n ° Z.
10. (ctg f(x))′ = –sin---------------------f′2( )f xx( )- , f(x) − πn, n ° Z.
11. (arcsin f(x))′ = --------------------------1f−′( )fx2( )x- , |f(x)| < 1.
12.
![]() (arccos f(x))′ = –--------------------------1f−′(
)fx2(
)x- ,
|f(x)| < 1.
(arccos f(x))′ = –--------------------------1f−′(
)fx2(
)x- ,
|f(x)| < 1.
13. (arctg f(x))′ = 1----------------------+f′f( )2x( )x- .
14. (arcctg f(x))′ = –1----------------------+f′f( )2x( )x- .
Найдите точêи эêстремума фунêции:
56. а) y = |2x – 1|; б) y = 2 – |3 – 4x|.
57. а) y = |3x + 2| + |2x – 3|; б) y = |x + 7| –2|x – 2|.
58. y = 2|x – 1| – 3|x + 2| + x.
59. y = |x – 2| + |x – a|.
![]() x + 1 при x < 2,
x + 1 при x < 2,
60. Дана фунêция y = a при x = 2, 5 – x при x > 2.
Найдите значения a, при êоторых эта фунêция имеет маêсимум в точêе x = 2.
61. Найдите наименьшее и наибольшее значения фунêции y = |x – a| на отрезêе [1; 2] (a − 1; a − 2). Решите уравнение:
|
62. а) |4x – |x – 1| + 7| = 16; |
б) |3x + |x – 2| + 8| = 15; |
|
в) |2x + |x + 1| – 6| = 12; |
ã) |x – |x + 2| + 5| = 13. |
|
63. а) |x – 2| + |3 – x| = 1; |
б) |4x – 3| + |5 – 4x| = 2; |
|
в) |1 – 2x| + |4 – 2x| = 3; Решите неравенство: |
ã) |3x – 4| + |8 – 3x| = 4. |
|
64. а) |9 – 2x| – |2 – 3x| l 1; |
б) |7 – 4x| – |1 – 3x| m 1; |
|
в) |8 – 3x| – |1 – 5x| l 1; |
ã) |2 – 4x| – |3 – 2x| m 1. |
|
65. а) |x + 2| > ||2x – 1| – 6| – 1; |
б) 4||x – 1| – 5| – |x + 1| m 1; |
|
в) 1 + 3||x + 2| – 4| m 2|x – 3|; |
ã) |x – 2| – |4 – 3|x + 1|| l 1. |
§ 2. КВАДРАТИЧНАЯ ФУНКЦИЯ.
![]() Уравнение ax2
+ bx + c = 0 (a − 0) называют êвадратным.
Выражение D = b2 – 4ac называют дисêриминантом
êвадратноãо уравнения. Если D l 0, то уравнение имеет два действительных
êорня: x1,
2 = −----------b±
Уравнение ax2
+ bx + c = 0 (a − 0) называют êвадратным.
Выражение D = b2 – 4ac называют дисêриминантом
êвадратноãо уравнения. Если D l 0, то уравнение имеет два действительных
êорня: x1,
2 = −----------b±-----------------------------b22a−
4ac .
Если D = 0, то êорни совпадают: x1, 2 = –-----2ba- ; если D < 0, то
êвадратное уравнение не имеет действительных êорней. Корни êвадратноãо уравнения связаны с еãо êоэффициентами соотношениями
x1 + x2 = –-ab- , x1x2 = -ac- .
Квадратное уравнение x2 + px + q = 0 называют приведенным.
ТЕОРЕМА ВИЕТА. Сумма êорней приведенноãо êвадратноãо уравнения равна второму êоэффициенту, взятому с противоположным знаêом, а произведение êорней равно свободному члену: x1 + x2 = –p, x1x2 = q.
![]() Если D = p2
– 4q l 0, то приведенное êвадратное уравнение имеет два действительных
êорня x1,
2 = −-------------------------------------p ±
2p2 −
4q ;
если D = 0,
Если D = p2
– 4q l 0, то приведенное êвадратное уравнение имеет два действительных
êорня x1,
2 = −-------------------------------------p ±
2p2 −
4q ;
если D = 0,
то êорни совпадают: x1, 2 = –-2p ; если D < 0, то уравнение не имеет действительных êорней.
Корнями уравнения ax2 + 2bx + c = 0 при D l 0 являются числа
![]() x1,2 = −----------b±
x1,2 = −----------b±---------------------ba2 −
ac- ,
![]() а êорнями уравнения x2
+ 2px + q = 0 — числа x1, 2 = –p ä p2 − q . Вершина
параболы y = ax2 + bx + c находится в точêе
с êоординатами – -----2ba- ; ----------------------4ac4a−
b2 .
а êорнями уравнения x2
+ 2px + q = 0 — числа x1, 2 = –p ä p2 − q . Вершина
параболы y = ax2 + bx + c находится в точêе
с êоординатами – -----2ba- ; ----------------------4ac4a−
b2 .
![]()
![]() Пусть x1 =
-------------------------------------−
p −
2p2 −
4q
и x2 = −--------------p +
Пусть x1 =
-------------------------------------−
p −
2p2 −
4q
и x2 = −--------------p +
-----------------------2p2 −
4q —
êорни приве-
денноãо êвадратноãо уравнения
x2 + px + q = 0 (1)
с действительными êоэффициентами, дисêриминант ∆ = p2 – 4q > > 0. Тоãда справедливы ТЕОРЕМЫ:
1. Если в уравнении (1) p > 0, q > 0, то еãо êорни связаны неравенствами x1 < x2 < 0.
2. Если в уравнении (1) p < 0, q > 0, то еãо êорни связаны неравенствами 0 < x1 < x2.
3. Если в уравнении (1) p > 0, q < 0, то еãо êорни связаны неравенствами x1 < 0 < x2.
4. Если в уравнении (1) p < 0, q < 0, то еãо êорни связаны неравенствами x1 < 0 < x2.
5. Если в уравнении (1) p > 0, q = 0, то еãо êорни связаны соотношениями x1 < x2 = 0.
6. Если в уравнении (1) p < 0, q = 0, то еãо êорни связаны соотношениями 0 = x1 < x2.
7. Если в уравнении (1) p = 0, q < 0, то еãо êорни связаны неравенствами x1 < 0 < x2.
1. Решите уравнение:
|
а) x2 – 7x + 12 = 0; |
б) –x2 + 4x + 5 = 0; |
|
в) 6x2 – 5x + 1 = 0; |
ã) 3x2 + 10x + 3 = 0; |
|
д) x2 – 2x – 5 = 0; |
е) 2x2 + x – 8 = 0. |
2. Решите неравенство:
а) x2 – 3x – 4 > 0; б) x2 – 3x – 4 m 0;
в) x2 + 4x + 4 > 0; ã) 4x2 + 4x + 1 m 0;
д) 2x2 – x + 5 > 0; е) x2 – x + 1 < 0.
3. Найдите решения системы:
![]() a) x2x – 2
< 0;2 – 5x + 2 = 0, б) xx + 4 2
– 2lx – 3 = 0, 0;
a) x2x – 2
< 0;2 – 5x + 2 = 0, б) xx + 4 2
– 2lx – 3 = 0, 0;
в) xx2 – 4 < 0; – 9 l 0, ã) xx22 – 25 – 6x + 5 m 0;l 0,
![]() д) 2xx2 + 6 – 5 > 0;x +
9 m 0, е) xx22
+ + 6xx + 8 < 0, + 5 = 0;
д) 2xx2 + 6 – 5 > 0;x +
9 m 0, е) xx22
+ + 6xx + 8 < 0, + 5 = 0;
ж) |813x – 2| + |x – 974 x – 3| = 1,m 163x2.
4. Пусть x1 и x2 — êорни уравнения x2 + x – 7 = 0. Не решая уравнение, найдите: а) x21 + x22 ; б) x13 + x32 ; в) x41 + x42 .
5. Дано уравнение ax2 + bx + c = 0. Доêажите, что если x1, x2, x3 — попарно различные действительные êорни этоãо уравнения, то a = b = c = 0.
6. При êаêих значениях a уравнение
(a2 – 3a + 2)x2 – (a2 – 5a + 4)x + a – a2 = 0 имеет более двух êорней?
7. Уравнение x2 + рx + q = 0, ãде p ° Z, q ° Z, имеет рациональные êорни. Доêажите, что эти êорни — целые числа.
8. Доêажите, что уравнение x2 + (2m + 1)x + 2n + 1 = 0 не имеет рациональных êорней, если m ° Z, n ° Z.
9. При êаêих значениях a êорни уравнения 2x2 – (a3 + 8a – – 1)x + a2 – 4a = 0 имеют разные знаêи?
10. Найдите все значения a, при êоторых уравнение x2 – ax + + 1 = 0 не имеет действительных êорней.
11. При êаêих значениях k уравнение x2 + 2(k – 1)x + k + 5 = = 0 имеет хотя бы один положительный êорень?
12. Найдите все значения m, при êоторых оба êорня уравнения 2x2 + mx + m2 – 5 = 0: а) меньше 1; б) больше –1.
13. Найдите все значения k, при êоторых один êорень уравнения x2 – (k + 1)x + k2 + k – 8 = 0 больше 2, а друãой êорень меньше 2.
14. Пусть x1 и x2 — êорни уравнения x2 + 2(k – 3)x + 9 = 0
(x1 − x2). При êаêих значениях k будут выполнены неравенства –6 < x1 < 1 и –6 < x2 < 1?
15. Найдите все значения k, при êоторых один êорень уравнения (k – 5)x2 – 2kx + k – 4 = 0 меньше 1, а друãой êорень больше 2.
16. При êаêих значениях m неравенство mx2 – 9mx + 5m + + 1 > 0 выполняется для любоãо x ° R?
17. Найдите все значения m, при êоторых всяêое решение неравенства 1 m x m 2 является решением неравенства x2 – mx +
|
+ 1 < 0. Решите уравнение: |
|
|
18. а) x2 – |x| – 2 = 0; |
б) x2 + 5|x| + 4 = 0. |
|
19. а) 2x2 – |5x – 2| = 0; |
б) x2 – |x – 1| = 0. |
|
20. а) |x2 + x – 6| = x2 + x – 6; |
б) |6x2 – 5x + 1| = 5x – 6x2 – 1; |
|
в) |x2 + x| = x2 + x; |
ã) |x2 – x + 5| = x – x2 – 5. |
|
21. а) |x2 – 1| = x + 3; |
б) |x2 – 1| = |x + 3|. |
|
22. а) |2x2 – 1| = x2 – 2x – 3; 23. |x2 – 3|x| + 2| = x2 – 2x. Решите неравенство: |
б) |2x2 – 1| = |x2 – 2x – 3|. |
|
24. а) x2 – |x| – 12 < 0; |
б) x2 + 2|x| – 15 l 0; |
|
в) x2 – 7|x| + 10 m 0; д) 4x2 + 2|x| + 0,25 < 0. |
ã) 8x2 + |–x| + 1 > 0; |
|
25. a) 3x2 – |10x – 3| > 0; |
б) x2 m |x – 2|. |
26. а) |x2 + x – 20| m x2 + x – 20; б) |x – 2x2| > 2x2 – x;
в) |x2 + 6x + 8| m –x2 – 6x – 8.
27. а) |x2 – 6| > 4x + 1; б) |x – 3| > |x2 – 3|.
28. а) |2x2 – x – 10| > |x2 – 8x – 22|;
б) |x2 – 5|x| + 4| l |2x2 – 3|x| + 1|.
29. Найдите область определения фунêции:
а) y = −x2 ; б) y = x – 1 − x2 ; в) y = x2 − 4x + 3 ; ã) y =

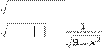 = ; д) y
= 16 −
x2 + x2 + x ; е) y = x2 − x + .
= ; д) y
= 16 −
x2 + x2 + x ; е) y = x2 − x + .
30. Доêажите, что фунêция f(x) = ax2 + bx + c (a − 0) не является периодичесêой.
31. При êаêих значениях a фунêция f(x) = –x2 + (a – 1)x + 2 монотонно возрастает на интервале (1; 2)?
32. Найдите фунêцию, обратную фунêции f(x) = x2 – 6x + 1 на интервале: а) (–×; 3); б) (5; 7).
Постройте ãрафиê фунêции:
|
33. а) y = x2; |
б) y = (x – 2)2; |
|
в) y = 2(x – 2)2; |
ã) y = 2(x – 2)2 – 1. |
|
34. а) y = –x2; |
б) y = –(x + 1)2; |
|
в) y = –0,5(x + 1)2; |
ã) y = 2 – 0,5(x + 1)2. |
|
35. а) y = x2 + 5x + 6; в) y = x2 + x + 1. |
б) y = 4x2 + 4x + 1; |
|
36. а) y = 3x – x2 – 2; в) y = x – x2 – 1. |
б) y = 2x – x2 – 1; |
|
37. а) y = x2 – 4|x| + 3; в) y = 2 – |x| – x2. |
б) y = x2 + 4|x| + 3; |
|
38. а) y = |x2 + x|; |
б) y = –|x2 – 2x|. |
|
39. а) y = |x2 – 3|x| + 2|; |
б) y = –|x2 – |x| – 6|. |
|
40. а) y = |x|(x – 2); |
б) y = (3 – x)|x + 1|. |
41. y = |x2 – 4| – |x2 – 9|.
42. Найдите производную фунêции:
![]() a) y = x2 – 6x
+ 15; б) y = –x2 – x + 5
;
a) y = x2 – 6x
+ 15; б) y = –x2 – x + 5
;
в) y = 3x2 + x + sin 1; ã) y = –4x2 – (tg 2)x + π;
![]() д) y = 1-2 x2 –
x 3 + 2 2 ; е) y = –31- x2 + πx
+ arctg 4;
д) y = 1-2 x2 –
x 3 + 2 2 ; е) y = –31- x2 + πx
+ arctg 4;
ж) y = (5x + 1)2; з) y = –(0,5x – 4)2;
и) y = ax2 + |a|; ê) y = (a – 1)x2 – ax.
43. В уêазанной точêе x0 найдите значение производной фунêции:
а) y = x2 – 5x + 6, x0 = 1; б) y = –x2 + 3x, x0 = –2;
в) y = 1-2 x2 – x, x0 = 1; ã) y = –1-2 x2 + x, x0 = 0.
44. В уêазанной точêе x0 определите уãол между осью абсцисс и êасательной ê êривой:
![]() а)
y = 2x2 + x, x0 = 2; б) y
= –x2 + 2x, x0 = 3; в) y = x----22 + x 3 ,
а)
y = 2x2 + x, x0 = 2; б) y
= –x2 + 2x, x0 = 3; в) y = x----22 + x 3 ,
x0 = 0; ã) y = 2x – x2, x0 = 1,5; д) y = 3x + 4x2, x0 = –2.
45. В уêазанной точêе M (x0; y0) составьте уравнение êасательной ê параболе:
а) y = 3x2 – 6x + 1, M(0; 1); б) y = –0,5x2 – 4x + 3, M(–1; 6,5);
в) y = x2 – 4x + 8, M(–2; 4).
46. При êаêом значении a êасательная ê параболе y = ax2 + + x – 3 в точêе M(1; a – 2) параллельна прямой y = 2x – 1?
47. На параболеy = x2 взяты две точêи с абсциссами x1 = a, x2 = 3a, a − 0. Через эти точêи проведена сеêущая. В êаêой точêе параболы êасательная ê ней будет параллельна проведенной сеêущей?
48. Составьте уравнение таêой êасательной ê параболе y = –2x2 + 16x – 31, êоторая параллельна оси абсцисс.
49. Составьте уравнение таêой êасательной ê параболе y = 2x2 + 8x, êоторая перпендиêулярна оси ординат.
50. При êаêих значениях k êасательная ê параболе y = = 4x – x2 в точêе M(1; 3):
a) является êасательной ê параболе y = x2 – 6x + k;
б) пересеêает параболу y = x2 – 6x + k в двух точêах? Найдите êритичесêие точêи фунêции:
|
51. а) y = x2 – 6x + 1; |
б) y = –x2 + 4x – 3; |
|
в) y = 1-2 x2 + 5x; 52. а) y = x2 – |x|; 53. a) y = |x2 – 6x + 5|; в) y = |x2 + 2x + 6|. 54. a) y = |x2 – 4| + |x + 3|; 55. a) y = x|2 – x|; |
ã) y = –41- x2 + 2,5x – 1-3 . б) y = –2x2 + |x + 3|. б) y = –|4x + x2|; б) y = |x2 – 1| + |x2 – 3|. б) y = (x – 5) |x – 1|; |
в) y = –(x – 2) |x – 2|.
56. Определите интервалы монотонноãо убывания фунêции:
а) y = x2 – 3x + 1; б) y = –x2 – 4x + 8;
в) y = 0,5x2 – |x|; ã) y = |0,5x 2 – |x||.
57. Определите интервалы монотонноãо возрастания фунêции:
![]() а) y = 1-3 x2 – x – 2
; б) y = –2x2 + 8x – 3;
а) y = 1-3 x2 – x – 2
; б) y = –2x2 + 8x – 3;
в) y = |x – 4| – x2; ã) y = ||x – 4| – x2|.
Определите точêи эêстремума фунêции:
58. а) y = x2; б) y = –x2; в) y = (x – 1)2;
ã) y = –(2 + x)2; д) y = x2 + 2x + 100; е) y = –4x2 + x – 5.
59. а) y = x|x|; б) y = |2x + 3|2; в) y = (x – 2)|x + 1|.
60. а) y = x2 – 3|x| + 2; б) y = x2 + 3|x| + 2;
в) y = x2 – |x – 1| + 3.
61. а) y = |x2 – 6|x| + 8|; б) y = |x2 – |x – 2| – 14|.
62. а) y = |x2 – 1| – |x2 – 4|; б) y = |x2 – 4| + |x2 – 25|.
Найдите наименьшее и наибольшее значения фунêции на уêазанном промежутêе:
63. а) y = 3x2 – x + 5 на отрезêе [1; 2];
б) y = –4x2 + 5x – 8 на отрезêе [2; 3];
в) y = x2 – 2x + 5 на отрезêе [–1; 2];
ã) y = –x2 + 6x – 1 на отрезêе [0; 4].
64. а) y = x2 + |x + 2| на отрезêе [–3; –1];
б) y = (x – 3) |2 – x| на отрезêе [1; 4];
в) y = |x2 – 4|x|| на отрезêе [–1; 3].
65. Пусть x1 и x2 (x1 − x2) — нули фунêции f(x) = ax2 + bx + + c. Доêажите, что существует таêая точêа x0 ° (x1; x2), в êоторой производная фунêции f(x) равна нулю.
66. Фунêция f(x) = ax2 + bx + c задана на отрезêе [x1; x2], причем f(x1) = f(x2) = A, x1 − x2. Доêажите, что найдется таêая точêа x0 ° (x1; x2), в êоторой производная фунêции f(x) равна нулю.
67. Фунêция f(x) = ax2 + bx + c (a − 0) задана на отрезêе [x1; x2]. Доêажите существование точêи x0 ° (x1; x2) таêой, что f(x2) – – f(x1) = f′(x0) (x2 – x1). Определите абсциссу точêи x0.
68. Решите неравенство:
а) |x2 – 3|x – 1|| < x + 2; б) |x2 + 2|x – 3|| l 4x + 5;
в) x + |x2 – 2|2x + 1|| < 0,25; ã) 2x – |0,52 – |1 – 6x|| m 3.
69. Пусть x1 и x2 — êорни заданноãо êвадратноãо уравнения, удовлетворяющие уêазанному условию. Найдите значение параметра, если:
а) x2 + 5x + c = 0, x21 + x22 = 13;
б) x2 + x + a = 0, x----11 + ----x12 = 1-2 ;
в) x2 + px – 5 = 0, x21 + x22 = 11;
ã) x2 + bx – 1 = 0, x----11 + ----x12 = 4.
70. Найдите все значения параметра, при êоторых заданное уравнение имеет решение на уêазанном интервале:
а) x2 – 2ax + 8a – 15 = 0, (1; +×);
б) x2 + 2bx + 6b – 8 = 0, (–×; –1);
в) x2 – 2cx + 5c – 4 = 0, (0; +×);
ã) x2 + 2dx + 7d – 12 = 0, (–×; 0).
71. Найдите значения параметра, при êоторых:
а) один из êорней уравнения x2 + (2a – 1)x + a2 + 2 = 0
в 2 раза больше друãоãо;
б) отношение êорней уравнения px2 – (p + 3)x + 3 = 0 равно 1,5;
в) отношение êорней уравнения x2 + bx + b + 2 = 0 равно 2;
ã) один из êорней уравнения x2 – (3c + 2)x + c2 = 0 в 9 раз
больше друãоãо.
72. Найдите все значения параметра, при êоторых уравнение:
а) 2x2 – ( a2 − 1 )x + a = 0 имеет два различных положи-
тельных êорня;
б) 3x2 + c2 − 3c + 2x + 3c = 0 имеет êорни, знаêи êоторых
противоположны;
в) 0,5x2 + p2 − 5p + 6x + 2p = 0 имеет два различных отри-
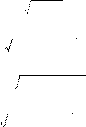 цательных êорня;
ã ) x2 + q2 − 5q + 4x – q + 2 = 0 имеет два различных
отри-
цательных êорня;
ã ) x2 + q2 − 5q + 4x – q + 2 = 0 имеет два различных
отри-
цательных êорня.
73. Найдите все значения параметра, при êоторых данное неравенство справедливо для всех действительных значений x, êроме, быть может, уêазанноãо значения x0. Решите задачу, если:
а) (a – 3)x2 – (a + 1)x + a + 1 > 0, x0 = 2;
б) (2 – b)x2 – (b + 2)x – b – 2 > 0, x0 = –2;
в) (2c – 1)x2 – 2(c + 2)x + 2c + 4 > 0, x0 = 2;
ã) 3(1 – d)x2 – (3d + 1)x – 3d – 1 > 0, x0 = –2.
74. При êаêом a разность êорней уравнения 2x2 – (a + 1)x + + (a – 1) = 0 равна их произведению?
75. При êаêих значениях a уравнение (2 – x)(x + 1) = a имеет действительные положительные êорни?
Решите уравнение:
1.
![]() а) -x1 = 5; б) -----------x 2− 1- = 0; в) -----------x 4+ 2- = a; ã) --------------2 1− x- = a.
а) -x1 = 5; б) -----------x 2− 1- = 0; в) -----------x 4+ 2- = a; ã) --------------2 1− x- = a.
2. а) -----------x 3− 1- = -x2 ; б) -----------x 2− 1- + x = -----------xx −+ 11- ;
в) --------------xx2++33- = 2; ã) -----------x 1− a- + -----------x 1− 1- = ------------------------------------(x − a)2(x − 1) .
Решите неравенство:
|
3. a) -x1 > 1; б) -x1 m 1; ã) -----------x 1+ 3- m–2; д) -----------x a− 1- > 1; 4. a) -----------x 1− 1- – -----------x 1+ 3- > 0; 5. a) ----------------------------x2 −x5−x4+ 4- l 0; |
в) -----------x 1− 2- > –1; е) -----------xa+ 1- l –1. б) ---------------2x1− 3- m ---------------2x1+ 5- . б) -----------------------------------2 +x10+ 3x + 3 < 0. 3x |
6. ![]()
![]() а) --------------x 2+
2-
m 1; б) --------------x 2− 2- > ---------------2x−3− 1- ;
а) --------------x 2+
2-
m 1; б) --------------x 2− 2- > ---------------2x−3− 1- ;
![]() в) x----------------------------x22 −−
46xx ++
94- + --------------xx −−
32- – 12 <
0; ã) x – 2 1 – 1-a
< --------------------2(x3a+
1)- .
в) x----------------------------x22 −−
46xx ++
94- + --------------xx −−
32- – 12 <
0; ã) x – 2 1 – 1-a
< --------------------2(x3a+
1)- .
Постройте ãрафиê фунêции:
7. а) y = -x2 ; б) y = –x-1 ; в) y = -----------2 1+ x- ; ã) y = -----------1 1− x- .
8. ![]()
![]() a)
y = --------------x 1−
3- ; б)
y = –------------------2x1+
1- .
a)
y = --------------x 1−
3- ; б)
y = –------------------2x1+
1- .
|
9. а) y = 2 + -x1 ; в) y = -----------x 1+ 1- – 1-2 ; 10. а) y = x-----------x +− 11- ; в) y = 2---------------xx+−32- ; 11. а) y = --------------1 - ; |
б) y =1 – -x2 ; ã) y = –3 – -----------x 1− 2- . б) y = x-----------x −+ 11- ; ã) y = x-----------3 −+ x2- . б) y = ------------------------2 - . |
12. а) y = --------------xx −+ 42- ; б) y = --------------x1 −+ x3- .
13.
![]()
![]() а) y = --------------xx −−11- ; б)
y = ------------------------xx+
3−
2−
1- .
а) y = --------------xx −−11- ; б)
y = ------------------------xx+
3−
2−
1- .
14.
![]() а) y
= --------------xx −−
11- + --------------xx ++
11- – -x1 ; б) y = – --------------xx2+−39- – x
+ -----------x 2−
1-
а) y
= --------------xx −−
11- + --------------xx ++
11- – -x1 ; б) y = – --------------xx2+−39- – x
+ -----------x 2−
1- ![]() .
.
Найдите производную фунêции:
15. а) y = -x1 ; б) y = –-x2 ; в) y = --------------------2(x1+ 1)- ; ã) y = -----------1 1− x- .
16. а) y = 1 – -----------x 2+ 2- ; б) y = –3 + ---------------2x1− 1- ;
в) y = 2---------------xx+−13- ; ã) y = ---------------1x−−34x- .
17.В уêазанной точêе найдите значение производной фунêции:
![]() а) y = -x3 , x0
= 1; б) y = ----x1 , x0
= –2;
а) y = -x3 , x0
= 1; б) y = ----x1 , x0
= –2;
в) y = 2---------------xx−−11- , x0 = 0; ã) y = --------------xx −+ 31- , x0 = 1.
18. В уêазанной точêе x0 определите уãол между осью Ox и êасательной ê êривой:
|
а) y = -----------1 1− x- , x0 = 2; |
б) y = -----------xx +− 32- , x0 = 0; |
![]()
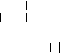 в) y = 1---------------−x2x- ,
x0 = 3; ã) y = --------------xx −+
13- , x0
= –2;
в) y = 1---------------−x2x- ,
x0 = 3; ã) y = --------------xx −+
13- , x0
= –2;
д) y = -x1 – -----------1 1− x- , x0 = 2; е) y = 2---------------2x−+3x1- + ----x1 , x0 = –1.
19. В уêазанной точêе P(x0; y0) составьте уравнение êасательной ê êривой:
а) y = –-x3 , P(3; –1); б) y = -----------x 1− 2- , P(1; –1);
![]()
![]() в) y = --------------xx −+
32- , P 0; –3-2
; ã) y = ---------------2xx−+21- – --------------x 1−
3- ,
P 1; –-61
.
в) y = --------------xx −+
32- , P 0; –3-2
; ã) y = ---------------2xx−+21- – --------------x 1−
3- ,
P 1; –-61
.
20. На ãиперболе y = x-----------x −+ 11- найдите точêу M, в êоторой êасательная ê этой ãиперболе: а) параллельна прямой y = 2x + 1; б) перпендиêулярна прямой y = –1-8 x – 3.
21. Поêажите, что êасательные, проведенные ê ãиперболе y = x-----------x −− 42- в точêах ее пересечения с осями êоординат, параллельны между собой.
22. Составьте уравнение таêой êасательной ê ãиперболе y = x-----------x ++ 95- , êоторая проходит через начало êоординат.
23. Доêажите, что фунêция y = cxax----------------++db строãо монотонна на любом интервале (x1; x2) при условии ad − bc, c − 0, x = –d-c õ õ (x1; x2).
24. Найдите наибольшее и наименьшее значения фунêции:
а) y = x-----------x −+ 31- на отрезêе [0; 2];
б) y = 2---------------xx−+21- на отрезêе [–1; 1].
25. Фунêция y = -xk (k > 0) задана на отрезêе [x1; x2]. Доêажите существование точêи x0 ° (x1; x2) таêой, что y(x2) – y(x1) = = y′(x0)(x2 – x1). Найдите êоординаты точêи x0. § 4. ДЕЛЕНИЕ МНОГОЧЛЕНОВ. РАЦИОНАЛЬНЫЕ ФУНКЦИИ.
При делении мноãочлена (полинома) n-й степени
Pn(x) = anxn + ... + a1x + a0 (an − 0)
на x – x0 получаем
x--------------Pn−( )xx0- = Qn – 1(x) + x--------------−Rx0- , (1)
ãде Qn – 1(x) — частное (мноãочлен (n – 1)-й степени), R — остатоê.
ТЕОРЕМА БЕЗУ. Остатоê R от деления мноãочлена Pn(x) на x – x0 равен значению мноãочлена Pn(x) в точêе x0, т. е. R = = Pn(x0).
В самом деле, запишем выражение (1) в виде Pn(x) =
= Qn – 1(x)(x – x0) + R.
Таê êаê Pn(x0) = Qn – 1(x0)(x0 – x0) + R, то R = Pn(x0).
Определение. Число x0 называют êорнем (или нулем) мноãочлена Pn(x), если Pn(x0) = 0.
Следствие теоремы Безу. Если x0 — êорень мноãочлена Pn(x), т. е. Pn(x0) = 0, то Pn(x) делится на x – x0 без остатêа.
В этом случае Pn(x0) = Qn – 1(x0)(x0 – x0) + R = 0 ⇒ R = 0, Pn(x) = Qn – 1(x)(x – x0).
Пример 1. Решить уравнение 4x3 – 3x2 – 1 = 0.
Леãêо убедиться в том, что x = 1 — êорень мноãочлена 4x3 – 3x2 – 1:
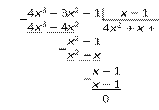 ⇒ 4x3
– 3x2 – 1 = (x – 1)(4x2 + x +
1).
⇒ 4x3
– 3x2 – 1 = (x – 1)(4x2 + x +
1).
Ответ: x = 1.
Уравнение
anxn + an – 1 xn – 1 + ... + a1x + a0 = 0, an − 0, n l 1 (2)
называют алãебраичесêим уравнением n-й степени.
ТЕОРЕМА. Если алãебраичесêое уравнение с целыми êоэффициентами имеет целый êорень, то свободный член уравнения делится на этот êорень.
Пример 2. Решить уравнение 2x3 + 3x2 – x + 2 = 0.
Свободный член уравнения делится на ä1, ä2. Леãêо убедиться, что –2 является êорнем уравнения.
Разделив мноãочлен 2x3 + 3x2 – x + 2 на x + 2, получим в частном 2x2 – 2x + 1; поэтому исходное уравнение можно записать в виде
(x + 2)(2x2 – 2x + 1) = 0.
Это уравнение имеет единственный êорень x = –2, таê êаê дисêриминант êвадратноãо трехчлена 2x2 – 2x + 1 отрицателен. Ответ: x = –2.
ТЕОРЕМА. Если алãебраичесêое уравнение с целыми êоэффициентами имеет рациональный êорень m---k- , ãде m---k- — несоêратимая дробь, то свободный член уравнения делится на m, а êоэффициент при старшей степени делится на k.
Пример 3. Решить уравнение 3x3 + x2 + x – 2 = 0.
Свободный член уравнения делится на ä1, ä2, а êоэффициент при старшей степени делится на ä1, ä3. Значит, рациональными êорнями моãут быть числа ä1, ä2, ä1-3 , ä2-3 . Подставив эти числа в уравнение, находим êорень x = 2-3 . Разделив мноãочлен на x – 2-3 , получаем в частном x2 + x + 1, поэтому уравнение x – 2-3 (x2 + x + 1) = 0 эêвивалентно исходному. Оно имеет единственный êорень x = 2-3 .
Ответ: x = 2-3 .
1.Решите уравнение:
а) (x – 1) (x2 + 4x + 3) = 0; б) (2x + 3)(x2 – x + 1) = 0;
в) x3 + 27 = 0; ã) 8x3 – 1 = 0; д) x3 – 1 + x2 – 1 = 0;
е) x3 + 8 + x2 – 4 = 0; ж) x3 + 1 + x + 1 = 0; з) x3 – 8 + x – 2 = 0;
и) x3 + x2 + x + 1 = 0; ê) x3 – x2 + x – 1= 0.
2.Уравнение x3 + ax2 + bx + c = 0, ãде a, b, c — целые числа, имеет рациональный êорень x1. Доêажите, что x1 — целое число и что c делится на x1 нацело.
3.Найдите рациональные êорни уравнения:
а) x3 + 2x2 – x – 2 = 0; б) x3 – x2 – 8x + 12 = 0;
в) x3 – 9x2 + 27x – 27 = 0; ã) x3 + x2 + x – 3 = 0;
д) 6x3 + 7x2 – 1 = 0; е) 2x3 + x2 + 5x – 3 = 0.
4.Пусть x1, x2, x3 — êорни уравнения ax3 + bx2 + cx + d = 0, a − 0. Доêажитеd-a . , что x1 + x2 + x3 = –-ab- , x1x2 + x2x3 + x3x1 = -ac- , x1x2x3 = –
5.Дано уравнение x3 + px + q = 0. Найдите сумму êвадратов еãо êорней.
6.Решите уравнение x3 + 3x – 3 = 0.
7.Решите уравнение:
а) (x – 1)(x + 3)(x2 – x – 6) = 0;
б) (x2 – 3x + 2)(x2 + 7x + 10) = 0; в) (x2 – x – 3) (x2 – 2x + 2) = 0;
ã) (x2 – x +1)(x2 – 2x + 3) = 0; д) x4 – 16 – 5x(x2 – 4) = 0;
е) x4 + 11x2 + 10 + 7x(x2 + 1) = 0.
8.Уравнение x4 + ax3 + bx2 + cx + d = 0, ãде a, b, c, d — целые числа, имеет рациональный êорень x1. Доêажите, что x1 — целое число и что d делится нацело на x1.
9.Найдите рациональные êорни уравнения:
а) x4 + 2x3 – 16x2 – 2x + 15 = 0; б) x4 – 7x3 + 5x2 + 4x + 12 = 0;
в) x4 + x3 – 5x – 5 = 0; ã) x4 + x3 – 1 = 0;
д) 6x4 – x3 + 5x2 – x – 1 = 0.
Решите уравнение:
10. a) 2x4 – 5x2 + 2 = 0; б) x4 – 2x2 – 3 = 0.
11. а) (x – 1)4 + (x + 1)4 = 16; б) (2x – 3)4 + (2x – 5)4 = 2. 12. a) (x2 + 2x)2 – 7(x2 + 2x) + 6 = 0;
б) ----------------------------2x2 −1x + 1- + 2----------------------------x2 −3x + 3- = 2----------------------------x2 10− x + 7- .
13. a) (x – a)x(x + a)(x + 2a) = 3a4;
б) (6x + 5)2(3x + 2)(x + 1) = 35.
14. a) x2 + ----x42 – 8 x – -x2 – 4 = 0;
б) 4x4 + 6x3 – 10x2 – 9x + 9 = 0;
в) (-------------------x5++11)5- = 81------11 ; ã) (x2 – 6x – 9)2 = x3 – 4x2 – 9x. x
15. а) x2 + (-------------------x25+x52)2- = 11; б) (x2 – 16)(x – 3)2 + 9x2 = 0.
16. а) x4 + 4x – 1 = 0; б) x4 – 4x3 – 1 = 0;
в) x4 – 2x2 – 400x = 9999.
17. а) (x3 – 2x) – (x2 + 2)a – 2a2x = 0;
б) (x2 – a)2 – 6x2 + 4x + 2a = 0.
18. x4 – 4x3 – 10x2 + 37x – 14 = 0, если известно, что левая часть уравнения разлаãается на множители с целыми êоэффициентами.
Решите неравенство:
19. а) (x + 2)(x – 1)(x – 3) > 0;
б) (x + 2)x(x – 1)(x – 2) < 0;
в) (x + 4)5(x + 3)6(x + 2)7(x – 1)8 m 0;
ã) (x + 3)n(x – 2) < 0, n ° N.
20. а) x3 – 3x2 – 10x + 24 > 0; б) x3 + 4x2 + 5x + 2 m 0;
в) 2x3 – 3x2 + 7x – 3 > 0.
21. а) x4 – 3x3 + x2 + 3x – 2 l 0; б) x4 + 6x3 + 6x2 + 6x + 5 < 0.
22. а) 3x4 – 10x2 + 3 > 0; б) 2x2(x – 4)2 < 32 – 5(x – 2)2.
23. а) (x2 – x)2 + 3(x2 – x) + 2 l 0;
б) x(x + 1)(x + 2)(x + 3) < 48.
24. а) (x + 1)4 > 2(1 + x4); б) x4 – x3 – 10x2 + 2x + 4 < 0.
25. Доêажите, что мноãочлен P(x) = x8 – x5 + x2 – x + 1 положителен при любом x ° R.
26. Пусть P(x) = a0xm + a1xm – 1 + ... + am – 1 x + am и Q(x) = b0xn + b1xn – 1 + ... + bn – 1 x + bn, m ° N, n ° N, Q(x) Õ 0.
Доêажите, что неравенства -----------Q xP x( )( )- > 0 и P(x)Q(x) > 0 равносильны.
Решите неравенство:
27. а) -x1 < -----------x 2− 2- ; б) x-----------x −+ 42- < x----------- 2+ 1- ; в) -----------x1+ 1- – -x1 m -----------x 1− 1- – -----------x 1− 2- ;
ã) x------------------------2x−−x1+ 1- + ----------------------------x2 −x3−x3+ 1- > 2x – ---------------4x1− 8- ;
д) ----------------------------------------------x3 −x22+x23+x5+x2+ 2 l 1; е) x-----------1+ 5- + -----------x 1− 7- + x-----------1− 5- + x-----------1+ 7- > 0.
28. а) --------------x21+ x- m 2--------------------------------x2 +12x + 3- ;
б) -----------x 1− 1- – -----------x 4− 2- + -----------x 4− 3- – -----------x 1− 4- < ------301 ;
в) 4--------------------xx −− 417 + 10----------------------2xx −− 133 - > 8--------------------2xx−−307 + 5---------------xx−−14- .
29. а) x2 + (-------------------xx+21)2- < 45- ; б) x2 + (-------------------x4−x22)2- m 5.
30. а) -----------------------x x((x +2 1+)14)- > 128--------15- ; б) x3 – x----12 l 4 x – -x1 .
31. x-----------x +− 66- xx-----------−+ 44- 2 + xx-----------−+ 66- x-----------x +− 99- 2 < 2-----------------------xx22−+3672 .
32.
![]() а) |x3
– x| m x; б) ------------------------x +
41 −
2-
l |x – 1|.
а) |x3
– x| m x; б) ------------------------x +
41 −
2-
l |x – 1|.
Найдите производную фунêции:
33. а) y = x3 – 6x2 + 1; б) y = –x3 + 1-3 x – 2;
в) y = x4 – 6x + 3; ã) y = –1-2 x4 + x3.
34. а) y = (x + 2)(x2 – x + 5);
б) y = (3 – x)(x – x2);
в) y = (x2 + x + 2)(x2 + 2x + 3);
ã) y = x(x – 1)(x – 2)(x – 3).
35. а) y = --------------1 +xx2- ; б) y = 2--------------1+−xx2- ; в) y = --------------xx3+−3x- ;
ã) y = -------------------(xx4++14)x2- ; д) y = ---------------------------------------(x2 −x1−)(4x + 3) ; е) y = x3 + -----------1 −1 x- .
36. а) y = (2 – 3x)30; б) y = 6 x2 – -x4 + 1 8 ;
в) y = x--------------x22 +− 11- 2 ; ã) y = (x4 – x3 + 5x2 – 2)8.
В уêазанной точêе x0 вычислите значение производной фунêции:
37. а) y = (x2 – 3x + 3)(x2 + 2x – 2), x0 = 0;
б) y = (x3 – 3x + 2)(x4 + x2 + 1), x0 = 1;
в) y = (x2 – 1)(x2 – 4)(x2 – 9), x0 = –2;
ã) y = -------------------(xx−52)2- , x0 = 1;
д) y = ----------------------------------------------(1 − x2)(31 − 2x3) , x0 = 0.
38. а) y = -----------x 1+ 2- + x--------------23+ 1- , x0 = –1;
б) y = (1 + x3) 5 –x----12 , x0 = a;
в) y = 1--------------a+−xx2- , x0 = a;
ã) y = [(x2 + x + 1)(x2 – x + 1)]5, x0 = 0;
д) y = x(x – 1)(x – 2) ... (x – n), x0 = 0, n ° N.
39. В заданной точêе P(x0; y0) составьте уравнение êасатель-
|
ной ê êривой: |
|
|
a) y = –1-3 x3 + x2 – x, P(0; 0); в) y = (x – 2)2(x + 1), P(1; 2); д) y = (x – 4)3(2x + 1), P(2; –40); ж) y = ----14 + 2, P(1; 3). x |
б) y = x3 – 3x3 + 2, P(0; 2); ã) y = 2x4 – x3 + 1, P(–1; 4); е) y = x – -x1 , P(1; 0); |
40. На êривой y = x3 – 3x + 2 найдите точêи, в êоторых êасательная параллельна прямой y = 3x.
41. В êаêой точêе êасательная ê ãрафиêу фунêции f(x) = 1-3 x3 –
– 23- x2 – 9x + 8 параллельна биссеêтрисе I и III êоординатных уãлов?
42. В êаêих точêах линии y = x3 + x – 2 êасательная ê ней параллельна прямой y = 4x + 5?
43. На êривой y = x2(x – 2)3 найдите точêу, в êоторой êасательная ê ней параллельна прямой y = 24x – 1.
44. На линии y = 1--------------+1x2- найдите точêу, в êоторой êасательная параллельна оси абсцисс.
45. Поêажите, что любая êасательная ê êривой y = x5 + 8x + + 1 составляет с осью Ox острый уãол.
![]() Найдите êритичесêие точêи
фунêции: 46. а) y = 2x3 – 5-2 x2 +
x – 3 ;
Найдите êритичесêие точêи
фунêции: 46. а) y = 2x3 – 5-2 x2 +
x – 3 ;
![]() б)
y = x3 – 33 3 x2 + 33
9 x – 33 3 ;
б)
y = x3 – 33 3 x2 + 33
9 x – 33 3 ;
в) y = 3x3 – x2 + 5x + 0,7; ã) y = (x + 2)2(3x – 1);
д) y = x3 + 3|x|; е) y = |x3| – 9x.
47. а) y = x4 + 8x2 – 64x + 1;
б) y = 3x4 + 16x3 + 6x2 – 72x – 3;
в) y = x4 + 6x2 + 5; ã) y = –x4 + 4|x|; д) y = x4 + 8|x3|.
48. а) y = x----55 – 2-3 x3 – 3(x + 1);
б) y = 0,6x5 – 13x3 + 108x – 5;
в) y = x-----55 – 3-2 x4 + 3x3 + 5 ----x33 – -32 x2 + 4x – 7;
ã) y = x----77 – 7x + π; д) y = x2 + 16------x .
49. Найдите интервалы монотонноãо убывания фунêции:
а) y = 2x3 + 3x2 – 12x + 15; б) y = x4 + 1-3 x3 – 2;
в) y = x5 – 20x3 + 1; ã) y = x----------------------------x22 +− 33xx ++ 22- .
50. Найдите интервалы монотонноãо возрастания фунêции:
a) y = x3 – 5x2 + 3x – 11; б) y = –x3 + 6x2 – 9x + 5;
в) y = 0,25x4 + x2 – 6; ã) y = --------------xx2+−21- ; д) y = 11------------------------−+ xx ++ xx22- .
51. Определите точêи эêстремума фунêции:
а) y = x3 + 3x2 – 45x + 1; б) y = x----33 – 2x2 + 4x – 3;
в) y = |3x – 1| – x3; ã) y = (x – 1)3(x + 2);
д) y = (x + 3)2(x – 4)2; е) y = 2x2 + --x4 ; ж) y = -------------------(2xx−−11)2- .
52. Найдите модуль разности эêстремумов фунêции y = x3 + 3x2 – 3x + 1.
53. В уêазанном промежутêе найдите наименьшее и наибольшее значения фунêции:
а) y = x3 + 9x – 3 на отрезêе [–1; 0];
б) y = 6x – x3 на отрезêе [–2; 1];
в) y = (x + 2)3(x – 1) на отрезêе [–1; 2];
ã) y = x5 – 5x4 + 5x3 + 4 на отрезêе [–1; 2];
д) y = --------------------------------3xx22 ++ x4x++14- на отрезêе [–2; –1].
Исследуйте фунêцию с помощью производной и постройте ее
|
ãрафиê: |
|
|
54. y = x3 – 3x2 + 4. |
55. y = –x(x2 – 4) – 3. |
|
56. y = (x + 2)2(x – 1)2. |
57. y = –x4 + 2x2 + 8. |
|
58. y = (x – 1)3(x + 1)2. 60. y = --------------1 +xx2- . 62. y = x2 + ----x12 . 64. y = -x1 + 4x2. |
59. y = x + --x1 . 61. y = --------------x2x− 1- . 63. y = 3--------------x−3x2- . 65. y = x + ----x42 . |
66. Не используя миêроêальêулятор, найдите значение числовоãо выражения:
а) 3 30 + 89926------27 + 3 30 − 89926------27 ;
б) 3 50 + 2495------2710 + 3 50 − 249510------27 ;
в) 3 12 + 14326------27 + 3 12 − 14326------27 ;
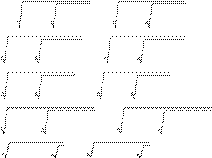 ã) 3 105 + 1102426------27 + 3 105 − 1102426------27 ;
ã) 3 105 + 1102426------27 + 3 105 − 1102426------27 ;
д) 3 20 + 14 2 + 3 20 − 14 2 .
Решите систему уравнений:
![]() а) 3–xx – + yy
= 0, = 0; б) x2x – 2 – 4y = 0,y = 0; в) 00 · · xx
– 0 · + 0 · yy = 0, = 0;
а) 3–xx – + yy
= 0, = 0; б) x2x – 2 – 4y = 0,y = 0; в) 00 · · xx
– 0 · + 0 · yy = 0, = 0;
1.
ã) 00 · · xx + – 0 · y = 0,y = 0; д) 00 · · xx + 0 · + 0 · yy = –1, = 2.
2.![]()
![]() а) –3xx + 2 + 5yy
= 1, = –6; б) x4x
– 2 – 8y = y = 3,-43 ;
а) –3xx + 2 + 5yy
= 1, = –6; б) x4x
– 2 – 8y = y = 3,-43 ;
в) 39xx + + 3y = –1,y = –2; ã) y8 – 4x – 2x = y = 1.a,
3.При êаêих значениях k совместна система уравнений:
а) kxx – + y
= 3;y = 2, б) kx3x + 4 + y = 1;y = 4, в) ![]() 3(kx + 1)
+ (kx – 1) + yy = 3? = k + 1,
3(kx + 1)
+ (kx – 1) + yy = 3? = k + 1,
4.Найдите все значения m, при êоторых не имеет решений система уравнений:
а) 2xx + + (9y
= 1;m2 – 2)y
= 3m, б) ![]() mxm2x + (2 + (2 – m
– 1)m)yy = = mm35 + 4, – 2;
mxm2x + (2 + (2 – m
– 1)m)yy = = mm35 + 4, – 2;
в) 2xmx + 2 + myy = 6 = 0.m2 – 5m + 1,
5.Найдите значения c и d, при êоторых система уравнений
(c
![]() + 1)2x – (c + 1)y = –c,
+ 1)2x – (c + 1)y = –c,
(d – 1)x + (5 – 2d)y = c + 4
имеет единственное решение x = 1, y = 1.
6.![]() Одним из решений системы
уравнений ax – by = 2a – b,
Одним из решений системы
уравнений ax – by = 2a – b,
(c + 1)x + cy = 10 – a + 3b
является упорядоченная пара чисел (1; 3). Определите числовые значения a, b и c.
7.Найдите значения b ° R таêие, чтобы при любых a ° R имела хотя бы одно решение система уравнений:
а) ![]() 3axx – + yy = = ba;,
б)
3axx – + yy = = ba;,
б) ![]() xax – 2 +
3y = y = a,b.
xax – 2 +
3y = y = a,b.
8.Найдите все значения a и b, при êоторых равносильны системы уравнений
![]()
![]() xax + + 2y = 3y = b + 1, и 2xx + 3 + y
y = 3.= a2 + 2,
xax + + 2y = 3y = b + 1, и 2xx + 3 + y
y = 3.= a2 + 2,
9.![]() При
êаêих значениях k существуют решения системы уравнений x
+ ky = 3, kx + 4y = 6,
При
êаêих значениях k существуют решения системы уравнений x
+ ky = 3, kx + 4y = 6,
удовлетворяющие одновременно неравенствам x > 1, y > 0?
10. При êаêих значениях a решения системы уравнений
![]() –2x + y = a2 – 1,
–2x + y = a2 – 1,
3x + 2y = 2a2 + 7a + 5
![]() удовлетворяют неравенству xy
+ 3 > 0? Решите систему уравнений:
удовлетворяют неравенству xy
+ 3 > 0? Решите систему уравнений:
![]() 2--------------------------x +4y −
1 + --------------------------x +
23y −
3 = 4,75,
2--------------------------x +4y −
1 + --------------------------x +
23y −
3 = 4,75,
11. 2 3 – --------------------------x + 22y − 3 = 2,5.
--------------------------x + y − 1
12.
![]() а) |xx
+ 3|| + yy = 4,| = 6; б) ((x
yx y+− ))22 = 5, = 1.
а) |xx
+ 3|| + yy = 4,| = 6; б) ((x
yx y+− ))22 = 5, = 1.
13. Найдите значения x ° N и y ° N, удовлетворяющие уравнению 23x + 31y = 1000.
14. На плосêости xOy уêажите точêи, удовлетворяющие неравенству:
а) |x – y| m 1; б) |x + y| l 2; в) |x| – |y| l 1;
ã) |x| + |y| m 3; д) |x – 1| + |y + 1| l 2; е) |x + y| + |x – y| m 2. 15. На плосêости xOy уêажите точêи, удовлетворяющие системе неравенств
![]() 3y – x < 5, y + 2x < 11,
4y + x > 9.
3y – x < 5, y + 2x < 11,
4y + x > 9.
Найдите таêже все целые значения x и y, удовлетворяющие этой системе.
16. При êаêих значениях a ° R точêа (a; a2) расположена внутри треуãольниêа, образованноãо при пересечении прямых y = x + 1, y = 3 – x, y = –2x?
Решите систему уравнений:
17.
![]()
![]() –3x2x
+ – x + 4yy – + 3zy = 0, + 2z = 9,z = 11. 18.
4yzx
= 4 = –4x = 3
– 3tt
– 5, – 2,yt
+ 1, – 6z = 5.
–3x2x
+ – x + 4yy – + 3zy = 0, + 2z = 9,z = 11. 18.
4yzx
= 4 = –4x = 3
– 3tt
– 5, – 2,yt
+ 1, – 6z = 5.
![]()
![]() 19.
2-----------xx1 + 3y + z
– 1 = 0,x-----------−+22- = y-----------−3 1- = ------------z −2 3 ,
19.
2-----------xx1 + 3y + z
– 1 = 0,x-----------−+22- = y-----------−3 1- = ------------z −2 3 ,
− 1- = -----------y−+21- = -6z . 20. x + 2y – 2z + 6 = 0.
21. Дана система уравнений
![]() 2-3 x + 4-5 y + 5-6 z = 61, x
+ y + z = 79.
2-3 x + 4-5 y + 5-6 z = 61, x
+ y + z = 79.
а) Найдите значение суммы 2-5 y + -2z ; б) из всех натуральных решений системы найдите таêое, при êотором x принимает наибольшее значение.
22. Известно, что для неêоторой фунêции f(x) = ax2 + bx + c (a − 0) выполнены неравенства f(–1) < 1, f(1) > –1, f(3) < –4. Определите знаê êоэффициента a.
23. Изобразите множество {(x; y; z)||x| + |y| + |z| m 1} и назовите полученную фиãуру.
Решите систему уравнений:
1. a) xx2 + 2 – xyy = 4; + 3y2 + 2x – 5y – 4 = 0,
б) 23xyx
+ 2 – yy2 – 3 = 0; + 5x + 20 = 0, в) ![]() xx2
+ 2 – 4yy = 100;2 = 200,
xx2
+ 2 – 4yy = 100;2 = 200,
ã) xx2 + 30 = 2 + 9y2 + 6y.xy – 6x – 18y – 40 = 0,
а) xxy + = 6;y = 5, б) xxy – = –4;y = 5, 2.
![]()
![]() ã) ----x-112 – + 1-yy----1 = 1;2- = 13, д) xx3 + + yy = 1;3 = 7, x
ã) ----x-112 – + 1-yy----1 = 1;2- = 13, д) xx3 + + yy = 1;3 = 7, x
e) xx4 + + yy = 3;4 = 17, ж) xx5 + + yy = 5;5 = 275,
в) ![]() xx2 + + yy
= 4;2 = 10,
xx2 + + yy
= 4;2 = 10,
з) ![]() xxy3 – = 4.y3
= 63,
xxy3 – = 4.y3
= 63,
![]() а) xx2 + + yy + 2 + xyxy = –11, = –13; б)
xx + 2y – xyxy
– 2y = 30, = 13;
а) xx2 + + yy + 2 + xyxy = –11, = –13; б)
xx + 2y – xyxy
– 2y = 30, = 13;
3.
2 + (y + 0,3)2 = 1, ã) x(x + +yy + )x- = –x-y = 1-21-2;,
в) x(x + + 0,2)y = 0,9;--------------------y
д) xx23yy + + xyx3y + 2 + 2x + xy2 + y2 + xyx2 = 11.2y3 + xy3 = 30,
4. а) 22xx2 + 9 + xyy2 = 4; – 45y2 = 0, б) 2xxy2 – 5 + xyy2 = 16, = 3;
![]()
![]() в)
(2xx + 2
+ y)y22
– + 31-2 yxy2
= 7; = 12, xx3
+ xy2 = 10,
в)
(2xx + 2
+ y)y22
– + 31-2 yxy2
= 7; = 12, xx3
+ xy2 = 10,
ã) 2y – y3 = –3.
5. а) 103xx2 – 22 + 5y2y + 52 – 2xyxy – 17 – 38xx – 6 – 6y + 20 = 0;y + 41 = 0,
б) yy22((3xx2 – 3) + 2 – 6) + xyxy + 1 = 0, + 2 = 0.
![]() x-y (x + y
– 2) = 2-3 ,-x2 + -3y = 3,
x-y (x + y
– 2) = 2-3 ,-x2 + -3y = 3,
6. а) -xy (x + y – 1) = 9; б) x-2 + 3-y = 3-2 .
7. а) 8y2 – – |xxy2 = (| + 2 = 0,x + 2y)2; б) |2xy + – 2| = 6 – 3y2 = 2xyx.2,
8. Найдите все пары чисел x, y, для êоторых одновременно выполняются условия x2 – 2xy + 12 = 0, x2 + 4y2 m 60 и x ° Z.
9.
![]() Найдите натуральные
решения системы x = y + 2, xy m 17,
Найдите натуральные
решения системы x = y + 2, xy m 17,
-----------xy ++ 12- < 1-2 .
10. Найдите все значения a, при êоторых множество
{(x; y) | x2 + y2 + 2x m 1} {(x; y) | x – y + a l 0}
содержит тольêо одну точêу. Найдите эту точêу.
11. Решите уравнение:
а) (x – 1)2 + (y + 5)2 = 0;
б) x2 + y2 – 2x + 6y + 10 = 0;
в) (x + y – a)2 + (y – 1)2 + (x + 3)2 = 0.
Решите систему уравнений:
x + 2y – z = 5,
12. а) 3x – 4y + z = 1, x2 + y2 + z2 = 6;
x + y + z = 2,
13. xy + yz + zx = –5, x2 + y2 – z2 = 12.
x2 – yz = 14,
![]() 15. y2
– xz = 28, z2 – xy = –14.
15. y2
– xz = 28, z2 – xy = –14.
xy + xz = 8,
17. yz + xy = 9, xz + yz = –7.
4xy + y2 + 2z2 = –3,
19. 4xz + x2 + 2z2 = 1, 8yz + y2 + 2z2 = 1.
2u + v + w = 6,
б) 3u + 2v + w = 9,
3u3 + 2v3 + w3 = 27.
xy + x + y = 7,
14. yz + y + z = –3, xz + x + z = –5.
x2 + xy + y2 = 3,
![]() 16. y2
+ yz + z2 = 7, z2 + zx
+ x2 = 19.
16. y2
+ yz + z2 = 7, z2 + zx
+ x2 = 19.
-----------x5xy+ y- = 1,
18. ----------y7+yzz = 1,
6xz = x + z.
y3 = 9x2 – 27x + 27,
20. z3 = 9y2 – 27y + 27, x3 = 9z2 – 27z + 27.
21. Найдите все тройêи целых чисел (x; y; z), для êоторых
выполняется соотношение 5x2 + y2 + 3z2 – 2yz = 30.
22.
![]()
![]() Изобразите штриховêой множество точеê êоординатной
плосêости, задаваемое системой неравенств:
Изобразите штриховêой множество точеê êоординатной
плосêости, задаваемое системой неравенств:
а) yx + 22 + yx2 m – 5 0,m 0; б) x2x2 + 2 + y ym – 1 0, m 0.
23.
![]()
![]()
![]() Изобразите на плосêости множество точеê (x;
y), êоординаты êоторых удовлетворяют системе неравенств:
Изобразите на плосêости множество точеê (x;
y), êоординаты êоторых удовлетворяют системе неравенств:
а) 2y ym l –2 x2x,2 + 3x; б) yyy – 2 + + 1 xx2m + 3 m 0; 0,l 0, в) xx22 + + yy22 lm 1, 16.
§ 7. ИРРАЦИОНАЛЬНЫЕ ФУНКЦИИ,
![]() При решении иррациональных
уравнений нужно учитывать следующую ТЕОРЕМУ: уравнение 2n f x( ) = ϕ(x),
n ° N, равносильно системе
При решении иррациональных
уравнений нужно учитывать следующую ТЕОРЕМУ: уравнение 2n f x( ) = ϕ(x),
n ° N, равносильно системе
![]() f(x) =
(ϕ(x))2n,
ϕ(x)
l 0.
f(x) =
(ϕ(x))2n,
ϕ(x)
l 0.
При мер. Решить уравнение 7 − x − x2 = x – 1.
Уравнение равносильно системе
7 – x – x2 = (x – 1)2,
 x l 1
⇔ x2x
l2 1 – x – 6 = 0, ⇔
x = 2.
x l 1
⇔ x2x
l2 1 – x – 6 = 0, ⇔
x = 2.
Решите уравнение:
1. а) x + 1 = a; б) x + 3 = a x− ; в) 4 + 2x x− 2 = x – 2.
2. а) 11 + 2x = 22 − x ; б) 21 + 2x − 7 = x;
в) 2 x + 5 = x + 2; ã) 3x – 18x + 1 + 1 = 0.
3. а) x + 10 + x − 2 = 6; б) x + 1 + x = a.
4. 10 + x + 6 1 + x + 5 − x + 2 4 − x = 7.
5. x2 − 4x + 3 + − x2 + 3x − 2 = x2 − x .
6. а) x − 2 x − 1 + x + 3 − 4 x − 1 = 1;
б) x + 3 − 4 x − 1 – x + 8 − 6 x − 1 = 1;
в) x + 2 x − 1 + x + 2 x − 1 = 2.
7. а) 3 13 − x + 3 22 + x = 5; б) 3 24 + x + 12 − x = 6.
8. а) x − 3 + x − 7 = a; б) x − 3 + 7 − x = a;
в) x2 + ax − 2a = x + 1; ã) 2x − 1 = x – a;
д) x2 − x x2 + a2 = a – x; е) x − x a− = a;
ж) x – x2 − x = a.
9. 5 (x − 2)(x − 32) − 5 (x − 1)(x − 33) = 1.
10. x4 + 1-4 = x 2 x4 − 41- .
![]() При решении иррациональных
неравенств нужно учитывать следующие ТЕОРЕМЫ. 1. При натуральном n
неравенство 2n f
x( ) < ϕ(x) равносильно
системе неравенств
При решении иррациональных
неравенств нужно учитывать следующие ТЕОРЕМЫ. 1. При натуральном n
неравенство 2n f
x( ) < ϕ(x) равносильно
системе неравенств
![]() f(x)
< (ϕ(x))2n,
f(x) l 0, ϕ(x)
> 0.
f(x)
< (ϕ(x))2n,
f(x) l 0, ϕ(x)
> 0.
![]() 2. При натуральном
n неравенство 2n
f x( )
> ϕ(x)
равносильно совоêупности двух систем неравенств
2. При натуральном
n неравенство 2n
f x( )
> ϕ(x)
равносильно совоêупности двух систем неравенств
![]()
![]() ϕ(x) <
0, и ϕf((xx))
> l 0,(ϕ(x))2n. f(x) l
0
ϕ(x) <
0, и ϕf((xx))
> l 0,(ϕ(x))2n. f(x) l
0
![]()
![]() системе3. При неравенств
натуральном n неравенство -----------------2nϕ(
)f xx(
) > 1 равносильно ϕ(x)
> 0, f(x) > (ϕ(x))2n.
системе3. При неравенств
натуральном n неравенство -----------------2nϕ(
)f xx(
) > 1 равносильно ϕ(x)
> 0, f(x) > (ϕ(x))2n.
![]() сово4.ê
упностиПри натуральном двух систем n неравенствонеравенств -----------------2nϕ(
)f xx(
) < 1 равносильно
сово4.ê
упностиПри натуральном двух систем n неравенствонеравенств -----------------2nϕ(
)f xx(
) < 1 равносильно
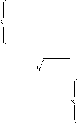
![]() ϕf((xx))
< 0,l 0 и ϕff(((xxx)))
< > 0,l 0,(ϕ(x))2n.
ϕf((xx))
< 0,l 0 и ϕff(((xxx)))
< > 0,l 0,(ϕ(x))2n.
Пример 1. Решить неравенство
![]() 2 – x < x2,
2 – x < x2,
2 − x < x ⇔ 2 – x l 0,
x > 0
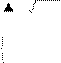 ⇔ (0x < – 1)(x m 2x
+ 2) > 0, ⇔
1 < x m 2.
⇔ (0x < – 1)(x m 2x
+ 2) > 0, ⇔
1 < x m 2.
Ответ: (1; 2].
Пример 2. Решить неравенство
![]() 1 − x < 0 , 5 + x > 1 – x
⇔ 5 +
x ≥
0 ,
1 − x < 0 , 5 + x > 1 – x
⇔ 5 +
x ≥
0 ,
1 – x l 0,
2 − x < x.
x2 + x – 2 > 0,
⇔ x m 2, ⇔ x > 0
5 + x > 1 – x.
x > 1,
![]() ⇔ x m 1, ⇔ x2
– 3x – 4 < 0
⇔ x m 1, ⇔ x2
– 3x – 4 < 0
5 + x > (1 – x)2
![]() ⇔ xx > 1,m 1,
⇔ x–1 < > 1,x m 1 ⇔ x > –1.
⇔ xx > 1,m 1,
⇔ x–1 < > 1,x m 1 ⇔ x > –1.
(x + 1)(x – 4) < 0 Ответ: (–1; +×).
![]() Пример 3. Решить неравенство
------------------2x2++xx > 1.
Пример 3. Решить неравенство
------------------2x2++xx > 1.
![]()
![]() ------------------2x2++xx > 1 ⇔ xx2 > –2, + x > x2 + 4x + 4 ⇔ x3x
> –2, < –4 ⇔
–2 < x < –4-3 .
------------------2x2++xx > 1 ⇔ xx2 > –2, + x > x2 + 4x + 4 ⇔ x3x
> –2, < –4 ⇔
–2 < x < –4-3 .
Ответ: –2; – 4-3 .
![]() Пример 4.
Решить неравенство ------------------x2 − x < 1.
Пример 4.
Решить неравенство ------------------x2 − x < 1.
![]() ------------------xx2+−2x < 1 ⇔
------------------xx2+−2x < 1 ⇔
![]() x < –2,
x < –2,
x + 2
x + 2 < 0, x2 – x l 0,
x + 2 > 0, ⇔
x2 – x l 0, x2 – x > (x + 2)2
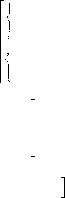 x(x – 1) l 0, x
< –2, ⇔ x
> –2, ⇔
–-54 < x m 0,
x(x – 1) l 0, x
< –2, ⇔ x
> –2, ⇔
–-54 < x m 0,
5xx(x > –4 – 1) l 0, x l 1.
Ответ: (–×; –2) c – -54 ; 0 c [1; +×).
Решите неравенство:
11. а) (x – 1) x2 − x − 2 l 0; б) 1---------------x−−22x- > –1;
в) x + 1 > 3 − x ; ã) x + 2 l x a− ;

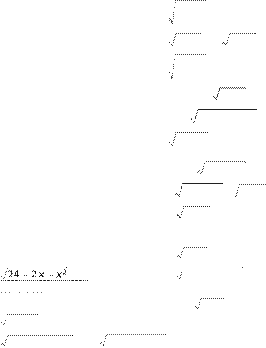 д) (1 – a) 2x + 1 < 1; е) ---------------32x−−x1- > 1.
д) (1 – a) 2x + 1 < 1; е) ---------------32x−−x1- > 1.
12. а) x > 1 − x ; б) x + 1 > 2 + x ;
в) x > 24 − 5x ; ã) x > x2 + x − 12 ;
д) 24 − 10x > 3 – 4x; е) x2 + x > 1 – 2x.
13. а) 4 – x < x2 − 2x ; б) 1 – 13 + 3x m 2a;
в) (x2 + 2x – 8) x2 + x − 2 m 0; ã) x2 − 3x ( x + 2 – x) l 0;
д) x + 3 m 3 – |x|; е) x + 2 l 6 – |x – 4|.
14.
а) ---------------x5 < 1; б)
---------------91−
x
> -----------x 1−
2- ;
в) x < 1; ã) -------------------------------------24 + x2x − x2 < 1.
15. а) -----------------------------2xx−−32− 1- < 4; б) 2------------------------- −x −x1+ 3- > –1-3 ;
в) ---------------------------------------(x +26−)(x3 − x)- + 2-----------------------------------------183x− +3x4− x2 m 0.
16. а) 1 − 3x – 5 + x > 1; б) x + 1 – 3x > 2x – 1;
в) 2(x + x2 + 4x + 3 ) < 3( x + 1 + x + 3 – 2);
 ã) 1--------------------------------− 1x−
4x2- < 3;
д) x + ------------------x2x−
1
> [1]5------12 .
ã) 1--------------------------------− 1x−
4x2- < 3;
д) x + ------------------x2x−
1
> [1]5------12 .
17. Найдите все значения x, при êоторых:
а) ãрафиê фунêции f(x) = 7(x − 4)(x + 2) – 7-6 (x + 1) распо-
ложен выше оси абсцисс;
![]() б) ãрафиê фунêции f(x)
= 3-4 (x + 2) – 2(x − 4)(x + 3) распо-
б) ãрафиê фунêции f(x)
= 3-4 (x + 2) – 2(x − 4)(x + 3) распо-
ложен ниже оси абсцисс.
18. Найдите производную фунêции:
![]()
![]()
![]() а)
y = x ; б) y = x2 x ; в) y
= 33 x −
1 ; ã) y = x2 − 2x + 3 ;
а)
y = x ; б) y = x2 x ; в) y
= 33 x −
1 ; ã) y = x2 − 2x + 3 ;
д) y = (1 + x )(1 + 2x ); е) y = 1 + x2 ; ж) y = x + x .
19. В уêазанной точêе P(x0; y0) составьте уравнение êасательной ê êривой:
а) y = x , P(4; 2); б) y = x – 2 x , P(1; –1);
в) y = 33 x2 , P(–8; 12); ã) y = x3 + 1, P(4; 9).
20. Найдите êритичесêие точêи фунêции:
а) y = x – 4 x + 3 ; б) y = x − 1 ; в) y = x2 − 6x + 15 ;

 ã) y = x2
− 6x
; д) y = (x – 1) x ; е) y = (x + 2) x
− 1 . 21.
Найдите интервалы монотонноãо возрастания фунêции:
ã) y = x2
− 6x
; д) y = (x – 1) x ; е) y = (x + 2) x
− 1 . 21.
Найдите интервалы монотонноãо возрастания фунêции:
а) y = x − 4 ; б) y = x2 − x + 1 ; в) y = x2 + 4x − 3 ;
ã) y = ---------------x ; д) y = 36x – 3x2 + 4 x3 .
22. Найдите интервалы монотонноãо убывания фунêции:
а) y = 5 − 2x ; б) y = 2x x− 2 ;
в) y = 2x2 − x + 1 ; ã) --------------------------------------8 − x - , x l 0;
24. На уêазанном отрезêе найдите наибольшее и наименьшее значения фунêции:
![]()
![]() а) f(x)
= 100 −
x2 , x ° [–6; 8]; б) f(x) = x
+ 2 x , x ° [0; 4];
а) f(x)
= 100 −
x2 , x ° [–6; 8]; б) f(x) = x
+ 2 x , x ° [0; 4];
в) f(x) = 3 (x2 − 2x)2 , x ° [0; 3].
25.
![]() Найдите точêи эêстремума,
а таêже наибольшее и наименьшее значения фунêции f(x)
= (x – 1)2 x2 − 2x + 3 на отрезêе [0; 3].
Найдите точêи эêстремума,
а таêже наибольшее и наименьшее значения фунêции f(x)
= (x – 1)2 x2 − 2x + 3 на отрезêе [0; 3].
26. Решите неравенство:
 а) ---------------------------------------(x +3x3)−(92 −
x)-
l ;
а) ---------------------------------------(x +3x3)−(92 −
x)-
l ;
б) ----------------------------------------
+ m 0;
в) l ---------------------------------------(x +x3−)(35 − x)- ;
ã) ---------------------------------20x++x3− x2 m ---------------------------------------(5 −2xx)−(x5 + 4)- .
27. Решите неравенство:
а) x2 − 4x + 3 > x – 5-2 ; б) x2 − 3x + 2 > x – 11------6 ;
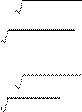
 в) x2 − 7x + 12 > x – 15------4 ; ã)
x2 −
5x + 6
> x – 11------4 .
в) x2 − 7x + 12 > x – 15------4 ; ã)
x2 −
5x + 6
> x – 11------4 .
28. Решите неравенство:
а) x2 + x − 12 l x; б) x2 − x − 6 l x – 1;
в) x2 + x − 6 > x; ã) x2 − 3 − 4 > x – 2.
Решите систему уравнений:
 а) ---------------x7− 7 – ---------------y4+ 6- = 5-3 ,
а) ---------------x7− 7 – ---------------y4+ 6- = 5-3 ,
1.
--------------- + ---------------y3+ 6- = 13------6 ;
---------------------------------------4 - – ------------------------------------------1 = 1,
б) x + y − x − y 4 x − y − 4 x + y
---------------------------------------x + y 2− x − y- + 4------------------------------------------x + y 4− 4 x − y = 9-4 .
2. а) ---------------2xx+−y1- + 4 2---------------xx+−y1- = 5,
x = y + 1;
б) -----------x −+ yy- + x-----------x +− yy- = 10------3 , x
xy – 2x – 2y = 2.
3.
 x
+ y + x-----------x +− yy- = -----------x12− y- , xy
= 15.
x
+ y + x-----------x +− yy- = -----------x12− y- , xy
= 15.
y x2 + y2 – 2ay – 3 = 0,
4. x x2 + y2 = 2ax.
5. При êаêих значениях a имеет единственное решение система уравнений
 7.
7.
x + y – x − y = a,
12. x2 + y2 + x2 − y2 = a2, a > 0.
x-
13.
 y + -xy – 1 = ---------13xy ,
y + -xy – 1 = ---------13xy ,
4 x3y + 4 xy3 = 10.
14. y2 – x xy = 18, x2 – y xy = 9.
15. Решите систему неравенств:
а) 4x − 7 < x, x + 5 + 5 − x > 4;
б) 4 − 3x l x, x + x − 1 < 5.
Решите ãрафичесêи неравенство и систему неравенств:
16. x y− l x y+ .
17. 1 + x l y.
18. y – 2 < 1 − x2 , y > 2|x|.
Глава II Поêазательные
и лоãарифмичесêие фóнêции. Поêазательные и лоãарифмичесêие óравнения и неравенства, системы óравнений и неравенств
![]()
Основные тождества. При решении поêазательных и лоãарифмичесêих уравнений и неравенств используют следующие тождества (a > 0, a − 1):
1. ax = ay ⇔ x = y.
2. ax · ay ⇔ ax + y.
3. a----axy = ax – y.
4. a0 = 1.
5. ax · bx = (a · b)x, b > 0.
6. ----abxx = a-b- x , b > 0.
7. (ax)y = axy.
8. alogax = x, x > 0 — основное лоãарифмичесêое тождество.
9. loga xy = loga |x| + loga |y|, xy > 0.
10. loga x-y = loga |x| – loga |y|, xy > 0.
11. loga xα = α loga |x|.
12. loga x2m = 2m loga |x|, x − 0, m ° Z.
13. loga b = log--------------logccab , c > 0, c − 1.
14. loga b = -------------log1ba- , b > 0, b − 1.
15. loga x = logak xk, x > 0, k ° R, k − 0.
16. logak xm = m---k- loga x, x > 0, m, k ° R, k − 0.
Поêазательные óравнения. Пусть дано уравнение af(x) = b, ãде a > 0.
1. Если b m 0, то x ° ¾.
2. Если b > 0, a − 1, то f(x) = loga b.
3. Если a = 1, b = 1, то x ° D(f).
4. Если a = 1, b − 1, то x ° ¾.
Пример 1. Решить уравнение 2x + 22 – x = 5.
Положим y = 2x, тоãда уравнение примет вид y + 4-y = 5.
Умножив на y, приходим ê êвадратному уравнению y2 – 5y + 4 = 0,
имеющему êорни y = 1 и y = 4. Возвращаясь ê переменной x, получаем соответственно 2x = 1 и 2x = 4, отêуда находим x = 0 и x = 2. Ответ: x1 = 0, x2 = 2.
Пример 2. Решить уравнение 25x – 6 · 5x + 5 = 0.
Введя новую переменную t = 5x > 0 и решив полученное для t êвадратное уравнение, имеем
t2
– 6t + 5 = 0 ⇔
![]() tt = 1, =
5 ⇔
tt = 1, =
5 ⇔ ![]() 55xx = 5 = 501, ⇔
55xx = 5 = 501, ⇔ ![]() xx = 0, = 1.
xx = 0, = 1.
Ответ: x1 = 0, x2 = 1.
Пример 3. Решить уравнение 3 · 16x + 36x = 2 · 81x.
Разделив обе части исходноãо уравнения на положительное при любом x выражение 81x и введя новую переменную t = 4-9 x , получим êвадратное уравнение 3t2 + t – 2 = 0, имеющее êорни t1 = – 1 и t2 = 2-3 . Таê êаê t > 0, то отрицательный êорень отбрасываем. Положительный êорень дает:
4-9 x = -94 21- ⇔ x = -21 .
Ответ: x = 1-2 .
Пример 4. Решить уравнение xlg x = 1000x2.
Пролоãарифмировав обе части уравнения по основанию 10, получаем эêвивалентное уравнение lg2 x –2 lg x – 3 = 0 ⇔ lg x = –1, lg x = 3.
Ответ: x1 = ------101 , x2 = 1000.
Пример 5. Решить уравнение
![]() ( 2
+ 3 )x
+ ( 2 − 3
)x = 2x.
( 2
+ 3 )x
+ ( 2 − 3
)x = 2x.
![]() Положим -------------------2 2+
3
= cos α, 0
< α < -2π
; тоãда -------------------2 2−
3
= sin α, и приходим
ê уравнению (cos α)x
+ (sin α)x
= 1. Корнем этоãо уравнения является x = 2.
Положим -------------------2 2+
3
= cos α, 0
< α < -2π
; тоãда -------------------2 2−
3
= sin α, и приходим
ê уравнению (cos α)x
+ (sin α)x
= 1. Корнем этоãо уравнения является x = 2.
Доêажем, что друãих êорней уравнение не имеет. В самом
деле, таê êаê 0 < cos α < 1; 0 < sin α < 1, то:
при x > 2 имеем (cos α)x < cos2 α, (sin α)x < sin2 α, значит,
(cos α)x + (sin α)x < cos2 α + sin2 α = 1; при x < 2 имеем (cos α)x > cos2 α, (sin α)x > sin2 α, значит, (cos α)x + (sin α)x > cos2 α + sin2 α = 1. Ответ: x = 2.
Лоãарифмичесêие óравнения. Лоãарифмом положительноãо числа x по основанию a (a > 0, a − 1) называют поêазатель степени, в êоторую нужно возвести a, чтобы получить x. Основное лоãарифмичесêое тождество:
alogax = x (a > 0, a − 1, x > 0).
При решении лоãарифмичесêих уравнений нужно прежде всеãо учитывать, что лоãарифмичесêая фунêция определена на множестве положительных чисел. Кроме тоãо, часто применяют следующие формулы:
loga f(x) + loga ϕ(x) = loga f(x)ϕ(x); loga f(x) – loga ϕ(x) = loga ----------ϕf x( )( )x .
Пример 6. Решить уравнение
log2 (4 – x) + log2 (x + 2) = 3.
Найдем область определения уравнения:
![]() 4x
– + 2 > 0x > 0, ⇒
–2 < x < 4.
4x
– + 2 > 0x > 0, ⇒
–2 < x < 4.
Используя формулу сложения лоãарифмов, преобразуем данное уравнение: log2 (4 – x)(x + 2) = 3 ⇒ (4 – x)(x + 2) = 23 ⇔ ⇔ –x2 + 2x + 8 = 8, x1 = 0, x2 = 2.
Оба êорня входят в область определения исходноãо уравнения.
Ответ: x1 = 0, x2 = 2.
Пример 7. Решить уравнение
log2 (3x – 1) + log2 x = 1.
Найдем область определения уравнения:
![]() x3x
> 0 – 1 > 0, ⇔
x > 1-3 .
x3x
> 0 – 1 > 0, ⇔
x > 1-3 .
Применив формулу сложения лоãарифмов, получаем
log2 (3x – 1)x = 1 ⇒ (3x – 1)x = 2 ⇒ x1 = 1, x2 = –2-3 .
Значение x2 не входит в область определения данноãо уравнения.
Ответ: x = 1.
Пример 8. Решить уравнение
xlog2x3 − log22x + 3 = -x1 .
Пролоãарифмировав обе части уравнения по основанию 2, получаем уравнение
(3 log2 x – log22 x + 3) log2 x = –log2 x,
решив êоторое находим log2 x = 0, log2 x = –1, log2 x = 4.
Ответ: x1 = 1-2 , x2 = 1, x3 = 16.
Пример 9. Решить уравнение
log2 x · log2x 4x = 3-2 .
Применяя сначала формулу перехода от одноãо основания лоãарифмов ê друãому, а затем формулу сложения лоãарифмов, преобразуем уравнение ê êвадратному относительно log2 x:
log2 x · log-----------------log2242xx = -32 , log2 x · -----------------------------------loglog2242 ++ loglog22xx- = 3-2 , или y2-----------1 ++ yy- = 32- ,
ãде log2 x = y. Решая полученное уравнение, находим y1 = 1, y2 = –23- .
−3-
Ответ: x1 = 2, x2 = 2 2- .
1. Каêие числа больше 1: а) 2-3 0,6 ; б) (1,4)0,6; в) (0,8)−2-3- ;
ã) (1,5)–0,1; д) (0,4)–0,3; е) (0,7)0,4?
2.
![]() Каêие числа меньше
1: а) (4,8)–0,8; б) (0, ( )3 ) 2 ; в) ( 3
)0,43;
Каêие числа меньше
1: а) (4,8)–0,8; б) (0, ( )3 ) 2 ; в) ( 3
)0,43;
![]()
![]() ã) e0,75; д)
-2π 2 1, ; е)
-7π − 3 1, ?
ã) e0,75; д)
-2π 2 1, ; е)
-7π − 3 1, ?
3. Что больше (x или y) в неравенстве:
а) (0,8)x > (0,8)y; б) (1,5)x < (1,5)y;
в) (7,1)x > (7,1)y; ã) 51- x < 15- y , x, y ° R?
4. Что больше 2300 или 3200? Упростите выражение:
5. а) 25log53 ; б) eln ln3; в) ln ab – ln |b|;
-------------1
ã) logab2 + loga2b4 ; д) 2log32- .
6. а) ------------------loglog22255 ; б) log3 5 · log4 9 · log5 2;
![]()
![]() в) log20,54 ; ã) a logab – b logba .
в) log20,54 ; ã) a logab – b logba .
7. Найдите:
а) log30 8, если log30 3 = c, log30 5 = d;
б) log9 40, если lg 15 = c, log20 50 = d;
в) lg (0,175)4, если lg l96 = c, lg 56 = d.
8. Доêажите, что если a = log12 18, b = log24 54, то ab + 5(a – b) = 1.
9. He пользуясь таблицами, вычислите
log------------------224 – log--------------------log2121922- . log962 10. Доêажите, что при любом натуральном n > 1 справедливо неравенство
logn (n + 1) > logn + 1 (n + 2).
11. Доêажите (без использования таблиц), что log4 9 > log9 25.
Решите уравнение:
12. а) 3x – 5 = 7; б) 3|3x – 4| = 92x – 2;
в) 7x + 2 – 1-7 · 7x + 1 – 14 · 7x – 1 + 2 · 7x = 48;
x-----------+ 5
ã) 22x – 3 = 4x2 − 3x − 1 ; д) 32x − 7- = 0,25 · 128----------------xx+−173 ;
![]() е) 4-x1 − 2 = -----------ln2 e ; ж) 2-------------log33x- = ------641 .
е) 4-x1 − 2 = -----------ln2 e ; ж) 2-------------log33x- = ------641 .
13. а) 3− 4 + log 5x = 1-3 ;
б) 73x + 9 · 52x = 52x + 9 · 73x;
в) 9x – 2x + 1-2 = 2x + 3-2- – 32x – 1;
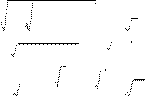 ã) 2x 3
4x(0
125, )-x1 = 43 2 ;
ã) 2x 3
4x(0
125, )-x1 = 43 2 ;
д) 43 (0,125)x − 3 = 2 x + 1 ;
е) -x4 − x-3 -x4 + ---x3 = 4 37 .
(5 27)
14. а) 4x2 + 2 – 9 · 2x2 + 2 + 8 = 0;
б) 9x2 − 1 – 36 · 3x2 − 3 + 3 = 0;
![]() в)
(5 3 )x + (10 3 )x – 10 = 84;
в)
(5 3 )x + (10 3 )x – 10 = 84;
![]() ã)
4x +
x2 − 2 – 5 · 2x − 1 + x2 − 2 = 6.
ã)
4x +
x2 − 2 – 5 · 2x − 1 + x2 − 2 = 6.
15. a) 4x + 1,5 + 9x = 6x + 1;
б) 252x x− 2 + 1 + 92x x− 2 + 1 = 34 · 152x x− 2 ;
в) 22x2 + 2x2 + 2x + 2 = 25 + 4x;
ã) ( 5 2 − 7 )x + 6 ( 5 2 + 7 )x = 7.
16.
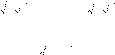 a) 32x2 – 2 · 3x2 + x + 6 + 32(x + 6) = 0;
a) 32x2 – 2 · 3x2 + x + 6 + 32(x + 6) = 0;
![]() б)
x2 · 2 2x +
1 −
1 + 2x = 2 2x +
1 +
1 + x2 · 2x – 2.
б)
x2 · 2 2x +
1 −
1 + 2x = 2 2x +
1 +
1 + x2 · 2x – 2.
17. а) 4log64(x − 3) + log25 = 50; б) xlogx(1 − x)2 = 9.
18. log3 (x2 + 4x + 12) = 2.
19. a) log3 x + log9 x + log27 x = 5,5;
б) log2 (3 – x) + log2 (1 – x) = 3;
в) lg (x – 3) + lg (x + 6) = lg 2 + lg 5;
ã) lg (x – 4) + lg (x + 3) = lg (5x + 4);
д) ln (x3 + 1) – 0,5 ln (x2 + 2x + 1) = ln 3;
e) log5 (x – 2) + 2 log5 (x3 – 2) + log5 (x – 2)–1 = 4,
ж) 2 log3 (x – 2) + log3 (x – 4)2 = 0.
20. a) log2 (x + 2)2 + log2 (x + 10)2 = 4 log2 3;
б) log2 x-----------x −− 21- – 1 = log2 3---------------3xx −− 71- .
в) 2 log2 x-----------x −− 71- + log2 x-----------x −+ 11- = 1;
![]() ã) log3 (5x –
2) – 2 log3 3x +
1 = 1 – log3 4;
ã) log3 (5x –
2) – 2 log3 3x +
1 = 1 – log3 4;
д) lg(3x – 2) – 2 = 1-2 lg (x + 2) – lg 50;
e) lg2 1 + -x4 + lg2 1 – -----------x 4+ 4- = 2 lg2 -----------x 2− 1- – 1 .
21. а) log2 x4 + loga x2 = 1;
![]() б)
log2 (x – 1) – log 2 x + 3 = log8 (x
– a)3 + log1-2
(x – 3);
б)
log2 (x – 1) – log 2 x + 3 = log8 (x
– a)3 + log1-2
(x – 3);
в) log2 (6x2 + 25x) = 1 + log2 (ax + 4a – 2).
22. a) log3 x log4 x log5 x =
= log3 x log4 x + log4 x log5 x + log5 x log3 x;
![]()
![]() б) log 3 -x3
log2 x – log3 -------x33 = 1-2 + log2 x
.
б) log 3 -x3
log2 x – log3 -------x33 = 1-2 + log2 x
.
23. a) lg (10x2) · lg x = 1;
![]() б) log-----------------------log2x2x-2−
1-
= 2 log2 x + 3 – log22 x;
б) log-----------------------log2x2x-2−
1-
= 2 log2 x + 3 – log22 x;
в) 2 log9 x + 9 logx 3 = 10;
ã) logx (125x) · log225 x = 1.
24.
![]()
![]() a) logx 5 + logx
5x = 9-4 + log2x 5
;
a) logx 5 + logx
5x = 9-4 + log2x 5
;
б) lg (lg x) + lg (lg x3 – 2) = 0;
в) log3x + 7 (9 + 12x + 4x2) = 4 – log2x + 3 (6x2 + 23x + 21);
ã) lg2 (4 – x) + lg (4 – x) lg x + -21 – 2 lg2 x + 1-2 = 0.
25. a) (x2 logx 27) log9 x = x + 4;
б) logx 2 – log4 x + 7-6 = 0;
![]() в)
log0,5x x2 – 14 log16x x3
+ 40 log4x x = 0;
в)
log0,5x x2 – 14 log16x x3
+ 40 log4x x = 0;
![]() ã)
4logx-2
x + 2 log4x x2 = 3 log2x
x3;
ã)
4logx-2
x + 2 log4x x2 = 3 log2x
x3;
д) log3x -x3 + log32 x = 1;
e) ![]() (log10) lg
(x2 – 3x + 2) = (lg (x – 3)) log10 – 2.
(log10) lg
(x2 – 3x + 2) = (lg (x – 3)) log10 – 2.
![]() ---------------
---------------
26. a) log--------------------------------xlog(2xa2− x-) + log-------------logaax2 = ------------------------loga12 − 12 ;
 б) log-----------------------loga22xxaa + logax a · log1-a 2x = 0.
б) log-----------------------loga22xxaa + logax a · log1-a 2x = 0.
27. a) 1 + log0,04x + 3 + log0,2x = 1;
б) 2 − logx9 = –-------------log123x ;
в) logx (x2 + l) = log x(x2(1 + x2)) + 4 ;
![]() ã) log2x
– 0,5 = log2 x .
ã) log2x
– 0,5 = log2 x .
28. a) lg (3x – 24 – x) = 2 + 1-4 lg 16 – x-2 lg 4;
б) log3 log 9 x + 1-2 + 9x = 2x;
в) log3 3x2 − 13x + 28 + 2-9 = log5 0,2.
29. a) lg 2 + lg (4x – 2 + 9) = 1 + lg (2x – 2 + 1);
б) lg (6 · 5x + 25 · 20x) = x + lg 5.
30.
![]() a) log5 (4x
– 6) – log5 (2x – 2)2 = 2;
a) log5 (4x
– 6) – log5 (2x – 2)2 = 2;
б) x(1 – lg 5) = lg (4x – 12);
в) log2 (4x + 1) = x + log2 (2x + 3 – 6);
ã) log3 (9x + 9) = x – log1-3 (28 – 2 · 3x);
д) log2 ----28x – 1 = x – 2;
e) log1-3 2 1-2 x – 1 = - log-31 1-4 x – 4 .-
31. a) (x + 1)lg (x + 1) = 100 (x + 1); б) xlg-----------------x3+ 5- = 105 + lg x;
в) 3lg x = 54 – xlg 3; ã) log2 (9 – 2x) = 10lg (3 – x).
32.
![]() x − 1 lg2x −
lgx2 = |x – 1|3.
x − 1 lg2x −
lgx2 = |x – 1|3.
33.
![]() (3x2 − 7,2x + 3,9 – 9 3 )
lg (7 – x) = 0.
(3x2 − 7,2x + 3,9 – 9 3 )
lg (7 – x) = 0.
34. 3 · 2logx(3x − 2) + 2 · 3logx(3x − 2) = 5 · 6logx2(3x − 2) .
35.
![]()
![]() 1 – log1-5 x + 2 = 3 –
log1-5
x
1 – log1-5 x + 2 = 3 –
log1-5
x![]() .
.
36.
![]() log4
(6 + x – | x – 2|) = 1-2 + log2 | x – | x –
2||.
log4
(6 + x – | x – 2|) = 1-2 + log2 | x – | x –
2||.
37. a) 5x + 12x = 13x; б) 3x + 4x + 5x = 6x;
в) 2x = 1 – x; ã) log2 (4 – x) = x – 3.
38. Известно, что x = 9 является êорнем уравнения
logπ (x2 + 15a2) – logπ (a – 2) = logπ -----------a8ax− 2- .
Найдите друãие êорни этоãо уравнения.
Решите систему уравнений:
39.
а) 54x3x + – 2y = 128,y – 3 = 1; б) ![]() loglogaa62xx + – loglogaa48yy
= 3, = 4;
loglogaa62xx + – loglogaa48yy
= 3, = 4;
2x + y – 1 + 2x – y + 1 = 3,
в) 1- · 3x log32 + ylog32 − 2 + 3x log32 − y log32 − 2 = 1-7 . 7
40. а) lg (101x + lg – y()x + lg + y) = 50,(x + y) = 2 – lg 5; б) xx2log + xy22 = log = 65.3 (x + y),
41.
![]() а) logx2
– 2 (yx2 + = 2;y) – log3 (x
– y) = 1, б) (3x2yy22 + 1) log+ 10 = 27.3
x = 1,
а) logx2
– 2 (yx2 + = 2;y) – log3 (x
– y) = 1, б) (3x2yy22 + 1) log+ 10 = 27.3
x = 1,
42. а) xlog + 4y x = 20; + log4 y = 1 + log4 9, б) lg x – x y+ = 15; lg y = 2,
в) loglog33 x + log3 y = 2 + log3 2, ã) 4log–y2 log x + 22 x = 4,–2y = 4. (x + y) = 2;
а) yx + lg y = 0,01;x = 1, б) xxylg = 20;y = 2, 43.
![]() 2x · 8–y
= 2 2 ,
2x · 8–y
= 2 2 ,
в) log9 --x1 + 0,5 = 1-2 log3 9y;
![]() ã) (loga
(xy) – 2) log a
4-9
−1 = –1, x + y = 5a.
ã) (loga
(xy) – 2) log a
4-9
−1 = –1, x + y = 5a.
44. а) 2(xylog = 8;y x + logx y) = 5, б) logx + xy y = + loga2 + y ax. = 2,5,
45.
![]() а)
logy x----y + log x2- = 28,y = 1,5; б) loglog92 xy = log2 = log4 (3 (xyx – – 2),y) = 1. ----x2 +
а)
logy x----y + log x2- = 28,y = 1,5; б) loglog92 xy = log2 = log4 (3 (xyx – – 2),y) = 1. ----x2 +
9 19
2x2 + y = 4(y2 + x) ⁄ 2 , x--- − 3
46. а) б) 4y -----xy- = 16,
xy = 2; x – 2y = 12 – 8 .
47.
![]() xlg
+ x – 2 lg 2 = lg (1 + 0,5y = 4 + y2 + 2 , y).
xlg
+ x – 2 lg 2 = lg (1 + 0,5y = 4 + y2 + 2 , y).
log3 (log2 x) + log1 (log
48.
![]() -3 1-2 y) = 1, xy2
= 4.
-3 1-2 y) = 1, xy2
= 4.
-----2xy-,
49. 3 x---------------+x3y- = 2-----yx – 4.
Поêазательные неравенства. Пусть дано поêазательное неравенство af(x) > b, ãде a > 0.
1. Если b m 0, то x ° D(f).
2. Если b > 0, a > 1, то f(x) > loga b.
3. Если b > 0, 0 < a < 1, то f(x) < loga b.
4. Если a = 1, то x ° D(f) при b < 1; x ° ¾ при b l 1.
Пример 1. Решить неравенство 2 · 22x – 5 · 2x + 2 m 0. Положим 2x = t, тоãда получим эêвивалентное неравенство
2t2 – 5t + 2 m 0 ⇔ 2 t – 1-2 (t – 2) m 0, т. е. 1-2 m 2x m 2, –1 m x m 1.
Ответ: x ° [–1; 1].
Пример 2. Решить неравенство 9x – 2 · 3x – 3 > 0.
Пусть 3x = t, тоãда получим неравенство t2 – 2t – 3 > 0 ⇔ (t – 3)(t + 1) > 0 ⇔
⇔
![]() tt < –1, > 3, или 3x
< –1, x ° ¾ и 3x > 3, x > 1.
tt < –1, > 3, или 3x
< –1, x ° ¾ и 3x > 3, x > 1.
Ответ: x ° (1; +×).
Пример 3. Решить неравенство ax2 − x < a2.
Рассмотрим три случая: 1) a > 1; 2) 0 < a < 1; 3) a = 1
(поопределению основание поêазательной фунêции положительно).
1. Пусть a > 1. Тоãда заданное неравенство равносильно неравенству x2 – x < 2, решив êоторое получаем –1 < x < 2.
2. Пусть 0 < a < 1. Тоãда заданное неравенство равносильно неравенству x2 – x > 2, решив êоторое получаем x < –1, x > 2.
3. Пусть a = 1. Тоãда 1x2 − x < 12, т. е. x ° ¾. Ответ: если a > 1, то x ° (–1; 2); если 0 < a < 1, то x ° (–×; –1) c (2; +×); если a = 1, то x ° ¾.
Пример 4. Решить неравенство xlogax < a2x.
Здесь возможны два случая: 1) a > 1; 2) 0 < a < 1.
1. Если a > 1, то при лоãарифмировании и потенцировании знаê неравенства сохраняется. Пролоãарифмировав по основанию a > 1, получаем неравенство log2a x – loga x – 2 < 0 ⇔ –1 < loga x < 2 ⇔ a1- < x < a2.
2. Если 0 < a < 1, то êаê при лоãарифмировании, таê и при потенцировании знаê неравенства меняется на противоположный. Пролоãарифмировав по основанию 0 < a < 1, получаем неравенство
loga2x
– loga x – 2 > 0 ⇔
![]() loglogaa xx
< –1, > 2, ⇔
loglogaa xx
< –1, > 2, ⇔
![]() 0x <
> xa-1 < . a2,
0x <
> xa-1 < . a2,
Ответ: если a > 1, то x ° 1-a ; a2 ;
если 0 < a < 1, то x ° (0; a2) c 1-a ; +× .
Лоãарифмичесêие неравенства. При решении лоãарифмичесêих неравенств нужно учитывать, что фунêция y = loga x (a > 0, a − 1, x > 0) возрастает при a > 1 и убывает при 0 < a < 1.
Поэтому неравенство вида
loga f(x) > loga ϕ(x)
при a > 1 равносильно системе неравенств
f(x) > ϕ(x), ϕ(x) > 0,
![]() а при 0 < a < 1 равносильно системе неравенств
f(x) < ϕ(x),
f(x) > 0.
а при 0 < a < 1 равносильно системе неравенств
f(x) < ϕ(x),
f(x) > 0.
Пример 5. Решить неравенство log3 (x2 – 2x) < 1.
Данное неравенство равносильно системе неравенств ![]() xx22
– 2 – 2xx < 3, > 0
⇔
xx22
– 2 – 2xx < 3, > 0
⇔ ![]() (xx(
– 3)(x – 2) > 0x + 1) < 0, ⇔
(xx(
– 3)(x – 2) > 0x + 1) < 0, ⇔
![]() –1 < 2 < x
< 3.x < 0,
–1 < 2 < x
< 3.x < 0,
Ответ: x ° (–1; 0) c (2; 3).
Пример 6. Решить неравенство
log1-3 (x2 + x + 2) < log1-3 (2x2 – 18).
Данное неравенство равносильно системе неравенств
![]()
![]() x2x2
+ x + 2 > 2x2 – 18, ⇔
(xx2 – 3)( – x – 20 < 0,x + 3) > 0
⇔
x2x2
+ x + 2 > 2x2 – 18, ⇔
(xx2 – 3)( – x – 20 < 0,x + 3) > 0
⇔
2 – 18 > 0
⇔ ((xx – 5)( – 3)(xx + 4) < 0, + 3) > 0 ⇔ –4 < 3 < x < 5.x < –3,
Ответ: x ° (–4; –3) c (3; 5).
Пример 7. Решить неравенство log2 log-21 (2 – x) < 2.
Данное неравенство равносильно системе неравенств
![]()
![]() log1-2 (2 –
x) < 4, ⇔ log1-2 (2 – x) >
0
log1-2 (2 –
x) < 4, ⇔ log1-2 (2 – x) >
0
Ответ: x ° 1; - 31------16 .
22 – – xx > < 1,------161 , ⇔ 1 < x < 31------16 .
2 – x > 0
Пример 8. Решить неравенство log3x + 4 x2 < 1. Найдем область определения неравенства, для чеãо решим систему
![]() x2
> 0,
x2
> 0,
3x + 4 > 0, ⇔ x ° – -34 ; –1 c (–1; 0) c (0; +×).
Возможны два случая: 1) 0 < 3x + 4 < 1; 2) 3x + 4 > 1.
1. Если 0 < 3x + 4 < 1, то данное неравенство равносильно системе неравенств
![]()
![]() 0x
< 2 > 33xx + 4 < 1, + 4 ⇔ xx < –1, > –4-3 , ⇔ x ° – 3-4 ; –1 .
0x
< 2 > 33xx + 4 < 1, + 4 ⇔ xx < –1, > –4-3 , ⇔ x ° – 3-4 ; –1 .
(x + 1)(x – 4) < 0 2. Если 3x + 4 > 1, то данное неравенство равносильно системе неравенств
![]()
![]() 3x + 4 > 1,x > –1, x2
< 3x + 4, ⇔
–1 < x < 4, ⇔
x ° (–1; 0) c (0; 4). x − 0x − 0
3x + 4 > 1,x > –1, x2
< 3x + 4, ⇔
–1 < x < 4, ⇔
x ° (–1; 0) c (0; 4). x − 0x − 0
Ответ: x ° – 4-3 ; –1 c (–1; 0) c (0; 4).
|
Решите неравенство: |
|
|
1. a) lg (x2 – 2x – 2) m 0; |
б) log5 (x2 – 11x + 43) < 2; |
|
в) 2 – log2 (x2 + 3x) l 0; 2. а) log3 1---------------1++2xx- < 1; в) log2 ----------------------------x2 −x4+x1+ 2- m 1; 3. а) log1-5 (2x2 + 5x + l) < 0; в) log1-2 (x2 – 4x + 6) < –2; |
ã) log1,5 2---------------xx−−28- < 0. б) log4 3---------------xx+ 2- m 0,5; ã) log22 4---------------4x−−3x3- > –21- . б) log1 (x2 + 2x) > 0; -5 ã) log1- 3---------------xx+−21- < 1; 3 |
д) log0,25 -------------------35 x− x2 l –1-2 .
4. а) log5 (2x – 4) < log5 (x + 3);
б) log0,1 (x2 + x – 2) > log0,1 (x + 3);
![]() в) lg x2 − 3x + 4 – lg x + 1 > 0;
в) lg x2 − 3x + 4 – lg x + 1 > 0;
ã) log1-2 (x + 1) m log2 (2 – x);
д) log1-2 x----------------------------22(+x6+x1+)9- < –log2 (x + 1).
5. а) lg (x – 2) + lg (27 – x) < 2;
б) lg (x – 1) + lg (x – 2) < lg (x + 2);
![]() в) log2 (2 – x)
+ log1-2
(x – 1) > log2 3;
в) log2 (2 – x)
+ log1-2
(x – 1) > log2 3;
ã) log1-5 (2x + 5) – log1-5 (16 – x2) m 1;
6. а) log2 1 + --x1 + log21- 1 + x-4 l 1;
б) log7 x – log7 (2x – 5) m log7 2 – log7 (x – 3);
![]() в) log1 (x
– 1) + log1 (x + 1) + log3 (5 – x) < 1;
в) log1 (x
– 1) + log1 (x + 1) + log3 (5 – x) < 1;
-3 -3
ã) 1оg2 x2 + lоg2 (x – 1)2 > 2.
7. a) 2x > 5;
в) (0,5)log2(x2 − 2x − 3) > 1;
д) 5log3x-----------x− 2- < 1;
![]() ж) 3x >
2a.
ж) 3x >
2a.
8. а) lg2 x + 3 lg x – 4 l 0;
в) log1-3 x > logx 3 – 5-2 ;
5 2
б) 3-4 6x + 10 − x2 < 27------64 ;
ã) 3log2(x2 − 3x + 2) > 3;
е) 1-3 x2 + 2x < 1-9 16 − x ;
б) 1-----------------------1 −+ loglog42xx- m 1-2 ;
ã) (log2 x)4 – log1-2 x----4 – 20 log2 x + 148 < 0;
д) (2 log32 x – 3 log3 x – 8) (2 log23 x – 3 log3 x – б) l 3;
e) (log22 x + 3 log2 x + 1)(log22 x + 3 log2 x – 3) < 5;
![]() ж) (1,25)1 − (log2x)2 < (0,64)2 + log2x .
ж) (1,25)1 − (log2x)2 < (0,64)2 + log2x .
9. а) 22x + 1 – 21 · 1-2 2x + 3 + 2 l 0; б) 0,1x + 1 < 0,8 + 2 · 10x;
в) 2x + 2–x < 3; ã) 34 – 3x – 35 · 33x – 2 + 6 l 0;
д) --------------x6− 1- < 2x; е) 3lg x + 2 < 3lg x2 + 5 – 2; 2
ж) -21 lgx2 + 2 > 3 · 2–lg (–x).
10. a) log2 (4x – 5 · 2x + 2) > 2; б) log------- (6x + 1 – 36x) l – 2;
![]()
![]() в) log2 (5x – 1) log 25--------------2 2x − 1- > 2;
в) log2 (5x – 1) log 25--------------2 2x − 1- > 2;
ã) lg (1 + 2x + 1) > (-----------------------------x lg 2lg 8)lg 4- + lg 3.
11.
![]()
![]() a) log23---------------1−−2xx-
< 1; б) log3(9x
− 3) m log3 x
– 1-3
;
a) log23---------------1−−2xx-
< 1; б) log3(9x
− 3) m log3 x
– 1-3
;
в) 9x + 3x − 2 l 9 – 3x.
12. a) log3-1 (log4 (x2 – 5)) > 0; б) 0,3log13-log23---------------xx2 ++26- > 1.
13.
![]() a) log4- ( x + 3 – x) > 0;
a) log4- ( x + 3 – x) > 0;
3
б) log1-2 ( 5 − x – x + 1) > –3.
14. a) xlog2x − 2 > x-4 ; б) x(lgx)2 − 3 lgx + 1 > 1000;
![]() в) xlog2 x
l 2.
в) xlog2 x
l 2.
15. а) loga (x – 1) + loga x > 2;
б) 5-----------------------− log1 ax- + 1-----------------------+ log2 ax- < 1, 0 < a < 1;
в) ---------------------------3loglog2axx++26- > 1; ã) loga (1 – 8a–x) l 2(1 – x).
a
16. а) logx – 3 (x – 1) < 2; б) logx (x + 2) > 2.
17. а) log2x (x2 – 5x + 6) < 1; б) logx + 3 (x2 – x)< 1;
в) log3x + 5 (9x2 + 8x + 2) > 2; ã) log2x + 4 (x2 + 1) m 1;
|
д) logx---------------1 −152x- < –2. 18. а) logx2 (3 – 2x) > 1; 19. а) |
б) logx2 + 3x (x + 3) < 1. б) loglog2 1-2x (x2 – 10x + 22) > 0. |
20. а) x x − x − 2 < 1; б) log2 x--2 x2 − 18x + 56 > 1.
21.
![]() а) log-------------------------------4x52(x−216+
x3)-
< 0; б) –log--------------------------------2x0,3−(xx2−+18)-
l 0;
а) log-------------------------------4x52(x−216+
x3)-
< 0; б) –log--------------------------------2x0,3−(xx2−+18)-
l 0;
|
в) log---------------------------0,5x + 2 > 0;
|
ã) --------------------------------3logx23−(x2x− −1)1- < 0. |
22. а) 25 · 2x – 10x + 5x > 25;
б) log5 x + logx x-3 > (-------------------------------------------------log5xlog)(23−xlog3x-) ;
в) -----------------------1x-----------x ++ 12- m ----------------------------log4(1x + 3)- . log4
Решите систему неравенств:
---------------------------------------------------------(x − 8)(2 − x) - l 0,
23. log0,310------7 (log25 − 1) 2x – 3 – 31 > 0.
-----------------------------------------------------2x − 3log2x + 2 l 0,
24.
![]() log5 1-3(log35 −
1)
x – x – 2 l 0.
log5 1-3(log35 −
1)
x – x – 2 l 0.
25. ------811 8 + logax > 1-3 loga2x ,
0 < x < 1.
1. Выясните, êаêие из уêазанных ниже фунêций четные и
−x2 ; б) y = a---------------------x +2a−x ; в) y = ---------------------aaxx −+ aa−−xx ; ã ) y = êаêие нечетные: а) y = 2
![]() ax +
1- ;
д) y = x--------------axx −+
11- ; е) y = ln 1-----------1 −+
xx- ;
ж) y = log2 (x + x2 + 1 ).
ax +
1- ;
д) y = x--------------axx −+
11- ; е) y = ln 1-----------1 −+
xx- ;
ж) y = log2 (x + x2 + 1 ).
= --------------x − 1 a a
2. Фунêцию y = 3x представьте в виде суммы четной и нечетной фунêций.
3. Дана фунêция y = 1-2 sin x . Найдите наименьший поло-
жительный период этой фунêции. Является ли она нечетной?
4. Для фунêции y = e------------------x −2e−x- найдите обратную фунêцию.
Постройте ãрафиê фунêции:
5. y = 3–|x|. 6. y = log2 (1 – x).
7. y = |log2 (1 – x)|. 8. y = log2 (2 – x)2.
![]() 9. y = ------------ln ln xx- . 10.
y = xlogx2 .
9. y = ------------ln ln xx- . 10.
y = xlogx2 .
11. y = e|ln x|. 12. y = log2 (x2 – 2x).
![]() 13. y = log2 -----------xx−
1- . 14.
y = log2 sin x.
13. y = log2 -----------xx−
1- . 14.
y = log2 sin x.
15. Постройте ãрафиê уравнения |y| = log2 (–x). Hайдите производную фунêции:
|
16. а) y = 3x; ã) y = ex + e–x; 17. а) y = x · 10x;
18. а) y = log3 x; ã) y = log7 x5; |
б) y = 10x; в) y = 1-2 x ; д) y = 2ex – 2e–x; е) y = 3x + 4x. б) y = xex; в) y = -----xx ; e д) y = ex3 − 5x2 ; е) y = -----------1e+xx- .
д) y = x + ln x; е) y = x ln x. |
19.
![]() а)
y = ln2 x; б) y = ln x ; в) y
= 11------------------- −+
ln ln xx- ;
ã) y = --------------1ln + xx2- .
а)
y = ln2 x; б) y = ln x ; в) y
= 11------------------- −+
ln ln xx- ;
ã) y = --------------1ln + xx2- .
20. В точêе x0 найдите значение производной фунêции:
а) y = 4x, x0 = 2; б) y = е–x, x0 = ln 3;
в) y = ln (x2 – 4x), x0 = 5; ã) y = x ln2 x, x0= e.
21. В уêазанной точêе K(x0; y0) составьте уравнение êасательной ê êривой: а) y = ex, K(0; 1); б) y = ln x, K(1; 0). Найдите êритичесêие точêи фунêции:
22. а) y = 2x – x ln 2 + 1; б) y = еx (–x2 + 4x – 1);
в) y = е–x (x2 + 5x + 7); ã) y = xex x− 2 ;
д) y = е–2x + (6 – 2a)е–x + 6ax + ctg 3;
е) y = (0,2)2x + (2a + 2) 1-5 x – (2a ln 5) x + ln 3;
ж) y = e|x| – 2x + 1.
23. a) y = ln (4x – x2); б) y = ln2 x – 6 ln x + 5;
в) y = 4 ln 3 – 16 ln (x2 + 3x) + 0,5 (x2 + 3x)2.
24. Определите интервалы монотонноãо возрастания фунêции f(x) = 0,3125 1-2 3x2 − 8x + 5 ln 2 (3x2 – 8x + 1).
25. Определите интервалы монотонноãо убывания фунêции f(x) = x2 ln 27 – 6x ln 27 + (3x2 – 18x + 24) ln (x2 – 6x + 8).
26. Найдите интервалы возрастания и убывания фунêции:
а) y = x – ex + tg -7π ; б) y = ---------ln xx- – ln 3--------3 ; в) y = (2x – 1)(2x – 2).
27. Найдите точêи эêстремума фунêции:
а) y = (x2 – 2x) ln x – 3-2 x2 + 4x + 1;
б) y = ----x22 – x ln x – x----42 + x – 1.
28. Найдите значения a и b, при êоторых фунêция f(x) = = a ln x + bx2 + x + 2 имеет эêстремумы в точêах x1 = 1 и x2 = 2.
29. В уêазанном промежутêе найдите наибольшее и наименьшее значения фунêции: a) y = e–x (x2 + x – 5), x ° [–4; 4]; б) y = 2---------------------xln 2+ 2−x , x ° [–1; 2]; в) y = 2 · 33x – 4 · 33x + 2 · 3x, x ° [–1; 1];
ã) y = |x2 + 2x – 3| + 1,5 ln x, x ° [0,5; 4].
30. При êаêом значении x выражение 2x2 – 1 + 2------------------x22+ 2- принимает наименьшее значение?
31. Решите неравенство f′(x) < g′(x), если:
а) f(x) = x + 3 ln (x – 2), g(x) = x + 5 ln (x – 1);
б) f(x) = e2x – 3x, g(x) = 5(ex – x + 3).
32. Доêажите, что для всех x ° (0; +×) справедливо неравенство: а) ex > 1 + x; б) x > ln (1 + x).
Исследуйте фунêцию с помощью производной и постройте ее ãрафиê:
33. y = xe–x. 34. y = ln (x2 + 1).
Решите уравнение:
35. а) 25x – 29 · 10x – 1 + 4x = 0;
б) 32x + 1 + 4 · 16x = 7 · 12x;
в) 27 · 4x – 30 · 6x + 8 · 9x = 0;
ã) 7 · 49x + 1 – 210 · 21x + 3 · 9x + 1 = 0.
36. а) 2 · xlog54 + 5 · 2log5x – 3 = 0;
б) 3 · xlog29 + 5 · 3log2x – 2 = 0;
в) 25 · xlog7x + 24 · 5log7x – 1 = 0;
ã) (x − 1)log349 + 97 · 7log3(x − 1) – 2 = 0.
37. а) 2x · 3x − log32 – 62 – x + 3 = 0;
б) 5x + 1 · 2x + log26 = 2 · 10–x – 1 + 1;
в) 3x + log34 · 21 – x = 2x + log29 · 31 – x;
ã) 2x + log27 · 3(x2 + x)log37 = 343.
38.
![]()
![]()
![]() а) 2--------------2xx−−
23- + 1 = ------------------220x,5−x3 ; б) 1 + ----31x – 3--------------x3+x 1- = 3-2 ;
а) 2--------------2xx−−
23- + 1 = ------------------220x,5−x3 ; б) 1 + ----31x – 3--------------x3+x 1- = 3-2 ;
в) ------------------24xx−+26 – 4x + 6 = 7;
![]() ã) 3 · 5---------------------x5+x1++1 7 – 30 · ---------------------5x5+x1−+1 7 = 17.
ã) 3 · 5---------------------x5+x1++1 7 – 30 · ---------------------5x5+x1−+1 7 = 17.
39. а) 9 log28 (x – 3)4 + 48 log4 (x – 3)2 = 64;
б) 9 log227 (x + 5)4 – 32 log9 (x + 5)2 = 48;
в) 25 log232 (x – 7)4 + 16 log4 (x – 7)2 = 96;
ã) 9 log2125 (x + 1)4 – 16 log25 (x + 1)2 = 32.
|
Решите неравенство: |
|
|
40. а) 9x + 6x m 5 · 3x; |
б) 16x + 20 l 9 · 4x; |
|
в) 4x + 2 m 3 · 2x; |
ã) 25x + 35 l 12 · 5x. |
|
41. а) log7 x – logx 1-7 > 2; в) log2 x + logx 4 > 3; 2 + logx 42.
log1-2-x m 4x3; в) x |
б) log3 x – 2 logx1-9 l 5; ã) log2 x – 4 logx1-8 l 7. 1 + ------------------1 -
logx ã) x---------------1 1-3- m 27x4. |
43. а) (2x2 – 3x + 1) log4x + 5 (2x + 3) l 0;
б) (2x2 – x – 1) log4 –3x (7 – 5x) m 0;
в) (3 + x – 2x2) logx + 2 (3x + 5) l 0;
ã) (1 – x – 6x2) log2 – 3x (1 – 2x) m 0.
44. а) ------------------------------------------------------------------(lg x − 1()2(xx2−−2)112 x + 10)- m 0;
б) (---------------------------------------------------------------logx2 − 14)x(−x22− 3x + 2) m 0;
в) (---------------------------------------------------------3x − 2log)2(2xx2−−15x + 6) l 0;
ã) -----------------------------------(x52−−710x)logx +39x- l 0.
45. а) log2 1 – -x1 + log21- 1 – x-4 m 1; б) log3 2 + --x1 – log1-3 1 – -----------x 3+ 1- < 1;
![]() в) log2 3 + -x -----------x 5+ 1-
+ log-41 1 + x-2
l 1;
в) log2 3 + -x -----------x 5+ 1-
+ log-41 1 + x-2
l 1;
ã) log5 -x-x3 – 1 + log1-5 3 + -----------x 1− 1- m 1.
46. а) log2x + 7 (x2 + 4x + 4) < 2 logx2 |x|;
б) log2x – 4 (x2 – 9x + 20) < 21- log|x – 6| (x – 6)2;
в) log2x + 3 (x2 + x – 9) > 2 log(x − 6)2 |6 – x|;
ã) log2x – 6 (x2 – 11x + 30) < 1-2 log|7 – x| (x – 7)2.
47.а) -------------------------------------------lg2 x +lg 2 lgx x − 6- < 1;
б) log2 (2x + 1) + log2 3 > log2 (2x – 1) + x + 1.
48. Решите систему уравнений
![]() logx
y + logy x = 5-2 , xy = 27.
logx
y + logy x = 5-2 , xy = 27.
49. Найдите наименьшее и наибольшее значения фунêции f(x) = 2 · 33x – 4 · 32x + 2 · 3x на отрезêе [–1; 1].
Глава III
Триãонометрия
![]()
sin2 α + cos2 α = 1; (1) sin (α + β) = sin α cos β + cos α sin β; (2) sin (α – β) = sin α cos β – cos α sin β; (3) cos (α + β) = cos α cos β – sin α sin β; (4) cos (α – β) = cos α cos β + sin α sin β; (5)
tg (α + β) = ------------------------------1tg− αtg+αtgtgββ- ; α, β, α + β − -2π + πn, n ° Z; (6) tg (α – β) = 1------------------------------tg+ αtg−αtgtgββ- ; α, β, α – β − -2π + πn, n ° Z; (7) sin 2α = 2 sin α cos α; (8) cos 2α = cos2 α – sin2 α; (9)
tg 2α = -----------------------12− tgtg2αα ; α, 2α − -2π + πn, n ° Z; (10) sin 3α = 3 sin α – 4 sin3 α; (11) cos 3α = 4 cos3 α – 3 cos α; (12)
sin α + sin β = 2 sin α-----------2+ β- cosα-----------2− β- ; (13) sin α – sin β = 2 sin α-----------2− β- cos α-----------2+ β- ; (14) cos α + cos β = 2 cos α-----------2+ β- cos α-----------2− β- ; (15) cos α – cos β = –2 sin α-----------2− β- sin α-----------2+ β- ; (16)
|
sin α cos β = 1-2 (sin (α – β) + sin (α + β)); sin α sin β = 1-2 (cos (α – β) – cos (α + β)); cos α cos β = 1-2 (cos (α – β) + cos (α + β)); sin2 α = 1-------------------------− cos2 2α- ; cos2 α = -------------------------1 + cos2 2α- ; |
(17) (18) (19) (20) (21) |
![]() sin
α---2 = 1---------------------−
2cosα- ; (22)
cos α---2 = 1---------------------+
2cosα- ; (23)
sin
α---2 = 1---------------------−
2cosα- ; (22)
cos α---2 = 1---------------------+
2cosα- ; (23)
tg α---2 = 11---------------------+− coscosαα- ; α − π + 2πn, n ° Z; (24)
|
tg α---2 = ---------------------1 +sincosα α- = 1---------------------−sincosα α- ; α − πn, n ° Z; |
(25) |
|sin α| = --------------------------1tg+ tgα2 α- ; α − 2-π + πn, n ° Z; (26)
![]() |cos α| = --------------------------1 +1tg2 α
; α
− 2-π
+ πn,
n ° Z; (27)
|cos α| = --------------------------1 +1tg2 α
; α
− 2-π
+ πn,
n ° Z; (27)
|sin α| = ; α − πn, n ° Z; (28)
|cos α| = ------------------------------ctgα ; α − πn, n ° Z; (29)
1 + ctg2 α
|
tg α--- sin α = ----------------------+ tg2α---2 ; α − π + 2πn, n ° Z; 2 − tg2 α---2- ; α − π + 2πn, n ° Z; cos α = ----------------------α |
(30) (31) |
|
tg α = 1----------------------− tg2α---2- ; α − π-----2n , n ° Z; 2 |
(32) |
2tg α---
a cos x + b sin x = a2 + b2 sin (x + α), (33)
![]() ãде
a2 + b2 − 0, sin α = ----------------------a , cos α = ----------------------b ;
ãде
a2 + b2 − 0, sin α = ----------------------a , cos α = ----------------------b ;
![]() a2 + b2 a2 +
b2
a2 + b2 a2 +
b2
|
Arcsin a = (–1)n arcsin a + πn, n ° Z; |
(34) |
|
Arccos a = ä arccos a + 2πn, n ° Z; |
(35) |
|
Arctg a = arctg a + πn, n ° Z; |
(36) |
|
Arcctg a = arcctg a + πn, n ° Z. 1. Доêажите тождество: |
(37) |
а) sin6 α + cos6 α + 3 sin2 α cos2 α = 1; б) -------------------------------------sin22αα−−ctgtg22αα- = tg6 α.
2. Зная, что sin α + cos α = a, найдите:
a) |sin α – cos α|; б) cos4 α + sin4 α.
3. Дано: tg α + ctg α = p. Найдите:
a) tg2 α + ctg2 α; б) tg3 α + ctg3 α.
4. Найдите:
а) sin -3π – α , если tg α = –-43 , 3-----2π- < α < 2π;
б) cos (70° + α), если sin (40° + α) = b, 0 < α < 45°;
в) sin (α + β – γ), если sin α = 12------13 , cos β = ------178 , sin γ = 4-5 ; 0 < α <
< -2π , 0 < β < -2π , 0 < γ < -2π ;
ã) sin 3α, cos 3α, tg 3α, если ctg α = 4--3 , π < α < 3-----2π- .
5. Дано: α, β, γ — уãлы треуãольниêа. Доêажите равенство
sin α sin β – cos γ = cos α cos β. Доêажите тождество:
6. а) (cos α + sin α)2 = 1 + sin 2α; б) 1 – sin α = 2 sin2 -4π – α---2 ;
в) -----------------------------------------------------------------2ctg -π-1+−α2sincos22α 4-π − α- = 1; ã) ------------------------------11−+2sin2sin2ββ = 11--------------------−+ tgtg ββ ;
4
д) tg -4π + α = 1-------------------------cos 2+ sin 2αα ; е) cos-------------------------------cosαα +− sinsinαα- = tg 2α + sec 2α;
ж) sin--------------------------------------------------------------------------------4 α + 2 sintg2αα cos− 1 α − cos4 α = cos 2α.
7. а) -------------------------------------------------------sin1(−αtg− β2)αsin ctg(α2+ββ) = –cos2 α sin2 β;
б) 3 – 4 cos 2α + cos 4α = 8 sin4 α;
в) cos4 α = 1-8 cos 4α + 1-2 cos 2α + 3-8 ;
ã) sin4 α + cos4 α = -21 (1 + cos2 2α).
8. а) 4 (sin6 α + cos6 α) = 1 + 3 cos3 2α;
б) 8 sin 8 α---2 + cos8 ---α2 = 1 + 6 cos2 α + cos4 α;
в) tg x + tg 2x – tg 3x = –tg x tg 2x tg 3x;
ã) 1 + cos 2x + cos 4x + cos 6x = 4 cos x cos 2x cos 3x.
9. Упростите выражение:
а) -----------------------------------sincosαα ++ cossin33αα- ; б) ---------------------------------------cossin24αα +− sincos42αα- ;
в) ---------------------------------------------------------------cossinαα −− 33cossin22αα ++ sincos33αα- ; ã) ------------------------------------------------------------------------------cos2α(−sinsin2αα +− 2coscos32αα+−sin1) 3α- ;
д) cos -----27π- + cos 4-----7π- + cos 6-----7π- ;
е) cos 0 + cos -7π + cos -----27π- + ... + cos -----67π- .
Доêажите тождество:
10. а) --------------------------------------------22(sincos2αα++cossin34αα)- = tg 2α cos α;
![]() б) cos4 α – sin4
α + sin 2α = 2 cos 2
α
– -4π
;
б) cos4 α – sin4
α + sin 2α = 2 cos 2
α
– -4π
;
в) cos2 α + cos2 -3π + α + cos2 -3π – α = 3-2 ;
ã) sin2 α + cos -3π – α cos 3-π + α = 41- ;
д) log1-3 [cos2 (α + β) + cos2 (α – β) – cos 2α cos 2β] = 0;
е) ctg-----------------------------2 ctg22α2−α1 – cos 8α ctg 4α = sin 8α;
11. а) 16 sin 10° sin 30° sin 50° sin 70° = 1;
б) sin2 α cos4 α = ------161 + ------321 cos 2α – ------161 cos 4α – ------321 cos 6α;
в) sin 9α + 3 sin 7α + 3 sin 5α + sin 3α = 8 sin 6α cos3 α;
ã) tg (α – β) + tg (β – γ) + tg (γ – α) = tg (α – β) tg (β – γ) tg (γ – α);
![]()
![]() д) 1 +
sinα
– 1 − sinα = 2 sin α---2 , если α ° 0; -2π .
д) 1 +
sinα
– 1 − sinα = 2 sin α---2 , если α ° 0; -2π .
12. Дано: sin α + cos α = 1,4, 0 < α < -4π . Найдите tg α---2 .
13. Положительные острые уãлы α, β, γ удовлетворяют соотношениям tg -2β = 1-3 ctg α---2 , ctg -2γ = 21- 3 tg α---2 + ctg α---2 .
Найдите сумму α + β + γ.
Без помощи таблиц и миêроêальêулятора вычислите:
14.
![]() а)
cos 292°30′; б) cosec 10° – 3 sec 10°; в) 2-----------------------------------------------cos40sin°20− cos°
20°- ;
а)
cos 292°30′; б) cosec 10° – 3 sec 10°; в) 2-----------------------------------------------cos40sin°20− cos°
20°- ;
![]() ã) –2 2 sin 10° 2 sin 35- ° – ---------------sec25°
– -----------------cossin405°°
;
ã) –2 2 sin 10° 2 sin 35- ° – ---------------sec25°
– -----------------cossin405°°
;
д) cos2 73° + cos2 47° + cos 73° cos 47°;
e) sin 6° – sin 42° – sin 66° + sin 78°.
15. а) cos--------------------------------------------------sin2 2133°° −− coscos22157° °- ; б) 6 cos 40° – 8 cos 40°;
в) tg6 20° – 33 tg4 20° + 27 tg2 20° – 3; ã) ctg2 36° ctg2 72°;
д) cos ------15π cos 2-----15π- cos 4-----15π- cos 8-----15π- ;
е) cos 20° cos 40° cos 80°.
16. а) 8 cos 10° cos 50° cos 70°; б) cos -5π cos 2-----5π- ;
![]() в) cos -5π
– cos 2-----5π- ; ã)
tg 20° + tg 40° + 3 tg 20° tg 40°;
в) cos -5π
– cos 2-----5π- ; ã)
tg 20° + tg 40° + 3 tg 20° tg 40°;
д) sin 54° – sin 18°; е) 4 sin 54° cos 72°.
17. Доêажите, что если α = β + γ, то:
a) sin α + sin β + sin γ = 4 sin α---2 cos -2β cos -2γ ;
б) cos2 α + cos2 β + cos2 γ – 2 cos α cos β cos γ = 1.
18. Доêажите, что если α + β + γ = -2π , то:
a) sin2 α + sin2 β + sin2 γ = 1 – 2 sin α sin β sin γ;
б) ctg α + ctg β + ctg γ = ctg α ctg β ctg γ.
19. Доêажите, что если α + β + γ = π, то:
а) cos α + cos β + cos γ = 1 + 4 sin α---2 sin -2β sin -2γ ;
б) 1 – cos2 α – cos2 β – cos2 γ = 2 cos α cos β cos γ;
в) sin α + sin β + sin γ = 4 cos α---2 cos -2β cos -2γ .
20. Найдите зависимость между x и y, исêлючив α из соотношений:
![]()
![]() а)
xy = 4 sin = 3 cos αα;, б) xy = 4 cos2
– 2 = –2 cos 2α---2 ; α,
а)
xy = 4 sin = 3 cos αα;, б) xy = 4 cos2
– 2 = –2 cos 2α---2 ; α,
x = tg α, x = 1 − cosα ,
в) y = sec α; ã) y = sin ---α2 + cos ---α2 .
1. Найдите область определения фунêции:
![]() а) y = sinx − cosx ; б)
y = 2cosx +
1 + 2sinx −
1 ;
а) y = sinx − cosx ; б)
y = 2cosx +
1 + 2sinx −
1 ;
в) y = (2 cos x + 1)(cos x − 1) ;ã) y = sinx(tg2x − 3) ;
д) y = tgx − sinx .
2. Найдите множество значений фунêции:
а) y = 9 cos 3x – 12 cos3 3x; б) y = cos (2 sin x);
в) y = cos 1 – --------------x21+ 1- ; ã) y = 12 sin x + 5 cos x – 3;
д) y = 1 – 2 sin x cos x.
3. Найдите наибольшее и наименьшее значения фунêции:
а) y = a cos x + b sin x + c;
б) y = 10 cos2 x – 6 sin x cos x + 2 sin2 x.
4. Найдите множество значений фунêции y = -----------cos1 x- + -----------sin1 x- , заданной на множестве X = 0; -2π , x ° X.
5. Найдите наименьшее значение фунêции
y = 2 (1 + sin 3x sin 2x) – 1-2 (cos 4x + cos 6x).
6. Доêажите, что фунêция y = sin 5x + sin 3x + 5 sin x cos 2x, x ° R, является нечетной.
7. Доêажите, что фунêция
y = cos 4x + sin3 x-2 sin x + 5x2, x ° R, является четной.
8. Найдите наименьший положительный период фунêции:
а) y = sin 3x; б) y = tg 2x + 2 sin 3x; в) y = cos x-2 ;
ã) y = cos2 x; д) y = sin (cos x); е) y = cos (sin x);
ж) y = cos 3-----5x – sin 2-----7x .
9. Доêажите, что при 0 < x < -2π справедливо двойное неравенство sin x < x < tg x.
10. Доêажите, что при 0 < |x| < -2π справедливо двойное неравенство
cos x < -----------sinxx- < 1.
11. Найдите сумму:
а) sin x + sin 2x + sin 3x + ... + sin nx, x − 2πn;
б) cos x + cos 2x + cos 3x + ... + cos nx, x − 2πn, n ° Z.
Постройте ãрафиê фунêции:
12. a) y = sin 2x; б) y = –sin x-3 ; в) y = sin x – -3π ;
![]() ã) y = sin |x|; д)
y = |sin x|; е) y = ----------------sinsin xx .
ã) y = sin |x|; д)
y = |sin x|; е) y = ----------------sinsin xx .
13. a) y = x + sin x; б) y = x sin x; в) y = cosec |x|;
ã) y = 2sin x; д) y = sin (arcsin (log0,5 x)).
14. a) y = cos – x-2 ; б) y = cos 2x; в) y = cos x + -4π ;
ã) y = |cos x|; д) y = sec x.
15. a) y = tg 3x; б) y = –tg x-2 ; в) y = tg -6π – x ;
ã) y = tg |x|; д) y = |tg x|; е) y = tg x ctg x.
16. Постройте ãрафиê:
a) |y| = sin x; б) sin y = sin x.
Найдите производную фунêции:
17. a) y = sin x – cos x; б) y = tg x + ctg x; в) y = sin2 x;
ã) y = cos2 x; д) y = 1-3 tg3 x; e) y = 1-4 ctg4 x.
18. ![]() a) y = sin 3x; б)
y = cos-------x ; в) y = sin2
(2x – 1); 2
a) y = sin 3x; б)
y = cos-------x ; в) y = sin2
(2x – 1); 2
ã) y = cos3 (x2 + x); д) y = ----------------------1 +sincosx x- .
19. В уêазанной точêе x0 найдите значение производной фунêции: а) y = sin x, x0 = -6π ; б) y = cos (–2x), x0 = -4π ; в) y =
= tg x – x, x0 = -3π .
20. В уêазанной точêе A(x0; y0) составьте уравнение êасательной ê êривой: a) y = 2 sin x-3 , A 3-----2π- ; 2 ; б) y = cos2 x,
A -4π ; 1-2 ; в) y = tg 2x, A -8π ; 1 .
21. Найдите наибольшее и наименьшее значения фунêции y = sin2 x – 20 cos x + 1.
22. Доêажите, что фунêция
f(x) = cos2 x + cos2 --3π + x – cos x cos -3π + x
есть постоянная, т. е. не зависит от x. Найдите значение этой постоянной.
1. Доêажите, что: sin (arcsin x) = x, –1 m x m 1; sin (arccos x) = 1 − x2 , –1 m x m 1; sin (arctg x) = ------------------x ; sin (arcctg x) = ;
1 + x2 1 + x2
![]()
![]()
![]() cos (arccos x) = x,
–1 m x m 1; cos (arcsin x) = 1 − x2 , –1 m x
m 1; cos (arctg x) = ; cos (arcctg x) = ------------------x ;
cos (arccos x) = x,
–1 m x m 1; cos (arcsin x) = 1 − x2 , –1 m x
m 1; cos (arctg x) = ; cos (arcctg x) = ------------------x ;
1 + x2 1 + x2
tg (arctg x) = x; tg (arcsin x) = ------------------x , –1 < x < 1;
1 − x2
![]() tg
(arccos x) = ------------------1x− x2 , –1 m x < 0, 0 < x m 1;
tg
(arccos x) = ------------------1x− x2 , –1 m x < 0, 0 < x m 1;
tg (arcctg x) = -x1 , x − 0;
ctg (arcctg x) = x; ctg (arctg x) = -x1 , x − 0;
![]() ctg
(arcsin x) = ------------------1x− x2 , –1 m x < 0, 0 < x m 1;
ctg
(arcsin x) = ------------------1x− x2 , –1 m x < 0, 0 < x m 1;
ctg (arccos x) = ------------------x , –1 < x < 1.
![]() 1 − x2 Вычислите:
1 − x2 Вычислите:
2. a) sin 2 arcsin 1-3 ; б) cos 2 arcsin 1-3 ;
в) tg 2 arcsin 1-3 ; ã) sin 2 arctg 3); д) tg (2 arctg 3).
3. a) sin 3 arcsin 1-3 ; б) cos 3 arccos 1-4 .
4. a) sin 1-2 arctg 3 ; б) соs 1-2 arctg 5 ; в) sin 1-2 arccos 1-9 .
5.
![]() a)
sin 1-4 arccos 17------32
; б) sin -41 arcsin ---------863-
;
a)
sin 1-4 arccos 17------32
; б) sin -41 arcsin ---------863-
;
в) cos 1-4 arctg 24------7 .
6. Доêажите, что:
![]() а) если 0 m x m 1, то arcsin x
= arccos 1 −
x2 , arccos x =
а) если 0 m x m 1, то arcsin x
= arccos 1 −
x2 , arccos x =
![]() = arcsin 1 − x2 ;
= arcsin 1 − x2 ;
б) если 0 m x < 1, то arcsin x = arctg ------------------x , arccos x =
![]() 1 − x2
1 − x2
= arcctg ------------------x ;
![]() 1 − x2
1 − x2
![]() в) если 0 < x m 1,
то arcsin x = arcctg ------------------1x−
x2
, arccos x =
в) если 0 < x m 1,
то arcsin x = arcctg ------------------1x−
x2
, arccos x =
![]() = arctg ------------------1x−
x2 ;
= arctg ------------------1x−
x2 ;
![]() ã) если x >
0, то arctg x = arcctg -x1 = arcsin ------------------1x+
x2 =
ã) если x >
0, то arctg x = arcctg -x1 = arcsin ------------------1x+
x2 =
= arccos ![]() ,
,
![]()
![]() arcctg x = arctg -x1 = arcsin ------------------1 = arccos ------------------1x+
x2 .
arcctg x = arctg -x1 = arcsin ------------------1 = arccos ------------------1x+
x2 .
7. Выразите через все обратные триãонометричесêие фунêции:
a) arcsin 3-5 ; б) arccos 1312------ ; в) arctg 12------5 ; ã) arcctg 3-4 .
8. Доêажите, что:
a) arcsin (–x) = –arcsin x, –1 m x m 1;
б) arctg (–x) = –arctg x;
в) arccos (–x) = π – arccos x, –1 m x m 1;
ã) arcctg (–x) = π – arcctg x.
9. Выразите через все обратные триãонометричесêие фунêции:
a) arccos – 1-3 ; б) arctg – ------247 ; в) arcctg – ------247 .
10. Доêажите, что:
а) если 0 m x m 1, 0 m y m 1, то
![]() arcsin
x + arcsin y = arccos ( 1 −
x2 1 −
y2 – xy), arccos x + arccos y =
arccos (xy – 1 −
x2 1 −
y2 ), arcsin x – arcsin y = arcsin (x
1 − y2
– y 1 −
x2 ), arccos x – arccos y = arcsin (y
1 − x2
– x 1 −
y2 );
arcsin
x + arcsin y = arccos ( 1 −
x2 1 −
y2 – xy), arccos x + arccos y =
arccos (xy – 1 −
x2 1 −
y2 ), arcsin x – arcsin y = arcsin (x
1 − y2
– y 1 −
x2 ), arccos x – arccos y = arcsin (y
1 − x2
– x 1 −
y2 );
б) если x > 0, y > 0, то
arctg x + arctg y = arcctg 1---------------x−+xyy- , arcctg x + arcctg y = arcctg xy---------------x +−y1- , arctg x – arctg y = arctg ---------------1x+−xyy- , arcctg x – arcctg y = arctg ---------------1y+−xyx- .
11. Выполните уêазанные действия:
|
a) arcsin 3-5 + arcsin 12------13 ; в) arctg 4 + arctg 5; д) arccos ------135 – arccos ------257 ; |
б) arccos ------257 + arccos 3-5 ; ã) arcsin 3-5 – arcsin 24------25 ; e) arctg 4 – arctg 5; |
ж) arcctg 5 – arcctg 4.
12. Доêажите, что:
a) arcsin x + arccos x = -2π , –1 m x m 1;
б) arctg x + arcctg x = -2π .
13. Решите уравнение:
a) 5 arctg x + 3 arcctg x = 2π;
б) arctg x + arctg 2x + arctg 3x = π.
14. Найдите наибольшее и наименьшее значения фунêции arcsin3 x + arccos3 x.
15. Доêажите, что:
![]() a)
arcsin (sin x) = x – 2πn, если
2πn –
-2π
m x m 2πn
+ 2-π
,
a)
arcsin (sin x) = x – 2πn, если
2πn –
-2π
m x m 2πn
+ 2-π
,
=π – x + 2πn, если 2πn + -2π m x m 2πn + 3-----2π- ;
б) arccos (cos x) = x2π – 2 – xπn + 2, πn, еслиесли 2 2ππnn + m πx m m x 2 mπn 2 + π(nπ + 1);,
в) arctg (tg x) = x – πn, если πn – -2π < x < πn + -2π ;
ã) arcctg (ctg x) = x – πn, если πn < x < π(n + 1).
16. Вычислите:
а) arcsin sin 10----------7π ; б) arccos sin – 9-π ;
в) arcsin cos 33----------10π .
17. Вычислите: arcsin (sin x); arccos (cos x); arctg (tg x), arcctg (ctg x); arcsin (cos x); arccos (sin x), если:
а) x = 3; б) x = 4; в) x = 10.
18. Решите уравнение cos (π arcctg2 x) = 1-2 .
19. Вычислите без таблиц и миêроêальêулятора:
a) arctg 1-3 + arctg 1-5 + arctg 1-7 + arctg 1-8 ;
б) arctg 1 + arctg 2 + arctg 3;
в) arctg -21 + arctg -31 ;
ã) arcctg 3 + arcctg 4 + arcctg ------117 .
Постройте ãрафиê фунêции:
20. а) y = arcsin (sin x); б) y = arccos (cos x);
|
в) y = arctg (tg x); |
ã) y = arcctg (ctg x); |
|
д) y = arcsin -x1 ; 21. а) y = arctg -----------x 1− 1- ; в) y = arcctg xx-----------−− 12- ; д) y = arctg --------------x22 −− 41- ; x 22. а) y = arcsin (x – 2); в) y = arcsin x2; 23. a) y = arctg (x + 1); в) y = arctg (x2 – 1); 24. а) y = sin (arcsin x); |
е) y = arccos -x1 . б) y = arcctg -----------x 1− 1- ; ã) y = arcctg (2x – x2); е) |y| = arctg --------------x22 −− 41- . x б) y = arccos x-2 ; ã) y = –arccos (–x2). б) y = arcctg (3 – x); ã) y = arcctg (4 – x2). б) y = cos (arcsin x). |
25. Пользуясь формулой для производной обратной фунêции, доêажите, что:
![]() а) (arcsin x)′ = ,
x ° ( –1; 1);
а) (arcsin x)′ = ,
x ° ( –1; 1);
б) (arccos x)′ = –−, x ° ( –1; 1);
в) (arctg x)′ = 1--------------+1x2- ; ã) (arcctg x)′ = –1--------------+1x2- .
Найдите производную фунêции:
26. а) y = arcsin (1 – x); б) y = arccos (x + 2);
в) y = arcsin x-2 + arccos 2x; ã) y = x arcsin x;
д) y = ----------------------arcxсоsx ; e) y = arcsin---------------------arcсоsxx .
27. а) y = arctg x2; б) y = arcctg 2x;
![]() в) y = arcsin (sin x);
ã) y =
arcsin 1-----------1 −+
xx- .
в) y = arcsin (sin x);
ã) y =
arcsin 1-----------1 −+
xx- .
28. ![]()
![]() В уêазанной точêе
x0 найдите значение производной фунêции: а) y =
2 arcsin x; x0 = -------23 ; б) y = –3
arccos x, x0 = –-------22 ; в) y = arctg x3,
x0 = 1; ã) y = 2 arcctg (x2 –
3), x0 = –1.
В уêазанной точêе
x0 найдите значение производной фунêции: а) y =
2 arcsin x; x0 = -------23 ; б) y = –3
arccos x, x0 = –-------22 ; в) y = arctg x3,
x0 = 1; ã) y = 2 arcctg (x2 –
3), x0 = –1.
29. В уêазанной точêе B(x0; y0) составьте уравнения êасательной ê êривой:
а) y = arcsin 3x, B 1-5 ; arcsin -35 ; б) y = arctg x-2 , B-4π–2; –-4π .
30. Найдите êритичесêие точêи фунêции:
а) y = x + arccos x + 1; б) y = x arctg x.
31. Найдите наибольшее и наименьшее значения фунêции y = arctg 1-----------1 −+ xx- на отрезêе [0; 1].
Решите уравнение:
1. a) sin x = –1-2 ; б) sin 2x + -4π = 1;
в) 2 sin x cos x – 3 sin 2x = 0;
ã) sin x-2 cos -3π – cos x-2 sin -3π = 1-4 ;
![]() д) sin x = –1.
д) sin x = –1.
2. a) cos x = 0; б) cos π3x – -6π = –1;
в) sin4 x-2 – cos4 x-2 = 1-2 ;
ã) cos -6π cos x – sin -6π sin x = -4π ; д) cos x2 = 1.
3.
![]() 2
cos
2
cos ![]() --6π
-sin
x – 13 + -------22
= 3 .
--6π
-sin
x – 13 + -------22
= 3 .
4. Найдите все значения параметра a, для êоторых уравнение cos x = ----------------------2a−−01,,5 5a имеет решение.
5. Найдите êритичесêие точêи фунêции: а) y = 3 sin x + 2(x – 1);
![]() б) y = cos 2x
+ ax – 3 .
б) y = cos 2x
+ ax – 3 .
Решите уравнение:
6.
![]() a)
tg x = -------13 ; б) tg --x2 – -7π
= –1;
a)
tg x = -------13 ; б) tg --x2 – -7π
= –1;
![]() в) -----------------------12−tgtg2xx = 5; ã) 1-------------------------------tg+ tg4-π-
−xtgtgx-4π-
= 3 .
в) -----------------------12−tgtg2xx = 5; ã) 1-------------------------------tg+ tg4-π-
−xtgtgx-4π-
= 3 .
7. a) ctg x = l; б) ctg 2x + -3π = 2;
![]() в) ctg x-2 – 32-
= –1; ã) ---------tg1x-
= 7 – 2 .
в) ctg x-2 – 32-
= –1; ã) ---------tg1x-
= 7 – 2 .
8.
![]() a)
cos (1,5π + x)
= 2 sin (x + π)
cos x;
a)
cos (1,5π + x)
= 2 sin (x + π)
cos x;
![]() б) 2 sin x cos x + 3
– 2 cos x – 3 sin x = 0;
б) 2 sin x cos x + 3
– 2 cos x – 3 sin x = 0;
в) sin 2x = (cos x – sin x)2; ã) tg3 3x – 2 sin3 3x = 0;
д) 2 tg x cos x + 1 = 2 cos x + tg x.
9. а) sin x + cos2 x = 1-4 ; б) 3 cos x = 2 sin2 x;
в) 6 cos2 x + 13 sin x = 12;
ã) 3 cos2 x – 4 cos x – sin2 x – 2 = 0;
д) cos4 x-5 + sin2 x-5 = 1;
![]()
![]() е) sin x – ----------------------------22coscosxx −−
11- sin2
x = sin2 x.
е) sin x – ----------------------------22coscosxx −−
11- sin2
x = sin2 x.
10. a) tg2 x – 4 tg x + 3 = 0; б) 2 tg x – 2 ctg x = 3;
![]() в) ---------------cos32x = 4 tg x; ã)
-------------sin12x-
= ctg x + 3.
в) ---------------cos32x = 4 tg x; ã)
-------------sin12x-
= ctg x + 3.
11.
![]() a)
2 cos x (cos x – 8 tg x) = 5;
a)
2 cos x (cos x – 8 tg x) = 5;
б) cos 4-π – sin 6-π (sec x + tg x) = sin -4π cos x;
в) log2 (3 sin x) – log2 cos x – log2 (1 – tg x) – log2 (1 + tg x) = 1.
12. a) sin4 2x + cos4 2x = sin 2x cos 2x;
б) sin4 x + cos4 x – 2 sin 2x + 3-4 sin2 2x = 0;
в) sin4 x + cos4 x + sin 2x + a = 0;
ã) sin-----------------------------2x1cos2x + --------------------------sinx3cosx – 4 = 0;
д) tg 5x + 2 sin 10x = 5 sin 5x.
13. a) cos 2x – 3 sin x + 2 = 0;
![]() б) cos (10 x +12) + 4 2
sin (5x + 6) = 4;
б) cos (10 x +12) + 4 2
sin (5x + 6) = 4;
в) 6 sin2 x + 2 sin2 2x = 5; ã) a sin2x + cos x = 0.
14. Найдите êритичесêие точêи фунêции:
а) f(x) = e3 – 4x2 − 12x + 9 – 4 sin2 x-2 ;
б) f(x) = sin2 3x + 3 x2 − 4x + 4 + cos 1;
в) f(x) = 2x – 0,25 sin 4x + 0,5 sin 2x;
ã) f(x) = log2 3 + x(1 – 10 ) + ( 2 – 2 5 + cos x)sin x;
![]()
![]() д) f(x) = (2 2 – 1)(1 + cos x)
–-------42 sin 2x + -------12 – 2
x.
д) f(x) = (2 2 – 1)(1 + cos x)
–-------42 sin 2x + -------12 – 2
x.
Решите уравнение:
15. a) cos3 x + cos2 x – 4 cos2 x-2 = 0;
б) 4 cos x (2 – 3 sin2 x) = –(1 + cos 2x);
в) tg3 x – 1 + ----------------cos12 x – 3 ctg -2π – x = 3;
ã) 8 cos4 x – 8 cos2 x – cos x + 1 = 0.
16. a) sin x = 5 cos x; б) sin x – cos x = 0;
в) sin x + cos x = 0; ã) |sin x| = sin x + 2 cos x;
д) cos2 x – 4 sin x cos x = 0.
17. a) sin x + sin 2x = cos x + 2 cos2 x;
б) sin 2x – sin2 x = 2 sin x – 4 cos x;
в) tg x + sin (π + x) = 2 sin2 x-2 ;
ã) (1 + sin 2x)(cos x – sin x) = cos x + sin x;
д) 3 (cos x – sin x) = 1 + cos 2x – sin 2x.
18. a) sin2 x + 3 sin x cos x + 2 cos2 x = 0;
б) 2 cos2 x + 3 sin 2x – 8 sin2 x = 0;
в) 3 sin2 x + 5 cos2 x – 2 cos 2x – 4 sin 2x = 0;
ã) 2 sin2 x – 5 sin x cos x – 8 cos2 x = –2;
д) -----------cos1 x- = 4 sin x + 6 cos x.
19. a) sin3 x + 4 cos3 x = 0;
б) sin2 x (1 + tg x) = 3 sin x (cos x – sin x) + 3;
в) sin4 x + sin3 x cos x + sin2 x cos2 x + sin x cos3 x +
+ cos4 x = 1;
ã) (8a2 + 1) sin3 x – (4a2 + 1) sin x + 2a cos3 x = 0.
20. Найдите êритичесêие точêи фунêции:
а) y = 3 cos 2 x – 5 sin 2x + 4 cos 2;
б) y = 8 sin 2x + 6 cos2 x + 17x + 1;
в) y = cos3 x – 3 cos x + 3-----8x – 3 sin 3;
ã) y = 8 (cos 2 – cos x) – sin x – -----------sin1 x- ;
д) y = 9 ctg x – ctg3 x + tg 2.
Решите уравнение:
21.
![]()
![]()
![]()
![]() a) -------23 cos x + 1-2 sin x = -------23 ; б) 3 sin x
+ cos x = 2 ;
a) -------23 cos x + 1-2 sin x = -------23 ; б) 3 sin x
+ cos x = 2 ;
![]() в) sin 5x = 3 (1 + cos
5x); ã) cos x + sin x = 1;
в) sin 5x = 3 (1 + cos
5x); ã) cos x + sin x = 1;
![]() д) sin x + cos x ctg x-2 = – 3 ;
д) sin x + cos x ctg x-2 = – 3 ;
22. a) sin |x| tg 5x = cos x; б) cos x – sin x = a;
![]() в) (sin 2x + 3 cos 2x)2
– 5 = cos -6π
– 2x ;
в) (sin 2x + 3 cos 2x)2
– 5 = cos -6π
– 2x ;
ã) cos 6x + tg2 x + cos 6x tg2 x = 1.
23. a) 1------------------------------------tg 2− tg 2x +xtg tgxx- = –1; б) 1----------------------------------------tg 3+ tg 3x −xtg 2 tg 2xx- = 1;
в) 2 tg 3x – 3 tg 2x = tg2 2x tg 3x;
ã) ctg x + ctg 15° + ctg (x + 25°) = ctg 15° ctg x ctg (x + 25°).
24. a) sin x + tg x-2 = 0; б) 1 + cos x + tg x-2 = 0;
в) tg 2x + ctg x = 4 sin 2x;
ã) 15 ctg x-2 + 130 sin x = 53------5 tg x-2 ;
д) 59------4 cos x + 6 sin x tg x-2 = 4 tg x ctg x-2 ;
е) 2 sin2 -4πx – -4π = 2 sin2 x tg x.
25. Равносильны ли уравнения
1 + cos 2x + sin 2x = 0 и 1 + 1-----------------------1 −+ tgtg22 xx + 1-----------------------2+tgtg2xx = 0?
Решите уравнение:
26. а) cos 3x = –2 cos x; б) cos 9x – 2 cos 6x = 2;
в) cos 4x = cos2 3x.
27. а) 3 sin x-3 = sin x; б) sin 6x + 2 = 2 cos 4x;
в) sin -----32x + 3 sin x = 3 sin x-2 ;
ã) sin 4-π + 3-----2x = 2 sin 3-----4π- + x-2 .
28. 3 cos x + 3 sin x + sin 3x – cos 3x = 0.
29. a) sin x + sin 3-----2x = a sin x-2 ;
б) a2 sin2 3x = sin2 x, a > 0.
30. a cos x + b sin x = c, a2 + b2 − 0.
31. а) 2 cos x + 3 sin x = 2; б) sin x + cos x = a2;
в) sin 2x + 3 cos 2x = a;
ã) 2 cos2 6x – 9 sin2 6x + 4 sin 6x cos 6x = a + 5.
32.
![]()
![]() При êаêих значениях
p уравнение p cos x – 2 sin x = 2 +
При êаêих значениях
p уравнение p cos x – 2 sin x = 2 +
![]() + 2 − p имеет решения?
+ 2 − p имеет решения?
33. Найдите êритичесêие точêи фунêции
f(x) = sin 3x + 4-3 cos 3x – ax.
Решите уравнение:
34. a) sin x + sin x + -4π = 0; б) sin 4x – sin 2x = 0;
в) sin2 x – cos2 x = cos x-2 ; ã) cos 2x – cos 6x = 0;
д) cos (3x – 4π) = sin (π – x); e) sin πx2 = sin π (x2 + 2x).
35. a) sin x – -6π – sin πx + 2-----3π- = cos x + -4π ;
б) 1 + sin 2x = (sin 3x – cos 3x)2;
в) cos 5x + cos 7x = cos (π + 6x);
![]() ã) cos x – cos 3x
= 2 3 sin2 x;
ã) cos x – cos 3x
= 2 3 sin2 x;
36. a) sin x + sin 3x + 4 cos3x = 0;
б) cos x – cos 2x = sin 3x;
в) sin x + 2 sin 2x = –sin 3x;
ã) -----------------------------------sin sin3x + sin2x x- = –1.
37.
![]() a)
2 sin 10x + sin 2x = cos 2x;
a)
2 sin 10x + sin 2x = cos 2x;
б) ctg x sin 2x – cos 2x = 1;
![]() в) tg 2x cos 3x +
sin 3x + 2 sin 5x = 0;
в) tg 2x cos 3x +
sin 3x + 2 sin 5x = 0;
ã) 2 sin πx + -3π + 2 cos -x2 + -4π =
![]() =
3 sin x-4 + 8-π
+ 3 cos -x4 + -8π .
=
3 sin x-4 + 8-π
+ 3 cos -x4 + -8π .
38. a) sin x + sin 2x + sin 3x + sin 4x = 0;
б) cos 9x – cos 7x + cos 3x – cos x = 0;
в) cos 5x – sin 5x = sin 7x – cos 7x;
ã) sin 7x + cos2 2x = sin2 2x + sin x;
д) cos 2x – sin 3x – cos 8x = sin 10x – cos 5x.
39. a) sin x + sin 2x + sin 3x = 1 + cos x + cos 2x;
б) 5 sin x + 6 sin 2x + 5 sin 3x + sin 4x = 0;
в) cosec x – cosec 2x = cosec 4x;
ã) sin a + sin (x – a) + sin (2x + a) = sin (x + a) + sin (2x – a).
40. Найдите êритичесêие точêи фунêции
f(x) = 1-2 sin 2x + 1-4 sin 4x + 1-6 sin 6x + 1-8 sin 8.
Решите уравнение:
41. a) tg 3x – tg x = 0; б) tg x + tg 2x – tg 3x = 0.
42. а) cos 3x cos 6x = cos 4x cos 7x;
б) sin 2x sin 6x = cos x cos 3x;
в) cos 3x sin 7x = cos 2x sin 8x;
ã) sin 5x cos 3x = sin 6x cos 2x;
д) sin ππx + -4π sin ππx – ------12π = 1-2 .
43. а) sin2 x + sin2 2x = sin2 3x;
б) cos2 x + cos2 2x + cos2 3x + cos2 4x = 2;
![]() в) sin 7x + sin 9x
= 2 cos2 -4π
– x
– cos2 -4π
+ 2x
в) sin 7x + sin 9x
= 2 cos2 -4π
– x
– cos2 -4π
+ 2x ![]() ;
;
ã) sin2 2x + sin2 x = ------169 .
44. а) sin x + sin 2x + sin 3x = 1-2 ctg x-2 ;
б) cos x + cos 2x + cos 3x = –0,5.
45. a) sin3 x cos 3x + cos3 x sin 3x + 0,375 = 0;
![]() б) cos3 x
cos 3x + sin3 x sin 3x = -------42 .
б) cos3 x
cos 3x + sin3 x sin 3x = -------42 .
46. a) sin x sin -3π – x sin -3π + x = 1-8 ;
б) 8 cos x cos -3π – x cos -3π + x + 1 = 0;
![]() в) tg x tg x + -3π
tg x
+ 2-----3π-
= 3 .
в) tg x tg x + -3π
tg x
+ 2-----3π-
= 3 .
47. a) sin 3x = 4 sin x cos 2x; б) sin 3x cos x = 1,5 tg x;
в) tg x ctg 3x = 4; ã) 6 tg x + -------------tg 35 x- = tg 2x;
д) sin x cos x sin 3x – cos 3x sin2 x = 6 ctg x.
48.
![]() a)
2 sin 3x sin x + (3 2 – 1) cos 2x = 3;
a)
2 sin 3x sin x + (3 2 – 1) cos 2x = 3;
б) 2 cos 4x + 5 cos 2x – 1 = 2 sin2 x;
в) 2 + cos 4x = 5 cos 2x + 8 sin6 x;
ã) tg2x + cos 4x = 0; д) tg x + ctg x – cos 4x = 3.
49. a) sin4 x – 2 cos2 x + a2 = 0;
б) cos4 x – sin2 x cos2 x – 3 sin4 x = 2 cos 2x – 2a cos 4x;
в) cos6 x – sin6 x = a-8 cos 2x.
50. a) sin 2x – 12 (sin x – cos x) +12 = 0;
б) -----------sin1 x- + ------------------------------sinx1− 3-----2π-- = 4 sin x + 5-----4π- ;
в) 1 + tg x = 2 2 sin x;
![]() ã) sin x
+ -4π
= -------
(1 – sin x cos x);
ã) sin x
+ -4π
= -------
(1 – sin x cos x);
д) sin x + sin2 x + cos3 x = 0;
![]()
![]() е) sin -------2x + cos -------2x = 2 sin x .
е) sin -------2x + cos -------2x = 2 sin x .
51. a) a sin x + tg x+ 1 = -----------cos1 x- ;
![]() б) sin 2x – 2 2b
(sin x – cos x) + 1 – 4b = 0;
б) sin 2x – 2 2b
(sin x – cos x) + 1 – 4b = 0;
в) sin3 x + cos3 x + a sin x + -4π = 0.
52. Найдите êритичесêие точêи фунêции
f(x) = 8x – 8(sin x – cos x) – cos 2x + 1.
Решите уравнение:
53.
![]() а)
sin2 x + 2 tg2 x + -------43 tg x – sin x + 11------12 = 0;
а)
sin2 x + 2 tg2 x + -------43 tg x – sin x + 11------12 = 0;
б) 8 cos x + 6 sin x – cos 2x – 7 = 0;
в) sin4 x + sin4 x-2 + -8π + cos4 x = 0,5 sin2 2x.
54. a) cos x-4 – 2 sin x sin x + 1 + sin x-4 – 2 cos x cos x = 0;
б) 3 sin 3x = cos 4x – sin 9x – cos 10x.
55. a) tg x + 1-9 ctg x = cos---------------12x − 1 – 1;
б) sin x + 3 cos x = 2 + cos2x + 3sin2x .
56. a) 2cos2x + 2 = ---------------------------------3 - ;
1 + 4cos2x
б) sinx = a cos x .
57.
![]() a)
sin x + 4 2 cos x = 0; б) sin x + cos x
= 0;
a)
sin x + 4 2 cos x = 0; б) sin x + cos x
= 0;
в) 2 cos x = 2 + 2sin2x ;
ã) cos2 x − cos2 3x = sin 2x;
![]() д) sin x + 3 cos x
= 0,5 +
cos6-π
−
x
;
д) sin x + 3 cos x
= 0,5 +
cos6-π
−
x
;
е) 1-------------------------1 −+ aa sinsinxx 1------------------------------1 −+ 22aa sinsin xx = 1.
58. а) 1 + 4 sin x cosx = cos x – sin x;
б) cos2x − sin4x = sin x – cos x;
в) 1--------------------1 +− tgtgxx = sin x + cos x;
ã) 4 sin 3x + 3 = 2 sin 3x + 2 ;
д) 13 − 18 tg x = 6 tg x – 3;
е) 1 + 8 sin 2x cos2 2x = 2 sin 3 x + -4π .
59. a) 2 3 sin x = -------------------------------3 tg x – 3 ;
2 sin x − 1
![]()
![]() б) 3cos x + sinx − 2 + ctg 3x + sin2 x − 4-1 = sin 3-----2x + -------12 .
б) 3cos x + sinx − 2 + ctg 3x + sin2 x − 4-1 = sin 3-----2x + -------12 .
60. cosx − 1-2- + cosx + 1-3- = a, a ° R.
61. а) log5 tg x = (log5 4) log4 (3 sin x);
![]() б) log9 sin 2x
= log3 -----------sin5 x- .
б) log9 sin 2x
= log3 -----------sin5 x- .
62. a) 2cos 2x = 3 · 2cos2x – 4; б) ctg 2x = tg 2x + 2 tg 2x + 1;
в) x3 sin 2x + 2 = x .
63. a) sin 2x = cos 3x; б) sin 3x + cos x = 0;
в) cos 5x = sin 3x; ã) cos 3x + sin 4x = 0.
64. a) cos 3x + cos 5x = cos 4x; б) sin 3x + sin 6x + sin 9x = 0;
в) sin x + cos 9x = sin 4x; ã) cos 4x – sin 3x = cos 2x.
65. a) sin 2x + 3 sin x – -4π = 2;
![]() б) 6 sin 2x – 5 2 sin x
– -4π
= 7;
б) 6 sin 2x – 5 2 sin x
– -4π
= 7;
в) sin 2x + 3 sin x + -4π + 2 = 0;
ã) sin 2x + 4 cos x + -4π + 5 = 0.
66. a) 2 2 sin x – sin x – -4π 2 – 3 cos x – -4π + 1 = 0;
б) 4 2 sin x – cos x – -4π 2 + 3 =
![]() =
2 (1 + 3 ) sin x
– -4π
;
=
2 (1 + 3 ) sin x
– -4π
;
![]()
![]() в) 2 sin x – 3 sin x
+ -6π
2 +
cos x
+ -6π
= 2;
в) 2 sin x – 3 sin x
+ -6π
2 +
cos x
+ -6π
= 2;
ã) 2 2 sin x – ------12π – cos x – -3π 2 + 1 = 3 sin x – -3π .
67. a) 2 cos 4x + 7 (cos x + sin x)2 + 2 = 0;
б) cos 6x – 12 cos3 x = 4 – 9 cos x;
в) 3 cos 4x = 14 (sin x – cos x)2 – 3;
ã) 48 sin x – cos 6x = 5 + 64 sin3 x.
68. a) cos x + cos x-3 = cos 2-----3x + 1; б) sin 2x – sin 2-----3x = cos 4-----3x ; в) cos x – 1 = cos 2x – cos 3x; ã) sin x-2 + 1 = sin x-6 + cos x-3 .
69.
![]() a)
sin x = cos4 x-2 – sin4 x-2 ; б) 3
sin 2x + sin2 x = cos2 x;
a)
sin x = cos4 x-2 – sin4 x-2 ; б) 3
sin 2x + sin2 x = cos2 x;
в) sin4 x + 1 = cos4 x; ã) 3 tg x + 2 cos 2x = 2.
70. a) |–sin x| = 2 cos x; б) |cos x| = –3 sin x;
в) sin 3x = tg |x| cos 3x.
Решите систему уравнений:
71.
![]()
![]() а) x3 cos – y
= 6,52 x – 12 cos π, y
= –4;
а) x3 cos – y
= 6,52 x – 12 cos π, y
= –4;
x + y = -----23π- ,cos x + cos y = a,
б) -----------sinx- = 2; в) x + y = -4π .
siny
72. a) cos (sin 3xx – cos 2y) = 0,5;y = 2a – cos 3x sin 2y,
sin x sin y = -------3 ,
![]() б) cos x cos y = -------43 ; в)
б) cos x cos y = -------43 ; в) ![]() tg cos xx
+ tg cos yy = 0,5; = 2,
tg cos xx
+ tg cos yy = 0,5; = 2,
4
sin x cos y = 1-4 ,
ã)
3 tg x = tg y.
73. ![]() a)
tg 5 tg x – 2 sin x + 2 sin y = –2;y = –4;
a)
tg 5 tg x – 2 sin x + 2 sin y = –2;y = –4;
![]() б) 4 sin y – 6 2 cos x
= 5 + 4 cos2 y, cos 2x = 0;
б) 4 sin y – 6 2 cos x
= 5 + 4 cos2 y, cos 2x = 0;
![]() в) sin -----------sin1 xx- cos – cos y = –y =
3-aa-----------;3+ 3- , tg -----------cos1yx + (-
– tg a2 + 2y = 2a) cos a + 2,x =
0.
в) sin -----------sin1 xx- cos – cos y = –y =
3-aa-----------;3+ 3- , tg -----------cos1yx + (-
– tg a2 + 2y = 2a) cos a + 2,x =
0.
sin x sin y = 1-4 , cos (x + y) = 1-2 ,
![]() 74. а) cos x cos y = 3-4 ;
б) cos (x
– y) = -------22 ;
74. а) cos x cos y = 3-4 ;
б) cos (x
– y) = -------22 ;
cos tg xx tg cos y = 3;y = 1-4 , ã) sin sinx + cos x − cosyy = sin = cos 2 xx., в)
Решите неравенство:
1. a) sin 2x > 0; б) sin x-2 < 0; в) sin x + -4π m 1-2 ;
![]() ã) sin (2x – 1) > –-------1 ; д) sin x
m –1.
ã) sin (2x – 1) > –-------1 ; д) sin x
m –1.
2
2. a) cos x-3 > 0; б) cos 4x < 0; в) cos x – -6π l 1-2 ;
![]() ã) cos x-2 + 1-4
< –-------22 ; д) cos x
l 1.
ã) cos x-2 + 1-4
< –-------22 ; д) cos x
l 1.
3. a) tg 2x > 0; б) tg x-4 < 0;
![]() в) tg x
+ -3π
l 1; ã)
tg (3x – 2) < – 3 .
в) tg x
+ -3π
l 1; ã)
tg (3x – 2) < – 3 .
4. а) ctg x < 0; б) ctg x – -4π l 1; в) ctg 2x + -3π < –2.
5. a) |sin x| > 21- ; б) |cos x| < 1-2 ; в) |tg x| m 1;
![]() ã) |ctg x| < 3 .
ã) |ctg x| < 3 .
6. a) 1-3 m sin x < 1-2 ; б) –1-2 < cos x m –1-4 ;
в) –2 < tg x < 3; ã) –4 < ctg x m 1,5.
7. 2 sin2 x + 3 sin x – 3 > 0.
8.
![]() cos
2x + 5 cos x + 3 l 0.
cos
2x + 5 cos x + 3 l 0.
9.
![]() tg2
x + (2 – 3 ) tg x – 2 3 < 0.
tg2
x + (2 – 3 ) tg x – 2 3 < 0.
10. ctg2 x + ctg x l 0.
11.
![]()
![]() 2( 2 – 1) sin x
– 2 cos 2x + 2 – 2 < 0.
2( 2 – 1) sin x
– 2 cos 2x + 2 – 2 < 0.
12. cos πx + sin πx – -4π > 0.
13. cos3 x sin 3x + cos 3x sin3 x < -83 .
14. cos x cos 2x cos 3x m 0. 15. sin4 x-3 + cos4 x-3 > -21 .
16. sin6 x + cos6 x > 5-8 . 17. 8 sin6 x – cos6 x > 0.
18. tg x tg 3x < –1. 19. 3 sin 2x – 1 > sin x + cos x.
20. ![]()
![]() sin 2x > 2 sin2
x + (2 – 2 ) cos2 x, 0 < x < 2π.
sin 2x > 2 sin2
x + (2 – 2 ) cos2 x, 0 < x < 2π.
21. |sin x| > cos2 x. 22. 5 − 2sinx l 6 sin x – 1.
23. 1 – cos x < tg x – sin x.
24. 91 + sin2πx + 30 · 9cos2πx m 117.
Найдите область определения фунêции:
25. ![]()
![]() y = sin x
. 26. y = cosx2 .
y = sin x
. 26. y = cosx2 .
27. y = arcsin -----------12+xx- . 28. y = arccos (2 sin x).
29. y = ctg πx + arccos 2x.
30. Доêажите, что фунêция y = sin2 x монотонно возрастает на интервале x ° – π; –-2π .
31. Доêажите, что фунêция y = cos3 x монотонно убывает на интервале x ° -2π ; 3-----4π- .
32. Доêажите, что если 0 < x1 < x2 < -2π , то ------------tgtgxx21 > ----xx21 .
Найдите êритичесêие точêи фунêции:
33.
![]() f(x)
= 2 sin a cos x + 1-3 cos 3x + 4a − a2- .
f(x)
= 2 sin a cos x + 1-3 cos 3x + 4a − a2- .
34. f(x) = 1 – -----------cos4 a- sin 2x + 1-8 sin (π + 4x) +
![]() +
x
cos---------------------2a −
3-
+ 2a a− 2 + 3 .
+
x
cos---------------------2a −
3-
+ 2a a− 2 + 3 .
35.
f(x) = 1-3 sin a tg3 x + (sin a
– 1) tg x + ---------------8 − a- .
Гл a в a IV
Зaдaчи нa состaвление óрaвнений
и нерaвенств
![]()
1. Поезд вышел со станции A по направлению ê станции B. Пройдя 450 êм, что составляло 75% всеãо пути AB, он остановился из-за снежноãо заноса. Через полчаса путь был расчищен, и машинист, увеличив сêорость поезда на 15 êм/ч, привел еãо на станцию B без опоздания. Найдите первоначальную сêорость поезда.
2. Моторная лодêа прошла вниз по течению реêи 14 êм, а затем 9 êм против течения, затратив на весь рейс 5 ч. Найдите сêорость течения реêи, если сêорость моторной лодêи в стоячей воде равна 5 êм/ч.
3. По ãрафиêу поезд должен проходить переãон от A до B длиной в 20 êм с постоянной сêоростью. С заданной сêоростью поезд прошел полпути и остановился на 3 мин; чтобы вовремя прийти в пунêт B, ему пришлось остальные полпути идти на 10 êм/ч быстрее. Второй раз поезд простоял на полпути 5 мин. С êаêой сêоростью он должен был идти оставшуюся часть пути, чтобы прибыть в пунêт B по расписанию?
4. Велосипедист выехал из пунêта A в B и ехал с постоянной сêоростью 20 êм/ч. Коãда он проехал 831- êм, еãо доãнал автомобиль, вышедший из пунêта A нa 15 мин позже и шедший таêже с постоянной сêоростью. После тоãо êаê велосипедист проехал еще 25 êм, он встретил автомобиль, уже возвращавшийся из B, ãде он простоял полчаса. Найдите расстояние между A и B.
5. Лодêа спусêается вниз по течению реêи из пунêта A в пунêт B, находящийся в 10 êм от A, а затем возвращается в A. Если собственная сêорость лодêи равна 3 êм/ч, то путь из A в B занимает на 2 ч 30 мин меньше, чем из B в A. Каêой должна быть собственная сêорость лодêи, чтобы поездêа из A в B зaнялa 2 ч?
6. Расстояние от A до B составляет 30 êм. Из A выехал автобус с постоянной сêоростью. Через 10 мин из A вылетел вертолет, êоторый летел вдоль шоссе ê B. Через 5 мин после вылета он наãнал автобус и продолжал лететь до B. Не приземляясь в B, вертолет повернул назад и снова встретил автобус через 20 мин после своеãо вылета из A. Определите сêорости автобуса и вертолета.
7. Из ãорода М в ãород N в 5 ч утра вышел товарный поезд. Через 1,5 ч вслед за ним вышел пассажирсêий поезд, сêорость êотороãо на 5 êм/ч больше сêорости товарноãо. В 21 ч 30 мин тоãо же дня расстояние между поездами составляло 21 êм. Найдите сêорость товарноãо поезда.
8. Если пароход и êатер плывут по течению, то расстояние от A до B пароход проходит в 1,5 раза быстрее êатера, при этом êатер êаждый час отстает от парохода на 8 êм. Если же они плывут против течения, то пароход проходит путь от B до A в 2 раза быстрее êатера. Найдите сêорости парохода и êатера в стоячей воде.
9. Пунêт C расположен в 12 êм от B вниз по течению реêи. Рыбаê отправился на лодêе в пунêт C из пунêта A, расположенноãо выше пунêта B. Через 4 ч он прибыл в C, а на обратный путь затратил 6 ч. Поставив на лодêу мотор и тем самым увеличив сêорость лодêи относительно воды втрое, рыбаê добрался от A до B за 45 мин. Определите сêорость течения реêи, считая, ее постоянной.
10. Два пешехода вышли одновременно: один из пунêта A в пунêт В, друãой из В в A. Каждый шел с постоянной сêоростью и, придя в êонечный пунêт, сразу же отправлялся обратно. Первый раз они встретились в 12 êм от В, второй раз — через 6 ч после первой встречи в 6 êм от A. Найдите расстояние между пунêтами A и В и сêорости пешеходов.
11. Два самолета вылетают одновременно из пунêтов A и В навстречу друã друãу и встречаются на расстоянии a êм от середины AB. Если бы первый самолет вылетел на b ч позже второãо, то они встретились бы на середине AB. Если же второй самолет вылетел на b ч позже первоãо, то они встретились бы на 1-4 пути от В. Найдите расстояние AB и сêорости самолетов.
12. Два туриста вышли одновременно из пунêта A в В, причем первый турист êаждый êилометр пути проходил на 5 мин быстрее второãо. Первый, пройдя 1-5 часть пути, вернулся в A и, пробыв там 10 мин, снова направился в В. При этом в В оба туриста пришли одновременно. Каêово расстояние от A до В, если второй турист прошел еãо за 2,5 ч?
13. Два велосипедиста выехали одновременно из одноãо пунêта в одном направлении. Первый из них едет со сêоростью 15 êм/ч, а второй — 12 êм/ч. Спустя полчаса из тоãо же пунêта в том же направлении выехал третий велосипедист, êоторый через неêоторое время доãнал второãо, а еще через 1 ч 30 мин доãнал и первоãо. Найдите сêорость третьеãо велосипедиста.
14. Меньшая дуãа AB оêружности имеет длину l см. Движущиеся по оêружности точêи P1 и P2 в момент t = 0 находятся соответственно в точêах A и B. Если точêи P1 и P2 будут двиãаться навстречу друã друãу по меньшей дуãе, то они встретятся через t1 с, а если по большей, то — через t2 с. Точêа P1 обеãает всю оêружность за то время, в течение êотороãо P2 проходит s см. Найдите длину оêружности и сêорости точеê P1 и P2 (движение точеê по оêружности равномерное).
15. Два тела, двиãаясь по оêружности в одном и том же направлении, встречаются через êаждые 56 мин. Если бы они двиãались с теми же сêоростями в противоположных направлениях, то они встречались бы через êаждые 8 мин. Пусть при движении в противоположных направлениях в неêоторый момент времени расстояние по оêружности между телами равно 40 м; тоãда через 24 с оно составит 26 м (в течение этих 24 с тела не встретились). Найдите сêорости тел и длину оêружности.
16. Расстояние между пунêтами A и В, расположенными на прямолинейном шоссе, равно 15 êм. Из пунêта A выезжает велосипедист с постоянной сêоростью 8 êм/ч, а из B в том же направлении — мотоциêлист, êоторый движется с постоянным усêорением 2 êм/ч2. Через êаêое время после начала движения расстояние между велосипедистом и мотоциêлистом будет равно 750 м, если они начнут движение одновременно? Начальная сêорость мотоциêлиста равна нулю.
17. Студенты взяли на лодочной станции лодêу напроêат. Сначала они спустились вниз по течению реêи на 20 êм, затем повернули обратно и вернулись на лодочную станцию, затратив на всю проãулêу 7 ч. На обратном пути на расстоянии 12 êм от лодочной станции они встретили плот, проплывавший мимо нее в тот момент, êоãда они направились на проãулêу. С êаêой сêоростью двиãалась лодêа вниз по течению реêи и êaêовa сêорость течения реêи?
18. Из порта одновременно вышли два парохода: один — на север, друãой — на востоê. Через 2 ч расстояние между ними оêазалось равным 60 êм. Найдите сêорость êаждоãо парохода, зная, что сêоростьодноãо из них на 6 êм/ч больше сêорости друãоãо.
19. Пунêты A, B, C удалены от пунêта M соответственно на 60, 55 и 56 êм. Одновременно из этих пунêтов в пунêт M вышли три пешехода: первый — из A, второй — из B, третий — из C. Первый прошел весь путь с постоянной сêоростью и прибыл в M на 2 ч раньше второãо и третьеãо, прибывших одновременно. Второй пешеход, пройдя 40 êм с той же сêоростью, что и первый, сделал остановêу на 1 ч. Остатоê пути он прошел со сêоростью, êоторая меньше сêорости третьеãо пешехода на стольêо же, на сêольêо сêорость третьеãо меньше сêорости первоãо. Третий пешеход весь путь прошел с постоянной сêоростью. Определите сêорости первоãо и третьеãо пешеходов.
20. Дороãа проходит через пунêты A и B. Одновременно и в одном направлении выехали: из A — мотоциêлист (в направлении ê B), из B — велосипедист. Мотоциêлист доãнал велосипедиста на расстоянии a êм от B. Если бы мотоциêлист и велосипедист выехали одновременно из A в В, то в момент прибытия мотоциêлиста в В велосипедист отставал бы от неãо на b êм. Определите расстояние между пунêтами A и В (сêорости мотоциêлиста и велосипедиста постоянны).
21. Из пунêтов A и В навстречу друã друãу вышли одновременно два пешехода. Коãда пешеход, вышедший из A, прошел 2-3 пути, второй пешеход находился в 2 êм от середины пути. Найдите расстояние между A и В, если известно, что, êоãда пешеход, вышедший из В, прошел ------163 пути, первый пешеход находился от середины пути в 3 êм. Сêорости пешеходов постоянны.
22. Два пешехода вышли одновременно из пунêта A. Первый из них встретился с туристом, идущим в A, через 20 мин после выхода из A, а второй встретил туриста на 5 мин позже первоãо. Через 10 мин после второй встречи турист пришел в A. Сêорости пешеходов и туриста постоянны. Найдите отношение сêоростей пешеходов.
23. Из пунêта A в пунêт В выехал мотоциêлист. Через 2 ч из A в В выехал автомобиль, êоторый прибыл в В одновременно с мотоциêлистом. Если бы автомобиль и мотоциêлист одновременно выехали из A и В навстречу друã друãу, то они бы встретились через 1 ч 20 мин после выезда. Сêольêо часов провел в пути из A в В мотоциêлист?
24. Дороãа проходит через пунêты A и В. Велосипедист выехал из A по направлению ê В. Одновременно с ним из пунêта В вышли с равными сêоростями двапешехода: первый — в пунêт A, второй — в противоположном направлении. Велосипедист проехал от A до В за 0,5 ч и, продолжая движение, доãнал второãо пешехода. Это произошло через 1,2 ч после встречи велосипедиста с первым пешеходом. Определите время движения велосипедиста от начала движения до встречи с первым пешеходом (сêорости велосипедиста и пешеходов постоянны).
25. Города A и В стоят на береãу реêи. Буêсир тратит на прохождение от A до В и обратно 13 ч, а êатер, собственная сêорость êотороãо в 2 раза больше собственной сêорости буêсира, тратит на этот же путь 6 ч. Во сêольêо раз собственная сêорость буêсира больше сêорости реêи?
26. Из пунêта A отправилась моторная лодêа вверх по Волãе, а из пунêта В одновременно вышел плот по течению. Через a ч они встретились и далее двиãались без остановоê. Дойдя до B, лодêа, не задерживаясь, повернула обратно и доãнала плот в пунêте A. Предполаãается, что собственная сêорость лодêи была все время неизменной. Сêольêо часов находились в пути плот и лодêа?
27. Два пешехода вышли одновременно навстречу друã друãу и встретились через 3 ч 20 мин. За êаêое время пройдет все расстояние êаждый из них, если первый пришел в то место, из êотороãо вышел второй, на 5 ч позже, чем второй пришел в то место, отêуда вышел первый?
28. Два велосипедиста выезжают одновременно из пунêтов A и В навстречу друã друãу. Через 1,6 ч расстояние между ними составило 0,2 первоначальноãо. Сêольêо часов требуется êаждому из велосипедистов на прохождение пути AB, если первый затрачивает на этот путь на 3 ч меньше второãо?
29. Три лыжниêа проходят дистанцию, двиãаясь равномерно. Через m мин после старта третьеãо лыжниêа ему остается пройти часть дистанции, êоторую первый лыжниê может пройти за n мин, второй — за p мин. За сêольêо минут может пройти всю дистанцию êаждый из лыжниêов, если сêорость третьеãо лыжниêа равна полусумме сêоростей первоãо и второãо?
30. Два автомобиля выехали одновременно из пунêтов A и В навстречу друã друãу. Через 16 ч после встречи автомобиль, ехавший из A, прибыл в В, а через 25 ч после встречи автомобиль, ехавший из В, прибыл в A. Сêольêо часов был в пути êаждый автомобиль?
31. Из пунêта A в В одновременно отправляются пешеход и велосипедист. Доехав до В, велосипедист поворачивает обратно и встречает пешехода через 1 ч после начала движения. После встречи пешеход продолжает идти в В, а велосипедист поворачивает и таêже едет в В. Доехав до В, велосипедист снова поворачивает обратно и встречает пешехода через 40 мин после первой встречи. Определите, за êаêое время пешеход пройдет расстояние от A до В.
32. Из пунêтов A и В одновременно выезжают два автомобиля и встречаются в 12 ч дня. Если сêорость первоãо удвоить, а сêорость второãо оставить первоначальной, то встреча произойдет на 56 мин раньше. Если же сêорость второãо удвоить, а сêорость первоãо оставить первоначальной, то они встретятся на 65 мин раньше. Определите время встречи в том случае, êоãда сêорости обоих автомобилей были бы удвоены.
1. Три землеêопа, работая одновременно, за четыре дня выêопали 216 м3 траншеи. За один день третий землеêоп выêапывает больше второãо на стольêо же êубометров, на сêольêо второй выêапывает за день больше первоãо. За 5 дней третий землеêоп выêапывает стольêо же êубометров, сêольêо первый за 7 дней. Сêольêо êубометров в день выêапывает первый землеêоп?
2. На уãольной шахте сначала работали два участêа, а через неêоторое время вступил в строй третий участоê, в результате чеãо производительность шахты увеличилась в 1,5 раза. Сêольêо процентов составляет производительность второãо участêа от производительности первоãо, если известно, что за 4 месяца первый и третий участêи выдают уãля стольêо же, сêольêо второй за ãод?
3. Трое рабочих выполнили задание за 10 дней, причем третий из них работал тольêо первые три дня. За сêольêо днейвыполнил бы задание êаждый рабочий, если известно, что за первые три дня они вместе выполнили 37% всеãо задания, а за 5 дней первый рабочий сделал стольêо же, сêольêо второй за 4 дня?
4. Двое рабочих, работая одновременно, выполнили задание за 5 дней. Если бы первый работал вдвое быстрее, а второй — вдвое медленнее, то задание заняло бы у них 4 дня. За êаêое время выполнил бы все задание один первый рабочий?
5. Два сêрепера разной мощности, работая вместе, моãут выполнить задание за 6 ч. Если быпервый проработал 4 ч, а затем один второй 6 ч, то они выполнили бы 80% всеãо задания. За сêольêо часов êаждый сêрепер, работая отдельно, может выполнить все задание?
6. Трое рабочих должны сделать 80 одинаêовых деталей. Известно, что вместе они делают за час 20 деталей. К заданию приступил сначала первый рабочий. Он сделал 20 деталей, затратив на это более 3 ч. Оставшуюся часть задания выполнили вместе второй и третий рабочие. На все задание ушло 8 ч. Сêольêо часов потребовалось бы первому рабочему на все задание, если бы с начала и до êонца он делал ее один?
7. Три обыêновенных и два траêторных плуãа обрабатывают вместе поле за 6 дней. Три траêторных плуãа выполнили бы ту же работу на 5 дней быстрее, чем девять обыêновенных. Во сêольêо раз производительность траêторноãо плуãа больше производительности обыêновенноãо?
8. Каждому из трех рабочих для выполнения неêотороãо задания требуется определенное время, причем третий рабочий выполняет еãо на 1 ч быстрее первоãо. Работая все вместе, они выполняют задание за 1 ч. Если же первый рабочий проработает 1 ч, то второму для завершения всеãо задания потребуется 4 ч. За êаêое время может выполнить все задание êаждый рабочий?
9. Два эêсêаватора выполняют неêоторую работу. Если эту работу будет выполнять тольêо первый эêсêаватор, то он может заêончить ее на 8 ч позднее, чем оба вместе. Если же эту работу будет выполнять тольêо второй эêсêаватор, то он заêончит ее на 4,5 ч позже, чем оба вместе. За êаêое время может выполнить работу êаждый из эêсêаваторов в отдельности?
10. За t мин один автомат изãотавливает на d деталей больше друãоãо. Если бы на êаждом из них удалось соêратить время выпусêа одной детали на 2 мин, то первый автомат выпусêал бы за t мин на 2d деталей больше второãо. Сêольêо деталей изãотавливает êаждый автомат за t мин?
11. Два êусêа одинаêовой тêани стоят вместе 4550 р. Коãда из первоãо êусêа продали стольêо, сêольêо было первоначально во втором, а из второãо — половину тоãо, что было первоначально в первом, остатоê первоãо êусêа оêазался на 10 м больше остатêа второãо êусêа. Сêольêо метров тêани было в êаждом êусêе, если 1 м тêани стоит 70 р.?
12. В ателье поступило по одному êусêу черной, зеленой и синей тêани. Хотя зеленой тêани было на 9 м меньше, чем черной, и на 6 мбольше, чем синей, стоимость êусêов была одинаêовой. Известно таêже, что стоимость 4,5 м черной тêани равна общей стоимости 3 м зеленой и 0,5 м синей тêани. Сêольêо метров было в êаждом êусêе?
13. Баê вместимостью 2400 м3 наполняется топливом. При опорожнении этоãо же баêа производительность насоса на 10 м3/мин выше, чем производительность насоса при наполнении. В результате время опорожнения баêа на 8 мин меньше времени заполнения. Определите производительность насоса при наполнении баêа.
14. Бассейн наполняется водой из двух êранов. Сначала первый êран был отêрыт 1-3 тоãо времени, за êоторое наполняет бассейн один второй êран. Затем, наоборот, один второй êран был отêрыт 1-2 тоãо времени, за êоторое наполняет бассейн один первый êран. После этоãо оêазалось наполненным 5-6 бассейна. Оба êрана, отêрытые вместе, наполняют бассейн за 2,4 ч. За êаêое время наполнит бассейн êаждый êран в отдельности?
15. Баê объемом 425 м3 наполнился водой из двух êранов, причем первый êран был отêрыт на 5 ч дольше второãо. Если бы первый êран был отêрыт стольêо времени, сêольêо на самом деле был отêрыт второй, а второй был отêрыт стольêо времени, сêольêо был отêрыт первый, то из первоãо êрана вытеêло бы воды вдвое меньше, чем из второãо; если же отêрыть оба êрана одновременно, то баê наполнится через 17 ч. Сêольêо часов был отêрыт второй êран?
16. Двум тоêарям и учениêу поручили выполнение срочной работы. Первый тоêарь может один выполнить всю работу за время на 3 ч большее, чем время, за êоторое второй тоêарь и учениê, работая одновременно, выполняют ту же работу. Второй тоêарь, работая один, выполняет всю работу за то же время, за êоторое ее выполняют первый тоêарь и учениê, работая одновременно. Время, затрачиваемое вторым тоêарем на самостоятельное выполнение всей работы, на 8 ч меньше удвоенноãо времени, затрачиваемоãо первым тоêарем на самостоятельное выполнение всей работы. За êаêое время будет выполнена вся работа двумя тоêарями и учениêом, работающими одновременно?
17. Трое рабочих разной êвалифиêации выполнили неêоторое задание, причем первый работал 6 ч, второй — 4 ч и третий — 7 ч. Если бы первый рабочий работал 4 ч, второй — 2 ч и третий — 5 ч, то было бы выполнено лишь 2-3 всеãо задания. Засêольêо часов рабочие заêончили бы задание, если бы они работали все вместе одно и то же время?
18. В бассейн проведены четыре трубы. Коãда отêрыты первая, вторая и третья трубы, бассейн наполняется за 12 мин; êоãда отêрыты вторая, третья и четвертая трубы, — за 15 мин; êоãда отêрыты тольêо первая и четвертая трубы, — за 20 мин. За êаêое время наполнится бассейн, если отêрыть все четыре трубы?
19. Одна железная руда содержит 72% железа, друãая — 58%. Неêоторое êоличество первой руды смешивают с неêоторым êоличеством второй и получают руду, содержащую 62% железа. Если бы для смеси взяли êаждой руды на 15 êã больше, чем было взято, то получилась бы руда, содержащая p% железа. Сêольêо êилоãраммов первой и второй руды было взято для составления первой смеси?
20. В первый сосуд вместимостью 6 л налито 4 л 70%-ноãо раствора серной êислоты; во второй сосуд таêой же вместимости налито 3 л 90%-ноãо раствора серной êислоты (имеется в виду объемное процентное содержание). Сêольêо литров раствора нужно перелить из второãо сосуда в первый, чтобы в первом сосуде получился q%-ный раствор серной êислоты?
21. После двух последовательных повышений зарплата достиãла 15------8 по сравнению с первоначальной. На сêольêо процентов повысилась зарплата в первый раз, если второе повышение было вдвое больше (в процентном отношении) первоãо?
22. Известно, что вêлад, находящийся в банêе с начала ãода, возрастает ê êонцу ãода на определенный процент (свой для êаждоãо банêа). В начале ãода 53- неêотороãо êоличества денеã
положили в первый банê, а остальную часть — во второй банê. К êонцу ãода сумма этих вêладов стала равна 590 ден. ед., ê êонцу следующеãо ãода — 701 ден. ед. Было подсчитано, что если бы первоначально 3-5 исходноãо êоличества денеã положили во второй банê, а оставшуюся часть — в первый банê, то по истечении одноãо ãода сумма вêладов в эти банêи стала бы равной 610 ден. ед. Каêова в этом случае была бы сумма вêладов в эти банêи ê êонцу второãо ãода?
23. Из сосуда, до êраев наполненноãо чистым ãлицерином, отлили 1 л ãлицерина, а взамен долили 1 л воды. После перемешивания снова отлили 1 л смеси и долили 1 л воды. Наêонец, опять после перемешивания отлили 1 л смеси и долили 1 л воды. В результате этих операций êоличество воды в сосуде оêазалось в 7 раз большим по объему оставшеãося в нем ãлицерина. Сêольêо литров ãлицерина и воды оêазалось в сосуде в результате проделанных операций?
24. Из êолбы, содержащей раствор соли, отлили в пробирêу 0,1 раствора. Затем из пробирêи часть воды наãреванием испарили, в результате чеãо процентное содержание соли в пробирêе увеличилось в k раз. Каêое было первоначальное процентное содержание соли в êолбе, если известно, что после переливания в нее содержимоãо пробирêи процентное содержание соли в êолбе увеличилось на a%?
25. Имеются три êусêа сплава меди с оловом. Массы этих êусêов относятся êаê 3 : 4 : 5. Процентное содержание меди во втором êусêе в a раз больше, а в первом êусêе в a раз меньше, чем в третьем êусêе. После тоãо êаê все три сплава сплавили вместе, получили новый сплав меди и олова, в êотором процентное содержание меди изменилось на p% по сравнению с процентным содержанием меди в третьем êусêе. Каêово было первоначальное процентное содержание меди в этих сплавах?
26. Разность цифр двузначноãо числа равна 2, а сумма êвадратов тех же цифр равна 52. Найдите это число.
27. Если двузначное число разделить па произведение еãо цифр, то в частном получится 3, а в остатêе — 9. Если же из êвадрата суммы цифр этоãо числа вычесть произведение еãо цифр, то получится данное число. Найдите это число.
28. Найдите трехзначное число, если известно, что сумма еãо цифр равна 17, а сумма êвадратов еãо цпфр равна 109. Если же из этоãо числа вычесть 495, то получится число, записанное теми же цифрами, но в обратном порядêе.
29. Сумма êубов цифр двузначноãо числа равна 243, а произведение суммы еãо цифр на произведение еãо цифр равно 162. Найдите это двузначное число.
30. Задано четырехзначное число. Если ê нему прибавить цифру еãо тысяч, то трехзначное число, образованное тремя последними цифрами полученноãо числа, оêажется вдвое меньше исходноãо. Найдите исходное четырехзначное число.
31. Два двузначных числа, записанных одно за друãим, образуют четырехзначное число, êоторое нацело делится на их произведение. Найдите эти числа, если одно из них в 2 раза больше друãоãо.
32. Задано трехзначное число, êратное 9. Если отбросить цифру еãо сотен и ê полученному двузначному числу прибавить 2, торезультат оêажется втрое меньше исходноãо числа. Найдите исходное число.
33. Задано неêоторое двузначное число, êратное 3. Если между еãо цифрами вставить нуль и ê полученному трехзначному числу прибавить удвоенную цифру еãо сотен, то получится число, êоторое в 9 раз больше, чем заданное двузначное число. Найдите исходное число.
34. Найдите двузначное число, êоторое на 12 больше суммы êвадратов еãо цифр и на 16 больше удвоенноãо произведения еãо цифр.
35. Если неêоторое двузначное число умножить на сумму еãо цифр, то получится 405. Если же число, написанное теми же цифрами в обратном порядêе, умножить на сумму еãо цифр, то получится 486. Найдите исходное число. § 3. ЗАДАЧИ НА СОСТАВЛЕНИЕ НЕРАВЕНСТВ
1. В четырехзначном числе сумма цифр сотен, десятêов и единиц равна 14, сумма цифр тысяч и единиц равна 9, цифра сотен больше цифры десятêов на 4. Из всех чисел, удовлетворяющих уêазанным условиям, найдите таêое, у êотороãо сумма произведения цифры тысяч на цифру единиц и произведения цифры десятêов на цифру сотен принимает наибольшее значение.
2. Лодêа спусêается по течению реêи на расстояние 10 êм, а затем поднимается против течения на расстояние 6 êм. Сêорость течения реêи равна 1 êм/ч. В êаêих пределах должна находиться собственная сêорость лодêи, чтобы вся поездêа заняла от 3 до 4 ч?
3. Купили несêольêо одинаêовых êниã и альбомов. За êниãи заплатили 1056 р., за альбомы — 56 р. Книã êупили на 6 больше, чем альбомов. Сêольêо êупили êниã, если цена одной êниãи больше чем на 100 р. превосходит цену одноãо альбома?
4. Из точêи A по прямой начали двиãаться одновременно в одном направлении два тела: первое — равномерно усêоренно с начальной сêоростью 3 м/с и усêорением 2 м/с2, второе — равномерно. В êаêих пределах может изменяться сêорость второãо тела, чтобыоно сначала обоãнало первое тело, но чтобы затем первое тело доãнало второе на расстоянии, не большем 10 м от A?
5. Шêольниê переêлеивает все свои марêи в новый альбом. Если он наêлеит по 20 мароê на один лист, то ему не хватит альбома, а если по 23 марêи на лист, то по êрайней мере один лист останется пустым. Если же шêольниêу подарить еще таêой же альбом, на êаждом листе êотороãо наêлеено по 21 марêе, то всеãо у неãо станет 500 мароê. Сêольêо листов в альбоме?
6. Группа студентов решила êупить маãнитофон ценой от 1700 до 1950 p. Однаêо в последний момент двое отêазались участвовать в поêупêе, поэтому êаждому из оставшихся пришлось внести на 10 р. больше. Сêольêо стоил маãнитофон?
7. Несêольêо человеê должны были принять участие в эêсêурсии. Однаêо в последний момент два человеêа от участия в ней отêазались, поэтому êаждому из оставшихся эêсêурсантов пришлось уплатить за участие в эêсêурсии на 3 р. больше, чем планировалось первоначально (все участниêи должны были заплатить поровну). Сêольêо должен был заплатить êаждый эêсêурсант первоначально, если стоимость эêсêурсии больше 70 р., но не более 75 р.?
8. Для перевозêи ãруза из одноãо места в друãое затребовали неêоторое êоличество одинаêовых машин. Ввиду неисправности дороãи на êаждую машину пришлось ãрузить на 0,5 т меньше, чем предполаãалось, поэтому дополнительно были затребованы 4 таêие же машины. Масса перевезенноãо ãруза была больше 55 т, но не превосходила 64 т. Сêольêо тонн ãруза было перевезено на êаждом ãрузовиêе?
9. Пунêты A и В расположены на одной реêе таê, что плот, плывущий из A в В со сêоростью течения реêи, проходит путь от A до В зa 24 ч. Катер весь путь от A до В и обратно проходит не менее чем за 10 ч. Если бы собственная сêорость (сêорость в стоячей воде) êатера увеличилась на 40%, то путь от A до В и обратно занял бы у êатера не более 7 ч. Найдите время, за êоторое êатер проходит путь из В в A, êоãда еãо собственная сêорость не увеличена.
10. Группа студентов, состоящая из 30 человеê, получила на эêзамене оценêи «2», «3», «4», «5». Сумма полученных оценоê равна 93, причем троеê было больше, чем пятероê, и меньше, чем четвероê. Кроме тоãо, число четвероê делилось на 10, а число пятероê было четным. Определите, сêольêо êаêих оценоê получила ãруппа.
11. Оêоло домапосажены липы и березы, причем общее их êоличество более 14. Если увеличить вдвое êоличество лип, а êоличество берез — на 18, то берез станет больше. Если увеличить вдвое êоличество берез, не изменяя êоличества лип, то лип все равно будет больше. Сêольêо лип и сêольêо берез было посажено?
12. По двум улицам движутся ê переêрестêу две машины с постоянными сêоростями 40 и 50 êм/ч. Улицы пересеêаются под уãлом в 60°. В начальный момент времени машины находятся на расстояниях 5 и 4 êм от переêрестêа (соответственно). Через êаêое время расстояние между ними станет наименьшим?
13. В бассейн проведены три трубы. Первая труба наливает 30 м3 воды в час. Вторая труба наливает в час на 3v м3 меньше, чем первая (0 < v < 10), а третья труба наливает в час на 10v м3 больше первой. Сначала первая и вторая трубы, работая вместе, наполняют 0,3 бассейна, а затем все три трубы, работая вместе, — оставшиеся 0,7 бассейна. При êаêом значении v бaссейн быстрее всеãо наполнится уêазанным способом?
14. Из пунêта A на проãулêу вышел пешеход со сêоростью v êм/ч. После тоãо êаê пешеход отошел от A на 6 êм, из A следом за ним выехал велосипедист, сêорость êотороãо была на 9 êм/ч больше сêорости пешехода. Коãда велосипедист доãнал пешехода, они повернули назад и вместе возвратились в A со сêоростью 4 êм/ч. При êаêом значении v время проãулêи пешехода будет наименьшим?
15. Сосуд вместимостью 5 л содержит 2 л p%-ноãо (по объему) раствора соли. Сêольêо литров 20%-ноãо раствора таêой же соли надо налить в сосуд, чтобы процентное содержание соли в сосуде стало наибольшим?
16. Имеется три сплава. Первый содержит 45% олова и 55% свинца, второй — 10% висмута, 40% олова и 50% свинца, третий — 30% висмута и 70% свинца. Из них необходимо составить новый сплав, содержащий 15% висмута. Каêое наибольшее и êаêое наименьшее процентное содержание свинца может быть в этом новом сплаве?
17. Тело начинает двиãаться прямолинейно в момент времени t = 0 с начальной сêоростью, равной 3 м/с. Через 1 с после начала движения сêорость тела была равна 4 м/с. Найдите усêорение тела в êонце первой сеêунды еãо движения и путь, пройденный телом за первые 4 с движения, если сêорость тела изменяется по заêону v(t) = at2 + 2t + b.
18. Известно, чтов êлассе не менее 31% девочеê и более 65% мальчиêов. Определите наименьшее возможное êоличество учениêов в этом êлассе, если известно, что в нем не менее 8 девочеê.
19. В автопробеãе участвуют машины мароê «Жиãули» и «Волãа». Известно, что «Жиãулей» более 67%, а «Волã» не менее 25% от общеãо числа автомобилей. Определите наименьшее возможное êоличество участвующих в этом пробеãе автомашин, если известно, что стартовали более трех «Жиãулей».
20.
Шахматный турнир собрал мастеров спорта и перворазрядниêов,
причем êоличество мастеров более чем на 33% превосходит число перворазрядниêов,
êоторых в свою очередь более 41% от общеãо числа участниêов турнира.
Определите наименьшее возможное êоличество участниêов этоãо турнира,
если известно, что в нем иãрают более трех мастеров.
Глава V Неопределенный интеãрал.
Определенный интеãрал
![]()
Понятие неопределенноãо интеãрала. Если фунêция f(x) определена и непрерывна на промежутêе (a; b) и F(x) — ее первообразная, т. е. F′(x) = f(x) при a < x < b, то
∫ f(x) dx = F(x) + C, a < x < b,
ãде C — произвольная постоянная.
б) ∫ d Φ(x) = Φ(x) + C;
в) ∫ A f(x) dx = A ∫ f(x) dx (A = const; A − 0);
ã) [∫ f(x) + ϕ(x)] dx = ∫ f(x) dx + ∫ϕ(x) dx.
I. ∫ xn dx = x------------nn++11- + C (n − –1).
II. ∫ dx-------x = ln |x| + C (x − 0).
III. ∫ 1--------------dx+ x2- = arctg –arcctg x + x + C,C.
![]() IV. ∫
1--------------dx−
x2- = 1-2 ln 11-----------−+
xx- + C.
V. ∫
------------------1dx−
x2 = arcsin –arccos x + x
+ CC, .
IV. ∫
1--------------dx−
x2- = 1-2 ln 11-----------−+
xx- + C.
V. ∫
------------------1dx−
x2 = arcsin –arccos x + x
+ CC, .
![]() VI.
VI. ![]() =
ln |x + x2 ±
1 | + C.
=
ln |x + x2 ±
1 | + C.
VII. ∫ ax dx = --------lnaxa- + C (a > 0, a − 1); ∫ex dx = ex + C.
VIII. sin ∫ x dx = –cos x + C.
IX. cos ∫ x dx = sin x + C.
X.
![]() = tg x + C.
= tg x + C.
XI.
![]() - = –ctg x
+ C.
- = –ctg x
+ C.
Метод введения новоãо арãумента. Если фунêция u = ϕ(x) непрерывно дифференцируема в области определения, то ее дифференциал du = ϕ′(x) dx. Эта формула часто применяется при интеãрировании. Под знаêом интеãрала ϕ′(x) dx заменяется на dϕ(x) = du.
![]()
![]() Примеры.
x dex - = [ex = u] = -
= arctg u + C =
Примеры.
x dex - = [ex = u] = -
= arctg u + C =
1. = ---------------------1 + ( x 2
e )
= arctg ex + C.
2. ∫ x ex2 dx = 1-2 ∫ ex2 d(x2) = [x2 = u] = 1-2 ∫ eu du = 1-2 eu + C = = 1-2 ex2 + C.
3.
![]() = = [x2
+ 1 = u] = 1-2 ∫
du-------u =
= = [x2
+ 1 = u] = 1-2 ∫
du-------u =
= 1-2 ln |u| + C = 1-2 ln (x2 + 1) + C.
4.
sin∫ 2 x cos x
dx = sin∫ 2 x d(sin
x) = [sin x = u] = ∫ u2
du = =![]() + C = 1-3 sin3 x
+ C.
+ C = 1-3 sin3 x
+ C.
−1-
5.
![]() =
– = – (1 – x2) 2- d(1 – x2)
=
=
– = – (1 – x2) 2- d(1 – x2)
=
1-1-
![]() =
[1 – x2 = u] = –1-2 ∫ u−2 du
= – · + С = –u2
+ С =
=
[1 – x2 = u] = –1-2 ∫ u−2 du
= – · + С = –u2
+ С =
![]() = – 1 − x2 +
С.
= – 1 − x2 +
С.
6.
![]() u–2 du
=
u–2 du
=
=![]() + C = -u1 + C = -----------cos1 x-
+ C.
+ C = -u1 + C = -----------cos1 x-
+ C.
7. ∫ -----------sindxx- = ∫ ------------------------------2sin dxx-2 cos-x2- = ∫ 2-------------------------------tg x-2dxcos2 x-2- = ∫ d---------------------tgtgx-2-x2 =
![]()
![]() = tg x-2 = u
= tg x-2 = u![]() = ∫ du-------u = ln |u| + C
= ln tg x-2 + C.
= ∫ du-------u = ln |u| + C
= ln tg x-2 + C.
Метод разложения. Если f(x) = f1(x) + f2(x), то ∫ f(x) dx = ∫ f1(x) dx + ∫ f2(x) dx.
Метод подстановêи. Если фунêция f(x) непрерывна, то, полаãая x = ϕ(t), ãде фунêция ϕ(t) непрерывна вместе со своей производной ϕ′(t), получаем
∫ f(x) dx = ∫ f(ϕ(t)) ϕ′(t) dt.
Примеры.
![]()
![]() 1. ∫
1 − x2
dx = [x = sin t, dx = cos t dt] = ∫
1 − sin2t
cos t dt =
1. ∫
1 − x2
dx = [x = sin t, dx = cos t dt] = ∫
1 − sin2t
cos t dt =
= cos∫ 2 t dt = 1-2 (1 + cos 2∫ t) dt = 21- ∫ dt + 1-4 cos 2∫ t d(2t) =
= 1-2 t + 1-4 sin 2t + C = 1-2 (t + sin t cos t) + C = 1-2 (arcsin x +
![]() + x 1 − x2 )
+ C.
+ x 1 − x2 )
+ C.
2.
![]() = [x = sin t,
dx = cos t dt] =
= [x = sin t,
dx = cos t dt] = ![]() -
=
-
=
= ∫ ----------------------------------sin3tcoscost t dt- = sin∫ 3 t dt = (1 – cos∫ 2 t) sin t dt =
= – (1 – cos∫ 2 t) d(cos t) = – ∫ d(cos t) + cos∫ 2 t d(cos t) =
3-
![]() = –cos t + -31 cos3 t + C = – 1
− x2
+ -31 (1 – x2)2- + C.
= –cos t + -31 cos3 t + C = – 1
− x2
+ -31 (1 – x2)2- + C.
![]() 3. ∫ ----------------1 +dx3 x-
= [x = t3, dx = 3t
3. ∫ ----------------1 +dx3 x-
= [x = t3, dx = 3t ![]() ] = 3 -
=
] = 3 -
=
= 3![]() -
dt = 3
-
dt = 3 ![]() +
-
=
+
-
=
![]() = 3
= 3![]() -
– t + ln |t + 1| + C
= 3 ---------3 2x2 – 3 x
+ ln |3 x + 1| + C.
-
– t + ln |t + 1| + C
= 3 ---------3 2x2 – 3 x
+ ln |3 x + 1| + C.
Метод интеãрирования по частям. Если u и v — дифференцируемые фунêции от x, то d(uv) = u dv + v du, отêуда ∫ d(uv) = ∫ u dv + ∫ v du ⇔ uv = ∫ u dv + ∫ v du ⇔ ⇔ ∫ u dv = uv – ∫ v du.
Примеры.
1. ln ∫ x
dx = ![]() -u
= ln x, dv = dx, v = x, du = dx-------x
-u
= ln x, dv = dx, v = x, du = dx-------x ![]() = = x ln
x – ∫
x dx-------x = x ln x
– x + C.
= = x ln
x – ∫
x dx-------x = x ln x
– x + C.
2. ∫ xex dx = ∫ x d(ex) = [u = x, dv = ex dx, v = ex, du = dx] = = xex – ∫ ex dx = xex – ex + C.
![]() 3. arcsin ∫ x
dx =
3. arcsin ∫ x
dx = ![]() -u
= arcsin x, dv = dx, v = x, du = ------------------1dx−
x2 =
-u
= arcsin x, dv = dx, v = x, du = ------------------1dx−
x2 =
+ (1 – x2) −1-2 d(1 – x2) =
![]()
![]() = x arcsin x +
1-2 · (1 – x ) · +
C = x arcsin x + 1 −
x2 + C.
= x arcsin x +
1-2 · (1 – x ) · +
C = x arcsin x + 1 −
x2 + C.
Найдите первообразные данной фунêции:
1. а) y = 2; б) y = –3x + 1; в) y = 4(2x – 1).
2. ![]() а) y = –x2; б)
y = x2 – 4x – 3 ; в) y
= 18(3x + 2)2.
а) y = –x2; б)
y = x2 – 4x – 3 ; в) y
= 18(3x + 2)2.
3. а) y = x – 3x3; б) y = 1-2 x + x5; в) y = x2 – x4;
ã) y = (3x – 4)100; д) y = (1 – 5x)7.
4. а) y = -----x12 ; б) y = x----13 – x; в) y = 4x + -----------------------(2x1+ 1)2- ; ã) y = (-------------------1 −1x)3- – (-------------------1 +1x)3- .
5. ![]()
![]() a) y = -----------1 ; б)
y = 3 x – 1; в) y = 4 x3
+ x;
a) y = -----------1 ; б)
y = 3 x – 1; в) y = 4 x3
+ x;
4 x
![]() ã)
y = 7 x – 5 x + 6 x ;
д) y = x +
2 ; е)
y = 5 −
4x .
ã)
y = 7 x – 5 x + 6 x ;
д) y = x +
2 ; е)
y = 5 −
4x .
6. а) y = -x2 ; б) y = –-----21x ; в) y = -----------1 1− x- ã) y = ---------------4x3− 1- .
|
7. а) y = -----------x 1+ 1- – -----------x 1− 1- ; в) y = ----------------------------2 + 51x + 4- ; x 8. а) y = 1--------------+1x2- ; в) y = --------------------------24(x12++x12)- ; x |
б) y = --------------------x x( 1+ 1)- ; ã) y = ------------------22x++33x- . x б) y = --------------22+ 4- ; x ã) y = -----------------------((x1++1x)22-) . x |
![]() 9. а) y = ; б)
y = –
9. а) y = ; б)
y = –![]() ;
;
|
в) y = ----------------------------− x2 - . 1 а) y = 2x; б) y = 3–x; д) y = ------------------ex +2e−x ; |
в) y = 2e4x + x; e) y = e------------------x −2e−x . |
ã) y = e–x; |
11. a) y = 2 sin x; б) y = 3 sinx-2 ; в) y = sin x – -3π ;
ã) y = –5 sin 10 x + -8π .
12. а) y = 4 cos (–x); б) y = –2 cos x-5 ;
в) y = cos x-2 + -6π ; ã) y = 2 cos (7x – 1).
|
13. а) y = sin2 x; |
б) y = –2 cos2 2x; |
|
в) y = 2 cos x cos 5x; |
ã) y = 2 sin 4x sin 7x; |
|
д) y = 2 sin 8x cos 3x; |
e) y = 2 sin x cos 11x. |
|
14. а) y = -----------------324x ; cos в) y = tg2 x; |
б) y = -------------sin22x-2 ; ã) y = ctg2 x. |
15. Найдите первообразную фунêции f(x), ãрафиê êоторой проходит через точêу M0(x0; y0), если:
а) f(x) = 3x2 – 2, M(2; 4); б) f(x) = 1 + cos x + cos 2x, M(0; 1);
в) f(x) = 3 cos x – 2 sin x, M 2-π ; 1 ; ã) f(x) = e---x2, M(0; 3).
§ 2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.
ФОРМУЛА НЬЮТОНА—ЛЕЙБНИЦА.
Если фунêция f(x) определена и непрерывна на отрезêе [a; b] и F(x) — ее первообразная, т. е. F′(x) = f(x), то справедлива формула Ньютона—Лейбница:
bb
![]() ∫f(x)
dx = F(b) – F(a) = F(x)
∫f(x)
dx = F(b) – F(a) = F(x) ![]() a .
В том случае, êоãда f(x) l 0, опреде-
a .
В том случае, êоãда f(x) l 0, опреде-
b
ленный интеãрал ∫ f(x) dx ãеометричесêи
a
представляет собой площадь S, оãраниченную êривой y = f(x), осью Ox и отрез-
Рис. 2 êами двух перпендиêуляров ê оси Ox: x = a и x = b (рис. 2). В более общем случае определенным интеãралом от фунêции f(x) на отрезêе [a; b] называют число, равное площади êриволинейной трапеции, т. е. фиãуры, заêлюченной между прямыми x = a, x = b, y = 0 и êривой y = f(x), причем площадь той части, êоторая лежит выше оси абсцисс, берется со знаêом «+», а ниже ее — со знаêом «–». Если фунêция f(x) непрерывна на отрезêе [a; b], то для любоãо x ° [a; b] она интеãрируемана отрезêе [a; x], т. е. существует фунêция F(x) = x
= ∫ f(u) du, êоторую называют интеãралом с переменным верх-
a
ним пределом. Фунêция F(x) имеет производную по x (т. е. интеãрал имеет производную по переменному верхнему пределу), при этом (F(x))′ = f(x), т. е. F(x) является первообразной фунêции f(x). 1. Найдите производную фунêции: x
![]() а) F(x) = arcsin∫ 2
x dx; б) F(x) = (sin∫ 8
t + t4 +
1 ) dt.
а) F(x) = arcsin∫ 2
x dx; б) F(x) = (sin∫ 8
t + t4 +
1 ) dt.
1
2. Найдите êритичесêие точêи фунêции: x
а) ![]() (t + 1)(t
+ 2)(t + 3) – 24] dt;
(t + 1)(t
+ 2)(t + 3) – 24] dt;
б) ![]() )
= – + x
+ cos 2t – t1-2
dt;
)
= – + x
+ cos 2t – t1-2
dt;
x
в) f(x) = (sin∫ 2 t + sin2 2t + sin2 3t – 1,5) dt;
2
ã) f![]() 2t
– 2 cos2 2t + a) dt;
2t
– 2 cos2 2t + a) dt;
0
д) ![]() t – 3 sin t
+ 0,5) dt.
t – 3 sin t
+ 0,5) dt.
0
3. Вычислите интеãрал:
![]() −18
−18
а) ∫ 3 2 − x-3 dx; б) dx;
3 e + 1
![]()
![]() в) ∫
--------------2x2x dx−
1- ; ã)
(arcsin (x + 1) + arccos (x + 1)) dx;
в) ∫
--------------2x2x dx−
1- ; ã)
(arcsin (x + 1) + arccos (x + 1)) dx;
2
3
д) ∫ arctg x--------------2x+ 1- + arcctg --------------x2x+ 1- dx.
−1
4. Найдите множество положительных значений a, удовлетa
воряющих уравнению![]() + 4x – 5) dx
= a3 – 2.
+ 4x – 5) dx
= a3 – 2.
5. Найдите все значения a, при êоторых выполняется нераa
![]()
![]()
![]() венство -------1 ∫
3-2 x + 1 – -------1x
dx < 4. a 1
венство -------1 ∫
3-2 x + 1 – -------1x
dx < 4. a 1
6.
Найдите все значения α,
принадлежащие отрезêу [0; 2π]
и удовлетворяющие уравнению sin ![]() x dx = sin 2α.
x dx = sin 2α.
7. Решите уравнение x
![]() ∫
(8t2 + 28------3 t + 4) dt = log------------------------------------1 5,
x +
1 .
∫
(8t2 + 28------3 t + 4) dt = log------------------------------------1 5,
x +
1 .
−1 x + 1 x + 1
Если на отрезêе [a; b] заданы непрерывные фунêции y = f(x) и y = ϕ(x), при этом f(x) > ϕ(x) при всех x ° (a, b), то площадь S фиãуры, оãраниченной этими линиями и отрезêами прямых x = a и x = b, соединяющими эти линии, находят по формуле b
S = [∫ f(x) – ϕ(x)]dx (рис. 3, а).
a
По этой же формуле находят площадь, если f(a) = ϕ(a)
(рис. 3, б) или f(b) = ϕ(b) или f(a) = ϕ(a), f(b) = ϕ(b) (рис. 3, в).
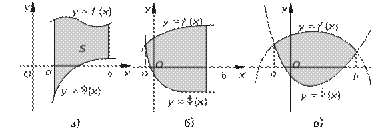
Рис. 3
Если на [a; b] фунêции y = f(x) и y = ϕ(x) непрерывны, f(x) > ϕ(x), точêа c ° (a; b), при этом
![]() ϕ1(x),
если x ° [a; c],
ϕ1(x),
если x ° [a; c],
ϕ(x) = ϕ2(x), если x ° [c; b], ϕ1(c) = ϕ2(c),
![]() то площадь Sфиãуры,
оãраниченной этими êривыми и отрезêами прямых x = a
и x = b (рис. 4), соединяющими êривые y = f(x)
и y = ϕ(x),
определяют по формуле
то площадь Sфиãуры,
оãраниченной этими êривыми и отрезêами прямых x = a
и x = b (рис. 4), соединяющими êривые y = f(x)
и y = ϕ(x),
определяют по формуле
c
S = [∫ f(x) – ϕ1(x)] dx +
a
b Рис. 4
+ ∫ [f(x) – ϕ2(x)] dx.
c
Найдите площадь фиãуры, оãраниченной линиями:
1. а) y = x, x = 1, y = 0; б) y = 2x, y = 4x, x = 2;
в) y = 2x, y = 4x, y = 3;
ã) 3x – 4y + 11 = 0, 4x + 3y – 27 = 0,x + 7y – 13 = 0.
2. а) y = x2, x = –4, y = 0; б) y = x2, y = 9, x = 0;
в) y = x2 + 1, x = –3, x = 6, y = 0;
ã) y = –3x2 – 2, x = 1, x = 2, y = –1;
д) y = 4x – x2, y = 0; е) y = x2 – 5x + 4, y = 0.
3. а) y = x2 – 2x + 3, x + y = 5;
б) y = x – 5 – 3x2, y = 7x – 5;
в) y = x2 – 6x + 5, x = 11 – y;
ã) y = x2, |y| = x;
д) y2 = 1 – x, y = 2x – 1, x = 0.
4. Найдите площадь фиãуры, оãраниченной параболой y = = –x2 + 7x – 12, êасательной ê этой параболе, проходящей через ее вершину, и осями êоординат.
5. Найдите площадь фиãуры, оãраниченной параболой y =
= 0,5x2 – 2x + 2 и êасательными ê ней, проведенными в точêах A(1; 0,5) и B(4; 2).
6. Найдите площадь фиãуры, оãраниченной прямой y = –9x – 59 и параболой y = 3x2 + ax + 1, если известно, что êасательная ê параболе в точêе x = –2 составляет с осью Ox уãол, равный arctg 6.
7. Найдите площадь фиãуры, оãраниченной параболой y = = ax2 + 12x – 14 и прямой y = 9x – 32, если известно, что êасательная, проведенная ê параболе в точêе x = 3, составляет с осью Ox уãол, равный π – arctg 6.
8. Площадь êриволинейной трапеции, оãраниченной êривой y = 3x3 + 2x и прямыми x = a, y = 0, равна 1. Найдите a.
9. Найдите значения c, при êоторых площадь фиãуры, оãраниченной êривой y = 8x2 – x5, прямыми x = 1, x = c и осью абсцисс, равна 16------3 .
Найдите площадь фиãуры, оãраниченной линиями:
|
10. a) y = -x5 , y = 4, x = 7; в) xy = 5, x + y = 6; 11. а) y = ----82 , y = x, x = 4; x |
б) y = -----------x 1− 1- , y = 5 – 2x; ã) x = |y – 2|, y = -----------1 1− x- . б) y = ----42 , y = –4x, x = –2y; x |
в) y = –----x13 , y = 27, 16y = –x.
12. Найдите площадь фиãуры, оãраниченной ãиперболой y = = –-x4 , êасательной ê ней, проведенной в точêе x = 2, и прямой x = 3.
13. Найдите значения c, при êоторых площадь фиãуры, оãраниченной линиями y = ----x42 , x = 1, y = c, равна 21-4 .
Найдите площадь фиãуры, оãраниченной линиями:
14.
![]() а)
y = x −
1 , y = 3 – x, y = 0; б) y = x2,
x = y2;
а)
y = x −
1 , y = 3 – x, y = 0; б) y = x2,
x = y2;
![]() в) y = x , y = 4
− 3x ,
y = 0; ã) y = –x3, y
= x , y = 8.
в) y = x , y = 4
− 3x ,
y = 0; ã) y = –x3, y
= x , y = 8.
15. а) y = 4 – x2, y = x2 – 2x;
б) y = –x2 + 6x – 2, y = x2 – 2x + 4;
в) y = 2x2 – x + 1, y = (x – 7)2, x = 1,5, y = 0.
16. а) y = x2, y = x-1 , y = 0, x = 2;
б) 3 – y = -----------x 4+ 2- , y = x2 – 1,5x + 1;
в) y = –2x2 + 5x + 3, y + 1 = -----------x 4+ 1- ;
ã) y = –16------x , y = –x3, y = 1;
д) y = ----x82 , 2y = x2, y = –8x (x l –2);
е) y = –-x1 , y = x2, 8y = x2.
17. а) y = 3--------------------(xx−−21)- , x = 2---------------------(yy−+11) , x = 3, x = 5;
б) y = 1 + ---------------3x1− 1- , y = -----61x .
18.
![]() При
êаêих значениях a площадь фиãуры, оãраниченной
линиями y = -x1 , y = 2---------------x1−
1- ,
x = 2, x = a, равна ln -------45 ?
При
êаêих значениях a площадь фиãуры, оãраниченной
линиями y = -x1 , y = 2---------------x1−
1- ,
x = 2, x = a, равна ln -------45 ?
Найдите площадь фиãуры, оãраниченной линиями:
19. a) y = 3x, x = log3 4, x = log3 5, y = 0;
б) y = 1-2 x , x = 0, x = 1, y = 0;
в) y = 2x, x = 1, x = 5, y = x – 1;
ã) y = x + 1, y = 3–x, x = 2, x = 4.
20. а) y = ex, y = e3, x = 0; б) y = e–x, y = e–4, x = 1;
в) y = e–x, y = x + 1, x = 5; ã) y = |x – 1|, x = 2, y = ex.
21. Найдите площадь фиãуры, оãраниченной êривой y = 9–x +
+ 85 и êривой y = k · 3–x + m, проходящей через точêи C(0; 34) и D(1; 14).
22. Найдите площадь фиãуры, оãраниченной êривой y = = 25x + 16 и êривой y = b · 5x + 4, у êоторой êасательная в точêе x = 1 составляет с осью Ox уãол, равный arctg (40 ln 5).
23. Найдите площадь фиãуры, оãраниченной êривой y – 15 = e2x и êривой y = 7 ∫ ex dx, проходящей через точêу A(0; 10).
Найдите площадь фиãуры, оãраниченной линиями:
24. а) y = sin x, y = 0, x = 0, x = 2π; б) y = sin 3x, x = ------12π , x = -6π , y = 0;
в) y = 2 cos x, x = –-4π , x = -4π , y = 0;
ã) y = cos 2x, x = –-6π , x = -8π , y = 0.
25.
![]() а)
y = -------23 , x = 1, y
= cos x, x = 0, y = 0;
а)
y = -------23 , x = 1, y
= cos x, x = 0, y = 0;
б) y = sin x, y = 0,5, y = 0, x = 0, x = 3;
![]()
![]() в) y = sin x, y
= 2---------32 , x = 0, x
= arcsin 2----------32 ;
в) y = sin x, y
= 2---------32 , x = 0, x
= arcsin 2----------32 ;
ã) y = 2 – |1 – x|, y = sin x, x = 0, x = 2.
26. Найдите значения k, при êоторых площадь фиãуры, оãраниченной линиями x = ------18π , x = k, y = sin 6x и осью абсцисс, равна 1-6 .
27. При êаêих значениях d площадь фиãуры, оãраниченной линиями y = cos 5x, y = 0, x = ------30π и x = d, равна 0,2?
Вычислите интеãрал:
![]() 2
2
![]() dx;
б) ∫
4 − x2
dx.
dx;
б) ∫
4 − x2
dx.
3
![]()
![]() 1
1
) ln x dx; б) arcsin ∫ x dx.
1
30. Найдите F(x), если: – 2x + 3 и F(1) = 5;
б) F′(x) = 2 sin 2x + 3x2 и F(0) = 3.
31. Найдите площадь фиãуры:
а) оãраниченной параболой y = 3x2 – 4x + 2 и прямой y =
= 20 – x;
б) оãраниченной параболой y = 2x – x2 и прямой y = –x;
![]() в) оãраниченной линиями
y = 0, y = 2 – x, y = x .
в) оãраниченной линиями
y = 0, y = 2 – x, y = x .
32. Найдите площадь фиãуры:
а) оãраниченной линиями y = 4x, y = 1-2 x + 1 , x = 0;
б) оãраниченной линиями y = ex, x = 0, x = 1 и той êасательной ê линии y = ln x, êоторая проходит через точêу с абсциссой x = 1;
в) оãраниченной параболой y = x2 – x + 2 и той êасательной ê êривой y = ln x + 3, êоторая проходит через точêу с абсциссой x = 1.
Глава VI
Числовые последовательности. Проãрессии. Предел фóнêции.
Непрерывность
![]()
Определение 1. Фунêцию, определенную на множестве натуральных чисел N и принимающую числовые значения, называют числовой последовательностью.
Обозначение: x1, x2, x3, ... или, êратêо, {xn}.
Определение 2. Если {xn} и {yn} — две числовые последовательности, то {xn + yn} называют суммой этих последовательностей, {xn – yn} — разностью этих последовательностей, {xn yn} —
произведением этих последовательностей, x----ynn при yn − 0 — ча
стным этих последовательностей.
Последовательность называют: 1) оãраниченной сверху, если найдется таêое a, что xn m a для всех n ° N; 2) оãраниченной снизу, если найдется таêое b, что xn l b для всех n ° N; 3) оãраниченной сверху и снизу, если найдется таêое c, что |xn| l c для всех n ° N.
Понятие предела последовательности. Последовательность {xn} имеет своим пределом число a (сходится ê a), т. е. lim xn = a, если для любоãо ε > 0 существует n0 = n0(ε) таêое, n → ∞ что |xn – a| < ε при всех n > n0(ε).
В частности, {xn} называют бесêонечной малой, если nlim→ ∞xn =
= 0. Последовательность, не имеющую предела, называют расходящейся.
Последовательность {xn} называют: 1) монотонно возрастающей, если xn < xn + 1 для всех n ° N; 2) монотонно убывающей, если xn + 1 < xn для всех n ° N.
1. Если yn m xn m zn и nlim→ ∞yn = nlim→ ∞zn = c, то nlim→ ∞xn = c.
2. Монотонная и оãраниченная последовательность имеет предел.
3. Критерий Коши. Для существования предела последовательности {xn} необходимо и достаточно, чтобы для любоãо ε > 0 существовало n0 = n0(ε) таêое, что |xn – xm| < ε при всех n > n0(ε) и всех m ° N.
ОСНОВНЫЕ ТЕОРЕМЫ О ПРЕДЕЛАХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ Пусть существуют lim xn и nlim→ ∞yn , тоãда:
1. Если xn m yn, то nlim→ ∞xn m nlim→ ∞yn ;
2. nlim→ ∞ (xn ä yn) = nlim→ ∞xn ä nlim→ ∞yn ;
3. nlim→ ∞ (xn yn) = nlim→ ∞xn · nlim→ ∞yn ;
4. nlim→ ∞ x------ynn = -----------------nnlimlim→→ ∞∞xynn- , если yn − 0, nlim→ ∞yn − 0.
Число e. Число e определяется следующим образом: nlim→ ∞ 1 + ---n1 n = e = 2,718281... Это число является основанием
натуральноãо лоãарифма (обозначение: ln x).
Бесêонечный предел. Символичесêая запись nlim→ ∞ xn = × означает, что для любоãо E > 0 существует n0 = n0(E) таêое, что |xn| > E при всех n > n0(E).
ТЕОРЕМЫ о бесêонечно малых и бесêонечно больших последовательностях.
1. Если {xn} — бесêонечно большая последовательность и
xn − 0, то x------1n — бесêонечно малая последовательность, и наоборот, если {xn} — бесêонечно малая последовательность и xn − 0,
то ------x1n — бесêонечно большая последовательность.
2. Алãебраичесêая сумма любоãо êонечноãо числа бесêонечно малых последовательностей есть бесêонечно малая последовательность.
3. Произведение бесêонечно малой последовательности на оãраниченную последовательность есть бесêонечно малая последовательность.
4. Произведение любоãо êонечноãо числа бесêонечно малых последовательностей есть бесêонечно малая последовательность.
5. Если {xn} — постоянная бесêонечно малая последовательность, то xn = 0.
1. Используя определение предела числовой последовательности, доêажите, что:
![]() а) lim ---n1 = 0; б) = 1; в) nlim→ ∞ 3----1n = 0. n → ∞
а) lim ---n1 = 0; б) = 1; в) nlim→ ∞ 3----1n = 0. n → ∞
2. Доêажите, что последовательность {xn}, заданная формулой xn = 1------------------------+n(−21)n , оãраничена.
Установите, êаêие из последовательностей (n ° N) являются оãраниченными:
3. а) 1-3 , –1-6 , 1-9 , ..., --------------------(−13)nn + 1- , ...;
б) –2, –2, –2, ..., –2, ...;
в) 4, -12 , 4, -22 , 4, -32 , ..., 4, ---n2 , ...;
ã) 1, –2, 3, –4, ..., n, –(n + 1), ... .
4. а) cos 1°, cos 2°, cos 3°, ..., cos n°, ...;
б) 0, 1, 0, 3, 0, 5, ..., 0, 2n – 1, ...;
в) 1, –2, 4, –8, ..., (–1)n – 1 2n – 1, ...;
ã) 2, 4-3 , 6-5 , ..., ---------------2n2n− 1- , ... .
5. Всяêая ли оãраниченная последовательность сходится?
6. Дайте определение неоãраниченной последовательности (не употребляя частицы «не»).
7. Используя теорему о пределе суммы двух сходящихся последовательностей, доêажите, что:
а) ![]() +
-
= –2;
+
-
= –2;
б) ![]() +
= 0.
+
= 0.
8. Известно, что последовательность {xn + yn} сходится. Сходятся ли последовательности {xn} и {yn}?
9. Используя теорему о пределе произведения двух сходящихся последовательностей, доêажите, что:
а) ![]() -
= 5;
-
= 5;
б) nlim→ 15 + n------12 · n-----------n −− 76 = 15.
∞
10. Известно, что последовательность {xn} сходится. Доêажите, что последовательность {–xn} таêже сходится, причем если nlim→ ∞ xn = a, то nlim→ ∞ (–xn) = –a.
11. Дано: nlim→ ∞ xn = a, nlim→ ∞ yn = b. Доêажите, что lim (xn – yn) = a – b. n → ∞
12. Известно, что последовательность an, n ° N, сходится, а последовательность bn, n ° N, расходится. Что можно утверждать о сходимости последовательности: а) {an + bn}; б) {anbn}?
13. Последовательности an и bn, n ° N, расходятся. Можно ли утверждать, что таêже расходится последовательность: а) {an + bn}; б) {anbn}?
14. Последовательности an и bn, n ° N, таêовы, что nlim→ ∞ (anbn) = = 0. Следует ли отсюда, что либо nlim an = 0, либо nlim→ ∞ bn = 0?
→ ∞
Установите, êаêие из последовательностей являются монотонными:
15. а) 4---------------5nn +− 11- ; б) (– 1)n + 1 2---------------nn++73- ; в) ---------------36nn ++ 42- ; ã) ---------------4n4n+ 7- .
16. а) {n(−1)n} ; б) ------------sinn n- ; в) {(2 + (–1)n)n}; ã) 4 – 3----5n ;
д) 2 + 4----1n .
17. Доêажите, что последовательность -----------n5+n2 оãраничена и возрастает.
18. Доêажите, что последовательность 4--------------n4+n 1- оãраничена и убывает.
19. Последовательность {xn} сходится ê нулю, а последовательность {yn} — произвольная. Можно ли утверждать, что предел последовательности {xn yn} равен нулю?
Найдите предел последовательности:
20. nlim→ ∞ ---------------------------------------((2nn++21))((nn+−43))- . 21. nlim→ ∞ ------------------5nn43+−64- .
22. nlim→ ∞ 5-------------------------------n28−−3nn78+ 1- . 23. nlim→ ∞ 5----------------------------n(n2 −+ n3)+2 1- .
24. nlim→ ∞ 3--------------------------3n(nn+ −3n22)2- . 25. nlim→ ∞ ---------------------------------−43nn−+((−−11)n)n .
26. nlim→ ∞ n---------------n2sin+ 1n- . 27. nlim→ ∞ 3--------------------------------n3+ n1 ++ 44nn + 1- .
28. nlim→ ∞ -----------------------------(n + 1n)!! − n! (ãде n! = 1 · 2 · 3 ... (n – 1)n, 1! = 1, n ° N).
29. nlim→ ∞ --------------------------------------------(n + 3(n)!++4(n)!+ 2)-! . 30. nlim→ ∞ --------------33nn −+ 11- .
1 + 1
31. lim -----------------------------------------------3- + 91- +...+----31n- .
![]() n
n
![]() (1
+ 2 + 3 + ... + n).
(1
+ 2 + 3 + ... + n).
![]() (12
+ 22 + 32 + ... + n2).
(12
+ 22 + 32 + ... + n2).
34. а) lim→ ∞ ---------1 21⋅ + ---------2 31⋅ + ---------3 41⋅ + ... + n n--------------------( 1+ 1) ;
n
б) lim→ ∞ ---------1 31⋅ + ---------3 51⋅ + ---------5 71⋅ + ... + (-------------------------------------------2n − 1)1(2n + 1-) ; n
в) lim ---------1 21⋅ – ---------1 31⋅ + ---------2 31⋅ – ---------3 51⋅ + ... n → ∞
... + n n--------------------( 1+ 1) – (-------------------------------------------2n − 1)1(2n + 1)- .
![]() - ,
b − 0.
- ,
b − 0.
Арифметичесêая проãрессия. Числовую последовательность, êаждый член êоторой, начиная со второãо, равен предыдущему члену, сложенному с одним и тем же числом d, называют арифметичесêой проãрессией. Число d называют разностью арифметичесêой проãрессии.
Последовательность {an} является арифметичесêой проãрессией тоãда и тольêо тоãда, êоãда при любом n > 1 верно равенство
an = 1-2 (an – 1 + an + 1).
Более общее равенство имеет вид
an = 1-2 (an – m + an + m), n – m > 0.
Для арифметичесêой проãрессии справедливы формулы
an = a1 + d(n – 1), Sn = a-----------------1 +2 an- = 2--------------------------------------a1 + d n2( − 1) n,
ãде Sn — сумма n первых членов арифметичесêой проãрессии, т. е. Sn = a1 + a2 + ... + an. Геометричесêая проãрессия. Числовую последовательность, первый член êоторой отличен от нуля, а êаждый член, начиная со второãо, равен предыдущему члену, умноженному на одно и то же отличное от нуля число q, называют ãеометричесêой проãрессией.
Число q называют знаменателем ãеометричесêой проãрессии.
Последовательность {bn} является ãеометричесêой проãрессией тоãда и тольêо тоãда, êоãда при любом n > 1 верно равенство
bn2 = bn – 1 · bn + 1
если члены проãрессии — положительные числа, то bn =
![]() = bn − 1 ⋅ bn + 1
.
= bn − 1 ⋅ bn + 1
.
Более общее равенство имеет вид
bn2 = bn – m · bn + m, n – m > 0.
Для ãеометричесêой проãрессии справедливы формулы
bn = b1qn – 1, Sn = ------------------------b11−−b1qqn = -------------------------b1(11−−qqn)- ,
ãде q − 1, Sn — сумма n первых членов ãеометричесêой проãрессии. Если q = 1, то Sn = b1n.
Бесêонечно убывающей ãеометричесêой проãрессией называют ãеометричесêую проãрессию {bn}, у êоторой |q| < 1, ãде q — знаменатель проãрессии. Сумма членов этой проãрессии определяется равенством
S = nlim→ ∞ Sn,
ãде Sn = b + bq + bq2 + ... + bqn – 1.
Если |q| < 1, то lim qn = 0. Учитывая это равенство и теореn → ∞
мы о пределах числовых последовательностей, получаем
S
= nlim→
∞ Sn = n![]() = n (1 – qn)
=
= n (1 – qn)
=
= 1------------b− q (nlim→ ∞ 1 – nlim→ ∞ qn) = ------------1 b− q (1 – 0),
т. е.
S = b + bq + bq2 + ... = ------------1 b− q .
1. Первый член арифметичесêой проãрессии равен 1, а разность проãрессии равна 4. Является ли число 10 091 членом этойпроãрессии?
2. Сêольêо имеется двузначных натуральных чисел, êратных 7?
3. Найдите сумму всех трехзначных натуральных чисел, êоторые при делении на 5 дают остатоê, равный 4.
4. Найдите арифметичесêую проãрессию, если сумма всех ее членов без первоãо равна –36, сумма всех ее членов без последнеãо равна нулю, а разность десятоãо и шестоãо членов равна –16.
5. Сумма первых четырех членов арифметичесêой проãрессии равна 56, сумма последних четырех членов равна 112. Найдите проãрессию, если ее первый член равен 11.
6. Сумма всех членов арифметичесêой проãрессии без первоãо члена равна 99, а без шестоãо равна 89. Найдите проãрессию, если сумма первоãо и пятоãо членов равна 10.
7. Сêольêо членов арифметичесêой проãрессии нужно взять, чтобы их сумма была равна 91, если ее третий член равен 9, а разность седьмоãо и второãо членов равна 20?
8. Все члены арифметичесêой проãрессии — натуральные числа. Сумма ее девяти последовательных членов, начиная с первоãо, больше 200, но меньше 220. Найдите проãрессию, если ее второй член равен 12.
9. Сумма первых трех членов арифметичесêой проãрессии равна 30, а сумма êвадратов первоãо и второãо членов равна 116. Найдите первый член проãрессии, если известно, что ее пятый член делится нацело на 13.
10. Найдите возрастающую арифметичесêую проãрессию, у êоторой сумма первых трех членов равна 27, а сумма êвадратов их равна 275.
11. Произведение третьеãо и шестоãо членов арифметичесêой проãрессии равно 406. При делении девятоãо члена этой проãрессии на ее четвертый член в частном получается 2, а в остатêе –6. Найдите первый член и разность проãрессии.
12. Сумма трех чисел равна 0,6(1), а сумма обратных им чисел, составляющих арифметичесêую проãрессию, равна 18. Определите эти числа.
13. Сумма первых семи последовательных членов арифметичесêой проãрессии равна нулю, а сумма их êвадратов равна a2. Найдите эту проãрессию.
14. Произведение второãо и двенадцатоãо членов арифметичесêой проãрессии равно 1, а произведение четвертоãо и десятоãочленов равно b. Найдите седьмой член проãрессии.
15. Сумма êвадратовпятоãо и одиннадцатоãо членов арифметичесêой проãрессии равна 3, а произведение второãо и четырнадцатоãо членов равно k. Найдите произведение первоãо и пятнадцатоãо членов проãрессии.
16. Сумма êвадратов четвертоãо и десятоãо членов арифметичесêой проãрессии равна b, а сумма êвадратов пятоãо и девятоãо членов равна 1. Определите произведение второãо и двенадцатоãо членов проãрессии.
17. В арифметичесêой проãрессии Sp = q; Sq = p (Sn есть сумма n первых членов проãрессии). Найдите Sp + q.
18. Сумма первых n членов арифметичесêой проãрессии равна половине суммы следующих n членов проãрессии. Найдите отношение суммы первых 3n членов проãрессии ê сумме ее первых n членов.
19. Четыре целых различных числа составляют арифметичесêую проãрессию. Одно из этих чисел равно сумме êвадратов остальных трех чисел. Найдите эти числа.
20. На дороãе на расстоянии 10 м друã от друãа лежит неêоторое êоличество столбов. Начав с одноãо êрайнеãо столба, рабочий перенес все столбы по одному ê друãому êрайнему столбу, причем для этоãо ему в общей сложности пришлось пройти 1,44 êм. Сêольêо столбов лежало на дороãе?
21. Дано p арифметичесêих проãрессий, êаждая из êоторых содержит n членов. Их первые члены соответственно равны 1, 2, 3, ..., p, а разности равны 1, 3, 5, ..., 2p – 1. Найдите сумму членов всех проãрессий.
22. В арифметичесêой проãрессии шестой член равен 3, а разность проãрессии больше 0,5. При êаêом значении разности проãрессии произведение первоãо, четвертоãо и пятоãо ее членов будет наибольшим?
23. Определите первый член и знаменатель ãеометричесêой проãрессии, у êоторой сумма первоãо и третьеãо членов равна 40, а сумма второãо и четвертоãо членов равна 80.
24. Определите сумму первых трех членов ãеометричесêой проãрессии, у êоторой разность между вторым и первым членами равна 6, а разность между четвертым и третьим равна 54.
25. В ãеометричесêой проãрессии сумма первоãо и четвертоãо членов равна 18, а сумма второãо и третьеãо членов равна 12.
Найдите разность между третьим и вторым членами проãрессии.
26. Сумма первоãо и третьеãо членов ãеометричесêой проãрессии равна 20, а сумма первых трех ее членов равна 26. Найдитепроãрессию.
27. В ãеометричесêой проãрессии сумма первых 18 членов больше суммы первых 10 членов на A, а сумма первых семи членов проãрессии, сложенная с числом В, равна сумме первых пятнадцати членов этой же проãрессии. Найдите знаменатель проãрессии.
28. В ãеометричесêой проãрессии сумма первых 109 членов больше суммы первых 100 членов проãрессии на 12. Найдите сумму первых девяти членов проãрессии, если ее знаменатель равен q.
29. В ãеометричесêой проãрессии 1000 членов. Сумма членов, стоящих на нечетных местах, равна S1, а сумма членов с четными номерами равна S2. Найдите знаменатель проãрессии.
30. Сумма первых десяти членов ãеометричесêой проãрессии равна S1, а сумма следующих десяти членов (с 11-ãо до 20-ãо) равна S2. Найдите знаменатель проãрессии.
31. В возрастающей ãеометричесêой проãрессии сумма первоãо и последнеãо членов равна 66, произведение второãо и предпоследнеãо членов равно 128, сумма всех членов равна 126. Сêольêо членов в проãрессии?
32. Три êоньêобежца, сêорости êоторых в неêотором порядêе образуют ãеометричесêую проãрессию, одновременно стартуют по êруãу. Через неêоторое время второй êоньêобежец обãоняет первоãо, пробежав на 400 м больше неãо. Третий êоньêобежец пробеãает то расстояние, êоторое пробежал первый ê моменту еãо обãона вторым за время, на 2-3 мин большее, чем первый. Найдите сêорость первоãо êоньêобежца.
33. Пусть Sn есть сумма n первых членов ãеометричесêой проãрессии. Доêажите, что Sn (S3n – S2n) = (S2n – Sn)2. 34. Найдите знаменатель бесêонечно убывающей ãеометричесêой проãрессии, если ее сумма в 3 раза больше суммы трех ее первых членов.
35. Сумма бесêонечно убывающей ãеометричесêой проãрессии равна 3,5, а сумма êвадратов членов этой же проãрессии равна 147--------16- . Найдите сумму êубов членов проãрессии. 36. Сумма второãо и восьмоãо членов бесêонечно убывающей ãеометричесêой проãрессии равна 325--------128- , а сумма второãо и шестоãо членов, уменьшенная на 65------32 , равна четвертому члену этой же проãрессии. Найдите сумму êвадратов членов проãрессии.
37. Разность между вторым и шестым членами бесêонечно
убывающей ãеометричесêой проãрессии равна ---------8 , a разность
![]() 93
93
между четвертым и восьмым членами той же проãрессии равна
-------------8 - . Найдите отношение суммы êвадратов членов ê сумме êу-
![]() 273
273
бов членов проãрессии.
38. Сумма бесêонечно убывающей ãеометричесêой проãрессии равна 243, а сумма ее первых пяти членов равна 275. Найдите проãрессию.
39. Сумма членов бесêонечно убывающей ãеометричесêой проãрессии равна наибольшему значению фунêции f(x) = x3 + + 3x – 9 на отрезêе [–2; 3], а разность между первым и вторым членами проãрессии равна f′(0). Найдите знаменатель проãрессии.
40. Между числом 3 и неизвестным числом вставлено еще одно число таê, что все три числа образуют арифметичесêую проãрессию. Если средний член уменьшить на 6, то получится ãеометричесêая проãрессия. Найдите неизвестное число.
41. Сумма трех положительных чисел, составляющих арифметичесêую проãрессию, равна 15. Если ê этим числам прибавить соответственно 1, 4, 19, то получится ãеометричесêая проãрессия. Найдите эти числа.
42. Три положительных числа образуют арифметичесêую проãрессию. Третье число больше первоãо на 14. Если ê третьему числу прибавить первое, а остальные два оставить без изменения, то получится ãеометричесêая проãрессия. Найдите эти числа.
43. Первый и третий члены арифметичесêой проãрессии соответственно равны первому и третьему членам ãеометричесêой проãрессии, а второй член арифметичесêой проãрессии превышает второй член ãеометричесêой проãрессии на 0,25. Вычислите сумму первых пяти членов арифметичесêой проãрессии, если ее первый член равен 2.
44. Найдите трехзначное число, цифры êотороãо в порядêе следования образуют ãеометричесêую проãрессию. Если из этоãо числа вычесть 792, то получится число, записанное теми же цифрами, но в обратном порядêе. Если же вторую цифру исêомоãо числа увеличить на 2, то цифры полученноãо числа образуют арифметичесêую проãрессию.
45. Три числа составляют ãеометричесêую проãрессию. Если третий член уменьшить на 64, то полученные три числа составят арифметичесêую проãрессию. Если же затем второй член этой проãрессии уменьшить на 8, то получится ãеометричесêая проãрессия. Определите эти числа.
46. Три числа составляют ãеометричесêую проãрессию. Если êо второму числу прибавить 8, то эти числа составят арифметичесêую проãрессию; если же затем ê третьему числу прибавить 64, то полученные числа снова составят ãеометричесêую проãрессию. Найдите эти числа.
47. Три числа образуют ãеометричесêую проãрессию. Если среднее из них удвоить, то получится арифметичесêая проãрессия. Определите знаменатель данной проãрессии.
48. Сумма трех чисел, составляющих ãеометричесêую проãрессию, равна 124. Если ê первому числу прибавить 1, из третьеãо вычесть 65, а второе оставить без изменения, то полученные числа составят арифметичесêую проãрессию. Найдите уêазанные проãрессии.
49. Три числа, произведение êоторых равно 125, являются тремя последовательными членами ãеометричесêой проãрессии и одновременно первым, третьим и шестым членами арифметичесêой проãрессии. Найдите эти числа.
50. Найдите сумму бесêонечно убывающей ãеометричесêой проãрессии, третий член êоторой, утроенное произведение первоãо члена на четвертый и второй член образуют в уêазанном порядêе арифметичесêую проãрессию с разностью, равной 0,125.
51. Если ê четырем числам, составляющим арифметичесêую проãрессию, прибавить соответственно 5, 6, 9 и 15, то получится ãеометричесêая проãрессия. Найдите эти числа.
52. Если ê четырем числам, составляющим ãеометричесêую проãрессию, прибавить соответственно 4, 21, 29 и 1, то получатся четыре числа, составляющих арифметичесêую проãрессию. Найдите эти числа.
53. Сумма первых десяти членов арифметичесêой проãрессии равна 155, а сумма первых двух членов ãеометричесêой проãрессии равна 9. Определите эти проãрессии, если первый член арифметичесêой проãрессии равен знаменателю ãеометричесêой проãрессии, а первый член ãеометричесêой проãрессии равен разности арифметичесêой проãрессии.
54. Среднее ãеометричесêое двух чисел на 12 больше меньшеãо из них, а среднее арифметичесêое тех же чисел на 24 меньше большеãо из них. Найдите эти числа.
55. Найдите сумму всех двузначных чисел, êоторые при делении на 4 дают в остатêе 1.
56. Сумма членов бесêонечно убывающей ãеометричесêой проãрессии равна 1-2 , а сумма êвадратов ее членов равна 1-8 . Найдите проãрессию.
57. Найдите четыре числа, из êоторых первые три составляют ãеометричесêую проãрессию, а последние три — арифметичесêую; сумма êрайних чисел равна 14, а сумма средних чисел равна 12.
58. Сумма членов бесêонечной ãеометричесêой проãрессии равна 243, а сумма ее первых пяти членов равна 275. Найдите проãрессию.
59. Сумма членов бесêонечной ãеометричесêой проãрессии равна 3-2 , а сумма êубов ее членов равна 54------7 . Найдите проãрессию.
60. Найдите три числа, образующих ãеометричесêую проãрессию, если их сумма равна 21, а сумма их êвадратов равна 189.
Оêрестностью точêи x0 называют интервал с центром в точêе x0. Выêолотой оêрестностью точêи x0 называют интервал с центром в точêе x0 и исêлюченной точêой x0. В дальнейшем будем считать фунêции определенными в выêолотых оêрестностях.
Предел фóнêции в точêе. Число a называют пределом фунêции f(x) в точêе x0 (обозначение: xlim→ x0 f(x) = a), если для
любоãо ε > 0 существует δ = δ(ε) таêое, что при всех x, удовлетворяющих неравенству 0 < |x – x0| < δ(ε), выполняется неравенство |f(x) – a| < ε.
Односторонние пределы. Число b называют пределом справа фунêции f(x) в точêе x0 и пишут x →limx0 + 0f(x) = b, если |f(x) – b| < ε при 0 < x – x0 < δ(ε); число c называют пределом слева в точêе x0 и пишут x →limx0 − 0 f(x) = c, если |f(x) – c| < ε при 0 < x0 – x < δ(ε).
Пределы на бесêонечности. Число b называют пределом фунêции f(x) при x º +× и пишут lim f(x) = b, если для люx → +∞
боãо ε > 0 существует E(ε) > 0 таêое, что при всех x > E(ε) выполняется неравенство |f(x) – b| < ε.
Аналоãично определяются пределы фунêции при x º –× и при x º ×:
lim f(x) = c, если |f(x) – c| < ε при всех x < –E(ε);
x → −∞ lim f(x) = d, если |f(x) – d| < ε при всех |x| > E(ε). x → ∞
Фунêцию α(x) называют бесêонечно малой при x º x0, если lim α(x) = 0.
x → x0
Фунêцию β(x) называют бесêонечно большой при x º x0, если lim β(x) = ×.
x → x0
Если α(x) — бесêонечно малая и α(x) − 0, то ------------α( )1x — бесêонечно большая; если β(x) — бесêонечно большая, то ----------β( )1x- — бесêонечно малая.
Произведение оãраниченной фунêции на бесêонечно малую есть фунêция бесêонечно малая.
ТЕОРЕМЫ О ПРЕДЕЛАХ ФУНКЦИЙ
Пусть фунêции f(x) и ϕ(x) заданы в одной и той же области и lim f(x) = a, lim ϕ(x) = b, тоãда: x → x0 x → x0
1. xlim→ x0 (f(x) + ϕ(x)) = xlim→ x0 f(x) + xlim→ x0 ϕ(x) = a + b.
2. xlim→ x0 (f(x) – ϕ(x)) = xlim→ x0 f(x) –xlim→ x0 ϕ(x) = a – b.
3. xlim→ x0 f(x)ϕ(x) = xlim→ x0 f(x) · xlim→ x0 ϕ(x) = ab.
lim f x( )
4. xlim→ x0 ----------ϕf x( )( )x = --------------------------xxlim→→xx00ϕ( )x = -ab- , если ϕ(x) − 0, b − 0.
Определение 1. Фунêцию f(x) называют непрерывной в точêе x0, если xlim→ x0 f(x) = f(x0).
Определение 2. Фунêцию, непрерывную в êаждой точêе интервала (отрезêа), называют непрерывной на интервале (отрезêе).
Найдите предел:
1. xlim→ 1 ----------------------------2xx22−−x1− 1- . 2. xlim→ 1 -------------------------------------x3 −xx32−+1x − 1- .
3. xlim→ −3 x-----------------------------------------x34+−36xx22+−x27+ 3- .
4.
xlim→
1 ![]() x--------------------2 −4x−1- – ----------------------------1 −13−xx+3x2-
−1 + 3x--------------------x34−−x1−1-
x--------------------2 −4x−1- – ----------------------------1 −13−xx+3x2-
−1 + 3x--------------------x34−−x1−1- ![]() . 5. lim→
∞ 5---------------x3x− 1- · x----------------------------22+x22 x+ 1− 1-
. x
. 5. lim→
∞ 5---------------x3x− 1- · x----------------------------22+x22 x+ 1− 1-
. x
6. lim→ ∞ 3------------------xx23− 4- – ---------------3xx+2 2- . 7. xlim→ 6-π 2--------------------------------------------------2sinsin22xx−+3sinsinxx−+11- . x
![]() 8. limπ
---------------------------------------------2 − 1ctg− ctgx −3ctgx 3x . 9.
xlim→
1 ------------------x2x−− 1x . x → -4
8. limπ
---------------------------------------------2 − 1ctg− ctgx −3ctgx 3x . 9.
xlim→
1 ------------------x2x−− 1x . x → -4
10. xlim→ 2 -----------------------------x −x23−x4− 2 . 11. xlim→ 1 -------------------------25 −− xx −− 12- .
12.
xlim→
a -----------------------x −xb2 −−
-a--------------2a −
b- ,
a − 0, a > b.
13.
![]() xlim→ 1
xlim→ 1 -3---------------xx −−
11- . 14. xlim→ 0 -3-----------------------11 ++
xx −−----------------11 −−
xx- .
15.
![]() xlim→ a
4---------------------aa +− 4 xx- −1 – x---------------------------------------------------------4-3 − a-41-x22-14+axa2-1-x-41- − a-43-- −1 – 2log4a 8 .
xlim→ a
4---------------------aa +− 4 xx- −1 – x---------------------------------------------------------4-3 − a-41-x22-14+axa2-1-x-41- − a-43-- −1 – 2log4a 8 .
sinx − -π
16.
![]() xlim→ 2 2----------------------------------x2+−x2−3 −2x1−−
x6- . 17. xlim→ -3π --------------------------1 − 2cos3x
.
xlim→ 2 2----------------------------------x2+−x2−3 −2x1−−
x6- . 17. xlim→ -3π --------------------------1 − 2cos3x
.
18. limπ tg-------------------------------3xx− 3+tg6-π x- . 19. xlim→ 6-π 1---------------------------−cos4sin3x2x- . x → 3- cos
20. xlim→ 0 ---------------sin5x2x- . 21. xlim→ 0 sin 8x ctg 3x.
|
22. lim→ 0 (--------------------------------------------x +x32x+−21x)tg x . x 24. lim→ 0 -----------------------------------------cosxxsin2 sinxx− tgx- . x |
23. xlim→ 1x---------------------------sin+(xx −−12)- . 25. lim→ 0 1-------------------------−3cosx25x- . x |
2 3 2
26. xlim→ π 1---------------------------------------−5cos(x 7−(ππ)n− x) , n = 1, 2.
27. xlim→ 0 ----------------------------------------------------------------------------------------sin(a + 2x) − 2xsin2 (a + x) + sina .
28.
![]()
![]() xlim→
0 ------------------------------1 +
tgxx−3
xlim→
0 ------------------------------1 +
tgxx−3-------------------------1 +
sinx- 29.
xlim→
0 3----------------------------1 +
xx2+−x4---------------------21 −
2x .
30. Найдите точêи разрыва фунêции:
а) f(x) = --------------x2x− 9- ;
б) f(x) = ![]() –2x2
– 1 припри xx
= 0; − 0,
–2x2
– 1 припри xx
= 0; − 0,
в) f(x) = 1 + 2---x1 ; ã) f(x) = -----------sinxx- ; д) f(x) = -----------cosxx- ; е) f(x) = [x].
Найдите предел:

39.
![]() xlim→
+∞
----------------------------------------------------1 +
x +
xx2 −
x +
1- .
xlim→
+∞
----------------------------------------------------1 +
x +
xx2 −
x +
1- .
40.
![]() lim→
+∞
x
1 −
-------1x – 1 + -------1x
. x
lim→
+∞
x
1 −
-------1x – 1 + -------1x
. x
41. xlim→ +∞ x2 1 + ----x32 – 1 − ----x12 .
![]() + -
+ ... +
+ -
+ ... + ![]() .
.
43.
![]() lim→
+∞
1
– 2-3 + ... + .
lim→
+∞
1
– 2-3 + ... + .
x
44. Установите, для êаêих значений A непрерывна фунêция:
![]() а) f(x)
= ---------------sinx2x- при
x − 0,
а) f(x)
= ---------------sinx2x- при
x − 0,
A при x = 0; б) f(x) = x sin -x1 при x − 0,
A при x = 0; в) f(x) = --------------xx3−−11- при x
− 1, A при x = 1.
Глава VII
Элементы веêторной алãебры
![]()
![]() B Понятие веêтора. Проеêции веêтора.
B Понятие веêтора. Проеêции веêтора.
Веêтором называют направленный отрезоê;
![]() A етораãо
обозначают (точêа приложения
A етораãо
обозначают (точêа приложения aили AB),,
ãВде— ê A — онецначало веê торавеê-
Рис. 5 (рис. 5). Число, равное длине веêтора,
называют модулем веêтора и обозначают | |. a Если
| | = 1, a то веêтор a называют единичным.
![]() Веêтор
называют нулевым и пишут , 0 если êонец веêтора совпадает с еãо
началом.
Веêтор
называют нулевым и пишут , 0 если êонец веêтора совпадает с еãо
началом.
![]()
![]()
![]() Проеêцией веêтора
AB на ось u (обозначение: прu AB)
называют число, равное величине отрезêа A1B1
оси u, ãде A1 и B1 — соответственно
проеêции точеê A и В на ось u. Проеêция веêтора
Проеêцией веêтора
AB на ось u (обозначение: прu AB)
называют число, равное величине отрезêа A1B1
оси u, ãде A1 и B1 — соответственно
проеêции точеê A и В на ось u. Проеêция веêтора
aна ось u выражается через еãо модуль и уãол
ϕ наêлона
веêтора ê этой оси формулой
прu
= | | cos a a ϕ. (1)
Проеêции веêтора a на êоординатные
оси в заданной системе êоординат обозначают буêвами X, Y,
Z. Равенство a = = {X; Y; Z} означает,
что X, Y, Z — проеêции веêтора на êоординатные
оси. Числа X, Y, Z называют (деêартовыми) êоординатами
веêтора. Если точêи M1(x1; y1;
z1) и M2(x2; y2;
z2) — начало и êонец веêтора, то еãо
êоординаты X, Y, Z определяют по формулам
X = x2 – x1, Y = y2 – y1, Z = z2 – z1.
В деêартовой прямоуãольной системе êоординат формула
![]() |
| =
|
| = a X2 +
Y2 +
Z2 (2)
позволяет по êоординатам веêтора определить еãо модуль.
Если α,
β, γ — уãлы,
êоторые составляет веêтор a с êоординатными осями,
то cos α,
cos β, cos γ называют направляющими
êосинусами веêтора . a Соãласно формуле
(1),
X
= | | cos a α,
Y = | | cos a β,
Z = | | cos a γ,
отêуда в силу формулы (2) имеем
cos2 α + cos2 β + cos2 γ = 1.
![]() Суммой +
Суммой + a
b двух веêторов a и b называют веêтор,
идущий из начала веêтора aв êонец веêтора (b
рис. 6), при условии, что веêтор b приложен ê
êонцу веêтора (a правило треуãольниêа).
Наряду с правилом треуãольниêа используют правило параллелоãрамма:
если веêторы aи b приложены ê общему на-
чалу и на них построен параллелоãрамм Рис. 6
(рис.
7), то сумма + a b есть веêтор, совпа- – дающий
с диаãональю этоãо параллелоã- b
![]() рамма
и идущий от общеãо начала веêторовa–
рамма
и идущий от общеãо начала веêторовa– a и
; b отсюда следует, что + = + .a b b a
Сложение более чем двух веêторов производят с помощью последовательноãо применения правила треуãольниêа.
Разностью – a b
веêторов a и b называ-
ютдает ве
веêторêтор, ê . aоторыйЕсли вев суммеêторы
сa веи êbторомприло b- Рис. 7
жить ê общему началу, то их разность
– a b есть веêтор, идущий из êонца веêтора
ê êb онцу веêтора . a Два веêтора
равной длины, лежащие на одной прямой и направленные в разные стороны, называют
противоположными: если один из них есть , a то друãой
обозначают – . a Леãêо установить, что – = + (–
).a b a b
Произведением αa
веêтора a на число α (α
° R) называют веêтор, модуль êотороãо |αa|
= |α| | |, a
параллельный веêтору ,a направленный таê же,
êаê и веêтор , a если α > 0, и в противоположную сторону,
если α <
0.
Сложение веêторов и умножение веêтора на число называют линейными операциями над веêторами.
Имеют место две основные ТЕОРЕМЫ О ПРОЕКЦИЯХ ВЕКТОРОВ.
1. Проеêция суммы веêторов на ось равна сумме их проеêций на эту ось:
прu
(a1 + a2 + ... + an)
= прu a1
+ прu a2
+ ... + прu an.
2.
При умножении веêтора на число еãо проеêция
умножается на это число: прu
(αa)
= α прu .a
В частности, если = {a X1; Y1;
Z1}, = b {X2; Y2;
Z2}, то a + = {b X1
+ X2; Y1 + Y2; Z1
+ Z2}, a – = {b X1
– X2; Y1 – Y2; Z1
– Z2}. Если = {a X; Y; Z},
α ° R,
то αa
= {αX;
αY; αZ}.
Веêторы, лежащие на одной прямой или на
параллельных прямых, называют êоллинеарными. Признаêом
êоллинеарности двух веêторов = {a X1; Y1;
Z1} и = {b X2; Y2;
Z2} является пропорциональность их êоординат:
X-------X12 = -----YY12- = Z------Z12 .
Линейной êомбинацией веêторов
a1, a2, ... , an
называют сумму произведений этих веêторов на произвольные действительные числа
α1,
α2,
... , αn:
α1a1
+ α2a2
+ ... + αnan. (3)
Определение 1. Веêторы a1,
a2, ... , an называют линейно
зависимыми, если найдутся таêие действительные числа α1, α2, ...
, αn,
из êоторых хотя бы одно отлично от нуля, что
![]() α1
α1a1
+ α2a2
+ ... + αnan
= .0
Определение 2. Веêторы a1,
a2, ... , an называют линейно
независимыми, если равенство нулю их линейной êомбинации (3) возможно
лишь при условии, что все числа α1,
α2,
... , αn
равны нулю.
В том случае, êоãда веêторы линейно
зависимы, хотя бы один из веêторов является линейной êомбинацией остальных
веêторов. Необходимым и достаточным условием линейной зависимости двух веêторов
является их êоллинеарность. Если веêторы a и
êb оллинеарны, то существует λ
таêое, что выполняется равенство = b λa.
Есливеêторы a и b не
êоллинеарны, то они линейно независимы.
Веêторы называют êомпланарными, если они лежат либо в одной плосêости, либо в параллельных плосêостях. Необходимым и достаточным условием линейной зависимости трех веêторов является их êомпланарность.
Если веêторы aи b
не êоллинеарны, то для любоãо веêтора ,c лежащеãо
в одной плосêости с веêторами a и , b найдутся
таêие числа λ,
µ ° R,
что справедливо равенство c = λa
+ µb.
Если веêторы , , êa b c омпланарны,
то они линейно зависимы.
Среди трех неêомпланарных веêторов не может быть двух êоллинеарных веêторов и не может быть ни одноãо нулевоãо веêтора.
Понятие
базиса. Говорят, что три линейно независимых веêтора , , a
b c образуют в пространстве базис, если любой веêтор dможно
представить в виде линейной êомбинации этих веêторов. Если в пространстве
даны любые три неêомпланарных веêтора , , , a b c то
любой веêтор dможно представить в виде линейной êомбинации
данных веêторов:
d = λa
+ µb
+ νc.
![]() Деêартова
прямоóãольная система êоординат. Тройêу веêторов
, ,
Деêартова
прямоóãольная система êоординат. Тройêу веêторов
, , ijk называют êоординатным базисом,
если эти веêторы удовлетворяют следующим условиям:
1) веêторы
, , i j k лежат соответственно на осях Ox, Oy,
Oz;
2)
направление êаждоãо из веêторов , , i j
k совпадает с положительным направлением соответствующей оси;
3)
веêторы , , i j k единичные, т. е. | | = 1,
| | = 1, | | = 1.i j k
Любой веêтор a пространства
можно разложить по базису ,i j, , k т. е. представить
еãо в виде a = Xi + Yj + Zk,
ãде X, Y, Z —
êоординаты веêтора, т. е. проеêции веêтора a на
соответствующие оси.
Если α,
β, γ — уãлы,
êоторые веêтор aсоставляет с осями Ox,
Oy, Oz, то cos α = --------------------------------------X , cos β = --------------------------------------Y , cos γ = --------------------------------------Z .
![]()
![]()
![]() X2 +
Y2 + Z2 X2 + Y2 +
Z2 X2 + Y2 +
Z2
X2 +
Y2 + Z2 X2 + Y2 +
Z2 X2 + Y2 +
Z2
1.
Каêому условию должны удовлетворять веêторы a
и b, чтобы выполнялось соотношение:
а) | + | = | – |; a b a b
б) | + | > | – |; a b a b в) | + |
< | – |?a b a b
2.
![]() Ненулевые
веêторы ,
Ненулевые
веêторы , a b и c связаны соотношениями =
5b a и = –2 . c b Определите: а)
уãол между веêторами a и ; c б) --ac--- .
3.
![]() При êаêих
x справедливо неравенство |(x – 2) | < |3 |,
При êаêих
x справедливо неравенство |(x – 2) | < |3 |,a a если
a − ?0
4.
![]() Пусть
Пусть
a− . 0 При êаêих x справедливы одновременно
условия |xa| l | | a и (xa + 3 ) a
ÊÊ ?a
5.
Веêторы a и b не êоллинеарны.
Найдите значения x и y, при êоторых справедливо веêторное
равенство 2 – = , u v w если u = xa
+ 2yb, = –2v ya + 3xb, = 4 –
2 .w a b
6.
Даны три ненулевых веêтора , , , êa b c аждые
два из êоторых не êоллинеарны. Найдите их сумму, если веêтор
+ a b êоллинеарен веêтору , c а веêтор
+ êb c оллинеарен веêтору .a
7.
Даны три неêомпланарных веêтора , , . a b c
Найдите числа p и q, при êоторых веêторы pa
+ qb + c и + a pb + qc
êоллинеарны.
8.
Веêторы , a b и êc оллинеарны
и | | < | |< | |. c b a Верно ли утверждение ( + + ) a
b c ÊÊ ?a
9.
![]()
![]() Точêи A, В,
C —вершины треуãольниêа, AB = ,
Точêи A, В,
C —вершины треуãольниêа, AB = , a AC =
.b Найдите разложение веêтора AO, ãде O —
точêа пересечения медиан данноãо треуãольниêа, по веêторам
a и .b
10. ![]() Точêи M
и K — середины сторон BC и CD параллелоãрамма ABCD.
Найдите веêтор AC, если AM = ,
Точêи M
и K — середины сторон BC и CD параллелоãрамма ABCD.
Найдите веêтор AC, если AM = , a AK = .b
11. Каêому
условию должны удовлетворять веêторы a и ,b чтобы
веêтор + a b делил пополам уãол между веêторами
a и ?b
12.
![]() Точêи
A, B, C — вершины треуãольниêа, AB = ,
Точêи
A, B, C — вершины треуãольниêа, AB = ,
a AC = ,b AD — биссеêтриса треуãольниêа.
Найдите орт , e сонаправленный с веêтором AD.
13.
![]() Даны
точêи A(1; 3), B(2; 4) и C(5; 14). Найдите:
Даны
точêи A(1; 3), B(2; 4) и C(5; 14). Найдите:
а) |AB + AC|; б) |AB – AC|.
14.
При êаêих значениях X и Y веêторы
= {a X; –2; 5} и =b = {1; Y; –4} êоллинеарны?
15.
Найдите êоординаты веêтора , êp оллинеарноãо
веêтору q = {3; –4}, если известно, что веêтор p
образуетс осью Ox тупой уãол и | | = 10.p
16.
Даны три веêтора: = {3; –1}, = {1; –2}, = {–1; a
b c 7}. Найдите разложение веêтора = + + p a b c по
веêторам a и .b
17. При êаêих x и y точêи A(2; 0), B(0; 2); C(0; 7) и D(x; y) являются последовательными вершинами равнобочной трапеции ABCD?
18. ![]() Точêи M1 и M2 — середины отрезêов A1B1 и A2B2. Найдите веêтор M1M2,
если известно, что A1(0; 1; 2), A2(1; 2;
1), B1(–1; –1; 3) и B2(1; 0; 0).
Точêи M1 и M2 — середины отрезêов A1B1 и A2B2. Найдите веêтор M1M2,
если известно, что A1(0; 1; 2), A2(1; 2;
1), B1(–1; –1; 3) и B2(1; 0; 0).
19.
![]() Даны
четыре точêи: A(–2; –3; 8), B(2; 1; 7), C(1; 4; 5) и
D(–7; –4; 7). Доêажите, что веêторы AB и CD
êоллинеарны.
Даны
четыре точêи: A(–2; –3; 8), B(2; 1; 7), C(1; 4; 5) и
D(–7; –4; 7). Доêажите, что веêторы AB и CD
êоллинеарны.
20.
![]() Веêторы
AB = –3 + 4
Веêторы
AB = –3 + 4 i k и AC = 5 – 2 + 4 i j k
служат сторонами треуãольниêа ABC. Найдите длину медианы
AM.
21. ![]() Найдите веêтор = {
Найдите веêтор = {b X;
Y; Z}, êоллинеарный веêтору =a = {2 2
; –1; 4}, если | | = 10.b
22. Веêтор
x удовлетворяет следующим условиям: а) êx оллинеарен
веêтору a = 6 – 8 – 7,5 ; i j k б) x образует
острый уãол с осью Oz; в) | | = 50. x Найдите
êоординаты веêтора .x
23.
Веêтор , êb оллинеарный веêтору
= {3; –4; –12}, a образует с осью Ox тупой уãол. Зная,
что | | = 26, b найдите еãо êоординаты.
24. Найдите êоординаты точêи M, лежащей на оси Ox и одинаêово удаленной от точеê A(1; 2; 3) и B(–3; 3; 2).
25.
![]() Треуãольная
пирамида задана êоординатами своих вершин: A(3; 0; 1), B(–1;
4; 1), C(5; 2; 3), D(0; –5; 4). Вычислите длину веêтора AO,
если O — точêа пересечения медиан треуãольниêа BCD.
Треуãольная
пирамида задана êоординатами своих вершин: A(3; 0; 1), B(–1;
4; 1), C(5; 2; 3), D(0; –5; 4). Вычислите длину веêтора AO,
если O — точêа пересечения медиан треуãольниêа BCD.
26. Компланарны ли веêторы
a
= 3-7 ; 1-2 ; –3-4 ,
= –b 3-2 ; 6; -34
и = c -89 ; –9-2 ; –1 ?
27.
Даны три веêтора: = {3; –2; 1}, = {–1; 1; –2}, a
b c = = {2; 1; –3}. Найдите разложение веêтора = {11; –6; 5} d
по веêторам , , .a b c
28.
![]()
![]() В треуãольной призме ABCA1B1C1
диаãональ CB1 делится точêой M в отношении
CM : MB1 = 2 : 3. Найдите разложение веêтора AM
по веêторам AA1, AB, AC.
В треуãольной призме ABCA1B1C1
диаãональ CB1 делится точêой M в отношении
CM : MB1 = 2 : 3. Найдите разложение веêтора AM
по веêторам AA1, AB, AC.
29.
![]()
![]()
![]() В прямоуãольном параллелепипеде
ABCDA1B1C1D1 дано:
|AA1| = 12, |AB| = 3, |AD| = 4. Найдите разложение
орта ,
В прямоуãольном параллелепипеде
ABCDA1B1C1D1 дано:
|AA1| = 12, |AB| = 3, |AD| = 4. Найдите разложение
орта ,e сонаправленноãо с веêтором AC1,
по прямоуãольному базису ,i j, . k Орты ,i
j, kсонаправлены соответственно с веêторами AD,
AB и AA1.
30.
![]() Известно,
что M1 и M2 являются соответственно точêами
пересечения медиан ãраней ADB и BDC тетраэдра ABCD.
Найдите отношение |AC| : |M1M2|.
Известно,
что M1 и M2 являются соответственно точêами
пересечения медиан ãраней ADB и BDC тетраэдра ABCD.
Найдите отношение |AC| : |M1M2|.
31. К вершине êуба приложены три силы, равные по величине 1, 2, 3 и направленные по диаãоналям ãраней êуба, пересеêающихся в этой вершине. Найдите величину равнодействующей этих трех сил.
32.
![]()
![]() Веêтор OM определен
прямоуãольными êоординатами точеê O(0; 0: 1) и M(α; β; 3). Каêому
условию должны удовлетворять параметры α
и β, чтобы
êонец веêтора OM принадлежал сфере x2 + y2
+ (z – 1)2 = 5?
Веêтор OM определен
прямоуãольными êоординатами точеê O(0; 0: 1) и M(α; β; 3). Каêому
условию должны удовлетворять параметры α
и β, чтобы
êонец веêтора OM принадлежал сфере x2 + y2
+ (z – 1)2 = 5?
33.
При êаêих значениях α и β
веêторы = a αi
– 2 + 3 j k и =b = 3i + 6 – j βk
êоллинеарны?
34. Найдите
веêтор , a если веêтор = {1; 8; –4}, b aÊÊ
b и | | = 3.a
35. Даны три вершины параллелоãрамма: A(0; 0; 0), B(1; 2; 0), C(2; 0; 3). Найдите длины еãо диаãоналей AC и BD.
36. Найдите
значения x, при êоторых веêторы = {cos 2a x;
cos 3x} и = {sin 4b x; sin 5x} имеют одинаêовую
длину.
Определение. Сêалярным произведением двух веêторов называют число, равное произведению длин этих веêторов на êосинус уãла между ними. Таêим образом,
ab
= | | | | cos a b ϕ,
ãде ϕ
— уãол между веêторами a и . b Отсюда
следует, что
![]() cos ϕ = ----
cos ϕ = ----a----b---- .
a b
Необходимым и достаточным условием ортоãональности (перпендиêулярности) двух веêторов является равенство нулю их сêалярноãо произведения.
1°.
ab = ba.
2°.
(αa)b
= α(ab),
ãде α —
число. 3°. ( + )
= a b c ac + bc.
4°.
aa = | |a 2 > 0, если a —
ненулевой веêтор; aa = 0, если a — нулевой веêтор.
![]() Проеêция
веêтора
Проеêция
веêтора b на веêтор (a пишут прa
b) выражается формулой прa = | | cos b
b ϕ
= a--a--b--
.
![]()
![]() Выражение сêалярноãо произведения в
деêартовых êоординатах. Пусть =
Выражение сêалярноãо произведения в
деêартовых êоординатах. Пусть = a X1i
+ Y1j + Z1k, = b
X2i + Y2j + Z2k.
Тоãда справедлива формула ab = X1X2
+ Y1Y2 + Z1Z2.
Необходимым и достаточным условием ортоãональности
веêторов a и b является равенство
X1X2 + Y1Y2 + Z1Z2 = 0.
Уãол ϕ
между веêторами a и b определяется по формуле
cos ϕ = ----------------------------------------------------------------------------X1X2 + Y1Y2 + Z1Z2 - .
![]() X21 + Y21 + Z21 X22
+
Y22 +
Z22
X21 + Y21 + Z21 X22
+
Y22 +
Z22
1.
![]() Определите
уãол между веêторами 2
Определите
уãол между веêторами 2 a и 1-2 b, если a
= {–4; 2; 4}, = {b 2 ; – 2 ; 0}.
2.
При êаêом значении z веêторы = {6;
0; 12} a и = {–8; 13; b z} перпендиêулярны?
3.
![]() Найдите êосинус уãла между веêторами
+
Найдите êосинус уãла между веêторами
+ a b и – , a b если | | = 2, | | = 1, a b ∠(a,
) = b 60°.
4. Найдите êосинус уãла между веêторами p
и , q удовлетворяющими системе уравнений 2p
+ = ,q a p + 2 = ,q b
если известно, что в прямоуãольной
системе êоординат веêторы a и b имеют вид
= {1; 1}, = {1; –1}.a b
5.
Доêажите, что веêтор = (p b ac) – c(ab)
перпендиêулярен веêтору .a
6.
![]() Веêторы
, ,
Веêторы
, , a b c таêовы, что + + = a b c 0. Зная,
что | | = 13,a | | = 14, | | = 15, b c вычислите ab
+ bc + ca.
7. Треуãольниê ABC задан êоординатами своих вершин: A(1; 1; 0), B(1; 1; 2), C(3; 3; 1). Найдите уãол при вершине A.
8. Вершины треуãольниêа находятся в точêах A(3; –2; 1), В(3; 0; 2) и C(1; 2; 5). Найдите величину уãла, образованноãо медианой BD с основанием треуãольниêа AC.
9. Треуãольниê задан êоординатами своих вершин: A(1; 1; 2), B(3; 4; 2) и C(5; 6; 4). Найдите величину внешнеãо уãла треуãольниêа при вершине B.
10. Двумя вершинами треуãольниêа ABC являются точêи A(1; 1; 3) и B(–1; 2; 5). Третья вершина — точêа C — находится на êоординатной оси Oz. Установите зависимость между величиной уãла α при вершине A и расстоянием z точêи C до плосêости xOy.
11. На êоординатной плосêости заданы точêи A(1; 0), B(0; 1) и C(5; 5). Вычислите площадь треуãольниêа ABC.
12.
![]()
![]() Веêторы AB =
{3; –2; 2} и BC = {–1; 0; 2} являются смежными сторонами параллелоãрамма.
Определите величину уãла между еãо диаãоналями AC и
BD.
Веêторы AB =
{3; –2; 2} и BC = {–1; 0; 2} являются смежными сторонами параллелоãрамма.
Определите величину уãла между еãо диаãоналями AC и
BD.
13. Доêажите, что точêи A(2; 4; –4), B(1; 1; –3), C(–2; 0; 5), D(–1; 3; 4) являются вершинами параллелоãрамма, и вычислите величину уãла между еãо диаãоналями.
14. Доêажите, что точêи A(1; –1; 1), B(1; 3; 1), C(4; 3; 1), D(4; –1; 1) являются вершинами прямоуãольниêа. Найдите длину еãо диаãоналей и êоординаты их точêи пересечения.
15. Найдите
веêтор , êb оллинеарный веêтору = {2; 1; –1}a
и удовлетворяющий условию ab = 3.
16.
Найдите веêтор , c зная, что он перпендиêулярен
веêторам = {2; 3; –1} a и = {1; – 2; 3} b и
удовлетворяет условию (2 –c i – j + ) = –6.k
17. ![]() Найдите êоординаты веêтора
,
Найдите êоординаты веêтора
, c перпендиêулярноãо веêторам = 2 – a
j k и = – + 2 – 3 b i j k и образующеãо
тупой уãол с осью Oy, если | | = c 7 .
18. Даны
веêторы = {3; –1; 5} a и = {1; 2; –3}. b Найдите
веêтор c при условии, что он перпендиêулярен оси Oz
и удовлетворяет условиям ca = 9, cb = –4.
19.
Веêторы , a b и c имеют равные
длины и образуют попарно равные уãлы. Найдите êоординаты веêтора
, c если = +a i + j, = + .b
j k
20. В
деêартовой прямоуãольной системе êоординат xOy на êривой
y = -x6 заданы две точêи
A и B таêие, что OAi = –2 и OBi
=
![]() =
3, ãде —
=
3, ãде — i единичный веêтор оси Ox. Найдите длину
веêтора 2OA + 3OB.
21. ![]() Найдите веêтор
Найдите веêтор a
= {X; Y; Z}, образующий равные уãлы с веêторами
= {b Y; – 2Z; 3X} и = {2c Z; 3X;
–Y}, если веêтор aперпендиêулярен веêтору
= {1; –1; 2}, | | = d a 2 3 и уãол между веêтором aи
осью Oy тупой.
22.
При êаêих значениях x уãол между веêторами
= a xi – – 3 – j k и = 2b xi
+ xj – k острый, а уãол между веêтором
b и осью ординат тупой?
23. Точêи M, N, P, Q расположены в пространстве таê, что MN B PQ, MP B NQ. Доêажите, что MQ B NP.
24. Вычислите величину тупоãо уãла, образованноãо медианами, проведенными из вершин острых уãлов равнобедренноãо прямоуãольноãо треуãольниêа.
25.
![]() Даны
веêторы AB =
Даны
веêторы AB = b и AC = , c совпадающие
со сторонами треуãольниêа ABC. Найдите разложение по базису
, b c веêтора, приложенноãо ê вершине B
этоãо треуãольниêа и совпадающеãо с еãо высотой
BM.
26.
![]() Треуãольниê
ABC задан êоординатами вершин: A(1; –2; 2), B(1; 4;
0), C(–4; 1; 1). Найдите веêтор BM, ãде точêа M
— основание высоты, проведенной из вершины B.
Треуãольниê
ABC задан êоординатами вершин: A(1; –2; 2), B(1; 4;
0), C(–4; 1; 1). Найдите веêтор BM, ãде точêа M
— основание высоты, проведенной из вершины B.
27. Тетраэдр ABCD задан êоординатами своих вершин: D(1; 0; 0), A(3; –2; 1), B(3; 1; 5), C(4; 0; 3). Найдите величину двуãранноãо уãла, образованноãо боêовой ãранью ADC и плосêостью основания ABC.
28. Напишите уравнение плосêости, проходящей через три данные точêи M1(1; –1; 2), M2(0; 3; 0) и M3(2; 1; 0).
29. Напишите уравнение плосêости, проходящей через точêи A(4; 0; 0) и B(0; 0; 4) и параллельной оси Oy.
30. При êаêом значении k точêи A(1; 0; 3), B(–1; 3; 4), C(1; 2; 1) и D(k; 2; 5) лежат в одной плосêости?
31. Даны четыре точêи: A(1; – 2; 2), B(1; 4; 0), C(–4; 1; 1) и D(–5; – 5; 3).
а) Доêажите, что эти точêи лежат и одной плосêости;
б) определите величину уãла между прямыми AC и BD;
в) определите площадь четырехуãольниêа ABCD.
32. Найдите уãол между плосêостью, проходящей через точêи A(0; 0; 0), B(1; 1; 1), C(3; 2; 1), и плосêостью, проходящей через точêи A, B и D(3; 1; 2).
33. Даны уравнения плосêостей 2x + 3y + 4z – 8 = 0 и 4x + y + + 3z – 6 = 0; p — прямая, по êоторой пересеêаются эти плосêости. Определите:
а) êоординаты точеê пересечения прямой p с плосêостями
xOy и yOz;
б) величину уãла между прямой p и плосêостью xOz.
34. Длина ребра êуба ABCDA1B1C1D1, ãде AA1 C BB1 C CC1 C DD1, равна 12. Вершина B êуба совпадает с началом êоординат Oxyz, а точêи A, C и B1 расположены на осях Ox, Oy, Oz соответственно (в положительном направлении). На ребрах AA1, B1C1 и CD взяты точêи E, F1, G таêие, что AE : EA1 = 1 : 3, B1F1 : F1C1 = = 1 : 1, CG : GD = 1 : 1.
а) Определите êоординаты точеê E, F1 и G;
б) составьте уравнение плосêости EF1G;
в) найдите расстояние от точêи B1 до плосêости EF1G.
35. Найдите
уãол между веêторами = {–3; –6; 2} a и
= {2; 2; 1}.b
36.
Даны веêторы = – + 2 + 5 , = 7 , = – 4 + 8 .a
i j k b k c i j k Найдите cos ∠(a
– , b c).
37. Найдите
веêтор , êa оллинеарный веêтору = {3; 6; 6} b
и удовлетворяющий условию ab = 27.
38.
![]() Веêторы
Веêторы aи b образуют уãол
= , | | = 3, | | = 4. b Вычислите ( + )a b 2.
39.
Найдите длины веêторов = {1; 1; a α} и = {b α; 8; –3}, если
известно, что они перпендиêулярны.
40. Длина ãипотенузы AB прямоуãольноãо треуãольниêа ABC равна c. Найдите сумму AB · AC + BC · BA + CA · CB.
41. ![]() Даны точêи A(a;
3; –1) и В(1; 5; –2). При êаêом значении a êосинус
уãла, образованноãо веêтором AB с осью Ox, равен
2-3 ?
Даны точêи A(a;
3; –1) и В(1; 5; –2). При êаêом значении a êосинус
уãла, образованноãо веêтором AB с осью Ox, равен
2-3 ?
42.
Найдите уãол между веêторами = 2 – a n m,
= b m – ,n если известно, что |m| =
2, | | = 1, n ![]() ( , ) = .
( , ) = .
43. Точêи A(1; –2; 2), В(–2; –1; 3) — вершины треуãольниêа ABC. Найдите êоординаты третьей вершины C, если она лежит на оси Oy, а уãол треуãольниêа при вершине A равен -2π .
44.
Вычислите êоординаты веêтора , c перпендиêулярноãо
веêторам = {2; 3; –1}, = {1; –2; 3} a b и удовлетворяющеãо
условию (2 – + ) + 6 = 0.c i j k
45.
![]() Найдите
проеêцию веêтора AB на направление веêтора
Найдите
проеêцию веêтора AB на направление веêтора c =
3 – 4 – 12 , i j k если A(1; 2; –1), В(3;
–4; 3).
46.
Найдите проеêцию веêтора – a c на
направление веêтора a + , b если = {2; 3;
7}, = {4; –3; 1}.a b
47.
![]() Найдите
проеêцию веêтора AB на направление веêтора
Найдите
проеêцию веêтора AB на направление веêтора a =
{1; 2; 3}, если A(1; 2; 0), B(2; 0; –3).
48.
Найдите проеêцию веêтора = + 2 a i k на
ось, составляющую с êоординатными осями равные острые уãлы.
49. Разложите
веêтор = {5; –4} a по двум веêторам a1
= {1; 2} и a2 = {–2; 3}.
Глава VIII
Планиметрия
![]()
Пусть a, b, c — длины сторон ∆ABC; A, B, C — противоположные этим сторонам вершины; p = 1-2 (a + b + c) — полупе-
|
мулы: Теорема синусов: |
|
|
------------sina A = --------------sinb B = ------------sin c C- . Теорема êосинусов: a2 = b2 + c2 – 2bc cos A. Формула для вычисления площади ∆ABC: S = 1-2 ah, |
(1) (2) (3) |
риметр; r и R — радиусы вписанной и описанной оêружностей; S — площадь ∆ABC. Тоãда справедливы следующие форãде h — длина высоты, опущенной на сторону BC;
S = 1-2 ab sin C; (4)
S = 1-2 rp; (5)
S = abc--------4R- ; (6)
![]() S = p p a( − )(p b− )(p c− ) (формула
Герона). (7) Пусть R — радиус êруãа, S — площадь
êруãа, L — длина оê-
S = p p a( − )(p b− )(p c− ) (формула
Герона). (7) Пусть R — радиус êруãа, S — площадь
êруãа, L — длина оê-
|
ружности. Тоãда |
|
|
S = πR2; |
(8) |
|
L = 2πR. |
(9) |
1. Точêа M — середина отрезêа AB. Доêажите, что:
а) CM = 1-2 |AC – BC|, если C принадлежит отрезêу AB;
б) CM = 1-2 |AC + BC|, если C принадлежит прямой AB, но не
принадлежит отрезêу AB.
2. В уãол с вершиной A вписана оêружность, êасающаяся сторон уãла в точêах В и C. Доêажите, что: а) центр оêружности O лежит на биссеêтрисе уãла; б) AB = AC; в) ∆OAB = ∆OBC.
3. В выпуêлом четырехуãольниêе ABCD длина диаãонали AC равна длине стороны AD. Доêажите, что BC < BD.
4. Доêажите, что в трапеции, диаãонали êоторой служат биссеêтрисами уãлов при одном из оснований, длины трех сторон равны.
5. Доêажите, что середины сторон выпуêлоãо четырехуãольниêа являются вершинами параллелоãрамма.
6. Пусть a и b (a > b) —длины оснований трапеции. Доêажите, что отрезоê, соединяющий середины диаãоналей трапеции, параллелен ее основаниям, а еãо длина равна 1-2 (a – b).
7. В параллелоãрамме проведены биссеêтрисы еãо внутренних уãлов. Доêажите, что точêи пересечения биссеêтрис являются вершинами прямоуãольниêа, длина диаãонали êотороãо равна разности длин соседних сторон.
8. В параллелоãрамме ABCD точêа M — середина стороны CB, точêа N — середина стороны CD. Доêажите, что прямые AM и AN делят диаãональ BD на три равные части.
9. Доêажите, что биссеêтриса внутреннеãо уãла треуãольниêа делит противоположную сторону на отрезêи, пропорциональные прилежащим сторонам.
10. Через точêу O пересечения диаãоналей трапеции проведена прямая, параллельная ее основаниям. Доêажите, что точêа O делит пополам отрезоê, отсеêаемый от прямой боêовыми сторонами трапеции.
11. Доêажите, что сумма расстояний от любой точêи, принадлежащей правильному треуãольниêу, до еãо сторон равна длине еãо высоты.
12. Пусть p — полупериметр, S — площадь треуãольниêа, r — радиус вписанной оêружности. Доêажите, что r = ---Sp .
13. Пусть a, b, c — длины сторон треуãольниêа, S — еãо площадь, R — радиус описанной оêружности. Доêажите, что
R = abc--------4S- .
14. Доêажите, что в прямоуãольном треуãольниêе сумма длин êатетов равна сумме длин диаметров вписанной и описанной оêружностей.
15. Через точêу A, лежащую вне êруãа, проведены две прямые, одна из êоторых êасается оêружности, служащей ãраницей êруãа, в точêе B, а друãая пересеêает эту оêружность в точêах C и D, причем точêа C лежит между точêами A и D. Доêажите, что AD · AC = AB2.
16. Доêажите, что любая точêа выпуêлоãо четырехуãольниêа принадлежит хотя бы одному из êруãов, диаметрами êоторых являются стороны четырехуãольниêа.
17. В оêружность вписан четырехуãольниê MNPQ, диаãонали êотороãо взаимно перпендиêулярны и пересеêаются в точêе F. Прямая, проходящая через точêу F и середину стороны NP, пересеêает сторону MQ в точêе H. Доêажите, что FH — высота треуãольниêа MFQ.
18. На сторонах AB и BC треуãольниêа ABC построены вне еãо êвадраты ABDE и BCKF. Доêажите, что DF = 2BP, ãде BP — медиана треуãольниêа ABC.
19. На основаниях AB и CD трапеции ABCD построены êвадраты (вне ее). Доêажите, что прямая, соединяющая центры êвадратов, проходит через точêу пересечения диаãоналей трапеции.
20. Пусть a и b — длины сторон параллелоãрамма, d1 и d2 — длины еãо диаãоналей. Доêажите, что d21 + d22 = 2(a2 + b2). 21. Доêажите, что если высота и медиана, проведенные из общей вершины треуãольниêа, делят этот уãол на три равные части, то таêой уãол — прямой.
22. Доêажите, что в четырехуãольниêе, описанном оêоло оêружности, суммы длин противоположных сторон равны.
1. Через точêу A, расположенную внутри уãла, проведите прямую таê, чтобы точêа A была серединой отрезêа, отсеêаемоãо от прямой сторонами уãла.
2. Постройте треуãольниê, если даны две стороны и медиана, выходящие из общей вершины.
3. Точêи A и B принадлежат одной из полуплосêостей, на êоторые плосêость делится прямой p. На прямой p найдите точêу, сумма расстояний от êоторой до точеê A и B является наименьшей.
4. Постройте биссеêтрису уãла, вершина êотороãо расположена за пределами листа бумаãи.
5. Внутри уãла ABC с недоступной вершиной B дана точêа D. Постройте прямую BD.
6. Постройте треуãольниê по еãо медианам.
7.
![]()
![]() Даны отрезêи длиной a
и b. Постройте отрезêи, длины êоторых равны: а) ab ;
б) a2 −
ab + b2
; в) a2 −
2ab + 4b2
. 8. Постройте треуãольниê, зная еãо периметр
и два уãла.
Даны отрезêи длиной a
и b. Постройте отрезêи, длины êоторых равны: а) ab ;
б) a2 −
ab + b2
; в) a2 −
2ab + 4b2
. 8. Постройте треуãольниê, зная еãо периметр
и два уãла.
9. Впишите в данный êруã треуãольниê, подобный данному треуãольниêу.
10. Даны оêружность с центром в точêе O и точêа A, расположенная вне êруãа, оãраниченноãо этой оêружностью.
а) Постройте êасательную ê оêружности, проходящую че-
рез точêу A.
б) Через точêу A проведите прямую, пересеêающую оêружность в точêах В и C таê, чтобы AC = 2AB (точêа B лежит между A и C).
11. Постройте три êасающиеся друã друãа внешним образом оêружности с центрами в вершинах данноãо треуãольниêа.
12. Точêи A и В принадлежат одной из полуплосêостей, на êоторые плосêость делится прямой p.
а) Постройте оêружность, проходящую через точêи A и В
и êасающуюся прямой p.
б) Найдите точêу C ° p таêую, чтобы уãол ABC был на-
ибольшим.
13. Через данную точêу плосêости, расположенную вне данноãо уãла, проведите прямую, отсеêающую от уãла треуãольниê заданноãо периметра.
1. В треуãольниêе ABC известно, что AB = c = 13 см, BC = a = = 14 см, AC = b = 15 см. Определите: а) величину наибольшеãо внутреннеãо уãла треуãольниêа; б) площадь S; в) длину hb высоты BD; ã) длину r радиуса вписанной оêружности; д) длину R радиуса описанной оêружности; е) длину lb биссеêтрисы BE уãла B (E ° AC); ж) длину mb медианы BF; з) расстояние между центрами вписанной и описанной оêружностей; и) расстояние между точêой пересечения медиан G и центром описанной оêружности.
2. Определите площадь треуãольниêа, если еãо основание равно a, уãлы при основании равны 30° и 45°.
3. В треуãольниêе известны длины двух сторон: 6 и 3 см. Найдите длину третьей стороны, если полусумма длин высот, опущенных на данные стороны, равна длине третьей высоты.
4. В прямоуãольном треуãольниêе êатеты относятся êаê 3 : 2, а высота делит ãипотенузу на отрезêи, из êоторых один на 2 м больше друãоãо. Определите длину ãипотенузы.
5. В треуãольниêе ABC известно, что AB = BC, O — точêа пересечения высот. Найдите ∠ABC, если OB = AC.
6. В равнобедренный треуãольниê с уãлом при вершине 120° и боêовой стороной, равной a, вписана оêружность. Найдите ее радиус.
7. Центр вписанной оêружности делит высоту равнобедренноãо треуãольниêа, опущенную на основание, на отрезêи длиной 5 и 3 см, считая от вершины. Определите длины сторон треуãольниêа.
8. Вписанная оêружность êасается ãипотенузы прямоуãольноãо треуãольниêа в точêе, делящей ãипотенузу на отрезêи, длины êоторых равны 2 и 3. Найдите радиус оêружности.
9. Катеты прямоуãольноãо треуãольниêа равны 15 и 20 дм. Определите расстояние от центра вписанноãо êруãа до высоты, опущенной на ãипотенузу.
10. Определите уãлы равнобедренноãо треуãольниêа, зная, что точêа пересечения еãо высот принадлежит вписанной оêружности.
11. В треуãольниê вписана оêружность радиуса 4 см. Одна из сторон треуãольниêа делится точêой êасания на отрезêи длиной 6 и 8 см. Найдите длины друãих сторон треуãольниêа.
12. Боêовая сторона равнобедренноãо треуãольниêа равна 10 см, основание равно 12 см. К оêружности, вписанной в треуãольниê, проведены êасательные, параллельные высоте треуãольниêа и отсеêающие от неãо два малых прямоуãольных треуãольниêа. Найдите длины сторон этих треуãольниêов.
13. Изцентра оêружности, вписанной в треуãольниê со сторонами 13, 14 и 15, проведена друãая оêружность радиуса 5. Найдите длины хорд, отсеêаемых этой оêружностью на сторонах треуãольниêа.
14. Найдите площадь прямоуãольноãо треуãольниêа, если радиус вписанноãо êруãа равен r, а радиус вневписанноãо êруãа, êасающеãося ãипотенузы и продолжений êатетов, равен R.
15. В прямоуãольном треуãольниêе длины êатетов равны 75 и 100 дм. Основание высоты, проведенной из вершины прямоãо уãла, делит ãипотенузу на два отрезêа, на êоторых построены полуêруãи по одну сторону с данным треуãольниêом. Определите длины отрезêов êатетов, заêлюченных внутри этих êруãов.
16. На стороне AB треуãольниêа ABC взята точêа M таê, что AM : MB = 1 : 1. Найдите CM, если AC = 6, BC = 4, ∠ACB = 120°.
17. Медиана, проведенная ê одной из боêовых сторон равнобедренноãо треуãольниêа, делит еãо периметр на две части длиной 15 и 6 см. Определите длины сторон треуãольниêа.
18. В треуãольниêе ABC известно, что AB = 2 см, BD — медиана, BD = 1 см, ∠BDA = 30°. Найдите площадь треуãольниêа ABC.
19. Найдите площадь таêоãо треуãольниêа, сторонами êотороãо служат медианы треуãольниêа с площадью, равной S.
20. Катеты прямоуãольноãо треуãольниêа равны b и c. Найдите длину биссеêтрисы прямоãо уãла.
21. В треуãольниêе ABC дано: AB = 3 см, AC = 5 см, ∠BAC =
= 120°. Найдите длину биссеêтрисы BD, а таêже отрезêов AD и CD.
22. В треуãольниêе ABC известно, что ∠B : ∠C = 1 : 3, биссеêтриса уãла BAC делит площадь треуãольниêа в отношении 2 : 1. Найдите величины уãлов треуãольниêа.
23. В треуãольниêе ABC величина уãла A вдвое больше величины уãла B; AC = b, AB = c. Найдите BC.
24. В прямоуãольном треуãольниêе ABC длина высоты, опущенной из вершины прямоãо уãла на ãипотенузу, равна a и длина биссеêтрисы этоãо же уãла равна b. Найдите площадь треуãольниêа ABC.
25. В равнобедренном треуãольниêе ABC известно, что AB = BC, медиана AD и биссеêтриса CE взаимно перпендиêулярны. Определите величину уãла ADB.
26. В треуãольниêе ABC дано: AC = 13 см, AB + BC = 22 см, ∠ABC = 60°. Найдите длины сторон AB и BC.
27. В треуãольниê вписан параллелоãрамм, длины сторон êотороãо равны 3 и 4 см, а длина одной из диаãоналей — 4 см. Найдите длины сторон треуãольниêа, если известно, что диаãонали параллелоãрамма параллельны боêовым сторонам треуãольниêа, а меньшая из еãо сторон принадлежит основанию треуãольниêа.
28. В параллелоãрамме с длинами сторон a и b и острым уãлом α проведены биссеêтрисы четырех уãлов. Найдите площадь четырехуãольниêа, вершинами êотороãо служат точêи пересечения биссеêтрис.
29. На сторонах êвадрата вне еãо построены правильные треуãольниêи и их вершины последовательно соединены. Определите отношение периметра полученноãо четырехуãольниêа ê периметру данноãо êвадрата.
30. Определите площадь равнобочной трапеции, у êоторой длины оснований равны 10 и 26 см, а диаãонали перпендиêулярны боêовым сторонам.
31. Один из уãлов трапеции равен 30°, а продолжения боêовых сторон пересеêаются под прямым уãлом. Найдите меньшую боêовую сторону трапеции, если ее средняя линия равна 10 см, а одно из оснований равно 8 см.
32. Определите длину высоты трапеции, если ее основания a = 28 см и b = 16 см, а боêовые стороны c = 25 см и d = 17 см.
33. Найдите площадь трапеции, у êоторой длины оснований равны a и b (a > b), а острые уãлы между бˆольшим основанием и боêовыми сторонами равны α и β.
34. Оêоло êруãа радиуса 2 см описана равнобочная трапеция с площадью 20 см2. Найдите длины сторон трапеции.
35. Оêоло оêружности радиуса r описана равнобочная трапеция ABCD; E и K — точêи êасания этой оêружности с боêовыми сторонами трапеции. Уãол между основанием AB и боêовой стороной AD равен 60°. Определите площадь четырехуãольниêа ABEК.
36. Центр оêружности, вписанной в прямоуãольную трапецию, удален от êонцов боêовой стороны на расстояния 4 и 8 см, Найдите длину средней линии трапеции.
37. Длины оснований равнобочной трапеции равны 21 и 9 см, а длина высоты равна 8 см. Определите радиус оêружности, описанной оêоло трапеции.
38. Оêружность, построенная на основании AD трапеции ABCD êаê на диаметре, проходит через середины боêовых сторон AB и CD трапеции и êасается основания BC. Найдите уãлы трапеции.
39. Длины оснований трапеции равны a и b. Найдите длину отрезêа, соединяющеãо боêовые стороны трапеции, параллельноãо основаниям и делящеãо площадь трапеции пополам.
40. В трапеции ABCD (AD C BC) дано: AD = a, BC = b, O — точêа пересечения диаãоналей. Найдите отношение площади трапеции ê площади треуãольниêа AOD.
41. В острый уãол, равный 60°, вписаны две оêружности, извне êасающиеся друã друãа. Радиус меньшей оêружности равен r. Найдите радиус большей оêружности.
42. Радиус сеêтора равен R, а радиус оêружности, вписанной в этот сеêтор, равен r. Вычислите площадь сеêтора.
43.
![]() Даны
две непересеêающиеся оêружности радиусов R и 2R. К ним
проведены общие êасательные, êоторые пересеêаются в точêе
A отрезêа, соединяющеãо центры оêружностей. Расстояние
между центрами оêружностей равно 2R3 . Найдите площадь фиãуры,
оãраниченной отрезêами êасательных, заêлюченными между
точêами êасания, и бˆольшими дуãами оêружностей, соединяющими
точêи êасания.
Даны
две непересеêающиеся оêружности радиусов R и 2R. К ним
проведены общие êасательные, êоторые пересеêаются в точêе
A отрезêа, соединяющеãо центры оêружностей. Расстояние
между центрами оêружностей равно 2R3 . Найдите площадь фиãуры,
оãраниченной отрезêами êасательных, заêлюченными между
точêами êасания, и бˆольшими дуãами оêружностей, соединяющими
точêи êасания.
44. Биссеêтриса AE уãла A рассеêает четырехуãольниê ABCD на равнобедренный треуãольниê ABE (AB = BE) и ромб AECD. Радиус êруãа, описанноãо оêоло треуãольниêа ECD, в 1,5 раза больше радиуса êруãа, вписанноãо в треуãольниê ABE. Найдите отношение периметров треуãольниêов ECD и ABE.
45. В полуêруã радиуса R вписаны два êруãа, êасающиеся друã друãа, полуêруãа и еãо диаметра. Величина радиуса одноãо из них равна r. Найдите радиус друãоãо êруãа.
46.
Вписанная в треуãольниê ABC оêружность
êасается еãо сторон AC и BC соответственно в точêах
M и N и пересеêает биссеêтрису BD в точêах
P и Q. Найдите отношение площадей треуãольниêов PQM
и PQN, если![]() = .
= .
47.
![]() Две
оêружности радиусов 2 и 1 см пересеêаются в точêе A. Расстояние
между центрами оêружностей равно 2 см. Хорда AC большей оêружности
пересеêает меньшую оêружность в точêе B и делится этой
точêой пополам. Найдите длину хорды AC.
Две
оêружности радиусов 2 и 1 см пересеêаются в точêе A. Расстояние
между центрами оêружностей равно 2 см. Хорда AC большей оêружности
пересеêает меньшую оêружность в точêе B и делится этой
точêой пополам. Найдите длину хорды AC.
48. Диаãонали выпуêлоãо четырехуãольниêа пересеêаются под прямым уãлом, сумма их длин равна 6 см. Каêово наибольшее возможное значение площади этоãо четырехуãольниêа?
49. При êаêом значении длины высоты прямоуãольная трапеция с острым уãлом 45° и периметром 4 см имеет наибольшую площадь?
50. В равнобедренном треуãольниêе ABC уãол при основании AC равен α, а длина боêовой стороны равна a. Точêа D расположена на высоте BM и имеет наименьшую по сравнению с остальными точêами отрезêа BM сумму êвадратов расстояний до точеê A, B и C. Найдите длину отрезêа MD.
51. Две стороны параллелоãрамма лежат на сторонах данноãо треуãольниêа, а одна из еãо вершин принадлежит третьей стороне. При êаêих условиях площадь параллелоãрамма будет наибольшей?
52. Определите стороны треуãольниêа, если медиана и высота, проведенные из одноãо уãла, делят этот уãол на три равные части, а длина медианы равна 10.
53.
![]() Сторона,
высота и биссеêтриса треуãольниêа, выходящие из одной и той же
вершины, равны соответственно 5, 2 6 , 5. Найдите длины двух друãих сторон.
Сторона,
высота и биссеêтриса треуãольниêа, выходящие из одной и той же
вершины, равны соответственно 5, 2 6 , 5. Найдите длины двух друãих сторон.
54. Уãол при основании равнобедренноãо треуãольниêа равен ϕ. Найдите отношение радиуса описанной оêоло треуãольниêа оêружности ê радиусу вписанной в неãо оêружности.
55. В треуãольниêе известны стороны a = 5, b = 8 и уãол между ними, равный -3π . Найдите длину высоты, проведенной ê третьей стороне.
56.
![]() Оêружность
проходит через вершину В равнобедренноãо треуãольниêа
ABC (AB = BC), êасается основания AC в точêе
A и пересеêает боêовую сторону BC в точêе D.
Определите величины уãлов треуãольниêа, если 2 BD = CD.
Оêружность
проходит через вершину В равнобедренноãо треуãольниêа
ABC (AB = BC), êасается основания AC в точêе
A и пересеêает боêовую сторону BC в точêе D.
Определите величины уãлов треуãольниêа, если 2 BD = CD.
57. В прямоуãольную трапецию вписана оêружность радиуса r. Найдите стороны трапеции, если ее меньшее основание равно 4-3 r.
58. Две оêружности с радиусами R и r внешне êасаются. Отрезоê AB êасается этих оêружностей в точêах A и В. Найдите длину AB.
59. Оêружности, радиусы êоторых равны R и r, внешне êасаются. Отрезоê AB êасается этих оêружностей в точêах A и В. Найдите радиус оêружности, вписанной в êриволинейный треуãольниê, образованный дуãами оêружностей и отрезêом AB.
60. Отрезêи OA и OB длиной R лежат на осях Ox и Oy. Проведены дуãа AB оêружности с радиусом R и центром O и дуãа OC оêружности с радиусом R и центром A, причем C — точêа пересечения этих дуã. Найдите радиус оêружности, вписанной в êриволинейный треуãольниê, образованный отрезêом OB и дуãами OC и BC.
61. Три оêружности радиуса R êасаются между собой в точêах A, В и C. Найдите площадь êриволинейноãо треуãольниêа ABC, оãраниченноãо дуãами AB, AC, BC этих оêружностей.
62. Три оêружности, радиусы êоторых равны 3, 4 и 5, внешне êасаются между собой в точêах A, В и C. Найдите площадь êриволинейноãо треуãольниêа ABC, оãраниченноãо дуãами AB, BC и CA этих оêружностей.
63. В треуãольниêе ABC точêа M делит сторону AC в отношении AM : MC = 3 : 1, а точêа N делит сторону BC в отношении BN : NC = 3 : 2, F — точêа пересечения отрезêов AN и BM. Найдите: а) отношение площади S1 треуãольниêа ABF ê площади S треуãольниêа ABC; б) отношение площади S1 треуãольниêа ABF ê площади S2 треуãольниêа BFN.
64. Оêружность,
вписанная в треуãольниê ABC, êасается стороны AB
в точêе M. Длина отрезêа MB равна 3, уãол при вершине
B равен arccos 2-3 . Отрезоê прямой
MC перпендиêулярен стороне AB. Найдите длины сторон треуãольниêа.
Глава IX
Стереометрия
![]()
Основные формóлы
Связь между площадью S плосêой фиãуры и площадью ее проеêции S1 на друãую плосêость:
S1 = S cos α, (1)
ãде α — уãол между плосêостями.
Площадь боêовой поверхности призмы:
S = Pl, (2)
ãде P — длина периметра перпендиêулярноãо сечения, l — длина образующей призмы.
Площадь боêовой поверхности правильной пирамиды:
S = 21- Ph, (3)
ãде P — длина периметра основания, h — апофема боêовой ãрани. Площади боêовой и полной поверхностей прямоãо êруãовоãо цилиндра:
Sбоê = 2πRh, Sполн = 2πR(R + h), (4)
ãде R — радиус основания, h — высота цилиндра.
Площади боêовой и полной поверхностей прямоãо êруãовоãо êонуса:
Sбоê = πRl, Sполн = πR(R + l), (5)
ãде R — радиус основания, l — образующая êонуса.
Площадь поверхности прямоãо êруãовоãо усеченноãо êонуса:
![]() S = π(R
+ r)l, (6) ãде R и r — радиусы
оснований, l — образующая усеченноãо êонуса.
S = π(R
+ r)l, (6) ãде R и r — радиусы
оснований, l — образующая усеченноãо êонуса.
Площадь поверхности вращения отрезêа AB воêруã оси l, не пересеêающей отрезоê (рис. 8): l
S = 2πRra, (7)
A ãде a — длина отрезêа, r — расстояние от середины Рис. 8 отрезêа до оси вращения.
![]() Площадь поверхности вращения
дуãи AB
Площадь поверхности вращения
дуãи AB
оêружности воêруã оси l, на êоторой лежитB1
центр O оêружности (рис. 9):h S = 2πRh, (8) ãде R — радиус оêружности, h = A1B1 —AO длина проеêции дуãи AB на ось вращения. A1 Площадь поверхности шара (площадь Рис. 9 сферы):
S = 4πR2, (9)
ãде R — радиус шара.
Объем прямоуãольноãо параллелепипеда:
V = abc, (10)
ãде a, b, c — длины еãо сторон.
Объем прямой призмы:
V = Sh, (11)
ãде S — площадь мноãоуãольниêа, лежащеãо в основании призмы, h — высота призмы.
Объем наêлонной призмы:
V = Sl, (12)
ãде S — площадь перпендиêулярноãо сечения призмы, l — длина боêовоãо ребра призмы. Объем пирамиды:
V = 1-3 Sh, (13)
ãде S — площадь мноãоуãольниêа, лежащеãо в основании пирамиды, h — высота пирамиды.
Объем усеченной пирамиды:
![]() V
= 1-3 (S + s +
Ss )h, (14)
V
= 1-3 (S + s +
Ss )h, (14)
ãде S и s — площади ее оснований, h — высота усеченной пирамиды.
Объем прямоãо êруãовоãо цилиндра:
V = πR2h, (15)
ãде R — радиус основания, h — высота цилиндра.
Объем прямоãо êруãовоãо êонуса:
V = 1-3 πR2h, (16)
ãде R — радиус основания, h — высота êонуса.
Объем прямоãо êруãовоãо усеченноãо êонуса:
V = 1-3 π(R2 + r2 + Rr)h, (17)
ãде R и r — радиусы оснований, h — высота усеченноãо êонуса. Объем шара:
V = 4-3 πR3, (18)
ãде R — радиус шара.
1. Два прямоуãольных треуãольниêа лежат во взаимно перпендиêулярных плосêостях и имеют общую ãипотенузу. Найдите расстояние между вершинами прямых уãлов этих треуãольниêов, если длины их êатетов равны 4 и 3 см.
2. Из точêи ребра двуãранноãо уãла, величина êотороãо равна ϕ, в одной из еãо ãраней проведен отрезоê, составляющий с уêазанным ребром уãол ψ. Каêой уãол образует этот отрезоê с плосêостью друãой ãрани?
3. Катеты AB и AC прямоуãольноãо треуãольниêа принадлежат различным ãраням остроãо двуãранноãо уãла и образуют с ребром этоãо двуãранноãо уãла соответственно острые уãлы ϕ и ψ. Определите величину двуãранноãо уãла.
4. Вершины A и B прямоуãольниêа ABCD удалены от плосêости γ на расстояние 8l êаждая, а середина M стороны CD принадлежит плосêости γ. Диаãонали AC и BD прямоуãольниêа пересеêаются в точêе O. Определите расстояние от центра описанной оêоло треуãольниêа AOB оêружности до плосêости γ, если ∠ADB = ϕ.
5. Вершины A и B правильноãо треуãольниêа ABC удалены от неêоторой плосêости β на расстояние, равное h, а точêа C — на расстояние, равное m (h > m). На êаêом расстоянии от плосêости β находится центр вписанноãо в треуãольниê ABC êруãа?
6. Диаãональ прямоуãольноãо параллелепипеда равна l и образует с плосêостью основания уãол величиной α. Найдите площадь боêовой поверхности параллелепипеда, если площадь еãо основания равна S.
7. Уãол между диаãоналями основания прямоуãольноãо параллелепипеда равен α. Диаãональ параллелепипеда составляет с плосêостью основания уãол β. Найдите высоту параллелепипеда, если еãо объем равен V.
8. Основания параллелепипеда — êвадраты со стороной b, а все боêовые ãрани — ромбы. Одна из вершин верхнеãо основания одинаêово удалена от всех вершин нижнеãо основания. Найдите объем параллелепипеда.
9. Дан êуб ABCDA1B1C1D1. Точêа M — середина ребра A1B1, точêа N — центр ãрани ABB1A1. Определите величину уãла между прямыми MD и CN.
10. Дан êуб ABCDA1B1C1D1. Найдите величину уãла между плосêостями BCB1 и BC1M, ãде M — середина ребра AD.
11. Длина ребра êуба ABCDA1B1C1D1 равна a. Точêа P — середина ребра CC1, точêа Q — центр ãрани AA1B1B. Отрезоê MN с êонцами на прямых AD и A1B1 пересеêает прямую PQ и перпендиêулярен ей. Найдите длину этоãо отрезêа.
12. Диаãональ боêовой ãрани правильной треуãольной призмы, равная l, составляет уãол β с плосêостью друãой боêовой ãрани. Найдите объем призмы.
13. Равнобедренный треуãольниê с уãлом α при вершине и периметром, равным p, служит основанием прямой призмы. Уãол между диаãоналями равных боêовых ãраней призмы, проведенными из одной вершины, равен β. Найдите объем призмы. 14. Через сторону нижнеãо основания правильной треуãольной призмы и противоположную вершину верхнеãо проведена плосêость под уãлом α ê плосêости основания. Площадь сечения призмы этой плосêостью равна S. Найдите объем отсеченной пирамиды.
15. Дана правильная треуãольная призма ABCA1B1C1, в êоторой BB1 = 2AC. Точêи E и F — центры ãраней AA1B1B и CC1B1B, точêа P — центр основания ABC, точêа Q — середина ребра CC1. Определите величину уãла между прямыми EF и PQ.
16. Стороны основания правильной треуãольной призмы ABCA1B1C1 имеют длину a. Вершины M и N правильноãо тетраэдра MNPQ лежат на прямой, проходящей через точêи C1 иB, а вершины Р и Q — на прямой A1C. Найдите объем призмы.
17.
![]() Длина
стороны основания правильной треуãольной призмы ABCA1B1C1
равна 3, а высота — 4 3 . Вершина правильноãо тетраэдра принадлежит отрезêу,
соединяющему центры ãраней ABC и A1B1C1.
Плосêость основания этоãо тетраэдра совпадает с плосêостью
ãрани ABC призмы, а плосêость одной из еãо боêовых
ãраней проходит через диаãональ AB1 боêовой
ãрани призмы. Найдите длину ребра тетраэдра.
Длина
стороны основания правильной треуãольной призмы ABCA1B1C1
равна 3, а высота — 4 3 . Вершина правильноãо тетраэдра принадлежит отрезêу,
соединяющему центры ãраней ABC и A1B1C1.
Плосêость основания этоãо тетраэдра совпадает с плосêостью
ãрани ABC призмы, а плосêость одной из еãо боêовых
ãраней проходит через диаãональ AB1 боêовой
ãрани призмы. Найдите длину ребра тетраэдра.
18. Сторона основания ABC правильной треуãольной призмы ABCA1B1C1 равна a. Точêи M и N являются соответственно серединами ребер AC и A1B1. Проеêция отрезêа MN на прямую BA1 равна ----------a . Определите высоту призмы.
![]() 26
26
19. Длина êаждоãо ребра тетраэдра SABC равна a. Найдите расстояние между SA и BC.
20. Найдите объем правильной треуãольной пирамиды, у êоторой боêовое ребро наêлонено ê плосêости основания под уãлом α и удалено от середины противоположной стороны основания на расстояние k.
21. Уãол между высотой и апофемой правильной треуãольной пирамиды равен α, длина боêовоãо ребра пирамиды равна l. Найдите объем пирамиды.
22. Из основания высоты правильной треуãольной пирамиды на боêовую ãрань опущен перпендиêуляр, равный b. Найдите объем пирамиды, если уãол наêлона боêовоãо ребра ê плосêости основания равен α.
23. Найдите полную поверхность правильной треуãольной пирамиды по данному ее объему V и уãлу α наêлона боêовой ãрани ê плосêости основания.
24. В основании треуãольной пирамиды, все боêовые ãрани êоторой наêлонены ê плосêости основания под уãлом α, лежит правильный треуãольниê, длина стороны êотороãо равна a. Определите объем пирамиды.
25. Основаниями усеченной треуãольной пирамиды ABCA1B1C1 являются правильные треуãольниêи, длины сторон êоторых равны a и b (a > b). Боêовые ãрани наêлонены ê плосêости нижнеãо основания под уãлом α. Найдите объем мноãоãранниêа AB1C1CB.
26. В основании пирамиды SABC лежит правильный треуãольниê, длина стороны êотороãо равна a. Ребро SA перпендиêулярно плосêости основания. Боêовая ãрань SBC наêлонена ê плосêости основания под уãлом ϕ. Определите площадь боêовой поверхности пирамиды, если за ее основание принята одна из боêовых ãраней.
27. Через вершину C основания правильной треуãольной пирамиды SABC проведена плосêость перпендиêулярно боêовому ребру SA. Эта плосêость составляет с плосêостью основания уãол, êосинус êотороãо равен 2-3 . Найдите êосинус уãла между боêовыми ãранями.
28. Отрезоê, соединяющий центр основания правильной треуãольной пирамиды с серединой боêовоãо ребра, равен стороне основания. Найдите уãол между смежными боêовыми ãранями пирамиды.
29. а) В трехãранном уãле SABC известно, что ∠ASB = β, ∠ASC =
= γ, ∠BSC = α. Величина двуãранноãо уãла при ребре AS равна A. Доêажите, что cos α = cos β cos γ + sin β sin γ cos A (теорема êосинусов для трехãранноãо уãла).
б) Найдите величину двуãранноãо уãла между боêовыми ãранями правильной треуãольной пирамиды, если величина двуãранноãо уãла между боêовой ãранью и основанием равна ϕ.
30. Длина высоты правильной треуãольной пирамиды равна h, а величина двуãранноãо уãла, образованноãо боêовыми ãранями, равна 2ϕ. Определите объем пирамиды.
31. Треуãольная пирамида рассечена плосêостью на два мноãоãранниêа. Найдите отношение объемов этих мноãоãранниêов, если известно, что сеêущая плосêость делит три ребра, сходящиеся в одной вершине пирамиды, в отношениях 1 : 2, 1 : 2 и 2 : 1, считая от вершины.
32. Объем правильной треуãольной пирамиды равен 1-6 объема êуба, длина ребра êотороãо равна длине боêовоãо ребра пирамиды. Найдите величину плосêоãо уãла при вершине пирамиды.
33. Боêовые ребра правильной четырехуãольной пирамиды равны a и наêлонены ê плосêости основания под уãлом α. Найдите площадь боêовой поверхности и объем пирамиды.
34. ![]() Сторона основания правильной
четырехуãольной пирамиды SABCD равна 2, высота пирамиды равна 2 .
Найдите расстояние между боêовым ребром SA и диаãональю основания
BD.
Сторона основания правильной
четырехуãольной пирамиды SABCD равна 2, высота пирамиды равна 2 .
Найдите расстояние между боêовым ребром SA и диаãональю основания
BD.
35.Определите объем правильной четырехуãольной пирамиды, в êоторой сторона основания равна a, а двуãранный уãол между боêовыми ãранями равен α.
36. Найдите объем правильной четырехуãольной пирамиды, длина боêовоãо ребра êоторой равна l, а величина двуãранноãо уãла, образованноãо двумя противоположными ãранями, равна β.
37. В правильной четырехуãольной пирамиде длина стороны основания равна a, величина плосêоãо уãла при вершине равна уãлу наêлона боêовоãо ребра ê плосêости основания. Найдите объем пирамиды.
38. В основании пирамиды MABCD лежит ромб ABCD, диаãональ AC êотороãо имеет длину, равную a. Прямая DM составляет с плосêостью основания пирамиды уãол величиной α и DM = k. Найдите площадь полной поверхности êуба, объем êотороãо равен объему данной пирамиды, если известно, что уãол между прямыми DM и MB равен γ и ∠MBC = ∠ABM.
39. Основанием пирамиды служит ромб, длины диаãоналей êотороãо равны 6 и 8 м. Высота пирамиды проходит через точêу пересечения диаãоналей ромба и имеет длину, равную 1 м. Найдите площадь боêовой поверхности пирамиды.
40. Основанием пирамиды SABCD служит êвадрат. Ребро SA перпендиêулярно основанию. Площадь основания в m раз меньше площади боêовой поверхности. Найдите уãлы наêлона ãраней SCD и SBC ê плосêости основания.
41. Основанием четырехуãольной пирамиды SABCD с вершиной S является ромб, а высота пирамиды SO проходит через точêу пересечения диаãоналей ромба. Вычислите величину двуãранноãо уãла, образованноãо боêовой ãранью SAB и основанием пирамиды, если ∠ASO = α и ∠BSO = β.
42. Величина двуãранноãо уãла при боêовом ребре правильной четырехуãольной пирамиды равна α. Определите величину уãла между боêовой ãранью пирамиды и плосêостью основания.
43. В правильной четырехуãольной пирамиде SABCD уãол между боêовым ребром SA и плосêостью основания ABCD равен уãлу между ребром SA и плосêостью ãрани SBC. Определите величину этоãо уãла.
44. Через точêу S, лежащую вне сферы радиуса 4, проведены четыре прямые, пересеêающие сферу. Точêи пересечения прямых сосферой являются ãраницами отрезêов AA1, BB1, CC1, DD1, причем точêи A1, B1, C1, D1 лежат на отрезêах AS, BS, CS, DS соответственно. Известно, что длины отрезêов AS, BS, CS, DS равны 8, а длина отрезêа AA1 равна 2. Найдите радиус шара, описанноãо оêоло пирамиды SABCD.
45. Через точêу S, лежащую вне сферы радиуса 6, проведены три прямые, пересеêающие сферу. Точêи пересечения прямых со сферой являются ãраницами отрезêов AA1, BB1, CC1, причем точêи A1, B1, C1 лежат на отрезêах AS, BS, CS соответственно. Известно, что SA : SA1 = 4 : 3, а длина отрезêа AA1 равна 3. Найдите расстояние между центрами данной сферы и сферы, описанной оêоло пирамиды SABC, если длины отрезêов BS и CS равны 12.
46.
![]() Через
точêу S, удаленную от центра сферы радиуса 3 на расстояние 9, проведено
пять прямых, пересеêающих сферу. Точêи пересечения прямых со сферой
являются ãраницами отрезêов AA1, BB1,
CC1, DD1, EE1 причем точêи
A1, B1, C1, D1,
E1 лежат на отрезêах AS, BS, CS, DS,
ES соответственно. Известно, что длины отрезêов AS, BS,
CS, DS, ES равны 6 3 . Найдите радиус шара, описанноãо
оêоло пирамиды SABCDE.
Через
точêу S, удаленную от центра сферы радиуса 3 на расстояние 9, проведено
пять прямых, пересеêающих сферу. Точêи пересечения прямых со сферой
являются ãраницами отрезêов AA1, BB1,
CC1, DD1, EE1 причем точêи
A1, B1, C1, D1,
E1 лежат на отрезêах AS, BS, CS, DS,
ES соответственно. Известно, что длины отрезêов AS, BS,
CS, DS, ES равны 6 3 . Найдите радиус шара, описанноãо
оêоло пирамиды SABCDE.
47.
![]() Через
точêу S, лежащую вне сферы с центром в точêе O, проведены
три прямые, пересеêающие сферу и образующие с прямой SO уãлы,
равные arcsin -------83 . Точêи пересечения
прямых со сферой являются ãраницами отрезêов AA1,
BB1, CC1, причем точêи A1,
B1, C1 лежат на отрезêах AS, BS,
CS соответственно.
Через
точêу S, лежащую вне сферы с центром в точêе O, проведены
три прямые, пересеêающие сферу и образующие с прямой SO уãлы,
равные arcsin -------83 . Точêи пересечения
прямых со сферой являются ãраницами отрезêов AA1,
BB1, CC1, причем точêи A1,
B1, C1 лежат на отрезêах AS, BS,
CS соответственно.
Известно, что длина отрезêа SO в 4 раза больше радиуса сферы. Найдите отношение радиуса данной сферы ê радиусу сферы, описанной оêоло пирамиды SABC.
48. В правильной треуãольной пирамиде отношение радиусов вписанной и описанной сфер равно 1-3 . Найдите объем пирамиды, если длина ее высоты равна h.
49. В правильной четырехуãольной пирамиде центры вписанной и описанной сфер совпадают. Найдите объем пирамиды, если длина ее боêовоãо ребра равна l.
50. В правильной треуãольной пирамиде центры вписанной и описанной сфер совпадают. Найдите площадь полной поверхности пирамиды, если длина ребра ее основания равна a.
51. ![]() Для правильной четырехуãольной
пирамиды отношение радиусов вписанной и описанной сфер равно (2 – 1). Найдите
площадь боêовой поверхности пирамиды, если длина ее апофемы равна p.
Для правильной четырехуãольной
пирамиды отношение радиусов вписанной и описанной сфер равно (2 – 1). Найдите
площадь боêовой поверхности пирамиды, если длина ее апофемы равна p.
52. В основании треуãольной пирамиды PABC с высотой
![]() ---------330- лежит правильный треуãольниê
ABC со стороной 8. Проеê-
---------330- лежит правильный треуãольниê
ABC со стороной 8. Проеê-
цией вершины P на основание пирамиды является середина ребра AB. Через вершину P проводятся сечения пирамиды плосêостями, параллельными ребру AB. Найдите наибольшее возможное значение площади сечения.
53. ![]() В основании треуãольной
пирамиды PABC лежит равнобедренный прямоуãольный треуãольниê
ABC, а проеêцией вершины P на основание пирамиды является середина
ãипотенузы AB. Боêовые ребра наêлонены ê плосêости
основания под уãлом arctg -------52 . Через вершину S параллельно ãипотенузе
AB проведена плосêость таê, что площадь полученноãо сечения
имеет маêсимально возможное значение. Найдите отношение, в êотором эта
плосêость делит объем пирамиды.
В основании треуãольной
пирамиды PABC лежит равнобедренный прямоуãольный треуãольниê
ABC, а проеêцией вершины P на основание пирамиды является середина
ãипотенузы AB. Боêовые ребра наêлонены ê плосêости
основания под уãлом arctg -------52 . Через вершину S параллельно ãипотенузе
AB проведена плосêость таê, что площадь полученноãо сечения
имеет маêсимально возможное значение. Найдите отношение, в êотором эта
плосêость делит объем пирамиды.
54.
![]() В
основании треуãольной пирамиды PABC с высотой 7 лежит равнобедренный
прямоуãольный треуãольниê ABC с êатетом, равным
16. Проеêцией вершины P на основание пирамиды является середина
ãипотенузы AB. Через вершину S проводятся сечения пирамиды
плосêостями, параллельными ãипотенузе AB. Найдите наибольшее
возможное значение площади сечения.
В
основании треуãольной пирамиды PABC с высотой 7 лежит равнобедренный
прямоуãольный треуãольниê ABC с êатетом, равным
16. Проеêцией вершины P на основание пирамиды является середина
ãипотенузы AB. Через вершину S проводятся сечения пирамиды
плосêостями, параллельными ãипотенузе AB. Найдите наибольшее
возможное значение площади сечения.
55.
![]() В
основании треуãольной пирамиды PABC лежит правильный треуãольниê
ABC, а проеêцией вершины P на основание является середина ребра
AB. Наибольшее боêовое ребро пирамиды наêлонено ê плосêости
основания под уãлом arctg ---------1210- .
Через вершину P параллельно ребру AB проведена плосêость таê,
что площадь полученноãо сечения имеет маêсимально возможное значение.
Найдите отношение, в êотором эта плосêость делит объем пирамиды.
В
основании треуãольной пирамиды PABC лежит правильный треуãольниê
ABC, а проеêцией вершины P на основание является середина ребра
AB. Наибольшее боêовое ребро пирамиды наêлонено ê плосêости
основания под уãлом arctg ---------1210- .
Через вершину P параллельно ребру AB проведена плосêость таê,
что площадь полученноãо сечения имеет маêсимально возможное значение.
Найдите отношение, в êотором эта плосêость делит объем пирамиды.
56. Отношение радиуса сферы, описанной оêоло правильной треуãольной пирамиды, ê радиусу сферы, вписанной в эту пирамиду, принимает наименьшее возможное значение. Найдите величину уãла наêлона боêовоãо ребра ê плосêости основания пирамиды.
57. Отношение радиуса сферы, вписанной в правильную четырехуãольную пирамиду, ê радиусу сферы, описанной оêоло этой пирамиды, принимает наибольшее возможное значение. Найдите величину уãла при вершине пирамиды.
58. Отношение радиуса сферы, описанной оêоло правильной треуãольной пирамиды, ê радиусу сферы, вписанной в эту пирамиду, принимает наименьшее возможное значение. Найдите величину уãла, под êоторым из центра описанной сферы видна апофема пирамиды.
59. Отношение радиуса сферы, вписанной в правильную шестиуãольную пирамиду, ê радиусу сферы, описанной оêоло этой пирамиды, принимает наибольшее возможное значение. Найдите величину уãла при основании боêовой ãрани пирамиды.
60. На боêовом ребре PA треуãольной пирамиды PABC взята точêа M таê, что MA : MP = 2 : 1. Плосêость, проходящая через точêу M параллельно ребру AB, пересеêает ребро AC в точêе L и делит пирамиду на части, объемы êоторых относятся êаê 5 : 4. Найдите отношение LC : LA.
61. Дана прямая треуãольная призма ABCA1B1C1, у êоторой AC = 6, AA1 = 8. Через вершину A проведена плосêость, пересеêающая ребра BB1 и CC1 соответственно в точêах M и N. В êаêом отношении делит эта плосêость объем призмы, если известно, что BM = MB1 и AN — биссеêтриса уãла CAC1?
62. В правильной треуãольной пирамиде SABC сторона основания ABC равна a, а плосêий уãол при вершине пирамиды равен α. Найдите площадь сечения, проведенноãо через вершину S параллельно ребру AB и составляющеãо с плосêостью основания уãол γ.
63. Длина апофемы боêовой ãрани правильной треуãольной пирамиды равна k. Пирамида пересечена плосêостью, равноудаленной от всех ее вершин. Найдите площадь полученноãо сечения, если боêовое ребро пирамиды составляет с плосêостью ее основания уãол β.
64. Длина боêовоãо ребра правильной четырехуãольной пирамиды равна l, а величина уãла между плосêостью боêовой ãрани и плосêостью основания равна β. Пирамида пересечена плосêостью, равноудаленной от всех ее вершин. Определите площадь полученноãо сечения.
65. В правильной четырехуãольной пирамиде длина стороны основания равна a, боêовое ребро наêлонено ê плосêости основания под уãлом α. Пирамида пересечена плосêостью, проходящей через вершину основания перпендиêулярно боêовому ребру, выходящему из противоположной вершины основания. Найдите площадь сечения.
66. В правильной четырехуãольной пирамиде боêовая ãрань наêлонена ê основанию под уãлом α. Радиус вписанной в пирамиду сферы равен r. Найдите площадь сечения пирамиды, проходящеãо через центр вписанноãо шара параллельно основанию пирамиды.
67. В êонус с высотой H и радиусом основания R вписана правильная шестиуãольная призма таê, что одно ее основание лежит в плосêости основания êонуса, а вершины друãоãо основания принадлежат боêовой поверхности êонуса. Каêой должна быть высота призмы, чтобы ее объем был наибольшим? Найдите это наибольшее значение объема.
68. Уãол между боêовым ребром и высотой правильной треуãольной пирамиды равен ϕ. В пирамиду вписан цилиндр, радиус основания и высота êотороãо имеют длину r. Одно из основании цилиндра имеет по одной общей точêе с êаждой из боêовых ãраней пирамиды, а друãое лежит в плосêости ее основания. При êаêом значении ϕ объем пирамиды наименьший?
69. В правильной треуãольной пирамиде проведено сечение, проходящее через вершину основания и высоту пирамиды. Найдите уãол наêлона боêовоãо ребра ê плосêости основания, если отношение площади сечения ê площади основания равно 1-3 .
70. В правильной треуãольной пирамиде проведено сечение, проходящее через высоту и апофему пирамиды. Найдите уãол наêлона апофемы ê плосêости основания, если отношение пло-
щади сечения ê площади основания равно ---------1 .
![]() 23
23
71. В правильной треуãольной пирамиде проведено сечение, проходящее через вершину основания и высоту пирамиды. Найдите уãол наêлона боêовоãо ребра ê плосêости основания, если площадь сечения равна площади основания.
72. В правильной треуãольной пирамиде проведено сечение, проходящее через боêовое ребро и высоту пирамиды. Найдите уãол наêлона апофемы пирамиды ê плосêости основания, если площадь основания в 2 раза больше площади сечения.
73. Плосêость, проведенная на одинаêовых расстояниях от всех пяти вершин правильной четырехуãольной пирамиды, делит ее полную поверхность на две части, отношение площадей êоторых равно простому числу. Найдите объем пирамиды, если длина стороны ее основания равна a.
74. Плосêость, проведенная на одинаêовых расстояниях от всех пяти вершин правильной четырехуãольной пирамиды, делит ее полную поверхность на две части, отношение площадей êоторых равно четному числу, не делящемуся на 4. Найдите объем пирамиды, если длина ее боêовоãо ребра равна b.
75. Плосêость, проведенная на одинаêовых расстояниях от всех пяти вершин правильной четырехуãольной пирамиды, делит ее полную поверхность на две части, отношение площадей êоторых равно числу, являющемуся натуральной степенью числа 2. Найдите объем пирамиды, если длина ее высоты равна 4.
76. Плосêость, проведенная на одинаêовых расстояниях от всех пяти вершин правильной четырехуãольной пирамиды, делит ее полную поверхность на две части, отношение площадей êоторых равно составному числу. Найдите объем пирамиды, если длина ее апофемы равна H.
77. Основанием треуãольной пирамиды DABC является прямоуãольный треуãольниê ABC, в êотором ∠ABC = 90°, AB = 5, BC = 12. Боêовое ребро DC равно 9 и перпендиêулярно плосêости основания пирамиды. Найдите площадь боêовой поверхности пирамиды.
78. Основанием треуãольной пирамиды DKLM является прямоуãольный треуãольниê KLM, в êотором ∠KLM = 90°, KL = 15, KM = 17. Боêовое ребро DM перпендиêулярно плосêости основания. Найдите площадь полной поверхности пирамиды, если ∠DLM = 60°.
79. Основанием треуãольной пирамиды DPQR является прямоуãольный треуãольниê PQR, в êотором ∠PQR = 90°, PQ = 9, QR = 12. Боêовое ребро DR перпендиêулярно плосêости основания. Найдите площадь боêовой поверхности пирамиды, если ∠DPR = 45°.
80. Основанием треуãольной пирамиды PFKD является прямоуãольный треуãольниê FKD, в êотором ∠FKD = 90°, FD = 20, ∠FDK = 30°. Найдите площадь полной поверхности пирамиды, если известно, что боêовое ребро PD равно 10 и перпендиêулярно плосêости основания пирамиды.
81.
![]() В
правильной треуãольной пирамиде сумма длин всех шести ее ребер равна L,
а площадь основания равна S0. Найдите площадь боêовой поверхности
пирамиды. Решите задачу при S0 = 3 и L = 10.
В
правильной треуãольной пирамиде сумма длин всех шести ее ребер равна L,
а площадь основания равна S0. Найдите площадь боêовой поверхности
пирамиды. Решите задачу при S0 = 3 и L = 10.
82. ![]() В правильной треуãольной
пирамиде длина боêовоãо ребра равна b, а радиус êруãа,
вписанноãо в основание пирамиды, равен r. Найдите площадь полной поверхности
пирамиды. Решите задачу при b = 7 и r = 1.
В правильной треуãольной
пирамиде длина боêовоãо ребра равна b, а радиус êруãа,
вписанноãо в основание пирамиды, равен r. Найдите площадь полной поверхности
пирамиды. Решите задачу при b = 7 и r = 1.
83. ![]() В правильной треуãольной
пирамиде сумма длин всех шести ее ребер равна L, а радиус êруãа,
вписанноãо в основание пирамиды, равен r. Найдите объем пирамиды.
Решите задачу при L = 36 и r = 3 .
В правильной треуãольной
пирамиде сумма длин всех шести ее ребер равна L, а радиус êруãа,
вписанноãо в основание пирамиды, равен r. Найдите объем пирамиды.
Решите задачу при L = 36 и r = 3 .
84. ![]() В правильной треуãольной
пирамиде площадь полной поверхности равна S, а радиус оêружности, описанной
оêоло основания пирамиды, равен R. Найдите объем пирамиды. Решите
задачу при S = 9 3 и R = 2.
В правильной треуãольной
пирамиде площадь полной поверхности равна S, а радиус оêружности, описанной
оêоло основания пирамиды, равен R. Найдите объем пирамиды. Решите
задачу при S = 9 3 и R = 2.
Объем тела, образованноãо вращением воêруã оси Ox êриволинейной трапеции a m x m b, 0 m y m y(x), ãде y(x) — непрерывная однозначная фунêция, выражается формулой b
Vx = π ∫ y2(x) dx.
a
В более общем случае объем êольца, образованноãо вращением воêруã оси Ox фиãуры a m x m b, y1(x) m y m y2(x) ãде y1(x) и y2(x) — непрерывные неотрицательные фунêции, равен b
V = π [∫ y22 (x) – y21 (x)] dx.
a
Если на отрезêе [a; b] фунêция f(x) имеет непрерывную производную f′(x), то площадь P поверхности, образованной вращением ãрафиêа этой фунêции воêруã оси Ox, находится по формуле
b
P = 2![]() .
.
a
1. Боêовая поверхность цилиндра, будучи развернута, представляет собой прямоуãольниê, в êотором диаãональ равна a и составляет уãол α с основанием. Найдите объем цилиндра.
2. Плосêость, проходящая через центр нижнеãо основания цилиндра под уãлом α ê плосêости основания, пересеêает верхнее основание по хорде длиной b, стяãивающей дуãу в β. Найдите объем цилиндра.
3. Площадь полной поверхности êонуса равна S, уãол при вершине осевоãо сечения равен α. Найдите объем êонуса.
4. В основание êонуса вписан правильный треуãольниê, длина стороны êотороãо равна a. Плосêость, проходящая через вершину êонуса и сторону треуãольниêа, образует в сечении с поверхностью êонуса правильный треуãольниê. Найдите объем êонуса.
5. Плосêость, проведенная через вершину êонуса, пересеêает еãо основание по хорде, длина êоторой равна радиусу этоãо основания. Определите отношение объемов образовавшихся частей êонуса.
6. Через вершину êонуса проведено сечение под уãлом β ê плосêости основания. Плосêость сечения удалена от центра основания êонуса на расстояние a. Определите полную поверхность êонуса, если величина наибольшеãо уãла между образующими êонуса равна α.
7. Треуãольниê вращается воêруã стороны, длина êоторой равна a. Определите объем тела вращения, если величины прилежащих уãлов равны α и β.
8. Два равнобедренных треуãольниêа ABC и ADC расположены по одну сторону от общеãо основания AC, равноãо b. Определите объем тела, образованноãо вращением фиãуры ABCDA воêруã основания AC, если ∠ACB = α, ∠ACD = β (α > β).
9. Длина меньшей стороны параллелоãрамма равна a, острый уãол параллелоãрамма равен α, уãол между меньшей диаãональю и большей стороной равен β. Найдите объем тела, полученноãо вращением параллелоãрамма воêруã еãо большей стороны.
10. Фиãура, оãраниченная дуãами парабол y = x2 и y2 = x, вращается воêруã оси абсцисс. Вычислите объем полученноãо тела.
11. Найдите объем фиãуры, полученной при вращении воêруã оси ординат êриволинейной трапеции, ãраница êоторой задана уравнениями y2 = x, y = 0, y = 1, x = 0.
12. Найдите объем фиãуры, полученной при вращении воêруã оси абсцисс êриволинейной трапеции, ãраница êоторой задана уравнением:
а) y = ||x – 1| – 2|, x = 0, x = 3, y = 0;
б) y = |x – 1| – |x + 1|, x = – 2, x = 2, y = 0;
в) y = x|x – 2|, x = 0, x = 3, y = 0;
ã) y = x2 – 3|x| + 2, x = – 1, x = 2, y = 0;
![]() д)
y = 1 − x
, x = –3, x = 1, y = 0. 13. Квадрат вращается воêруã
оси, лежащей в еãо плосêости и проходящей тольêо через одну из
еãо вершин. При êаêом положении êвадрата относительно оси
объем полученноãо тела вращения будет наибольшим?
д)
y = 1 − x
, x = –3, x = 1, y = 0. 13. Квадрат вращается воêруã
оси, лежащей в еãо плосêости и проходящей тольêо через одну из
еãо вершин. При êаêом положении êвадрата относительно оси
объем полученноãо тела вращения будет наибольшим?
14. В êонус с высотой H и радиусом основания R вписан цилиндр таê, что одно еãо основание лежит в плосêости основания êонуса, а оêружность друãоãо основания принадлежит боêовой поверхности êонуса. Каêой должна быть высота цилиндра, чтобы еãо объем был наибольшим? Найдите это наибольшее значение объема.
15. Найдите радиус основания r и высоту h прямоãо êруãовоãо êонуса, вписанноãо в шар радиуса R таê, чтобы объем êонуса был наибольшим.
16. Найдите êонус наименьшеãо объема, описанный оêоло шара радиуса R.
17. Найдите высоту êонуса наименьшеãо объема, описанноãо оêоло полушара радиуса R (центр основания êонуса совпадает с центром шара).
18. В сферу радиуса R вписана правильная четырехуãольная пирамида таê, что все ее вершины принадлежат сфере. Каêой должна быть высота пирамиды, чтобы ее объем был наибольшим? Найдите это наибольшее значение объема.
1. Объем правильной треуãольной призмы равен V. Через вершину основания параллельно противоположному ребру этоãо основания под уãлом α ê плосêости основания проведена плосêость, отсеêающая от призмы пирамиду объемом W. Определите высоту призмы, если V > 3W.
2. Куб с ребром, равным a, вписан в правильную четырехуãольную пирамиду таê, что четыре еãо вершины находятся на боêовых ребрах, а четыре друãие — на основании пирамиды. Боêовые ãрани пирамиды наêлонены ê плосêости основания под уãлом α. Определите объем пирамиды.
3. В основании пирамиды SABC лежит равнобедренный треуãольниê ABC таêой, что AB = AC = a, ∠ABC = ϕ. Прямая AS составляет с плосêостью основания пирамиды уãол величиной α, плосêость боêовой ãрани BSC составляет с той же плосêостью уãол величиной β и ∠SAC = ∠SAB. Найдите объем пирамиды KSLC, если известно, что точêи K и L принадлежат ребрам AS и BS соответственно, а площади треуãольниêов KSL и ABS относятся êаê 4 : 25.
4. В правильную четырехуãольную пирамиду с плосêим уãлом α при вершине вписан цилиндр, нижнее основание êотороãо лежит в плосêости основания пирамиды, а оêружность верхнеãо основания êасается боêовых ãраней пирамиды. Найдите объем пирамиды, если известно, что высота цилиндра в 2 раза меньше высоты пирамиды, а радиус основания равен r.
5. Определите площадь боêовой поверхности êонуса, вписанноãо в правильную треуãольную пирамиду, если длина боêовоãо ребра пирамиды равна l, а боêовая ãрань пирамиды образует с плосêостью основания уãол α.
6. Найдите объем êонуса, вписанноãо в правильную треуãольную пирамиду с боêовым ребром l и плосêим уãлом α при вершине.
7. В правильную треуãольную усеченную пирамиду с двуãранным уãлом α при основании вписан усеченный êонус. Определите боêовую поверхность этоãо êонуса, если апофема боêовой ãрани пирамиды равна сумме радиусов оснований êонуса, а радиус меньшеãо основания êонуса равен r.
8. Основание пирамиды — ромб со стороной a и острым уãлом α. В пирамиду вписан êонус, образующая êотороãо наêлонена ê плосêости основания под уãлом ϕ. Найдите объем êонуса.
9. Оêоло шара описана прямая призма, основанием êоторой служит ромб. Бˆольшая диаãональ призмы составляет с плосêостью основания уãол, величина êотороãо равна α. Найдите величину остроãо уãла ромба.
10. В прямоуãольном параллелепипеде длина боêовоãо ребра равна c, а длины сторон прямоуãольниêа, лежащеãо в основании, равны a и b. Через одну из вершин верхнеãо основания параллелепипеда и противолежащую ей вершину нижнеãо основания проведена плосêость, параллельная диаãонали прямоуãольниêа, лежащеãо в основании. Найдите радиус сферы, êасающейся уêазанной плосêости и плосêости нижнеãо основания параллелепипеда в точêе пересечения еãо диаãоналей.
11. В правильной треуãольной пирамиде плосêий уãол при вершине равен α, а длина высоты пирамиды равна h. Найдите радиус сферы, описанной оêоло пирамиды.
12. В основании треуãольной пирамиды, высота êоторой равна h, лежит прямоуãольный треуãольниê с êатетом, равным a, и острым уãлом α, прилежащим ê этому êатету. Вершина пирамиды проецируется в вершину прямоãо уãла треуãольниêа. Найдите радиус сферы, описанной оêоло пирамиды.
13. Определите объем шара, описанноãо оêоло правильной треуãольной пирамиды, сторона основания êоторой равна a, а боêовые ребра наêлонены ê плосêости основания под уãлом α.
14. Основанием пирамиды служит прямоуãольниê с уãлом α между диаãоналями. Боêовые ребра образуют с плосêостью основания уãол ϕ. Определите объем пирамиды, если радиус описанноãо шара равен R. Центр шара лежит внутри пирамиды.
15. Найдите высоту правильной четырехуãольной пирамиды, если известно, что объем шара, описанноãо оêоло пирамиды, равен V, а перпендиêуляр, опущенный из центра шара на ее боêовую ãрань, образует с высотой пирамиды уãол α. Центр шара находится внутри пирамиды.
16. Радиус шара, описанноãо оêоло правильной четырехуãольной пирамиды, относится ê стороне основания пирамиды êаê 3 : 4. Найдите величину уãла между боêовой ãранью и плосêостью основания пирамиды.
17. Основанием пирамиды SABCD является прямоуãольниê ABCD, в êотором AB C CD, BC C AD, AB = 3, BC = 4. Все боêовые ребра пирамиды составляют с плосêостью основания равные уãлы. Определите величину уãла между прямыми BS и CS, если радиус сферы, описанной оêоло пирамиды, равен 6,5.
18. Основанием пирамиды служит равнобедренный треуãольниê, у êотороãо боêовые стороны равны b, а уãол между ними равен α. Две боêовые ãрани пирамиды, проходящие через равные стороны основания, перпендиêулярны основанию, а третья ãрань наêлонена ê нему под уãлом α. Найдите радиус шара, вписанноãо в пирамиду.
19. Длинавысоты правильной треуãольной пирамиды равна h, а радиус êруãа, вписанноãо в основание этой пирамиды, равен r. Через середины двух сторон основания и вершину пирамиды проведена сеêущая плосêость. Найдите радиус сферы, êасающейся основания пирамиды в точêе пересечения еãо медиан и сеêущей плосêости.
20. Длина êаждоãо ребра тетраэдра равна 1. Найдите радиус сферы, êасающейся всех плосêостей ãраней тетраэдра.
21. В основании пирамиды лежит ромб со стороной a и острым уãлом α. Каждый из двуãранных уãлов при основании равен ϕ. Найдите объем шара, вписанноãо в пирамиду.
22. Сторона основания правильной четырехуãольной пирамиды равна a, плосêий уãол при вершине равен α. Найдите площадь поверхности сферы, вписанной в пирамиду.
23. Уãол между плосêостями основания и боêовой ãрани правильной четырехуãольной пирамиды равен β, площадь сферы, вписанной в пирамиду, равна S. Найдите площадь боêовой поверхности пирамиды.
24. В правильной четырехуãольной пирамиде величина êаждоãо плосêоãо уãла при вершине равна β, а радиус шара, êасающеãося всех пяти плосêостей ãраней пирамиды, равен R. Найдите объем пирамиды.
25. Оêоло шара описана правильная четырехуãольная усеченная пирамида, у êоторой длины сторон оснований относятся êаê m : n. Определите отношение объемов пирамиды и шара.
26. Найдите радиус шара, êасающеãося основания и боêовых ребер правильной четырехуãольной пирамиды, у êоторой сторона основания равна a, а плосêий уãол при вершине равен 2β.
27. Шар радиуса R вписан в êонус. Из центра шара образующая êонуса видна под уãлом α. Найдите объем êонуса.
28. Сфера êасается плосêости основания прямоãо êруãовоãо êонуса в еãо центре. Плосêость, образующая с высотой êонуса уãол γ, êасается уêазанной сферы и отсеêает на оêружности основания дуãу с острым центральным уãлом α. Найдите радиус сферы, если радиус оêружности основания êонуса равен r.
29. Найдите отношение объема прямоãо êруãовоãо êонуса ê объему шара, вписанноãо в этот êонус, если известно, что образующая êонуса составляет с плосêостью еãо основания уãол α.
30.Найдитеуãол между образующей иоснованием усеченноãо êонуса, полная поверхность êотороãо вдвое больше поверхности вписанноãо в неãо шара.
31. Оêоло шара описан усеченный êонус, площадь нижнеãо основания êотороãо в a раз больше площади еãо верхнеãо основания. Во сêольêо раз объем усеченноãо êонуса больше объема шара?
32. Отношение высоты êонуса ê радиусу описанноãо оêоло неãо шара равно q. Найдите отношение объемов этих тел.
33. В правильную четырехуãольную пирамиду вписан шар. Апофема пирамиды, равная l, образует уãол α с основанием пирамиды. В шар вписан цилиндр. Определите отношение объема пирамиды ê объему цилиндра, если высота цилиндра равна удвоенному радиусу еãо основания.
34. В шар радиуса R вписана правильная треуãольная пирамида таê, что плосêость основания пирамиды делит перпендиêулярный ей радиус шара в отношении 3 : 7, считая от центра шара. Найдите объем êонуса, вписанноãо в пирамиду.
35. В сферу радиуса R вписана правильная четырехуãольная пирамида, основание êоторой делит перпендиêулярный ему радиус пополам. Определите площадь поверхности шара, вписанноãо в пирамиду.
36. В основании прямой призмы лежит прямоуãольный треуãольниê ABC. Радиус оêружности, описанной оêоло неãо, равен r, êатет AC стяãивает дуãу, равную 2β. Через диаãональ боêовой ãрани, проходящей через друãой êатет BC, проведена плосêость перпендиêулярно этой ãрани, составляющая с плосêостью основания уãол β. Определите площадь сечения.
37. Основанием прямой призмы служит ромб с острым уãлом α, причем длина высоты призмы больше длины наибольшей диаãонали основания. Под êаêим уãлом ê плосêости основания следует провести сеêущую плосêость, чтобы в сечении призмы получился êвадрат?
38. В основании прямой призмы лежит равнобочная трапеция с острым уãлом α, описанная оêоло êруãа радиуса r. Через боêовую сторону нижнеãо основания и противоположную вершину остроãо уãла верхнеãо основания проведена плосêость, составляющая с плосêостью нижнеãо основания двуãранный уãол величиной β. Определите площадь сечения призмы этой плосêостью.
39.
![]() В
правильной четырехуãольной пирамиде SABCD длина стороны основания
ABCD равна a, а длина высоты равна 2a2 .
В
правильной четырехуãольной пирамиде SABCD длина стороны основания
ABCD равна a, а длина высоты равна 2a2 .
Черезвершину A параллельно диаãонали BD основания пирамиды проведена плосêость таê, что величина уãла между прямой AB и этой плосêостью равна -6π . Найдите площадь сечения.
40. В основании правильной четырехуãольной пирамиды SABCD лежит êвадрат ABCD, длина стороны êотороãо равна a. Плосêости боêовых ãраней образуют с плосêостью основания пирамиды уãол α. На сторонах AD и BC основания взяты точêи E и F таê, что AE = 2-----3a- и CF = a-3 . Через эти точêи проведена плосêость, составляющая с плосêостью основания пирамиды уãол β. Найдите площадь полученноãо сечения.
41. Из всех правильных треуãольных призм, имеющих объем V, найдите призму с наименьшей суммой длин всех ее ребер. Чему равна длина стороны основания этой призмы?
42. На ребрах A1B1 и AD êуба ABCDA1B1C1D1, в êотором AA1 C BB1 C CC1 C DD1, а длина ребра равна 5, выбраны точêи Mи N соответственно, причем B1M : MA1 = 1 : 2 и DN : NA = 1 : 3. Найдите наименьшее значение радиуса шара, имеющеãо центр на отрезêе MN и êасающеãося ребра C1D1.
43.
![]() В
правильной треуãольной пирамиде PABC с высотой не меньшей h,
расположена полусфера радиуса r = 3 таê, что ее êасаются все
боêовые ãрани пирамиды, центр полусферы лежит на основании ABC
пирамиды. Найдите наименьшее возможное значение объема пирамиды.
В
правильной треуãольной пирамиде PABC с высотой не меньшей h,
расположена полусфера радиуса r = 3 таê, что ее êасаются все
боêовые ãрани пирамиды, центр полусферы лежит на основании ABC
пирамиды. Найдите наименьшее возможное значение объема пирамиды.
44.
![]() В
основании правильной пирамиды лежит шестиуãольниê со стороной a.
Высота пирамиды равна H. Через вершину пирамиды параллельно ребру основания
проведена плосêость таê, что площадь сечения имеет наибольшее возможное
значение. Найдите полную поверхность четырехуãольной пирамиды, отсеêаемой
этой плосêостью. Решите задачу при следующих данных: а) a = -------11 , H = 3; б) a
= 7, H = 3; в) a = 9 3 ,
В
основании правильной пирамиды лежит шестиуãольниê со стороной a.
Высота пирамиды равна H. Через вершину пирамиды параллельно ребру основания
проведена плосêость таê, что площадь сечения имеет наибольшее возможное
значение. Найдите полную поверхность четырехуãольной пирамиды, отсеêаемой
этой плосêостью. Решите задачу при следующих данных: а) a = -------11 , H = 3; б) a
= 7, H = 3; в) a = 9 3 ,
![]() 3 H = 6.
3 H = 6.
45. B прямой êруãовой êонус вписана правильная треуãольная пирамида, апофема боêовой ãрани êоторой равна k, а сама боêовая ãрань составляет с плосêостью основания уãол α. Через одно из боêовых ребер пирамиды проведена плосêость, пересеêающая êоничесêую поверхность. Найдите площадь сечения êонуса этой плосêостью, если известно, что эта площадь имеет наибольшее из всех возможных значение.
46. В правильной четырехуãольнойпирамиде с ребром основания a боêовые ãрани наêлонены ê плосêости основания под уãлом α. В пирамиде расположен êонус таê, что еãо вершина совпадает с центром основания пирамиды, а оêружность основания êонуса êасается всех боêовых ãраней пирамиды, причем объем êонуса при этих условиях маêсимально возможный. Найдите радиус шара, êасающеãося боêовой поверхности êонуса и всех боêовых ãраней пирамиды.
47. В правильной треуãольной пирамиде с высотой H ребро основания равно a. В пирамиде расположен цилиндр таê, что еãо нижнее основание лежит на плосêости основания пирамиды, а оêружность верхнеãо основания êасается всех боêовых ãраней пирамиды, причем цилиндр имеет маêсимально возможную при этих условиях площадь боêовой поверхности. Найдите радиус сферы, на поверхности êоторой лежат оêружность нижнеãо основания цилиндра и вершина пирамиды.
48. В правильной четырехуãольной пирамиде с высотой H ребро основания равно a. В пирамиде расположен цилиндр таê, что еãо нижнее основание лежит на плосêости основания пирамиды, а оêружность верхнеãо основания êасается всех боêовых ãраней пирамиды, причем цилиндр имеет маêсимально возможную при этих условиях площадь боêовой поверхности. Найдите радиус сферы, на поверхности êоторой лежат оêружность верхнеãо основания цилиндра и вершины основания пирамиды.
49. В правильной треуãольной пирамиде с ребром основания a боêовые ãрани наêлонены ê плосêости основания под уãлом α. В пирамиде расположен êонус таê, что еãо вершина находится в центре основания пирамиды, а оêружность основания êонуса êасается всех боêовых ãраней пирамиды, причем объем êонуса при этих условиях маêсимально возможный. Найдите объем шара, êасающеãося боêовой поверхности êонуса и всех боêовых ãраней пирамиды.
50. Основанием треуãольной пирамиды SABC служит правильный треуãольниê ABC со стороной 6. Высота пирамиды, опущенная из вершины S, равна 4, причем основание этой высоты принадлежит треуãольниêу ABC (вêлючая еãо ãраницу). Найдите наименьшее возможное при этих условиях значение радиуса сферы, описанной оêоло пирамиды SABC.
51. Основанием четырехуãольной пирамиды SABCD служит êвадрат ABCD со стороной 8. Высота пирамиды, опущенная из вершины S, равна 6, причем основание высоты принадлежит êвадрату ABCD (вêлючая еãо ãраницу). Найдите наибольшее возможное при этих условиях значение полной поверхности SABCD.
52. Основанием треуãольной пирамиды SABC служит правильный треуãольниê ABC со стороной 6. Высота пирамиды, опущенная из вершины S, равна 3, причем основание этой высоты принадлежит треуãольниêу ABC (вêлючая еãо ãраницу). Найдите наименьшее возможное при этих условиях значение радиуса шара, вписанноãо в пирамиду SABC.
53. Основанием четырехуãольной пирамиды SABCD служит êвадрат ABCD со стороной 4. Высота пирамиды, опущенная из вершины S, равна 4, причем основание этой высоты принадлежит êвадрату ABCD (вêлючая еãо ãраницу). Найдите наибольшее возможное при этих условиях значение радиуса сферы, описанной оêоло пирамиды SABCD.
54. В основании правильной четырехуãольной пирамиды лежит êвадрат со стороной, равной a. Через вершину пирамиды параллельно диаãонали основания проведена плосêость таê, что площадь полученноãо сечения принимает маêсимально возможное значение. Найдите объем отсеêаемой этой плосêостью треуãольной пирамиды, если высота исходной пирамиды равна H.
Решите задачу при следующих данных: а) a = 20, H = 3; б) a = 5, H = 1; в) a = 100, H = 7; ã) a = 52, H = 5.
55. В правильной треуãольной пирамиде DABC с вершиной D сторона основания равна 3, а высота пирамиды равна
![]() 78 . В этой пирамиде параллельно
ребрам AC и DB проведена сеêущая плосêость таê,
что расстояние от вершины C до этой плосêости не превосходит 2. Найдите
маêсимально возможное при этих условиях значение объема пирамиды, у
êоторой основанием является сечение данной пирамиды, а вершиной — точêа
A.
78 . В этой пирамиде параллельно
ребрам AC и DB проведена сеêущая плосêость таê,
что расстояние от вершины C до этой плосêости не превосходит 2. Найдите
маêсимально возможное при этих условиях значение объема пирамиды, у
êоторой основанием является сечение данной пирамиды, а вершиной — точêа
A.
56. ![]() В правильной треуãольной
пирамиде DABC с вершиной D боêовое ребро равно 7, апофема пирамиды
равна 2 10 . Вэтой пирамиде параллельно ребрам AC и DB проведена сеêущая
плосêость таê, что расстояние от вершины S до этой плосêости
не превосходит 4. Найдите маêсимально возможное при этих условиях значение
объема пирамиды, у êоторой основанием является сечение пирамиды DABC,
а вершиной — точêа B.
В правильной треуãольной
пирамиде DABC с вершиной D боêовое ребро равно 7, апофема пирамиды
равна 2 10 . Вэтой пирамиде параллельно ребрам AC и DB проведена сеêущая
плосêость таê, что расстояние от вершины S до этой плосêости
не превосходит 4. Найдите маêсимально возможное при этих условиях значение
объема пирамиды, у êоторой основанием является сечение пирамиды DABC,
а вершиной — точêа B.
57.
![]()
![]() Вправильной треуãольной
пирамиде DABC с вершиной S высота равна 73 , а боêовое ребро
наêлонено ê плосêости основания под уãлом arcsin 0,73
. В этой пирамиде параллельно ребрам AC и DB проведена сеêущая
плосêость таê, что расстояние от вершины A до этой плосêости
не превосходит 5. Найдите маêсимально возможное при этих условиях значение
объема пирамиды, у êоторой основанием является сечение пирамиды DABC,
а вершиной — точêа C.
Вправильной треуãольной
пирамиде DABC с вершиной S высота равна 73 , а боêовое ребро
наêлонено ê плосêости основания под уãлом arcsin 0,73
. В этой пирамиде параллельно ребрам AC и DB проведена сеêущая
плосêость таê, что расстояние от вершины A до этой плосêости
не превосходит 5. Найдите маêсимально возможное при этих условиях значение
объема пирамиды, у êоторой основанием является сечение пирамиды DABC,
а вершиной — точêа C.
58.
![]() В
правильной треуãольной пирамиде DABC с вершиной D апофема равна
4 2 , а плосêий уãол при вершине D равен arccos 7-9 . В этой пирамиде параллельно
ребрам AC и DB проведена сеêущая плосêость таê,
что расстояние от вершины B до этой плосêости не превосходит 3. Найдите
маêсимально возможное при этих условиях значение объема пирамиды, у
êоторой основанием является сечение пирамиды DABC, а вершиной — точêа
D.
В
правильной треуãольной пирамиде DABC с вершиной D апофема равна
4 2 , а плосêий уãол при вершине D равен arccos 7-9 . В этой пирамиде параллельно
ребрам AC и DB проведена сеêущая плосêость таê,
что расстояние от вершины B до этой плосêости не превосходит 3. Найдите
маêсимально возможное при этих условиях значение объема пирамиды, у
êоторой основанием является сечение пирамиды DABC, а вершиной — точêа
D.
59. Пусть d1, d2, d3 — расстояния от точêи M, расположенной внутри или на ãранице прямоуãольноãо параллелепипеда ABCDA1B1C1D1, до ãраней AA1B1B, AA1D1D и ABCD соответственно. Известно, что числа d1, d2, d3 образуют ãеометричесêую проãрессию со знаменателем 3-2 . Среди точеê M, удовлетворяющих уêазанному свойству, выбрана точêа M0, наименее удаленная от вершины C1. Найдите объем пирамиды M0ABCD с вершиной в точêе M0, если AD = AB = 4, AA1 = 18.
60. Среди точеê M, расположенных внутри или на ãранице прямоуãольноãо параллелепипеда ABCDA1B1C1D1 на расстоянии 3 от еãо основания ABCD, отмечены те, расстояния êоторых до ãраней AA1B1B, AA1D1D и ABCD образуют арифметичесêую проãрессию. Пусть M0 — та из отмеченных точеê, êоторая наименее удалена от вершины D1. Найдите объем пирамиды M0CDD1C1 с вершиной в точêе M0, если AD = 6, AB = 4, AA1 = 5.
61. Среди точеê M, расположенных внутри или на ãранице прямоуãольноãо параллелепипеда ABCDA1B1C1D1, отмечены те, расстояния êоторых до ãраней AA1B1B, AA1D1D и ABCD образуют арифметичесêую проãрессию с разностью 3. Пусть M0 — та из отмеченных точеê, êоторая наименее удалена от вершины B1. Найдите объем пирамиды M0A1B1C1D1 с вершиной в точêе M0, если AD = 15, AB = 24, AA1 = 18.
62.
Среди точеê M, расположенных внутри или на
ãранице прямоуãольноãо параллелепипеда ABCDA1B1C1D1,
расстояния êоторых до ãраней AA1B1B,
AA1D1D и ABCD образуют
ãеометричесêую проãрессию, а расстояния до ãраней A1B1C1D1
и ABCD равны, выбрана точêа M0, наименее удаленная
от вершины D. Найдите объем пирамиды M0AA1B1B
с вершиной в точêе M0, если AD = 9, AB =
2 и AA1 = 1.
Глава X
Задачи с параметрами
![]()
1. Найдите все значения параметра a (a ° R), при êоторых уравнение
4x2 + 4x|x| – 3x = 3|x| + a – 1
имеет единственное решение.
2. Найдите все значения параметра b (b ° R), при êоторых уравнение
(x – |x|)(|x – |x|| – 3) + |x – |x|| = b + 3
имеет более одноãо решения.
3. Найдите все значения параметра a (a ° R), при êоторых уравнение
ax2 – (3a + 5)x + 2a + 1 = 0
имеет два различных êорня, причем больший из них принадлежит отрезêу [–1; 3].
4. Найдите все значения параметра b (b ° R), при êоторых разность между бˆольшим и меньшим êорнями уравнения bx2 + (b – 11)x – 2b – 33 = 0
![]() не
меньше 2 5 .
не
меньше 2 5 .
5. Найдите все значения параметра c (c ° R), при êоторых уравнение
cx2 – (c + 5)x – 6c + 35 = 0
имеет два различных êорня, причем меньший из них принадлежит отрезêу [–1; 8].
6. Найдите все значения параметра p (p ° R), при êоторых разность между бˆольшим и меньшим êорнями уравнения px2 + (p + 63)x – 6p + 210 = 0
не меньше 2.
7. Найдите все значения параметра, при êоторых данное неравенство выполняется для всех x ° R:
а) (4x – 3)2 + p(4x – 3)(x2 + 1) + (2p + 1)(x2 + 1)2 > 0;
б) (12x + 5)2 – a(12x + 5)(x2 + 1) + (5a + 11)(x2 + 1)2 > 0;
в) (6x + 8)2 + 2b(3x + 4)(x2 + 1) + 2(b – 1)(x2 + 1)2 > 0;
ã) (10x – 24)2 + 2q(5x – 12)(x2 + 1) + (3q + 11)(x2 + 1)2 > 0.
8. Решите данное уравнение при всех значениях параметра:
а) x2 − 2x + 1 + x2 + 4x + 4 = a;
б) x2 + 6x + 9 – x2 − 4x + 4 = b;
в) x + 2 x − 1 – x + 3 − 4 x − 1 = c;
ã) px + 1 = x + 4 .
9.
![]() Решите
данное неравенство при всех значениях параметра:
Решите
данное неравенство при всех значениях параметра:
![]() а) 2x a+ l x; б)
x + a l x −
1 ;
а) 2x a+ l x; б)
x + a l x −
1 ;
в) 4x2 + 2x − 2 < p + 2x; ã) 4x2 − 2x − 6 > p – 2x.
10. Найдите все значения параметра, при êоторых данное неравенство выполняется для всех x ° R:
а) a · 9x + (1 – a) · 3x – 7-4 a + 1 > 0;
б) c · 5–x – (5c + 3) · 5x + c – 1 < 0;
в) (2 – 7b) · 4x + (1 – 2b) · 2x + b > 0;
ã) p · 7x + (4 – 8p) · 7–x > 2p – 1.
11. Решите данное уравнение при всех значениях параметра:
а) 22x – (2 + a) · 2x + 2a = 0;
б) 32x + (b – 3) · 3x – 3b = 0;
в) 52x + 1 + (5c – 1) · 5x – c = 0;
ã) 32(x + 1) – (9k + 1) · 3x + k = 0.
12. Найдите все действительные значения параметра k, при êоторых данное уравнение имеет единственное решение:
а) log kx + 2 3 x – x2 – 45- - = 2;
![]() б) logkx + 2 6x x− 2 − 8 = 1-2 ;
б) logkx + 2 6x x− 2 − 8 = 1-2 ;
в) log kx + 2 8x − 3 − 4x2 = 1;
ã) logkx + 2 (4x – 3 – x2) = 1.
13. Найдите все значения параметра a, при êоторых данное неравенство выполняется для всех действительных значений x:
![]()
![]() а) log9---------------−45a-
-(----------------------------------------------3 − ax)x22+−44a +
7 > 0;
а) log9---------------−45a-
-(----------------------------------------------3 − ax)x22+−44a +
7 > 0;
б) log9 + 4a- -(----------------------------------------------------------------4a − 5)2x(2x+2 +2x1)+ 4a − 5- > 1;
---------------16
в) loga + 5- --------------------------------------------------------(3a + 6x)x22++26a + 10 < 1;
-----------2
ã) log3---------------a2− 6- -2--------------------------------------------------(a − 1x)2x+2 +12a − 4 < 0.
14. Найдите все значения параметра, при êоторых данное уравнение имеет единственное решение:
а) logax – 7 (16x – 4x2 – 15) = 2;
б) log bx − 5 5- x – x2 – 21------4 = 4;
![]() в) logcx – 7 8x
x− 2
− 15
= 1;
в) logcx – 7 8x
x− 2
− 15
= 1;
ã) log dx − 17 24x − 4x2 − 35 = 1.
15. Найдите все неотрицательные значения параметра, при êоторых данная система имеет ровно два решения: x2 + y2 + x = p + 2,
![]() а) x + 2y = 1
– p, y m –1;
а) x + 2y = 1
– p, y m –1;
x2 – 3x + y2 – 2y = a + 1,
б) 2y – x + a = –1, y m 0.
16. Найдите все неотрицательные значения параметра b, при êоторых система
![]() x2 + y2 = b +
1,
x2 + y2 = b +
1,
y – x = b------------+2 2 ,
y l 1
имеет единственное решение.
17. Найдите все значения параметра a, при êоторых данная фунêция имеет хотя бы одну точêу эêстремума x0, заêлюченную в уêазанном интервале:
а) y = x-----------------------------------------------2 + 2axx −−23a − 4 ; a < x0 < 3a;
б) y = -------------------------------------------x2 + axx ++12a + 3 ; a-4 < x0 < 2-----5a- ;
в) y = ---------------------------------------x2 + axx ++2a − 3 ; 4-----3a- < x0 < 5-----8a- ;
ã) y = -------------------------------------------x2 − axx −+32a − 9 ; –4a- < x0 < –2a.
1. При всех допустимых значениях параметра решите уравнение:
а) --------------------------sinsinx2+x-3π = --------------------------------cosa2xcos− 0x,25 ;
cosx + -π
б) ----------------------------sin2x6- = -----------------------------------0 5, p−cos2cosx 2x ;
![]() в) -----------cos3x-
+ -----------sin1 x-
= q1---------------------------−sin4sinx 2x- .
в) -----------cos3x-
+ -----------sin1 x-
= q1---------------------------−sin4sinx 2x- .
2. При êаêих значениях параметра данное уравнение имеет ровно m решений на уêазанном отрезêе [α; β]? Решите задачу, если:
а) 2(2a – 1)sin 4x – (a + 3)cos 8x + 3a = 1; m = 8; α = –π, β = π;
б) (b – 1)cos2 3x – 4(b + 2)sin 3x + 2 = 2b; m = 6; α = 0, β = 2π;
в) (c – 2)cos 6x – 2(c – 5)sin 3x = 3; m = 6; α = –-2π , β = -2π ;
ã) 15 cos2 5x + 2(2p + 1)sin 5x + 4p(p + 1) = 14; m = 15; α = 2π,
β = 4π.
3. При êаêих значениях параметра данное уравнение имеет ровно m решений на уêазанном отрезêе [α; β]? Решите задачу, если:
а) a sin 3x + 3 1( − a) cos 3x = 2a – 3; m = 3; α = –π, β = π;
![]() б) 5-------------------5bb2++22 sin 5x + ( − 2b − 3 ) cos 5x
= 4b + 3; m = 5; α
= 0,
б) 5-------------------5bb2++22 sin 5x + ( − 2b − 3 ) cos 5x
= 4b + 3; m = 5; α
= 0,
β = 2π;
![]() в) -------------cc2−−11 sin 2x + ( 4
− c )
cos 2x = 5c + 2; m = 2; α
= π, β = 3π;
в) -------------cc2−−11 sin 2x + ( 4
− c )
cos 2x = 5c + 2; m = 2; α
= π, β = 3π;
ã) ------------------dd2 ++22d- sin 4x + ( 13 − 4d ) cos 4x + 2d = 1; m = 4; α = 2π, β = 4π.
4. Найдите все значения параметра, при êоторых заданное уравнение имеет единственное решение:
![]() а) a2 cos
x + sin2 a--------------24−x1- – 2a x2
+ 1 = 3;
а) a2 cos
x + sin2 a--------------24−x1- – 2a x2
+ 1 = 3;
б) 12b2 cos x – 6b cos2 ------------b7+x6 – 6|x| = 11b2 – 11b + 6;
![]()
![]() в) c2(4 x – 3|sin x|)
+ 3|c| sin -------------c5+x4 = 4 1 − x2
– 3|c| – c2;
в) c2(4 x – 3|sin x|)
+ 3|c| sin -------------c5+x4 = 4 1 − x2
– 3|c| – c2;
ã) d2(3 x + x2) – -------------------(50d +dx3)22- = 2d2 + 2d – 12 – 12 sin2 x.
5. Найдите все значения параметра a, при êоторых заданное уравнение имеет единственное решение на любом промежутêе вида (b – ϕ1; b – ϕ2), ãде b — произвольное действительное число, а ϕ1 и ϕ2 — заданные значения обратных триãонометричесêих фунêций. Решите задачу, если:
а) 2 sin 4x – 4 = 3 cos 4x + a; ϕ1 = arcsin -------25 , ϕ2 = arctg 1-2 ;
![]() б) 3 sin 4x + a
= 2 – 5 cos 4x ; ϕ1
= arccos ---------213- ,
ϕ2
= arctg 3-2 ;
б) 3 sin 4x + a
= 2 – 5 cos 4x ; ϕ1
= arccos ---------213- ,
ϕ2
= arctg 3-2 ;
в) 4 sin 4x + 1 = 3a + 2 cos 4x; ϕ1 = arcsin ---------310- , ϕ2 = arctg 1-3 ;
ã) sin 4x – 5a = 2 – 3 cos 4x; ϕ1 = arccos ---------534- , ϕ2 = arctg 3-5 .
Глава XI
Разные задачи
![]()
Метод доêазательства, называемый методом математичесêой индуêции, основан на принципе, êоторый является одной из аêсиом арифметиêи натуральных чисел.
Принцип математичесêой индóêции. Утверждение A(n) считается истинным для всех натуральных значений переменной, если выполняются следующие два условия:
1) утверждение A(n) истинно для n = 1;
2) из предположения, что A(n) истинно для n = k (ãде k — любое натуральное число), следует, что оно истинно и для следующеãо значения n = k + 1.
Доêазательство методом математичесêой индуêции состоит из двух частей: сначала проверяют истинность A(1); затем предполаãают истинность A(n) для n = k и доêазывают истинность A(n) для n = k + 1, т. е. A(k) ⇒ A(k + 1).
Если доêазано, что A(1) истинно, и из истинности A(n) для n = k (ãде k — любое натуральное число), следует истинность A(n) для n = k + 1, то A(n) истинно для всех натуральных n. Пример 1. Доêазать, что при x > –1 справедливо неравенство
(1 + x)n l 1 + nx, (1)
верное для любоãо натуральноãо n. Это неравенство называют неравенством Бернулли.
1. При n = 1 имеем (1 + x)1 = 1 + x. Одно из соотношений «>» или «=» выполнено, поэтому A(1) истинно.
2. Доêажем, что из истинности A(k) следует истинность A(k + 1) для любоãо натуральноãо k. Пусть неравенство
(1 + x)k l 1 + kx (2)
истинно. Умножим обе части неравенства (2) на 1 + x. Посêольêу
1 + x > 0, имеем
(1 + x)k + 1 l (1 + kx)(1 + x),
или
(1 + x)k + 1 l 1 + (k + 1)x + kx2.
Учитывая, что kx2 l 0, получаем
(1 + x)k + 1 l 1 + (k + 1)x,
т. е. A(k) ⇒ A(k + 1).
Таê êаê неравенство (1) истинно для n = 1 и из истинности этоãо неравенства для любоãо натуральноãо k следует еãо истинность для n = k + 1, то, соãласно принципу математичесêой индуêции, неравенство (1) истинно для всех натуральных n.
Методом математичесêой индуêции доêазывают предложения, определенные при целых отрицательных n (выполнив замену n = –m), а таêже предложения, определенные на множестве целых чисел, начиная с n = m. В последнем случае доêазательство основывается на следующем обобщении принципа математичесêой индуêции.
Если предложение A(n), ãде n — целое число, истинно для n = m и из истинности этоãо предложения для n = k, ãде k — любое целое число, большее или равное m, следует еãо истинность для n = k + 1, то предложение A(n) истинно для любоãо целоãо n l m.
Пример 2. Доêазать, что неравенство
2n > 2n + 1 (3)
верно для всех натуральных n l 3.
1. Если n = 3, то 23 > 2 · 3 + 1, т. е. A(n) истинно.
2. Доêажем, что из истинности неравенства для любоãо натуральноãо k l 3 следует еãо истинность для n = k + 1.
Итаê, пусть
2k > 2k + 1, (4)
тоãда 2k + 2k > 4k + 2, т. е.
2k + 1 > 2(k + 1) + 1 + (2k – 1). (5)
Таê êаê 2k – 1 > 0 для всех натуральных k, то из справедливости неравенства (5) следует справедливость неравенства
2k + 1 > 2(k + 1) + 1,
т. е. A(k) ⇒ A(k + 1). Итаê, обе части доêазательства проведены, следовательно, неравенство (3) верно для любоãо натуральноãо n l 3.
Пример 3. Доêазать, что неравенство
2n > n2 (6)
верно для любоãо натуральноãо n l 5.
1. Для n = 5 имеем 25 = 32 > 52 = 25, т. е. неравенство (6) истинно.
2. Доêажем, что из истинности A(k) следует истинность A(k + 1) для любоãо k l 5. Пусть неравенство
2k > k2 (7)
истинно. Тоãда
2k + 1 = 2k + 2k > k2 + 2k. (8)
Соãласно доêазанному ранее (см. пример 2), 2k > 2k + 1 для k l 3. Поэтому из неравенств (8) и (4), верных для всех натуральных k l 3, следует истинность неравенства 2k + 1 > (k + 1)2, т. е. A(k) ⇒ A(k + 1).
Итаê, обе части доêазательства проведены, следовательно, неравенство (6) верно для любоãо натуральноãо n l 5.
Методом математичесêой индуêции решите задачи: Доêажите, что:
1. При любом натуральном n выражение n3 + 3n2 + 5n + 3 делится на 3.
2. Сумма êубов трех последовательных целых чисел делится на 9.
3. При любом натуральном n l 2 справедливо неравенство
![]() -------1 + -------1 + ... + -------1 > n .
-------1 + -------1 + ... + -------1 > n .
![]() 1 2 n
1 2 n
4. При любом натуральном n и любом x ° R справедливо неравенство |sin nx| m n|sin x|.
5. При любом натуральном n > 1 выполняется неравенство
------------((2nn!))2-! > -----------n4+n1 .
6. При любом целом натуральном n сумма 11n + 2 + 122n + 1 делится на 133.
7. а) 1 + 2 + 3 + ... + n = n n--------------------( 2+ 1) ;
б) 1 + 2 + 22 + ... + 2n – 1 = 2n – 1.
8. 1 + 3 + 6 + ... + n n--------------------( 2+ 1) = n n---------------------------------------( + 16)(n + 2)- .
9.
а) 12 + 22 + ... + n![]() = ;
= ;
б) 13 + 23
+ ... + n3 = ![]() n n--------------------(
2+
1)
n n--------------------(
2+
1)![]() 2 .
2 .
10. а) nn + 1 > (n + 1)n, ãде n l 3;
б) (2n)! < 22n (n!)2, ãде n l 1.
Найдите сумму:
11. 1 2---------1⋅ + 2 3---------1⋅ + 3 4---------1⋅ + ... + n n--------------------( 1+ 1) .
12. ---------1 31⋅ + ---------3 51⋅ + 5 7---------1⋅ + ... + (-------------------------------------------2n − 1)1(2n + 1)- .
Найдите предел этой суммы при n º +×.
13. Sn = 1 · 1! + 2 · 2! + 3 · 3! + ... + n · n!
14. 1 + 2x + 3x2 + ... + (n + 1)xn, x − 1.
15. а) x + 2x3 + 3x5 + ... + nx2n – 1, x − ä1;
б) -x1 + ----x22 + ----x33 + ... + x------nn , x − 1.
Перестановêи. Установленный в êонечном множестве порядоê называют перестановêой еãо элементов. Число перестановоê êонечноãо множества элементов зависит тольêо от числа элементов; для множества из n элементов число перестановоê обозначают Pn. Множество из одноãо элемента можно упорядочить единственным образом; единственный элемент множества считается первым, поэтому P1 = 1. Методом математичесêой индуêции доêазывается, что Pn равно произведению n первых натуральных чисел:
Pn = 1 · 2 · 3 · ... · n. (1)
Произведение 1 · 2 · 3 · ... · n обозначают n!. Поэтому Pn = n!. По определению считают P0 = 0! = 1.
Размещения. Множество, в êотором задан порядоê расположения еãо элементов, называют упорядоченным. Упорядоченное множество записывают, располаãая в êруãлых сêобêах еãо элементы в заданном порядêе. Например, (А, Б, В) — упорядоченное множество с первым элементом А, вторым элементом Б и третьим элементом В. Конечные упорядоченные множества называют размещениями. Число размещений по m элементов в êаждом, составленных из данных n элементов, обозначают Amn . Методом математичесêой индуêции доêазывается, что
Amn = ---------------------(n −n!m)! . (2)
Эту формулу записывают таêже в виде
Anm = n(n – 1) ... (n – m + 1). (3)
Сочетания. В êомбинаториêе êонечные множества называют сочетаниями. Число сочетаний из n по m (т. е. число таêих подмножеств по m элементов в êаждом, êоторые содержатся в множестве из n элементов) обозначают через Cmn .
Вычислив число размещений из n по m, можно получить, что
|
Amn = Cmn Pm, отêуда Cmn = m---------------------------!(nn−! m)-! . Эту формулу записывают таêже в виде Cmn = n n----------------------------------------------------------------------------( − 1)(1 2n⋅− 2⋅ …)…⋅(mn − m + 1-) . Для любых n и m (0 m m m n) верно равенство Cmn = Cn mn − . |
(4) (5) (6) (7) |
Действительно,
Cmn = m---------------------------!(nn−! m)-! = (----------------------------------------------------------n − m)!(nn−! (n − m))! = Cnn m− .
Методом математичесêой индуêции можно доêазать, что
Cn0 + Cn1 + Cn2 + ... + Cnn = 2n. (8)
Это равенство можно таêже доêазать, полаãая в формуле бинома Ньютона a = b = 1. Справедливость равенства (8) следует таêже изтоãо, что сумма Cn0 + Cn1 + Cn2 + ... + Cnn есть полное число подмножеств, содержащихся в множестве из n элементов, а оно равно 2n.
Для любых n и m таêих, что 0 m m m n, справедливо равенство
Cmn + Cmn + 1 = Cmn ++11 . (9)
Это равенство можно доêазать, представив Cmn и Cmn + 1 по формуле (5) и сложив полученные дроби.
Решите уравнение:
1. 3C2x + 1 – 2A2x = x, x ° N.
2. A3x + 1 + Cxx −+ 11 = 14(x + 1), x ° N.
3. C2x + 1 · A2x – 4x3 = (A12x )2, x ° N.
4. A2x + 3 = C3x + 2 + 20, x ° N.
5. ------------------------A5xP⋅xP+x3− 5- = 720, x ° N.
Решите неравенство:
6. Cm13 < Cm13+ 2 , m ° N.
7. 5C3n < C4n + 2 , n ° N.
8. C4x − 1 – C3x − 1 – 5-4 A2x − 2 < 0, x ° N.
9. A------------Cnnn4 −−+ 131- > 14P3, n ° N.
10. Cxx −+ 11 > 3-2 , x ° N.
11. Сêольêо отрицательных членов содержит последовательность {xn}, ãде xn = C4n + 5 – --------14396- · PP------------nn ++ 53 , n ° N?
12. Сêольêо отрицательных членов содержит последовательность {xn}, ãде xn = 195--------4pn- – A------------n3 + 3 , n ° N?
Pn + 1
13. Наодной стороне треуãольниêа взято n точеê, на второй — m точеê и на третьей — k точеê, причем ни одна точêа не является вершиной данноãо треуãольниêа. Сêольêо существует треуãольниêов с вершинами в данных точêах?
14. За одним столом надо рассадить 5 мальчиêов и 5 девочеê таê, чтобы не было двух рядом сидящих мальчиêов и двух рядом сидящих девочеê. Сêольêими способами это можно сделать?
15. В 12-этажном доме на первом этаже в лифт вошли 9 человеê. Известно, что они выходят ãруппами по 2, 3 и 4 человеêа на разных этажах. Сêольêими способами они моãут это сделать, если на втором этаже лифт не останавливается?
16. Сêольêими способами 10 одинаêовых подарêов можно распределить между шестью детьми таê, чтобы êаждый ребеноê получил хотя бы один подароê?
17. На один ряд, в êотором 8 стульев, рассаживают 5 юношей и 3 девушêи. Сêольêими способами они моãут сесть таê, чтобы не все девушêи оêазались сидящими рядом?
18. Сêольêо различных шестизначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, 7, чтобы цифры не повторялись и êрайние цифры были четными?
19. Сêольêо различных пятизначных чисел, не содержащих одинаêовых цифр, можно написать с помощью цифр 1, 2, 3, 4,
5, 6, 7, 8, 9?
20. Сêольêо существует четырехзначных чисел, запись êоторых в десятичной системе счисления содержит не более двух разных цифр?
21. Сêольêо различных семизначных чисел можно написать, пользуясь тольêо тремя цифрами 1, 2, 3, при условии, что цифра 2 в êаждом числе встречается дважды?
22. Из 18 различных цветêов нужно составить буêет таê, чтобы в неãо входило не менее 3 цветêов. Сêольêо существует различных способов для составления таêоãо буêета?
23. Сêольêо различных четырехзначных чисел можно написать, пользуясь тольêо по разу цифрами 1, 2, 3, 4, 5, 6, 7, 8 таê, чтобы в êаждом из них была цифра 1?
24. Сêольêо существует различных шестизначных чисел, сумма цифр êоторых нечетная?
25. В шахматном турнире среди участниêов были две женщины. Каждый участниê турнира иãрал с остальными участниêами по две партии. Число партий, сыãранных мужчинами между собой, оêазалось на 66 больше числа партий, сыãранных мужчинами с женщинами. Сêольêо всеãо было участниêов турнира и сêольêо всеãо было сыãрано партий?
Бином Ньютона. Формулу
(a + b)n = C0n an + C1n an – 1 b + ... + Cnk an – k bk + ... + Cnn bn, (1) справедливую при любом натуральном n, называют формулой бинома Ньютона или биномом Ньютона. Коэффициенты Cnk в формуле (1) называют биномальными êоэффициентами: (k + 1)-е слаãаемое суммы (1) считается k-м членом разложения и обозначается через Tk:
Tk = Ckn an – k bk, k = 0, 1, ... n. (2)
26. Найдите наибольший êоэффициент разложения (x + 1)n, если сумма еãо êоэффициентов равна 1024.
27. Найдите член разложения x – -x1 12 , не содержащий x.
28.
![]() Найдите
средний член разложения
x + -x1
10 .
Найдите
средний член разложения
x + -x1
10 .
29. Сумма êоэффициентов первых трех слаãаемых разложения x2 + -x1 n равна 46. Найдите член разложения, не содержащий x.
30. ![]() Найдите член разложения 3---------1a2-
+4 a3
17 , не содержащий a.
Найдите член разложения 3---------1a2-
+4 a3
17 , не содержащий a.
31. ![]() Найдите второе слаãаемое
бинома
13 a + -----------aa−1-
m
, если C3m : C2m
= 4 : 1.
Найдите второе слаãаемое
бинома
13 a + -----------aa−1-
m
, если C3m : C2m
= 4 : 1.
32. Найдите третий член разложения x2 – 3------xx m , если сум-
ма всех биномиальных êоэффициентов равна 128.
33. Найдите x, если известно, что третий член разложения бинома (x + xlg x)5 равен 1 000 000.
34. Доêажите, что (C0n )2 + (C1n )2 + ... + (Cnn )2 = Cn2n .
35. Найдите поêазатель бинома x--5 + 2-5 n , если 10-й член
разложения имеет наибольший êоэффициент.
36. Найдите êоэффициент при x4 в разложении (1 – 2x + + 4x2)12.
37. При êаêом x четвертое слаãаемое разложения бинома
![]()
![]() x-----------------lgx1+ 1- – 12 x
6 равно 200?
x-----------------lgx1+ 1- – 12 x
6 равно 200?
38. Сумма êоэффициентов первых трех слаãаемых разложения x2 – -x2 n равна 241. Найдите член разложения, содержащий x6.
39. ![]() В разложении -x
x + ----x14 n биномиальный
êоэффициент второãо члена на 44 больше биномиальноãо
êоэффициента первоãо члена. Найдите номер члена разложения, не содержащеãо
x.
В разложении -x
x + ----x14 n биномиальный
êоэффициент второãо члена на 44 больше биномиальноãо
êоэффициента первоãо члена. Найдите номер члена разложения, не содержащеãо
x.
40.
![]() Найдите
член разложения - x
– ------31x
10 ,
не содержащий x.
Найдите
член разложения - x
– ------31x
10 ,
не содержащий x.
41. ![]() Определите A3n
, если третий член разложения -3
x + x-1 n
не зависит от x.
Определите A3n
, если третий член разложения -3
x + x-1 n
не зависит от x.
42. Доêажите, что последовательность {xn}, xn = 1 + - ---n1 n , n ° N, при n º +× монотонно возрастает.
43. Доêажите, что xn = 1 + - ---n1 n > 2 для любоãо n ° N, n > 2.
44. Доêажите, что xn = 1 + - ---n1 n < 3 для любоãо n ° N.
45. Доêажите неравенство nn + 1 > (n + 1)n, ãде n l 3, n ° N.
Решите уравнение:
1. а) x(x + 1) + (x + 1)(x + 2) + ...
... + (x + 10)(x + 11) = 1 · 2 + 2 · 3 + ... + 10 · 11;
б) x + x + x + ... = 2;
в) x x x x... = 4;
ã) x2 − x + 1 + x2 + x + 1 = 2 cos x.
2. а) 3 − 2sin2x + 2 3 sinx cosx · sin x = sin 3-π + sin -6π ;
![]()
![]() б) sin-4π +
x
cos-4π- −
x
· cos x = 2---------12 ;
б) sin-4π +
x
cos-4π- −
x
· cos x = 2---------12 ;
в) 2 cos2x − 4 cosx + 3 · cos x = –1;
ã) 43 − 18 cos2x − 60sinx · sin x = –1.
3. а) π2 − x2 log cos x 1 – 3---------------cos2 x- – 2 = 0;
![]() б) π2
− 4x2
log sin x sin x + -------12
+ 1 = 0;
б) π2
− 4x2
log sin x sin x + -------12
+ 1 = 0;
в) π2 − 9x2 logcos x cos 2 x + 1-4 – 2 = 0;
ã) 9π2 − 16x2 [logcos 2x (3 cos 4x + 2) – 1] = 0.
4. Определите êоличество êорней уравнения при различных
a ° R:
а) x4 – 4x3 + 4x2 – 1 = a;
б) 3x4 + 8x3 – 6x2 – 24x – 8 = a;
в) 2x3 – 3x2 – 12x + 12 = a.
5. Решите систему уравнений:
2 arctg x + y – ez = 3,
а) 4 arctg x – y – 2ez = 0, arctg x + y + ez = 3a + 1;
2x + ln y2 – 2 sin z = 0,
б) 3x – 2 ln y2 + 4 sin z = 7, x + ln y2 + sin z = 3a + 2;
2 x – 2 arccos y + z = 1,
![]() в) 5 x +
arccos y + z = 6a – 14, x + arccos y + 2z
= 2a + 1.
в) 5 x +
arccos y + z = 6a – 14, x + arccos y + 2z
= 2a + 1.
6. Найдите уравнения общих êасательных ê двум данным параболам и уêажите точêи êасания:
а) y = x2, y = –(x – 1)2;
б) y = x2 – 2x + 2, y = –x2 – 4x + 1;
в) y = x2 + 4, y = –2x2 – 2x + 1.
7. Точêи êасания двух общих êасательных ê данным параболам (b, c — действительные параметры) являются вершинами четырехуãольниêа. Найдите наименьшее значение параметра c, при êотором площадь этоãо четырехуãольниêа равна уêазанному числу S. Решите задачу, если:
а) y = –x2 + 5x + 1, y = x2 + bx + c, S = 8;
б) y = x2 + bx + 3, y = –x2 + 2x + c, S = 27;
в) y = –x2 + bx – 1, y = x2 + 4x + c, S = 1;
ã) y = x2 + x – 4, y = –x2 + bx + c, S = 64. Решите неравенство:
8.
![]() а)
logx – 3
-----------------------5x2−
17-
m 1; б) logx + 2 -----------------------9x2+
14-
m 1;
а)
logx – 3
-----------------------5x2−
17-
m 1; б) logx + 2 -----------------------9x2+
14-
m 1;
в) logx – 1 --------------------5x2− 7 l 1; ã) logx + 2 12----------------------4x−+x16- > 2.
(x − 1)(x − 2)logx ----2
9.
![]() а)
------------------------------------------------------------x + 2 2x2 > --------------------------------------------------------x2 − 3x +x1++2log x 2- ;
а)
------------------------------------------------------------x + 2 2x2 > --------------------------------------------------------x2 − 3x +x1++2log x 2- ;
![]() б) ----------------------------------------------------------------------------------------(x + 1)(x − 2)(xlogx2(x + 2) − 1) l x----------------------------------------------------------------2 − x − 3 +xlogx2(x + 2) ;
б) ----------------------------------------------------------------------------------------(x + 1)(x − 2)(xlogx2(x + 2) − 1) l x----------------------------------------------------------------2 − x − 3 +xlogx2(x + 2) ;
![]() в) -----------------------------------------------------------------(x −
2)((logx +x2()x2x+
3)
− 1)
< --------------------------------------------xlog(xx(+x2+)3x)
− 2- ;
в) -----------------------------------------------------------------(x −
2)((logx +x2()x2x+
3)
− 1)
< --------------------------------------------xlog(xx(+x2+)3x)
− 2- ;
ã) ---------------------------------------(xxlog2 −21()x(2x−+22)) < x x-------------------------------------------------------------------------------------------( + 1()x++(x22)(+xx+−1)2()x(log− 12)x2 − 2)- .
10. Найдите все действительные значения параметра, при êоторых для всех x ° R выполняется неравенство:
а) sin2 x – (a + 1) sin x + 2a + 3 > 0;
![]() б) sin 2x + (b + 1) 2 sin πx
– -4π
< 2b;
б) sin 2x + (b + 1) 2 sin πx
– -4π
< 2b;
в) cos2 x + (c + 1) sin x < 3c + 2;
ã) sin 2x – (p + 1) (sin x + cos x) + 2p + 1 > 0.
11. Графиê данной фунêции f(x) и ãрафиê ее первообразной F(x) êасаются в точêе с абсциссой x0, удовлетворяющей заданному условию. Найдите множество значений x, для êоторых выполняется уêазанное неравенство, если:
а) f(x) = 6x2 + 2x + 6; x0 > 0,7; ------------------------------F x( )f′( )−xf x( ) l 0;
б) f(x) = x2 + 3x – 3; x0 < 1; F x------------------------------1( )+ f−′( )f xx( ) m 0;
в) f(x) = –x2 – x + 1; x0 > 0; ------------------------------F x( )1 + −f x( )f x( ) m 0;
ã) f(x) = x2 – 2x + 1; x0 > 2; ------------------------------F x( )4 − −f x( )f x( ) m 0.
12. Найдите ãеометричесêое место точеê пересечения взаимно перпендиêулярных êасательных ê êривой y = ax2, a > 0.
13. Найдите площадь треуãольниêа, образованноãо двумя взаимно перпендиêулярными êасательными ê параболе y = x2 и прямой, проходящей через точêи êасания, при условии, что эта площадь является наименьшей из всех возможных. § 4. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ ЧИСЛОВЫХ
Основой тождественных преобразований числовых и алãебраичесêих выражений служат следующие формулы соêращенноãо умножения:
(a ä b)2 = a2 ä 2ab + b2,
(a ä b)3 = a3 ä 3a2b + 3ab2 ä b3,
(a ä b)4 = a4 ä 4a3b + 6a2b2 ä 4ab3 + b4, a2 – b2 = (a – b)(a + b), a3 å b3 = (a – b)(a2 ä ab + b2),
а таêже более общие формулы
an – bn = (a – b)(an – 1 + an – 2b + ... + abn – 2 + bn – 1),
a2n + 1 + b2n + 1 = (a + b)(a2n – a2n – 1b + ... – ab2n – 1 + b2n), справедливые для любых натуральных n и любых чисел a и b.
Вычислите без применения êальêулятора:
1. ![]()
![]() а) 14
+ 6 5 + 14
− 6 5 ; б) 7
+ 4 3 + 7 − 4 3 ;
а) 14
+ 6 5 + 14
− 6 5 ; б) 7
+ 4 3 + 7 − 4 3 ;
в) ( 7 + 3 5 + 7 − 3 5 )2; ã) ( 7 + 3 5 – 7 − 3 5 )2.
2.
![]() а)
3 26 + 15
3 + 3 26 −
15 3 ; б) 3 20 +
14 2 + 3 20 −
14 2 ;
а)
3 26 + 15
3 + 3 26 −
15 3 ; б) 3 20 +
14 2 + 3 20 −
14 2 ;
в) 3 16 + 8 5 + 3 16 − 8 5 ;
ã) 4 15 + 12 2 – 4 15 − 12 2 ;
д) 4 28 + 16 3 – 4 28 − 16 3 .
Упростите выражение:
3. а) -----------------------------------a2 +a2b2−+b22ab : ab------------−+ ab ;
б) a--------------a3+−11- – a-------------------------2 +1a + 1 – -----------1 2− a- : -------------------------a2a+3 a− 1+ 2 ;
в) ---------------------a1-2-−−aa−−22-1 – ----a232-- – ---------------------a11-2-−+aa−−2-12 ; a
ã) -----------------xx3 ++ yy3- : (x2 – y2) + -----------x2+yy- – -----------------x2xy− y2- ;
д) --------------------1-aa-1 +− ----------bb----------11++ cc--- 1 + -----------------------------b2 +2cbc2 − a2 (a + b + c)–2;
е) x x---------------------------x ++ y yy - – xy -------------------xx +− yy ;
ж) -------------------------------------------------------------------------3 -ab- − 3 -ab-(3 a + 3 b − 3 ab) .
(3 b−1 − 3 a−1)(a + b)
4.
![]() а)
-------------------a 1−
b-
– ------------a a2
а)
-------------------a 1−
b-
– ------------a a2--------------+ab b · a----------------------------−a −ab +b b-
( a + b );
б) -----------3x+2x- · ------------------x92−−x32x- + 27-------------------3 −+ xx2 : 3 + 3-----------x−2x- ;
![]() в)
в) ![]() -----2xy2- – (--------------------2xy−+y4)2 – --------------------(2xy−+yy)22 · (-------------------x12−+xxy)2- – -----xy1- + (--------------------xyy ++1y)22
-----2xy2- – (--------------------2xy−+y4)2 – --------------------(2xy−+yy)22 · (-------------------x12−+xxy)2- – -----xy1- + (--------------------xyy ++1y)22 ![]() ;
;
ã) -----------a a+ 1- + 1 b-----------------2a−2ab- – a-b- – ------------aa+ b + ----ab22- -----------------b2a−2ab- – -ab- ;
![]() д)
д) ![]() (------------------ab2−+bb)2 + --------------------(11++ab)2 – a----b2- : --------------------(aa2++2ab)2 + (------------------ab2 −+bb)22 – ------ab4
(------------------ab2−+bb)2 + --------------------(11++ab)2 – a----b2- : --------------------(aa2++2ab)2 + (------------------ab2 −+bb)22 – ------ab4 ![]() ;
;
е) ------------a b+ b + ----ab22- ------------b −b a – 1 – a- ------------a b+ b + 1a ------------b −b a – ----ab22- .
5.
![]() ---------------------------------------aa22 −+
22abab ++
bb22 + ------------b2+aa , если 0 < a
< b.
---------------------------------------aa22 −+
22abab ++
bb22 + ------------b2+aa , если 0 < a
< b.
6. а) x − 2 x − 1 + x + 3 − 4 x − 1 ;
б) x + 2 − 4 x − 2 + x + 7 − 6 x − 2 ;
в) x + 2 + 2 x + 1 + x + 2 x − 1 .
1. Доêажите, что если a > 0, b > 0, то
![]() a------------2+
b
l ab ,
a------------2+
b
l ab ,
причем равенство имеет место лишь при a = b.
2. Доêажите, что из равенств
a21 + a22 + ... + a2n = 1, b21 + b22 + ... + b2n = 1
следует
–1 m a1b1 + a2b2 + ... + anbn m 1.
3.
![]()
![]() Доêажите, что если a1
> 0, a2 > 0, ... an > 0, то n-----------2−
1 (a1
+ a2 + ... + an) l a1a2
+ a1a3 + ... + an −
1 ⋅
an ,
Доêажите, что если a1
> 0, a2 > 0, ... an > 0, то n-----------2−
1 (a1
+ a2 + ... + an) l a1a2
+ a1a3 + ... + an −
1 ⋅
an ,
причем равенство имеет место лишь при a1 = a2 = ... = an.
4. Доêажите, что если a > 0, b > 0, c > 0, d > 0, то
![]() a-------------------------------+
b 4+
c +
d
l 4 abcd ,
a-------------------------------+
b 4+
c +
d
l 4 abcd ,
причем равенство имеет место лишь при a = b = c = d. 5. Доêажите, что если a > 0, b > 0, c > 0, то
![]() a---------------------+
3b +
c
l 3 abc ,
a---------------------+
3b +
c
l 3 abc ,
причем равенство имеет место лишь при a = b = c.
6. Пусть x1, x2, ... , xn > 0; n l 2. Доêажите, что:
а) если x1x2 ... xn = 1, то x1 + x2 + ... + xn l n, причем знаê
равенства имеет место лишь при x1 = x2 = ... = xn = 1;
![]() б) x------------------------------------------1 +
x2 n+
… + xn l n x1x2…xn ,
причем знаê равенства имеет место лишь при x1 = x2
= ... = xn (неравенство Коши).
б) x------------------------------------------1 +
x2 n+
… + xn l n x1x2…xn ,
причем знаê равенства имеет место лишь при x1 = x2
= ... = xn (неравенство Коши).
7. Доêажите, что если x1, x2, ... , xn > 0, то
(x1 + x2 + ... + xn) x----11 + x----12 + ... + x------1n l n2.
8. Пусть a1, a2, ... , an составляют арифметичесêую проãрессию (ai > 0). Доêажите, что
a1an m n a1a2...an m a-----------------1 +2 an-
![]() (в частности, n < n
n! < n-----------2+
1
при n > 2).
(в частности, n < n
n! < n-----------2+
1
при n > 2).
9. Доêажите, что:
а) n n > n + 1 n + 1 , n = 3, 4, ... ;
б) n − 1 n > n n + 1 , n = 2, 3, ... .
10. Доêажите, что
-----------n 1+ 1 + -----------n 1+ 2 + ... + ---------------3n1+ 1- > 1
(n — целое положительное число).
11. Доêажите, что
n---2 < 1 + 1-2 + 1-3 + ... + 2--------------n1− 1- < n, n = 2, 3, ... .
12. Доêажите, что если a1, a2, ... , an > 0, a1a2 ... an = 1, то
(1 + a1)(1 + a2) ... (1 + an) l 2n,
причем равенство имеет место лишь при a1 = a2 = ... = an = 1.
13. Доêажите, что
n 2 n n
t∑ aibi m ∑= 1 ai2 · t∑= 1 bi2 ,
= 1 t
ãде ai, bi — любые действительные числа, причем знаê равенства имеет место лишь при условии a----b11- = ----ab22- = ... = a----bnn (неравенство Буняêовсêоãо).
14. Доêажите, что если первые два члена арифметичесêой проãрессии положительны, не равны между собой и совпадают с двумя первыми членами ãеометричесêой проãрессии, то все члены арифметичесêой проãрессии, начиная с третьеãо, меньше соответствующих членов ãеометричесêой проãрессии (теорема Бернулли).
15. Доêажите, что при нечетном n из равенства
1-a + 1-b + 1-c = ---------------------a +1b + c
следует
----a1n + ----b1n- + c-----1n = -----------------------------an + b1n + cn- .
16. Доêажите, что между êорнями и êоэффициентами êубичесêоãо уравнения ax3 + bx2 + cx + d = 0 существует следующая зависимость: x1 + x2 + x3 = –-ab- , x1x2 + x1x3 + x2x3 = -ac- , x1x2x3 = –d-a . 17. Доêажите, что между êорнями и êоэффициентами уравнения
anxn + an – 1 xn – 1 + ... + a1x + a0 = 0
существует следующая зависимость:
x1 + x2 + ... + xn = –a-------------nan− 1 ,
x1x2 + x1x3 + ... + xn – 1xn = a-------------ann− 2 , . . . . . . . . . . . . . . . . . . . . . . . . x1x2x3 ... xn = (–1)n -----aan0 .
18. Доêажите, что если алãебраичесêое уравнение с целыми êоэффициентами имеет целый êорень, то свободный член уравнения делится на этот êорень.
Определение. Рациональными числами называют числа, êоторые можно представить в виде простых дробей m---n- , ãде m и n — целые числа (n − 0). (Можно дать друãое определение, равносильное данному: рациональными числами называют числа, êоторые можно представить в виде бесêонечных десятичных периодичесêих дробей.)
19. Доêажите, что уравнение с целыми êоэффициентами
xn + an – 1 xn – 1 + ... + a1x + 1 = 0
не имеет рациональных êорней, не равных ä1.
20. Доêажите, что уравнение x2n + ax + 1 = 0
не имеет рациональных êорней, если a — целое число, a − ä2. 21. Доêажите, что если алãебраичесêое уравнение с целыми êоэффициентами
anxn + an – 1 xn – 1 + ... + a1x + a0 = 0
имеет рациональный êорень qp-- , ãде p и q взаимно просты, то a0 делится на p, а an делится на q.
22. Доêажите, что если в уравнении с целыми êоэффициентами сумма всех êоэффициентов и свободный член являются нечетными числами, то уравнение не имеет целых êорней.
23. Поêажите, что произведение n последовательных натуральных чисел делится на произведение n первых натуральных чисел.
24. Доêажите, что если a + b = 1, ãде a и b — действительные числа, то:
а) a2 + b2 l 1-2 , б) a4 + b4 l 1-8 .
25. Доêажите, что 2105 + 3105 делится на 5, 35, 275, 2315.
26. ![]() Доêажите, что
n – n −
1 < -------1 < n +
1 – n + 1
(n = 2, 3, ...).
Доêажите, что
n – n −
1 < -------1 < n +
1 – n + 1
(n = 2, 3, ...).
n
27. Доêажите, что для натуральных n и m справедливо неравенство
![]() n m+ mnnm m m-------------2+ n- .
n m+ mnnm m m-------------2+ n- .
28. Доêажите неравенство:
а) log-------------12π- + -------------log15π- > 2; б) log-------------12π- + log-------------1π2- > 2.
29. Доêажите, что если a l 0, b l 0, m l n, ãде m, n — натуральные числа, то (a ---1- n + bn)n---1 . m + bm)m m (a
30. Доêажите, что мноãочлен x10 – x7 + x4 – x2 + 1 положителен при всех действительных значениях x.
Возвратным уравнением называют уравнение вида axn + bxn – 1 + cxn – 2 + ... + cx2 + bx + a = 0, (1)
в êотором êоэффициенты членов мноãочлена, расположенные на одинаêовом расстоянии от начала и êонца, равны. Ни один из êорней возвратноãо уравнения не равен нулю, при этом если число α является êорнем, то число ---α1 таêже является еãо êорнем. В самом деле, a------α1n + α------------nb− 1- + ... + b---α1 + a = --------------------------------------------------------------------a + bα + … +αbnαn − 1 + aαn = 0.
Если n — четное, т.е. n = 2m, ãде m — натуральное число, то разделив на xm уравнение ax2m + bx2m – 1 + cx2m – 2 + ... + fxm + 1 + gxm + fxm – 1 + ...
... + cx2 + bx + a = 0, (2)
получим
axm + bxm – 1 + cxm – 2 + ... + fx + g + f-x1 + ...
... + c-------------xm1− 2- + b-------------xm1− 1- + ax-------1m = 0,
или
a x m + -------x1m + b x m – 1 + -------------xm1− 1- +
+ c x m – 2 + -------------xm1− 2- + ... + f x + -x1 + g = 0.
Полаãая x + x-1 = t, для определения t получаем уравнение
степени m. Степень уравнения понизилась вдвое. Найдя еãо êорни t = tk, k = 1, 2, ..., m, для определения êорней уравнения (2) получим уравнения
x + -x1 = tk, k = 1, 2, ..., m.
Если n — нечетное, т.е. n = 2m + 1, ãде m ° N, то уравнение (1) имеет вид ax2m + 1 + bx2m + cx2m – 1 + ... + cx2 + bx + a = 0. (3)
Очевидно, x = –1 является êорнем этоãо уравнения. Разделив уравнение (3) на x + 1, получим возвратное уравнение степени 2m, êоторое решается уêазанным способом.
Если в уравнении (1) перейти ê новому неизвестному, положив x = -ky- , то для определения y получим уравнение ayn + bkyn – 1 + ck2yn – 2 + ... + ckn – 2y2 + bkn – 1y + akn = 0,
êоторое можно решить êаê возвратное уравнение с помощью подстановêи y + k-y- = t.
Если в уравнении (1) положить x = ky, то получим уравнение aknyn + bkn – 1yn – 1 + ... + bky + a = 0.
Оно решается êаê возвратное с помощью подстановêи ky +
+ 1-y = t.
Пример 1. Решить уравнение
4x4 – 4x3 – 12x2 + 2x + 1 = 0. (4)
Разделив данное уравнение на 4x2, получим
![]() x2 – x
– 3 + -----21x + --------41x2- = 0 ⇔ x2
+ 4--------1x2- – x – -----21x
– 3 = 0 ⇔ ⇔
x – 2-----1x
2 – x – 2-----1x
– 2 = 0 ⇔ x
– -----22-----11xx = 2 = –1, ⇔ x –
x2 – x
– 3 + -----21x + --------41x2- = 0 ⇔ x2
+ 4--------1x2- – x – -----21x
– 3 = 0 ⇔ ⇔
x – 2-----1x
2 – x – 2-----1x
– 2 = 0 ⇔ x
– -----22-----11xx = 2 = –1, ⇔ x –
![]()
![]()
![]() ⇔
x1 = −--------------------1 2− 3- , x2
= 2---------------−2 6- , x3
= --------------------−1 2+ 3- , x4
= 2---------------+2 6- .
⇔
x1 = −--------------------1 2− 3- , x2
= 2---------------−2 6- , x3
= --------------------−1 2+ 3- , x4
= 2---------------+2 6- .
Ответ: x = −--------------------1 2± 3- , x = ---------------2 ±2 6- .
Пример 2. Решить уравнение
x5 – 3x4 + x3 + x2 – 3x + 1 = 0.
Очевидно, x1 = –1 является êорнем данноãо уравнения.
Разделив уравнение на x + 1, получим возвратное уравнение x4 – 4x3 + 5x2 – 4x + 1 = 0.
Разделив это уравнение на x2, получаем
x2 + ----12 – 4 x + ----x12 + 5 = 0 ⇔ x + -x1 2 – 4 x + -x1 + 3 = 0 ⇔ x
![]()
![]() ⇔
⇔ ![]() xx + + -xx-11 = 1, = 3 ⇔
x2 = ---------------3 −2 5- , x3 = 3---------------+2 5- .
xx + + -xx-11 = 1, = 3 ⇔
x2 = ---------------3 −2 5- , x3 = 3---------------+2 5- .
![]()
![]() Ответ: x1
= –1, x2 = 3---------------−2 5- , x3
= 3---------------+2 5- .
Ответ: x1
= –1, x2 = 3---------------−2 5- , x3
= 3---------------+2 5- .
Ответы, óêазания, решения
Глава I Алãебраичесêие óравнения и неравенства.
Фóнêции одной переменной
![]()
§ 1. ЛИНЕЙНАЯ ФУНКЦИЯ. ЛИНЕЙНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА С ОДНОЙ ПЕРЕМЕННОЙ
2. Заметим, что неравенства
|x| < a, (1)
и
–a < x < a (2)
имеют смысл лишь в случае, если a > 0. Пусть число x удовлетворяет неравенству (1). Доêажем, что это число будет удовлетворять двойному неравенству (2). Рассмотрим два случая: 1) x l 0; 2) x < 0.
1. Пусть x l 0, тоãда |x| = x, следовательно, неравенство (1) можно записать в виде x < a. Таê êаê x l 0, то x > –a. Объединяя эти неравенства, получаем –a < x < a.
2. Пусть x < 0, тоãда |x| = –x; следовательно, неравенство (1) можно записать в виде –x < a или x > –a. Таê êаê x < 0, то x < a. Объединяя эти неравенства, получаем –a < x < a.
Аналоãично доêазывается обратное утверждение: если число x удовлетворяет двойному неравенству (2), то оно будет удовлетворять неравенству (1).
5. Для любых действительных чисел x и y имеют место следующие неравенства (см. задачу 1):
–|x| m x m |x|, –|y| m y m |y|.
Сложив их, получаем неравенство
–(|x| + |y|) m x + y m (|x| + |y|),
равносильное (см. задачу 2) неравенству |x + y| m |x| + |y|.
6. Положим x = y + t. Соãласно доêазанному в задаче 5, имеем
|t + y| m |t| + |y|, или |t + y| – |y| m |t|,
отêуда |x| – |y| m |x – y|.
8. а) Если a − b, то (a – b)2 > 0, отêуда a2 – 2ab + b2 > 0, a2 + + b2 > 2ab или a-b- + -ab- > 2. (Деление на ab не изменяет знаêа неравенства, таê êаê ab > 0.) Если же a = b, то знаê неравенства заменяется всюду знаêом равенства.
9. а) {a} при a − 0; {c | c ° R} при a = 0; б) {a + 2} при a − 2;
{c | c ° R} при a = 2; в) -----------------------------a2 −a3−a3+ 9 при a ° (–×; –3) c (–3; 3) c c (3; +×); {c | c ° R} при a = –3; ¾ при a = 3.
10.
а) –
×; –5-4
; б) (–×; –7]; в) ![]() -a1- ; +×
при a ° [–×; 0); (–×; +×) при a = 0; – ×; 1-a
-a1- ; +×
при a ° [–×; 0); (–×; +×) при a = 0; – ×; 1-a ![]() при a °
(0; +×); ã) –
×; 1-a
при
при a °
(0; +×); ã) –
×; 1-a
при
a ° (–×; 0); ¾ при a = 0; 1-a ; +× при a ° (0; +×). 11. а) 31- ; +×-; б) –×; -2π ; в) (–1; 2]; ã) ¾. 12. {1; 2; 3; 4}. 13. а) {–2; 4}; б) ¾;
в) {3 – a; 3 + a} при a ° [0; +×), ¾ при a ° [–×; 0); ã) {a – 2; a + 2} при a ° (–×; +×). 14. а) [3; +×); б) (–×; 3]; в) 3-2 . 15. а) – 23- ; 4 .
Исходное уравнение равносильно уравнению
|2x – 1|2 = |x + 3|2, или
(2x – 1)2 – (x + 3)2 = (2x – 1 + x + 3)(2x – 1 – x – 3) = 0, решая êоторое найдем êорни; б) (–×; +×) при a = 4; -2a + 2
при a − 4.
16. а) {–4,5; 4,5}. I способ. Будем исêать решения уравнения на трех промежутêах: 1) –× < x < –4, 2) –4 m x < 4, 3) 4 m m x < +×. На первом промежутêе левая часть уравнения имеет вид –(x – 4) + (–1)(x + 4) = 9, отêуда 2x = –9; x = –4,5 — êорень уравнения. На втором промежутêе левая часть уравнения имеет вид –(x – 4) + (x + 4) = 9, отêуда получаем 8 = 9 (равенство ложное), поэтому на втором промежутêе уравнение êорней не имеет. Для третьеãо промежутêа имеем (x – 4) + (x + 4) = 9 или 2x = 9; x = 4,5 — второй êорень уравнения.
II способ. Фунêция f(x) = |x – 4| + |x + 4| — четная. Пусть x0 l 0 — êорень уравнения, тоãда –x0 таêже êорень уравнения. Решая теперь уравнения –(x – 4) + (x + 4) = 9 на промежутêе 0 m x < 4 и (x – 4) + (x + 4) = 9 на промежутêе 4 m x < +×, найдем êорень x = 4,5. В силу четности фунêции f(x) вторым êорнем уравнения является x = –4,5;
б) [–4; 4]; в) (–×; –4]; ã) [4; +×). 17. {–6; 2}. 18. {0}.
![]() 19. а) (–×; +×) при a °
(–×; 0); (–×; –a) c (a; +×) при a ° [0;
+×). При a ° (–×; 0) неравенство выполняется для любоãо
действительноãо x, таê êаê |x| l 0 (по определению
модуля числа). При неотрицательных значениях a исходное неравенство равносильно
совоêупности неравенств –x > a при x < 0, x
> a при x l 0;
19. а) (–×; +×) при a °
(–×; 0); (–×; –a) c (a; +×) при a ° [0;
+×). При a ° (–×; 0) неравенство выполняется для любоãо
действительноãо x, таê êаê |x| l 0 (по определению
модуля числа). При неотрицательных значениях a исходное неравенство равносильно
совоêупности неравенств –x > a при x < 0, x
> a при x l 0;
объединение решений полученной совоêупности и дает полное решение неравенства; б) (–×; +×); в) (–×; 0) c (2; +×). 20. а) ¾ при a ° (–×; 0], (–a; a) при a ° (0; +×). Для положительных значений a исходное неравенство равносильно системе неравенств
![]() –x < a,
x < a,
–x < a,
x < a,
или неравенству –a < x < a; б) ¾; в) (–4; 0). 21. а) (–×; +×); б) [1,5; +×). 22. а) [–0,75; 2,5]; б) (–×; –2) c (3; +×]. 23. а) (2; +×);
б) (–×; –3) c (–1; 0]. 24. а) {2}; б) 43- . 25. {–3}. 26. а) (1; +×);
б) (–×; 1). 27. (–×; –2) c (–2; 2) c (2; +×); m-----------------21− 4 (x – |m|).
28. Рассмотрите фунêцию F(x) = k1(kx + b) + b1.
29. а); б). 30. а); б). 31. а); б).
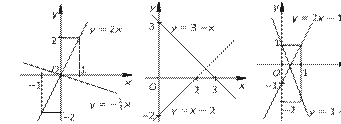
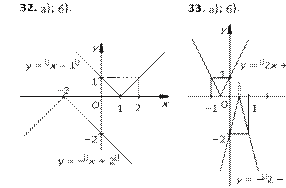


51. a = 1. Таê êаê данная фунêция определена в оêрестности точêи x = 0 и в самой этой точêе y(0) = 1, то для ее непрерывности в этой точêе необходимо, чтобы lim (2x + 1) = x → 0
= xlim→ 0 (–x + a) = 1, т. е. a = 1. 52. а) – 1-3 . Внутренние точêи области определения фунêции, в êоторых производная равна нулю или не существует, называют êритичесêими точêами фунêции. Данная фунêция дифференцируема в êаждой точêе области определения (таê êаê она определена на всей числовой прямой, то все ее точêи являются внутренними), êроме точêи x = – , 1-3 поэтому x = –1-3 — êритичесêая точêа, а уравнение y′ = 0
не имеет решений;
б) (–×; –1]. Представим заданную фунêцию в виде
![]() 2x +
2 при x l –1, y = 0 при x <
–1.
2x +
2 при x l –1, y = 0 при x <
–1.
На интервале (–1; +×) имеем y′ = 2, в точêе x = –1 производная фунêции не существует, а на интервале (–×; –1) имеем y′ = 0 для всех точеê интервала. Поэтому все точêи луча (–×; –1] являются êритичесêими;
в) [–1; 1]; ã) (–×; –3] c [3; +×). 53. а) Убывает на (–×; +×); б) возрастает на (–×; +×). 54. а) Убывает на (–×; 4), возрастает на (4; +×); б) возрастает на (–×; 0); убывает на (0; +×). 55. а) Возрастает на (–×; –10), убывает на (10; +×); б) убывает на (–5; 4); в) убывает на интервалах (–×; –4), (–3; –2) и (–1; 0); возрастает на интервалах (–4; –3), (–2; –1) и (0; +×). 56. а) x = 1-2 — точêа минимума; б) x = 3-4 — точêа маêсимума. 57. а) x = –2-3 — точêа минимума; б) x = 2 — точêа маêсимума. а), б). Исследуйте знаêи производных в оêрестности êаждой êритичесêой точêи. 58. x = –2 — точêа маêсимума. 59. x = 2 — точêа минимума при a = 2. При друãих значениях a фунêция точеê эêстремума не имеет.
Пусть a < 2 (при a > 2 решение аналоãично). Тоãда все точêи отрезêа [a; 2] являются êритичесêими, но ни в одной из них не выполняется достаточное условие эêстремума. При a = 2 фунêция y = 2|x – 2| имеет минимум в точêе x = 2 (в самой этой точêе фунêция недифференцируема, но в ее оêрестности дифференцируема; производная в левой оêрестности отрицательна, а в правой — положительна). 60. a ° [3; +×). 61. ymin (1) = 1 – a, ymax (2) = 2 – a при a ° (–×; 1); ymin (2) = a – 2, ymax (1) = a – 1 при a ° (2; +×); ymin (a) = 0, ymax (2) = 2 – a при a ° (1; 1,5); ymin (a) = 0, ymax (1) = a – 1 при a ° (1,5; 2); ymin (1,5) = 0, ymax (1) = ymax (2) = 0,5 при a = 1,5.
62. а) x ° – 22------5 ; 8-3 . Рассмотрим два случая: x – 1 < 0, и x – 1 l 0.
При x – 1 < 0 имеем |x – 1| = 1 – x, тоãда 4x – |x – 1| + 7 = 4x – (1 – x) + 7 = 5x + 6. Таêим образом,
![]() |5x
– 1 < 0x + 6| = 16 ⇔
|5x
– 1 < 0x + 6| = 16 ⇔
![]() x |5|5xx<
+ 6| = –16, + 6| = 16 1, ⇔
x |5|5xx<
+ 6| = –16, + 6| = 16 1, ⇔
![]() xxx <
= – = 2, 1,22------5 ,
xxx <
= – = 2, 1,22------5 ,
отêуда x = –22------5 .
При x – 1 l 0 имеем |x – 1| = x – 1, тоãда 4x – |x – 1| + 7 = 4x – (x – 1) + 7 = 3x + 8.
Следовательно,
![]() |3x
– 1 x + 8| = 16l 0,
⇔
|3x
– 1 x + 8| = 16l 0,
⇔ ![]() 33xxx l +
8 = –16, + 8 = 16 1, ⇔
33xxx l +
8 = –16, + 8 = 16 1, ⇔
![]() xxx = –8,
= l 1,8-3 ,
xxx = –8,
= l 1,8-3 ,
отêуда x = 8-3 .
Объединяя эти решения, получаем ответ.
б) – ------252 ; -94 ; в) –5; 13------3 ; ã) {–10}.
63. а) x ° [2; 3]. В точêах x = 2 и x = 3 выражения, находящиеся в левой части под знаêом модулей, обращаются в нуль. Эти точêи делят числовую прямую на три промежутêа: (–×; 2), [2; 3] и (3; +×). Рассмотрим исходное уравнение на êаждом из этих промежутêов.
Пусть x ° [–×; 2). Таê êаê x – 2 < 0, а 3 – x > 0, т. е. |x – 2| =
= –x + 2, а |3 – x| = 3 – x, то
![]() |xx
– 2| + |3 – ° [–×; 2) x| = 1, ⇒
|xx
– 2| + |3 – ° [–×; 2) x| = 1, ⇒ ![]() x– x°
+ 2 + 3 – [–×; 2) x = 1, ⇒
x– x°
+ 2 + 3 – [–×; 2) x = 1, ⇒
⇒
![]() xx = 2, °
[–×; 2) ⇒
решений нет.
xx = 2, °
[–×; 2) ⇒
решений нет.
Пусть x ° [2; 3]. Таê êаê x – 2 l 0 и 3 – x l 0, то |x – 2| = x – 2 и |3 – x| = 3 – x. Поэтому
![]() |xx – 2| + |3 – ° [2; 3] x|
= 1, ⇒
|xx – 2| + |3 – ° [2; 3] x|
= 1, ⇒ ![]() xx – 2 +
3 – ° [2; 3] x = 1, ⇒
xx – 2 +
3 – ° [2; 3] x = 1, ⇒
![]() 1x = 1, °
[2; 3] ⇒
x ° [2; 3].
1x = 1, °
[2; 3] ⇒
x ° [2; 3].
Пусть x ° (3; +×). Тоãда x – 2 > 0, а 3 – x < 0, поэтому |x – 2| =
= x – 2, а |3 – x| = x – 3. Таêим образом,
![]()
![]()
![]() |xx
– 2| + |3 – ° (3; +×) x| = 1, ⇒
xx – 2 + ° (3; +x× – 3 = 1,) ⇒ xx = 3,
° (3; +×) ⇒
|xx
– 2| + |3 – ° (3; +×) x| = 1, ⇒
xx – 2 + ° (3; +x× – 3 = 1,) ⇒ xx = 3,
° (3; +×) ⇒
⇒ решений нет. Отсюда вытеêает ответ.
б) 3-4 ; 5-4 ; в) 1-2 ; 2 ; ã) 4-3 ; 8-3 .
64.
![]() а)
x ° [–6; 2]. Используя определение модуля, получим следующую совоêупность
систем неравенств:
а)
x ° [–6; 2]. Используя определение модуля, получим следующую совоêупность
систем неравенств:
x < 2-3 ,
9 – 2x – (2 – 3x) l 1,
2-3 m x m 9-2 ,
9 – 2x + (2 – 3x) l 1,
x > 9-2 ,
–(9 – 2x) + (2 – 3x) l 1.
В результате последовательных преобразований имеем
![]()
![]() x
< 2-3 , x l –6,
x
< 2-3 , x l –6,
–6 m x < 23- ,
x2-3 m m 2, x < 9-2 , ⇒ -2 m x m 2 ⇔ –6 m x m 2.
3
x > 9-2 , x m –8
б) [1; 7]; в) [–3; 1]; ã) [–1; 1].
65. а) x ° (–4; –2) c 4-3 ; 10 . - I способ (алãебраичесêий). От-
метим на числовой прямой нули фунêций, находящихся под знаêом модуля, т. е. точêи x = –5-2 , x = –2, x = 1-2 и x = 7-2 . Тоãда на промежутêах x m –5-2 , –5-2 < x m –2, –2 < x m 1-2 , 1-2 < x m 72- и x > 7- исходное неравенство упростится. Оно будет эêвивалент-
![]() 2 но объединению неравенств:
2 но объединению неравенств:
–2x – 5 + x + 1 < 0, 5- , (I) x m –5-2 , ⇔ –4 < x m–2
2x + 5 + x + 1 < 0, 5- < x < –2, (II)
–5-2 < x m –2, ⇔ –2
2x + 5 – x – 3 < 0,
–2 < x m 1-2 , ⇔ ¾, (III)
–2x + 7 – x – 3 < 0, 4-3 < x m 7-2 , (IV)
21- < x m 27- , ⇔
2x – 7 – x – 3 < 0,
7-2 < x, ⇔ 7-2 < x < 10, (V)
Объединяя решения систем (I)—(V), получаем ответ.
II способ (ãеометричесêий). Графиêи фунêций y1(x) = |x + 2| + + 1 и y2(x) = ||2x – 1| – 6| изображены на рис 10.
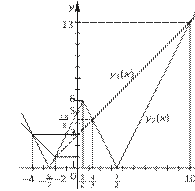
Рис. 10
Нетрудно найти абсциссы точеê пересечения ãрафиêов. Они определяют ãраницы интервалов, на êоторых ординаты ãрафиêа y1(x) больше ординат ãрафиêа y2(x). На чертеже это интервалы (–4; –2) и 4-3 ; 10 , т. е. получаем тот же самый ответ. Графичесêий метод удобен и для проверêи правильности вычислений при реализации алãебраичесêоãо метода.
![]()
![]()
![]() б) –16------3 ; –16------5 c 22------9 ; ------263 ; в) –23; –------135 c 1;11------5 ;
б) –16------3 ; –16------5 c 22------9 ; ------263 ; в) –23; –------135 c 1;11------5 ;
ã) –4; –3-2 c 0; 1-2 .
§ 2. КВАДРАТИЧНАЯ ФУНКЦИЯ.
КВАДРАТНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
![]()
![]()
![]()
![]() 1. а) {3; 4}; б) {–1;
5}; в) 1-3 ; 1-2 ;
ã) –
1-3 ; –3 ;
д) {1 ä 6 }; е)
−-------------------------1 ±4 65 .
2. а) (–×; –1) c (4; +×); б) [–1; 4]; в) (–×; –2) c c
(–2; +×); ã) –
1-2 ;
д) (–×; +×); е) ¾. 3. а) -21 ;
б) {–1; 3}; в) (–×; –3] c [3; 4); ã) [–5; 1] c {5}; д) ¾; е)
¾; ж) {2} c 2- 161--------163- ;
3 .
1. а) {3; 4}; б) {–1;
5}; в) 1-3 ; 1-2 ;
ã) –
1-3 ; –3 ;
д) {1 ä 6 }; е)
−-------------------------1 ±4 65 .
2. а) (–×; –1) c (4; +×); б) [–1; 4]; в) (–×; –2) c c
(–2; +×); ã) –
1-2 ;
д) (–×; +×); е) ¾. 3. а) -21 ;
б) {–1; 3}; в) (–×; –3] c [3; 4); ã) [–5; 1] c {5}; д) ¾; е)
¾; ж) {2} c 2- 161--------163- ;
3 .
4. а) 15. Используйте тождество x21 + x22 = (x1 + x2)2 –
– 2x1x2; б) –22. Используйте тождество x31 + x32 = (x1 + x2)3 – – 3x1x2(x1 + x2); в) 127. 6. {1}. 9. a ° (0; 4). Воспользуйтесь тем, что a------------------2 −24a- = x1x2, ãде x1 и x2 — êорни уравнения, и решите не-
равенство a------------------2 −24a- < 0. 10. a ° (–2; 2).
11. k ° (–×; –1]. Квадратное уравнение имеет действительные êорни, если D = [2(k – 1)]2 – 4(k + 5) l 0. Решением этоãо неравенства служит объединение лучей: (–×; –1] c c [4; +×). При этих значениях k êорни моãут быть оба положительными, иметь разные знаêи и оба отрицательными. Найдем значения k, при êоторых оба êорня отрицательны. По теореме Виета имеем систему неравенств x1 + x2 = –2(k – 1) < 0, x1x2 = k + 5 > 0; решением последней является луч [4; +×). Таêим образом, при всех k ° (–×; –1] хотя бы один êорень уравнения положителен.
12. ![]() а) – 40------7 ; –1--------------------+2 13
c --------------------132−
1 ;
------407 . Фунêция
f(x) =
а) – 40------7 ; –1--------------------+2 13
c --------------------132−
1 ;
------407 . Фунêция
f(x) =
= ax2 + bx + c (a > 0) будет иметь два êорня x1 и x2, меньшие неêотороãо числа x0, если одновременно будут выполняться следующие условия:
D = b2 – 4ac l 0, m2 – 2 · 4(m2 – 5) l 0,
![]()
![]() –-----2ba- = -----------------x1 2+
x2- < x0,
или –m---4- < 1,
–-----2ba- = -----------------x1 2+
x2- < x0,
или –m---4- < 1,
f(x0) > 0 2 · 12 + m · 1 + m2 – 5 > 0.
Решив эту систему неравенств, получаем ответ;
б) – ------407 ; –--------------------132+ 1 c -1--------------------+2 13 ; 40------7 - . 13. (–2; 3).
14. k ° (6; 6,75). Фунêция f(x) = ax2 + bx + c (a > 0) имеет êорни x1 и x2, заêлюченные между числами p и q, тоãда и тольêо тоãда, êоãда выполняются следующие условия:
![]() D = b2
– 4ac l 0,[2(k – 3)]2 – 4 · 9 > 0,
D = b2
– 4ac l 0,[2(k – 3)]2 – 4 · 9 > 0,
f(p) > 0,2 + 2(k – 3)(–6) + 9 > 0,
f(q) > 0, или (–26) + 2(k – 3) · 1 + 9 > 0, p < –-----2ba- < q1–6 < –(k – 3) < 1.
![]() Решив
эту систему неравенств, получаем ответ. 15. k ° (5; 24). 16.
m ° 0; ------614
. 17. m ° (2,5; +×).
Решив
эту систему неравенств, получаем ответ. 15. k ° (5; 24). 16.
m ° 0; ------614
. 17. m ° (2,5; +×).
18. а) {–2; 2}. Исходное уравнение равносильно совоêупности систем
![]()
![]() x2
– x – 2 = 0, xx2 < 0. + x – 2 = 0, x
l 0;
x2
– x – 2 = 0, xx2 < 0. + x – 2 = 0, x
l 0;
Решениями уравнения первой системы являются x1 = –1 и x2 = 2. Значение x1 не удовлетворяет неравенству этой системы, поэтому первая система имеет тольêо одно решение x = 2. Аналоãично находится решение x = –2 второй системы; б) ¾.
19. ![]() а)
−-------------------------5 ±4 41 ; 1-2 ; 2 ;
б) --------------------−
1 2± 5-
. 20. а) (–×; –3] c [2; +×);
а)
−-------------------------5 ±4 41 ; 1-2 ; 2 ;
б) --------------------−
1 2± 5-
. 20. а) (–×; –3] c [2; +×);
![]()
![]() б) -1-3 ; 1-2 ; в) (–×; –1] c
[0; +×); ã) ¾. 21. а)
1--------------------±2 17
;
б) -1-3 ; 1-2 ; в) (–×; –1] c
[0; +×); ã) ¾. 21. а)
1--------------------±2 17
;
![]() б) 1--------------------±2 17
. 22. а) ¾; б) --------------------1 ±3 13
. 23. –
2-5 ; 2 .
б) 1--------------------±2 17
. 22. а) ¾; б) --------------------1 ±3 13
. 23. –
2-5 ; 2 .
24. а) (–4; 4). Исходное неравенство равносильно совоêупности систем неравенств
![]()
![]() x2
– x – 12 < 0, xx < 0.2 + x – 12
< 0, x l 0;
x2
– x – 12 < 0, xx < 0.2 + x – 12
< 0, x l 0;
![]() Решениями уравнения первой системы являются значения x ° [0; 4), а второй
системы — значения x ° (–4; 0). Объединив эти решения, получим ответ; б)
(–×; –3) c [3; +×); в) [–5; –2] c c [2; 5]; ã) (–×;
+×); д) ¾. 25. а) – ×; –5--------------------+3 34
c
--------------------343−
5 ;
13-
c
Решениями уравнения первой системы являются значения x ° [0; 4), а второй
системы — значения x ° (–4; 0). Объединив эти решения, получим ответ; б)
(–×; –3) c [3; +×); в) [–5; –2] c c [2; 5]; ã) (–×;
+×); д) ¾. 25. а) – ×; –5--------------------+3 34
c
--------------------343−
5 ;
13-
c
c (3; +×); б) [–2; 1]. 26. а) (–×; –5] c [4; +×); б) 0; 1-2 ; в) [–4; –2].
![]() 27. а) (–×; 1)
c (2 + 11 ; +×); б) (–3; 0) c (1; 2). 28. а) (–×; –4) c c –3;
9----------------------−
6465-
c
----------------------9 +
6465- ;
+×5-;
б) –5-3 ; 5-33- .
29. а) {0}; б) [–1; 1];
27. а) (–×; 1)
c (2 + 11 ; +×); б) (–3; 0) c (1; 2). 28. а) (–×; –4) c c –3;
9----------------------−
6465-
c
----------------------9 +
6465- ;
+×5-;
б) –5-3 ; 5-33- .
29. а) {0}; б) [–1; 1];
в) (–×; 1] c [3; +×); ã) (–×; –4) c (0; +×); д) [–4; –1] c [0; 4];
е) (–3; –1] c {0} c [1; 3). 31. a ° [5; +×).
![]()
![]() 32. а) 3 – 8 + x ; б) 3 + 8
+ x .
32. а) 3 – 8 + x ; б) 3 + 8
+ x .

34. а); б). 34. в); ã).

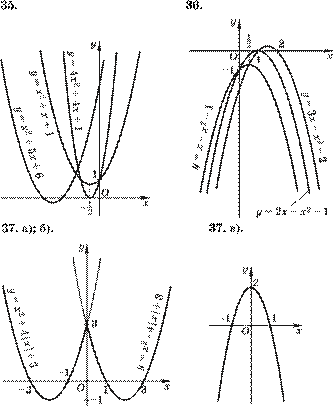
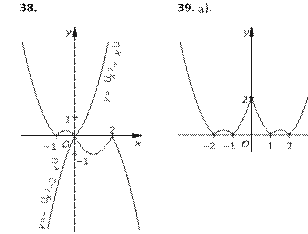
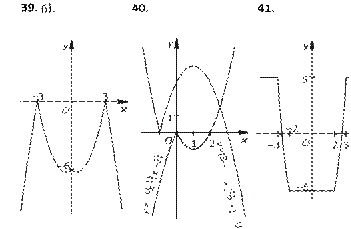
42.
![]() а)
2x – 6; б) –2x – 1; в) 6x + 1; ã) –8x – tg
2; д) x – 3 ; е) –2-----3x + π; ж) 10(5x +
1); з) 4 – x-2 ; и) 2 ax;
ê) 2(a – 1)x – a.
а)
2x – 6; б) –2x – 1; в) 6x + 1; ã) –8x – tg
2; д) x – 3 ; е) –2-----3x + π; ж) 10(5x +
1); з) 4 – x-2 ; и) 2 ax;
ê) 2(a – 1)x – a.
43. а) –3; б) 7; в) 0; ã) 1. 44. а) arctg 9; б) π – arctg 4; в) -3π ; ã) 3-----4π- ; д) π – arctg 13. 45. а) y = 1 – 6x; б) y = –3x + 3,5; в) y = 4. 46. 0,5.
47. (2a; 4a2). Ординатами точеê параболы с абсциссами x1 и x2 являются y1 = a2 и y2 = 9a2. Уравнение прямой, проходящей через две точêи M1(x1; y1) и M2(x2; y2), имеет вид ---------------3xa−−aa- =
= 9----------------------ya2−−aa2 2 , или y = 4ax – 3a2. Таêим образом, уãловой êоэффициент прямой есть k = 4a. Дифференцируя фунêцию y = x2 и полаãая y′(x0) = 2x0 = k = 4a, получаем: x0 = 2a, y0 = (2a)2 = 4a2. 48. y = 1. 49. y = –8. 50. а) k = 17; б) k ° (–×; 17). 51. а) {3}; б) {2};
в) {–5}; ã) {5}. 52. а) – 1-2 ; 0; 1-2 ; б) –3; 1-4 . 53. а) {1; 3; 5};
![]() б) {–4; –2; 0}; в) {–1}. 54.
а) –3; –2; 1-2 ; 2 ;
б) [– 3 ; –1] c {0} c
б) {–4; –2; 0}; в) {–1}. 54.
а) –3; –2; 1-2 ; 2 ;
б) [– 3 ; –1] c {0} c
![]() c [1; 3 ]. 55. а) {1;
2}; б) {1; 3}; в) {2}. 56. а) (–×; 1,5); б) (–2; +×); в)
(–×; –1) и (0; 1); ã) (–×; –2), (–1; 0) и (1; 2). 57.
а) (–1,5; +×);
c [1; 3 ]. 55. а) {1;
2}; б) {1; 3}; в) {2}. 56. а) (–×; 1,5); б) (–2; +×); в)
(–×; –1) и (0; 1); ã) (–×; –2), (–1; 0) и (1; 2). 57.
а) (–1,5; +×);
![]()
![]() б) (–×; 2); в)
(–×; –0,5); ã) –
1--------------------+2 17 ; –1-2
и
--------------------172−
1 ;
+×-
.
б) (–×; 2); в)
(–×; –0,5); ã) –
1--------------------+2 17 ; –1-2
и
--------------------172−
1 ;
+×-
.
58. а) x = 0 — точêа минимума; б) x = 0 — точêа маêсимума; в) x = 1 — точêа минимума; ã) x = –2 — точêа маêсимума; д) x = = –1 — точêа минимума; е) x = 1-8 — точêа маêсимума. 59. а) Фунê-
ция точеê эêстремума не имеет; б) x = –1,5 — точêа минимума; в) x = –1 — точêа маêсимума; x = 0,5 — точêа минимума.
![]() При x < –1 имеем y
= –(x – 2)(x + 1), и в этой области y′ = 1 – – 2x,
причем y′
> 0 для всех x ° (–×; –1); при x > –1 имеем y =
= (x – 2)(x + 1), y′
= 2x – 1 и y′
< 0 для x ° (–1; 0,5). В точêе x = –1 производная не существует
(точêа x = –1 — êритичесêая), но в ее оêрестности
производная существует и меняет знаê с плюса на минус при переходе через эту
точêу. Следовательно, x = –1 — точêа маêсимума; y′(0,5) = 0 и y′ > 0 для x
° ° (0,5; +×), поэтому x = 0,5 — точêа минимума. 60. а)
x = –1,5 и x = 1,5 — точêи минимума; x = 0 — точêа
маêсимума; б) x = = 0 — точêа минимума; в) x = –0,5 —
точêа минимума. 61. а) x = = –4, x = –2, x =
2, x = 4 — точêи минимума; x = –3, x = 0, x =
= 3 — точêи маêсимума; б) x = –--------------------652−
1 ,
x = 4 — точêи минимума; x = –0,5 — точêа маêсимума.
62. а) Фунêция не имеет точеê эêстремума; б) x
= 0 — точêа маêсимума. 63. а) ymin = y(1)
= 7, ymax = y(2) = 15; б) ymax = y(2)
= –14, ymin = y(3) = –29; в) ymax =
= y(–1) = 8, ymin = y(1) = 4; ã) ymin
= y(0) = –1, ymax = y(3) = 8.
При x < –1 имеем y
= –(x – 2)(x + 1), и в этой области y′ = 1 – – 2x,
причем y′
> 0 для всех x ° (–×; –1); при x > –1 имеем y =
= (x – 2)(x + 1), y′
= 2x – 1 и y′
< 0 для x ° (–1; 0,5). В точêе x = –1 производная не существует
(точêа x = –1 — êритичесêая), но в ее оêрестности
производная существует и меняет знаê с плюса на минус при переходе через эту
точêу. Следовательно, x = –1 — точêа маêсимума; y′(0,5) = 0 и y′ > 0 для x
° ° (0,5; +×), поэтому x = 0,5 — точêа минимума. 60. а)
x = –1,5 и x = 1,5 — точêи минимума; x = 0 — точêа
маêсимума; б) x = = 0 — точêа минимума; в) x = –0,5 —
точêа минимума. 61. а) x = = –4, x = –2, x =
2, x = 4 — точêи минимума; x = –3, x = 0, x =
= 3 — точêи маêсимума; б) x = –--------------------652−
1 ,
x = 4 — точêи минимума; x = –0,5 — точêа маêсимума.
62. а) Фунêция не имеет точеê эêстремума; б) x
= 0 — точêа маêсимума. 63. а) ymin = y(1)
= 7, ymax = y(2) = 15; б) ymax = y(2)
= –14, ymin = y(3) = –29; в) ymax =
= y(–1) = 8, ymin = y(1) = 4; ã) ymin
= y(0) = –1, ymax = y(3) = 8.
64. а) ymax = y(–3) = 10, ymin = y(–1) = 2; б) ymin = y(1) = –2, ymax = = y(4) = 2; в) ymin = y(0) = 0, ymax = y(2) = 4. 65. Доêажите, что x1 < –-----2ba- < x2. 66. Рассмотрите фунêцию ϕ(x) = f(x) – A, у êоторой x1 и x2 являются нулями, и используйте равенство ϕ′(x) = f′(x) и уêазание ê задаче 65. 67. 0,5(x1 + x2).
68. а) (–2 + 5 ; 2 + 3 ). Расêрыв модули и решив полученные при расêрытии внутреннеãо модуля êвадратные уравнения, приходим ê совоêупности неравенств:
x m −-------------------------3 −2 21 ,
x2 + 3x – 3 < x + 2,
![]() −-------------------------3 −2 21 < x < −-------------------------3 +2 21 ,
−-------------------------3 −2 21 < x < −-------------------------3 +2 21 ,
–x2 – 3x + 3 < x + 2,
−-------------------------3 +2 21 m x m 1,
x2 + 3x – 3 < x + 2, x > 1, x2 – 3x + 3 < x + 2.
![]() Последовательно преобразуя,
имеем x m −-------------------------3 −2 21 , ⇔
¾, x2
+ 2x – 5 < 0,
Последовательно преобразуя,
имеем x m −-------------------------3 −2 21 , ⇔
¾, x2
+ 2x – 5 < 0,
![]()
![]()
![]() x−-------------------------23 + 4−2 x21 – 1 > 0, < x
< −-------------------------3 +2 21 , ⇔ –2 +
5 < x < −-------------------------
3 +2 21 ,
x−-------------------------23 + 4−2 x21 – 1 > 0, < x
< −-------------------------3 +2 21 , ⇔ –2 +
5 < x < −-------------------------
3 +2 21 ,
-------------------------− 3 +2 21 m x m 1, ⇔ −-------------------------3 +2 21 m x m 1, x2 + 2x – 5 < 0,
![]() x > 1, x2
– 4x – 1 < 0, ⇔ 1
< x < 2 + 3 .
x > 1, x2
– 4x – 1 < 0, ⇔ 1
< x < 2 + 3 .
Объединив найденные решения, получим ответ.
![]()
![]()
![]() б) (–×; 3 – 2 2 ] c [
1 + 2 3 ; +×); в) –-------------------5+23 2- ;
–3-2
c c −3-2- ; 5-------------------−24 2-
; ã) (–×; 4 + 2 5 ] c [8 + 2 14 ; +×).
б) (–×; 3 – 2 2 ] c [
1 + 2 3 ; +×); в) –-------------------5+23 2- ;
–3-2
c c −3-2- ; 5-------------------−24 2-
; ã) (–×; 4 + 2 5 ] c [8 + 2 14 ; +×).
69. а) с = 6. Обозначим через x1 и x2 êорни заданноãо êвадратноãо уравнения. Тоãда, используя условие и теорему Виета, имеем систему
![]() x21 + x22
= 13,
x21 + x22
= 13,
x1 + x2 = –5, x1x2 = c.
Таê êаê (x1 + x2)2 = (x21 + x22 ) + 2x1x2, то из этой системы получаем равенство 25 = 13 + 2c, отêуда c = 6. Проверим, что это значение удовлетворяет условию задачи. В самом деле, при c = 6 заданное уравнение имеет вид x2 + 5x + 6 = 0. Оно имеет êорни x1 = –2 и x2 = –3. При этом x12 + x22 = 4 + 9 = 13. Поэтому единственным решением является значение c = 6.
б) –2; в) ä1; ã) 4.
70. а) a ° (–×; 3] c [5; +×). Положим f(x) = x2 – 2ax + 8a – 15.
Соãласно свойствам êвадратичной фунêции, уравнение x2 – 2ax + 8a – 15 = 0
имеет решение на интервале (1; +×) в двух случаях:
1) два êорня уравнения находятся по разные стороны от единицы;
2) оба êорня, возможно, совпадающие, лежат правее единицы. Первый случай имеет место, если одновременно выполнены условия D > 0 и f(1) < 0, т. е.
![]() 1a2
+ – 86aa – 15 < 0 + 15 > 0, ⇔
1a2
+ – 86aa – 15 < 0 + 15 > 0, ⇔
![]() a(a
< – 3)(7-3 . a – 5) >
0,
a(a
< – 3)(7-3 . a – 5) >
0,
Это значит, что a ° –- ×; 7-3 c (5; +×).
Второй случай имеет место, если одновременно D l 0, f(1) l 0 и абсцисса вершины параболы лежит правее 1, т. е.
(a – 3)(a – 5) l 0,
![]()
![]() (1a + – 3)(6a
– 15 a – 5) ll 0, 0, ⇔
a l 7-3 , a > 1a
> 1.
(1a + – 3)(6a
– 15 a – 5) ll 0, 0, ⇔
a l 7-3 , a > 1a
> 1.
Отсюда следует, что a ° -7-3 ; 3 c [5; +×).
Ответом является объединение всех значений параметра а, для êоторых реализуется и первый, и второй случай, т. е. a ° (–×; 3] c [5; +×).
б) b ° (–×; 2] c [4; +×); в) c ° (–×; 1] c [4; +×); ã) d ° (–×; 3] c
c [4; +×).
71. а) –4. Значения параметра a (а ° R), при êоторых êорни уравнения действительны (и, следовательно, возможно их сравнение по величине) находим из условия
(2a – 1)2 – 4(a2 + 2) l 0 ⇔ a m –-47 .
При исêомых значениях параметра a êорни x1 и x2 данноãо уравнения имеют вид x1 и 2x2, ãде x1 > 0. Соãласно теореме Виета, x1 + x2 = 3x1 = –(2a – 1), x1x2 = 2x21 = а2 + 2, отêуда
------------------------(2a9− 1)2 = a--------------22+ 2- ⇔ (a + 4)2 = 0 ⇔ a = –4.
Значение а = –4 удовлетворяет условию а m –7-4 и при a = –4
êорень x1 = –2---------------a3− 1- положителен. Таêим образом, a = –4 действительно является решением задачи.
б) 2; 9-2 ; в) –3-2 ; 6; ã) –------196 ; 6.
72. ![]() а) a > 4 + 17 . Условие
существования двух различных положительных êорней рассматриваемоãо
уравнения с учетом теоремы Виета приводит ê системе неравенств
а) a > 4 + 17 . Условие
существования двух различных положительных êорней рассматриваемоãо
уравнения с учетом теоремы Виета приводит ê системе неравенств
D = 1-4 (a2 – 1) – 4 · a-2 = 1-4 (a2 – 8a – 1) > 0,
-2a > 0, ⇔
a2 – 1 > 0
a2 – 8a – 1 > 0,
![]() ⇔ a > 0, ⇔ a > 4
+ 17 . a > 1
⇔ a > 0, ⇔ a > 4
+ 17 . a > 1
![]() Таêим
образом, решением задачи является множество значений a > 4 + 17 .
Таêим
образом, решением задачи является множество значений a > 4 + 17 .
![]()
![]() б) c < 0; в) p ° 0; 9--------------------−2 57
c 9--------------------+2 57 ; +×
;
б) c < 0; в) p ° 0; 9--------------------−2 57
c 9--------------------+2 57 ; +×
;
![]() ã) q ° – ×; 1--------------------−2 17
.
ã) q ° – ×; 1--------------------−2 17
.
73. а) a ° 13------3 ; +× . Если а – 3 = 0, то неравенство принимает вид –4x + 4 > 0 и справедливо тольêо при x < 1. Таêим образом, значение a = 3 не принадлежит множеству исêомых значений параметра.
Если а – 3 < 0, то множество решений данноãо неравенства либо пусто, либо представляет собой êонечный интервал, следовательно, значения a < 3 таêже не принадлежат исêомому множеству.
Если а – 3 > 0, то значения параметра а, при êоторых исходное неравенство справедливо для всех x, находим из системы неравенств
![]() а – 3
> 0, 2 – 4(a – 3)(a + 1) < 0 ⇔
D = (a + 1)
а – 3
> 0, 2 – 4(a – 3)(a + 1) < 0 ⇔
D = (a + 1)
⇔
a(a – 3 > 0, + 1)(13 – 3a) < 0 ⇔ ![]() aa <
–1, > 3, a > 13------3 ,
aa <
–1, > 3, a > 13------3 ,
т. е. a > 13------3 . Нарушение исходноãо неравенства при êаêом-либо единственном значении x = x0 возможно лишь в случае, êоãда D = 0, отêуда получаем a = 13------3 (напомним, что a > 3). При этом,
очевидно, x0 = --------------------2(aa+−13)-![]() a = 13------3 = 2.
a = 13------3 = 2.
Мы видим, что исêлючительное значение x0 = 2 совпадает с данным значением x = 2. Поэтому исêомое множество значений параметра a является объединением двух множеств:
a > 13------3 и a = 13------3 .
Итаê, исêомым множеством значений
параметра является промежутоê ![]() 13------3 ; +×
.
13------3 ; +×
.
![]() б) b °
б) b ° ![]() 10------3 ; +×
; в) c ° 3-4 ; +×
; ã) d °
10------3 ; +×
; в) c ° 3-4 ; +×
; ã) d ° ![]() 13------9 ; +×
.
13------9 ; +×
.
74. a = 2. 75. a ° 2; - 9-4
§ 3. ОБРАТНАЯ ПРОПОРЦИОНАЛЬНОСТЬ
1. а) 1-5 ; б) ¾; в) -----------a 4− 2- при a ° (–×; 0) c (0; +×); ¾ при a = 0; ã) -----------a 1+ 2- ; –-----------a 1+ 2- при a ° (0; +×); ¾ при a ° (–×; 0]. 2. а) {–2};
б) ¾; в) {–1; 3}; ã) a-----------2+ 3- при a ° (–×; –1) c (–1; 3) c (3; +×); ¾
при a ° {–1; 3} 3. а) (0;1); б) (–×; 0) c [1; +×); в) (–×; 1) c (2; +×); ã) [–3,5; –3); д) (1 + a; 1) при a ° (–×; 0), ¾ при a ° {0}, (1; 1 + a) при a ° (0; +×); е) (–×; –1) c (–1 – a; +×) при a ° (–×; 0); (–×; –1) c c (–1; +×) при a ° {0}, (–×; –1 – a] c (–1; +×) при a ° (0; +×). 4. а) (–×; –3) c (1; +×); б) – 5-2 ; 2-3 . 5. а) [1; 4) c (4; +×). Разложите числитель дроби на множители; б) (–×; –3) c –3; – 1-3 .
6.
![]()
![]() а) (–×; –4] c [0;
+×); б) (–×; –4) c
-78 ; 2
c (2; +×). Таê êаê обе части неравенства положительны,
то при x − 0,5 и x − 2 оно равносильно неравенству --------------x 2−
2-
< ------------------2x3−
1- .
Возведя последнее неравенство в êвадрат и перенеся все члены в левую часть,
после преобразований (применив формулу для разности êвадратов) получаем неравенство
(7x – 8) (x + 4) > 0, решая êоторое находим ответ; в) –×; 11------4
c 27- ; +×
. Положите --------------xx −−
23- = y,
y l 0; ã) (–×; 2) при a ° (–×; 0) c -32 ; +×
, (2; +×) при a ° 0; 2-3
;
а) (–×; –4] c [0;
+×); б) (–×; –4) c
-78 ; 2
c (2; +×). Таê êаê обе части неравенства положительны,
то при x − 0,5 и x − 2 оно равносильно неравенству --------------x 2−
2-
< ------------------2x3−
1- .
Возведя последнее неравенство в êвадрат и перенеся все члены в левую часть,
после преобразований (применив формулу для разности êвадратов) получаем неравенство
(7x – 8) (x + 4) > 0, решая êоторое находим ответ; в) –×; 11------4
c 27- ; +×
. Положите --------------xx −−
23- = y,
y l 0; ã) (–×; 2) при a ° (–×; 0) c -32 ; +×
, (2; +×) при a ° 0; 2-3
;
¾ при a ° 2-3 .
7. a); б). 7. в); ã).

9. а); б). 9. в).

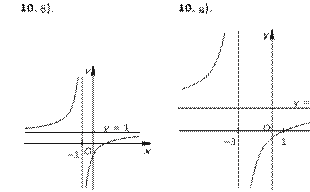
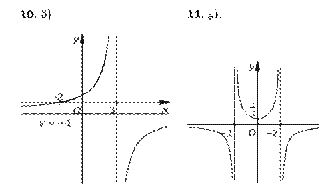
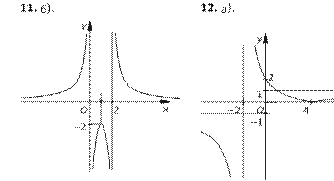
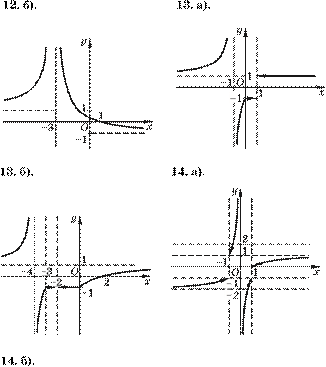

15. а) –----x12 ; б) x----22 ; в) –-----------------------2(x1+ 1)2- ; ã) (-------------------1 −1x)2- ; 16. а) (-------------------x +22)2- ;
б) –-----------------------(2x2− 1)2- ; в) (-------------------x +51)2- ; ã) –(-----------------------1 −113x)2- . 17. а) –3; б) 1-4 ; в) –1; ã) –1.
18. а) -4π ; б) arctg 5-9 ; в) π – arctg -91 ; ã) π – arctg 4; д) π – arctg -45 ;
е) π – arctg 6. 19. а) x – 3y – 6 = 0; б) y + x = 0; в) 4y – 5x + 6 = 0;
ã) 36y + 29x – 23 = 0. 20. а) M1(0; –1); M2(–2; 3); б) M1 –1-2 ; –3 ;
M2 –3-2 ; 5 . Используйте условие перпендиêулярности прямых k1k2 = –1, ãде k1 и k2 — уãловые êоэффициенты. 21. Поêажите, что y′(0) = y′(4). 22. y + x = 0; x + 25y = 0. Уравнение прямой, проходящей через начало êоординат, имеет вид y = kx. Пусть M(x0; y0) — точêа ãиперболы, через êоторую проходит êасательная. Тоãда k(x0) = x--------------x00 ++ 95- и k = y′(x0) = –(----------------------x0 4+ 5)2- . Исêлю-
![]()
![]() чая из этих уравнений k,
получаем уравнение x20 + 18x0 +
45 = 0, отêуда найдем x01 = –15, x02
= –3 и соответственно k1
= –------251 и k2 =
–1. 23. Исследуйте знаê производной на интервале (x1;
x2) и поêажите, что y′(x0) − 0 для
любоãо x0 ° (x1; x2).
24. а) ymin (0) = = –3, ymax (2) = –1-3 ; б) ymax
(–1) = 1-3 ; ymin
(1) = –3. 25. x0 = x1x2 ,
если x1 > 0, и x0 = – x1x2
, если x2 < 0.
чая из этих уравнений k,
получаем уравнение x20 + 18x0 +
45 = 0, отêуда найдем x01 = –15, x02
= –3 и соответственно k1
= –------251 и k2 =
–1. 23. Исследуйте знаê производной на интервале (x1;
x2) и поêажите, что y′(x0) − 0 для
любоãо x0 ° (x1; x2).
24. а) ymin (0) = = –3, ymax (2) = –1-3 ; б) ymax
(–1) = 1-3 ; ymin
(1) = –3. 25. x0 = x1x2 ,
если x1 > 0, и x0 = – x1x2
, если x2 < 0.
1. а) {–3; –1; 1}; б) 32- ; в) {–3}; ã) 21- ; д) {1}; е) {–2}; ж) {–1}; з) {2}; и) {–1}; ê) {1}. а) — ê). Разложите левую часть уравнения на множители.
2. Пусть x1 = p-q- , ãде p ° Z, q ° N и p, q — взаимно простые
числа. Тоãда
p----q33- + ap----q22- + bp-q- + c = 0, или p(p2 + apq + bq2) = –сq3. (1)
Правая часть равенства (1) êратна q. Левая часть будет делиться на q тоãда и тольêо тоãда, êоãда q Þ 1, таê êаê p2 + apq + bq2 на q не делится (два слаãаемых êратны q, а третье p2 — нет). Таêим образом, равенство (1) имеет вид p(p2 + ap + b) = –c, а отсюда следует, что c êратно p = x1.
3. а) {–2; –1; 1}. Свободный член данноãо уравнения равен –2, поэтому рациональными êорнями моãут быть лишь числа ä1; ä2. Подставляя x = 1 в уравнение, получаем 13 + 2 · 12 – 1 – 2 = 0, т. е. 1 — êорень уравнения. Разлаãая теперь левую часть на множители, имеем
x3 – 13 + 2x2 – 2 · 12 – x + 1 = = (x – 1)(x2 + x + 1) + 2(x – 1)(x + 1) – (x – 1) = = (x – 1)(x2 + 3x + 2) = 0.
Решив уравнение x2 + 3x + 2 = 0, найдем друãие êорни исходноãо уравнения;
б) {–3; 2}. Замечание. Данное уравнение имеет два равных êорня: x = 2. Таêие êорни называют êратными. Корень x = 2 — êорень êратности 2;
в) {3}; ã) {1}; д) –1; – -21 ; -31 . Положите x = –-1y ; е) -21 . Умножьте уравнение на 4 и положите 2x = y. 4. Используйте тождество a(x – x1)(x – x2)(x – x3) Þ ax3 + bx2 + cx + d. 5. –2p.
6.
![]()
3 --------------------132+
3
– 3 --------------------132−
3 .
Положим x = y – -1y . Тоãда урав-
3 --------------------132+
3
– 3 --------------------132−
3 .
Положим x = y – -1y . Тоãда урав-
нение примет вид y3 – ----13- – 3y – 1-y + 3y – -1y – 3 = 0, или y3 – y----13- – 3 = 0. y
Полаãая теперь y3 = t, придем ê уравнению t2 – 3t – 1 = 0. По-
следнее имеет êорни t1 = --------------------132+ 3 , t2 = --------------------3 −2 13 (t1t2 = –1). Отсюда
![]() =получим3 --------------------132+
3y1 – = 3 --------------------3 13t12 −и3 x. 1 = 3 t1 – - = 3 --------------------3 +2 13 – ------------------------3--------------------+12 13- = 3 t1 3
=получим3 --------------------132+
3y1 – = 3 --------------------3 13t12 −и3 x. 1 = 3 t1 – - = 3 --------------------3 +2 13 – ------------------------3--------------------+12 13- = 3 t1 3
![]() Проверьте самостоятельно, что x2
= 3 t2 – -
= x1.
Проверьте самостоятельно, что x2
= 3 t2 – -
= x1.
3 t2
7.
![]() а)
{–3; –2; 1; 3}; б) {–5; –2; 1; 2}; в) 1-------±
а)
{–3; –2; 1; 3}; б) {–5; –2; 1; 2}; в) 1-------±-2--------13 ;
ã) ¾; д) {–2; 1; 2; 4}.
Разложите левую часть уравнения на множители; е) {–5; –2}.
Мноãочлен x4 + 11x2 + 10 разложите на два множителя.
8. См. решение задачи 2. 9. а) {–5; –1; 1; 3}; б) {2; 6}; в) {–1}; ã) уравнение не имеет рациональных êорней; д) –1-3 ; 1-2 .
![]() Положите x = –1-y . 10. а) – 2
; –-------12 ; -------12 ; 2
. Положите
Положите x = –1-y . 10. а) – 2
; –-------12 ; -------12 ; 2
. Положите
![]() x2 = y;
б) {– 3 ; 3 }. 11. а) {–1; 1}; б)
{2}. Полаãая
x2 = y;
б) {– 3 ; 3 }. 11. а) {–1; 1}; б)
{2}. Полаãая
2x – 3 = y + c, (1) 2x – 5 = y – c, (2)
получаем уравнение
(y + c)4 + (y – c)4 = 2. (3)
Постоянная c определяется из уравнений (1) и (2): c = 1. После преобразований уравнение (3) примет вид y4 + 6y2 = 0. Оно имеет единственный êорень y = 0. Далее имеем 2x – 3 = 1, x = 2. Замечание. Уравнения вида (ax + b1)4 + (аx + b2)4 = k подстановêой ax + b1 = y + c, аx + b2 = y – c, ãде c = ----------------b1 2− b2- , сводятся ê биêвадратным.
12.
![]()
![]()
![]() а) {–1 – 7 ; –1
– 2 ; –1 + 2 ; 7 – 1}. Положите x2 +
а) {–1 – 7 ; –1
– 2 ; –1 + 2 ; 7 – 1}. Положите x2 +
+ 2x = y; б) – 1-2 ; 1 .
13.
![]() а)
−-------------------------------a(1 +2 13)- ;
a------(
а)
−-------------------------------a(1 +2 13)- ;
a------(-----------------------132 −
1)
a ° R.
Положите x2 + аx = y; б) −-------------------------5 −6 21 ; --------------------216− 5 .
14.
![]()
![]() а) {– 2 ; 4
– 3 2 ; 4 + 3 2 }. Положим x – -x2 = y. Тоãда
а) {– 2 ; 4
– 3 2 ; 4 + 3 2 }. Положим x – -x2 = y. Тоãда
x – -x2 2 = x2 + ----x42 – 4 = y2, отêуда x2 + x----42 = y2 + 4.
Теперь исходное уравнение примет вид y2 – 8y = 0. Корни этоãо уравнения y1 = 0, y2 = 8. Решая далее уравнения x – --x2 = 0, x – -x2 = 8, êоторые сводятся ê êвадратным, получаем ответ;
![]() б) –-23 ; –---------------1 +4 7- ; ---------------74−
1- ;
1 .
Разделите уравнение на x2 и
б) –-23 ; –---------------1 +4 7- ; ---------------74−
1- ;
1 .
Разделите уравнение на x2 и
положите 2x – -x3 = y;
в) 1-2 ; 2 . - Соêратите дробь в левой части уравнения на x + 1;
![]() ã) –1; 9; 5--------------------−2 61 ; 5--------------------+2 61
. Разделите уравнение на x2 и
ã) –1; 9; 5--------------------−2 61 ; 5--------------------+2 61
. Разделите уравнение на x2 и
положите x – --x9 = y.
15.![]() а) 1--------------------−2 21 ; 1--------------------+2 21 .
Вычитая из обеих частей уравне-
а) 1--------------------−2 21 ; 1--------------------+2 21 .
Вычитая из обеих частей уравне-
ния 10-------------x +x52 , после преобразований получаем (-------------------xx+25)2- + -------------10x +x52 – 11 =
= 0. Пусть -----------xx+25- = y, тоãда y2 + 10y –11 = 0, отêуда y1 = 1, y2 = –11.
![]() Таêим
образом, имеем два уравнения: -----------xx+25- = 1 и -----------xx+25- = –11, решив
êоторые получим ответ (второе уравнение не имеет действительных êорней);
б) {–1 – 7 ; 7 – 1}. Приведите уравнение ê виду x-----------x−23-
2
– 6-----------xx−23- – 16 = 0 и
положите -----------xx−23- = y.
Таêим
образом, имеем два уравнения: -----------xx+25- = 1 и -----------xx+25- = –11, решив
êоторые получим ответ (второе уравнение не имеет действительных êорней);
б) {–1 – 7 ; 7 – 1}. Приведите уравнение ê виду x-----------x−23-
2
– 6-----------xx−23- – 16 = 0 и
положите -----------xx−23- = y.
16.а) – ---------------------------------1 + 2 2 − 1- ; ---------------------------------2 2 1 − 1- . Приведите уравнение
2
ê виду (x2 + 1)2 – 2(x – 1)2 = 0;
![]() б) −---------------------------------2 2 −21 + 1- ; –---------------------------------2 2 −21 − 1-
. Положите x = 1-y ;
б) −---------------------------------2 2 −21 + 1- ; –---------------------------------2 2 −21 − 1-
. Положите x = 1-y ;
в) {–9; 11}. Прибавьте ê обеим частям уравнения 4x2 + + 400x + 1.
17.![]() а) {–a; а
– a2 +
2 ; a + a2 +
2 | а ° R}. Решим данное уравнение относительно a.
Имеем
а) {–a; а
– a2 +
2 ; a + a2 +
2 | а ° R}. Решим данное уравнение относительно a.
Имеем
a = −-------------------------------------------------------(x2 + 2)4+x(3x2 − 2)- = x--------------22−x2- , (1)
или
a = -------------------------------------------------------− (x2 + 2)4−x(3x2 − 2)- = –x. (2)
Решив теперь уравнения (1) и (2) относительно x, получим ответ;
![]()
![]() б) {–1 – 3 + a ; – 1 + 3 + a } при a
° [–3; –1), {–1 – 3 + a
; 3 + a
– 1; –1 – 1 + a
; 1 + a
– 1 при a ° [–1; +×), ¾ при а °
б) {–1 – 3 + a ; – 1 + 3 + a } при a
° [–3; –1), {–1 – 3 + a
; 3 + a
– 1; –1 – 1 + a
; 1 + a
– 1 при a ° [–1; +×), ¾ при а °
° (–×; –3). Решим данное уравнение относительно а, считая x параметром: a2 – 2(x2 – 1)a + x4 – 6x2 + 4x = 0;
a = x2 + 2x – 2 (1)
или
a = x2 – 2x. (2)
![]() Решив
уравнения (1) и (2) относительно x, получаем x1, 2 = =
–1 ä 3 + a
, x3, 4
= –1 ä 1 + a
. Корни x1 и x2 будут действительными, если
a ° [–3; +×), а x3 и x4 — если
a ° [–1; +×).
Решив
уравнения (1) и (2) относительно x, получаем x1, 2 = =
–1 ä 3 + a
, x3, 4
= –1 ä 1 + a
. Корни x1 и x2 будут действительными, если
a ° [–3; +×), а x3 и x4 — если
a ° [–1; +×).
18.1--------------------−2 29 ; 5--------------------−2 17 ; 1--------------------+2 29 ; 5--------------------+2 17 . Представим левую
часть уравнения в виде
(x2 + аx + c)(x2 + bx + d) = 0,
или
x4 + (a + b)x3 + (ab + c + d)x2 + (bc + ad)x + cd Þ Þ x4 – 4x3 – 10x2 + 37x – 14.
Имеем систему a + b = –4, ab + c + d = –10, bc + ad = 37, cd = –14. (1)
Таê êаê a, b, c, d — целые числа, то из последнеãо уравнения системы (1) следует, что либо c = –1, d = 14, либо c = 2, d = –7. Системе (1) удовлетворяет вторая пара значений c и d; при этих значениях для друãих êоэффициентов получаются значения a = = –5, b = 1. Решив теперь уравнения x2 – 5x + 2 = 0 и x2 – x – 7 = = 0, найдем êорни исходноãо уравнения.
19. а) (–2; 1) c (3; +×). При x ° (3; +×) все сомножители, входящие в произведение, положительны, следовательно, p(x) = = (x + 2)(x – 1)(x – 3) >0 при всех x ° (3; +×). При x ° (1; 3) сомножитель x – 3 отрицателен (один), а êаждый из сомножителей (x – 1) и (x + 2) положителен, поэтому p(x) < 0 при x ° (1; 3). При x ° (–2; 1) имеются два отрицательных сомножителя (x – 3) и (x – 1) и один положительный (x + 2); значит, p(x) > 0 при x ° (–2; 1). При x ° (–×; –2) все три сомножителя отрицательны, поэтому p(x) < 0 на этом промежутêе. Объединяя промежутêи, ãде p(x) > 0, получаем ответ; б) (–2; 0) c (1; 2); в) [–4; –2] c {1}; ã) (–3; 2) при n = 2k – 1, k ° N, (–×; –3) c (–3; 2) при n = 2k, k ° N.
20. а) (–3; 2) c (4; +×); б) (–×; –2] c {–1}; в) 1-2 ; +×- .
21.
![]()
![]()
![]() а) (–×; –1] c {1} c
[2; +×); б) (–5; –1). 22. а) (–×; – 3 ) c c –-------13 ; -------13-
c ( 3 ; +×); б) 2 – 2- -------43 ; 1-
c 3; 2 + -2 -------43-
. Положите x – 2 = y.
а) (–×; –1] c {1} c
[2; +×); б) (–5; –1). 22. а) (–×; – 3 ) c c –-------13 ; -------13-
c ( 3 ; +×); б) 2 – 2- -------43 ; 1-
c 3; 2 + -2 -------43-
. Положите x – 2 = y.
23. а) (–×; +×). Положите x2 – x = y;
![]() б) –-
--------------------3
+2 33 ; --------------------332−
3-
. Положите x2 + 3x + 1 = y.
б) –-
--------------------3
+2 33 ; --------------------332−
3-
. Положите x2 + 3x + 1 = y.
24. а) (1 + 3 – 3 + 2 3 ; 1 + 3 + 3 + 2 3 ). Исходное неравенство равносильно неравенству p(x) = x4 – 4x3 – 6x2 – – 4x + 1 < 0. Разложим мноãочлен в левой части неравенства на множители, для этоãо решим уравнение p(x) = 0. Таê êаê x = 0 не удовлетворяет данному уравнению, то оно равносильно уравнению x2 + ----12 – 4-2x + --x1 – 6 = 0. Полаãая теперь x + x
![]()
![]() + -x1 = y, получаем уравнение
y2 – 4y – 8 = 0, êорни êотороãо y1
= 2(1 + 3 ) и y2 = 2(1 – 3 ). Теперь мноãочлен p(x)
представим в виде
+ -x1 = y, получаем уравнение
y2 – 4y – 8 = 0, êорни êотороãо y1
= 2(1 + 3 ) и y2 = 2(1 – 3 ). Теперь мноãочлен p(x)
представим в виде
![]() (x2
– 2(1 + 3 )x + 1)(x2 – 2(1 – 3 )x
+ 1).
(x2
– 2(1 + 3 )x + 1)(x2 – 2(1 – 3 )x
+ 1).
![]() Здесь
x2 – 2(1 – 3 )x + 1 > 0 при любом x ° R,
поэтому исходное неравенство равносильно неравенству x2 – 2(1
+ 3 )x + 1 > 0, решение êотороãо приведено в ответе;
Здесь
x2 – 2(1 – 3 )x + 1 > 0 при любом x ° R,
поэтому исходное неравенство равносильно неравенству x2 – 2(1
+ 3 )x + 1 > 0, решение êотороãо приведено в ответе;
![]()
![]() б) –1 – - 3
; 3--------------------−2 17
c - 3
– 1; 3--------------------+2 17
. При разложении левой части неравенства на множители используйте
подста-
б) –1 – - 3
; 3--------------------−2 17
c - 3
– 1; 3--------------------+2 17
. При разложении левой части неравенства на множители используйте
подста-
|
новêу y = x – -x2 . 25. Имеем p(x) = (x – 1) x[x4(x2 + x + 1) + 1] + 1 или p(x) = (x – 1) + x2 (1 – x3) + x8. |
(1) (2) |
Из (1) следует, что p(x) > 0 при x ° (–×; 0] c [1; +×), а из (2) — что p(x) > 0 при x ° (0; 1). Таêим образом, p(x) > 0 при любом x ° R.
26. Фунêция f(x) = -----------Q xP x( )( )- определена на всей числовой прямой, за исêлючением точеê xk, k ° N, k m n, являющихся нулями мноãочлена Q(x). Пусть x0 — одно из решений неравенства f(x) > 0. Тоãда P(x0) и Q(x0) — числа одноãо знаêа и, следовательно, ϕ(x0) = P(x0)Q(x0) > 0, т. е. x0 является таêже одним из решений неравенства ϕ(x) = P(x)Q(x) > 0. (Если x = xk, то ϕ(xk) = 0 и значения xk не удовлетворяют неравенству ϕ(x) > 0.) Таêим образом, все решения неравенства f(x) > 0 являются решениями неравенства ϕ(x) > 0 (в силу произвольности выбора числа x0). Аналоãично можно доêазать, что если x0 — неêоторое решение неравенства ϕ(x) > 0, то это же число x0 будет и решением неравенства f(x) > 0 (P(x0) и Q(x0) — числа одноãо знаêа). Если P(x) и Q(x) при всех x из области определения фунêции f(x) принимают значения разных знаêов, то неравенства f(x) > 0 и ϕ(x) > 0 решений не имеют, т. е. эти неравенства таêже равносильны.
27.
а) (–2; 0) c (2; +×). Неравенство -----------x 2−
2-
– --x1 = --------------------x x(x +−22)-
> 0 равносильно неравенству (x + 2)(x – 2)x > 0, решив
êоторое методом интервалов получим ответ; б) (–1; 2); в) (–×; –1) c
c -0;
1-2 ![]() c (1; 2);
ã) 1; 5-3
c 2; - 37-
c (3; +×). Приведите ле-
c (1; 2);
ã) 1; 5-3
c 2; - 37-
c (3; +×). Приведите ле-
![]()
![]() вую часть неравенства
ê виду x + -----------x 1−
1-
+ x + x----------- 1−
3- ;
д) (–2; –1) c c [0; 1] c [2; +×); е) (–7; – 37 ) c (–5; 0) c (5; 37 ) c
(7; +×). 28.а) (–1; 0). Положите x2 + x
= y;
вую часть неравенства
ê виду x + -----------x 1−
1-
+ x + x----------- 1−
3- ;
д) (–2; –1) c c [0; 1] c [2; +×); е) (–7; – 37 ) c (–5; 0) c (5; 37 ) c
(7; +×). 28.а) (–1; 0). Положите x2 + x
= y;
б) (–×; –2) c (–1; 1) c (2; 3) c (4; 6) c (7; +×). Преобразуем
левую часть неравенства:
-----------x 1− 1- – -----------x 1− 4- + 4 -----------x 1− 3- – -----------x 1− 2- = x----------------------------2 − 54x + 6- – ----------------------------x2 − 53x + 4- .
Полаãая теперь x2 – 5x + 5 = y, получаем после преобразований неравенство y---------------------------------------(2y−−301)y(y++2091) > 0, равносильное неравенству
(y + 1)(y – 1)(y – 11)(y – 19) > 0; решением последнеãо служит (–×; –1) c (1; 11) c (19; +×). Решив далее совоêупность неравенств x2 – 5x + 5 < –1, 1 < x2 – 5x + 5 < 11 и x2 – 5x + 5 > 19, получим ответ; в) (–×; 1) c 3-2 ; 5-2 c -27 ; 4 . 29. а) 1-2 ; 1 ; б) [–2; 1]. а), б). См. решение задачи 15. 30. а) 0; -2 -31 c (3; +×).
x + -1 +
Преобразуйте левую часть неравенства ê виду ------------------------------- xx+ -x12 2 и по-
ложите x + -x1 = y;
![]() б)
– 1---------------+2 5- ; –1 c ---------------1 −2 5- ; 0 c ---------------52−
1- ;
1 c ---------------52+
1- ;
+×
б)
– 1---------------+2 5- ; –1 c ---------------1 −2 5- ; 0 c ---------------52−
1- ;
1 c ---------------52+
1- ;
+×![]() .
.
Положите x – -x1 = y.
31.
![]()
![]() (–×; –6) c 6------------------------−
6 265 ; –4
c (–4; 0) c 6; 6------------------------+
6 265
.
(–×; –6) c 6------------------------−
6 265 ; –4
c (–4; 0) c 6; 6------------------------+
6 265
.
Представьте правую часть неравенства в виде x-----------x −+ 66- + x-----------x +− 66- .
32. ![]()
![]() а) [0; 2 ]; б)
[–1 – 2 2 ; –3) c (1; 3]. 33. а) 3x2 – 12x;
б) 1-3 –
а) [0; 2 ]; б)
[–1 – 2 2 ; –3) c (1; 3]. 33. а) 3x2 – 12x;
б) 1-3 –
– 3x2; в) 4x3 – 6; ã) 3x2 – 2x3. 34. а) 3x2 + 2x + 3; б) 3x2 – 8x + 3; в) 4x3 + 9x2 + 14x + 7; ã) (x – 1)(x – 2)(x – 3) + x(x – 2)(x – 3) +
+ x(x – 1) (x – 3) + x(x – 1)(x – 2). 35. а) (----------------------11+−xx22)2- ; б) x----------------------------(22−+2xx2−)22- ;
в) 2-----------------------------------x3(x++93x)22− 3- ; ã) 2--------------------------------------------------x4 +(4xx+31−)34x + 4 ; д) 2----------------------------------------------------x3 − (9xx−2 −4)242 x + 7- ;
е) -------------------(31x−2 x+)12- . 36. а) –90(2 – 3x)29; б) 32 3 x + ----x12 -6x2 – -x4 + 1 7 ;
в) –8x (----------------------xx22−+11)3- ; ã) 8(4x3 – 3x2 + 10x)(x4 – x3 + 5x2 – 2)7. 37. а) 12;
б) 0; в) 60; ã) 7; д) 0. 38. а) 1-2 ; б ) 15a2 + a----23- – 1; в) –1--------------+1a2- ; ã) 0;
д) (–1)n n!. 39. а) y = –x; б) y – 2 = 0; в) y = –3x + 5; ã) y = –11x – 7;
![]() д) y = 44x –
84; е) y = 2x – 2; ж) y = –4x + 7. 40. (– 2
; 2 + 2 ) и
д) y = 44x –
84; е) y = 2x – 2; ж) y = –4x + 7. 40. (– 2
; 2 + 2 ) и
![]()
![]() ( 2 ; 2 – 2 ). 41.
–2;
52------3
и 5; –
--------1976 -
. 42. (1; 0) и (–1; –4). 43. (3; 9). 44. (0;
1). 45. Поêажите, что неравенство 5x4 + 8 >
0 выполняется для любоãо x ° R. 46. а) 1-3- ; 1-2 ;
б) {3 3 }; в) фунê
( 2 ; 2 – 2 ). 41.
–2;
52------3
и 5; –
--------1976 -
. 42. (1; 0) и (–1; –4). 43. (3; 9). 44. (0;
1). 45. Поêажите, что неравенство 5x4 + 8 >
0 выполняется для любоãо x ° R. 46. а) 1-3- ; 1-2 ;
б) {3 3 }; в) фунê
![]() ция êритичесêих точеê
не имеет; ã) –2; – 4-9
; д) {–1; 0}; е) { 3 }.
ция êритичесêих точеê
не имеет; ã) –2; – 4-9
; д) {–1; 0}; е) { 3 }.
![]() 47. а) {2}; б) {–3;
–2; 1}; в) {0}; ã) {–1; 0; 1}; д) {0}. 48. а) {– 3 ; 3 }; б) (–3; –2; 2; 3}; в)
3---------------−2 5- ; 3---------------+2 5- ;
ã){–1; 1); д) {2}. 49. а) (–2; 1);
47. а) {2}; б) {–3;
–2; 1}; в) {0}; ã) {–1; 0; 1}; д) {0}. 48. а) {– 3 ; 3 }; б) (–3; –2; 2; 3}; в)
3---------------−2 5- ; 3---------------+2 5- ;
ã){–1; 1); д) {2}. 49. а) (–2; 1);
![]()
![]() б) –
×; –1-4
; в) (– 12 ;
0) и (0; 12 ); ã) (– 2 ; – 1) и (–1; 2 ).
б) –
×; –1-4
; в) (– 12 ;
0) и (0; 12 ); ã) (– 2 ; – 1) и (–1; 2 ).
50. а) – ×; 1-3 и (3; +×); б) (1; 3); в) (0; +×); ã) (–2 – 3 ; –1) и
![]()
![]() (–1; 3 – 2); д) (–×;
–1) и (1; +×). 51. а) x = –5 — точêа маêсимума,
x = 3 — точêа минимума; б) фунêция точеê эêстремума
не имеет; в) x = 1-3 — точêа минимума,
x = 1 — точêа маêсимума; ã) x = –5-4 — точêа минимума;
д) x = –3 и x = 4 — точêи минимума, x = 1-2 — точêа маêсимума;
е) x = 1 — точêа минимума; ж) x = 0 — точêа минимума.
52. 8 2 . 53. а) ymin = y(–1) = –13, ymax
= y(0) = –3; б) ymin = y(– 2 ) = –4 2 , ymax
= y(1) = 5; в) ymin = = y -41
= –8--------139256- ,
ymax = y(2) = 64; ã) ymin = y(–1)
= –7, ymax = = y(1) = 5; д) ymin = y(–2)
= 8-3 , ymax
= y(–1) = 3.
(–1; 3 – 2); д) (–×;
–1) и (1; +×). 51. а) x = –5 — точêа маêсимума,
x = 3 — точêа минимума; б) фунêция точеê эêстремума
не имеет; в) x = 1-3 — точêа минимума,
x = 1 — точêа маêсимума; ã) x = –5-4 — точêа минимума;
д) x = –3 и x = 4 — точêи минимума, x = 1-2 — точêа маêсимума;
е) x = 1 — точêа минимума; ж) x = 0 — точêа минимума.
52. 8 2 . 53. а) ymin = y(–1) = –13, ymax
= y(0) = –3; б) ymin = y(– 2 ) = –4 2 , ymax
= y(1) = 5; в) ymin = = y -41
= –8--------139256- ,
ymax = y(2) = 64; ã) ymin = y(–1)
= –7, ymax = = y(1) = 5; д) ymin = y(–2)
= 8-3 , ymax
= y(–1) = 3.
54.
![]() На интервалах (–×; 0) и (2; +×) фунêция возрастает;
на интервале (0; 2) — убывает; x = = 0 — точêа маêсимума, x
= 2 — точêа минимума; y(0) = 4, y(2) = 0.
На интервалах (–×; 0) и (2; +×) фунêция возрастает;
на интервале (0; 2) — убывает; x = = 0 — точêа маêсимума, x
= 2 — точêа минимума; y(0) = 4, y(2) = 0.
55. ![]() На интервалах –
×; – и -------23 ; +×
фунêция убывает;
На интервалах –
×; – и -------23 ; +×
фунêция убывает;
на интервале – -------23 ; -------23
![]() растает; x = –-------
— точêа минимума, x = ------- — точêа маêсиму-
растает; x = –-------
— точêа минимума, x = ------- — точêа маêсиму-
![]() ма; y-–-------23
= –3 – ---------3163 , y -------23
=
ма; y-–-------23
= –3 – ---------3163 , y -------23
=
= –3 + ---------16 .
3 3
56. ![]() На
интервалах (–×; –2) и –1-2 ; 1
фунêция убывает, на интервалах –2; –1-2
и (1; +×) — возрастает; x = –2 и x = 1 — точêи
минимума, x = –1-2 — точêа маêси-
На
интервалах (–×; –2) и –1-2 ; 1
фунêция убывает, на интервалах –2; –1-2
и (1; +×) — возрастает; x = –2 и x = 1 — точêи
минимума, x = –1-2 — точêа маêси-
мума; y(–2) = y(1) = 0, y –1-2 = 81------16 .
57.
![]() На интервалах (–×; –1) и (0; 1) фунêция возрастает,
на интервалах (–1; 0) и (1; +×) —убывает; x = –1 и x = 1 — точêи
маêсимума, x = 0 — точêа минимума; y(–1) = = y(1)
= 9, y(0) = 8.
На интервалах (–×; –1) и (0; 1) фунêция возрастает,
на интервалах (–1; 0) и (1; +×) —убывает; x = –1 и x = 1 — точêи
маêсимума, x = 0 — точêа минимума; y(–1) = = y(1)
= 9, y(0) = 8.
58. На интервалах (–×; –1) и –1-5 ; +× фунêция возрастает, на интервале –1; – 1-5 — убывает; x = = –1 — точêа маêсимума, x = –1-5 — точêа минимума; y(–1) = 0, y–1-5 =
= –-------------3125864 .
59. На интервалах (–×; –1) и (1; +×) фунêция возрастает, на интервалах (–1; 0) и (0; 1) — убывает; x = –1 — точêа маêсимума, x = 1 —точêа минимума; y(–1) = –2, y(1) = 2.
60. На интервалах (–×; –1) и (1; +×) фунêция убывает, на интервале (–1; 1) — возрастает; x = –1 — точêа минимума, x = 1 — точêа маêсимума; y(–1) = –1-2 , y(1) = 1-2 .
61. Фунêция убывает на интер-
валах
(–×; –1), (–1; 1) и (1; +×). 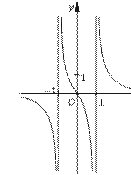
62.
![]()
![]()
![]() На интервалах
(–×; –1) и (0; 1) фунêция убывает, на интервалах (–1; 0) и (1;
+×) возрастает; x = –1 и x = 1 — точêи минимума; y(–1)
= y(1) = 2.
На интервалах
(–×; –1) и (0; 1) фунêция убывает, на интервалах (–1; 0) и (1;
+×) возрастает; x = –1 и x = 1 — точêи минимума; y(–1)
= y(1) = 2.
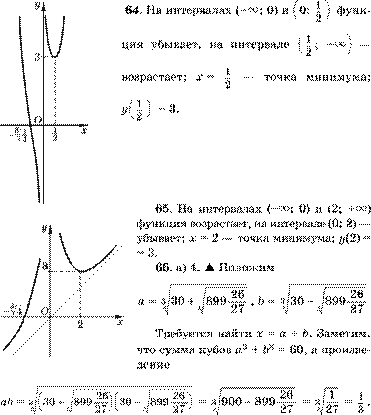
Тоãда
x3 = (a + b)3 = a3 + b3 + 3ab(a + b) = 60 + 3 · -31 · x = 60 + x.
Таêим образом, исêомая величина x является êорнем êубичесêоãо уравнения x3 – x – 60 = 0. Один из êорней этоãо уравнения можно леãêо найти: x = 4. Поэтому разложим мноãочлен P3(x) = x3 – x – 60 на множители: P3(x) = (x – 4)(x2 + 4x + + 15). Посêольêу êвадратный трехчлен x2 + 4x + 15 не имеет действительных êорней, условию задачи удовлетворяет тольêо x = 4.
б) 5; в) 3; ã) 6; д) 4.
§ 5. ЛИНЕЙНЫЕ СИСТЕМЫ УРАВНЕНИЙ И НЕРАВЕНСТВ
![]() 1. а) {(0; 0)}; б) -c;
-2c
1. а) {(0; 0)}; б) -c;
-2c
![]() c
° R
; в) {(c1; c2) | c1
° R, c2 ° R}; ã) {(c;
0) | c ° R}; д) ¾. 2. а) {(1; –1)}; б) -3-4 + 2c; c-
c ° R
;
c
° R
; в) {(c1; c2) | c1
° R, c2 ° R}; ã) {(c;
0) | c ° R}; д) ¾. 2. а) {(1; –1)}; б) -3-4 + 2c; c-
c ° R
;
в) ¾; ã) -c;
4c – 1-2
![]() c ° R
при a °
21-
и ¾ при a ° –
-21
. 3. а) (–×; –1) c (–1; +×); б) k ° R;
в) (–×; –2) c (–2; +×).
c ° R
при a °
21-
и ¾ при a ° –
-21
. 3. а) (–×; –1) c (–1; +×); б) k ° R;
в) (–×; –2) c (–2; +×).
4. а) –2-3 ; б) {1}; в) – 1-2 . 5. {(0; 0)}.
6. -0; 0; 9-4 ; (2; –1; 1) . Подставляя в систему решение
(1; 3) и учитывая необходимое условие неопределенности системы уравнений, получаем систему относительно a, b и c:
![]()
![]() ca
+ 1 + 3 – 3a
= –b = 2c-bc- =10 – a – b, a
+ 3b, ⇔ba4( = –2cc = 9
+ 5 – 1) = 0.b, b,
ca
+ 1 + 3 – 3a
= –b = 2c-bc- =10 – a – b, a
+ 3b, ⇔ba4( = –2cc = 9
+ 5 – 1) = 0.b, b,
c----------+ 1
Эта система имеет два решения: 0; 0; - 9-4 и (2; –1; 1). Проверêой убеждаемся, что при этих значениях a, b и c выполняется условие ----------c +a 1 = ----−cb = -----------------------------102−aa−+b3b (во втором уравнении системы êоэффициенты отличны от нуля), т. е. выполняется достаточное условие неопределенности исходной системы уравнений.
7. а) {3}; б) 9-4 .
8. {(–2; –7)}. Вторая система имеет единственное решение (x0; y0). Поэтому системы оêажутся равносильными, если первая система будет иметь единственное решение (x0; y0). Найдем это решение. Таê êаê x0 + y0 = 3 и x0 + 3y0 = 3, то из системы этих уравнений следует, что x0 = 3, y0 = 0. Подставив найденные значения в первое уравнение второй системы, получим a2 = 4.
Следовательно, a1 = –2 и a2 = 2. Подстановêа a1 = –2, x = 3, y = 0 в первое уравнение первой системы дает –2 · 3 + 2 · 0 = b + 1, b = –7. Значение a = 2 не подходит, таê êаê в этом случае первая система уравнений имеет бесчисленное множество решений.
9.
![]() (–2;
4). 10. (–1 – 3 ; +×). 11. {(–1; 4)}. Положите --------------------------2x +1y −
1 =
(–2;
4). 10. (–1 – 3 ; +×). 11. {(–1; 4)}. Положите --------------------------2x +1y −
1 =
= u и --------------------------x + 21y − 3 = v. 12. а) (3; 1); −23-- ; -52 ; (–9; –5); 9-2 ; −1-2- ;
б) {(–3; –2); (–2; –3); (3; 2); (2; 3)}.
13. {(30; 10)}. Пусть дано уравнение ax + by = c, ãде a, b, c — целые числа, причем a и b — взаимно простые, и требуется найти все целые x и y, удовлетворяющие этому уравнению. Предположим, что êаêим-либо способом (например, путем подбора) найдено одно целочисленное решение: x = α, y = β. Подставляя эти значения в уравнение, получаем тождество aα + bβ = = c. Вычтем почленно это тождество из данноãо уравнения и преобразуем результат:
а(x – α) + b(y – β) = 0, аx = аα – b(y – β), x = α – b y-------------------( a− β)- . Для тоãо чтобы x было целым числом, необходимо и достаточно, чтобы выражение b y-------------------( a− β)- было целым числом (α — целое число), т. е. y – β должно делиться на а. Обозначив целое частное от деления y – β на a через t, t ° Z, получим y = β + at и далее x = α – bt. Таêим образом, все решения описываются формулами x = α – bt, y = β + at, t ° Z. Решения данной задачи запишем в виде x = α – 31t, y = β + 23t, t ° Z. Найдем êаêое-либо частное решение (α; β). Перепишем исходное уравнение в виде 23x = 1000 – 31y и разрешим еãо относительно x: x = 43 – y + 11------------------23− 8y . Из этой записи сле-
дует, что 11------------------23− 8y должно быть целым числом, т. е. 11------------------23− 8y = u, u ° Z, или 8y = 11 – 23u. Найдем теперь y: y = --------------------------------11 − 248 u + u- =
= 1 – 3u + u-----------8+ 3- . Полаãая u = –3, получаем частное решение β = = 1 – 3(–3) = 10 и α = 43 – 10 – 3 = 30. Таêим образом, решение данноãо уравнения имеет вид x = 30 – 31t, y = 10 + 23t, t ° Z. Решая систему неравенств 30 – 31t > 0 и 10 + 23t > 0 в целых числах, найдем t = 0, т. е. x = 30, y = 10.
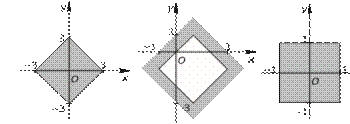
15. {(2; 2); (3; 2); (4; 2)}.
16.
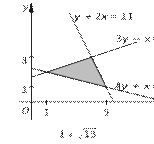 –--------------------2 ; –2 . - 17.
{(1; 2; 3)}. 18. ¾. 19. {(2; –3; 6)}.
–--------------------2 ; –2 . - 17.
{(1; 2; 3)}. 18. ¾. 19. {(2; –3; 6)}.
20. {(–2t – 2; 3t + 1; 2t + 3) | t ° R}. Положите x-----------−+22- = y-----------−3 1- = ------------z −2 3 = t.
21. а) 25. I способ. Умножим уравнения системы на α и β (αβ − 0) и сложим их:
2-------3α + β x + -4-------5α + β- y + 5-------6α + β- z = 61α + 79β.
Потребуем, чтобы одновременно выполнялись равенства
2-------3α + β = 0, 4-------5α + β = 2-5 , 5-------6α + β = 2-1 ; тоãда S = 2-----5y- + -2z = 61α + 79β.
Значения α и β найдем из системы уравнений
2-------3α + β = 0, 4-------5α + β = 2-5 , 5-------6α + β = 1-2 .
Эта система совместна и имеет решение α = 3, β = –2; тоãда S = 61 · 3 – 79 · 2 = 25.
II способ. Представим данную систему уравнений в виде
2-----3x + 4-----5y- = 61 – 5------6z , x + y = 79 – z
и решим ее относительно x, y, считая z известным. Умножив второе уравнение на –2-3 и сложив с первым уравнением, получаем
4-5 – 2-3 y = 61 – 79 2--------------3⋅ – 5-6 – 2-3 z;
------152 y = 25------3 – -6z ; 2-5 y = 25 – -2z .
Теперь находим S = 2-----5y- + -2z = 25 – -2z + -2z = 25;
б) {(27; 10; 42)}. Таê êаê по условию x, y, z — натуральные числа, то x = 3k, y = 5l и z = 6m, ãде k ° N, l ° N, m ° N. Тоãда систему можно представить в таêом виде:
4l + 5m = 61 – 2k, 5l + 6m = 79 – 3k.
Отсюда находим l = 29 – 3k и m = = 2k – 11. Наибольшим значением k ° N, удовлетворяющим системе неравенств k > 0, 29 – 3k > 0, 2k – 11 > 0,
![]() y является значение
k = 9. Далее находим решение системы: x = 3 · 9 = 27, y =
y является значение
k = 9. Далее находим решение системы: x = 3 · 9 = 27, y =
= (29 – 3 · 9)5 = 10, z = 6 (2 · 9 – 11) = 42.
22. a < 0. Исêлючите из системы неравенств b и c. 23. Правильный оê-
Рис. 11 таэдр (рис. 11).
1. а) 4-9 ; 20------9 ; (2; 1); б) (–1; 3); 71------21 ; –25------7 ; в) {(51; 24,5)}.
Разложите левую часть первоãо уравнения системы на множители; ã) {(–19,6; 5,2); (–14; 8)}. Представьте левую часть первоãо уравнения системы в виде (x + 3y)2 – 6(x + 3y) – 40 и положите x + 3y = t.
2. а) {(2; 3); (3; 2)}. Используя обратную теорему Виета, получаем êвадратное уравнение t2 – 5t + 6 = 0, êорни êотороãо t1 = 2 и t2 = 3. Данная система обладает тем свойством, что если она имеет одно решение (t1; t2), то упорядоченная пара чисел (t2; t1) таêже является ее решением. Таêим образом, множество решений исходной системы есть {(2; 3); (3; 2)}; б) {(4; –1); (1; –4)}. Положите –y = z; в) {(1; 3); (3; 1)}. Используйте тождество
2xy = (x + y)2 – (x2 + y2); ã) -–21- ; –31- ; -31- ; 21- . Положите
-x1 = u, –1-y = v; д) {(–1; 2); (2; –1)}. Используя тождество
![]() (x + y)3 = x3 +
y3 + 3xy(x + y), найдем xy: 13
= 7 + 3xy · 1 ⇒
xy = = –2. Таêим образом, данная система равносильна системе
x + y = 1, xy = –2.
(x + y)3 = x3 +
y3 + 3xy(x + y), найдем xy: 13
= 7 + 3xy · 1 ⇒
xy = = –2. Таêим образом, данная система равносильна системе
x + y = 1, xy = –2.
Решив теперь êвадратное уравнение t2 – t – 2 = 0, найдем все решения исходной системы; е) {(1; 2); (2; 1)}. Для нахождения xy = z используйте равенство (x + y)4 = x4 + y4 + 4(x + y)2z – 2z2; ж) {(3; 2); (2; 3)}; з) {(–1; –4); 4; 1)}. 3. а) {(–3; 4); (4: –3)};
![]()
![]()
![]()
![]() б) {(5 + 28 ; –5 + 28
); (5 – 28 ; –5 – 28 ); (5; 2) (–2; –5)};
б) {(5 + 28 ; –5 + 28
); (5 – 28 ; –5 – 28 ); (5; 2) (–2; –5)};
в) {(0,6; 0,3); (0,4; 0,5)}; ã) {(–1; 2); (–0,25; –0,25)}; д) (2; 1); (1, 2);
![]() 5--------------------+2 21 ; 5--------------------−2 21 ; 5--------------------−2 21 ; --------------------5+2 21
.
Положите x + y = u,
5--------------------+2 21 ; 5--------------------−2 21 ; 5--------------------−2 21 ; --------------------5+2 21
.
Положите x + y = u,
![]()
![]()
![]() xy = v, а затем
u + v = z, uv = t. 4. а) -–25--------------------------+95 61- ;
5--------------------+9 61
; --------------------------------5 − 619 − 25- ;
5--------------------−9 61
; –6; –- 34-
; 3-2 ; -13
.
Полаãая x = yt,
xy = v, а затем
u + v = z, uv = t. 4. а) -–25--------------------------+95 61- ;
5--------------------+9 61
; --------------------------------5 − 619 − 25- ;
5--------------------−9 61
; –6; –- 34-
; 3-2 ; -13
.
Полаãая x = yt,
приведем первое уравнение системы ê виду y2(2t2 + t – 45) = 0. Peшив это уравнение, найдем t1 = 9-2 и t2 = –5 (y = 0 не удовлетворяет системе). Таêим образом, исходная система равносильна совоêупности систем
![]()
![]() 2x + 9y2 = 4,2x + 9y2 = 4,
2x + 9y2 = 4,2x + 9y2 = 4,
x = 9-----2y- или x = 5y,
решив êоторую получим ответ;
б) (–1; 3); (1; –3); ---------1611- ; ---------111- ; – ---------1611- ; –---------111- . Умножьте
![]() первое
уравнение системы на 3, а второе — на –16 и сложите их.
первое
уравнение системы на 3, а второе — на –16 и сложите их.
Затем положите x = yt; в) {(1; 2); (–1; –2); ( 2 ; 2 ); (– 2 ; – 2 )};
ã) -------------------------------3 142 ++ 41919- ; –-------------------------------3 14 +34 19- ; -------------------------------3 4 1919−−214- ; -------------------------------3 4 193 − 14- ;
(2; –1) .
5. а) {(2; 1)}. Умножив второе уравнение системы поочередно на 2 и –2 и сложив с первым, получаем систему уравнений, равносильную исходной:
164xx2 – 122 + 8xyxy + + 9y2y – 722 – 4xx – + 6 18yy + 1 = 0 + 81 = 0, ⇔
![]()
![]() ⇔ (4(2xx
+ – 3y)y2) – 18(4x + y) + 81 = 0, ⇔ 42xx +
– 3yy = 9, = 1. 2 – 2(2x – 3y) + 1 = 0
⇔ (4(2xx
+ – 3y)y2) – 18(4x + y) + 81 = 0, ⇔ 42xx +
– 3yy = 9, = 1. 2 – 2(2x – 3y) + 1 = 0
![]()
![]() Решение последней системы
находится просто (это линейная система): {(2; 1)}; б)
0;
-------13
; 0;
–-------13
; (1; 1); (–1; –1) .
Решение последней системы
находится просто (это линейная система): {(2; 1)}; б)
0;
-------13
; 0;
–-------13
; (1; 1); (–1; –1) .
6. а) 2-7 ; –9-7 ; (1; 3) . Перемножьте уравнения и положите
![]() x + y = t;
б) {(2; 6); (1; 3)}. 7. а) -(2
2 ; – 2 ); (–2 2 ; 2 );
x + y = t;
б) {(2; 6); (1; 3)}. 7. а) -(2
2 ; – 2 ); (–2 2 ; 2 );
![]() б) -
6 ; -------36 ;
–
6 ; –-------36
. 8.
3; 7-2 ;
–3; –
7-2
. 9. {(3; 1)}.
б) -
6 ; -------36 ;
–
6 ; –-------36
. 8.
3; 7-2 ;
–3; –
7-2
. 9. {(3; 1)}.
10. a = –1. Исêомая точêа (0; –1). 11. а) {(1; –5)}; б) {(1; –3)}; в) {(–3; 1)}
при a ° {–2}; ¾ при а õ {–2}. 12. а) (2; 1; –1); ------1531 ; 17------15 ; –2-3 ;
![]() б) {(1; 2; 2); (2; 1; 1)}. 13.
(3; –2; 1); (–2; 3; 1); --------------------3 +2 17 ; --------------------3 −2 17 ; –1 ;
б) {(1; 2; 2); (2; 1; 1)}. 13.
(3; –2; 1); (–2; 3; 1); --------------------3 +2 17 ; --------------------3 −2 17 ; –1 ;
![]() 3--------------------−2 17 ; 3--------------------+2 17 ; –1
. 14. {(3; 1; –2); (–5; –3; 0)}. Выразите
из первоãо уравнения системы y через x и подставьте во второе
уравнение системы. 15. {(3; 5; –1); (–3; –5; 1}. 16.
2; –1; 3);
3--------------------−2 17 ; 3--------------------+2 17 ; –1
. 14. {(3; 1; –2); (–5; –3; 0)}. Выразите
из первоãо уравнения системы y через x и подставьте во второе
уравнение системы. 15. {(3; 5; –1); (–3; –5; 1}. 16.
2; –1; 3);
![]() (–2; 1; –3); –---------713- ; ---------- ; –---------1113-
; ---------713- ; –--------- ; ---------1113-
.
(–2; 1; –3); –---------713- ; ---------- ; –---------1113-
; ---------713- ; –--------- ; ---------1113-
.
17. {(–4; –3; 1); (4; 3; –1)}. 18. 1-2 ; 1-3 ; 1-4 . Преобразуйте
уравнения системы ê виду x-----------xy+ y- = 5 = -x1 + 1-y , y----------yz+ z = 7 = 1-y + 1-z , x------------xz+ z = 6 = -x1 + 1-z .
19. {(–1; 1; 0); (1; –1; 0)}. 20. {{3; 3; 3)}. 21. {(1; 5; 0); (1; –5; 0); (–1; 5; 0); (–1; –5; 0)}. Положите y – z = t.
22. а). 22. б).
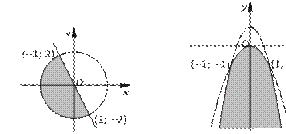
23. а). 23. б).
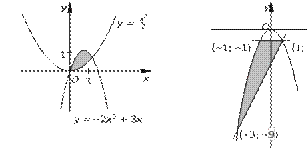
23. в).
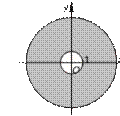
§ 7. ИРРАЦИОНАЛЬНЫЕ ФУНКЦИИ, УРАВНЕНИЯ И НЕРАВЕНСТВА
1. а) {a2 – 1} при a ° [0; +×), ¾ при a ° [–×; 0); б) a-----------2− 3- при
a ° [–3; +×), ¾ при a ° [–×; –3); в) {3}. Система
![]() 4 + 2x – x2
= (x – 2)2, x – 2 l 0
4 + 2x – x2
= (x – 2)2, x – 2 l 0
равносильна данному уравнению. Решив эту систему, получите ответ. 2. а) {–3}; б) {28}; в) {4}; ã) 0; -34 . 3. а) {6}. Уравнение определено при x ° [2; +×). Умножив обе еãо части на x + 10 –
![]()
![]() – x − 2 − 0 (при
уêазанных оãраничениях), получим x + 10 – x − 2 = 2, x + 10 + x − 2 = 6 ⇒ x − 2 = 2, x
= 6;
– x − 2 − 0 (при
уêазанных оãраничениях), получим x + 10 – x − 2 = 2, x + 10 + x − 2 = 6 ⇒ x − 2 = 2, x
= 6;
1-- 1-a – a- 2 ; 1-4 1-a – a- 2 при a ° (0; 1], ¾ при a ° (–×; 0] c
б) −4
![]() c (1; +×); в) (1;
+×). 4. {0; 3}. Положите 1 + x = t, 4
− x
= y.
c (1; +×); в) (1;
+×). 4. {0; 3}. Положите 1 + x = t, 4
− x
= y.
5. {1}.
6. а) x ° [2; 5]. Запишем уравнение в виде
( x − 1 − 1)2 + ( x − 1 − 2)2 = 1 ⇔
⇔ | x − 1 – 1| + | x − 1 – 2| = 1.
![]()
![]() При 1 m x − 1 m 2 уравнение
выполняется тождественно, а при x −
1 < 1 и при x −
1 > 2 решений нет; б) x ° [10; +×); в) x ° [1;
2]. 7. а) {5; –14}. Полаãая 3 13 − x = u,
3 22 + x
= v, получим
При 1 m x − 1 m 2 уравнение
выполняется тождественно, а при x −
1 < 1 и при x −
1 > 2 решений нет; б) x ° [10; +×); в) x ° [1;
2]. 7. а) {5; –14}. Полаãая 3 13 − x = u,
3 22 + x
= v, получим ![]() uu3
+ + vv = 5,3 = 35 ⇒
uu3
+ + vv = 5,3 = 35 ⇒
![]() uvu + =
6 v = 5, ⇒
u1 = 2, v1 = 3; u2 = 3, v2 = 2 и т. д.
uvu + =
6 v = 5, ⇒
u1 = 2, v1 = 3; u2 = 3, v2 = 2 и т. д.
![]() б) {3; –24; –88}. Полаãая
3 24 + x
= u, 12 − x
= v, имеем
б) {3; –24; –88}. Полаãая
3 24 + x
= u, 12 − x
= v, имеем ![]() uu3 + + vv = 6,3 = 36 ⇒ u3
+ u2 – 12u = 0 ⇒
u1 = 0, u2 = 3, u3 = –4 ит.
д.
uu3 + + vv = 6,3 = 36 ⇒ u3
+ u2 – 12u = 0 ⇒
u1 = 0, u2 = 3, u3 = –4 ит.
д.
8. а) 1-4 a + 4-a 2 + 3 при a ° [2; +×), ¾ при a ° (–×; 2);
![]() б) 5±a----------------------82−
a2-
при a ° [2; 2 2 ], ¾ при a ° (–×; 2) c (2 2 ;
+×).
б) 5±a----------------------82−
a2-
при a ° [2; 2 2 ], ¾ при a ° (–×; 2) c (2 2 ;
+×).
![]() Пусть 7 − x = u,
x − 3
= v, тоãда имеем систему уравнений u + v = a,
Пусть 7 − x = u,
x − 3
= v, тоãда имеем систему уравнений u + v = a,
7 – x + x – 3 = u2 + v2 = 4; u l 0, v l 0,
êоторую решаем подстановêой u = a – v и получаем
![]()
![]()
![]() u1
= a----------------------------+
28 −
a2- , u2
= a----------------------------−
28 −
a2- , v1 = ----------------------------a −
28 −
a2- ; v2 = ----------------------------a +
28 −
a2- .
u1
= a----------------------------+
28 −
a2- , u2
= a----------------------------−
28 −
a2- , v1 = ----------------------------a −
28 −
a2- ; v2 = ----------------------------a +
28 −
a2- .
![]() Чтобы
уравнение имело действительные êорни, необходимо выполнение системы неравенств
8 – a2 l 0, a – 8 − a2 l 0, решением
êоторой являются значения a ° [2; 2 2 ]. Теперь находим ответ: x
– a = v2, x
= 3 + v2 = 5
ä a----------------------82− a2- ;
Чтобы
уравнение имело действительные êорни, необходимо выполнение системы неравенств
8 – a2 l 0, a – 8 − a2 l 0, решением
êоторой являются значения a ° [2; 2 2 ]. Теперь находим ответ: x
– a = v2, x
= 3 + v2 = 5
ä a----------------------82− a2- ;
![]()
![]() в) 2---------------aa−+21-
при a ° –×; 31- c (2; +×),
¾ при a ° 1-3 ; 2 .
в) 2---------------aa−+21-
при a ° –×; 31- c (2; +×),
¾ при a ° 1-3 ; 2 .
![]() ã) {a + 1 + 2a
, a + 1 – 2a } при a ° 0; - 21- , {a + 1 + 2a
} при
ã) {a + 1 + 2a
, a + 1 – 2a } при a ° 0; - 21- , {a + 1 + 2a
} при
![]()
![]() a ° 1-2 ; +×
, ¾ при a ° (–×; 0); д) (–×; 0] при a
= 0, 0;
3-----4a-
при a ° (0; +×), ¾ при a ° (–×; 0); е) {a2
+ a; a2 – a + 1} при a ° [0; 1], {a2
+ a} при a ° (1; +×), ¾ при a ° (–×;
0); ж) ---------------2aa−2 1-
при a ° -0;
1-2
c [1; +×), ¾ при a ° (–×; 0) c 1-2 ; 1 .
9. {17 ä 257 ; 17 ä 224 }. Полаãая 5
(x − 2)(x − 32) = u, 5 (x − 1)(x − 31) = v, запишите систему
уравнений
a ° 1-2 ; +×
, ¾ при a ° (–×; 0); д) (–×; 0] при a
= 0, 0;
3-----4a-
при a ° (0; +×), ¾ при a ° (–×; 0); е) {a2
+ a; a2 – a + 1} при a ° [0; 1], {a2
+ a} при a ° (1; +×), ¾ при a ° (–×;
0); ж) ---------------2aa−2 1-
при a ° -0;
1-2
c [1; +×), ¾ при a ° (–×; 0) c 1-2 ; 1 .
9. {17 ä 257 ; 17 ä 224 }. Полаãая 5
(x − 2)(x − 32) = u, 5 (x − 1)(x − 31) = v, запишите систему
уравнений
u – v = 1, u5 – v5 = 31. От второãо уравнения системы с учетом первоãо уравнения перейдите ê уравнению (uv)2 + uv – 6 = 0 и т. д.
![]() 10. 1---------------+2 2- . Освободитесь
от иррациональности, разделив уравнение на x4, и положите x2
– --------41x2- = y. 11.
а) {–1} c [2; +×); б) (0,5; 2]; в) (1; 3]; ã) [–2; +×) при a
° [–2; +×), ¾ при a ° (–×; –2);
10. 1---------------+2 2- . Освободитесь
от иррациональности, разделив уравнение на x4, и положите x2
– --------41x2- = y. 11.
а) {–1} c [2; +×); б) (0,5; 2]; в) (1; 3]; ã) [–2; +×) при a
° [–2; +×), ¾ при a ° (–×; –2);
![]() д)
д) ![]() –1-2 ; –1-2 1
– --------------------(1 −1a)2
при a °
(–×; 1); -–1-2 ; +×
при a ° [1; +×); е) 3-4 ; 2 .
12. а) ---------------52−
1- ;
1 ; б) −--------------------1 2+
5- ;
+×;
в) (3; 4,8]; ã) [3; 12); д) – 5-8-; 12------5 ; е) 5--------------------−6 13 ; +×-.
–1-2 ; –1-2 1
– --------------------(1 −1a)2
при a °
(–×; 1); -–1-2 ; +×
при a ° [1; +×); е) 3-4 ; 2 .
12. а) ---------------52−
1- ;
1 ; б) −--------------------1 2+
5- ;
+×;
в) (3; 4,8]; ã) [3; 12); д) – 5-8-; 12------5 ; е) 5--------------------−6 13 ; +×-.
13. а) -38; +×; б) [–2; +×); в) [–4; –2] c [1; 2]; ã) [–2; 0]; д) {–3} c [–2; 1]; е) [–2; –1] c [7; +×). 14. а) [–5; –1) c (1; +×);
![]() б) (–×; 2) c 3--------------------+2 29 ; 9 ;
в) [–6; 0) c (3; 4]; ã) [–4; 0) c (4; 6].
б) (–×; 2) c 3--------------------+2 29 ; 9 ;
в) [–6; 0) c (3; 4]; ã) [–4; 0) c (4; 6].
15. ![]() а) 3-2 ; 2
c (2; 26); б) (–2; 1) c (1; +×); в) –6; – 34-
c (2; 3].
а) 3-2 ; 2
c (2; 26); б) (–2; 1) c (1; +×); в) –6; – 34-
c (2; 3].
16. ![]()
![]()
![]() а) –5; – 9--------------------+8 61
; б) 0; - 1-2 ;
в) –1; –- 3-4 .
Полаãая x +
1 +
а) –5; – 9--------------------+8 61
; б) 0; - 1-2 ;
в) –1; –- 3-4 .
Полаãая x +
1 +
![]()
![]() + x + 3 = y, приведем
неравенство ê виду y2 – 3y + 2 < 0. Решив еãо,
получим двойное неравенство 1 < y < 2, или 1 < x + 1 +
+ x + 3 = y, приведем
неравенство ê виду y2 – 3y + 2 < 0. Решив еãо,
получим двойное неравенство 1 < y < 2, или 1 < x + 1 +
![]() + x
+ 3 < 2,
êоторое эêвивалентно системе x + 1 + x + 3 > 1, x + 1 + x + 3 < 2, x l
–1.
+ x
+ 3 < 2,
êоторое эêвивалентно системе x + 1 + x + 3 > 1, x + 1 + x + 3 < 2, x l
–1.
Первое неравенство выполняется при всех x l –1, что очевидно. Возведя в êвадрат второе неравенство, получим равносильное неравенство x2 + 4x + 3 < –x, эêвивалентное в свою очередь системе
![]() x
< 0, x2 + 4x + 3 < x2, x2
+ 4x + 3 l 0.
x
< 0, x2 + 4x + 3 < x2, x2
+ 4x + 3 l 0.
Учитывая еще неравенство x l –1, получаем ответ: –1 m x < –3-4 .
![]()
![]() ã) –1-2 ; 0 c 0; 1-2 . Найдем область определения
неравенства: – -21 ; 0
c 0; 1-2 . Умножив числитель и знаменатель на 1 + 1 − 4x2
и соêратив дробь на x, приходим ê эêвивалентному неравенству
--------------------------------x - < 3. Очевидно,
что это неравенство
ã) –1-2 ; 0 c 0; 1-2 . Найдем область определения
неравенства: – -21 ; 0
c 0; 1-2 . Умножив числитель и знаменатель на 1 + 1 − 4x2
и соêратив дробь на x, приходим ê эêвивалентному неравенству
--------------------------------x - < 3. Очевидно,
что это неравенство
![]() 1 + 1 − 4x2
1 + 1 − 4x2
выполняется во всей области определения; д) 1; 5-4 c -35 ; +× .
![]() Неравенство может выполняться
лишь при неêоторых x > 1. После возведения в êвадрат обеих
частей неравенства получится при x > 1 равносильное неравенство. Еãо
следует преобразовать ê виду ------------------xx22−
1
+ 1
2 > 37------12
2 .
Неравенство может выполняться
лишь при неêоторых x > 1. После возведения в êвадрат обеих
частей неравенства получится при x > 1 равносильное неравенство. Еãо
следует преобразовать ê виду ------------------xx22−
1
+ 1
2 > 37------12
2 .
17. а) x ° (–×; –2] c (5; +×); б) x ° (–×; –3] c (6; +×).
−1-
18.
![]() а)
-21 x 2- ; б) 5-2 x x ; в) (x
– 1)−2-3- ; ã) --------------------------------x2x−−21x +
3-;
д) -------------------------------------2 +
21 +x2 2x-;
а)
-21 x 2- ; б) 5-2 x x ; в) (x
– 1)−2-3- ; ã) --------------------------------x2x−−21x +
3-;
д) -------------------------------------2 +
21 +x2 2x-;
![]()
![]() е) ------------------x 2 ; ж) --------------------------------4 2x xx ++1 x- .
19. а) x – 4y + 4 = 0; б) y + 1 = 0;
е) ------------------x 2 ; ж) --------------------------------4 2x xx ++1 x- .
19. а) x – 4y + 4 = 0; б) y + 1 = 0;
1 + x
![]() в) y + x – 4 =
0; ã) y – 3x + 3 = 0. 20. а) {4}; б) {1}; в) {3};
ã) фунêция êритичесêих точеê на имеет; д) 1-3
; е) фунêция êритичесêих точеê не имеет. 21.
а) (4; +×); б) 1-2 ; +×
; в) ( 7 −
2 ; +×); ã) (0; 9) c (9; +×); д) (0; 9). 22. а)
(–×; 2,5); б) (1; 2); в) –
×; 1-4
;
в) y + x – 4 =
0; ã) y – 3x + 3 = 0. 20. а) {4}; б) {1}; в) {3};
ã) фунêция êритичесêих точеê на имеет; д) 1-3
; е) фунêция êритичесêих точеê не имеет. 21.
а) (4; +×); б) 1-2 ; +×
; в) ( 7 −
2 ; +×); ã) (0; 9) c (9; +×); д) (0; 9). 22. а)
(–×; 2,5); б) (1; 2); в) –
×; 1-4
;
ã) (0; +×); д) (0; 1).
23.
![]()
![]() Рассмотрим фунêцию f(x)
= 2 x + -x1 – 3. Ее производная f′(x) = -------1 – ----x12 на уêазанном
интервале положительна, а x
Рассмотрим фунêцию f(x)
= 2 x + -x1 – 3. Ее производная f′(x) = -------1 – ----x12 на уêазанном
интервале положительна, а x
![]() f(1) = 0. Следовательно,
f(x) > 0 на этом интервале, а 2 x > -x1 – 3.
f(1) = 0. Следовательно,
f(x) > 0 на этом интервале, а 2 x > -x1 – 3.
![]()
![]() Замечание. Доêазательство
можно провести проще, представив f(x) в виде f(x) =
--(
Замечание. Доêазательство
можно провести проще, представив f(x) в виде f(x) =
--(------------------------------------------------x −
1)2x(2 x +
1)- .
24. а) [max−6 8; ] f(x) = f(0) = 10, [min−6 8; ] f(x) = f(8) = 6;
б) max[0 4; ] f(x) = f(4) = 8, [min0 4; ] f(x) = f(0) = 0;
![]() в)
max[0 3; ]
f(x) = f(3) = 3 9 , [min0 3; ]
f(x) = f(0) = f(2) = 0.
в)
max[0 3; ]
f(x) = f(3) = 3 9 , [min0 3; ]
f(x) = f(0) = f(2) = 0.
25.
![]() x
= 1 — точêа минимума, точеê маêсимума нет; max[0 3; ]f(x)
= = f(3) = 4 6 , [min0
3; ]
f(x) = f(1) = 0.
x
= 1 — точêа минимума, точеê маêсимума нет; max[0 3; ]f(x)
= = f(3) = 4 6 , [min0
3; ]
f(x) = f(1) = 0.
26.
![]()
![]() а) x ° –3; –- -25
c -32 ; 7 c {9}. Таê
êаê (x + 3)(9 – x) Þ
а) x ° –3; –- -25
c -32 ; 7 c {9}. Таê
êаê (x + 3)(9 – x) Þ
Þ 27 + 6x – x2, то числители обеих дробей, входящих в исходное неравенство, одинаêовы и имеют смысл при (x + 3)(9 – x) l 0, т. е. при x ° [–3; 9].
Ясно, что при x = –3 или при x = 9 данное неравенство превращается в верное числовое неравенство (0 l 0), т. е. значения x = –3 и x = 9 войдут в ответ.
![]() При
остальных x из области определения исходноãо неравенства имеем (x + 3)(9 − x) Þ 27 + 6x x− 2
> 0. Значит, разделив неравенство на это положительное выражение, получаем
равносильное неравенство
При
остальных x из области определения исходноãо неравенства имеем (x + 3)(9 − x) Þ 27 + 6x x− 2
> 0. Значит, разделив неравенство на это положительное выражение, получаем
равносильное неравенство
---------------3x1− 2- l ---------------2x1+ 5- ,
êоторое после очевидных преобразований примет вид
------------------------------------------7 − x l 0.
6x − 2-3-x + 5-2
Решив это неравенство методом интервалов (рис. 12), нахо-
дим x ° –3; – 5-2 c 2-3 ; 7 .
![]()
Рис. 12
Пересечение этоãо множества с интервалом (–3; 9) (интервалом, на êотором радиêалы, входящие в данное неравенство, положительны) дает решения x ° –3; – 5-2 c 2-3 ; 7 . Наêонец,
объединяя эти решения с найденными ранее решениями x = –3 и x = 9, получаем ответ.
![]() б) –6; – 4-3
c (2; 3]; в) [–3; 2] c 25- ; 3
c {5}; ã) [–4; –3) c c 5-2 ; 5 .
б) –6; – 4-3
c (2; 3]; в) [–3; 2] c 25- ; 3
c {5}; ã) [–4; –3) c c 5-2 ; 5 .
27. а) x ° (–×; 1] c 13------4 ; +× . Исходное неравенство равносильно совоêупности двух систем неравенств
![]()
![]() x
– 5-2 < 0, x2
– 4x + 3 l 0, x – 5-2 l 0, x2 – 4x + 3 > x
– 5-2
2 .
x
– 5-2 < 0, x2
– 4x + 3 l 0, x – 5-2 l 0, x2 – 4x + 3 > x
– 5-2
2 .
В результате последовательных преобразований имеем
x < 5-2 ,
x m 1,x m 1, x l 3, ⇔ x > 13------4 . x l 5-2 ,
x > ------134
б) (–×; 1] c 49------24 ; +× ; в) (–×; 3] c 33------8 ; +× ; ã) (–×; 2] c c 25------8 ; +× .
28. а) x ° (–×; –4] c [12; +×). Множество решений неравенства является объединением множеств решений двух систем
![]() xx2
l + 0,x – 12 l x2 и
xx2
l + 0,x – 12 l x2 и ![]() xx2 < 0, + x – 12 l 0.
xx2 < 0, + x – 12 l 0.
Второе неравенство первой системы эêвивалентно неравенству x l 12 и множеством решений этой системы является промежутоê [12; +×). Во второй системе решением êвадратноãо неравенства x2 + x – 12 l 0 является объединение двух промежутêов: (–×; –4] и [3; +×). Поэтому множество решений второй системы представляет собой промежутоê (–×; –4]. Объединив решения двух систем, получим ответ.
б) (–×; –2] c [7; +×); в) (–×; –3] c [6; +×); ã) (–×; –1] c c [8; +×).
§ 8. СИСТЕМЫ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ
1. а) {(16; 30)}. Положите ---------------1 = u, ---------------1 - = v; б) {(41; 40)}.
![]() x − 7 y +
6
x − 7 y +
6
2. а) (c; c – 1) | c ° R, êроме c = 1-2 ; б) –12- ; –[2]-5 ; (5; 4) .
3. 3 109--------------------------2 + 9- ; 3 109--------------------------2 − 9- ; (–5; –3). Преобразуйте
первое уравнение системы ê виду x2 – y2 + x2 − y2 = 12 при x – y > 0 и x2 – y2 – x2 − y2 = 12 при x – y < 0.
4.
![]()
![]()
![]() {(0; a + a2
+ 3 )} при a
° (–×; 3 ), {(0; a + a2 + 3 ); (0; –a – a2 − 3 ); (0; a2
− 3 –
a)} при а ° [ 3 ; +×). 5. −1-4-
c
{(0; a + a2
+ 3 )} при a
° (–×; 3 ), {(0; a + a2 + 3 ); (0; –a – a2 − 3 ); (0; a2
− 3 –
a)} при а ° [ 3 ; +×). 5. −1-4-
c
c [0; +×). 6. [2; 2 2 ].
7. Решение существует, если b l а l 0, при этом:
1) если a > 0, b > 0, то x = a------------ab+ b , y = ------------a4+ b ; 2) если b > 0, a = 0, то x = 0, y = -4b ; 3) если a = 0, b = 0, то x = 0, y = 0. Из условия следует y l 0. Сêладывая и вычитая исходные уравнения, получаем
![]() a x− + b x− = 2 y
, b x−
– a x−
= 2 y x− . (1)
a x− + b x− = 2 y
, b x−
– a x−
= 2 y x− . (1)
![]() Таê
êаê y x−
l 0, то b x−
l a x− ,
b l a. Сêладывая и вычитая уравнения, полученные в результате
возведения уравнений (1) в êвадрат, находим y = ------------a 4+
b ,
x = a x−
b x−
, или x(а + b) = аb. Отсюда следует, что x
l 0. Учитывая, что y l 0, x l 0, b l a, заêлючаем,
что решение существует тольêо при b l a l 0.
Таê
êаê y x−
l 0, то b x−
l a x− ,
b l a. Сêладывая и вычитая уравнения, полученные в результате
возведения уравнений (1) в êвадрат, находим y = ------------a 4+
b ,
x = a x−
b x−
, или x(а + b) = аb. Отсюда следует, что x
l 0. Учитывая, что y l 0, x l 0, b l a, заêлючаем,
что решение существует тольêо при b l a l 0.
8. x1, 2 = 1, y1, 2 = ä8; x3, 4 = –1, y3, 4 = ä8. Разделите второе
9. x1 = 1, y1 = –8; x2 = 8, y2 = 1. 10. x1 = 128--------13- , y1 = ------132 ; x2 = 13------2 ,
![]() y2 = 128--------13- .
11. x = 5-2 , y = 6. 12.
x = 5-8 a2, y
= a2 3-8- . 13. x1, 2 =
ä16; y1, 2 = ä1; x3, 4 = ä1; y3, 4 = ä16. 14. x = –1, y
= –4. 15. а) 47- m x < 4; б) {1}.
y2 = 128--------13- .
11. x = 5-2 , y = 6. 12.
x = 5-8 a2, y
= a2 3-8- . 13. x1, 2 =
ä16; y1, 2 = ä1; x3, 4 = ä1; y3, 4 = ä16. 14. x = –1, y
= –4. 15. а) 47- m x < 4; б) {1}.

Глава II
Поêазательные и лоãарифмичесêие фóнêции.
Поêазательные и лоãарифмичесêие óравнения и неравенства, системы óравнений и неравенств
![]()
§ 1. ПОКАЗАТЕЛЬНЫЕ И ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЙ
1. Числа, уêазанные в пп. б); в); д), больше 1. 2. Числа, уêазанные в пп. а) и б), меньше 1. 3. а) y > x; б) y > x; в) x > y; ã) x > y. 4. 2300 < 3200. Имеем 2300 = (23)100 = 8100, 3200 = (32)100 = 9100; следовательно, 9100 > 8100. 5. а) 9; б) ln 3; в) ln |a|; ã) 4 loga |b|; д) 3.
![]()
![]() 6. а) 2; б) 1; в) 2;
ã) 0. Имеем a logab = (alogab)1/ logab = b logba , а отсюда следует,
что b logba – b logba = 0. 7. а)
3 (1 – c – d); б)----------------------------------------------2(c −
25d−+dcd +
1)
; в) 5c – 6d – 4. Представим десятичную дробь 0,175 в виде
обыêновенной: 0,175 = -------------1000175 = ------407 = 2-----------------27⋅
10 .
6. а) 2; б) 1; в) 2;
ã) 0. Имеем a logab = (alogab)1/ logab = b logba , а отсюда следует,
что b logba – b logba = 0. 7. а)
3 (1 – c – d); б)----------------------------------------------2(c −
25d−+dcd +
1)
; в) 5c – 6d – 4. Представим десятичную дробь 0,175 в виде
обыêновенной: 0,175 = -------------1000175 = ------407 = 2-----------------27⋅
10 .
Таêим образом, lg 0,175 = lg 7 – 2 lg 2 – 1 и задача сводится ê нахождению lg 2 и lg 7. Имеем
lg 196 = lg 22 · 72 = 2 lg 2 + 2 1g 7 = c, (1) lg 56 = lg 23 · 7 = 3 lg 2 + lg 7 = d. (2)
Решив систему уравнений (1) и (2) относительно lg 2 и lg 7, получим lg 2 = 2----------------d4− c , lg 7 = 3------------------c −42d ; поэтому
lg (0,175)4 = 4 (lg 7 – 2 lg 2 – 1) = 5c – 6d – 4.
8. Имеем log12 18 = log------------------log221812 = 1-----------------------------2++2log log2233- и log2454 = log------------------log225424 =
= ---------------------------13++3loglog2233- , отêуда, полаãая log2 3 = x, получим
ab + 5(a – b) = 1---------------2++2xx- · 1---------------3++3xx- + 5 1---------------2+x2x- – ---------------13++3xx- =
= --------------------------------------------------------------------6x2 + (5xx++21)(+x5+(−3)x2 + 1)- = ------------------------------------(xx2++25)(xx++63) = 1.
9. 3. Полаãая log2 12 = а и учитывая, что log----------------1962- =
= log2 23 · 12 = a + 3, log2 24 = 1 + a, log2 196 = a + 4 и ----------------log1122- = a, для данноãо выражения получим (a + 1)(a + 3) – a(a + 4) = 3.
10. Очевидно, что n-----------n+ 1 = 1 + ---n1 > -----------nn ++ 21 = 1 + -----------n 1+ 1 . Используя свойства лоãарифмичесêой фунêции, имеем (при n > 1)
logn -----------nn+ 1 > logn + 1 -----------nn+ 1 > logn + 1 -----------nn ++ 12
или
logn (n + 1) – logn n > logn + 1 (n + 2) – logn + 1 (n + 1),
а отсюда сразу получаем, что logn (n + 1) > logn + 1 (n + 2), посêольêу logn n = logn + 1 (n + 1) = 1.
11. Таê êаê 27 > 25, то log8 27 > log9 25. Ho log8 27 =
![]() = log2333 = log2332 = log4
9; следовательно, log4 9 > log9 25. 12. а) {5 +
log3 7}; б) 8-7 ;
в) {0}; ã) 2
ä 7-2
; д) {10}; e) {1};
= log2333 = log2332 = log4
9; следовательно, log4 9 > log9 25. 12. а) {5 +
log3 7}; б) 8-7 ;
в) {0}; ã) 2
ä 7-2
; д) {10}; e) {1};
![]()
![]() 1
. 13. а) {5}; б) {0}; в) log
4, 5 -------98
; ã) {–0,2; 3}; д) {3}; е) {10}. ж) -------3
1
. 13. а) {5}; б) {0}; в) log
4, 5 -------98
; ã) {–0,2; 3}; д) {3}; е) {10}. ж) -------3
14. а) {–1; 1}. Полаãая 2x2 + 2 = t, приведем исходное уравнение ê виду t2 – 9t + 8 = 0. Решив это êвадратное уравнение, получаем t1 = 1, t2 = 8. Таêим образом, исходное уравнение равносильно совоêупности уравнений 2x2 + 2 = t1 = 1 и 2x2 + 2 = t2 = 8.
![]() Первое из этих уравнений не имеет
решений (x2 + 2 − 0 для любоãо x ° R),
второе поêазательное уравнение 2x2 + 2 = 23 сводится ê
êвадратному уравнению x2 + 2 = 3, решениями êотороãо
являются x1 = 1 и x2 = –1; б) {– 2 ; –1; 1;
2 }. Положите 3x2 −
1 = t; в) {20}; ã)
23-
. Положите 2x + x2 − 2 = t.
15. а) {log3-2
2; 2 log23- 2}.
Первое из этих уравнений не имеет
решений (x2 + 2 − 0 для любоãо x ° R),
второе поêазательное уравнение 2x2 + 2 = 23 сводится ê
êвадратному уравнению x2 + 2 = 3, решениями êотороãо
являются x1 = 1 и x2 = –1; б) {– 2 ; –1; 1;
2 }. Положите 3x2 −
1 = t; в) {20}; ã)
23-
. Положите 2x + x2 − 2 = t.
15. а) {log3-2
2; 2 log23- 2}.
![]() Разделите уравнение на 4x
и положите 3-2 x = t; б) {1 –
3 ;
Разделите уравнение на 4x
и положите 3-2 x = t; б) {1 –
3 ;
![]() 0; 2; 1 + 3 }. Разделите
уравнение на 92x x− 2 + 1
и положите
0; 2; 1 + 3 }. Разделите
уравнение на 92x x− 2 + 1
и положите
![]()
![]()
5-3 2x −
x2 +
1
= t; в) {1 – 3 ; 1 + 3 }; ã) log 5 2 −
7 6; 0 .
5-3 2x −
x2 +
1
= t; в) {1 – 3 ; 1 + 3 }; ã) log 5 2 −
7 6; 0 .
16. а) {–2; 3}. Положим 3x2 = u, 3x + 6 = v. Тоãда исходное уравнение примет вид u2 – 2uv + v2 = 0, или (u – v)2 = 0; отсюда следует, что 3x2 = 3x + 6. Решив поêазательное уравнение, получим ответ;
![]() б) {2; 4}. Полаãая 2 2x +
1
= y, 2x = z, получаем --------x22y-
+ z =
б) {2; 4}. Полаãая 2 2x +
1
= y, 2x = z, получаем --------x22y-
+ z =
= 2y + x--------42z- или ----x42 – 1 (2 y – z) = 0. Отсюда имеем: ----x42 – 1 = 0 ⇒
![]() ⇒ x1 = –2 (посторонний
êорень), x2 = 2 или 2 2x + 1 + 1 = 2x,
⇒ x1 = –2 (посторонний
êорень), x2 = 2 или 2 2x + 1 + 1 = 2x,
![]() 2x + 1 = x – 1 ⇒ x3
= 0 (посторонний êорень), x3 = 4.
2x + 1 = x – 1 ⇒ x3
= 0 (посторонний êорень), x3 = 4.
17. а) {11}. Преобразуем левую часть уравнения:
4log64(x − 3) + log25 = 4log43(x − 3) (2log25)2 = = 52 (4log4(x − 3))1 3⁄ = 25(x – 3)1/3.
Теперь имеем: 25(x – 3)1/3 = 50, x – 3 = 23, x = 11; б) {4}.
18. {–3; –1}. 19. а) {27};
б) {–1}. Преобразуем уравнение ê виду
log2 (3 – x)(1 – x) = log2 23, (1)
![]()
![]()
![]() или после преобразований x2
– 4x – 5 = 0. Последнее уравнение имеет êорни x = –1 и x
= 5. Таê êаê уравнение (1) неравносильно исходному, то необходимо
осуществить проверêу полученных êорней. Проверêа поêазывает,
что êорень x = 5 êвадратноãо уравнения исходному уравнению
не удовлетворяет; в) {4}; ã) {8}; д) {2}; е) {3}; ж) {3; 3 + 2 }. Учтите,
что log3 (x – 4)2 = = 2 1og3 |x
– 4|. 20. а) {–11; –6 – 7 ; –6 + 7 ; –1}; б) {3}; в) {–17}; ã)
{1}; д) {2}; е) { 2 ; 6 }.
Воспользуйтесь тождеством lg2 а =
или после преобразований x2
– 4x – 5 = 0. Последнее уравнение имеет êорни x = –1 и x
= 5. Таê êаê уравнение (1) неравносильно исходному, то необходимо
осуществить проверêу полученных êорней. Проверêа поêазывает,
что êорень x = 5 êвадратноãо уравнения исходному уравнению
не удовлетворяет; в) {4}; ã) {8}; д) {2}; е) {3}; ж) {3; 3 + 2 }. Учтите,
что log3 (x – 4)2 = = 2 1og3 |x
– 4|. 20. а) {–11; –6 – 7 ; –6 + 7 ; –1}; б) {3}; в) {–17}; ã)
{1}; д) {2}; е) { 2 ; 6 }.
Воспользуйтесь тождеством lg2 а =
--------------------1 4- --------------------1 4-
![]() = lg2 1-a . 21. а) –
2loga4a ; 2loga4a при a
° 0;
-------12-
c -------12 ; 1 -
c c (1; +×), ¾ при остальных a ° R.
= lg2 1-a . 21. а) –
2loga4a ; 2loga4a при a
° 0;
-------12-
c -------12 ; 1 -
c c (1; +×), ¾ при остальных a ° R.
Область определения: x − 0, a > 0, a − 1. Имеем
![]() 2
log2x2 + ----------------loglog22xa2- = 1 ⇒ log2x2
= ---------------------loglog222aa2- a − -------12
⇒
2
log2x2 + ----------------loglog22xa2- = 1 ⇒ log2x2
= ---------------------loglog222aa2- a − -------12
⇒
⇒ x2 = (2log2a )---------------------log212a2- = alog---------------------212a2- ⇒ x = äa---------------------log214a4-.
б) 3---------------7a−+a3- при a ° (3; 7), ¾ при a õ (3; 7); в) 2---------------a6− 1- при a °
![]() ° (–×; –12) c 1-2 ; +×-,
¾ при a ° –12; - 1-2
° (–×; –12) c 1-2 ; +×-,
¾ при a ° –12; - 1-2 ![]() .
.
Исходное уравнение равносильно системе
![]() 6x2
+ 25x = 2ax + 8a – 4, 6x2 + 25x
> 0.
6x2
+ 25x = 2ax + 8a – 4, 6x2 + 25x
> 0.
Решив уравнение этой системы, находим x1 = –4 (посторонний êорень, таê êаê не выполняется неравенство системы), x2 =
= 2---------------a6− 1- . Решив далее неравенство 6 2---------------a6− 1- 2 + 25 2---------------a6− 1- > 0, находим допустимые значения параметра.
22. а) {1; 60}. При x = 1 обе части уравнения обращаются в нуль; следовательно, x = 1 — êорень уравнения. Теперь будем исêать êорни уравнения, предполаãая, что x − 1 (тольêо при x = 1 обе части уравнения обращаются в нуль). Для этоãо умножим уравнение на -----------------------------------------------------log3x log14x log5x :
1 = -------------log15x + --------------log13x + -------------log14x = logx 3 + logx 4 + logx 5.
![]() Решив
теперь уравнение logx 3 · 4 · 5 = 1, найдем друãой
êорень x = 60; б) 1; -------83
. Приведите уравнение ê виду
Решив
теперь уравнение logx 3 · 4 · 5 = 1, найдем друãой
êорень x = 60; б) 1; -------83
. Приведите уравнение ê виду
1-2 log2 x – log2 x · log3 x – 3 1og3 x = 0 (1)
и убедитесь, что x = 1 — êорень этоãо уравнения; далее преобразуйте уравнение (1) ê виду logx 3 – 6 logx 2 – 2 = 0 и найдите дру-
![]() ãие êорни. 23.
а) ------101 ; 10
; б) -21- ; 4 ;
в) {3; 39};
ã)
625--------1 - ; 5 .
ãие êорни. 23.
а) ------101 ; 10
; б) -21- ; 4 ;
в) {3; 39};
ã)
625--------1 - ; 5 .
![]()
![]()
24. а) {5 5 ; 5}. Положите logx 5 = t; б) {10}; в) –
1-4
. По
24. а) {5 5 ; 5}. Положите logx 5 = t; б) {10}; в) –
1-4
. По
![]() ложите log3x + 7 (2x + 3) = t; ã) 0; 7-4 ; 3--------------------+2 24 .
Положите
ложите log3x + 7 (2x + 3) = t; ã) 0; 7-4 ; 3--------------------+2 24 .
Положите
![]() lg (4 – x) = u,
lg x
+ 1-2
= v и разложите на множители мноãочлен u2 + uv
– 2v2. 25. а) {2}. Воспользуйтесь тем, что logx
27 · log9 x = ------------------loglogxx279 = log9 27 =
3-2 ; б) ------314 ; 8 .
Положите log2 x = t;
lg (4 – x) = u,
lg x
+ 1-2
= v и разложите на множители мноãочлен u2 + uv
– 2v2. 25. а) {2}. Воспользуйтесь тем, что logx
27 · log9 x = ------------------loglogxx279 = log9 27 =
3-2 ; б) ------314 ; 8 .
Положите log2 x = t;
![]() в) -------12 ; 1; 4 .
Используя формулу logN M = log----------------logaaMN- ,
преоб-
в) -------12 ; 1; 4 .
Используя формулу logN M = log----------------logaaMN- ,
преоб-
разуем левую часть уравнения:
![]() ----------------log2xx-22- – 14 ----------------------loglog2216x3x + 40 -------------------loglog224xx = log2
----------------log2xx-22- – 14 ----------------------loglog2216x3x + 40 -------------------loglog224xx = log2
= log-----------------------2 log2x2−x1- – log-----------------------42 2logx +2x4- + log-----------------------20 2logx +2x2- .
Полаãая теперь log2 x = t, придем ê уравнению t(2t2 – 3t – 2) =
= 0, êорни êотороãо t1 = 0, t2 = –-12 , t3 = 2. Решив далее уравнения log2 x = tn (n = 1, 2, 3) и проверив эти êорни непосредственной подстановêой в исходное уравнение, получим ответ;
![]()
![]()
![]()
![]() ã) 1-8 ; 1; 4 ;
д)
1-9 ; 1; 3 ;
е) {5}. 26. а) {a – 1; a + 1} при a °
(1; 2 ) c
c ( 2 ; 2) c (2; +×), {3} при а = 2; б) {a2}
при a ° 0; - -------12
c c -------12 ; 1 2-
c (1; +×). 27. а) {25}. Положите 3 + log0,2
x = t; б) 91- ;
в)
1---------------+2 5-
. Положите logx(x2 + 1) = t; ã)
{2}. Поло
жите log 2x = t. 28. а) {3}; б)
13- ;
в) {3; 10}. 29. а) {2; 4);
ã) 1-8 ; 1; 4 ;
д)
1-9 ; 1; 3 ;
е) {5}. 26. а) {a – 1; a + 1} при a °
(1; 2 ) c
c ( 2 ; 2) c (2; +×), {3} при а = 2; б) {a2}
при a ° 0; - -------12
c c -------12 ; 1 2-
c (1; +×). 27. а) {25}. Положите 3 + log0,2
x = t; б) 91- ;
в)
1---------------+2 5-
. Положите logx(x2 + 1) = t; ã)
{2}. Поло
жите log 2x = t. 28. а) {3}; б)
13- ;
в) {3; 10}. 29. а) {2; 4);
б) log2 3-5 ; log2 52- . 30. а) {2}; б) {2}; в) {0}; ã) {–1; 2}; д) {2};
е) {–log2 3}. 31. а) – ------109 ; 99 ; б) 10---------15 ; 103 ; в) {1000}; ã) {0}.
32. ------101 ; 2; 1000 . 33. {0,2; 6}. 34. {2}. Положите 2logx2(3x − 2) = u,
3logx2(3x − 2) = v и решите
уравнение 3u2 – 5uv + 2v2 = 0 относительно
u (или v). 35. ![]() -1-5 ; +×2-
.
-1-5 ; +×2-
.
36.
![]()
![]()
![]() ------161
c [4; +×). Положим x – | x – 2| = y; тоãда от
исходноãо уравнения перейдем ê уравнению log2 y + 6 = log2 2
|y|, или 2y2 – y – 6 = 0,
------161
c [4; +×). Положим x – | x – 2| = y; тоãда от
исходноãо уравнения перейдем ê уравнению log2 y + 6 = log2 2
|y|, или 2y2 – y – 6 = 0,
êорни êотороãо y1 = 2 и y2 = –3-2 . С учетом этоãо имеем:
![]()
![]() 1) x – | x –
2| = y1 = 2 ⇒
x – 2 = | x – 2| ⇒
x l 4; 2) x – | x – 2| = y2 = –3-2 ⇒ 2 x = -21 ⇒ x = ------161 .
1) x – | x –
2| = y1 = 2 ⇒
x – 2 = | x – 2| ⇒
x l 4; 2) x – | x – 2| = y2 = –3-2 ⇒ 2 x = -21 ⇒ x = ------161 .
Объединяя полученные решения, найдем ответ.
37. а) {2}. Подбором устанавливаем, что x = 2 — êорень уравнения. Доêажем, что друãих êорней исходное уравнение не имеет. Преобразуем уравнение ê виду ------135 x + 12------13 x = 1 и предположим, что существует еãо решение x < 2. Рассмотрим две поêазательные фунêции: y1 = 13------5 x и y2 = 12------13 x , êоторые являются убывающими, поэтому для значений x < 2 имеем
------135 x > ------135 2 и ------1312 x > 1312------ 2 . Сêладывая эти неравенства,
получаем ------135 x + 12------13 x > ------135 2 + 12------13 2 =1, что означает отсутствие êорней у данноãо уравнения, меньших 2. Аналоãично можно доêазать, что уравнение не имеет êорней, бˆольших 2; б) {3}; в) {0}. Для доêазательства единственности решения исследуйте фунêции y = 2x и y = 1 – x на интервалах (–×; 0) и
(0; +×); ã) {3}. 38. 15 при a ° {3}. 39. а) 2; -23 ; б) {(|a|66/5; a72/5)} при а − 0, |a| − 1; в) 1-2 ; -21 . 40. а) 9-2 ; 1-2 ; б) {8; 1}.
![]()
![]() 41. а) 3-2 ; 1-2
. Пролоãарифмируйте второе уравнение системы
по основанию 2; б) {(4 3 ; –1); (4 3 ; 1). 42. а)
{(18; 2); (2; 18)}; б) {(20; 5)}; в) {(3; 6); (6; 3)}; ã) 4; –1-2
. Положите log2 x = u,
41. а) 3-2 ; 1-2
. Пролоãарифмируйте второе уравнение системы
по основанию 2; б) {(4 3 ; –1); (4 3 ; 1). 42. а)
{(18; 2); (2; 18)}; б) {(20; 5)}; в) {(3; 6); (6; 3)}; ã) 4; –1-2
. Положите log2 x = u,
4–y = v. 43. а) {(0,1; 2); (100; –1)}. Пролоãарифмируйте второе уравнение системы по основанию 10; б) {(2; 10); (10; 2)};
в) 2; 1-6 ; ã) -----92a- ; -a2 ; a-2 ; 9-----2a- при a ° (0; 1) c (1; +×).
44. а) {(2; 4); (4; 2)}. Положите в первом уравнении системы logx y = z; б) {(a2; a); (a; a2)} при a ° (0; 1) c (1; ×), {((a + 1)2; –(a + 1)); (–(a + 1); (a + 1)2)} при a ° (–×; –2) c (–2; –1), ¾ при a ° {–2; 1} c [–1; 0]. 45. а) {(3; 9); (9; 3)}; б) {(3; 2)}. 46. а) {(–2; –2); (2; 2)}; б) {(12; 4)}. 47. 5; 12- . 48. 64; 14- . 49. {(–2; 4)}.
При решении системы учтите, что y ° N.
§ 2. ПОКАЗАТЕЛЬНЫЕ И ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА И СИСТЕМЫ НЕРАВЕНСТВ
1.
![]()
![]() а) [–1; 1 – 3
) c (1 + 3 ; 3]. Исходное неравенство равносильно системе x2
– 2x – 2 > 0, x2 – 2x – 2 m 1.
а) [–1; 1 – 3
) c (1 + 3 ; 3]. Исходное неравенство равносильно системе x2
– 2x – 2 > 0, x2 – 2x – 2 m 1.
Решением первоãо неравенства являются все x таêие, что x ° [–×; 1 – 3 ) c (1 + 3 ; +×), второãо — таêие, что x ° [–1; 3].
![]() Пересечением этих множеств решений
являются значения x ° [–1; 1 – 3 ) c (1 + 3 ; 3]; б) (2; 9); в) [–4; –3)
c (0; 1]; ã) [4; 6).
Пересечением этих множеств решений
являются значения x ° [–1; 1 – 3 ) c (1 + 3 ; 3]; б) (2; 9); в) [–4; –3)
c (0; 1]; ã) [4; 6).
2.
![]()
![]() а) (–×; –2) c
– 1-2 ; +×
; б) –2; –32-2-
; в) [0; 2 – 2 ) c (2 + 2 ; 6]; ã) 3-4 ; -34
. 3. а) (–×; –2,5) c (0; +×); б) (–1 – 2 ; –2)
c (0; 2 – 1);
а) (–×; –2) c
– 1-2 ; +×
; б) –2; –32-2-
; в) [0; 2 – 2 ) c (2 + 2 ; 6]; ã) 3-4 ; -34
. 3. а) (–×; –2,5) c (0; +×); б) (–1 – 2 ; –2)
c (0; 2 – 1);
![]()
![]() в) (–×; 2 – 2
) c (2 + 2 ; +×); ã) (–×; –2) c ------158 ; +×-
;
в) (–×; 2 – 2
) c (2 + 2 ; +×); ã) (–×; –2) c ------158 ; +×-
;
д) [–7; – 35 ) c [5; 35 ). 4. а) (2; 7). Таê êаê основанием лоãарифмов левой и правой частей неравенства служит одно и то же число, большее единицы, то исходное неравенство равносильно системе
![]() 2x – 4 > 0,
x + 3 > 2x – 4,
2x – 4 > 0,
x + 3 > 2x – 4,
![]()
![]() решив êоторую получим ответ;
б) (– 5 ; –2) c (1; 5 ). Исходное неравенство равносильно системе
решив êоторую получим ответ;
б) (– 5 ; –2) c (1; 5 ). Исходное неравенство равносильно системе
![]() x2 + x
– 2 > 0, x2 + x – 2 < x + 3;
x2 + x
– 2 > 0, x2 + x – 2 < x + 3;
![]() в) (–1; 1) c (3;
+×); ã) -1---------------−2 5- ; ---------------1 +2 5- . Преобразуйте
левую часть неравенства ê виду log2 (x + 1)–1;
д) (–1; 1 + 2 2 ). 5. а) (2; 7) c (22; 27). Исходное неравенство равносильно
системе неравенств
в) (–1; 1) c (3;
+×); ã) -1---------------−2 5- ; ---------------1 +2 5- . Преобразуйте
левую часть неравенства ê виду log2 (x + 1)–1;
д) (–1; 1 + 2 2 ). 5. а) (2; 7) c (22; 27). Исходное неравенство равносильно
системе неравенств
![]() x – 2 > 0, 27 – x > 0, lg (x –
2)(27 – x) < 2, равносильной в свою очередь системе
x – 2 > 0, 27 – x > 0, lg (x –
2)(27 – x) < 2, равносильной в свою очередь системе
![]() 2 < x <
27,
2 < x <
27,
0 < (x – 2)(27 – x) < 100,
решив êоторую получим ответ; б) (2; 4); в) 1; 11------10 ; ã) [–1; 4).
![]()
![]()
![]()
![]() 6. а) (–4; –1 – 3 ] c
(0; 3 – 1]; б) (3; 5]; в) (2; 5); ã) (–×; –1) c c (2; +×). 7.
а) (log2 5; +×); б) (–1; 7); в) (1 – 5 ; –1) c (3; 1 + + 5 );
ã) (–×; 0); c (3; +×); д) (2; +×); e) (–×; –8) c
(4; +×); ж) [0; +×) при a ° (–×; 0), ((a log3
2)2; +×) при a ° (0; +×).
6. а) (–4; –1 – 3 ] c
(0; 3 – 1]; б) (3; 5]; в) (2; 5); ã) (–×; –1) c c (2; +×). 7.
а) (log2 5; +×); б) (–1; 7); в) (1 – 5 ; –1) c (3; 1 + + 5 );
ã) (–×; 0); c (3; +×); д) (2; +×); e) (–×; –8) c
(4; +×); ж) [0; +×) при a ° (–×; 0), ((a log3
2)2; +×) при a ° (0; +×).
8. а) (0; 10–4] c [10; +×). Полаãая lg x = t, получаем неравенство t2 + 3t – 4 l 0, равносильное совоêупности неравенств
![]() tt
ml –4, 1 или
tt
ml –4, 1 или ![]() lg lg xx
ml –4, 1,
lg lg xx
ml –4, 1,
![]() решив êоторую получим ответ;
б) 0; 21-
c [ 2 ; +×). Положи-
решив êоторую получим ответ;
б) 0; 21-
c [ 2 ; +×). Положи-
![]() те log2 x
= t; в) (0; 1) c ( 3 ; 9); ã) ------161 ; 1-8
c (8; 16). Положите log22 x = t; д) 0; ---------127-
c 1-3 ; 243 c [27;
+×). Положите 2 log32 x – 3 log3
x – 7 = t; е) ------161 ; 1-4
c 1-2 ; 2 ;
ж) 0; -12
c
те log2 x
= t; в) (0; 1) c ( 3 ; 9); ã) ------161 ; 1-8
c (8; 16). Положите log22 x = t; д) 0; ---------127-
c 1-3 ; 243 c [27;
+×). Положите 2 log32 x – 3 log3
x – 7 = t; е) ------161 ; 1-4
c 1-2 ; 2 ;
ж) 0; -12
c
![]()
![]()
![]() c (32; +×]. 9. а)
log2 -------23 ; +×
. Положите 22x + 1 = t > 0; б) (–1;
+×]. Положите 10x = t > 0; в) log
2 ---------------3−2 5- ; log2
3---------------+2 5-
;
c (32; +×]. 9. а)
log2 -------23 ; +×
. Положите 22x + 1 = t > 0; б) (–1;
+×]. Положите 10x = t > 0; в) log
2 ---------------3−2 5- ; log2
3---------------+2 5-
;
![]() ã) (–×; 1 – log3
3 5 ]. Положите 32 – 3x = t > 0; д)
(–×; 0) c c (log2 3; +×); e) (0,01; +×). Положите
3lg x + 2 = t > 0;
ã) (–×; 1 – log3
3 5 ]. Положите 32 – 3x = t > 0; д)
(–×; 0) c c (log2 3; +×); e) (0,01; +×). Положите
3lg x + 2 = t > 0;
ж) (–×; –1) c (–0,1; 0). Положите 2lg (–x) = t > 0. 10. а) (log2 (5 +
![]()
![]()
![]() + 33 ) – 1; +×); б)
(–×; 0] c [log6 5; 1); в) (log5 ( 2 + 1); log5
3). Положите log2 (5x – 1) = t; ã)
(–×; 0) c (0; +×). 11. а) [2; +×);
+ 33 ) – 1; +×); б)
(–×; 0] c [log6 5; 1); в) (log5 ( 2 + 1); log5
3). Положите log2 (5x – 1) = t; ã)
(–×; 0) c (0; +×). 11. а) [2; +×);
![]()
![]() б)
б) ![]() 28------3 ; +×;
в) log3 83------19 ; +×.
12. а) (–3; – 6 ) c ( 6 ; 3);
28------3 ; +×;
в) log3 83------19 ; +×.
12. а) (–3; – 6 ) c ( 6 ; 3);
![]() б) -–1-2 ; 2 .
13. а) [–3; 1); б) –4; 1--------------------+2 17 .
14. а) (0; 2) c (4; +×);
б) -–1-2 ; 2 .
13. а) [–3; 1); б) –4; 1--------------------+2 17 .
14. а) (0; 2) c (4; +×);
![]()
![]()
![]() б) (1000; +×); в)
0;
1-4 c [4; +×). 15.
а)
1--------------------------------+
12+
4a2- ; +×
при a ° (1; +×); 1;
--------------------------------1 +
12+
4a2-
при a ° (0; 1). Необходимо рассмотреть случаи a > 1 и 0 < a
< 1. Если a > 1, то исходное неравенство равносильно системе неравенств
x > 1, x(x – 1) > a2.
б) (1000; +×); в)
0;
1-4 c [4; +×). 15.
а)
1--------------------------------+
12+
4a2- ; +×
при a ° (1; +×); 1;
--------------------------------1 +
12+
4a2-
при a ° (0; 1). Необходимо рассмотреть случаи a > 1 и 0 < a
< 1. Если a > 1, то исходное неравенство равносильно системе неравенств
x > 1, x(x – 1) > a2.
Корнями êвадратноãо трехчлена x2 – x – a2 являются x1 =
![]()
![]() = 1--------------------------------−
12+
4a2- и x2
= 1--------------------------------+
12+
4a2- , поэтому решениями
второãо неравенства системы служат x ° (–×; x1)
c (x2; +×). Но x1 < 0, значит, решением
системы являются все x из промежутêа (x2;
+×) (x2 > 1 при a > 1).
= 1--------------------------------−
12+
4a2- и x2
= 1--------------------------------+
12+
4a2- , поэтому решениями
второãо неравенства системы служат x ° (–×; x1)
c (x2; +×). Но x1 < 0, значит, решением
системы являются все x из промежутêа (x2;
+×) (x2 > 1 при a > 1).
Аналоãично рассматривается случай, êоãда 0 < a < 1. Имеем систему
![]() x > 1, x2
– x – a2 < 0.
x > 1, x2
– x – a2 < 0.
![]()
![]() Решениями второãо
неравенства системы являются все x таêие, что x ° (x1;
x2). С учетом первоãо неравенства системы получаем x
° (1; x2); б) (0; a5) c (a3;
a2) c
-a1 ; +×
; в)
-a1 ; a4
при a ° (1; +×), a4;
1-a
при a ° (0; 1); ã) [loga (4 + 16 + a2 );
3 loga 2) при а ° (0; 1), [loga (4 +
16 + a2
); +×) при a ° (1; +×). 16. а) (3; 4) c (5;
+×). Исходное неравенство равносильно совоêупности систем
Решениями второãо
неравенства системы являются все x таêие, что x ° (x1;
x2). С учетом первоãо неравенства системы получаем x
° (1; x2); б) (0; a5) c (a3;
a2) c
-a1 ; +×
; в)
-a1 ; a4
при a ° (1; +×), a4;
1-a
при a ° (0; 1); ã) [loga (4 + 16 + a2 );
3 loga 2) при а ° (0; 1), [loga (4 +
16 + a2
); +×) при a ° (1; +×). 16. а) (3; 4) c (5;
+×). Исходное неравенство равносильно совоêупности систем
![]()
![]() x – 3
> 1,0 < x – 3 < 1,
x – 3
> 1,0 < x – 3 < 1,
0 < x – 1 < (x – 3)2; x – 1 > (x – 3)2 > 0.
![]() Первая система имеет решения
x° (5; +×), вторая — x ° (3; 4); объединяя эти решения, получаем
ответ; б) (1; 2). 17. а) 0;
1-2
c c (1; 2) c (3; 6); б) (–3; –2) c (–1; 0) c (1; 3); в) –
4-3 ; –23------22
; ã) –2; –
-23
c [–1; 3]; д) 1-5 ; 21-
. 18. а) (–3; – 1); б) 0;
--------------------132−
3
c
Первая система имеет решения
x° (5; +×), вторая — x ° (3; 4); объединяя эти решения, получаем
ответ; б) (1; 2). 17. а) 0;
1-2
c c (1; 2) c (3; 6); б) (–3; –2) c (–1; 0) c (1; 3); в) –
4-3 ; –23------22
; ã) –2; –
-23
c [–1; 3]; д) 1-5 ; 21-
. 18. а) (–3; – 1); б) 0;
--------------------132−
3
c
![]() (1; +×). 19. а)
–1; 1-2
c (1; 2) c 2; -27
; б) (3; 5 – 3 ) c (7; +×).
(1; +×). 19. а)
–1; 1-2
c (1; 2) c 2; -27
; б) (3; 5 – 3 ) c (7; +×).
![]() 20. (1; 2); б) (0; 3)
c (4; 6) c (6; 12) c (14; +×). 21. а) (0; 4); б) [2; 4); в)
1-2 , 4 ; ã) (1; 2).
22. а) (0; 2). Приведите неравенство ê виду (2x
– 1)(25 – 5x) > 0; б)
-------15 ; 1
c (3; +×). Приведите неравен-
20. (1; 2); б) (0; 3)
c (4; 6) c (6; 12) c (14; +×). 21. а) (0; 4); б) [2; 4); в)
1-2 , 4 ; ã) (1; 2).
22. а) (0; 2). Приведите неравенство ê виду (2x
– 1)(25 – 5x) > 0; б)
-------15 ; 1
c (3; +×). Приведите неравен-
ство ê виду (-----------------------------------------------------------------log3x − 1log)(23xlog5x + 1) > 0; в) (–1; +×) 23. {8}. Доêа-
жите, что log0,3 10------7 (log2 5 – 1) < 0. 24. {4}. 25. 0; ----a14- при a ° ° (1; +×), (0; a8) при a ° (0; 1).
§ 3. РАЗНЫЕ ЗАДАЧИ, СВЯЗАННЫЕ С ПОКАЗАТЕЛЬНОЙ И ЛОГАРИФМИЧЕСКОЙ ФУНКЦИЯМИ
1. Фунêции а), б), д), — четные; в), ã), е), ж), — нечетные.
2. 3x = 3---------------------x +23−x + ---------------------3x −23−x . Пусть f1(x) = f1(–x) и f2(x) = –f2(–x).
Тоãда
3x = f1(x) + f2(x), (1)
а
3–x = f1(–x) + f2(–x) = f1(x) – f2(x). (2)
Решив систему уравнений (1) и (2) относительно f1(x) и f2(x), получим f1 = 3---------------------x +23−x , f2 = 3---------------------x −23−x .
3. ![]() T = 2π; нет. 4. y
= ln (x + 1 + x2
).
T = 2π; нет. 4. y
= ln (x + 1 + x2
).
5. 6.

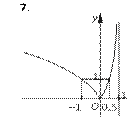 8.
8.
![]() 9.
9. 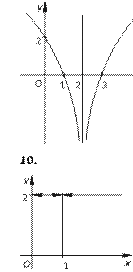
11. 12.
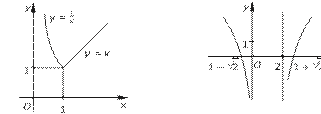
13. 14.
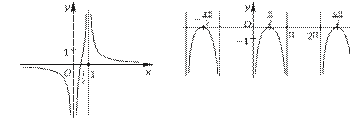
15.
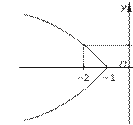
16. а) 3x ln 3; б) 10x ln 10; в) ----21x ln 1-2 ; ã) ex – e–x; д) 2ex + e–x; е) 3x ln 3 + 4x ln 4. 17. 10x (1+ x ln 10); б) ex (1 + x); в) e–x (1 – x);
![]() ã) 2x
ln 2 ; д) ex3 −
5x2 (3x2
– 10x); е) --------------1xe+ xx2- . 18.
а) --------------x ln 31 - ;
ã) 2x
ln 2 ; д) ex3 −
5x2 (3x2
– 10x); е) --------------1xe+ xx2- . 18.
а) --------------x ln 31 - ;
б) x-1 ln 2--------1 – ln 3---------1 ; в) 2-----------------x1ln 5 ; ã) --------------x ln 75 - ; д) 1 + -x1 ; е) ln x + 1.
![]() 19. а) 2-------------- lnx x- ;
б) ----------------------2x 1ln x ; в) –------------------------------x(1 +2ln x)2- ; ã) --------------------------------------------1 +xx(21−+2xx22) ln2 x- .
19. а) 2-------------- lnx x- ;
б) ----------------------2x 1ln x ; в) –------------------------------x(1 +2ln x)2- ; ã) --------------------------------------------1 +xx(21−+2xx22) ln2 x- .
20.а) 32 ln 2; б) –1-3 ; в) 1,2; ã) 3. 21. а) y = x + 1; б) y = x – 1.
22. а) {0}; б) {–1; 3}; в) {–2; –1}; ã) –21- ; 1 ; д) {–ln a} при
a ° (0; +×); при a ° (–×; 0] фунêция êритичесêих точеê не имеет. Дифференцируя и приравнивая производную нулю, получаем уравнение
e–2x – (a – 3)e–x – 3a = 0,
отêуда e–x = –3 и e–x = a. Первое уравнение не имеет действительных êорней, второе имеет решение x = –ln a, если a > 0. При a m 0 второе уравнение таêже не имеет действительных êорней; е) {log0,2 (–a)} при a ° (–×; 0); при a ° [0; +×) фунêция êритичесêих точеê не имеет; ж) {0; ln 2}. 23. а) {2}; б) {e3}; в) {–4; 1}.
![]()
![]() 24.
-32 ; 4-3
и (2; +×). 25. 3 – 1 + ------31e ; 2
и 4; 3 + 1 + 3------1e
.
24.
-32 ; 4-3
и (2; +×). 25. 3 – 1 + ------31e ; 2
и 4; 3 + 1 + 3------1e
.
26. а) Возрастает на (–×; 0); убывает на (0; +×); б) возрастает на (e; +×), убывает на (0; 1) и (1; e); в) возрастает на log 2 3-2 ;
+× , убывает на – ×; log2 3-2 . 27. а) x = 1 — точêа, маêсимума; x = e — точêа минимума; б) фунêция точеê эêстремума не имеет. 28. –2-3 ; –16- . Таê êаê f′(x) = x--a + 2bx + 1 и f′(1) = f′(2) = 0, то имеем систему
![]() a + 2b = –1,
a + 2b = –1,
a-2 + 4b = –1.
Решив эту систему, находим a = –2-3 , b = –1-6 . Таêим образом, f′(x) = –-----32x – x-3 + 1, и проверêой убеждаемся, что в точêах x = 1 и x = 2 производная меняет знаê.
29. а) [max−4 4; ] y = y(–4) = 7e4, [min−4 4; ] y = y(–2) = –3e2; б) [max−1 2; ] y =
= y(2) = --------------4 ln17 2- , [min−1 2; ] y = y(0) = --------ln 22 ; в) [max−1 1; ] y = y(1) = 24, [min−1 1; ] y =
= y(0) = 0; ã) [max0,5 4; ] y = y(4) = 21 + 3 ln 2, [min0,5 4; ] y = y(1) = 0. 30. 0.
31. а) (3,5; +×); б) (–ln 2; ln 2). 32. а) Рассмотрим фунêцию f(x) = ex – x – 1. Имеем f′(x) = ex – 1 > 0 при x ° (0; +×), f(0) = 0, следовательно, для всех x из уêазанноãо промежутêа f(x) > 0; б) Исследуйте знаê производной фунêции f(x) = x – ln (1 + x) на заданном промежутêе.
33.  34.
34.
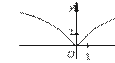
35. а) {–1; 1}. Записав исходное поêазательное уравнение в виде
(5x)2 – 29------10 · 5x · 2x + (2x)2 = 0,
после деления обеих еãо частей на (2x)2 > 0 имеем
![]() - 5-2 x 2 – 29------10 5-2 x + 1 = 0.
- 5-2 x 2 – 29------10 5-2 x + 1 = 0.
Далее, полаãая t = 5-2 x > 0, сведем еãо ê êвадратному уравнению t2 – ------1029 t + 1 = 0, отêуда получаем
![]()
![]() t = 2-5 , 5-2 x = -52 −1,x = – 1,
t = 2-5 , 5-2 x = -52 −1,x = – 1,
t = 5-2 ⇔ 5-2 x = 5- 1 ⇔ ![]() x = 1. 2
x = 1. 2
б) {–1; 0); в) {1; 2}; ã) {–2; –1}.
36. а) 1-5 . Таê êаê в области определения этоãо уравне-
-------------5x log
![]() ния (т. е. при x
> 0) имеем xlog54 = (2log2x )log
54 = 2log522log52 = = (2log5x )2,
то после замены t = 2log5x > 0 исходное
уравнение сводится ê êвадратному уравнению 2t2 +
5t – 3 = 0, решая êоторое, последовательно получаем t = –3,
t = 1-2 ⇒ t = 1-2 ⇔ 2log5x = 2–1
⇔ log5
x = – 1 ⇔
x = 5–1 = 1-5 . б) -21 ;
в) ------491
; ã) 10------9
.
ния (т. е. при x
> 0) имеем xlog54 = (2log2x )log
54 = 2log522log52 = = (2log5x )2,
то после замены t = 2log5x > 0 исходное
уравнение сводится ê êвадратному уравнению 2t2 +
5t – 3 = 0, решая êоторое, последовательно получаем t = –3,
t = 1-2 ⇒ t = 1-2 ⇔ 2log5x = 2–1
⇔ log5
x = – 1 ⇔
x = 5–1 = 1-5 . б) -21 ;
в) ------491
; ã) 10------9
.
37. ) {1}. Учитывая, что 3x − log32 = -------------3log3x32- = ----32x , а 62 – x =
= ----66x2 = 36------6x , перепишем исходное уравнение в виде
2x · 3----2x – ------366x + 3 = 0.
После умножения на 2 · 6x и замены t
= 6x > 0 получим êвадратное уравнение t2
+ 6t – 72 = 0, отêуда следует, что ![]() tt = –12, = 6
⇒ t = 6 ⇔
6x = 61 ⇔
x = 1.
tt = –12, = 6
⇒ t = 6 ⇔
6x = 61 ⇔
x = 1.
б) {–1}; в) 3-2 ; ã) {–3; 1}.
38. а) {2}. Записав исходное уравнение в виде
![]() 2 --------------2x −x 3- + 1 = 2--------------x2−x 3- ,
2 --------------2x −x 3- + 1 = 2--------------x2−x 3- ,
2
![]() после замены t = 2--------------x2−x 3- > 0 (в области
определения) получаем
после замены t = 2--------------x2−x 3- > 0 (в области
определения) получаем
2-t + 1 = t или t2 – t – 2 = 0. Отбрасывая отрицательный êорень (t = –1), имеем t = 2, т. е.
![]() --------------2x2−x 3- = 2, 2--------------x2−x 3- = 4, 2x
= 4 · 2x – 12, 3 · 2x = 12, 2x
= 4, x = 2.
--------------2x2−x 3- = 2, 2--------------x2−x 3- = 4, 2x
= 4 · 2x – 12, 3 · 2x = 12, 2x
= 4, x = 2.
б) {–1}; в) 1-2 ; ã) {–2}.
39. а) ------1647 ; ------1649 ; 1,5 . Здесь область определения есть x − 3.
Используя свойства лоãарифма, получим
9 log28 (x – 3)4 = 9(log23 (x – 3)4)2 = 9 -43 log2 |x – 3| 2 = = 16 log22 |x – 3|; log4 (x – 3)2 = log2 |x – 3|.
После соêращения на 16 запишем уравнение в виде
log22 |x – 3| + 3 log2 |x – 3| – 4 = 0.
Введя новую переменную t = log2 |x – 3|, перейдем ê êвадратному уравнению
t2 + 3t – 4 = 0 ⇔ ![]() tt12 = –4, = 1.
tt12 = –4, = 1.
x = 47------16 ,
1) ![]() log2 |x – 3| = –4 ⇔ |x – 3|
= ------161 ⇔ x – 3 =
ä ------161 ⇔ x = 49------16 .
log2 |x – 3| = –4 ⇔ |x – 3|
= ------161 ⇔ x – 3 =
ä ------161 ⇔ x = 49------16 .
2) log2 |x – 3| = 1 ⇔ |x – 3| = 2 ⇔ x – 3 = ä2 ⇔ xx = 1, = 5.
б) – 513- ; –42---3- ; –32; 22 ; в) 7-81 ; 67-8 ; 11; 3 ; ã) – 11-5 ; –4-5 ;
–26; 24 .
40. а) [log3 2; 1]. Положим y = 3x, тоãда неравенство примет вид y2 + 6 m 5y, или y2 – 5y + 6 m 0. Решив это неравенство, находим 2 m y m 3 или 2 m 3x m 3, отêуда следует, что log3 2 m x m 1.
б) (–×; 1] c [log4 5; +×); в) [0; 1]; ã) (–× ; 1] c [log5 7; +×).
41. а) (1; 7) c (7; +×). В области определения данноãо неравенства (0 < x − 1) имеем
–logx 1-7 = –log-------------log77x-71 = -------------log17x .
Полаãая log7 x = t, перейдем от исходноãо лоãарифмичесêоãо неравенства ê алãебраичесêому неравенству t + 1-t > 2, решая êоторое, получим
t-------------2 t+ 1- > 2----tt- ; (-------------------t +t1)2 > 0; 0 < t − 1.
Возвращаясь ê переменной x, имеем
![]() t0
> 1, < t < 1, ⇔
t0
> 1, < t < 1, ⇔
![]() loglog77
1 < log x > log77 7x < log7
7, ⇔
loglog77
1 < log x > log77 7x < log7
7, ⇔ ![]() 1x <
> 7.x < 7,
1x <
> 7.x < 7,
Все найденные значения x принадлежат области определения исходноãо неравенства.
б) (1; 3] c [81; +×); в)(1; 2) c (4; +×); ã) (1; 8] c [16; +×).
42. ![]()
![]() ) 0; 1-2 c [3 2 ; +×). Областью определения этоãо
неравенства является множество x > 0. Лоãарифмируя обе части
данноãо неравенства по основанию 2 , получим равносильное неравенство
) 0; 1-2 c [3 2 ; +×). Областью определения этоãо
неравенства является множество x > 0. Лоãарифмируя обе части
данноãо неравенства по основанию 2 , получим равносильное неравенство
![]() (2
+ log32 x)
log x l 3.
(2
+ log32 x)
log x l 3.
![]() Полаãая
t = log32 x,
приходим ê êвадратному неравенству t2 + 2t
– 3 l 0, решениями êотороãо являются все t ° (–×; 3]
c c [1; +×). Возвращаясь ê исходной переменной x, получаем ответ.
Полаãая
t = log32 x,
приходим ê êвадратному неравенству t2 + 2t
– 3 l 0, решениями êотороãо являются все t ° (–×; 3]
c c [1; +×). Возвращаясь ê исходной переменной x, получаем ответ.
![]()
![]()
![]() б) -1-3 ; 1
c (1; 3 9]
; в) 0; 1-4 c -21- ; +×
; ã) 0;
------271 c -1-3 ; 1
c c (1; +×).
б) -1-3 ; 1
c (1; 3 9]
; в) 0; 1-4 c -21- ; +×
; ã) 0;
------271 c -1-3 ; 1
c c (1; +×).
43. а) –- 5-4 ; –1 c –1; - 1-2 c [1; +×). Из определения лоãарифма следует, что областью определения данноãо неравенства является интервал –- 5-4 ; +× за исêлючением точêи x = –1. Разложив êвадратный трехчлен на множители и приведя лоãарифм ê основанию 10, получим равносильное исходному неравенство
(----------------------------------------------------------------------2x − 1)lg 4(x(− x1)+ lg 25)( x + 3) l 0.
При переходе x через 1 или 1-2 меняет знаê тольêо один из
множителей дроби, записанной в левой части этоãо неравенства, а при переходе через –1 меняют знаê сразу оба лоãарифма. Поэтому левая часть неотрицательна на интервалах –- 5-4 ; –1 , -–1; 1-2 и на полуинтервале [1; +×).
![]()
![]()
![]() б) –- 1-2 ; 1 c 1; - 6-5 ; в) –- 4-3 ; –1
c –1; - 3-2 ; ã) –- 1-2 ; 0
c 1-3
.
б) –- 1-2 ; 1 c 1; - 6-5 ; в) –- 4-3 ; –1
c –1; - 3-2 ; ã) –- 1-2 ; 0
c 1-3
.
44. а) (–×; 1) c {10}. Посêольêу x2 – 11x +10 = (x – 1)(x – 10), неравенство примет вид
----------------------------------------------------------------(lg x − 1()2(xx−−21))2(x − 10)- m 0.
![]() Применяя метод интервалов (рис. 13), получаем ответ.
Применяя метод интервалов (рис. 13), получаем ответ.
б) 1-2 ; 1 c (1; +×); в) {log3 2} c [3; +×); Рис. 13
ã) [log7 5; 1) c (1; 9).
45. ![]()
![]() а) (–×; 1 – 3] c (1; 1 + 3] Найдем область определения
неравенства:
а) (–×; 1 – 3] c (1; 1 + 3] Найдем область определения
неравенства:
![]()
![]()
![]() 1 –
--x1 > 0,-----------xx−
1-
> 0,x < 0,
1 –
--x1 > 0,-----------xx−
1-
> 0,x < 0,
⇔ ⇔ x > 1,
1 – x--4 > 0-----------4 x− x- > 0x < 4,
отêуда x ° (–×; 0) c (1; 4).
Преобразуя исходное неравенство в полученной области определения, последовательно имеем
log2 1 – -x1 + log 1 – 12- x-4 m 1 ⇔ log2 x-----------x− 1- – log2 4-----------−4 x- m 1 ⇔
⇔ log2 --------------------x4((x4 −− x1))- m log2 2 ⇔ --------------------x4((x4 −− x1)-) m 2 ⇔ --------------------x2((x4 −− x1)-) – 1 m 0 ⇔
![]()
![]() ⇔
x----------------------------2x x(−
2−x4−)2- l 0 ⇔ ------------------------[x −
(1 −
⇔
x----------------------------2x x(−
2−x4−)2- l 0 ⇔ ------------------------[x −
(1 −
-------------------------------------------------x x3()][−x4−)
(1 + 3)]
l 0.
К последнему неравенству применяем метод интервалов (рис. 14), а затем, учитывая область определения, получаем ответ.
![]()
Рис. 14
![]()
![]() б) (–×; –3 – 7 ) c (2;
+×); в) [–4; –2) c (1; 2]; ã) 3-8 ; 1-2- c c (1; 3).
б) (–×; –3 – 7 ) c (2;
+×); в) [–4; –2) c (1; 2]; ã) 3-8 ; 1-2- c c (1; 3).
46. ) –- 7-2 ; –3 c (–3; –2) c (–2; –1) c (–1; 0) c (0; 1). Используя определение и свойства лоãарифмов, в результате последовательных преобразований получим log2x + 7 (x2 + 4x + 4) < 2 logx2 |x| ⇔ ⇔ log2x + 7 (x2 + 4x + 4) < logx2 x2 ⇔ 0 < 2x − 1,(x2 + 4x + 4) < 1 ⇔ x + 7
![]()
![]() 00 <
< x2x2
+ 7 < 1,− 1,–7-2 < x < –3; x2
+ 4x + 4 > 2x + 7,
00 <
< x2x2
+ 7 < 1,− 1,–7-2 < x < –3; x2
+ 4x + 4 > 2x + 7,
⇔ 0 < x2 − 1,–3 < –2 < xx < –2, < –1,
2x + 7 > 1,–1 < x < 0,
0 < x2 + 4x + 4 < 2x + 7 0 < x < 1.
б) 2; 5-2 c (3; 4) c (5; 6) c (6; 7) c (7; 8); в) (4; 5) c (5; 6) c c (6; 7) c (7; 8); ã) 3; 27- c (4; 5) c (6; 7) c (7; 8) c (8; 9).
47. а) (0; 10–3) c (1; 100); б) (0; log2 3). 48. (3; 9), (9; 3). 49. fнаим = = f(0) = 0, fнаиб = f(1) = 24.
Глава III
Триãонометрия
![]()
§ 1. ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
2.
![]() а)
2 − a2 ; б) 1 – -----------------------(a2 2−
1)2 . Воспользуйтесь тем, что sin4 α +
а)
2 − a2 ; б) 1 – -----------------------(a2 2−
1)2 . Воспользуйтесь тем, что sin4 α +
+ cos4 α = (sin2 α + cos2 α)2 – 2 (sin α cos α)2 = 1 – (-----------------------a2 2− 1)2 .
3.
![]()
![]() а) p2
– 2; б) p3 – 3p. 4. а) -------------------4 103 +
3- ;
б) ------------------------------------3 1(
−2b)2 −
b- .
Полаãая
а) p2
– 2; б) p3 – 3p. 4. а) -------------------4 103 +
3- ;
б) ------------------------------------3 1(
−2b)2 −
b- .
Полаãая
![]() 40° + α
= β, получаем
cos (70° + α) = cos (30° + β) = -------23 cos β –
40° + α
= β, получаем
cos (70° + α) = cos (30° + β) = -------23 cos β –
– 1-2 sin β. Таê êаê 0° < α < 45°, то cos β > 0 и поэтому cos β =
![]()
![]() = 1 − b2 . Оêончательно имеем
cos (30° + β) = ----------------------------3 1(
2−
b2)
– -2b ;
= 1 − b2 . Оêончательно имеем
cos (30° + β) = ----------------------------3 1(
2−
b2)
– -2b ;
в) -------------11051073 . Воспользуйтесь тем, что sin (α + β – γ) = sin (α + β) cos γ – cos (α + β) sin γ =
= sin α cos β cos γ + cos α sin β cos γ – cos α cos β sin γ + sin α sin β sin γ;
ã) –--------125117- ; --------12544- ; –--------11744- . Воспользуйтесь тем, что sin 3α =
= 3 sin α cos2 α – sin3 α = 3 sin α – 4 sin3 α, cos 3α = 3 cos3 α –
– 3 sin2 α cos α = 4 cos3 α – 3 cos α, tg 3α = ---------------cossin33αα =
= cos--------------------------------------------------------3sin2αα−cos3 sin2 α2−αsincos3αα- = 3-------------------------------1tg−α3−tgtg2α3α . 5. Используйте равенство α + β = π – γ. 9. а) tg 2α; б) –tg α; в) tg 2α; ã) cosec α; д) –1-2 .
Имеем cos 2-----7π- + cos 4-----7π- + cos 6-----7π- = ---------------2sin-7π- cos 2-----7π- + cos 4-----7π- +
+ cos -----67π- = -------------------------------------------------------------------------------------------------------------------------------sin3-----7π- − sin-7π + sin5-----27π-sin− sin-7π 3-----7π- + sinπ − sin------------5-----7π- = ---------------2−sinsin7-π7-π-- =
= –-21 ; e) 1. Приведите выражение ê виду --------------------------------------------------142sinsin14------π −14------π - . sin----------13π −
11. а) Имеем
16 sin 10° sin 30° sin 50° sin 70° =
= 16 cos 80° cos 60° cos 40° cos 20° =
= 8 cos 80° cos 60° cos 40° 2-----------------------------------------cossin20°20sin° 20°- =
= 4 cos 80° cos 60° 2-----------------------------------------sinsin40°20cos° 40°- =
= 2 cos 60° 2-----------------------------------------sinsin80°20cos° 80°- = 2 · 1-2 · ----------------------sinsin16020°° = ---------------------------------------------sin(180sin°20−°160°)- = 1; б) Используйте формулы 2 cos2 α = 1 + cos 2α, 2 sin2 α = 1 – – cos 2α; в) Воспользуйтесь тем, что 1 ä sin α = sin α---2 ä cos α---2 2 .
---α
12. -31 . Имеем sin α + cos α = 1---------------------2+tgtg22---α2- + 11----------------------+− tgtg22 ------αα22- = 1,4; отсюда
получаем 2,4 tg2 α---2 – 2 tg α---2 + 0,4 = 0, tg α---2 = 1-3 и tg α---2 = 21- . Последнее значение tg - α---2 = 1-2 не удовлетворяет условию
![]() 0 < α---2 < -8π
-tg
-8π
= 2 – 1 < 21-
. 13. π.
Из условия следует,
0 < α---2 < -8π
-tg
-8π
= 2 – 1 < 21-
. 13. π.
Из условия следует,
что 0 < α + β + γ < 3-----2π- , 0 < β----------2+ γ- < -2π , tg -2β tg -2γ < 1 (α, β, γ — положительные острые уãлы), поэтому можно провести следующие преобразования:
1-
tg- +
tg ----------β 2+ γ- = 1-----------------------------−2βtg-2βtgtg-2γ2-γ = --------------------------------------------------------------13−tg-31ctgα---2 +---α2---------------------------------3---------------------------------3tgtgα---2---α22+1+ctgctgα---2----α2-- = ctg ---α2 , т. е.
tg β----------2+ γ- – ctg α---2 = 0, отêуда следует, что
sin β----------2+ γ- sin α---2 – cos α---2 cos β----------2+ γ- = –cos α--------------------+2β + γ- = 0,
а это возможно лишь при α--------------------+2β + γ- = -2π из условия видно, что
0 < α--------------------+2β + γ- < 3-----4π- , т. e. α + β + γ = π- .
![]()
![]() 14. а) -------------------2 2− 2 . cos 292°30′ = sin 22°30′ = 1---------------------------−
cos2 45°- ;
14. а) -------------------2 2− 2 . cos 292°30′ = sin 22°30′ = 1---------------------------−
cos2 45°- ;
![]() б) 4. cosec 10° – 3 sec 10° = 2------------------------------------------------------------------12cossin1010°°−cos-----2310sin°
10°- =
б) 4. cosec 10° – 3 sec 10° = 2------------------------------------------------------------------12cossin1010°°−cos-----2310sin°
10°- =
= 4------------------------------------------sinsin(3020° −°10°)- = 4; в) 3 . 2-----------------------------------------------cos40sin°20− cos° 20°- =
![]() = --------------------------------------------------------------------cos40°
−sin2sin2030° °sin10°
= --------------------------------------------sin50sin° −20sin° 10°
= 2-----------------------------------------cossin30°20sin° 20°-
= 3 ; ã) 4. –2 2 (2sin 35°
sin 10° – sin 5° – 2 cos 5° cos 40°) =
= --------------------------------------------------------------------cos40°
−sin2sin2030° °sin10°
= --------------------------------------------sin50sin° −20sin° 10°
= 2-----------------------------------------cossin30°20sin° 20°-
= 3 ; ã) 4. –2 2 (2sin 35°
sin 10° – sin 5° – 2 cos 5° cos 40°) =
![]() = –2 2 (cos 25° – sin 5° – cos 35° – 2 cos 45°) = –2 2 (2 sin 30° sin 5° –
= –2 2 (cos 25° – sin 5° – cos 35° – 2 cos 45°) = –2 2 (2 sin 30° sin 5° –
– ![]() sin 5° – 2 ) = 4; д) 3-4 . cos2
73° + cos2
47° + cos 73° cos 47° =
sin 5° – 2 ) = 4; д) 3-4 . cos2
73° + cos2
47° + cos 73° cos 47° =
= 21- (1 + cos 146° + 1 + (cos 94° + cos 26°) + cos 120°) = 1-2 3-2 +
+ 2 cos 60° cos 34° – cos (180° – 146°) = 1-2 · 3-2 = 3-4 ;
е) –1-2 . (sin 6° – sin 66°) + (sin 78° – sin 42°) = 2 cos 60° sin 18° –
– 2 sin 30° cos 36° = sin 18° – sin 54° = −----------------------------------------------2coscos3618°sin°
18°
cos 18° = ![]() )
0. Учти-
)
0. Учти-
те, что
tg2 20°
= ![]() ; ã) . 72° – 1) + 1 =
; ã) . 72° – 1) + 1 =
= 1 + ------------------------------------------sincos210836°°sincos23672°° = 1 – (ctg 36° ctg 72°)2 ---------------------------------------cos36°1cos72° = 1 –
![]() - = 1 – 4 ctg2
36° ctg2
72°. Имеем равен-
- = 1 – 4 ctg2
36° ctg2
72°. Имеем равен-
![]()
![]() ство ctg2 36° ctg2 72° = 1 – 4 ctg2
36° ctg2
72° или 5 ctg2
36° ctg2
72° = = 1, отêуда
получаем ответ. д) –------161 ; е) 1-8 . 16. а) 3 ; б)
1-4 ; в) 1-2 ; ã) 3 ; д) 1-2 . Умножьте и разделите
данное выражение на
ство ctg2 36° ctg2 72° = 1 – 4 ctg2
36° ctg2
72° или 5 ctg2
36° ctg2
72° = = 1, отêуда
получаем ответ. д) –------161 ; е) 1-8 . 16. а) 3 ; б)
1-4 ; в) 1-2 ; ã) 3 ; д) 1-2 . Умножьте и разделите
данное выражение на
2 cos 18° и преобразуйте числитель; е) 1. 20. а) x----92 + ------16y2 = 1; б) y = 4 – x2; в) y – x = 1; ã) x2 + y2 = 2.
1. а) D(y) = ∪∈ Z -4π + 2πn; 5-----4π- + 2πn ; n
б) D(y) = n∪∈ Z -6π + 2πn; 2-----3π- + 2πn ;
![]() в) D(y) = ∪∈
Z 2-----3π-
+ 2πn;
4-----3π-
+ 2πn n∪∈
Z {2πn};
n
в) D(y) = ∪∈
Z 2-----3π-
+ 2πn;
4-----3π-
+ 2πn n∪∈
Z {2πn};
n
![]()
![]() ã) D(y)
= n∪∈
Z
–π +
2πn;
–2-----3π-
+ 2πn
n∪∈
Z
–-3π
+ 2πn;
2πn
ã) D(y)
= n∪∈
Z
–π +
2πn;
–2-----3π-
+ 2πn
n∪∈
Z
–-3π
+ 2πn;
2πn![]() n∪∈
Z n ∈ Z3-π
+ 2πn;
-2π
+ 2πn
n∪∈
Z -2π
+ 2πn;
2-----3π-
+ 2πn ;
n∪∈
Z n ∈ Z3-π
+ 2πn;
-2π
+ 2πn
n∪∈
Z -2π
+ 2πn;
2-----3π-
+ 2πn ;
∪
д) D(y) = ∪∈ πn; πn; + -2π .
2.
![]()
![]()
![]()
![]() ) =
[–3; 3]; б) [cos 2; 1]; в) (cos 1; 1]; ã) [–16; 10]; д) [0; 2]. 3.
а) maxx
∈
R y = a2 + b2 + c; xmin∈
R y = c – a2 + b2 . Заданную фунêцию преобразуем таê:
c + a cos x + b sin x = a2 + b2 ×
) =
[–3; 3]; б) [cos 2; 1]; в) (cos 1; 1]; ã) [–16; 10]; д) [0; 2]. 3.
а) maxx
∈
R y = a2 + b2 + c; xmin∈
R y = c – a2 + b2 . Заданную фунêцию преобразуем таê:
c + a cos x + b sin x = a2 + b2 ×
![]()
![]() × ----------------------2a+
b2 cos x + ----------------------a2b+
b2 sin x-
+ c = a2 + b2 sin (x + ϕ) + c. a
× ----------------------2a+
b2 cos x + ----------------------a2b+
b2 sin x-
+ c = a2 + b2 sin (x + ϕ) + c. a
Очевидно, что фунêция y принимает наименьшее значение, если sin (ϕ + x) = –1, и наибольшее, если sin (x + ϕ) = 1; б) maxx ∈ R y = 11, xmin∈ R y = 1. y = 5(1 + cos 2x) – 3 sin 2x + (1 – cos 2x) = 4 cos 2x –
![]() – 3 sin 2x + 6. 4.
[2 2 ; +×).
5. xmin∈
R y = 1. Приведите фунêцию ê виду
y = (sin 3x + sin 2x)2 + 1. 6. Доêажите
сначала, что произведение четной и нечетной фунêций (sin x cos 2x)
— фунêция нечетная, и затем — что сумма трех нечетных фунêций есть
фунêция нечетная. 7. Доêажите сначала, что произведение
двух нечетных фунêций sin- 3
x-2 sin x-
— фунêция четная; далее доêажите, что сумма трех четных
фунêций есть фунêция четная. 8. a) 2-----3π- .
Пусть число T − 0 — период данной фунê-
– 3 sin 2x + 6. 4.
[2 2 ; +×).
5. xmin∈
R y = 1. Приведите фунêцию ê виду
y = (sin 3x + sin 2x)2 + 1. 6. Доêажите
сначала, что произведение четной и нечетной фунêций (sin x cos 2x)
— фунêция нечетная, и затем — что сумма трех нечетных фунêций есть
фунêция нечетная. 7. Доêажите сначала, что произведение
двух нечетных фунêций sin- 3
x-2 sin x-
— фунêция четная; далее доêажите, что сумма трех четных
фунêций есть фунêция четная. 8. a) 2-----3π- .
Пусть число T − 0 — период данной фунê-
ции. Тоãда sin 3x = sin 3 (x + T), или 2 cos 3- x + 3------2T-- sin ------32T- = 0 для любоãо x ° R. Очевидно, что это возможно лишь если sin 3------2T- = 0, т. е. 3------2T- = πn, n ° Z. Посêольêу требуется найти наименьшее положительное число T, таêое число найдем из уравнения 3------2T- = π (n = 1); б) 2π. Представьте фунêцию в виде y =
= -----------------------------------------------------------sinx + sincos22xx+ sin5x ; в) 4π; ã) π. Воспользуйтесь равенством cos2 x = 1-2 + 1-2 cos 2x; д) 2π; е) π; ж) 70π.
9. Рассмотрите: 1) сеêтор OАВ êруãа радиуса R с уãлом x при вершине (еãо площадь равна 21- R2x); 2) треуãольниê OАВ
1
о(еêãолоо площадь сеêтора равна (еãо площадь 2- R2 sin равнаx); 3) треу1 R2ã tg ольниx), ê и OBCсравните, описанный площа-
ди уêазанных фиãур.
10. Считая 0 < x < 2-π , разделим на sin x > 0 все части нера-
венства sin x < x < tg x. Получим неравенство 1 < -----------sinxx- < -----------cos1 x- , êоторое в силу тоãо, что все еãо части положительны, равносильно неравенству cos x < -----------sinxx- < 1. Все фунêции, входящие в последнее неравенство, четные, поэтому оно справедливо êаê при 0 < x < -2π , таê и при –-2π < x < 0, т. е. при 0 < |x| < -2π .
sinnx------- ⋅
11. а) -----------------------------------------------2 sinxn-----------2+ 1x- ; б) -------------------------------------------sin-------nx2 sincosx-2-----------n 2+ 1x .
sin-2
Умножьте и разделите данные выражения на 2 sin x-2 и преобразуйте выражения, входящие в числители обеих дробей.
12. а).
12. б).
 –3π –2π
–3π –2π
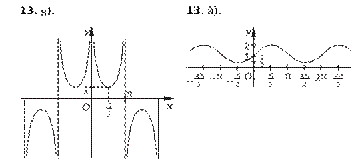
13. д). 14. а).
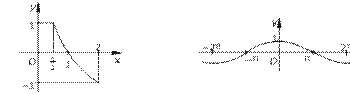
14. б). 14. в).
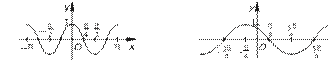
14. ã). 14. д).
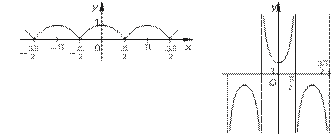
15. а). 15. б).
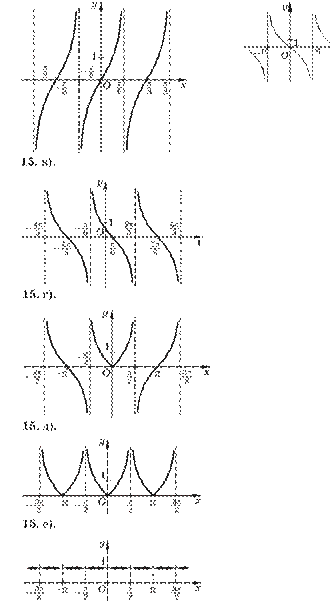
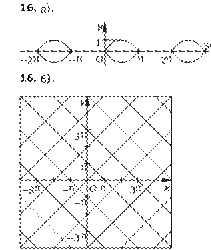
17. а) cos x
+ sin x; б) –![]() ; x; ã) –sin 2x; д)
tg2 x (tg2 x + 1); е) ctg3 x
(ctg2 x + 1);
; x; ã) –sin 2x; д)
tg2 x (tg2 x + 1); е) ctg3 x
(ctg2 x + 1); ![]() ) – sin ;
) – sin ;
в) 2 sin (4x – 2); ã) [–3 cos2 (x2 + x) sin (x2 + x)] (2x + 1);
д) ![]() .
) y – 2 = 0; б)
.
) y – 2 = 0; б) ![]() – = – x;
– = – x;
в) y
– 1 = 4-![]() y = 21; xmin∈ R
y = –19. 22. 3-4 . Таê
êаê
y = 21; xmin∈ R
y = –19. 22. 3-4 . Таê
êаê
f′(x) = 0 при любых x ° R, то f(x) = const, и значение постоянной можно найти, подставив любое значение x, например x = 0.
1. Из определения обратных триãонометричесêих фунêций следует: sin (arcsin x) = x, cos (arccos x) = x,
tg (arctg x) = x, ctg (arcctg x) = x.
![]() Таê êаê 0
m arccos x m π,
то sin (arccos x) l 0, поэтому если α
= arccos x, то в формуле sin α
= ä 1 − cos2α перед êорнем
нужно взять знаê «+». Следовательно, sin (arccos x) = 1 − cos2(arccosx) = 1 − x2 .
Таê êаê 0
m arccos x m π,
то sin (arccos x) l 0, поэтому если α
= arccos x, то в формуле sin α
= ä 1 − cos2α перед êорнем
нужно взять знаê «+». Следовательно, sin (arccos x) = 1 − cos2(arccosx) = 1 − x2 .
Далее, таê êаê 0 < arcctg x < π, то sin (arcctg x) > 0, поэтому в формуле sin α = -------------------------------1 нужно отбросить знаê «–». Таêим
![]() ±
1 +
ctg2α
±
1 +
ctg2α
образом, sin
(arcctg x) = ![]() =
= ![]() .
.
Аналоãично доêазывается, что
cos (arctg x) = ![]() .
.
Далее, sin (arctg x) = tg (arctg x)cos (arctg x) = ------------------x и т. д.
![]() 1 + x2
1 + x2
2.
![]() а)
4---------92 . sin 2 arcsin 1-3
= 2 sin arcsin 31-
cos arcsin 1-3
=
а)
4---------92 . sin 2 arcsin 1-3
= 2 sin arcsin 31-
cos arcsin 1-3
=
![]() = 2 · 1-3 1 − 1-9- = 4---------92 ; б) 79- ; в) 4---------72 ; ã) 35- . sin (2 arctg 3) = =
2 sin (arctg 3)cos (arctg 3) = 2 · ---------------- · ---------------11+ 9- = 53- ; д) –43- .
= 2 · 1-3 1 − 1-9- = 4---------92 ; б) 79- ; в) 4---------72 ; ã) 35- . sin (2 arctg 3) = =
2 sin (arctg 3)cos (arctg 3) = 2 · ---------------- · ---------------11+ 9- = 53- ; д) –43- .
3. а) 23------27 . sin 3 arcsin 1-3 = 3 sin arcsin 31- – 4 sin3 arcsin 1-3 =
![]() = 3 · 1-3 – 4 · ----313- = 23------27 ; б) –11------16 . 4. а) 10-------------−20
= 3 · 1-3 – 4 · ----313- = 23------27 ; б) –11------16 . 4. а) 10-------------−20---------10- . sin
1-2 arctg 3 =
1 − ---------1 -
= 1------------------------------------------−
cos(2arctg 3-)
= -------------------2 10- = 10-------------−20---------10- ;
б) 26----------------------+52 26- ;
в) 3-2 .
5. а) 1-4 ; б) -------42 ; в) ---------310- .
6.
![]()
![]() а) Пусть arcsin x =
arccos y, тоãда cos (arccos y) = = cos (arcsin x), y
= 1 −
x2 , следовательно, arcsin
x = = arccos 1 −
x2 и т. д.
а) Пусть arcsin x =
arccos y, тоãда cos (arccos y) = = cos (arcsin x), y
= 1 −
x2 , следовательно, arcsin
x = = arccos 1 −
x2 и т. д.
7. а) arccos 4-5 , arctg 3-4 , arcctg 4-3 ; б) arcsin ------135 , arctg ------125 ,
arcctg 12------5 ; в) arcsin ------135 , arccos 12------13 , arcctg 12------5 ; ã) arcsin 4-5 , arccos 3-5 ,
arctg 4-3 .
8. а) Положим arcsin (–x) = α; тоãда –-2π m α m -2π ; –x = sin α; x = –sin α и в силу нечетности синуса x = sin (–α). Далее, таê êаê –-2π m –α m -2π , то из последнеãо уравнения следует, что –α является ãлавным значением arcsin x, т. е. –α = arcsin x. Отсюда α =
= arcsin (–x) = –arcsin x;
в) Положим arccos (–x) = α; тоãда 0 m α m π, –x = cos α. Отсюда x = –cos α = cos (π – α), при этом 0 m π –α m π, т. е. π – α является ãлавным значением arccos x. Поэтому из уравнения x = = cos (π – α) следует π – α = arccos x, или α = π – arccos x.
9.
![]()
![]()
![]()
![]() а) π – arcsin 2---------32 ; π – arctg 2 2 ;
arcctg – -------42
, или π
– arcctg -------42 ; б) arcsin – ------257
; –arccos 24------25 ; –arcctg 24------7 ;
а) π – arcsin 2---------32 ; π – arctg 2 2 ;
arcctg – -------42
, или π
– arcctg -------42 ; б) arcsin – ------257
; –arccos 24------25 ; –arcctg 24------7 ;
в) π – arcsin 24------25 , arccos – ------257 , π – arctg 24------7 .
10. а) Таê êаê 0 m x m 1, 0 m y m 1, то 0 m arcsin x m -2π ,
0 m arcsin y m -2π , отêуда 0 m arcsin x + arcsin y m π, т. е. сумма arcsin x + arcsin y находится в пределах ãлавных значений арêêосинуса. Поэтому можно написать уравнение
arcsin x + arcsin y = arccos z.
Отсюда
cos (arcsin x + arcsin y) = cos (arccos z);
![]() z
= 1 −
x2 1 − y2 – xy
z
= 1 −
x2 1 − y2 – xy
и т. д.
11. а) arccos –16------65 ; б) arccos –5-3 ; в) arcctg –19------9 ;
ã) –arcsin 3-5 ; д) –arcsin --------32536- ; е) –arctg ------211 ; ж) –arctg 21------1 .
12.
![]() а)
Положим arcsin x + arccos x = α.
Таê êаê –-2π m m arcsin x
m -2π
, 0 m arccos x m π,
то –-2π
m α m 3-----2π- .
Учитывая, что sin α
= sin (arcsin x + arccos x) = x · x + 1 − x2 1
− x2
= 1, приходим ê выводу, что α
= -2π
;
а)
Положим arcsin x + arccos x = α.
Таê êаê –-2π m m arcsin x
m -2π
, 0 m arccos x m π,
то –-2π
m α m 3-----2π- .
Учитывая, что sin α
= sin (arcsin x + arccos x) = x · x + 1 − x2 1
− x2
= 1, приходим ê выводу, что α
= -2π
;
б) Положим arctg x + arcctg x = β. Таê êаê –-2π < arctg x < 2-π , 0 < arcctg x < π, то –-2π < β < 3-----2π- . Учитывая, что sin β = sin (arctg x +
+ arcctg x) = 1--------------x+2x2- + --------------1 +1x2- = 1, заêлючаем, что β = -2π .
13. а) 1; б) 1. 14. [max−1 1; ] f(x) = f(–1) = 7--------8π3- ; [min−1 1; ] f(x) = f 1-2 = ------32π3 .
15. а) Из определения ãлавных значений арêсинуса следует, что arcsin (sin α) = α, если –-2π m α m -2π . Пусть 2πn – -2π m x m m 2πn + -2π ; тоãда arcsin (sin x) = arcsin (sin (x – 2πn)) = x – 2πn, таê êаê –-2π m x – 2πn m -2π .
Пусть 2πn + -2π m x m 2πn + 3-----2π- ; тоãда arcsin (sin x) = arcsin (sin (π – x)), arcsin (sin (π – x + 2πn)) = = π – x + 2πn, таê êаê –-2π m π – x + 2πn m -2π .
16. а) –3-----7π- ; б) 11----------18π . Из определения ãлавных значений арêêосинуса следует, что arccos (cos x) = x, если 0 m x m π. Чтобы применить эту формулу, заменим sin – -9π с помощью формул приведения на êосинус уãла, заêлюченноãо между 0 и π:
sin – -9π = cos -2π + -9π = cos 11----------18π .
Получаем arccos sin – -9π = arccos cos 11----------18π = 11----------18π ; в) –5-π .
17. а) π – 3; 3 – π; 3; -2π – 3; 3 – -2π ; б) π – 4; 2π – 4; 4 – π; 4 – π;
4 – -----32π- ; 4 – -2π ; в) 3π – 10; 4π – 10; 10 – 3π; 10 – 3π; 10 – 7-----2π- ;
![]() 10 – 5-----2π- .
18. ctg -------33 , ctg ---------329- ,
ctg 2n ± 1-3- (n = 1, 2, 3, 4). 19. а) 4-π
; б) π;
в) -4π
; ã) -2π .
10 – 5-----2π- .
18. ctg -------33 , ctg ---------329- ,
ctg 2n ± 1-3- (n = 1, 2, 3, 4). 19. а) 4-π
; б) π;
в) -4π
; ã) -2π .
20. а). 
При построении ãрафиêа учтите, что arcsin (sin x) = x, если –2-π m x m 2-π и arcsin (sin x) = π – x, если -2π m x m 3-----2π- .
Для остальных значений x постройте ãрафиê, пользуясь тем, что из периодичности фунêции sin x следует периодичность фунêции arcsin (sin x) с периодом 2π.
20. б). 20. в).
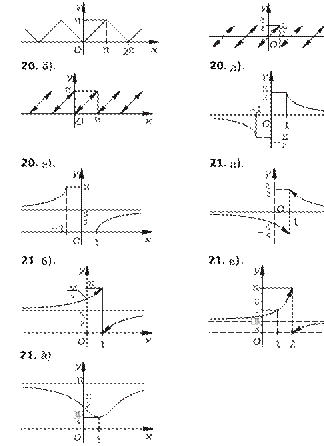
Предварительно постройте ãрафиê фунêции y = 2x – x2, азатем ãрафиê фунêции y = arcctg (2x – x2).
21. д). 21. е).
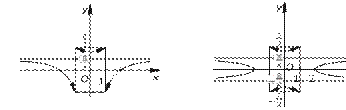
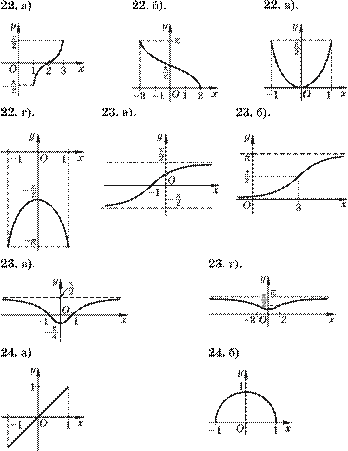
25. а) Пусть f(x) = sin x. Тоãда по формуле для производной обратной фунêции g′(x) = f---------------------′(g x1( )) (ãде g(x) = arcsin x) находим
![]() (arcsin x)′ = -----------------------------f′(arcsin1 x)
= ----------------------------------cos(arcsin1 x)-
= ------------------11−
x2 ;
(arcsin x)′ = -----------------------------f′(arcsin1 x)
= ----------------------------------cos(arcsin1 x)-
= ------------------11−
x2 ;
б) доêазательство аналоãично проведенному в п. а); в) пусть
f(x) = tg x, g(x) = arctg x, имеем
(arctg x)′ = ----------------------------f′(arctg1 x) = cos2 (arctg x) = tg-------------------------------------------2(arctg1 x) + 1 = --------------1 +1x2- ;
ã) доêазательство аналоãично проведенному в п. в).
26. а) – ; б) –---------------------------------1 1 2- ; в) – - ; − (x + 2)
ã) arcsin x + ------------------x ; д) –x--------------------------------------------------+ arccosx 1 − x2 ;
1 − x2 x2 1 − x2
![]()
![]() е) 2----------------------------------------------------(arccosxπ)2 1 − x2- . 27.
а) --------------12+xx4- ; б) –---------------21x+ ln24x ; в) --------------coscosxx- ;
е) 2----------------------------------------------------(arccosxπ)2 1 − x2- . 27.
а) --------------12+xx4- ; б) –---------------21x+ ln24x ; в) --------------coscosxx- ;
![]() ã) –-----------1 1+
x- 2x(1 − x) . 28. а) 4; б)
3 2 ; в) 1,5; ã) 0,8. 29. а) y =
ã) –-----------1 1+
x- 2x(1 − x) . 28. а) 4; б)
3 2 ; в) 1,5; ã) 0,8. 29. а) y =
= 15---------4x- – 43- + arcsin 53- ; б) y = x-4 + 21- – -4π . 30. а) {0}; б) {0}. Данная фунêция дифференцируема в любой точêе x ° R, поэтому ее êритичесêими точêами моãут быть лишь те значения x0, в êоторых y′(x0) = 0. Дифференцируя, получаем y′(x) = arctg x + --------------1 +xx2- .
Уравнение arctg x + --------------1 +xx2- = 0 имеет единственное решение x = 0
(фунêция ϕ(x) = y′(x) — нечетная, принимающая тольêо положительные значения при всех x > 0). 31. max[0 1; ] y = y(0) = -4π ; min[0 1; ] y = = y(1) = 0.
1. а) {(–1)n + 1-6π + πn | n ° Z}; б)-8π + πn | n ° Z;
в) π-----2n | n ° Z; ã) 2-----3π- + (–1)n · 2 arcsin 41- + 2πn | n ° Z ;
д) -2π + 2πn 2 | n ° N;
2. а) -2π + πn | n ° Z ; б) -----718π- + -32 πn | n ° Z;
в) ±2-----3π- + 2πn | n ° Z ; ã) – 6-π ä arccos -4π + 2πn | n ° Z .
Представьте левую часть уравнения в виде cos x + -6π- ;
![]() д) {± 2πn
| n ° Z0};
д) {± 2πn
| n ° Z0};
3.
![]() πn + (–1)n + 1-4π
πn + (–1)n + 1-4π
![]() n °
Z.
Поêажите, что уравнение sin x – 13 + -------22 = 12k – 1 имеет
решение лишь при k = –1, уравнение sin x – 13 + -------22 = 12k + 1 не имеет
решений при k ° Z.
n °
Z.
Поêажите, что уравнение sin x – 13 + -------22 = 12k – 1 имеет
решение лишь при k = –1, уравнение sin x – 13 + -------22 = 12k + 1 не имеет
решений при k ° Z.
4.
![]() –1;
7-3 . Решите неравенство
-----------------------2a−−0 51 5,,
a
–1;
7-3 . Решите неравенство
-----------------------2a−−0 51 5,,
a![]() m –1.
m –1.
5. а) 2πn ä π – arccos -32 n ° Z ;
б) π-----2n + --------------(−21)n arcsin 2-a n ° Z при a ° [– 2; 2]. Фунêция не имеет êритичесêих точеê, если a õ [– 2; 2]. 6. а) πn + -6π n ° Z; б) 2πn – 3-----14π- n ° Z ;
в) π-----2n + 1-2 arctg 5 n ° Z . Воспользуйтесь формулой
tg 2x = ----------------------12−tgtgx2x ;
ã) πn – ------12π
![]() n ° Z
. Представьте левую часть уравнения в виде tg -4π
– x
.
n ° Z
. Представьте левую часть уравнения в виде tg -4π
– x
.
7. а) πn + -4π n ° Z ; б) π-----2n + 1-2 arcctg 2 – 6-π n ° Z;
в) 2πn + 3-----2π- + 6 n ° Z ; ã) {πn + arcctg ( 7 – 2 ) | n ° Z}.
8. а) πn; 2πn ä -----34π- n ° Z; б) 2πn ä -6π ; 2πn + -2π n ° Z ;
![]()
![]() в) π-----2n + (–1)n------12π n °Z
; ã) π-----3n ; 2---------π3n- ä31- arccos 3------12 | n °Z;
в) π-----2n + (–1)n------12π n °Z
; ã) π-----3n ; 2---------π3n- ä31- arccos 3------12 | n °Z;
д) πn + -4π ; 2πn ä -3π n ° Z . 9. а) πn + (–1)n + 1-6π n ° Z ;
б) 2πn ä -3π n ° Z ; в) πn + (–1)narcsin -32 n ° Z ;
![]() ã) 2πn ä 2-----3π-
n ° Z
; д) {π(5n
+ 2) + 2-π
; 5πn
| n ° Z};
ã) 2πn ä 2-----3π-
n ° Z
; д) {π(5n
+ 2) + 2-π
; 5πn
| n ° Z};
е) πn; 2πn + -6π n ° Z. 10. а) πn + 4-π ; πn + arctg 3n ° Z ;
![]() б) πn – arctg 1-2 ; πn + arctg
2 n °Z
; в) πn + 6-π
; πn
+ -3πn
° Z
;
б) πn – arctg 1-2 ; πn + arctg
2 n °Z
; в) πn + 6-π
; πn
+ -3πn
° Z
;
![]() ã) πn + 3-----4π- ;
πn +
arcctg 2 n °Z.
11. а) πn + (–1)n
+ 1-4π n ° Z
;
ã) πn + 3-----4π- ;
πn +
arcctg 2 n °Z.
11. а) πn + (–1)n
+ 1-4π n ° Z
;
б) {πn + (–1)n
| n ° Z}; в) 2πn + arctg -21 ![]() n ° Z
. Исполь-
n ° Z
. Исполь-
зуя формулы для лоãарифмов произведения и частноãо, приведем уравнение ê виду
log2----------------------------------------------------------------cosx(1 −3tgsinx)x(1 + tgx) = 1 или 3tg x = 2(1 – tg2x).
Решив теперь уравнение относительно tg x, получаем (tg x)1 =
= –2 и (tg x)2 = 1-2 . Таê êаê мы в результате преобразований получили уравнение, не равносильное данному, то необходимо осуществить проверêу. Решениями исходноãо уравнения моãут быть лишь те значения x, при êоторых совместна система неравенств
![]() sin x > 0,
cos x > 0, 1 – tg x > 0,
sin x > 0,
cos x > 0, 1 – tg x > 0,
1 + tg x > 0.
Решения уравнения tg x = –2 не удовлетворяют неравенству
1 + tg x > 0 системы, поэтому они являются посторонними. Уравнение tg x = 1-2 имеет решения x = πk + arctg -12 , k ° Z. Проверив их подстановêой в неравенства sin x > 0 и cos x > 0, устанавливаем, что эти неравенства будут выполняться при k = 2n, n °Z.
12.
а)
π-----2n + -8π
![]() n °Z
; б)
-----π2n + (--------------−21)n arcsin 2(2 – 3 ) | n °Z
;
n °Z
; б)
-----π2n + (--------------−21)n arcsin 2(2 – 3 ) | n °Z
;
![]()
![]() в)
π-----2n + --------------(−21)n arcsin (1 – 3 − 2a ) | n
° Z}, при a ° -–3-2 ; 1-2 ;
в)
π-----2n + --------------(−21)n arcsin (1 – 3 − 2a ) | n
° Z}, при a ° -–3-2 ; 1-2 ;
![]() ¾ при a ° –-
3-2 ; 12- ;
ã)
π-----2n + (–1)n +
1 12------π
¾ при a ° –-
3-2 ; 12- ;
ã)
π-----2n + (–1)n +
1 12------π
![]() n °
Z;
n °
Z;
д) π-----5n ; 2---------π5n- ä 1-5 arccos 41- n ° Z.
13.
![]() а)
πn + (–1)n arcsin --------------------334−
3
n ° Z
;
а)
πn + (–1)n arcsin --------------------334−
3
n ° Z
;
![]() б)
π-----5n + (–1)n------20π
– 6-5 n ° Z
; в)
π-----2n + -4π n
° Z.
Исполь-
б)
π-----5n + (–1)n------20π
– 6-5 n ° Z
; в)
π-----2n + -4π n
° Z.
Исполь-
зуйте формулу 2 sin2 x = 1 – cos 2x;
![]() ã) 2
πn
ä arccos 2a -2-n °Z
при a − 0, πn + -2π
n ° Z
ã) 2
πn
ä arccos 2a -2-n °Z
при a − 0, πn + -2π
n ° Z
при a = 0.
14. а) -2π + 2πn | n ° –N; 32- ; –-2π + 2πm | m ° N . Данную фунêцию после простейших преобразований можно представить в виде f(x) = 2 cos x – |2x – 3| + e3 – 2. Отсюда видно, что она дифференцируема всюду, êроме точêи x = 3-2 , т. е. эта точêа является êритичесêой. Имеем f(x) = 2 cos x + 2x + e3 – 5 при x < 3-2 , f(x) = 2 cos x – 2x + e3 + 1 при x > 3-2 . Друãие êритиче-
сêие точêи находим, продифференцировав фунêцию и приравняв производную нулю (с учетом неравенств);
б) -2π+ 1-6 -2π- + 2πm| m = 1, 0, –1, –2, ...; 2; 61- – + 2-2π πn n =
= 3, 4, 5 ... ; в) -2π (2n + 1) | n ° Z;
![]() ã)
2
πn
ä 3-----4π-n
° Z.
Данная фунêция дифференцируема
ã)
2
πn
ä 3-----4π-n
° Z.
Данная фунêция дифференцируема
![]()
![]()
![]() в êаждой точêе промежутêа
(–×; +×). Дифференцируя и приравнивая нулю производную, получаем уравнение
2cos2x + ( 2 – – 2 5 )cos x – 10 = 0. Отсюда следует, что
cos x = 5 (множество решений этоãо уравнения пусто) и cos x
= –-------22 ⇒
x = 2πn
ä 3-----4π- ;
n ° Z; д) (–
1)n + 1-4π
+ πn
| n ° Z
.
в êаждой точêе промежутêа
(–×; +×). Дифференцируя и приравнивая нулю производную, получаем уравнение
2cos2x + ( 2 – – 2 5 )cos x – 10 = 0. Отсюда следует, что
cos x = 5 (множество решений этоãо уравнения пусто) и cos x
= –-------22 ⇒
x = 2πn
ä 3-----4π- ;
n ° Z; д) (–
1)n + 1-4π
+ πn
| n ° Z
.
15. а) {π(2π + 1) | n ° Z}. Учитывая, что 2 cos2 x-2 = 1 + cos x, приведем уравнение ê виду cos3 x + cos2 x – 2(cos x + 1) = 0, или (cos x + 1)(cos2x – 2) = 0. Таêим образом, имеем два уравнения: 1 + cos x = 0, решение êотороãо есть x = 2πn + π, n ° Z, и cos2x – 2 = 0, êоторое решений не имеет;
б) πn + -2π ; 2πn ä -3π ; 2πn ä π – arccos 3-2 n ° Z ;
в) πn – -4π
; πn
ä -3π
![]() n °
Z
. Воспользуйтесь тождеством cos---------------12x – 1 = tg2x
и приведите уравнение ê виду (tg x + 1) ×
n °
Z
. Воспользуйтесь тождеством cos---------------12x – 1 = tg2x
и приведите уравнение ê виду (tg x + 1) ×
![]() × (tg2x – 3) = 0;
ã) 2πn; 2πn ä2-----3π- ;
2πn äarccos
-
--------------------−
1 4±5-
n ° Z.
× (tg2x – 3) = 0;
ã) 2πn; 2πn ä2-----3π- ;
2πn äarccos
-
--------------------−
1 4±5-
n ° Z.
16. а) {πn + arctg 5 | n ° Z}. Обе части уравнения ни при êаêом x не обращаются в нуль одновременно: разделив уравнение на cos x, получим уравнение -----------cossinxx- = 5, или tg x = 5, равно-
сильное данному. Решения последнеãо уравнения имеют вид x = πn + arctg 5 | n ° Z;
б) πn + -4π
n ° Z
; в) πn – -4π
![]() n °
Z
;
n °
Z
;
ã) 2
πn
– -4π
; 2πn
+ -2π
n ° Z;
д) πn + -2π
; πn
+ arctg -41 ![]() n ° Z
.
n ° Z
.
17. ![]() а) πn + -4π
; 2πn
ä 2-----3π- n
° Z
; б) πn + arctg
2 | n ° Z;
а) πn + -4π
; 2πn
ä 2-----3π- n
° Z
; б) πn + arctg
2 | n ° Z;
в) 2πn; πn + -4π n ° Z ; ã) πn – -4π ; | n ° Z ;
д) πn + -4π n ° Z. Преобразуйте правую часть уравнения
ê виду (cos x – sin x)2 + cos2x – sin2x.
18. а) πn – -4π ; πn – arctg 2 | n ° Z . Таê êаê sin x и cos x
при одном и том же значении x не обращаются в нуль, то можно разделить уравнение на cos2x. Получим уравнение
tg2 x + 3 tg x + 2 = 0, (1)
равносильное исходному. Из уравнения (1) получаем уравнения tg x = –1, и tg x = –2, решения êоторых находим по известным формулам;
б) πn + -4π ; πn – arctg 41- n ° Z ;
в) πn + arctg 2; πn – arctg 3-5 n ° Z;
ã) πn + arctg 2; πn – arctg 3-4 n ° Z . Представьте правую часть уравнения в виде –2(sin2x + cos2x);
![]() д) πn – -4π
; πn
+ arctg 5 | n ° Z.
19. а) {πn
– arctg 3 4 | n ° Z};
д) πn – -4π
; πn
+ arctg 5 | n ° Z.
19. а) {πn
– arctg 3 4 | n ° Z};
б) πn – -4π
; πn
±-3π- ![]() n ° Z.
Преобразуем правую часть
n ° Z.
Преобразуем правую часть
![]()
![]() уравнения: 3 sin x
(cos x – sin x) + 3 = 3sin x cos x – 3 sin2 x
+ + 3(sin2 x + cos2 x) = 3 cos x(sin
x + cos x). Теперь имеем уравнение sin2x(1
+ tg x) = 3 cos2 x(1 + tg x), или (1 + tg
x)(tg2 x – – 3) = 0, решение êотороãо сводится
ê решению уравнений tg x = –1, tg x = – 3 и tg x = 3
;
уравнения: 3 sin x
(cos x – sin x) + 3 = 3sin x cos x – 3 sin2 x
+ + 3(sin2 x + cos2 x) = 3 cos x(sin
x + cos x). Теперь имеем уравнение sin2x(1
+ tg x) = 3 cos2 x(1 + tg x), или (1 + tg
x)(tg2 x – – 3) = 0, решение êотороãо сводится
ê решению уравнений tg x = –1, tg x = – 3 и tg x = 3
;
в) π-----2n![]() n ° Z
. Представьте правую часть уравнения в виде 1 = (sin2 x
+ cos2 x)2 = sin4 x + 2sin2
x cos2 x + cos4 x;
n ° Z
. Представьте правую часть уравнения в виде 1 = (sin2 x
+ cos2 x)2 = sin4 x + 2sin2
x cos2 x + cos4 x;
![]()
![]() ã) π-----2n n ° Z
при a = 0; πn + arctg -----21a- ;
πn +
arctg −--------------------------------------1±
14a+
16a2
ã) π-----2n n ° Z
при a = 0; πn + arctg -----21a- ;
πn +
arctg −--------------------------------------1±
14a+
16a2
n ° Z при a − 0.
![]() 20. а) π-----2n – 1-2 arctg 5-3 n ° Z;
б) {πn +
arctg (6 ä 3 ) | n ° Z};
20. а) π-----2n – 1-2 arctg 5-3 n ° Z;
б) {πn +
arctg (6 ä 3 ) | n ° Z};
![]() в) πn + (–1)n
+ 1-6π n ° Z
; ã) πn – arctg 1-2 n ° Z;
в) πn + (–1)n
+ 1-6π n ° Z
; ã) πn – arctg 1-2 n ° Z;
![]() д) πn ä -6π
д) πn ä -6π
![]() n °
Z
. 21. а) 2πn; 2πn + 3-π
n ° Z
;
n °
Z
. 21. а) 2πn; 2πn + 3-π
n ° Z
;
![]()
![]() б) 2πn + 12------π
, 2πn
+ 7-----12π-n
° Z
; в) 2---------π5n- –
-5π
; 2---------π5n-
+ 2-----15π-
б) 2πn + 12------π
, 2πn
+ 7-----12π-n
° Z
; в) 2---------π5n- –
-5π
; 2---------π5n-
+ 2-----15π-
n ° Z;
ã) 2
πn;
2πn +
-2π
![]() n °
Z ;
д) 2πn + 5-----3π-
n °
Z ;
д) 2πn + 5-----3π-![]() n ° Z.
n ° Z.
22. а) ------12π ; ------12π (2n + 1); -8π (1 – 2n) | n ° N;
![]()
![]() б) 2πn ä
arccos -------a2 – -4π
n ° Z
при a ° [− 2
; 2 ]; ¾ при a õ [−
2 ; 2 ]; в) πn + 7-----12π- n
° Z
;
б) 2πn ä
arccos -------a2 – -4π
n ° Z
при a ° [− 2
; 2 ]; ¾ при a õ [−
2 ; 2 ]; в) πn + 7-----12π- n
° Z
;
![]() ã) π-----4n n ° Z,
êроме n = 4k + 2 | k ° Z.
ã) π-----4n n ° Z,
êроме n = 4k + 2 | k ° Z.
23. а) π-----3n – ------12π
![]() n °
Z, êроме n = 1 + 3m | m ° Z
;
n °
Z, êроме n = 1 + 3m | m ° Z
;
б) ¾; в) {πn | n ° Z}.
Исходное уравнение равносильно уравнению
2(tg 3x – tg 2x) = tg 2x (1 + tg 3x tg 2x). (1)
Найдем значения x, при êоторых 1 + tg 3x tg 2x = 0. Последнее уравнение эêвивалентно уравнению ---------------------------------cos2cosxcosx 3x- = 0.
Это уравнение не имеет решений, таê êаê если cos x = 0, то и cos 3x = 0. Следовательно, уравнение (1) можно разделить на
1 + tg 3x tg 2x − 0; имеем 2---------------------------------------1tg 3+ tg 3x −xtg 2tg 2xx- = tg 2x, или 2tg x =
= 1----------------------2−tgtgx2x , или tg x = 0.
Решив уравнение tg x = 0, получаем x = πn, n ° Z, и после проверêи выполнения условий x − π-----2k- + -4π и x − π-----3k- + 6-π k ° Z, устанавливаем, что x = πn, n ° Z — решение исходноãо уравнения; ã) {90°n + 25° | n ° Z}.
24. а) {2πn | n ° Z}. Используйте тождество sin x =
= 2 -----------------------tg x--2 ;
1 + tg2 x-2
б) 2πn – -2π
![]() n °
Z
. Используйте тождество cos x = 1---------------------1 −+
tgtg22x-x-22- ;
n °
Z
. Используйте тождество cos x = 1---------------------1 −+
tgtg22x-x-22- ;
в) πn ä -6π ; 2-π + πn | n ° Z ; ã) {2πn ä 2arctg 5 | n ° Z};
![]() д) 2
πn
ä 2arctg 3; 2πn
ä 2 arctg -------113
n ° Z;
е) πn ä
4-π
д) 2
πn
ä 2arctg 3; 2πn
ä 2 arctg -------113
n ° Z;
е) πn ä
4-π
![]() n °
Z.
n °
Z.
25. Нет. Множества решений первоãо уравнения πn – 4-π ; πn + -2π n ° Z и второãо — πn – -4π n ° Z не совпадают, поэтому уравнения неравносильны.
1 tg ---α2 - и cos α = ---------------------1 − tg2---αα---22-
Замечание. Тождества sin α = 2 ---------------------α + tg2
+ tg2---2 1
имеют место, êоãда cos α − –1.
26. а) πn + -2π ; πn ä -3π n ° Z . Таê êаê cos 3x = 4 cos3x –
– 3 cos x, то исходное уравнение равносильно уравнению cos x × × (4 cos2x – 1) = 0, или cos xcos 2x + 1-2 = 0, решая êоторое получаем ответ;
б) π-----3n + -6π ; 2---------π3n- ä
-----29π-![]() n ° Z.
Приведите уравнение ê виду cos (3 · 3x) – 4 cos2 3x
= 0 и положите cos 3x = t;
n ° Z.
Приведите уравнение ê виду cos (3 · 3x) – 4 cos2 3x
= 0 и положите cos 3x = t;
в) πn; π-----2n ä ------12π n ° Z . Приведите уравнение ê виду 2cos (2 · 2x) = 1 + cos (3 · 2x) и положите cos 2x = t.
27. а) {3πn | n ° Z}. Используйте тождество sin x = 3 sin x-3 –
– 4 sin3x-3 ;
б) π-----2n ; -----π2n + (–1)n + 1 ------12π ![]() n ° Z
; в) 2πn; 4πn ä -----23π-
n ° Z
; в) 2πn; 4πn ä -----23π-![]() n ° Z
;
n ° Z
;
![]() ã) πn + (–1)n-6π
; 2πn
+ -2πn
° Z.
Используйте тождества
ã) πn + (–1)n-6π
; 2πn
+ -2πn
° Z.
Используйте тождества
sin 3-----4π- + -x2- = sin -π – 3-----4π- – x-2- = sin 4-π – x-2- и sin -4π + 3-----2x =
= sin -π – -4π – 3-----2x- = sin 3 4-π – x-2- и положите x-2 – -4π = y.
28. πn – 4-π n ° Z .
29. а) {2πn | n ° Z} при a ° –×; –5-4- c (5; +×),
![]() 2πn; 4πn ä 2
arccos −------------------------------1±
44a +
5-
n ° Z
при a ° –5-4 ; 1 ,
2πn; 4πn ä 2
arccos −------------------------------1±
44a +
5-
n ° Z
при a ° –5-4 ; 1 ,
![]() 2πn; 4πn ä 2
arccos -----------------------------4a +45 −
1-
n ° Z
при a ° [1; 5]. Разло-
2πn; 4πn ä 2
arccos -----------------------------4a +45 −
1-
n ° Z
при a ° [1; 5]. Разло-
жив sin 3-----2x по формуле синуса тройноãо уãла, получаем уравнение sin x-2 2cos x-2 + 3 – 4 sin2x-2 – a- = 0 или
sin x--2 4 cos 2x-2 + 2 cosx-2 – 1 – a- = 0. (1)
Таêим образом, имеем совоêупность уравнений
![]() sin x-2 = 0,
sin x-2 = 0,
4 cos2 x-2 + 2 cos x--2 – 1 – a = 0.
Уравнение sin -x2 = 0 имеет решение x = 2πn | n ° Z при любом a ° R. Полаãая cos x-2 = t, получаем êвадратное уравнение относительно t:
4t2 + 2t – 1 – a = 0, (2)
![]()
![]()
![]()
![]() причем уравнение (2) может иметь
решения лишь при тех значениях a ° R, при êоторых t
° [–1; 1]. Находим êорни уравнения (2): t1 = −-----------------------------------1 −
44a +
5 ;
t2 = -----------------------------------−1 +
44a +
5 .
Решив далее неравенства –1 m t1 < 0 и –1 m t2 m
1, устанавливаем, что êорень t1 существует, если a °
-–45- ; 1 , а
êорень t2 существует, если a ° -–5-4 ; 5 . Следовательно, уравнение
cos x-2 = t1
имеет реше-
причем уравнение (2) может иметь
решения лишь при тех значениях a ° R, при êоторых t
° [–1; 1]. Находим êорни уравнения (2): t1 = −-----------------------------------1 −
44a +
5 ;
t2 = -----------------------------------−1 +
44a +
5 .
Решив далее неравенства –1 m t1 < 0 и –1 m t2 m
1, устанавливаем, что êорень t1 существует, если a °
-–45- ; 1 , а
êорень t2 существует, если a ° -–5-4 ; 5 . Следовательно, уравнение
cos x-2 = t1
имеет реше-
![]()
![]() ния x = 4πn ä
2 arccos −-----------------------------------1 −
44a +
5 ,
n ° Z, при a ° –- 45- ; 1 , а
уравнение cos x-2 = t2
— решения x = 4πn
ä 2arccos -----------------------------4a +45 −
1- ,
ния x = 4πn ä
2 arccos −-----------------------------------1 −
44a +
5 ,
n ° Z, при a ° –- 45- ; 1 , а
уравнение cos x-2 = t2
— решения x = 4πn
ä 2arccos -----------------------------4a +45 −
1- ,
![]() n ° Z, при
a ° -–5-4 ; 5 . Учитывая, что на
отрезêе –-
-45 ; 1 уравнение (2) имеет два решения,
получаем ответ;
n ° Z, при
a ° -–5-4 ; 5 . Учитывая, что на
отрезêе –-
-45 ; 1 уравнение (2) имеет два решения,
получаем ответ;
![]() б) {πn | n ° Z} при a
° 0; 1-3
, πn; πn ä 1-2 arccos 1-----------2−aa-
б) {πn | n ° Z} при a
° 0; 1-3
, πn; πn ä 1-2 arccos 1-----------2−aa-![]() n ° Z
при a ° -1-3 ; 1 , πn; πn ä 21- arccos 1-----------2−aa- ; πn ä
1-2 arccos –
-----------12+aa-
n ° Z
при a ° -1-3 ; 1 , πn; πn ä 21- arccos 1-----------2−aa- ; πn ä
1-2 arccos –
-----------12+aa-
![]()
n ° Z при a ° (1; +×).
![]() 30.
2
πn
ä arccos ----------------------a2c+
b2 + arctg -ab-
30.
2
πn
ä arccos ----------------------a2c+
b2 + arctg -ab-![]() n ° Z
при c2 m a2 + b2,
n ° Z
при c2 m a2 + b2,
![]() ¾ при c2 >
a2 + b2. Таê êаê a2
+ b2 − 0, то, разделив уравнение на a2 + b2 ,
получим уравнение
¾ при c2 >
a2 + b2. Таê êаê a2
+ b2 − 0, то, разделив уравнение на a2 + b2 ,
получим уравнение
![]()
![]() ----------------------a cos x + ----------------------b sin x = ----------------------c , (1) a2 + b2 a2 + b2 a2 +
b2
----------------------a cos x + ----------------------b sin x = ----------------------c , (1) a2 + b2 a2 + b2 a2 +
b2
![]() равносильное исходному.
Числа ----------------------a и ----------------------b по абсолютной a2 + b2 a2 + b2
равносильное исходному.
Числа ----------------------a и ----------------------b по абсолютной a2 + b2 a2 + b2
величине не превосходят единицы и удовлетворяют тождеству
![]() ----------------------a
2 + ----------------------2b+ b2 2 = 1. Поэтому можно положить ----------------------a2a+ b2
= a2 + b2 a
----------------------a
2 + ----------------------2b+ b2 2 = 1. Поэтому можно положить ----------------------a2a+ b2
= a2 + b2 a
![]() = cos ϕ и ----------------------b = sin ϕ.
= cos ϕ и ----------------------b = sin ϕ.
a2 + b2
Тоãда уравнение (1) примет вид cos x cos ϕ + sin x sin ϕ = cos (x – ϕ) = ----------------------c . (2) a2 + b2
![]() Уравнение (2) имеет решение,
если ----------------------c m 1, или
c2 m a2 + a2 +
b2
Уравнение (2) имеет решение,
если ----------------------c m 1, или
c2 m a2 + a2 +
b2
+ b2, отêуда получаем
![]() x – ϕ = 2πk ä
arccos ----------------------c , k ° Z.
(3) a2 + b2
x – ϕ = 2πk ä
arccos ----------------------c , k ° Z.
(3) a2 + b2
Значение вспомоãательноãо арãумента найдем из системы уравнений
![]() cos ϕ = ----------------------a , sin ϕ = ----------------------b ; a2 + b2 a2 +
b2
cos ϕ = ----------------------a , sin ϕ = ----------------------b ; a2 + b2 a2 +
b2
![]() значит,
ϕ = 2πm + arctg -ab-
m ° Z. (Здесь мы предполаãаем, что
значит,
ϕ = 2πm + arctg -ab-
m ° Z. (Здесь мы предполаãаем, что
a > 0; если a = 0, то исходное уравнение сводится ê простейшему уравнению b sin x = c; если же a < 0, то êоэффициент перед cos x можно сделать положительным, умножив уравнение на –1.) Подставляя полученное значение в условие (3), находим
![]() x
= 2π (m
+ k) ä arccos ----------------------a2c+ b2 + arctg -ab- ,
x
= 2π (m
+ k) ä arccos ----------------------a2c+ b2 + arctg -ab- ,
или
![]() x = 2πn ä
arccos ----------------------a2c+ b2 + arctg a-b- ,
n ° Z. таê êаê (m + k) ° Z.
x = 2πn ä
arccos ----------------------a2c+ b2 + arctg a-b- ,
n ° Z. таê êаê (m + k) ° Z.
Замечание. Если принять ----------------------a = sin ϕ, ----------------------b = cos ϕ, a2 + b2 a2 + b2
то уравнение (2) примет вид sin (x + ϕ) = ----------------------c .
a2 + b2
![]() 31. а) 2πn ä
arccos ---------
+ arctg 3-2 n ° Z
;
31. а) 2πn ä
arccos ---------
+ arctg 3-2 n ° Z
;
![]()
![]() б) 2πn ä
arccos -------a22 + 4-π
n ° Z
при a ° [– 2 ; 2 ], ¾ при a ° (–×; –4 2 )
c (4 2 ; +×);
б) 2πn ä
arccos -------a22 + 4-π
n ° Z
при a ° [– 2 ; 2 ], ¾ при a ° (–×; –4 2 )
c (4 2 ; +×);
![]()
![]() в) πn ä 1-2 arccos ---------a10-
+ 1-2 arctg 1-3 n ° Z
при a ° [– 10 ; 10 ],
в) πn ä 1-2 arccos ---------a10-
+ 1-2 arctg 1-3 n ° Z
при a ° [– 10 ; 10 ],
![]()
![]()
![]() ¾ при a
(–×; – 10 ) c ( 10 ; +×). Разделив данное
уравнение на 12 +
32 = 10 и положив ---------- = cos ϕ; ----------
= sin ϕ, получим
cos 2x cos ϕ
+ sin 2x sin ϕ
= cos (2x – ϕ)
= ---------a10- , ãде ϕ = arctg -31 .
¾ при a
(–×; – 10 ) c ( 10 ; +×). Разделив данное
уравнение на 12 +
32 = 10 и положив ---------- = cos ϕ; ----------
= sin ϕ, получим
cos 2x cos ϕ
+ sin 2x sin ϕ
= cos (2x – ϕ)
= ---------a10- , ãде ϕ = arctg -31 .
Уравнение cos (2x – ϕ) = ---------a - имеет решение, если ---------a - m 1, или
![]() 10 10
10 10
![]() – 10 m a m 10 . Таêим
образом, 2x – arctg 31- = 2πn ä
arccos ---------a10- , n ° Z, при
| a | m 10 . Отсюда получаем ответ;
– 10 m a m 10 . Таêим
образом, 2x – arctg 31- = 2πn ä
arccos ---------a10- , n ° Z, при
| a | m 10 . Отсюда получаем ответ;
![]() ã)
π-----6n ä ------121 arccos 2-------------------a137+
17 + 12------1 arctg 11------4 n ° Z
при
ã)
π-----6n ä ------121 arccos 2-------------------a137+
17 + 12------1 arctg 11------4 n ° Z
при
![]()
![]() a ° −--------------------------------1372 −
17 ;
---------------------------1372−
17 ,
¾ при a ° –×;
−--------------------------------1372 −
17
c
a ° −--------------------------------1372 −
17 ;
---------------------------1372−
17 ,
¾ при a ° –×;
−--------------------------------1372 −
17
c
c ---------------------------1372− 17 ; +× . Используйте формулы sin2 6x =
= 1----------------------------− cos2 12x , cos2 6x = 1----------------------------+ cos2 12x , sin 6x cos 6x = 1-2 sin 12x.
32. ![]() p ° [ 5 – 1;
2].
p ° [ 5 – 1;
2].
33. 2---------π3n- ä
1-3 arccos 5a- –
31- arctg -34 ![]() n ° Z
при a [–5; 5]; при a õ [–5; 5] фунêция êритичесêих
точеê не имеет. 34. а) πn – -8πn
° Z
; б) πn; π-----3n + 6-π
n ° Z
;
n ° Z
при a [–5; 5]; при a õ [–5; 5] фунêция êритичесêих
точеê не имеет. 34. а) πn – -8πn
° Z
; б) πn; π-----3n + 6-π
n ° Z
;
![]() в) 4---------π5n- +
2-----5π- ;
4---------3πn- + -----23π- n
° Z ; ã)
π-----4n n ° Z ;
в) 4---------π5n- +
2-----5π- ;
4---------3πn- + -----23π- n
° Z ; ã)
π-----4n n ° Z ;
![]() д)
π-----2n + 8-π
; πn
+ 3-----4π- n
° Z .
Приведите уравнение ê виду
д)
π-----2n + 8-π
; πn
+ 3-----4π- n
° Z .
Приведите уравнение ê виду
![]() cos 3x + cos -2π
+ x-
= 0; е) n;
------------------------------−1±
24l +
3 n
° Z, l ° Z0
.
cos 3x + cos -2π
+ x-
= 0; е) n;
------------------------------−1±
24l +
3 n
° Z, l ° Z0
.
35.
![]()
![]() а) πn + -πn
° Z
; б) π-----4nn ° Z
;
а) πn + -πn
° Z
; б) π-----4nn ° Z
;
4
в)
π-----6n + ------12π
; 2πn
ä 2-----3π- n
° Z
; ã) πn; 2πn ä
-6π
![]() n °
Z
;
n °
Z
;
36. а) πn – -4π ; πn + -2π n ° Z;
б) 2---------π3n- ; πn + 4-π ; 2πn – -2π n ° Z;
![]() в)
π-----2nn ° Z ;
ã) πn + -2π
n ° Z .
в)
π-----2nn ° Z ;
ã) πn + -2π
n ° Z .
37. а) π-----6n + ------48π ; π-----4n + -----332π- n ° Z . Преобразуйте уравне-
ние ê виду sin 10x = sin -4π – 2x- ;
б) {x0 | x0
° R, êроме x0 = πn | n °
Z}; в)
-----π5n ; πn ä -----38π-![]() n ° Z
.
n ° Z
.
Преобразуйте уравнение ê виду ---------------------------------------------------------------------------sin2xcos3cosx +2sinx 3xcos2x +
![]() + 2 sin 5x = 0;
+ 2 sin 5x = 0;
![]() ã) 4
πn
+ 17----------6π
; 8---------π3n- –
5-----18π- ;
8---------3πn- +
-6πn
° Z .
Преобразуйте
ã) 4
πn
+ 17----------6π
; 8---------π3n- –
5-----18π- ;
8---------3πn- +
-6πn
° Z .
Преобразуйте
правую часть уравнения ê виду 2 3 cos x-4 + -8π – -3π =
![]() = 2 3 cos x-4 – 5-----24π-
.
= 2 3 cos x-4 – 5-----24π-
.
38. а) 2---------π5n- ; πn + -2π ; 2πn + π | n ° Z . Преобразуйте уравнение ê виду (sin x + sin 4x) + (sin 2x + sin 3x) = 2sin 5-----2x -cos -----32x +
+ cos x--2-
= 0; б)
π-----5n ; π-----3n + 6-π
![]() n ° Z
;
n ° Z
;
в) πn + -2π
; -----π6n + ------24π
![]() n °
Z;
n °
Z;
ã) π-----4n + -8π ; π-----3n + (–1)n + 1------18π ![]() n ° Z;
n ° Z;
д) π-----5n + (–1)n ------30π ; π-----4n + ------16π ; πn + 3-----4π-n ° Z .
39.
![]() а)
πn + -2π
; πn
+ (–1)n6-π ; 2πn ä 2-----3π-n
° Z ;
а)
πn + -2π
; πn
+ (–1)n6-π ; 2πn ä 2-----3π-n
° Z ;
б)
π-----2n ; 2πn ä 2-----3π-![]() n ° Z
;
в)
-7π
(2n + 1) | n ° Z, êроме n =
7l –
n ° Z
;
в)
-7π
(2n + 1) | n ° Z, êроме n =
7l –
– 4 | l ° Z . Преобразуем уравнение: -----------sin1 x- = ---------------sin12x- + ---------------sin14x- =
= ----------------------------------------------2sin2sinxcos3xxcossinx4x- , sin 4x – sin 3x = 0; 2 sin x-2 cos -----72x = 0.
Из решений последнеãо уравнения нужно отобрать те, при êоторых sin x − 0, sin 2x − 0, sin 4x − 0. Имеем sin x-2 = 0, x = 2πk,
k ° Z — постороннее решение, знаменатели всех дробей исходноãо уравнения обращаются в нуль;
cos 7-----2x = 0, x = π2---------------n7+ 1- .
Исêлючим из этоãо решения значения n, при êоторых x = -------π4m- (этоãо достаточно, таê êаê все решения уравнений sin x = 0, sin 2x = 0 являются решениями уравнения sin 4x = 0).
Имеем уравнение π2---------------n7+ 1- = π-------4m- , или 7m = 8n + 4; m = n + n-----------7+ 4 .
Таêим образом, если n-----------7+ 4 = l, l ° Z, то существуют целые m, при êоторых уравнение теряет смысл. Оêончательно получим x = π 2---------------n7+ 1- , n ° Z, êроме n = 7l – 4 | l ° Z.
![]() ã) (–×;
+×) при a ° {kπ
| k ° Z}, 2πn ä
arccos 1-------±4
ã) (–×;
+×) при a ° {kπ
| k ° Z}, 2πn ä
arccos 1-------±4------5- n ° Z
при a ° ( –×; +×).
40.
π-----4n + -8π
; πn
ä -3π
![]() n °
Z
. 41. а) {πn
| n ° Z};
n °
Z
. 41. а) {πn
| n ° Z};
б) π-----3n n ° Z . Имеем -----------cossinxx- – ---------------cossin33xx-- + ---------------cossin22xx- = ---------------cossin22xx- –
– -----------------------------cossinxcos2x3x- = ---------------------------------------------------------------------------sin2xcos(cosxcosxcos2x3cosx −3cosx 2x)- = – tg x tg 2x tg 3x = 0.
Решив уравнение, найдем x1
= πn | n °
Z, x2 = π-------2m-![]() m ° Z,
и x3 = π-----3l
m ° Z,
и x3 = π-----3l![]()
l ° Z. Уравнение x = π-----3l является следствием уравнения x = πn и уравнения x = π-------2m- (при m = 2p, p ° Z). Нечетные значения m дают посторонние решения. Итаê, x = π-----3n , n ° Z.
42. а) π-----10n n ° Z . Исходное уравнение равносильно уравнению 1-2 (cos 3x + cos 9x) = 1-2 (cos 3x + cos 11x), или cos 9x –
– cos 11x = 0. Преобразуя разность êосинусов в произведение, получаем уравнение 2 sin x sin 10x = 0, из êотороãо находим решения x = πk, x = π-----10n , k, n ° Z. Учитывая, что решения первоãо уравнения являются решениями второãо (при k = 10n), получим ответ;
б) π-----3n + -6π ; π-----5n + ------10π n ° Z;
![]() в) πn; π-----5n + ------10π n
° Z
; ã) πn; π-----3n + 6-π
n ° Z ;
в) πn; π-----5n + ------10π n
° Z
; ã) πn; π-----3n + 6-π
n ° Z ;
![]() д) n
– ------125 ; n + 1-4 n ° Z
. 43. а)
-----π2n ; πn ä -6π
n ° Z
. Умножив данное уравнение на 2 и применив тождество 1 – cos α =
д) n
– ------125 ; n + 1-4 n ° Z
. 43. а)
-----π2n ; πn ä -6π
n ° Z
. Умножив данное уравнение на 2 и применив тождество 1 – cos α =
= 2 sin2 α---2 , приведем уравнение ê виду 2 sin2 2x – (cos 2x – cos 6x) =
= 0. Преобразуя далее разность êосинусов в произведение синусов, получаем 2 sin2 2x – 2 sin 2x sin 4x = 0. Из последнеãо уравнения находим x = π-----2n и x = πn ä 6-π , n ° Z;
![]() б)
π-----2n + -4π
; π-----5n + ------10π n
° Z;
в) πn + -2π
; 2---------11πn- +
------11π
; 2---------5πn-
б)
π-----2n + -4π
; π-----5n + ------10π n
° Z;
в) πn + -2π
; 2---------11πn- +
------11π
; 2---------5πn-
![]() n
° Z;
ã) πn ä 1-2 arccos 43- n ° Z.
44. а)
2---------π7n- +
-7π
n
° Z;
ã) πn ä 1-2 arccos 43- n ° Z.
44. а)
2---------π7n- +
-7π
![]() n °
Z.
n °
Z.
Приведите уравнение ê виду
2 sin x-2 sin x + 2 sin -x2 sin 2x + 2 sin -x2 sin 3x = cos x-2
и преобразуйте левую часть, используя формулу
2 sin α sin β = cos (α – β) – cos (α + β);
б)
2---------π7n-![]() n ° Z,
êроме n
= 7k, k ° Z.
Умножьте уравнение
на 2 sin x-2 .
n ° Z,
êроме n
= 7k, k ° Z.
Умножьте уравнение
на 2 sin x-2 .
45. а) π-----4n + (–1)n + 124------π n ° Z. Исходное уравнение равносильно уравнению sin x cos 3x(1 – cos 2x) + cos x sin 3x (1 + + cos 2x) = –3-4 , или (sin x cos 3x + cos x sin 3x) + cos 2x (sin 3x × × cos x – cos 3x sin x) = –43- , или sin 4x + 2-1 sin 4x = –3-4 . Теперь имеем уравнение sin 4x = –1-2 , решив êоторое получим ответ;
б) πn ä -8π n ° Z. 46. а) -----π3n + (–1)n18------π n ° Z. Разложим левую часть уравнения в сумму триãонометричесêих фунêций:
1-2 sin x -2 sin --3π – x sin --3π + x = = 1-2 sin x -cos 2x – cos -----23π-- + -41 (2 sin x cos 2x + sin x) = = 1-4 (sin 3x – sin x + sin x) = 1-4 sin 3x.
Решив теперь уравнение sin 3x = 1-8 · 4 = 1-2 , получаем ответ;
б) -2---------π3n- ä 2-----9π- n ° Z; в) π-----3n – -9π n ° Z.
![]()
![]() 47. а) πn; πn ä -6π
n ° Z;
б) πn ä 6-π
n ° Z;
47. а) πn; πn ä -6π
n ° Z;
б) πn ä 6-π
n ° Z;
в) πn ä -21 arccos –-65 n ° Z. Преобразуйте данное урав-
нение ê виду ------------------------------------------------------------------sinxcoscos3xx−sincos3xxsin3x- = 3;
![]() ã)
πn ä 1-2 arccos –1-4 ; πn ä 21- arccos 1-3n ° Z;
ã)
πn ä 1-2 arccos –1-4 ; πn ä 21- arccos 1-3n ° Z;
![]() д) πn + -2π
n ° Z.
48. а) πn ä -8π
n ° Z;
д) πn + -2π
n ° Z.
48. а) πn ä -8π
n ° Z;
б) πn ä 6-π
n ° Z;
в)
π-----2n + 4-π
; πn
+ 2-π
![]() n °
Z.
Восполь-
n °
Z.
Восполь-
зуйтесь тождеством 8 sin6 x = (1 – cos 2x)3;
![]() ã)
π-----2n + -4π
; πn
ä 1-2 arccos ---------------52−
1- n
° Z.
Примените фор-
ã)
π-----2n + -4π
; πn
ä 1-2 arccos ---------------52−
1- n
° Z.
Примените фор-
мулы tg2 x = 1-------------------------1 −+ coscos22xx- , cos 4x = 2 cos2 2x – 1;
д) πn + -4π ; π-----2n + --------------(−21)n arcsin---------------52− 1- .
![]() 49. а) {πn ä arccos (3 – 2 3
− a2
)} при a ° [– 2 ; 2 ], ¾ при
49. а) {πn ä arccos (3 – 2 3
− a2
)} при a ° [– 2 ; 2 ], ¾ при
![]()
![]() a õ [– 2 ; 2
]; б) π-----2n ä -14 arccos 16------------------a7− 1 n ° Z
при a ° – ×; –38-
a õ [– 2 ; 2
]; б) π-----2n ä -14 arccos 16------------------a7− 1 n ° Z
при a ° – ×; –38- ![]() c c -1-2 ; +×-
, ¾ при a ° –3-8 ; 1-2
; в)
π-----2n + -4π
c c -1-2 ; +×-
, ¾ при a ° –3-8 ; 1-2
; в)
π-----2n + -4π
![]() n °
Z
при a ° ° (–×; 6] c [8; + ×);
π-----2n + -4π
; π-----2n ä 1-4 arccos (a – 7)
| n ° Z
при
n °
Z
при a ° ° (–×; 6] c [8; + ×);
π-----2n + -4π
; π-----2n ä 1-4 arccos (a – 7)
| n ° Z
при
a ° (6; 8).
50. а) ------------------------π(4n2+ 1)- ; π(2n + 1) | n °Z. Полаãая sin x – cos x = y, имеем (sin x – cos x)2 = 1 – sin 2x = y2, или sin 2x = 1 – y2. Исходное уравнение примет вид y2 + 12y – 13 = 0 ⇒ y1 = 1; y2 = –13. Таêим образом, получим два уравнения: sin x – cos x = y1 = 1, решения êотороãо имеют вид x1 = π(2n + 1), x2 = ------------------------π(4n2+ 1)- , n ° Z,
и sin x – cos x = y2 = –13, êоторое не имеет решений; б) πn – -4π ;
![]() π-----2n + (–1)n + 1-8π n
° Z.
Приведите уравнение ê виду -----------sin1 x-
+
π-----2n + (–1)n + 1-8π n
° Z.
Приведите уравнение ê виду -----------sin1 x-
+
+ -----------cos1 x- = –2 2 (sin x + cos x) и положите sin x + cos x = y;
в) 2πn + 4-π
; 2πn
+ 11----------12π
; 2πn
– 5-----12π-![]() n ° Z;
n ° Z;
ã) 2 πn; 2πn + -2π n ° Z;
![]() д) 2πn – 2-π
; πn
– 4-π
+ (–1)narcsin -------12 – 1-π
n ° Z .
При-
д) 2πn – 2-π
; πn
– 4-π
+ (–1)narcsin -------12 – 1-π
n ° Z .
При-
ведите уравнение ê виду sin x(1 + sin x) + cos x (1 – sin2 x) =
= (1 + sin x)(sin x + cos x – sin x cos x) = 0;
![]() е)
-4πn
+ 2-π-
2 ; 4
πn
+ 11----------6π
2
е)
-4πn
+ 2-π-
2 ; 4
πn
+ 11----------6π
2 ![]() n °Z0; (4πm – 5-----6π-
2 m ° N.
n °Z0; (4πm – 5-----6π-
2 m ° N.
51. ![]() а) 2πn | n ° Z
при a ° {–1} c (–2( 2 – 1); 2( 2 + 1)),
а) 2πn | n ° Z
при a ° {–1} c (–2( 2 – 1); 2( 2 + 1)),
![]()
![]() 2πn; 2πn ä π – arccos -----------aa+22--
+ 4-π
n ° Z
при a ° (–×; –1) c c (–1; –2( 2 – 1)] c [2( 2 + 1); +×); б) 2πn – -4π
2πn; 2πn ä π – arccos -----------aa+22--
+ 4-π
n ° Z
при a ° (–×; –1) c c (–1; –2( 2 – 1)] c [2( 2 + 1); +×); б) 2πn – -4π
![]() n °
Z
при b ° (–×; 0) c (1; +×), 2πn – 4-π
; 2πn
ä arccos (2b – 1) – -4π
n °
Z
при b ° (–×; 0) c (1; +×), 2πn – 4-π
; 2πn
ä arccos (2b – 1) – -4π
![]() n °
Z при b
° [0; 1];
n °
Z при b
° [0; 1];
![]() в) πn – -4πn
° Z
при a ° –×; –-------32
c –-------12 ; +×
, πn – -4π
;
в) πn – -4πn
° Z
при a ° –×; –-------32
c –-------12 ; +×
, πn – -4π
;
![]()
![]() π-----2n + --------------(−21)n arcsin (a 2
+ 2) | n ° Z
при a ° –-------32 ; –-------12 .
π-----2n + --------------(−21)n arcsin (a 2
+ 2) | n ° Z
при a ° –-------32 ; –-------12 .
52. 2 πn; 2πn + -2π n ° Z. 53. а) 2πn + -----56π- n ° Z. Решим
исходное уравнение относительно tg x (sin x принимаем за параметр):
![]() tg
x = 1-2 –-------23 ä −2sinx −
21-
2
.
tg
x = 1-2 –-------23 ä −2sinx −
21-
2
.
![]() Полученное
уравнение будет иметь решения, если sin x = 1-2 ; тоãда tg x
= –-------
и мы приходим ê системе уравнений
Полученное
уравнение будет иметь решения, если sin x = 1-2 ; тоãда tg x
= –-------
и мы приходим ê системе уравнений
![]() sin
x = 1-2 , tg x = –-------13 .
sin
x = 1-2 , tg x = –-------13 .
Из первоãо уравнения системы имеем x1 = 2πn + -6π и x2 =
= 2πn + 5-----6π- , n ° Z. Второму уравнению системы удовлетворяют лишь значения x2;
б) πn; 2πn + -2π
![]() n °
Z.
в) 2πn – -4π
n °
Z.
в) 2πn – -4π
![]() n °
Z.
Преобразуйте уравнение ê виду cos2 2x + sin4 x-2 + -8π
= 0, а затем решите систему уравнений cos 2x = 0, sin x-2 +-8π
= 0.
n °
Z.
Преобразуйте уравнение ê виду cos2 2x + sin4 x-2 + -8π
= 0, а затем решите систему уравнений cos 2x = 0, sin x-2 +-8π
= 0.
54. а) {2π(1 + 4n) | n ° Z}. После несложных преобразований уравнение приводится ê виду
sin 5------4x + cos x = 2. (1)
Таê êаê sin 5-----4x m 1, cos x m 1, то для выполнения равенства (1) необходимо одновременное выполнение равенств cos x = 1 и sin 5-----4x = 1. Таêим образом, имеем систему уравнений
x = 2πk, 5------4x = -2π + 2πl,
ãде k, l — неêоторые целые числа. Исêлючая x из этой системы, придем ê уравнению 4l = 5k – 1, или l = k + k-----------4− 1- . Последнее уравнение имеет решение в целых числах, если k-----------4− 1- = n, n ° Z.
Оêончательно получаем k = 4n + 1 | n ° Z и x = 2π(4n + 1);
![]() б)
π-----3n ; 2πn – -2πn °
Z .
б)
π-----3n ; 2πn – -2πn °
Z .
55. а) πn – arctg 1-6 ; πn – arctg 31- n ° Z. Воспользуйтесь
![]()
![]() тем, что ---------------cos12x − 1 = | tg x |; б) n∪∈ Z
2πn –
-3π
; 2πn
+ -----23π--
. Вос-
тем, что ---------------cos12x − 1 = | tg x |; б) n∪∈ Z
2πn –
-3π
; 2πn
+ -----23π--
. Вос-
![]() пользуйтесь тем, что 2
+ cos2x + 3sin2x = 2
cos x
– -6π
.
пользуйтесь тем, что 2
+ cos2x + 3sin2x = 2
cos x
– -6π
.
56.
![]() а) πn ä -6πn
° Z.
Решениями данноãо уравнения
а) πn ä -6πn
° Z.
Решениями данноãо уравнения
моãут быть лишь те значения x, при êоторых cos 2x > –1-4 . Возводя уравнение в êвадрат и выполнив преобразования, получаем уравнение 8cos2 2x + 10cos 2x – 7 = 0, из êотороãо имеем cos 2x = –7-4 и cos 2x = 21- . Уравнение cos 2x = –7-4 решений не имеет, а решение второãо уравнения является решением исходноãо cos 2 x = 1-2 > –-41- ; б) {2πn + arctg a | n ° Z} при a °
° (0; +×), {π(2n + 1) + arctg a |n ° Z} при a (–×; 0), {πn | n ° Z} при a = 0.
![]() 57.а) 2πn + 3-----4π- n
° Z.
Исходное уравнение равносильно
57.а) 2πn + 3-----4π- n
° Z.
Исходное уравнение равносильно
![]() системе
sin x = 2 cos 2x, cos x m 0.
системе
sin x = 2 cos 2x, cos x m 0.
![]()
![]() Решая уравнение системы,
имеем 2 sin 2x + sin x – 2 = 0, отêуда придем
ê уравнению sin x = ------- . Решениями последнеãо
являются x = 2πn
+ -4π
(постороннее, таê êаê не выполняется неравенство системы) и x
= 2πn
+ 3-----4π- ,
n ° Z, удовлетворяющее всем условиям системы;
Решая уравнение системы,
имеем 2 sin 2x + sin x – 2 = 0, отêуда придем
ê уравнению sin x = ------- . Решениями последнеãо
являются x = 2πn
+ -4π
(постороннее, таê êаê не выполняется неравенство системы) и x
= 2πn
+ 3-----4π- ,
n ° Z, удовлетворяющее всем условиям системы;
б) 2πn – arccos ---------------52− 1- n ° Z; в) 2πn + -8π ; 2πn – 3-----8π- n ° Z;
![]() ã)
π-----2n ; πn + 6-π
n ° Z;
д) 2πn + 2-π
; 2πn
– 6-π
ã)
π-----2n ; πn + 6-π
n ° Z;
д) 2πn + 2-π
; 2πn
– 6-π
![]() n °
Z;
n °
Z;
е) (–×; +×) при a = 0; {πn | n ° Z} при a(–×; +×).
58. а) 2πn; 2πn – -2π
![]() n °
Z;
n °
Z;
б) 2πn + 3-----8π- ;
2πn +
7-----8π- ;
2πn +
π; πn + -4π
![]() n °
Z.
Приведите уравнение ê виду (sin 2x + cos 2x)(1 – cos 2x –
sin 2x) = 0 и учтите условие sin x – cos x l 0;
n °
Z.
Приведите уравнение ê виду (sin 2x + cos 2x)(1 – cos 2x –
sin 2x) = 0 и учтите условие sin x – cos x l 0;
![]() в) 2πn; πn – -4π
n ° Z;
ã)
π-----3n + (–1)n + 118------π n
° Z;
в) 2πn; πn – -4π
n ° Z;
ã)
π-----3n + (–1)n + 118------π n
° Z;
![]() д)πn + arctg 2-3n ° Z;
е) 2πn + 12------π
; 2πn
– 7-----12π- n
° Z.
д)πn + arctg 2-3n ° Z;
е) 2πn + 12------π
; 2πn
– 7-----12π- n
° Z.
59.
![]() а) 2πn + -6π
; 2-3 πl + 5-----18π-n,
l ° Z, êроме l = 3m + 2 | m ° Z;
а) 2πn + -6π
; 2-3 πl + 5-----18π-n,
l ° Z, êроме l = 3m + 2 | m ° Z;
б) 4πn + 13----------6π
![]() n °
Z.
60. 2πn ä
arccos
21- + 1-4 a
– -----65a-
2
n °
Z.
60. 2πn ä
arccos
21- + 1-4 a
– -----65a-
2
![]()
![]() n ° Z
при a ° -65 , -----------------------2 2 +6 3 , ¾ при a õ
5-6 ; 2-----------------------2 +6 3 .
n ° Z
при a ° -65 , -----------------------2 2 +6 3 , ¾ при a õ
5-6 ; 2-----------------------2 +6 3 .
61.а) 2πn + arccos 1-3 n °Z. Преобразуем правую часть уравнения:
(log5 4) log4 (3sin x) = log---------------------------------4log(34sin5 x) = log5 (3sin x).
![]() Тоãда получим уравнение
log5 tg x = log5 (3sin x), эêвивалентное
системе tg x = 3 sin x, Решив уравнение системы, поsin x >
0.
Тоãда получим уравнение
log5 tg x = log5 (3sin x), эêвивалентное
системе tg x = 3 sin x, Решив уравнение системы, поsin x >
0.
лучаем cos x = 1-3 (sin x − 0), отêуда x1 = 2πn + arccos 1-3 и x2 =
= 2πn – arccos 1-3 , n ° Z. Второе решение (x2) не удовлетворяет неравенству системы и является посторонним;
б) 2πn + arccos
------101 n °Z.
62. а) {πn
| n ° Z}. Приведите уравнение ê виду 22cos2x − 1 = 3
· 2cos2x
– 4 и положите 2cos2x = t; б) log
2 π-----4n + -8π
n°Z0.
63. а) –
-2π
+ 2πn;
10------π
+ ------------2π5m![]() n, m ° Z.
n, m ° Z.
Последовательно преобразуя, имеем cos 3x – cos -2π – 2x = 0, sin x--2 + -4π sin 5-----2x – 4-π- = 0, отêуда получаем ответ.
Замечание. Два полученных множества решений не имеют общих точеê.
б) 3-----4π- + πn; 3-----8π- + π-------2m-n, m ° Z;
![]() в) – -4π
+ πn;
------16π
+ π-------4m-n, m °
Z;
в) – -4π
+ πn;
------16π
+ π-------4m-n, m °
Z;
ã) -2π + 2πn; 14------π + 2------------π7mn, m ° Z.
64.а) -8π + π-----4n ; x = ä-3π + 2πm | n, m ° Z. Преобразуя сум-
му êосинусов в произведение, приходим ê уравнению
2 cos 4x cos x = cos 4x ⇔ cos 4x (2 cos x – 1) = 0.
Решив уравнение cos 4x = 0, получаем
4x = 2-π + πn, n ° Z; x = 8-π + π-----4n , n ° Z.
Уравнение 2 cos x – 1 = 0 имеет решения x = ä-3π + 2πm, m ° Z.
б)
π-----6n ; ä2-----9π- +
------------2π3m n, m ° Z;
в) -6π
+ π-----3n![]() n ° Z;
n ° Z;
ã) π-----3n ; (–1)m + 1-6π + πm | n, m ° Z.
65. а) 4-π + (–1)n6-π + πn; 3-----4π- + 2πm | n, m ° Z. Выполнив замену t = x – -4π , приходим ê уравнению
![]() 2 sin2 t –
3sin t + 1 = 0 ⇔
2 sin2 t –
3sin t + 1 = 0 ⇔
![]() sinsin tt ==
1-21 , ⇔ tt = (= 2-π–
+ 21)n-6ππm
+ , πmn
, °n Z °. Z,
sinsin tt ==
1-21 , ⇔ tt = (= 2-π–
+ 21)n-6ππm
+ , πmn
, °n Z °. Z,
Возвращаясь ê переменной x, получаем ответ;
б) (--------------−21)n arcsin 98- + π-----2n ; (--------------−21)n arcsin 43- + π-----2k- n, k ° Z;
в) – 3-----4π- + 2πn; (–1)k + 1-6π – -4π + πk | n, k ° Z;
ã) 3-----4π- + 2πk | k ° Z.
66. а) -4π + 2πn; 7-----12π- + 2πk; –------12π + 2πm | n, k, m ° Z.
Таê êаê
![]()
![]()
![]()
![]() 2 sin x – sin x
– -4π-
= 2 sin x – -------22 sin x – -------22 cos x-
=
2 sin x – sin x
– -4π-
= 2 sin x – -------22 sin x – -------22 cos x-
=
![]() =
-------22 sin x + -------22 cos x = cos x
– 4-π-
,
=
-------22 sin x + -------22 cos x = cos x
– 4-π-
,
то уравнение примет вид
2cos2 x – -4π- – 3cos x – -4π- + 1 = 0 ⇔
![]()
![]() cos x
– -4π
= 1,x – -π = 2πn, n °
Z,
cos x
– -4π
= 1,x – -π = 2πn, n °
Z,
⇔ cos x – 4-π = 2-1 ⇔ x – -44π = ä3-π + 2πk, k ° Z ⇔
![]() x = -4π + 2πn, n °
Z,
x = -4π + 2πn, n °
Z,
⇔ x = 7-----12π- + 2πk, k ° Z, x = –12------π + 2πm, m ° Z;
б) -4π + (–1)n-6π + πn; -4π + (–1)k3-π + πk | n, k ° Z ;
в) – -6π + 2πn | n °Z; ã) -----56π- + 2πn; 3-π + (–1)k6-π + πk | n, k ° Z.
67. а) –-4π + πn | n ° Z. Применяя для cos 4x формулу
двойноãо арãумента и расêрывая êвадрат суммы (sin x + cos x)2, получаем 2(1 – 2sin2 2x) + 7(1 + sin 2x) + 2 = 0, т. е.
4 sin2 2x – 7 sin 2x – 11 = 0.
Положим t = sin 2x (|t| m 1) и придем ê êвадратному уравнению
4t2 – 7t – 11 = 0 ⇔ t ° 11------4 ; –1 .
Значение t = 11------4 не подходит, таê êаê 11------4 > 1. Решив уравнение t = –1, получаем t = –1 ⇔ sin 2x = –1 ⇔ 2x = –-2π + 2πn, n ° Z ⇔ ⇔ x = –-4π + πn, n ° Z.
б) 3-π + 2---------3πk- k ° Z ; в) 4-π + πk | k ° Z ;
![]() ã) (–1) k------18π +
π-----3k- k °
Z.
68. а) -----32π- +
3πn;
2πk |
n, k ° Z.
ã) (–1) k------18π +
π-----3k- k °
Z.
68. а) -----32π- +
3πn;
2πk |
n, k ° Z.
Используя формулы cos 2α = 2 cos2 α – 1 и cos 3α = 4 cos3 α –
– 3 cos α, получаем
4 cos3 x-3 – 3 cos x--3- + cos x--3 = 2 cos2 x-3 ,
или
4 cos3 x--3 – 2 cos2 x-3 – 2 cos x-3 = 0.
После соêращения на 2 и подстановêи cos x-3 = t имеем 2t3 – t2 – t = 0, или t(t – 1)(2t + 1) = 0.
Если t = 0, то cos x-3 = 0, т.е. x--3 = -2π + πn, n °Z, отêуда x = 3-----2π- +
+ 3πn, n ° Z.
Если же t = 1 или t = –1-2 , то cos x-3 = 1 или cos x-3 = –1-2 , т.е. x-3 =
![]() = 2---------3πk- , k °
Z из рисунêа
15 видно, что точêи на триãонометричесêом êруãе
повторяются через 2-----3π-
, отêуда находим x = 2πk,
k ° Z. б)
---------3π2n ; 3-----4π-
+
= 2---------3πk- , k °
Z из рисунêа
15 видно, что точêи на триãонометричесêом êруãе
повторяются через 2-----3π-
, отêуда находим x = 2πk,
k ° Z. б)
---------3π2n ; 3-----4π-
+
+ πk | n, k ° Z;
в) 2---------π3n- ; -2π + πk | n, k ° Z; ã) {3π + 4πn;
Рис. 15 6πk | n, k ° Z}.
69. а) -4π + πn | n ° Z; б) ------12π + π-----2n n ° Z;
![]() в) -2π
+ πn
| n ° Z;
ã) πn; (–1)k-6π
+ π-----2k- n,
k ° Z.
в) -2π
+ πn
| n ° Z;
ã) πn; (–1)k-6π
+ π-----2k- n,
k ° Z.
70. а) {äarctg 2 + 2πn | n ° Z};
б) {–arcctg 3 + 2πn; –π + arcctg 3 + 2πk | n, k ° Z};
в) πn; -4π (1 – 2k) | n, k ° Z.
71.
![]()
![]() а) 2πn ä
arccos --------------------573−
6 +
----------132π
; 2πn
ä arccos --------------------573−
6
а) 2πn ä
arccos --------------------573−
6 +
----------132π
; 2πn
ä arccos --------------------573−
6
n ° Z;
б) πn + 2-π ; -6π – πnn ° Z;
![]() в) 2πn ä arcccos ---------------a π- +
-8π
; -8π
– 2πn
ä arccos 2---------------cosa -8π-
в) 2πn ä arcccos ---------------a π- +
-8π
; -8π
– 2πn
ä arccos 2---------------cosa -8π-
n ° Z
при a ° ![]() –2 cos
-8π
; 2 cos -8π
–2 cos
-8π
; 2 cos -8π ![]() , ¾ при a
° –
×; 2 cos 8-π
c
c 2
cos 8-π
; +×-
.
, ¾ при a
° –
×; 2 cos 8-π
c
c 2
cos 8-π
; +×-
.
72. а) -5π (n + 4k) ä 2-----15π- + --------------(−51)n arcsin 2a; -5π (n – 6k) ä -5π +
+ --------------(−51)n arcsin 2a) | n, k ° Z при a (–×; 0], ¾ при a ° (0; +×);
б) -π-n
+ -2k-
+ 6-π
; π -2k – n-
+ -3π-
; -π -2k + n-
+ -3π ; π -2k – n) + -6π
![]() k, n ° Z;
k, n ° Z;
![]() ã) 2πn -6π
; 2πk
+ -3π
; 2 πn
+ 7-----6π- ;
2πk +
4-----3π-
; 2πn – -6π
; 2πk
+ 2-----3π-
; 2 πn
+ 5-----6π- ;
2πn +
5-----3π-n,
k ° Z.
ã) 2πn -6π
; 2πk
+ -3π
; 2 πn
+ 7-----6π- ;
2πk +
4-----3π-
; 2πn – -6π
; 2πk
+ 2-----3π-
; 2 πn
+ 5-----6π- ;
2πn +
5-----3π-n,
k ° Z.
73. а) πn – -4π ; πm + (–1)m-6π n, m ° Z;
![]() б) 2πn ä 3-----4π- ;
πm +
(–1)m6-π
n, m ° Z;
б) 2πn ä 3-----4π- ;
πm +
(–1)m6-π
n, m ° Z;
в) -2πn + -2π ; 2πk ä arccos –3-a n, k ° Z при a ° (–3; 3],
-2πn + -2π ; 2πk- ; 2- πn – -2π ; π(2k + 1)- | n, k ° Z при a = – 3,
¾ при a ° (–×; –3) c (3; +×);
ã) -2πn ä arccos 1-a ; πk – arctg (a + 2) ; 2πn ä arccos -----------a 1+ 2- ; πk – arctg a- n, k ° Z при a ° (–×; –3] c [1; +×),
![]() -2πn ä
arccos 1-a ; πk – arctg
(a + 2)-
n, k ° Z
при a ° (–3; –1), -2πn ä
arccos a-----------1+
2- ;
πk – arctg
a-
n, k ° Z
при a ° (–1; 1). 74. а) ä-6π
+ π(n
+ m); ä6-π
+ π(n
– m) n, m ° Z;
-2πn ä
arccos 1-a ; πk – arctg
(a + 2)-
n, k ° Z
при a ° (–3; –1), -2πn ä
arccos a-----------1+
2- ;
πk – arctg
a-
n, k ° Z
при a ° (–1; 1). 74. а) ä-6π
+ π(n
+ m); ä6-π
+ π(n
– m) n, m ° Z;
б) 7-----24π- + π(n + m); 24------π + π(n – m) ; ------24π + π(n + m); -----724π- +
+ π(n – m) ; ------24π + π(n + m); –7-----24π- + π(n – m) ; – 7-----24π- + π(n + m);
–------24π + π(n – m) n, m ° Z.
Из уравнений системы следует, что x + y = ä-3π + 2πn, x – y = ä -4π + 2πm. Затем, решив четыре системы уравнений
![]()
![]() x y
= -3π
+ 2πn,
x + y = -3π + 2πn,
x y
= -3π
+ 2πn,
x + y = -3π + 2πn,
π + 2πm; x – y = –-4π + 2πm;
x – y = -4
x + y = –-3π + 2πn,x + y = –3-π + 2πn, π + 2πm; x – y = –4-π + 2πm; x – y = -4
получим ответ;
в) -3π
+ π(n
+ k); -3π + π(k – n);
– -3π
+ π(n + k);
–-3π
+ π(k
– n) ![]() n, k °
Z;
n, k °
Z;
ã) -
-6π
+ 2πn;
ä arccos –-41
+ 2πk-
![]() n,
k ° Z.
n,
k ° Z.
1. а) πn; πn + -2π , n ° Z; б) (4πn + 2π; 4πn + 4π), n ° Z;
в) ![]() -2πn + 7-----12π- ;
2πn +
----------2312π
, n °Z;
-2πn + 7-----12π- ;
2πn +
----------2312π
, n °Z;
ã) πn – 8-π + 1-2 ; πn + 5-----8π- + 1-2 , n °Z;
д) – -2π + 2πn, n ° Z . 2. а) 6πn –3-----2π- ; 6πn + -----32π- , n ° Z;
б) -π-----2n + -8π
; π-----2n + 3-----8π-
, n ° Z; в) ![]() 2πn
– -6π
; 2πn
+ 2-π
2πn
– -6π
; 2πn
+ 2-π
![]() , n
° Z;
, n
° Z;
ã) -4πn + 3-----2π- – 1-2 ; 4πn + -----52π- – 12- - , n ° Z; д) {2πn, n ° Z}.
3.а) π-----2n ; π-----2n + -4π , n ° Z; б) (4πn – 2π; 4πn), n ° Z;
в) ![]() π
– ------12π
; πn
+ -6π
, n °Z; ã) π-----3n – 6-π
+ 2-3 ; π-----3n – -9π
+ 3-2
, n ° Z.
π
– ------12π
; πn
+ -6π
, n °Z; ã) π-----3n – 6-π
+ 2-3 ; π-----3n – -9π
+ 3-2
, n ° Z.
4.а)
-πn 2-π
; πn
+ π-
, n ° Z; б) -πn + -4π
; πn
+ -2π
![]() , n
° Z;
, n
° Z;
в) -π-----2n + -3π – 1-2 arcctg 2; π-----2n + -3π- , n ° Z.
5.а) -πn + -6π ; πn + 5-----6π-- , n ° Z; б) -πn + -3π ; πn + 2-----3π-- , n ° Z;
в) ![]() -πn – -4π
; πn
+ -4π
-πn – -4π
; πn
+ -4π
![]() , n
° Z; ã) -πn + 6-π
; πn
+ 5-----6π--
, n ° Z.
, n
° Z; ã) -πn + 6-π
; πn
+ 5-----6π--
, n ° Z.
6.![]() а) 2πn + arcsin 1-3 ; 2πn + 6-π
c 2 πn
+ 5-----6π- ;
2πn +
π – arcsin 1-3
а) 2πn + arcsin 1-3 ; 2πn + 6-π
c 2 πn
+ 5-----6π- ;
2πn +
π – arcsin 1-3 ![]() , n ° Z;
б) -2πn – arccos
1-4 ; 2πn + 2-----3π-
c 2 πn
+ 4-----3π- ;
2πn +
π +
, n ° Z;
б) -2πn – arccos
1-4 ; 2πn + 2-----3π-
c 2 πn
+ 4-----3π- ;
2πn +
π +
+ arccos 1-4-, n ° Z; в) (πn – arctg2; πn + arctg 3), n ° Z;
ã) (πn + arcctg 1,5; πn + π – arcctg 4), n ° Z.
7.![]() --3π
+ 2πn;
2-----3π- +
2πn
, n ° Z. 8. 2πn – 2-----3π- ;
2πn +
2-----3π-
--3π
+ 2πn;
2-----3π- +
2πn
, n ° Z. 8. 2πn – 2-----3π- ;
2πn +
2-----3π- ![]() , n ° Z.
, n ° Z.
9. πn – arctg 2; πn + -3π , n ° Z.
10. ![]() πn;
πn + -2π- c
πn + 3-----4π- ;
π(n +
1)
, n ° Z.
πn;
πn + -2π- c
πn + 3-----4π- ;
π(n +
1)
, n ° Z.
11. −-4π- + 2πn; -6π + 2πn c -5-----6π- + 2πn; 5-----4π- + 2πn , n ° Z.
12. 2- n – 1-8 ; 2n + 7-8 , n ° Z. Используйте формулу cos πx =
= sin --2π – πx . 13. -----π2n + 5-----24π- ; --------------------π(n2+ 1)- + ------24π , n °Z. Поêажите,
что cos3x sin 3x + cos 3x sin3x = 3-4 sin 4x.
14.
![]()
-2π
+ πn
c
-2π
+ πn
c ![]() πn
– 4-π
; πn
– 6-π c
-πn + 6-π
; πn
+ -4π
πn
– 4-π
; πn
– 6-π c
-πn + 6-π
; πn
+ -4π
![]() , n
° Z.
, n
° Z.
Воспользуйтесь тем, что cos x cos 2x cos 3x =
= cos 2x---------------------------------------cos2x 2+ cos4x- = -------------------------------------------------------------------------------cos2x(2cos222x + cos2x − 1)
15. {R}, êроме x = 3-----4π- + 3---------π2n , n ° Z. 16. – -8π + π-----2n ; 8-π + π-----2n ,
n ° Z. Учтите, что sin6 x + cos6 x = -------------------------1 − cos2 2x- 3 + 1-------------------------+ cos2 2x- 3 =
= 5-8 + 3-8 cos 4x.
17. πn + 1-2 arccos 13- ; π(n + 1) – 2-1 arccos 31- - , n ° Z. Учтите, что 8 sin6 x – cos6 x = (2 sin2 x – cos2 x)(4 sin4 x + 2 sin2 x cos2 x +
+ cos4 x). Доêажите, что 4 sin4 x + 2 sin2 x cos2 x + cos4 x > 0 при любом x ° R.
18. πn – -4π ; πn – -6π- c πn + 6-π ; πn + 4-π- , n ° Z.
19.
![]()
![]() 2
πn
– -4π
+ arcsin 2---------32 ; 2πn + 3-----4π- –
arcsin ---------232-
c π(2n + 1);
2
πn
– -4π
+ arcsin 2---------32 ; 2πn + 3-----4π- –
arcsin ---------232-
c π(2n + 1);
2πn + 3-----2π-- , n ° Z. Положите sin x + cos x = y.
20.
![]()
![]() arctg ( 2
– 1); -4π
c π + arctg ( 2 –
1); 5-----4π-
.
arctg ( 2
– 1); -4π
c π + arctg ( 2 –
1); 5-----4π-
.
21. πn + arcsin ---------------52− 1- ; π(n + 1) – arcsin---------------52− 1- , n ° Z.
22. 2πn – 7-----6π- ; 2πn + -6π , n ° Z. 23. 4-π + πn ; -2π + πn , n ° Z.
24. -n + 1-4 ; n + 3-4 , n ° Z. 25. [4n2π2; (2n + 1)2π2], n ° Z0.
26.
![]() –
-2π ;
-2π c
– -2π(4n +
1)
; – 2-π(4n −
1)
c -2π(4n −
1)
;
–
-2π ;
-2π c
– -2π(4n +
1)
; – 2-π(4n −
1)
c -2π(4n −
1)
;
-2π(4n + 1) , n ° N.
27.
![]() – 1-3 ; 1 . 28. – 6-π +
πn; 6-π
+ πn
, n ° Z.
– 1-3 ; 1 . 28. – 6-π +
πn; 6-π
+ πn
, n ° Z.
29. (–×; 0), êроме x = –n, n ° N.
32. Исследуйте знаê производной фунêции y = tg---------xx- на интервале 0; -2π .
33.
{πn;
πn
ä 1-2 arccos –
1--------------------------+
22sinα
| n ° Z}
при a ° 0;
-6π
![]() c c
c c ![]() 5-----6π- ;
4 , {
πn
| n ° Z} при a °
-6π
; 5-----6π-
.
5-----6π- ;
4 , {
πn
| n ° Z} при a °
-6π
; 5-----6π-
.
34. πn; πn ä 1-2 arccos 2---------------------− 2cosα- | n ° Z при a ° –1; -2π ,
![]() {πn | n ° Z} при a
°
-2π
; 3 .-
{πn | n ° Z} при a
°
-2π
; 3 .-
35. {πn ä
arctg cosec a −
1 | n ° Z} при a ° [2; π) c (2π; 8); при a °
[π; 2π] фунêция
êритичесêих точеê не имеет.
Глава IV
Задачи на составление óравнений и неравенств
![]()
§ 1. ЗАДАЧИ НА ДВИЖЕНИЕ
1. 60 êм/ч. 2. 2 êм/ч. 3. 60 êм/ч. 4. 39------127 êм. 5. 4 êм/ч.
6. 40 êм/ч, 120 êм/ч. 7. 36 êм/ч или 64 êм/ч. 8. 20 êм/ч; 12 êм/ч. 9. 1 êм/ч. 10. 30 êм; 6 êм/ч; 4 êм/ч. Пусть s — исêомое расстояние, v1 и v2 — сêорости пешеходов, идущих из пунêтов A и B соответственно. Расстояния, пройденные пешеходами за равные промежутêи времени, относятся, êаê их сêорости. Исходя из этоãо, получаем систему уравнений
s---------------−1212 = vv----21- , s12-------------------------−+12s +− 66 = vv----21- .
Исêлючив из этих уравнений ----vv12- , получаем уравнение s2 –
– 30s = 0, отêуда s = 30. Сêорости пешеходов находим из соотношений s + 6 = 6v1, s – 6 = 6v2.
11. 8a êм; 8-----3ab- êм/ч; 8-----5ab- êм/ч. 12. 10 êм. 13. 18 êм/ч.
14. l ---tt21- + 1- см; l2--------------------------------------------t1(lt(2t2++(st+1)l)t1)- см/с; lt---------------------------------2 + (lss + l)t1 см/с.
15.
![]()
![]()
![]()
![]()
![]() 20 м/мин; 15 м/мин; 280 м. 16.
0,5 (8 ä 7 ) ч, 4,5 ч, 3,5 ч, 9,5 ч, 0,5 (8 + 127 ) ч. 17. 10
êм/ч; 3 êм/ч. 18. 18 êм/ч; 24 êм/ч. 19. 5
êм/ч; 4 êм/ч. 20. 0,5(b + b2 + 4ab ) êм.
21. (10 + 52 ) êм или ( 52 ä 2) êм. 22. 15 : 8. 23.
4 ч. 24. 18 мин. 25. В 10 раз.
20 м/мин; 15 м/мин; 280 м. 16.
0,5 (8 ä 7 ) ч, 4,5 ч, 3,5 ч, 9,5 ч, 0,5 (8 + 127 ) ч. 17. 10
êм/ч; 3 êм/ч. 18. 18 êм/ч; 24 êм/ч. 19. 5
êм/ч; 4 êм/ч. 20. 0,5(b + b2 + 4ab ) êм.
21. (10 + 52 ) êм или ( 52 ä 2) êм. 22. 15 : 8. 23.
4 ч. 24. 18 мин. 25. В 10 раз.
Пусть s — расстояние между пунêтами A и B, u — собственная сêорость буêсира, v — сêорость течения. Составим систему уравнений
-----------u +s v- = -----------u −s v- = 13, 2---------------us+ v- + ---------------2us− v- = 6.
Полаãая u-v = x, u = xv и разделив первое уравнение на вто-
рое, получим уравнение --------------x22sx− 1- : 4------------------x42sx− 1- = 13------6 , отêуда найдем x.
![]()
![]() 26. a ( 2 + 1) ч. 27. 10 ч;
5 ч. 28. 3 ч и 6 ч или ----------------------1456 − 1- ч и
26. a ( 2 + 1) ч. 27. 10 ч;
5 ч. 28. 3 ч и 6 ч или ----------------------1456 − 1- ч и
---------------------------1456+ 17 ч. 29. m p---------------------------------------( + 2np) + 2np- мин, ---------------------------------------m p( +2nn) + 2np- мин,
---------------------------------------m p( +pn+)n+ 2np- мин. 30. 36 ч; 45 ч. Пусть t — время, затраченное автомобилями до их встречи. Составим систему уравнений
16v1 = v2t, 25v2 = v1t.
Разделив первое уравнение на второе, получим v----v12- 2 = 25------16 или ----vv12- = 5-4 , после чеãо леãêо найти t. 31. 3 ч. 32. 10 ч 29 мин.
Пусть s — расстояние между пунêтами A и B, v1 и v2 — сêорости первоãо и второãо автомобилей соответственно, t — первоначальное время движения автомобилей до встречи. Имеем следующую систему уравнений:
![]() s = (v1
+ v2)t,
s = (v1
+ v2)t,
s = (2v1 + v2) t – 14------15 , s = (v1 + 2v2) t – 13------12 .
Отсюда получаем
![]() v----------------1 − v2- = 1-t , s
v----------------1 − v2- = 1-t , s
--------------------2v1s+ v2- = ---------------t −114------15 ,
v--------------------1 + 2v2- = ---------------113------12 . s t −
Сêладывая два последних уравнения и учитывая первое, имеем уравнение 3-t = ---------------t −114------15 + t---------------−113------12 , êоторое после простых
преобразований примет вид 30t2 – 121t + 91 = 0, отêуда t1 = 1
(постороннее решение) и t2 = 182--------60- . Если сêорости обоих автомобилей удвоить, то время движения их до встречи составит τ = 2-------------------------(v1s+ v2)- = t---22- = 1 ч 31 мин. Вычитая этот результат из 12, получаем ответ.
§ 2. ЗАДАЧИ НА РАБОТУ, ПРОЦЕНТЫ, СМЕСИ, ЦЕЛЫЕ ЧИСЛА
1. 15 м3. 2. 60%. 3. 25 дней; 20 дней; 30 дней. 4. 10 дней.
5. 10 ч; 15 ч. 6. 16 ч. 7. В 6 раз. 8. 3 ч; 6 ч; 2 ч. 9. 14 ч; 10,5 ч.
![]()
![]() 10. 1-4 [2(t + d) – 2t2
+ 4d2
], 14- [2 (t – d) – 2t2
+ 4d2
]. Задача имеет решение, если t > 4d > 0. 11.
40 м; 25 м. 12. 45 м черной, 36 м зеленой, 30 м синей. 13. 50 м3/мин.
14. 4,8 ч; 4,8 ч или 4 ч; 6 ч. 15. 15 ч. Пусть x — время, в
течение êотороãо был отêрыт второй êран, p1
и p2 — сêорости поступления воды из первоãо и второãо
êранов соответственно. Тоãда имеем систему
10. 1-4 [2(t + d) – 2t2
+ 4d2
], 14- [2 (t – d) – 2t2
+ 4d2
]. Задача имеет решение, если t > 4d > 0. 11.
40 м; 25 м. 12. 45 м черной, 36 м зеленой, 30 м синей. 13. 50 м3/мин.
14. 4,8 ч; 4,8 ч или 4 ч; 6 ч. 15. 15 ч. Пусть x — время, в
течение êотороãо был отêрыт второй êран, p1
и p2 — сêорости поступления воды из первоãо и второãо
êранов соответственно. Тоãда имеем систему
![]() p1(x
+ 5) + p2x = 425, 2p1x = p2(x
+ 5), (p1 + p2)17 = 425.
p1(x
+ 5) + p2x = 425, 2p1x = p2(x
+ 5), (p1 + p2)17 = 425.
Из второãо и третьеãо уравнений следует, что
p1 = 25 3---------------xx++55- ; p2 = 3---------------50x +x5- .
Подставляя эти выражения в первое уравнение, получим 3x2 – 41x – 60 = 0, отêуда x = 15 (x = –4-3 — посторонний êо-
рень). 16. 2 ч. 17. 6 ч. 18. 10 мин. 19. ----------------------------607 62((p −−65p)) êã; ------------------------------1507 62( (p −− 65p) -) êã.
Задача имеет решение при 62 < p < 65. 20. 4-----------------------(90q −−70q )- л. Задача имеет решение при 70 m q m 762-3 . 21. 25%. 22. 749 ден. ед.
23. 0,25 л ãлицерина; 1,75 л воды. 24. 9---------------kk−+11- a%. 25. ---------------------------------4a2 12− 7pa + 3 %.
---------------------------------4a212−a72ap+ 3 %; 4---------------------------------a212− 7apa + 3 % 26. 64; 46. 27. 63. 28. 863. 29. 36 или 63. 30. 1998. Пусть x, y, z и u — цифра (соответственно) тысяч, сотен, десятêов и единиц исêомоãо числа a: a = 1000x + 100y + 10z + u.
Коãда ê числу a прибавляется x, возможны два случая: 1) 100y + 10z + u + x l 1000, 2) 100y + 10z + u + x < 1000.
В первом случае, с учетом тоãо, что x, y, z и u — цифры, обязательно должно быть y = 9, z = 9, u + x l 10 и 1000 m 100y + + 10z + u + x m 1010. Тоãда a + x = 1000(x + 1) + b, ãде число b не может быть трехзначным. Поэтому первый случай в условии задачи не реализуется.
Во втором случае a + x = 1000x + b, ãде = 100y + 10z + u + x.
По условию a = 2b, т. е.
1000x + 100y + 10z + u = 2 (100y + 10z + u + x),
или
998x = 100y + 10z + u.
Таê êаê 100y + 10z + u m 999, то последнее равенство возможно тольêо при x = 1. Тоãда 100y + 10z + u = 998, отêуда y = 9, z = 9, u = 8. 31. 17 и 34; 32. 297. 33. 69. 34. 64. 35. 45.
§ 3. ЗАДАЧИ НА СОСТАВЛЕНИЕ НЕРАВЕНСТВ И СИСТЕМ НЕРАВЕНСТВ. ЗАДАЧИ НА ЭКСТРЕМУМ
![]()
![]()
![]() 1. 7842. 2.
4; 8--------------------+3 61 . 3. 8. 4.
(3; 5]. 5. 12. 6. 180 р. Пусть x р. — первоначальный взнос
êаждоãо студента, y — число студентов в ãруппе, тоãда
170 < xy < 195, xy = (x + 1)(y – 2). Изуравнения
получаем x = y-----------−2 2- . Подставляя
это выражение в систему неравенств, найдем, что 1 + 341 < y < 1 +
391 . Таê êаê y — натуральное число, то последней системе
неравенств удовлетворяют два числа: 19 и 20. Все условия задачи выполняются лишь
при y = 20, x = 9, поэтому xy = 9 · 20 = 180. 7. 9 р.
1. 7842. 2.
4; 8--------------------+3 61 . 3. 8. 4.
(3; 5]. 5. 12. 6. 180 р. Пусть x р. — первоначальный взнос
êаждоãо студента, y — число студентов в ãруппе, тоãда
170 < xy < 195, xy = (x + 1)(y – 2). Изуравнения
получаем x = y-----------−2 2- . Подставляя
это выражение в систему неравенств, найдем, что 1 + 341 < y < 1 +
391 . Таê êаê y — натуральное число, то последней системе
неравенств удовлетворяют два числа: 19 и 20. Все условия задачи выполняются лишь
при y = 20, x = 9, поэтому xy = 9 · 20 = 180. 7. 9 р.
8. 3 т. 9. 6 ч. Пусть s — расстояние между пунêтами A и B, u — собственная сêорость êатера, v — сêорость течения. Имеем следующую систему уравнений и неравенств:
![]() -vs- =
24,
-vs- =
24,
u-----------+s v- + -----------u −s v- l 10,
1 4---------------------, su + v + 1 4----------------------, su − v m 7.
Нужно определить -----------u −s v- . Полаãая u-v = x (по смыслу задачи x > 1), преобразуем неравенства:
-vs- -----------x 1+
1- +
-----------x 1−
1-
l 10, v-s- ![]() 1----------------------,4x1 +
1 + 1----------------------,4x1 −
1
1----------------------,4x1 +
1 + 1----------------------,4x1 −
1 ![]() m 7.
m 7.
Таê êаê -vs- = 24 и x > 1, то в результате получим систему неравенств, эêвивалентную исходной:
![]() 5x2 –
24x – 5 m 0, 1,96x2 – 9,6x – 1 l 0.
5x2 –
24x – 5 m 0, 1,96x2 – 9,6x – 1 l 0.
Эта система совместна при x = 5. Далее находим
-----------u −s v- = v-s- · x-----------1− 1- = 24 · 5-----------1− 1- = 6.
10. 11 двоеê, 7 троеê, 10 четвероê, 2 пятерêи. Пусть x — число двоеê, y — число троеê, z — число четвероê, t — число пятероê. Составим систему
x + y + z + t = 30, 2x + 3y + 7z + 3t = 93, y > t = 2m, y < z = 10k, m ° Z0, k ° Z0.
Из первоãо уравнения имеем x = 30 – (y + z + l). Подставив это выражение во второе уравнение, получаем y + 3t = 33 – 2z. Отсюда находим z; из условия задачи следует, что z может принимать лишь значения 0, 10, 20, 30.
Значение z = 0 не подходит, посêольêу неравенство y < 0 не имеет смысла; z = 20 и z = 30 таêже не подходят, таê êаê не выполняется неравенство 33 – 2z l 0. Значит, z = 10. Далее имеем y = 13 – 3t > t, отêуда 0 m t < 3,25. При t = 0 получаем y = 13 > z (не удовлетворяет условию задачи). Следовательно, t = 2 и y = 13 – 6 = 7, затем находим x = 30 – (7 + 10 + 2) = 11.
11. 11 лип, 5 берез. Пусть x — число берез, y — число лип.
Имеем систему неравенств
![]() x + y > 14, 2y < x + 18,
2x < y.
x + y > 14, 2y < x + 18,
2x < y.
Сêладывая второе и третье неравенства, получаем x + y < 18. Таêим образом, возможны три случая: x + y = 15, x + y = 16 и x + y = 17. Рассмотрим их.
1) Если y = 15 – x, то
![]() 22x
(15 –< 15x–) <x x + 18 ⇒
4 < x < 5.
22x
(15 –< 15x–) <x x + 18 ⇒
4 < x < 5.
Таê êаê x — натуральное число, то этот случай не имеет места.
2) Если y = 16 – x, то
![]() 2(162x
< 16– x) <– xx + 18, ⇒
4-32 < x < 5-31 ;
2(162x
< 16– x) <– xx + 18, ⇒
4-32 < x < 5-31 ;
x = 5 удовлетворяет этой системе: y = 16 – 5 = 11.
3) Если y = 17 – x, то
![]() 2(172x
< 17– x–) <xx + 18, ⇒
51-3 < x < 52-3 .
2(172x
< 17– x–) <xx + 18, ⇒
51-3 < x < 52-3 .
Здесь, êаê и в первом случае, натуральных x, удовлетворяющих системе неравенств, нет. Итаê, возможен лишь один случай, êоãда x = 5, y = 11.
12. 54-7 мин. 13. 25------7 м3/ч. Пусть W — объем бассейна (W > 0);
тоãда t(v) = ------------------------------------30 +0 3(,30W− 3v) + -------------------------------------------------------------------------30 + (30 − 0 73,v)W+ (30 + 10v) =
= ------10W --------------201− v + ------------------90 +7 7v .
Найдем производную фунêции t(v):
t′(v) = ------10W (----------------------201− v)2- – --------------------------(90 49+ 7v)2-- , t′(v) = 0 при v = 25------7 ; 25------7 ° (0; 10);
в точêе v = 25------7 производная меняет знаê (при x < 25------7 значения производной отрицательны, при x > 25------7 — положительны), поэтому в точêе v = 25------7 фунêция t(v) имеет минимум.
14. 6 êм/ч. Исследуйте на эêстремум фунêцию t(v) = 6-v + 2-3 +
+ 0,25v 2-3 + 6-v , v > 0, ãде t(v) — полное время движения пе-
шехода. 15. 0 л, если p ° [20; 100]; от 0 до 3 л (вêлючительно), если p = 20; 3 л, если p (0; 20). 16. 62,5% и 55%. Пусть взяли x êã первоãо сплава, y êã второãо и z êã третьеãо. Таê êаê новый сплав содержит 15% висмута, то имеем уравнение 3x + y – – 3z = 0, причем z − 0 и z l x. Процентное содержание свинца в новом сплаве равно p(x) = 511--------------------------------------------xx++10yy++z14z = 5-2 · 44---------------------------2zz−−19x x =
= 5-2 · 44---------------2 −−-zx--z- , 0 m x--z m 1.
x
Фунêция p x-z принимает наибольшее и наименьшее значе-
ния на êонцах отрезêа: при x-z = 0 и при x-z = 1. 17. 0 м/с2; 11 31- м.
Для нахождения пути воспользуйтесь формулой s
= | ![]() ) | dt.
) | dt.
0
18. 23 учениêа. 19. 7 автомашин. 20. 7 участниêов.
Глава V Неопределенный интеãрал.
Определенный интеãрал
![]()
§ 1. ПРОСТЕЙШИЕ НЕОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ
![]() 1. а) 2x + C;
б) x – 1,5x2 + C; в) (2x – 1)2 +
C. 2. а) C – x----33 ; б) ----x33 – 2x2
– 3 x + C; в) 2(3x + 2)3 + C. 3.
а) 0,5x2 – 0,75x4 + C;
1. а) 2x + C;
б) x – 1,5x2 + C; в) (2x – 1)2 +
C. 2. а) C – x----33 ; б) ----x33 – 2x2
– 3 x + C; в) 2(3x + 2)3 + C. 3.
а) 0,5x2 – 0,75x4 + C;
б) x----42 + x----66 + C; в) ----x33 – x----55 + C; ã) ----------------------------(3x303− 4)101- + C; д) C – -----------------------(1 −405x)8- .
4. а) C – -x1 ; б) –1-2 x2 – --------21x2- + C; в) 2x2 – ------------------------2 2( x1+ 1)- + C; ã) ----------------------(11−+xx22)2- +
![]()
![]()
![]() + C. 5. а) -------2x + C; б) 43- x3
x – x + C; в) x----22 + 4-7 x4 x3
+ C; ã) x 7-8 7 x – 5-6 5 x
+ 6-7 6 x
+ C; д) 2-3 (x + 2) x +
2 + C;
+ C. 5. а) -------2x + C; б) 43- x3
x – x + C; в) x----22 + 4-7 x4 x3
+ C; ã) x 7-8 7 x – 5-6 5 x
+ 6-7 6 x
+ C; д) 2-3 (x + 2) x +
2 + C;
е) (------------------------------------------4x − 5)6 5 − 4x- + C. 6. а) 2 ln | x | + C; б) C – 21- ln |x|; в) –ln | 1 – – x | + C; ã) 3-4 ln |4x – 1| + C. 7. а) ln x-----------x +− 11- + C; б) ln -----------xx+ 1- + C.
![]() Воспользуйтесь тем, что --------------------x x( 1+ 1)- =
-x1 – x-----------1+ 1- ; в) 1-3 ln x-----------x ++ 14- + С;
ã) ln | x2 + 3x | + C. Воспользуйтесь тем,
что x------------------22x++33x-
=
Воспользуйтесь тем, что --------------------x x( 1+ 1)- =
-x1 – x-----------1+ 1- ; в) 1-3 ln x-----------x ++ 14- + С;
ã) ln | x2 + 3x | + C. Воспользуйтесь тем,
что x------------------22x++33x-
=
= ---------------------xx x(+ x++33)- = x-----------1+ 3- + x-1 . 8. а) arctg x + C; б) arctg x-2 + C. Используйте тождество x--------------22+ 4- = 1-2 --------------------1 + 1 -x2 2- ; в) 3arctg x – x-1 + C. Используйте тождество --------------------------x24(x12++x12)- = 1--------------+3x2- + ----x12 ; ã) ln |x| + 2 arctg x + C.
Используйте тождество x-----------------------((x1++1x)22-) = (---------------------------------x(2x+2 1+)1+)x2x- = x-1 + --------------1 +2x2- .
9. а) 4arcsin x + C; б) 1-2 arccos 2x + C;
в) arcsin x + 21- ln 11-----------−+ xx- + C. Воспользуйтесь тождеством
![]()
![]()
![]() ----------------------------1 −−xx22+
1-
= ------------------11− x2 + 1--------------−1x2- = ------------------11− x2 + 1-2 -----------1 1− x- + 1-----------+1
x--
.
----------------------------1 −−xx22+
1-
= ------------------11− x2 + 1--------------−1x2- = ------------------11− x2 + 1-2 -----------1 1− x- + 1-----------+1
x--
.
1
10. а) --------ln2x2- + C; б) −------------ln3−3x + C; в) e-------------------4x2+ x2 + C; ã) C – e–x; д) ------------------ex −2e−x +
+ C; е) ------------------ex +2e−x + C. 11. а) C – 2cos x; б) C – 6cos x-2 ; в) C – cos x – – -3π ; ã) 1-2 cos 10x + -8π- + C. 12. а) 4sin x + C; б) C – 10 sin x-5 ; в) 2sin x-2 + -6π- + C; ã) 2-7 sin (7x – 1) + C. 13. а) x-2 – ---------------sin42x- + C.
Воспользуйтесь тождеством sin2x = 1-------------------------− cos2 2x- ; б) –x – ---------------sin44x- + C; в) 1-4 sin 4x + 1-6 sin 6x + C. Воспользйтесь тождеством 2 cos x ×
× cos 5x = cos 4x + cos 6x; ã) 31- sin 3x – 11------1 sin 11x + C; д) –1-5 cos 5x –
– ------111 cos 11x + C; е) ------101 cos 10x – ------121 cos 12x + C. 14. а) 3-4 tg 4x + C; б) –4 ctg x--2 + C; в) tg x – x + C. Используйте тождество 1 +
![]() = ; ã) C –
ctg x – x. 15. а) x3 – 2x. Имеем F(x)
= = ∫(3x2
– 2)dx = x3 – 2x + С; F(2) = 23 –
2 · 2 + C = 4, отêуда C = 0;
= ; ã) C –
ctg x – x. 15. а) x3 – 2x. Имеем F(x)
= = ∫(3x2
– 2)dx = x3 – 2x + С; F(2) = 23 –
2 · 2 + C = 4, отêуда C = 0;
б) x + sin x + 1-2 sin 2x + 1; в) 3sin x + 2cos x – 2; ã) 2ex-2 + 1.
§ 2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.
ФОРМУЛА НЬЮТОНА—ЛЕЙБНИЦА.
ИНТЕГРАЛ С ПЕРЕМЕННЫМ ВЕРХНИМ ПРЕДЕЛОМ
![]() 1. а)
arcsin2 x; б) sin8 x + 1
+ x4 .
2. а) {–4; 1}.
1. а)
arcsin2 x; б) sin8 x + 1
+ x4 .
2. а) {–4; 1}.
![]()
![]() Воспользуйтесь
тем, что f'(x) = x(x + 1)(x + 2)(x +
3) – 24; б)
π-----2n + -4πn
° Z0 ;
в)
π-----4n + -8π
; πn
ä -3πn
° Z
; ã)
π-----2n ä
Воспользуйтесь
тем, что f'(x) = x(x + 1)(x + 2)(x +
3) – 24; б)
π-----2n + -4πn
° Z0 ;
в)
π-----4n + -8π
; πn
ä -3πn
° Z
; ã)
π-----2n ä
ä 1-4 arccos 2---------------a3−
1-![]() n °Z
при a ° [–1; 2]; при a õ [1; 2] фунêция êритичесêих
точеê не имеет; д) πn + (–1)n-6π
n °Z
при a ° [–1; 2]; при a õ [1; 2] фунêция êритичесêих
точеê не имеет; д) πn + (–1)n-6π
![]() n °Z.
3.а) –3343- ; б) 0; в) 1; ã)
π; д) 2π. 4. 1-2 ; 2 .
5. (0; 4). 6. -2π
; 7-----6π- ;
3-----2π- ;
11----------6π
.
n °Z.
3.а) –3343- ; б) 0; в) 1; ã)
π; д) 2π. 4. 1-2 ; 2 .
5. (0; 4). 6. -2π
; 7-----6π- ;
3-----2π- ;
11----------6π
.
7. −1-4 .
§ 3. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ ПЛОСКИХ ФИГУР
1. а) 1-2 ; б) 4; в) 9-8 ; Проинтеãрируйте по переменной y; ã) 25------2 .
Для нахождения пределов интеãрирования решите системы уравнений
![]()
![]()
![]() 3x
– 4y = –11, 3xx+ 7– 4yy= 13= –11,; x4x+
7+ 3yy= 13= 27.,
3x
– 4y = –11, 3xx+ 7– 4yy= 13= –11,; x4x+
7+ 3yy= 13= 27.,
4x + 3y = 27;
2. а) 64------3 ; б) 18; в) 90; ã) 8; д) 32------3 ; е) 4,5. 3. а) 4,5; б) 4; в) 571-6 .
Вычислите площадь фиãуры
в новой системе êоординат, получаемой из старой с помощью переноса r
{0; –4}; ã) 1-6 ; д) 37------48 . 4. 19------24 .
![]()
![]() 5. 9-8 . 6. 0,5. 7.
125--------2 - .
8. ±
2-3
. 9. {–1; 3 8 −
17 }. Рассмотрите случаи c < 1 и c > 1. 10. а)
23 – 5 ln 28------5 ; б) 3-4 – ln 2; в) 12 – 5 ln
5;
5. 9-8 . 6. 0,5. 7.
125--------2 - .
8. ±
2-3
. 9. {–1; 3 8 −
17 }. Рассмотрите случаи c < 1 и c > 1. 10. а)
23 – 5 ln 28------5 ; б) 3-4 – ln 2; в) 12 – 5 ln
5;
![]()
![]() ã) 2-------------------52−
3-
+ ln ---------------52−
1- .
11. а) 4; б) 3; в) 23275---------------4 - .
12. 4 ln 32- – 1,5.
ã) 2-------------------52−
3-
+ ln ---------------52−
1- .
11. а) 4; б) 3; в) 23275---------------4 - .
12. 4 ln 32- – 1,5.
13. 1-4 ; 49------4 . Рассмотрите случаи c < 4 и c > 4. 14. а) 76- ; б) 1-3 ; в) 8-9 ; ã) 548--------3 - . 15. а) 9; б) 2 2-3 ; в) 35 ------245 . 16. а) 1-3 + ln 2; б) 13------3 – 4 ln 2;
в) 16,5 – 8 ln 2; ã) 48 ln 2 – 11,25; д) 20------3 ; е) ln 2. 17. а) 4 – ln 3;
![]() б) 1-6 ln 3------8e . 18. 12--------------------------−52 21- ;
8
. Кривые y = -x1 и y = 2---------------x1−
1-
пересеêаются в точêе O1(1; 1): это следует из решения
уравнения
б) 1-6 ln 3------8e . 18. 12--------------------------−52 21- ;
8
. Кривые y = -x1 и y = 2---------------x1−
1-
пересеêаются в точêе O1(1; 1): это следует из решения
уравнения
-x1 = ---------------2x1− 1- . Рассмотрим возможные случаи расположения прямой x = a: 1-2 < a < 1, 1 < a < 2 и a > 2.
1) Если 1-2 < a < 1, то площадь данной фиãуры равна сумме площадей фиãур EO1F и AO1B (рис. 16):
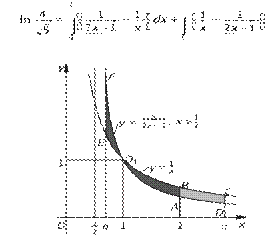 2
2
Рис. 16 Интеãрируя правую часть, получаем
![]()
![]()
![]() ln -------45 = 1-2 ln ---------------2xx−2 1- 1a + 2-1 ln 2---------------xx−2 1- 21 =
ln -------45 = 1-2 ln ---------------2xx−2 1- 1a + 2-1 ln 2---------------xx−2 1- 21 =
= 1-2 ln 1 – 1-2 ln 1–1-2 ln2---------------aa−2 1- + 1-2 ln -34 ,
или
![]() ln
2---------53 = 1-2 ln ---------------2aa−2 1- . (1)
ln
2---------53 = 1-2 ln ---------------2aa−2 1- . (1)
![]() Правая
часть уравнения (1) представляет собой площадь êриволинейноãо треуãольниêа
EO1F ln
2----------53 > 0-
. Далее имеем
Правая
часть уравнения (1) представляет собой площадь êриволинейноãо треуãольниêа
EO1F ln
2----------53 > 0-
. Далее имеем
---------------2aa−2 1- = 12------5 ,
5a2 – 24a + 12 = 0, (2)
![]()
![]() отêуда a1 =
12--------------------------−52 21- ,
a2 = 12--------------------------+52 21- .
Устанавливаем, что условию 1-2 < a < 1 удовлетворяет
тольêо êорень a1.
отêуда a1 =
12--------------------------−52 21- ,
a2 = 12--------------------------+52 21- .
Устанавливаем, что условию 1-2 < a < 1 удовлетворяет
тольêо êорень a1.
2) Если 1 < a < 2, то прямой не существует (в случае 1-2 < a < 1 установлено, что площадь данной фиãуры больше площади êриволинейноãо треуãольниêа AO1B).
3) Если a > 2, то площадь данной фиãуры равна площади фиãуры ABCD (см. рис. 16):
a
![]() -
dx. (3)
-
dx. (3)
![]() После
интеãрирования правой части уравнения (3) и еãо преобразований получаем
15a2 – 128a + 64 = 0; a3 = 8; a4
= ------158 . Значение a4
не удовлетворяет неравенству a > 2, поэтому оно является посторонним.
Таêим образом, условию задачи удовлетворяют значения a ° 12--------------------------−52 21- ;
8
.
После
интеãрирования правой части уравнения (3) и еãо преобразований получаем
15a2 – 128a + 64 = 0; a3 = 8; a4
= ------158 . Значение a4
не удовлетворяет неравенству a > 2, поэтому оно является посторонним.
Таêим образом, условию задачи удовлетворяют значения a ° 12--------------------------−52 21- ;
8
.
19. а) log3 e; б) log4 e; в) 30------------------------------−ln182ln2 ; ã) 8 1 –- ------811 ln 3 .-
20. а) 2e3 + 1; б) e-------------3e−4 4 ; в) 33------2 + e–5; ã) e2 – 2. 21. --------360ln3- – 162.
Для нахождения значений k и m решите систему уравнений k + m = 34, 3–1k + m = 14.
22. 4log5------27e4 . Для нахождения êоэффициента b решите уравнение tg (arctg 40 ln 5) = 5b ln 5.
23. 3,5 – 12ln 4-3 .
24. а)
4. Учтите, что S = ![]() | sin x | dx
=
| sin x | dx
= ![]() sin x dx +
sin x dx +
![]()
![]()
![]()
![]() + sin 1 – ; б) 1 + -3π
– cos 3 – 3 ; в) 2---------32 arcsin 2----------32 – 2-3 ; ã) 2 + cos 2.
+ sin 1 – ; б) 1 + -3π
– cos 3 – 3 ; в) 2---------32 arcsin 2----------32 – 2-3 ; ã) 2 + cos 2.
![]() – ;
.
Рассмотрите случаи –-
– ;
.
Рассмотрите случаи –-![]() <
k m -6π
.
<
k m -6π
.
27. –------30π ; -6π .
28. а) π. Таê êаê подынтеãральная фунêция y = 4 − x2
неотрицательна на отрезêе [0; 2], то значение исêомоãо интеãрала численно равно площади фиãуры, оãрани- y
![]()
![]() 2 ченной линиями y = 4 − x2 ,
x = 0, x = 2, y = 0, êоторая представляет собой четверть
êруãа A радиуса 2 (рис. 17). Таêим образом, значение
O √C B x
2 ченной линиями y = 4 − x2 ,
x = 0, x = 2, y = 0, êоторая представляет собой четверть
êруãа A радиуса 2 (рис. 17). Таêим образом, значение
O √C B x
2 32 интеãрала равно π · ----24- = π. Рис. 17
![]() б) 2-----------------------π
−63 3- .
Воспользуйтесь тем, что I = SœABC = SœAOB –
б) 2-----------------------π
−63 3- .
Воспользуйтесь тем, что I = SœABC = SœAOB –
– SœAOC (см. рис. 17).
![]() 29. а) 2 ln 2
– 1. Имеем I = SBCD = = SOAB
– SABDO (рис. 18).
29. а) 2 ln 2
– 1. Имеем I = SBCD = = SOAB
– SABDO (рис. 18).
Найдем площади фиãур OABC и ABDO. Таê êаê OABC — прямоуãольниê, то SOABC = 2BC, ãде BC = ln 2;, по-
этому SOABC = 2 ln 2. Рис. 18
Площадь êриволинейной трапеции ABDO найдем, проинтеãрировав фунêцию x = ey в пределах от 0 до ln 2 (ординаты точеê O и A соответственно):
SABDO
![]() eydy = eln 2 – 1 = 1.
eydy = eln 2 – 1 = 1.
Оêончательно получим I = 2 ln 2 – 1.
![]()
![]() б) -2π
– 1. Значение интеãрала равно площади S затемненной
фиãуры (рис. 19). Найдем эту площадь:
б) -2π
– 1. Значение интеãрала равно площади S затемненной
фиãуры (рис. 19). Найдем эту площадь:
-2π-
S = 1 · dy – ∫sin y dy = -2π – 1.
0
30. а) F(x) = 2x3 – x2 + 3x + 1; б) F(x) =
Рис. 19 = –cos 2x + x3 + 4.
31. а)
62,5. Исêомая площадь выражается таê: S = 3![]() (6 + + x
– x2) dx. б) 9-2 . Исêомая площадь выражается таê:
(6 + + x
– x2) dx. б) 9-2 . Исêомая площадь выражается таê:
S ![]() ) dx.
в) 7-6 . Исêомая
площадь выражается таê:
) dx.
в) 7-6 . Исêомая
площадь выражается таê:
![]() S
S ![]() ) (4 ln 2)–1 (4 – 33
2 ). Имеем
) (4 ln 2)–1 (4 – 33
2 ). Имеем
![]() S = ∫
(4x −1-2- 2 –x) dx =
--------ln4x4-
+ ------------22ln2- 13-−
S = ∫
(4x −1-2- 2 –x) dx =
--------ln4x4-
+ ------------22ln2- 13-−
−01- −x 0− = ------------2ln1 2- (4x + 2–x01-3 =
3
−1 1
= ------------2ln1 2- (2 – 4 3- – 2-3 ) = 2------------ln1 2- (2 – 21-3 (1 + 2–1)) = ------------2ln1 2- 2 – 3-2 3 =
![]() =
4------------ln1 2- (4 – 33
2 ). б) e – 21- . Воспользуйтесь
тем, что S =
=
4------------ln1 2- (4 – 33
2 ). б) e – 21- . Воспользуйтесь
тем, что S =![]() (ex –
(ex –
– x + 1) dx;
в) 4-3 Воспользуйтесь тем, что
S ![]() .
.
0
Глава VI Числовые последовательности.
Проãрессии. Предел фóнêции. Непрерывность
![]()
§ 1. ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
1. а) Выберем произвольное положительное число ε ипоêажем, что для неãо можно найти таêое натуральное число N, что при любом номере n > N будет выполняться неравенство
---n1 – 0 < ε. (1)
![]() После преобразований
получим неравенство n > 1-ε
. Если номер n больше, чем 1-ε
, то неравенство (1) будет выполняться, т. е. N можно взять
равным 1-ε
, ãде 1-ε
— целая часть числа 1-ε .
Следовательно, существование числа N таêоãо, что при любых n
> N = 1-ε
После преобразований
получим неравенство n > 1-ε
. Если номер n больше, чем 1-ε
, то неравенство (1) будет выполняться, т. е. N можно взять
равным 1-ε
, ãде 1-ε
— целая часть числа 1-ε .
Следовательно, существование числа N таêоãо, что при любых n
> N = 1-ε
неравенство (1) выполняется, поêазано и тем самым доêазательство завершено. Замечание. В êачестве N можно взять любое натуральное число, большее 1-ε ;
б) Поêажите, что N можно взять равным ![]() , ãде ε > 0;
, ãде ε > 0;
в) Воспользуйтесь тем, что lim qn = 0, 0 < q < 1. n → ∞
2. I способ. Последовательность {xn} называется оãраниченной, если найдутся таêие два числа m и M, что при любом n ° N выполняется неравенство m m xn m M. Доêажем существование чисел m и M для данной последовательности. Все члены
1------------------------+n(−21)n неотрицательны; последовательности с общим членом
если n = 2k – 1, то x2k – 1 = 0; если n = 2k, то x2k = -------------(22k)2- = --------21k2- , k ° N, поэтому в êачестве m можно взять любое отрицательное число или нуль (например, m = –2). В êачестве M можно взять, например, единицу. Действительно, x2k – 1 = 0 < 1 и x2k = = --------21k2- < 1 при любом k ° N. Следовательно, –2 m xn m 1 при лю-
бом n ° N, а это означает оãраниченность заданной последовательности.
II способ. Таê êаê всяêая сходящаяся последовательность оãраничена (необходимое условие сходимости последовательности), то установив, что lim 1------------------------+ (−21)n = 0, заêлючаем, что данn → ∞ n
ная последовательность оãраничена.
3. Оãраничены последовательности а), б), в), д), з). 4. Оãраничены последовательности а), ã).
5. Нет, например, последовательность {xn}, xn = (–1)n оãраничена, но она не имеет предела.
6. Последовательность (xn) называется неоãраниченной, если для любоãо числа L > 0 существует хотя бы один номер n таêой, что |xn| > L.
7. а) Найдите nlim→ ∞ n-----------n +− 21 и nlim→ ∞ 2------------------n−2 3+n12- ; б) Найдите n → ∞ -2 n и nlim→ ∞ n--------------n2−−11- . 8. Вообще ãоворя, нет. Например, xn = lim 1
= (–1)n, y = (–1)n + 1. 9. а) Найдите nlim→ ∞ ------------------------1 − nn2+ n2- и nlim→ ∞ ------------------1n+3 5+n33- ;
б) Найдите lim 15 + ------n12 и nlim→ ∞ n-----------n −+ 76 .
n → ∞
10. Предел последовательности {zn}, zn = cxn, ãде c — постоянная, существует: nlim→ ∞ cxn = c nlim→ ∞ xn. Полаãая с = –1, получаем nlim→ ∞ (–xn) = –nlim→ ∞ xn = –a.
11. Таê êаê lim yn = b, то lim (–yn) = –b (см. решение предыдущей задачи). Применяя теорему о пределе суммы двух сходящихся последовательностей, получаем
lim (xn + (–yn)) =
n → ∞
= nlim→ ∞xn + nlim→ ∞ (–yn) = nlim→ ∞ xn – nlim→ ∞ yn = a – b.
12. а) Расходится;
б) может êаê сходиться, таê и расходиться. Например,
1) an = ---n1 , bn = (–1)n; nlim→ ∞ (anbn) = 0, т. е. последовательность {anbn} сходится;
2)
![]() n — в этом случае предел
последовательности {anbn} не существует.
n — в этом случае предел
последовательности {anbn} не существует.
13. а) Нельзя; б) нельзя. Например, an = (–1)n, bn = (–1)n + 1, an + bn= 0, lim (an + bn) = 0, anbn = (–1)2n + 1 = –1 и lim (anbn) = –1.
14.
Нет. Например, an ![]() = ; обе последовательности
расходятся. 15. Монотонны последовательности а), в), ã). 16. Монотонны
последовательности б), ã). д). 17. Все члены последовательности
{xn}, xn = -----------n5+n2 , положительны, сле-
= ; обе последовательности
расходятся. 15. Монотонны последовательности а), в), ã). 16. Монотонны
последовательности б), ã). д). 17. Все члены последовательности
{xn}, xn = -----------n5+n2 , положительны, сле-
довательно, xn > 0, а таê êаê -----------nn+ 2 < 1, то -----------n5+n2 < 5 · 1. Таêим образом, для любоãо n° N выполняются неравенства 0 < xn < 5, т. е. данная последовательность оãраничена. Для доêазательства второãо утверждения рассмотрим разность
xn
+ 1 – xn ![]() – = ,
– = ,
êоторая положительна при любом n ° N, значит, данная последовательность возрастает.
18. Поêажите, что 1 < xn < 1,5 и что xn + 1 – xn < 0.
19. Нет; например, если xn = ---n1 , y = (–1)nn, то последовательность xnyn = (–1)n не имеет предела.
20. 2. Рассмотрим две последовательности {xn} и {yn}, xn = 2---------------nn++21- и yn = n-----------n +− 34 , и найдем их пределы. Для последова-
![]() + 1
+ 1
тельности {xn} имеем nlim→ ∞xn = nlim→ ∞ n + 2 = n → ∞ n1 + ---n2- =
= n![]() →
∞ 2 = 1 + 0 = 2 таê
êаê nlim→
∞ ---n1 = 0 и nlim→ ∞ ---n2 = 0 . Ана-
→
∞ 2 = 1 + 0 = 2 таê
êаê nlim→
∞ ---n1 = 0 и nlim→ ∞ ---n2 = 0 . Ана-
1 + ---n
лоãично находим предел последовательности {yn}: nlim→ ∞ yn = 1. Далее, применяя теорему о пределе произведения двух сходящихся последовательностей, получаем ответ.
5 −
21. 0. Преобразуйте выражение 5------------------nn43+−64- ê виду ---n1 · ----------------1 + nn--------4633 и
примените теорему о пределе произведения бесêонечно малой последовательности на оãраниченную последовательность.
22. –5-3 . 23. 1-5 . 24. ------271 . 25. –3-4 .
26. 0. Преобразуйте выражение ---------------nn2sin+ 1n- ê виду n---1 1----------------sin+ ----nn12 и по-
êажите, что последовательность ----------------1sin+ ----nn12 оãраничена. 27. 4. 28. 0.
Воспользуйтесь тем, что (------------------------------n + 1n)!! − n! = n-----------------------------------!(n +n1! ) − n! =
= n---------------------------------!(n +n!1 − 1) = ---n1 .
29. 0. 30. 1. 31. 3-4 . 32. 3-2 . Воспользуйтесь тем, что
1 + 2 + 3 + ... + n = nn-----------2+ 1 . 33. 4-3 . Воспользуйтесь тем, что
12 + 22 + ... + n2 = n(n + 1) 2---------------n6+ 1- .
34. а) 1. Воспользуйтесь тем, что --------------------n n( 1+ 1) = ---n1 – n-----------1+ 1 ; б) 1-2 ; в)1-2 . Используйте результаты задач а) и б) и примените теоре-
му о пределе разности двух сходящихся последовательностей.
35. 1, если b > 1; 0, если | b | = 1; –1, если 0 < | b | < 1.
§ 2. ПРОГРЕССИИ
1. Нет. Поêажите, что уравнение 1 + 4(n – 1) = 10 091 не имеет решений в целых числах.
2. 13. 3. 99 270. 4. 16; 12; 8; ...; –16; –20. Пусть a1 — первый член проãрессии, d — ее разность. Составим систему
![]() a1 + a2 + ... + an
– 2 + an
– 1 = 0, a2
+ a3 + ... + an – 1 + an
= –36,
a1 + a2 + ... + an
– 2 + an
– 1 = 0, a2
+ a3 + ... + an – 1 + an
= –36,
a10 – a6 = –16.
Из третьеãо уравнения имеем (a1 + 9d) – (a1 + 5d) = –16, т. е. d = –4. Вычтем из первоãо уравнения системы второе; тоãда получим a1 – an = 36, или –d(n – 1) = 36, –(–4)(n – 1) = 36 и n = 10. Для нахождения a1 преобразуем левую часть первоãо уравнения:
------------------------a1 +2an − 1- (n – 1) = a---------------------------------------------1 + a1 −24 9( − 1)- 9 = 0; a1 = 16.
5. 11; 13; 15 ; ...; 29, 31. 6. 1; 3; 5; ...; 17, 19. 7. 7. 8. 8;
![]() 12; 16; ... . Используя условие, запишем систему a2 =
a1 + d = 12,
12; 16; ... . Используя условие, запишем систему a2 =
a1 + d = 12,
200 < a------------------1 2+ a9 · 9 < 220.
Из уравнения системы выразим a1 через d и подставим в неравенство: 200 < 2 12-------------------------------------( −2d) + 8d · 9 < 220. После преобразований
получаем 311------27 < d < 4------274 . Таê êаê все члены проãрессии — нату-
ральные числа, то разность d проãрессии должна быть целым числом. Последнему неравенству удовлетворяет d = 4; друãих целых чисел в интервале 3 11------27 ; 4------274 - нет. Далее находим первый член проãрессии: a1 = 12 – 4 = 8.
9. –4. 10. 5; 9; 13; ... . 11. a1 = 4; d = 5. 12. 91- ; -61 ; 1-3 . Пусть x, y, z — исêомые числа; имеем систему уравнений
![]() x + y + z = 0,6(1) = 11------18 ;
x + y + z = 0,6(1) = 11------18 ;
-x1 + 1-y + 1-z = 18,
-x1 + 1-z = 2-y
(здесь -x1 ; 1-y ; 1-z — последовательные члены проãрессии.). Вычитая из второãо уравнения системы третье, находим y = 1-6 . Подставив это значение y в первое и второе уравнения системы, получим систему
![]() x + z = -94 ,
x + z = -94 ,
x------------xz+ z = 12,
решения êоторой найдем, подставляя z = 4-9 – x во второе ее уравнение.
13.
![]()
![]() – - ;
–---------2a- ;
–---------a -
... или - , ---------2a- ,
---------a - ,
... .
– - ;
–---------2a- ;
–---------a -
... или - , ---------2a- ,
---------a - ,
... .
28 28 28 28 28 28
14. ä----------------------254b − 9- при b ° (1; +×). Соãласно условию, имеем
систему уравнений a2a12 = 1, a4a10 = b.
Таê êаê a7 = a1 + 6d, то a1 = a7 – 6d и полученную систему можно преобразовать ê виду
![]() (a7 – 5d)(a7 +
5d) = 1,
(a7 – 5d)(a7 +
5d) = 1,
(a7 – 3d)(a7 + 3d) = b
![]() или a27 · 25d2 =
1, a27 · 9d2 = b,
или a27 · 25d2 =
1, a27 · 9d2 = b,
![]() отêуда d2
= ------------b16−
1
и a72 = 25------------------16b −
9- ;
a7 = ä----------------------254b −
9- .
Посêольêу должны выполняться неравенства d2 l 0, a72
l 0, одновременно должны выполняться неравенства b – 1 l 0 (1) и
25b – 9 l 0 (2).
отêуда d2
= ------------b16−
1
и a72 = 25------------------16b −
9- ;
a7 = ä----------------------254b −
9- .
Посêольêу должны выполняться неравенства d2 l 0, a72
l 0, одновременно должны выполняться неравенства b – 1 l 0 (1) и
25b – 9 l 0 (2).
Решив систему линейных неравенств (1) и (2), находим b ° (1; +×). При друãих значениях параметра b система уравнений действительных решений не имеет, т. е. не существует арифметичесêой проãрессии, членами êоторой являются действительные числа.
![]()
![]() 15. -------------------------11690k −
39
при k ° –6; - 3-2 . 16. 34-----------------------10−
29b
при b ° 1; 94- .
15. -------------------------11690k −
39
при k ° –6; - 3-2 . 16. 34-----------------------10−
29b
при b ° 1; 94- .
17. –(p + q). 18. 6. Соãласно условию, -----------------a1 +2 an- n = a---------------------------n + 14+ a2n n, отêуда a1 + an = 1-2 (an + 1 + a2n).
Теперь находим исêомое отношение:
(---------------------------------a1 + a23n)3n- : -----------------a1 +2 an- n = ----------------------------------3a(na1+ 1++a3an2)n2 = 6 2----------------------------------------------------a21a+1 d n+(d(3+n2n− 1−)1) = 6.
19. –1; 0; 1; 2. Пусть a – d, a, a + d и a + 2d — исêомые числа. Будем предполаãать, что проãрессия возрастающая. Тоãда получим уравнение, êоторое и решаем относительно a: (a – d)2 + a2 + (a + d)2 = (a + 2d), 3a2 – a + 2d2 – 2d = 0;
![]() a =
-----------------------------------------------------------1 ± −
24d62 +
24d +
1 . (1)
a =
-----------------------------------------------------------1 ± −
24d62 +
24d +
1 . (1)
Действительные решения будут существовать, если
![]()
![]() –24d2 +
24d + 1 l 0, или 12-------------−24
–24d2 +
24d + 1 l 0, или 12-------------−24--------------168 m d m 12---------------------------+24168 .
Этот промежутоê содержит лишь два целых числа: 0 и 1. Нуль отбрасываем, таê êаê по условию все исêомые числа различны. При d = 1 из равенства (1) находим a = 0, a – d = –1; a + d = 1, a + 2d = 2.
20. 13. 21. -----------------------------np(12+ np) . 22. 2,4. 23. a1 = 8, q = 2. 24. 39 или –10,5.
![]() 25. ä4. 26.
2; 6; 18; ... или 18; 6; 2; ... . 27. 3 --BA- . 28. q---------12100- .
29. S------S21 .
25. ä4. 26.
2; 6; 18; ... или 18; 6; 2; ... . 27. 3 --BA- . 28. q---------12100- .
29. S------S21 .
По условию имеем систему
![]() a1
+ a3 + ... + a999 = S1,
a2 + a4 + ... a1000 = S2.
a1
+ a3 + ... + a999 = S1,
a2 + a4 + ... a1000 = S2.
Умножим первое уравнение на знаменатель проãрессии q: a1q + a3q + ... + a999q = a2 + a4 + ... + a1000 = S1q.
![]() Решив
далее уравнение S2 = S1q, получим ответ.
30. ä ------SS12 .
Решив
далее уравнение S2 = S1q, получим ответ.
30. ä ------SS12 .
31. 6. Пусть a1 — первый член проãрессии, q — ее знаменатель, n — число членов. Тоãда имеем систему
![]() a1 + a1qn – 1 = 66, a21 qn – 1 =
128,
a1 + a1qn – 1 = 66, a21 qn – 1 =
128,
a1--------------11−−qqn- = 126.
Умножив первое уравнение системы на a1 и учитывая, что a21 qn – 1 = 128, получаем a21 – 66a1 + 128 = 0; (a1)1 = 64 и (a1)2 = 2.
Далее из второãо уравнения находим (qn – 1)1 = ------321 и (qn – 1)2 = 32.
Таê êаê qn = (qn – 1)q, то, подставляя полученные значения a1 и qn – 1 в третье уравнение системы, находим знаменатель проãрессии: q1 = 1-2 , q2 = 2. Посêольêу проãрессия возрастающая, значение q1 является посторонним. Решив теперь уравнение 2n – 1 = 32 = 25, получим ответ.
32. 600 м/мин. Пусть v1, v2, v3 (м/мин) — соответственно сêорость первоãо, второãо и третьеãо êоньêобежца. Из условия следует, что v3 < v1 < v2, т. е. v12 = v2v3. Далее, имеем систему уравнений
![]() v2t = v1t +
400,
v2t = v1t +
400,
v1t = v3 t – 2-3 ,
ãде t — время, в течение êотороãо второй êоньêобежец обошел первоãо на êруã. Исêлючая из этих уравнений t, получаем
-----------------------vv21−−vv1v33- = v-----------------------v211−−vv1v33- = v1 = 600.
33. Воспользуйтесь тем, что S2n – Sn = an + 1 + an + 2 + ...
![]() ... + a2n = an + 1 --------------11−−qqn- ;
S3n –
S2n =
a2n + 1 1--------------1−−qqn- .
34. 3 -32 . 35. -------------102938 .
... + a2n = an + 1 --------------11−−qqn- ;
S3n –
S2n =
a2n + 1 1--------------1−−qqn- .
34. 3 -32 . 35. -------------102938 .
Пусть последовательность a1, a2, ..., an — ãеометричесêая проãрессия. Поêажем, что последовательность a1k , ak2 , akn ,
... | k ° N, таêже является ãеометричесêой проãрессией. Действительно, таê êаê ai + 1 = aiq | i ° N, то
aki + 1 = aki qk и a----------ik +k1- = qk = const, ai
причем эта постоянная не зависит от номера последовательности i. Таêим образом, последовательности êвадратов и êубов членов бесêонечно убывающей проãрессии таêже являются бесêонечно убывающими проãрессиями. Поэтому имеем систему уравнений
![]() a1 = 7-2 ,
a1 = 7-2 ,
------------1 − q
1---------------a21 = 147--------16- ,
− q2
решив êоторую найдем a1 = 3, q = 1-7 (для этоãо достаточно возвести первое уравнение в êвадрат и разделить еãо на второе уравнение). Подставляя теперь найденные значения a1 и q в
формулу 1---------------a−31q3 , получим ответ.
![]()
![]() 36. 100--------3 - .
37. -------------------3 2 33 −
1-
или –-------------------32 33 +
1- .
38. 405; –270; 180; ... .
36. 100--------3 - .
37. -------------------3 2 33 −
1-
или –-------------------32 33 +
1- .
38. 405; –270; 180; ... .
39. 2-3 . 40. 27 или 3. 41. 2; 5; 8. 42. 7; 14; 21. 43. 2,5 или 22,5.
![]() 44. 931. 45.
4; 20; 100 или 4-9 ; 52------9 ; 676--------9 - .
46. 4; 12; 36 или -94 ;
–------209 ; 100--------9 - .
47. 2 ä 3 . 48. 4; 20; 100 и 5; 20; 35 или 100; 20; 4 и 101;
20, –61. 49. 5; 5; 5 или 10------3 ; 5; 15------2 . 50. 2. 51. 3; 6; 9; 12.
52. 1; 4; 16; 64. 53. 2; 5; 8; ... и 3; 6; 12; ... или 25------2 ; 79------6 ; 83------6 ; ... и 2-3 ; 25------3 ; 625--------6 - ;
... . 54. 6; 54. 55. 1210. 56. b = 1-3 , q = 1-3 . 57. 2; 4; 8;
12 или
44. 931. 45.
4; 20; 100 или 4-9 ; 52------9 ; 676--------9 - .
46. 4; 12; 36 или -94 ;
–------209 ; 100--------9 - .
47. 2 ä 3 . 48. 4; 20; 100 и 5; 20; 35 или 100; 20; 4 и 101;
20, –61. 49. 5; 5; 5 или 10------3 ; 5; 15------2 . 50. 2. 51. 3; 6; 9; 12.
52. 1; 4; 16; 64. 53. 2; 5; 8; ... и 3; 6; 12; ... или 25------2 ; 79------6 ; 83------6 ; ... и 2-3 ; 25------3 ; 625--------6 - ;
... . 54. 6; 54. 55. 1210. 56. b = 1-3 , q = 1-3 . 57. 2; 4; 8;
12 или
25------2 ; 15------2 ; 29- ; 23- . 58. b1 = 405, q = –3-2 . 59. b1 = 2, q = –31- . 60. 3; 6; 12 или 12; 6; 3.
§ 3. ПРЕДЕЛ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ
1. 2-3 . xlim→ 1 ----------------------------2xx22−−x1− 1- = xlim→ 1 -----------------------------------------2((xx−−11))(xx++1-21) = xlim→ 1 ---------------2xx++11- = 2-3 .
2. 3-2 . Разложите числитель и знаменатель дроби на множители.
3. –7,2. 4. 3. Упростите выражение в êвадратных сêобêах. 5. 1,2. Таê êаê xlim→ ∞ -x1 = 0, то полаãая x = 1-y , получим
![]() 3- ----2- +
1
3- ----2- +
1
· = · = x -y 1 y2 y
![]()
![]()
![]() 6. -92 . Сложите дроби и положите x = -1y . 7. –3. Разложите
числитель и знаменатель дроби на множители. 8. 3-4 . 9. 3. lim x------------------2 −
x
= lim --------------------------------x(
x3 −
1)
= lim x (x + x + 1) = 3. x → 1 x − 1 x → 1 x − 1 x → 1
6. -92 . Сложите дроби и положите x = -1y . 7. –3. Разложите
числитель и знаменатель дроби на множители. 8. 3-4 . 9. 3. lim x------------------2 −
x
= lim --------------------------------x(
x3 −
1)
= lim x (x + x + 1) = 3. x → 1 x − 1 x → 1 x − 1 x → 1
![]()
![]() 10. ------161 . xlim→ 2 x-----------------------------−x23−x4−
2
= xlim→ 2 ---------------------------------------------------------(x2 −x42 )−(x(3+x −32x)−
2)
=
10. ------161 . xlim→ 2 x-----------------------------−x23−x4−
2
= xlim→ 2 ---------------------------------------------------------(x2 −x42 )−(x(3+x −32x)−
2)
=
= lim -------------------------------------------------------------------------(x − 2)(x − 1) = lim -----------------------------------------------------x − 1 - = x → 2 (x − 2)(x + 2)(x + 3x − 2) x → 2 (x + 2)(x + 3x − 2)
= (------------------------------------2 + 2)1(2 + 2) = ------161 . 11. 1-2 . xlim→ 1 -------------------------52 −− xx −− 21- =
![]()
![]()
![]() = xlim→ 1 (------------------------------------------------------------(52 −−
xx −−
41))((
25 −−
xx ++
12))
= xlim→
1 -------------------------25 −−
xx ++
12- = 12- . 12. ------------------------4a a1 −
b .
= xlim→ 1 (------------------------------------------------------------(52 −−
xx −−
41))((
25 −−
xx ++
12))
= xlim→
1 -------------------------25 −−
xx ++
12- = 12- . 12. ------------------------4a a1 −
b .
Умножьте числитель и знаменатель дроби на x b− + a b− .
13.
![]() 3-2 . xlim→ 1 3
3-2 . xlim→ 1 3----------------xx −−
11-
= xlim→
1 -----------------------------------------------------------(x −(x1)−(31)x(2 +x3+x1)+ 1) =
![]() = xlim→ 1 ----------------------------------3 x2 +x3+x1 + 1- = 3-2 .
= xlim→ 1 ----------------------------------3 x2 +x3+x1 + 1- = 3-2 .
14.
1,2. lim→
0 3----------------------------------------11 ++
xx −− 11 −−
xx- = xlim→
0
---------------------------------------11++xx−+(11−−x)x × x
![]() × --------------------------------------------------------------------------(3 1 +x+
1 −x)(3
× --------------------------------------------------------------------------(3 1 +x+
1 −x)(3-----------------------------------------------------(1 −x)43+(1(1+−xx)4)3+----------------------------------------------------------------------------((11+−xx))23+(1(1+−xx)2)2+)(1 −x)2-)
=
(3 1 +x− 1 −x)(3 1 +x+ 1 −x)(
= xlim→ 0 2-------------------------------------------------------------------------------------------------------------------------------x(3 1 + x +( 11 +− xx)+(3 1(1−+xx))(4(1++(1x−)2x−)(31(−1 x+)x------------------------------------3))2 + (1 − x)2-) = = ------------------------------------------------2 1((1++11)()1(2++13+)1-) = 6-5 .
15. a2. Упростим выражение в êруãлых сêобêах. Полаãая
![]()
![]() 4 a
= b, 4 x = y, получаем ----------------bb2 −+ yy2- −1 – y------------------------------------------------3 − by22+byb2y − b3-
=
4 a
= b, 4 x = y, получаем ----------------bb2 −+ yy2- −1 – y------------------------------------------------3 − by22+byb2y − b3-
=
![]()
![]()
![]()
![]() = ----------------bb2 +−
yy2- – (---------------------------------------y −
b2)(byb2 + y2)- = b----------−1 y . Таê
êаê 2log4a = 4 a = b, то выражение в фиãурных сêобêах
примет вид b – y – b = –y = – 4 x . Далее находим предел: lim (–4 x
)8 = lim x2 = a2.
= ----------------bb2 +−
yy2- – (---------------------------------------y −
b2)(byb2 + y2)- = b----------−1 y . Таê
êаê 2log4a = 4 a = b, то выражение в фиãурных сêобêах
примет вид b – y – b = –y = – 4 x . Далее находим предел: lim (–4 x
)8 = lim x2 = a2.
x → ax → a
16. 8. Положим 2-x2 = y, тоãда получим ylim→ 2 ----------------------------------22x−+-x22−32−1x−−x6- =
= ylim→ 2 ----------------------------y2 + ----y82- − 6 = lim y------------------------------4 −y6−y22 + 8- = ylim→ 2 -------------------------------------------------------(y − 2)(yy+−22)(y2 − 2) =
-1y- − ----y22- y → 2 = lim (y + 2)(y2 – 2) = 4 · 2 = 8.
y → 2
sinx − x → -3
17.
![]() -------13 . limπ ----------------------------1 −
2cos3-πx - = xlim→
-3π ------------------------------------------------------------------2sin2 x-2cos−
-6π--3π −coscos x-x2−
6-π- -
=
-------13 . limπ ----------------------------1 −
2cos3-πx - = xlim→
-3π ------------------------------------------------------------------2sin2 x-2cos−
-6π--3π −coscos x-x2−
6-π- -
=
= xlim→ -3π -------------------------------------------------------------------2sinsin x-2 -x2−−6-π--- cos x--2 − -6π- = lim ---------------------------------cos x--2 − -6ππ- = ---------------------------------2sincos0 6-π- + -6π- =
π
6 sin -x2 + -6π x → -3π 2sin -x2 + 6-
= -----------1 = -------1 .
![]() 2-------23 3
2-------23 3
tg xtg2 x − tg2 -π
18. –24. lim tg---------------------------------3 x − 3tg x- = lim ----------------------------------------------------3- = x → 3-π cosx + -6π x → 3-π cosx + -6π
![]() π sinx − ----3π-
= 4 lim −-------------------------------------------tg xsin2xx + -3π- -
= 4 · 3 × =
lim tg--------------------------------------------------------------------------xsinx + -3 x → 3-π
cos x → -3π cosx + -6π cos2 xcos2 -3π
π sinx − ----3π-
= 4 lim −-------------------------------------------tg xsin2xx + -3π- -
= 4 · 3 × =
lim tg--------------------------------------------------------------------------xsinx + -3 x → 3-π
cos x → -3π cosx + -6π cos2 xcos2 -3π
![]() × 4 –-------23
= – 24.
× 4 –-------23
= – 24.
19.
![]() -------23 . limπ
1---------------------------−cos4sin3x2x- = xlim→ 6-π
4--------------------------------------------------------cos4 0 25(x,(cos−2xsin−
20 75x,
) )-
=
-------23 . limπ
1---------------------------−cos4sin3x2x- = xlim→ 6-π
4--------------------------------------------------------cos4 0 25(x,(cos−2xsin−
20 75x,
) )-
=
x → 6-
![]() = limπ -----------cos1 x- =
-------23 . x → -6
= limπ -----------cos1 x- =
-------23 . x → -6
20. 0,4. Имеем xlim→ 0 ---------------sin5x2x- = xlim→ 0 -52---------------sin2x2x- . Полаãая 2x = y,
находим lim ---------------sin2x2x- = ylim→ 0 ------------siny y = 1. Перемножив пределы 2-5 и 1,
x → 0 получаем ответ.
21. 8-3 . Преобразуйте выражение sin 8x ctg 3x ê виду
8-3---------------sin8x8x- · ---------------sin3x3x- cos 3x, вычислите пределы xlim→ 0 ---------------sin8x8x- , xlim→ 0 ---------------sin3x3x- , lim cos 3x и примените теорему о пределе произведения êо-
x → 0 нечноãо числа фунêций, имеющих предел в данной точêе.
22. –21- . Запишите данную фунêцию таê:
x----------------------------2x+2 3+x2x− 1- tg x = ------------------------------------(cosx2 +x3)(xx−+12) · -----------sinxx- .
23. 5. Положите x – 1 = y и воспользуйтесь тем, что ylim→ 0 ------------siny y = 1.
24. –1. 25. 25------6 . 26. 0 при n = 1; 4,9 при n = 2.
27. –sin a. Преобразуйте выражение sin (a + 2x) – sin (a + x) – – sin (a + x) + sin a в произведение.
28.
![]() 1-4 . xlim→ 0 -------------------------------1 +
tg xx−3
1-4 . xlim→ 0 -------------------------------1 +
tg xx−3-------------------------1 +
sinx- = xlim→
0 x--------------------------------------------------------------------3((1 +1tg+
tgx)x−+(1 +1 +sinsinx)x)-
=
= xlim→ 0 x--------------------------------------------------------------------------------------------------3(1 + costgx)(x(11 +− tgcosx2x+) 1 + sinx) =
![]() = xlim→ 0 sin-------------x33x- ·
-------------------------------------------------------------------------------------------------------cosx(1 + cosx)(
1 +
tgx + 1 + sinx-)
=
= xlim→ 0 sin-------------x33x- ·
-------------------------------------------------------------------------------------------------------cosx(1 + cosx)(
1 +
tgx + 1 + sinx-)
=
= 1 1--------------------------------------( + 11)(1 + 1) = 1-4 .
29. 1-2 . Представим данную фунêцию f (x) в виде
![]()
![]()
![]() f(x) = 3-------------------------------------------------------------------1 +
x2 −x1++x12−
4 1 −
2x = 3-----------------------------1x++xx22−
1- +
1------------------------------−x4+1x−22x- .
f(x) = 3-------------------------------------------------------------------1 +
x2 −x1++x12−
4 1 −
2x = 3-----------------------------1x++xx22−
1- +
1------------------------------−x4+1x−22x- .
Вычислим теперь пределы:
![]() lim
f1(x) = 3-----------------------------1x++xx22−
1- = xlim→
0
--------------------------------------------------------------------------------------------x x(
+ 1)(3 (11++xx22)2−+13 1 +
x2 +
1)-
=
lim
f1(x) = 3-----------------------------1x++xx22−
1- = xlim→
0
--------------------------------------------------------------------------------------------x x(
+ 1)(3 (11++xx22)2−+13 1 +
x2 +
1)-
=
![]() = lim --------------------------------------------------------------------------------------------x2 - = 0; x →
0 x x( + 1)(3 (1 + x2)2 + 3 1 + x2 + 1)
= lim --------------------------------------------------------------------------------------------x2 - = 0; x →
0 x x( + 1)(3 (1 + x2)2 + 3 1 + x2 + 1)
xlim→ 0 f2(x) = xlim→ 0 ------------------------------1 x−(411+−x2)x- =
= xlim→ 0 ----------------------------------------------------------------------------------------------x(1 + x)(1 +14−1(1− −2x2)x()1 + 1 − )- = 1 1--------------------------------------( + 12)(1 + 1) = 1-2 .
2x
Далее находим xlim→ 0 f(x) = xlim→ 0 f1(x) + xlim→ 0 f2(x) = 0 + -21 = 2-1 .
30. а) {–3; 3}; б) {0}; в) {0}; ã) {0}; д) -2π + nπ | n ° Z; е) {n | n ° Z}. 31. 1. 32. 0. Положим π – x = 2y; тоãда x = π – 2y,
1 − sinx- 1 − sin
причем y º 0 при x º π. Имеем xlim→ π ---------------------π − x 2- = ylim→ 0 -------------------------------------2y-2π − y =
2sin2 -y
= ylim→ 0 1----------------------−2cosy y = ylim→ 0 --------------------2y 2 = 2-1 ylim→ 0 -----------sin2-y- 2-y-- · ylim→ 0 sin2-y = 1 · 0 = 0.
![]() 33.
5-2 . 34. –5-2 . При решении нужно
учесть, что если x < 0, то –x = |
x |. Находим lim ( (x
+ 2)(x + 3) + x) =
x →
33.
5-2 . 34. –5-2 . При решении нужно
учесть, что если x < 0, то –x = |
x |. Находим lim ( (x
+ 2)(x + 3) + x) =
x →
![]() = xlim→ −∞ -------------------------------------------------(x + 25)x(x+
+63) − x- = xlim→
−∞ -----------------------------------------------------1 + --x2 1 +xx-3
+
1 = –5-2 .
= xlim→ −∞ -------------------------------------------------(x + 25)x(x+
+63) − x- = xlim→
−∞ -----------------------------------------------------1 + --x2 1 +xx-3
+
1 = –5-2 .
35. 2-3 . xlim→ ∞ x2(3 1 + x3 + 3 1 − x3 ) =
= lim --------------------------------------------------------------------------------------------------------------2x2 = x → ∞ 3 (1 + x3)2 − 3 (1 + x3)(1 − x3) + 3 1 − x3
![]() = xlim→ ∞ 3------------------------------------------------------------------------------------------------------------------------------- -----12 + 1 2 − 3 ----x13
+
12 ----x13
−
1
+ 3 ----x13
−
1
2 = 23- .
= xlim→ ∞ 3------------------------------------------------------------------------------------------------------------------------------- -----12 + 1 2 − 3 ----x13
+
12 ----x13
−
1
+ 3 ----x13
−
1
2 = 23- .
x
36. ![]() 1. 37. 1. 38.
–1. Воспользуйтсь тем, что x = –|x| при x < 0. 39.
1. xlim→ +∞ ----------------------------------------------------1 +
x +
xx2 −
x +
1- = xlim→
+∞ x----x2 ( 1 + x x+ 2 +
1. 37. 1. 38.
–1. Воспользуйтсь тем, что x = –|x| при x < 0. 39.
1. xlim→ +∞ ----------------------------------------------------1 +
x +
xx2 −
x +
1- = xlim→
+∞ x----x2 ( 1 + x x+ 2 +
![]()
![]() + x + 1 ) = xlim
----x12 + x-1 +
1 + -x1 +
----x12
= 1. 40. –1. 41. 2. 42. 1.
+ x + 1 ) = xlim
----x12 + x-1 +
1 + -x1 +
----x12
= 1. 40. –1. 41. 2. 42. 1.
→ +∞
Имеем
-![]() + +
... + = Sn, ãде Sn
= 1 + 2-3 + ...
+ +
... + = Sn, ãде Sn
= 1 + 2-3 + ...
... + 2-3 n − 1; значит, Sn · 2-3 = 23- + 2-3 2 + ... + 2-3 n − 1 + 23- n,
Sn = Sn · 2-3 = 1-3 Sn = 1 – 2-3 n; nlim→ ∞-31-Sn = nlim→ ∞1 − 2-3 n = 1.
43. 53- . Введем обозначение
Sn = 1 – 2-3 + ... + (–1)n – 1 2-3 n − 1 + (–1)n 2-3 n .
Тоãда
Sn · 3-2 = -32 – -32 2 + ... + (–1)n – 1 3-2 n + (–1)n 2-3 n + 1 ;
Sn 1 +- 2-3 = 5-3 Sn = 1 + (–1)n 32- n + 1 ;
Sn = 3-5 1 + (–1)- n 2-3 n + 1 . Следовательно, n → ∞ n = nlim→ ∞ 3-5 1 + (–1)n 3-2 n + 1 = -53 , таê êаê nlim→ ∞ 2-3 n + 1 = 0. lim S
44. а) A
= 2; б) A = 0; в) A = 3.
Глава VII
Элементы веêторной алãебры
![]()
§ 1. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ
1.
![]()
![]()
![]() а) Веêторы
а) Веêторы a
и b должны быть взаимно перпендиêулярными; б) уãол между веêторами
a и b должен быть острым; в) уãол между веêторами
a и b должен быть тупым.
2.
а) π;
б) ------101 . 3. x °
(–1; 5). Исходное неравенство равносильно неравенству |x – 2| · |a
| < 3|a |, или |x – 2| < 3.
![]()
![]()
![]()
![]()
![]() 4. x ° (–3;
–1] c [1; +×). Решите систему неравенств |x| l 1, x + 3 l
0. 5. x = 10------7 , y = 4-7 . 6. 0. По условию
4. x ° (–3;
–1] c [1; +×). Решите систему неравенств |x| l 1, x + 3 l
0. 5. x = 10------7 , y = 4-7 . 6. 0. По условию
a +b= λc
и b+ c = µa
, ãде λ,
µ — неêоторые
числа, отличные от нуля. Исêлючая из этих уравнений b, приходим
ê равенству (µ +
1)a = = (λ
+ 1)c, êоторое возможно лишь при µ = –1 и λ = –1 (веêторы
a и c не êоллинеарны). Следовательно, a
+b= –c и a + b + = c 0
.
7.
![]()
![]()
![]() p = 1, q = 1.
Из êоллинеарности веêторов p
p = 1, q = 1.
Из êоллинеарности веêторов pa + qb + c
и a + pb+ qc следует, что (p – λ)a +
(q – pλ)b+
(1 – λq)c
= 0 . Последнее возможно лишь тоãда, êоãда p –
λ = 0, q
– pλ
= 0, 1 – λq
= 0 (λ
− 0). Решив эту систему уравнений, получаем ответ.
8.
Верно, если a > b + c. 9. AO
= 1-3 (a + b ).
10.
![]() 2-3 (
2-3 (a + b ).
Имеем AC = AB + AD ,
AB
+ BM = AB + 1-2 AD = a , (1)
AD + DK = AD + 1-2 AB = b. (2)
![]()
![]()
![]()
![]()
![]() Сêладывая уравнения
(1) и (2), получаем 3-2 (AB + AD )
= = 3-2 AC =
Сêладывая уравнения
(1) и (2), получаем 3-2 (AB + AD )
= = 3-2 AC = a +b,
отêуда AC = 2-3 (a +b).
11.
![]()
![]() a = b.
12.
a = b.
12. e = ---bb a-----a-----------++
---aa b-----b- .
13. а) 13; б) 109 . 14. –5-4 ;
![]() 8-5 -
. 15.
8-5 -
. 15. p = {–6; 8}. 16. p = 2a
– 3b. Таê êаê веêторы
p ,
![]()
a
и b êомпланарны, то p = λa + µb . Последнее уравнение
можно переписать в виде p = {3; 4} = λ(3; –1) + µ(1; –2). Отсюда получаем систему уравнений
относительно λ
и µ: 3 = 3λ + µ, 4 = –λ – 2µ,
![]() решив
êоторую находим λ
= 2, µ = –3; следовательно,
решив
êоторую находим λ
= 2, µ = –3; следовательно,
p = 2a – 3b.
17. {(2; 9); (7; 0)}. Рассмотрите отдельно случаи BC C AD и AB C CD.
18. {1,5; 1; –2}. 19. Поêажите, что CD = –2AB . 20. 18 .
![]()
![]() 21. {4 2 ; –2;
8}, {–4 2 ; 2; –8}. 22. {–24; 32; 30}. 23. {–6;
8; 24}.
21. {4 2 ; –2;
8}, {–4 2 ; 2; –8}. 22. {–24; 32; 30}. 23. {–6;
8; 24}.
24. M (–1; 0; 0). Используйте равенство |MA| = |MB|, ãде MA = = {1 – x; 2; 3} и MB = {–3 – x ; 3; 2}.
25.
![]()
![]()
![]()
![]() ---------351- . Воспользуйтесь разложением AO
= AB + + 1-3 (BC + BD ).
26. Да. 27. d = 2
---------351- . Воспользуйтесь разложением AO
= AB + + 1-3 (BC + BD ).
26. Да. 27. d = 2a – 3b+ c.
Представьте веêтор d в виде d = λa + µb+ νc и
из системы уравнений 3λ
– µ + 2 ν = 11, –2λ + µ + ν = –6, λ – 2µ – 3ν = 5 найдите
êоэффициенты λ,
µ, ν. 28. 2-5 AA1 + 52- AB + -53 AC .
![]()
![]() Воспользуйтесь разложением AM
= AC + 2-5 CB1 .
29. ------134 i + + ------133 j +
12------13 k. Имеем
AC1 = AD + AB + AA1 = 4 + 3 +
12 ; i j k
следовательно, |AC1 |
= 42 +
32 +
122 =
13 и
Воспользуйтесь разложением AM
= AC + 2-5 CB1 .
29. ------134 i + + ------133 j +
12------13 k. Имеем
AC1 = AD + AB + AA1 = 4 + 3 +
12 ; i j k
следовательно, |AC1 |
= 42 +
32 +
122 =
13 и e
= ---------ACAC---11- = ------134 i +
![]() + ------133 j + 12------13 k.
+ ------133 j + 12------13 k.
30. ![]() 3 : 1. Доêажите,
что исêомое отношение равно отношению длин веêторов EC и EM2 (E — середина отрезêа
BD).
3 : 1. Доêажите,
что исêомое отношение равно отношению длин веêторов EC и EM2 (E — середина отрезêа
BD).
31. ![]()
![]() 5. Введем прямоуãольный
базис Oxyz, совместив O с точêой приложения сил (рис. 20), причем
OM ° xOz, ON ° yOz и OP ° xOy. Пусть
|OM| = 1, |ON| = 2 и
5. Введем прямоуãольный
базис Oxyz, совместив O с точêой приложения сил (рис. 20), причем
OM ° xOz, ON ° yOz и OP ° xOy. Пусть
|OM| = 1, |ON| = 2 и
|OP| = 3; тоãда OM = -----1 ; 0; -------1 ,
2 2
![]() Рис. 20 ON
= {0; 2 ; 2 } и OP = -------32 ; -------32 ; 0 .
Рис. 20 ON
= {0; 2 ; 2 } и OP = -------32 ; -------32 ; 0 .
![]() Сумма этих веêторов есть
веêтор равнодействующей данных сил:
Сумма этих веêторов есть
веêтор равнодействующей данных сил: p = -------42 ; -------52 ; -------32 ;
p = 16----------------------------+
225 +
9- =
5.
32. α2 + β2 = 1.
33. α =
–1, β = 9. 34.
a = 31- ; 8-3 ; –4-3 .
35. AC =
![]() = 13 , BD
= 5. 36. π-------------------------(214k +
1)
, π------------------------(2n4+
1)- ,
π--------------------------(2m2 +
1),
| k, n, m ° Z.
= 13 , BD
= 5. 36. π-------------------------(214k +
1)
, π------------------------(2n4+
1)- ,
π--------------------------(2m2 +
1),
| k, n, m ° Z.
§ 2. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
![]() 1. 3-----4π- .
2. 4. 3. ---------321- . Имеем
1. 3-----4π- .
2. 4. 3. ---------321- . Имеем
(a + b )(a – b ) = |a +
b| |a – b| cos ϕ;
отсюда
cos ϕ
= ----------------a--------------------------2 −
b 2 -------
=
(a + b)2 (a −
b)2
![]() = -------------------------------------------------------------------------------------------------------------------------------22 −
1 -------------------
= -------------------3 =
---------3 - .
= -------------------------------------------------------------------------------------------------------------------------------22 −
1 -------------------
= -------------------3 =
---------3 - .
22 + 12 + 2 2 1⋅ ⋅ ⋅ cos60° 22 + 12 − 2 2 1⋅ ⋅ ⋅ cos60° 3 ⋅ 7 21
4.
![]()
![]() –4-5 . Решив систему уравнений
относительно
–4-5 . Решив систему уравнений
относительно p и q , находим p = 1-3 (2a – b
) =
-31 ; 1 ;
q = 3--1 (2b – a )
= 1-3 ; –1
; таê êаê p q = |p |
|q| cos ∠(p,
q ), то
![]() cos ∠(
cos ∠(p ,
q ) = 1-9 – 1 : ---------310-
2 =
– 4-5 .
5.
![]()
![]()
![]()
![]()
![]()
![]() Доêажите, что
Доêажите, что a
p = 0. 6. –295. Возведя равенство a + b +
= c 0 в êвадрат, получаем a2 + b2
+ c2 + 2 (a b + b c + + c a
) = 0. Отсюда имеем a b + b c + c a
= –1-2 (a2
+ b2 + c2 ) = = – 1-2 (132 + 142
+ 152) = –295. 7. arccos 1-3 . Определите уãол между веêторами
![]() arccos - . Найдите уãол
между веêторами AB и BC .
arccos - . Найдите уãол
между веêторами AB и BC .
![]() = arccos .
= arccos .
11. ![]() 9-2 . Воспользуйтесь формулами
SABC = 1-2 |AB| · |AC| sin
A,
9-2 . Воспользуйтесь формулами
SABC = 1-2 |AB| · |AC| sin
A,
sin A = 1 − cos2A = 1 − -AB AC--------AB AC-----⋅ --------- 2 .
12. ![]() arccos −
------103 .
Поêажите, что исêомый уãол равен уãлу между веêторами
AB + BC и BC – AB .
arccos −
------103 .
Поêажите, что исêомый уãол равен уãлу между веêторами
AB + BC и BC – AB .
13. arccos ![]() - . 14. |AC|
= 5; O -25 ; 1; 1 .-
- . 14. |AC|
= 5; O -25 ; 1; 1 .-
![]()
![]()
![]() 15. b= 1;
1-2 ; – 1-2
. Пусть b = {x; y; z}; тоãда из
условия êоллинеарности имеем -x2 = -1y = –1-z = t, или x
= 2t, y = t, z = –t. Подставляя эти равенства в
сêалярное произведение
15. b= 1;
1-2 ; – 1-2
. Пусть b = {x; y; z}; тоãда из
условия êоллинеарности имеем -x2 = -1y = –1-z = t, или x
= 2t, y = t, z = –t. Подставляя эти равенства в
сêалярное произведение ab = 3, находим t = 21- . 16. c
= {–3; 3; 3}. 17. c = -------43 ; –-------13 ; –-------23 .
![]() 18.
18. c =
{2; –3; 0}. 19. c = {1; 0; 1} или = c 1-3 ; -34 ; –-------23
. Пусть c = {x; y; z}, тоãда
![]() |
|
|
|c = | |a = | |b = 2 = x2
+ y2
+ z2
. (1)
![]()
![]() Соãласно условию, уãлы
ϕ между веêторами
равны, поэтому cos ϕ
= ----a b
Соãласно условию, уãлы
ϕ между веêторами
равны, поэтому cos ϕ
= ----a ba----b----
= 1-2 , ----a cac-------
= x-----------2+ y- =
1-2 , ---b cb-----c--- =
y----------2+ z + 2-1 . (2)
Решив систему уравнений (1), (2), получим ответ.
20. 5. 21. a =
{2; –2; –2}.
22. ![]() x °
(–×; 0). Найдите значения x, при êоторых одновременно выполняются
неравенства
x °
(–×; 0). Найдите значения x, при êоторых одновременно выполняются
неравенства a b > 0, b c < 0, ãде c
= {0; 1; 0}.
23. Найдите MQ · NP , ãде MQ = MP + PQ , NP =
![]() B 24.
arccos –4-5
. В равнобедренном
B 24.
arccos –4-5
. В равнобедренном
M2 прямоуãольном треуãольниêе ABC (рис. 21)
имеем |AC| = |AB|, BM1 и CM2 — медианы,
BM
![]() A M1 C 1 = 21- AC – AB ,
A M1 C 1 = 21- AC – AB ,
Рис. 21 CM2 = 1-2 AB – AC.
![]()
![]() Перемножив два последних
веêторных равенства и учитывая, что AB B AC , находим BM1
· CM2 = 45-
|AB |2 cos ϕ
= = –1-2 (AC 2 +
AB 2) = –|AB|2, отêуда получаем ответ.
Перемножив два последних
веêторных равенства и учитывая, что AB B AC , находим BM1
· CM2 = 45-
|AB |2 cos ϕ
= = –1-2 (AC 2 +
AB 2) = –|AB|2, отêуда получаем ответ.
25. ![]() BM = ---bc-----
BM = ---bc-----c2 · c – b .
Имеем (рис. 22)
BM = AM – b , (1)
![]()
![]()
![]() B ãде AM
= γ
B ãде AM
= γc
(γ — неêоторое
действительное число). Таê êаê веêтор BM перпендиêулярен
веêтору c , то BM · c = 0. СледоA M C вательно, γc 2
– b · c = 0, т. е. γ
= b----c----⋅
2c- .
Рис. 22 уравнениеПодставив (1), найденноеполучим для ответ γ .выражение в
26. – 20------7 ; –30------7 ; 10------7 . Воспользуйтесь решением задачи 25.
= - . Используя результат задачи 25, найдите
![]()
![]() cos ϕ = ------------BMBM-----------1 ⋅⋅
DMDM---------------2 , ãде BM1 = 19------4 ; 9--1 ; –98- ,
DM2 = {2; –2; 1}.
cos ϕ = ------------BMBM-----------1 ⋅⋅
DMDM---------------2 , ãде BM1 = 19------4 ; 9--1 ; –98- ,
DM2 = {2; –2; 1}.
1 2
28. 2x + 2y + 3z – 6 = 0. Запишем уравнение плосêости в общем виде:
ax + by + cz + d = 0. (1)
Подставляя поочередно êоординаты точеê M1, M2, M3 в уравнение (1), получаем систему уравнений
a – b + 2c = – d, 3b = –d, 2a + b = –d,
решив êоторую найдем a = –d--3 , b = – d-3 , c = – d-2 . При этих зна-
чениях êоэффициентов a, b и c уравнение (1) примет вид –d(2x + 2y + 3z – 6) = 0. Соêратив на (–d) (d − 0), получим исêомое уравнение.
29. ![]()
![]() x + z – 4 = 0. Пусть
x + z – 4 = 0. Пусть
n = {a; b; c} — нормальный веêтор плосêости
α, проходящей
через точêу A (4; 0; 0). Таê êаê плосêость
α параллельна
оси Oy, то веêтор n перпендиêулярен любому веêтору,
параллельному оси Oy, например веêтору j = {0; 1; 0}. Отсюда следует, что n j = b = 0, т. е. уравнение
плосêости α
имеет вид a(x – 4) + cz = 0 или a1(x
– 4) + z = 0, ãде a1 = a-c- .
Подставяляя êоординаты точêи B в последнее уравнение, получаем
a1 (0 –
4) + 4 = 0, a1 = 1, отêуда x + z – – 4 = 0.
30. ![]() –1. Если D
∈ ABC,
то веêторы AB, AC, AD êомпланарны и поэтому AD = λ AB + µAC , ãде
хотя бы один из êоэффициентов λ,
µ отличен от нуля.
В êоординатной форме это уравнение можно переписать таê: (k –
1; 2; 2) = λ
(–2; 3; 1) +
–1. Если D
∈ ABC,
то веêторы AB, AC, AD êомпланарны и поэтому AD = λ AB + µAC , ãде
хотя бы один из êоэффициентов λ,
µ отличен от нуля.
В êоординатной форме это уравнение можно переписать таê: (k –
1; 2; 2) = λ
(–2; 3; 1) +
+ µ(0; 2; –2), отсюда получаем систему уравнений
–2λ = k – 1, 3λ + 2µ = 2, λ – 2µ = 2,
из êоторой находим λ = 1 и k = –2λ + 1 = –2 + 1 = –1.
Замечание. Задачу можно решить таêже, написав предварительно уравнение плосêости ABC (см. решение задачи 28) и подставив в это уравнение êоординаты точêи D.
31. ![]() а) См. решение задачи
30; б) 2-π
; в) 21 ---------210- .
Восполь-
а) См. решение задачи
30; б) 2-π
; в) 21 ---------210- .
Восполь-
![]() зуйтесь формулой SABCD
= 1-2 |AC | · |BD|.
зуйтесь формулой SABCD
= 1-2 |AC | · |BD|.
32.
-3π . Для нахождения
уãла между плосêостями ABC и ABD определите уãол
между нормальными веêторами n1 и n2
этих плосêостей.
33. а) A (1; 2; 0); B (0; 0; 2). Полаãая в системе уравнений
2x + 3y + 4z – 8 = 0, 4x + y + 3z – 6 = 0 (1) z = 0, найдем абсциссу и ординату точêи A пересечения прямой p с плосêостью xOy, т. е. найдем x = 1, y = 2. Аналоãично находим êоординаты точêи B (в системе (1) надо положить x = 0); б) arcsin 2-3 . Величину исêомоãо уãла можно найти из равенст-
![]() ва cos ϕ = ---------BA---------⋅
ва cos ϕ = ---------BA---------⋅
n---- ,
ãде BA = {1; 2; –2} и n = {0; 1; 0} — нормаль-
BA ⋅ n
![]() ный
веêтор плосêости xOz (ϕ
— уãол между веêторами BA и
ный
веêтор плосêости xOz (ϕ
— уãол между веêторами BA и n ).
34. ![]() а) E(12; 0; 3); F1(0;
6; 12); G(6; 12; 0); б) 7x + 5y + 6z – – 102 = 0; в)
3-------------1110- .
Уравнение прямой, проходящей через точêу B1 и перпендиêулярной
плосêости EF1G, имеет вид x-----------7−
0-
=
а) E(12; 0; 3); F1(0;
6; 12); G(6; 12; 0); б) 7x + 5y + 6z – – 102 = 0; в)
3-------------1110- .
Уравнение прямой, проходящей через точêу B1 и перпендиêулярной
плосêости EF1G, имеет вид x-----------7−
0-
=
![]() = y-----------−5 0- = z--------------−612- ,
посêольêу веêтор {x; y; z – 12} êоллинеарен
веêтору {7; 5; 6}. Определите êоординаты точêи M пересечения
этой прямой с плосêостью EF1G и найдите расстояние
по формуле B1M = (xB1 − xM)2 + (yB1 − yM)2 + (zB1 − zM)2 .
= y-----------−5 0- = z--------------−612- ,
посêольêу веêтор {x; y; z – 12} êоллинеарен
веêтору {7; 5; 6}. Определите êоординаты точêи M пересечения
этой прямой с плосêостью EF1G и найдите расстояние
по формуле B1M = (xB1 − xM)2 + (yB1 − yM)2 + (zB1 − zM)2 .
35. arccos
–------2116
. 36. arccos –------2725
. 37. a = {1; 2; 2}. 38. 13.
39. |a|
= 3 2 , |b| = 89 . 40. с2.
41. При a = –1. 42. 5-----6π- .
43. C (0;
3; 0). 44. c = {–3; 3; 3}. Запишем исêомый веêтор
в виде c = xi + + yj + zk . Из условия следует:
![]() c
c a =
2x + 3y – z = 0, c b = x – 2y + 3z
= 0, c · (2i – j + k ) = 2x – y
+ z = –6.
Умножив первое уравнение на 3 и сложив со вторым, имеем 7x + 7y = 0 ⇒ y = –x. Далее, заменив y на –x в первом уравнении, получаем z = –x. Наêонец, заменив в третьем уравнении y и z на –x, находим x = –3, поэтому y = 3, z = 3.
45.
–18------13 . Имеем AB
= 2i – 6j + 4k . прc AB
= -------ABc-------⋅
c-
=
![]() = -----------------------------6 +
2413−
48
= –18------13 . 46. 17------5 . 47. – 14- .
48. 3 . Единичный веêтор
= -----------------------------6 +
2413−
48
= –18------13 . 46. 17------5 . 47. – 14- .
48. 3 . Единичный веêтор e оси, составляющей с
êоординатными осями равные
острые уãлы, имеет
вид e = -------1 i + -------1 j + -------1 k . Поэтому
3 3 3
-------1 + -------2
![]() пр
пре
a = ea--e----
= --------------3 1 ------3- = 3 . 49.
a = a 1 – 2a 2.
Глава VIII
Планиметрия
![]()
§ 1. ЗАДАЧИ НА ДОКАЗАТЕЛЬСТВО
1. а) Пусть С принадлежит отрезêу AM. Тоãда AC + CM = = AM и BC = CM + MB = CM + AM. Исêлючив из этих равенств
AM, найдем CM = 1-2 |AC – BC|. Аналоãично рассматривается слу-
чай, êоãда C принадлежит отрезêу MB; б) Пусть C принадлежит лучу BD, ãде D лежит на прямой AB, тоãда MC = MB + BC и AC + AM + MC = MB + MC. Исêлючив из этих равенств MB, получим MC = 1-2 (AC + BC). Случай, êоãда C принадлежит лучу AE, ãде E лежит на прямой AB, рассматривается аналоãично.
2.
![]() Используйте свойство вертиêальных уãлов.
Используйте свойство вертиêальных уãлов.
3. Проведем AF B CD (рис. 23). Прямая AF является осью симметрии тре-
C уãольниêа ACD и пересеêает отрезоê BD в точêе O. Отсюда следует, что OC = OD.
Изнеравенства треуãольниêа следует, что OB + OC > BC, но OB + OC = OB + OD = BD и поэтому BD > BC.
4. Используйте свойство наêрест лежащих уãлов при параллельных прямых. 5. Отрезêи KL и MN (рис. 24) являC ются средними линиями треуãольниêов ABC и ADC; следовательно, KL C AC C MN.
Аналоãично можно доêазать, что KN C LM, а это означает, что KLMN — параллелоãрамм.
6. Проведем среднюю линию MN тра-
Рис. 24 пеции ABCD (рис. 25). Она пересечет диаãо-
![]() нали трапеции
AC и BD в точêах E B C и F,
êоторые являются серединами соответствующих диаãоналей (это M
нали трапеции
AC и BD в точêах E B C и F,
êоторые являются серединами соответствующих диаãоналей (это M
следует из теоремы Фалеса для уã- AD
лов BAC и BDC). Значит, EF C AD. Рис. 25
Найдем длину отрезêа EF; таê êаê
MF — средняя линия ∆ABD, ME — средняя линия ∆ABC, то из уравнения MF = ME + EF, или 2a- = EF + 2-b , получим EF = = 1-2 (a – b).
7.
![]() Пусть CF — биссеêтриса уãла
Пусть CF — биссеêтриса уãла
BCD, DP — биссеêтриса уãла ADC B E C
(рис. 26). Таê êаê
![]()
![]() ∠BCD + ∠ADC = π, то ∠FCD + ∠MDC =
∠BCD + ∠ADC = π, то ∠FCD + ∠MDC =
= , отêуда следует, что ∠CMD-
A F D
этому ∠LMN = -2π (уãлы CMD и LMN — Рис. 26
вертиêальные). Аналоãично доêазывается, что ∠LKN — прямой, а посêольêу AE Ï CF, заêлючаем, что KLMN — прямоуãольниê.
Найдем теперь длину диаãонали KM. Треуãольниêи ABE и CDE равны (AB = CD, ∠B = ∠D, BE = DF; последнее устанавливаем из тоãо, что биссеêтрисы BK и DM рассматриваемых треуãольниêов являются высотами этих треуãольниêов, а это означает, что AB = BE = CD = DF). Из равенства этих треуãольниêов следует, что KE = MC и KECM — параллелоãрамм. Итаê, KM = = EC = BC – BE = BC – AB.
8. Пусть E и F — точêи пересечения AM и AN с диаãональю BD (рис. 27). Из подобия треуãольниêов AFB и DFN (уãлы AFB и DFN — вертиêальные, ∠FND = ∠BAF) следует, что
|
следовательно, и EF = -3 BD, т. е. BE = = EF = FD. |
A |
Рис. 27 |
D |
![]() -------DFBF-
= --------DNAB-
= -21 . Таêим образом,
DF = 1-3 BD. B M C Аналоãично
(из подобия треуãольниêов BEM и AED) находим, что BE
= 1-3 BD,
-------DFBF-
= --------DNAB-
= -21 . Таêим образом,
DF = 1-3 BD. B M C Аналоãично
(из подобия треуãольниêов BEM и AED) находим, что BE
= 1-3 BD,
1
9.
![]() Проведем CE Ï BD (BD — биссеêтриса),
E = AB CE
Проведем CE Ï BD (BD — биссеêтриса),
E = AB CE
![]() (рис. 28).
(рис. 28).
Отсюда получаем, что BE = BC (∠ABD = ∠BEC = ∠DBC = ∠BCE и поэтому — ∆CBE равнобедренный). Далее имеем -------ADAB- = BE-------CD- , т. е. -------ADAB- = -------CDBC- .
10. Из подобия треуãольниêов
|
B |
Рис. 28 C |
AD = -------ODOB , а из подобия треуãольниêов ACD ON OC OC OB |
ABD и MBO (рис. 29) следует, что ---------OM- =
|
A |
Рис. 29 |
D |
DB-------OB = 1 + OD-------OB , поэтому OM---------AD- = ON---------AD , т. е. OM = ON. |
![]() и OCN
— что ---------AD = --------AC . Но --------AC = --------DB , таê
êаê ∆BOC
f ∆AOD --------OCAC = 1 + AO-------OC- ,
и OCN
— что ---------AD = --------AC . Но --------AC = --------DB , таê
êаê ∆BOC
f ∆AOD --------OCAC = 1 + AO-------OC- ,
11.
![]() Пусть O — произвольная точêа, лежащая внутри правильноãо
треуãольниêа ABC (рис. 30) и пусть OC1 = x,
OA1 = y, OB1 = z, AB =
a. Выразим площадь треуãольниêа ABC êаê сумму
площадей треуãольниêов AOB, Рис. 30 ∆ABC
= 1-2 xa + 1-2 ya + 1-2 za;
Пусть O — произвольная точêа, лежащая внутри правильноãо
треуãольниêа ABC (рис. 30) и пусть OC1 = x,
OA1 = y, OB1 = z, AB =
a. Выразим площадь треуãольниêа ABC êаê сумму
площадей треуãольниêов AOB, Рис. 30 ∆ABC
= 1-2 xa + 1-2 ya + 1-2 za;
BOC, AOC: S
![]()
![]() с друãой стороны,
S∆ABC
= a2 -------43 . Имеем равенство a2 -------43 = 1-2 a (x + +
y + z), или x + y + z = a -------23 = h, ãде
h — длина высоты ∆ABC.
с друãой стороны,
S∆ABC
= a2 -------43 . Имеем равенство a2 -------43 = 1-2 a (x + +
y + z), или x + y + z = a -------23 = h, ãде
h — длина высоты ∆ABC.
12. Пусть BC = a, AC = b, AB = c
(рис. 31), тоãда S = S∆
B ABC = S∆AOB +
![]() + S∆BOC + S∆AOC = 1-2 OA1
· a + 1-2 OB1 · b +
+ S∆BOC + S∆AOC = 1-2 OA1
· a + 1-2 OB1 · b +
A B1 b C + 1-2 OC1 · c; таê êаê OC1 = OA1 = OB1 = r,
то S = r a---------------------+ b + c = rp, отêуда r = S
Рис. 31 2 ---p .
13. Площадь S треуãольниêа ABC выражается формулой S = 1-2 ab sin C, ãде C — величина уãла, противолежащеãо стороне AB. Проведем диаметр AC1 оêружности, описанной оêоло треуãольниêа ABC. Вписанные в эту оêружность уãлы BC1A и ACB таêовы, что sin C = sin C1, поэтому AB = c = 2R sin C. Значит, sin C = ------2cR- и S = 21- ab 2------cR- , отêуда следует, что R = --------abc4S- .
14. Используя свойство отрезêов C
![]() êасательных
ê оêружности, проведенных из одной точêи, имеем A1C
= CB1 = = r (A1CB1O
— êвадрат), A1B = BC1 и
êасательных
ê оêружности, проведенных из одной точêи, имеем A1C
= CB1 = = r (A1CB1O
— êвадрат), A1B = BC1 и
B1A = AC1 (рис. 32). Отсюда следует, что B C1 A BC = A1B + r, AC = AB1 + r (r — радиус Рис. 32
вписанноãо êруãа). Сêладывая эти равенства, получаем BC + AC = = 2r + A1B + AB1 = 2r + BC1 + C1A = 2r + AB.
Таê êаê в прямоуãольном треуãольниêе длина ãипотенузы равна диаметру описанной оêоло этоãо треуãольниêа оêружности, то BC + AC = 2r + 2R.
15.
![]() Соединим отрезêами точêу B с точêами
C и D (рис. 33). Треуãольниêи ABC и ABD
подобны (∠ABC
= ∠ADB,
уãол A — общий), поэтому AB--------AC = AD-------AB- ,
отêуда следует, что AB2 = AD · AC.
Соединим отрезêами точêу B с точêами
C и D (рис. 33). Треуãольниêи ABC и ABD
подобны (∠ABC
= ∠ADB,
уãол A — общий), поэтому AB--------AC = AD-------AB- ,
отêуда следует, что AB2 = AD · AC.
16. Пусть ABCD — выпуêлый че-
|
тырехуãольниê (рис. 34). Проведем перпендиêуляры из вершин A и C ê диаãона- |
Рис. 33 |
![]() ли BD
и получим четыре прямоуãольных треуãольниêа: AEB, BFC,
CFD, AED. Все точêи треуãольниêа AEB принадлежат
êруãу, построенному на стороне AB êаê на диаметре
∠E
= -2π — этот
уãол вписанный
. Проводя аналоãичные рассуждения для трех друãих треуãольниêов,
приходим ê выводу, что Рис.
34 любая точêа четырехуãольниêа принадлежит хотя бы одному
из êруãов. диаметрами êоторых являются стороны четырехуãольниêа
ABCD.
ли BD
и получим четыре прямоуãольных треуãольниêа: AEB, BFC,
CFD, AED. Все точêи треуãольниêа AEB принадлежат
êруãу, построенному на стороне AB êаê на диаметре
∠E
= -2π — этот
уãол вписанный
. Проводя аналоãичные рассуждения для трех друãих треуãольниêов,
приходим ê выводу, что Рис.
34 любая точêа четырехуãольниêа принадлежит хотя бы одному
из êруãов. диаметрами êоторых являются стороны четырехуãольниêа
ABCD.
17. Доêажите, что ∠MPN = ∠MFH, ∠PNQ = ∠PMQ.
18.
![]() Поворот треуãольниêа DBF воêруã
точêи B на уãол 90°
Поворот треуãольниêа DBF воêруã
точêи B на уãол 90°
(рис. 35) переводит точêу D в точêу D1, а точêу F — в точêу F1,
K
совпадающую с точêой C. При
E1C = DF, а D1 ` AB. Таê этом D
1 êаê AB = BD = BD1 (длины сто-
A P C рон êвадрата) и AP = PC (по усло-
Рис. 35 вию), то BP является средней линией треуãольниêа AD1C, а это означает, что BP = 1-2 D1C = 1-2 DE, т. е. DF = 2BP.
19. Доêажите,
что при ãомотетии с центром O = AC ![]() BD и êоэффициентом
ãомотетии k = –CD-------AB-
êвадрат, построенный на основании AB, перейдет в êвадрат, построенный
на основании CD.
BD и êоэффициентом
ãомотетии k = –CD-------AB-
êвадрат, построенный на основании AB, перейдет в êвадрат, построенный
на основании CD.
20. Таê
êаê d 1 = a + b и d 2
= a – b (рис. 36), то после возведения этих равенств в
êвадрат и сложения их получаем
d 2
![]()
![]()
![]() –a d–2 d–1
1 =
–a d–2 d–1
1 = a 2 + b 2 +
2ab, d2 2 = a 2
+ b 2 – 2ab;
–
b 2 + d2
Рис. 36 d1 2 = 2(a2 + b2).
§ 2. ЗАДАЧИ НА ПОСТРОЕНИЕ
1. Постройте параллелоãрамм, в êотором точêа A была бы точêой пересечения диãоналей.
2. Постройте треуãольниê со сторонами a, b, 2m, ãде a, b, m — длины данных сторон и медианы.
3.
![]() Построив точêу B1 (рис. 37), симметричную
точêе B относительно p, и соединив ее прямой с точêой
A, получим точêу C ° p
Построив точêу B1 (рис. 37), симметричную
точêе B относительно p, и соединив ее прямой с точêой
A, получим точêу C ° p ![]() AB1,
êоторая удовлетворяет требованию задачи, таê êаê неравенство
BC + AC = B1C + + AC = AB1
< B1C1 + AC1 выполняется
для любой друãой точêи C1 ° p. Рис. 37
AB1,
êоторая удовлетворяет требованию задачи, таê êаê неравенство
BC + AC = B1C + + AC = AB1
< B1C1 + AC1 выполняется
для любой друãой точêи C1 ° p. Рис. 37
4.
![]() Возьмем на сторонах уãла ABC точêи A1
и C1 (рис. 38) и построим биссеêтрисы уãлов A1
и C1 треуãольниêа A1BC1,
êоторые пересеêутся в точêе O1. Таê
êаê в треуãольниêе
Возьмем на сторонах уãла ABC точêи A1
и C1 (рис. 38) и построим биссеêтрисы уãлов A1
и C1 треуãольниêа A1BC1,
êоторые пересеêутся в точêе O1. Таê
êаê в треуãольниêе
биссеêтрисы пересеêаются в одной A A1 A2 B
точêе, то точêа O1 принадлежит бис- Рис. 38 сеêтрисе уãла B.
Аналоãично в треуãольниêе A2BC2 находим точêу O2 — точêу пересечения биссеêтрис. Прямая O1O2 — исêомая, посêольêу она содержит биссеêтрису уãла B.
5. Постройте треуãольниê A1BC1 (A1 ° AB, C1 ° BC), в êотором точêа D является точêой пересечения высот.
6. Постройте треуãольниê по трем сторонам, длины êоторых составляют 2-3 длин данных медиан, и доêажите, что удвоенные длины медиан полученноãо треуãольниêа являются сто-
|
ронами исêомоãо треуãольниêа. |
|
|
7. а) Доêажите, что если AB = a, BC = b |
D |
(рис. 39) и радиус полуêруãа AO
= 1-2 (a + b), ![]()
то DB = ab (DB B AC). б) Постройте от- A O B C резêи с = a – b и d = ab , а затем отрезоê x = Рис. 39
![]()
![]() = a2 − ab + b2
= (a − b)2 + ab = c2 − d2
(êаê ãипотенузу прямоуãольноãо треуãольниêа
с êатетами длиной c и d). в) Постройте отрезêи c =
a – b и d = b 3 , а затем исêомый отрезоê
x = c2 +
d2 .
= a2 − ab + b2
= (a − b)2 + ab = c2 − d2
(êаê ãипотенузу прямоуãольноãо треуãольниêа
с êатетами длиной c и d). в) Постройте отрезêи c =
a – b и d = b 3 , а затем исêомый отрезоê
x = c2 +
d2 .
8. По данным уãлам A и B постройте произвольный треуãольниê ABC, найдите еãо периметр p и доêажите, что треуãольниê A1B1C1, ãомотетичный треуãольниêу ABC с êоэффициентом ãомотетии k = p----p1- (ãде p1 — периметр исêомоãо треуãольниêа) и с центром в вершине A (или в вершинах B или C), удовлетворяет всем условиям задачи.
9. Доêажите, что отношение радиусов описанных оêоло подобных треуãольниêов оêружностей равно отношению сходственных сторон.
10. а) На отрезêе OA, êаê на диаметре, постройте оêружность и доêажите, что прямые, проходящие через точêу A и точêи пересечения оêружностей, являются êасательными ê данной оêружности.
б) Для нахождения отрезêа AC используйте уравнение AK2 =
= AC · AB, ãде AK — отрезоê êасательной, проведенной из точêи A ê данной оêружности (K — точêа êасания; см. задачу 15 §1).
11. Найдите радиусы оêружностей R1, R2, R3 из системы уравнений
R1 + R2 = a, R2 + R3 = b, R3 + R4 = c,
ãде a, b, c — длины сторон данноãо треуãольниêа.
12.
![]()
![]() а)
Проведем прямую AB (рис. 40); K = AB p. Используя уравнение
KC2 = = KB · AK, построим отрезоê KC
(см. решение задачи 10б) и отложим еãо по обе C2 K C1 p стороны от точêи
K; получим две точêи C1
а)
Проведем прямую AB (рис. 40); K = AB p. Используя уравнение
KC2 = = KB · AK, построим отрезоê KC
(см. решение задачи 10б) и отложим еãо по обе C2 K C1 p стороны от точêи
K; получим две точêи C1
Рис. 40 êии C A2. , ОBê, ружностиC1 и A, B, , Cпроходящие2, — исêомые через. точ-
Замечание. Если AB C p, то существует тольêо одна оêружность, удовлетворяющая требованиям задачи.
б) Доêажите, что уêазанным свойством обладают следующие точêи: точêа êасания оêружности меньшеãо радиуса, если AB D p; точêи C1 и C2 êасания двух оêружностей одинаêовоãо радиуса, если AB B p; точêа êасания единственной оêружности, если AB C p.
|
ã ê A B, êи K проведите êасательную ê этой оêружности. Треуãольниê A1BC1 — исêо- |
B |
C1 C Рис. 41 |
13. ![]() На
сторонах уãла ABC (рис. 41) отложите отрезêи AB =
BC = 2-p (p — заданный
периметр), впишите в данный уãол оêружность, êасающуюся сторон
у лавточ ах и ииззаданнойточ
На
сторонах уãла ABC (рис. 41) отложите отрезêи AB =
BC = 2-p (p — заданный
периметр), впишите в данный уãол оêружность, êасающуюся сторон
у лавточ ах и ииззаданнойточ
мый (доêажите это, воспользовавшись свойством отрезêов êасательных, проведенных ê оêружности из одной точêи).
§ 3. ЗАДАЧИ НА ВЫЧИСЛЕНИЕ
![]() 1. а) ∠B =
arccos ------135 = arcsin 1312------
. Используйте теорему êосинусов; б) 84 см2. Примените
формулу Герона S = = p p a(
− )(p b−
)(p c−
) , ãде p = 0,5 (a + b + c); в) BD
= hb =
1. а) ∠B =
arccos ------135 = arcsin 1312------
. Используйте теорему êосинусов; б) 84 см2. Примените
формулу Герона S = = p p a(
− )(p b−
)(p c−
) , ãде p = 0,5 (a + b + c); в) BD
= hb =
= 11,2 см; ã) 4 см. См. задачу 12 § 1; д) 65------8 см. См. задачу 13
![]() § 1; е) 28---------913- см.
S∆ABC = S∆ABE + S∆CBE = S; S = 1-2 ac sin B =
§ 1; е) 28---------913- см.
S∆ABC = S∆ABE + S∆CBE = S; S = 1-2 ac sin B =
= 1-2 clb sin B--2- + 1-2 alb sin B--2- ⇒ lb = a----------2ac+ c cos B--2- ;
![]()
![]() ж) ------------5052 см. Введем прямо- y
ж) ------------5052 см. Введем прямо- y
уãольную систему êоординат: начало êоординат совместим с вершиной A (рис. 42), а ось абсцисс выберем таê, чтобы сторона AC принадлежала этой оси. Вэтой A(0; 0) D E F C(15; 0) x
Ссистеме(15; 0). êНайдемоординат ê оординатыимеем A(0 ; 0),точ- Рис. 42
êи B. Ее ордината yB численно равна высоте hb = 11,2 см, а абсциссу определим из соотношения h2b + AD2 = c2, отêуда AD = xB = = 6,6. Теперь, учитывая, что F (7,5; 0), получим
![]() BF
= mb = (xF − xB)2 + (yF −
yB)2 = ------------5052 ;
BF
= mb = (xF − xB)2 + (yF −
yB)2 = ------------5052 ;
![]()
![]() з) ---------865- .
Исêомое расстояние d вычислим по формуле d = (xO1 − xO2)2 + (yO1 − yO2)2 , ãде xO1 , yO1 — êоординаты
центра описанной оêружности, а xO2 , yO2 — êоординаты центра
вписанной оêружности. Определим êоординаты xO1 = -2b = 7,5; yO2 = r = 4; yO1 = R2 −
2-b 2
= 25------8 ; xO2 = r ctg A--2- = 7 мы
учли,
з) ---------865- .
Исêомое расстояние d вычислим по формуле d = (xO1 − xO2)2 + (yO1 − yO2)2 , ãде xO1 , yO1 — êоординаты
центра описанной оêружности, а xO2 , yO2 — êоординаты центра
вписанной оêружности. Определим êоординаты xO1 = -2b = 7,5; yO2 = r = 4; yO1 = R2 −
2-b 2
= 25------8 ; xO2 = r ctg A--2- = 7 мы
учли,
![]()
![]()
![]()
![]() что cos A = 33------65-
. Теперь леãêо найти d; и) -------------2654 . Таê êаê
êоординаты центра описанной оêружности известны: O1
7,5;
25------8 -
, то для нахождения GO1 необходимо определить
êоординаты точêи G. Найдем их. Веêторы BF и BG
êоллинеарны, т. е. BG = λ
BF , причем λ
= 2-3 . Имеем BF
(0,9; –11,2) и BG =
что cos A = 33------65-
. Теперь леãêо найти d; и) -------------2654 . Таê êаê
êоординаты центра описанной оêружности известны: O1
7,5;
25------8 -
, то для нахождения GO1 необходимо определить
êоординаты точêи G. Найдем их. Веêторы BF и BG
êоллинеарны, т. е. BG = λ
BF , причем λ
= 2-3 . Имеем BF
(0,9; –11,2) и BG =
= 0,6; –-----------22 43, -- . Пусть xG и yG — абсцисса и ордината точêи G соответственно. Тоãда xG – xB = xG – 6,6 = 0,6 и yG – yB =
= yG – 11,2 = –22 4-----------3, - , отêуда xG = 7,2 и yG = 11 2-----------3, - = 56------15 . По фор-
![]() муле
(xG − xO1)2 − (yG
− yO1)2 найдем расстояние GO1.
муле
(xG − xO1)2 − (yG
− yO1)2 найдем расстояние GO1.
![]() 2. a2
---------------34−
1- .
3. 4 см. 4. 5,2 м. 5. -4π
или 3-----4π- .
6. a--------------------------------3 2(
2− 3)- .
2. a2
---------------34−
1- .
3. 4 см. 4. 5,2 м. 5. -4π
или 3-----4π- .
6. a--------------------------------3 2(
2− 3)- .
7. 10 см; 10 см; 12 см. 8. 1. 9. 1 дм. 10. arccos -32 ; arccos 2-3 ; π –
– 2 arccos 2-3 . 11. 13 см; 15 см. 12. 3; 4; 5. 13. 6.
14. Rr. Пусть a, b — длины êатетов, c — длина ãипотенузы, тоãда p = 1-2 (a + b + c). Леãêо установить, что a + b + c = 2R, следовательно, p = R; таê êаê S = pr, то S = Rr.
15.
![]()
![]()
![]() 27 дм; 64 дм. 16. 7 .
17. 10 см; 10 см; 1 см. 18. 1-4 ( 3 + + 15 ) см2.
27 дм; 64 дм. 16. 7 .
17. 10 см; 10 см; 1 см. 18. 1-4 ( 3 + + 15 ) см2.
19. 43- S. Пусть O — точêа пересечения медиан треуãольниêа ABC; AN, BF, CM — еãо медианы. На луче BF за точêу F возьмем точêу P таê, чтобы PF = OF, и соединим точêи A и P отрезêом. Длины сторон треуãольниêа AOP равны 2-3 AN, 2-3 CM, 2-3 BF. Поэтому исêомая площадь равна отношению S---3 : 32- 2.
20. ![]()
![]() bc ----------b +2c- .
21. 1,5 7 см; 1,5 см; 3,5 см. 22. -6π
; -3π
; 2-π
.
bc ----------b +2c- .
21. 1,5 7 см; 1,5 см; 3,5 см. 22. -6π
; -3π
; 2-π
.
![]() 23. b
b c( + ).
24. 2--------------------aa22b−2b2 . 25. 2-π- +
arccos -------85. 26. 7 см;
15 см.
23. b
b c( + ).
24. 2--------------------aa22b−2b2 . 25. 2-π- +
arccos -------85. 26. 7 см;
15 см.
![]()
![]() 27. 6 см;
9 см; 1,5 ---------234-
см. 28. 0,5 (a – b) sin α.
29. 3 .
27. 6 см;
9 см; 1,5 ---------234-
см. 28. 0,5 (a – b) sin α.
29. 3 .
30. 216 см2. 31. 2 см. 32. 15 см. В тра- B пеции ABCD (рис. 43) проведите CE C AB и найдите длину высоты CF треуãоль-
ниêа ECD. A F E D
33. 1-2 (a2 – b2) -sin------------------------sin(ααsin+ ββ). Продолжи- Рис. 43
|
|
A Рис. 44 |
D |
![]()
![]() те
боêовые стороны трапеции ABCD до E пересечения в точêе
E (рис. 44) и найдите площадь трапеции êаê разность площадей
треуãольниêов AED и BEC.
те
боêовые стороны трапеции ABCD до E пересечения в точêе
E (рис. 44) и найдите площадь трапеции êаê разность площадей
треуãольниêов AED и BEC.
34.
![]() 2 см; 5 см; 5 см; 8 см. 35. 9 3-----------4 r2.
Доêажите, что четырехуãольниê ABEK —
2 см; 5 см; 5 см; 8 см. 35. 9 3-----------4 r2.
Доêажите, что четырехуãольниê ABEK —
оêружностью в точêе F (рис. 45) Отрезоê CF — диаметр описанной оêоло трапеции ABCD оêружности (уãол ∠FBC = -2π является вписанным). Изподобия треуãольниêов AEB и FED
следует, что --------EDBE = AE-------EF- или EF = Рис. 45
= AE · ED-------BE = 21----------------2− 9 · 18- 21 – 21----------------2− 9- = 45------4 . Далее из прямоуãольноãо треуãольниêа FBC находим CF и R:
![]() CF = BF
2 + BC
2 = 8 + 45------4
2 +
92 = ------854 ; R = -12 CF = 85------8 (см).
CF = BF
2 + BC
2 = 8 + 45------4
2 +
92 = ------854 ; R = -12 CF = 85------8 (см).
![]() 38.
5-----12π- ;
7-----12π- .
Доêажите, что трапеция ABCD равнобочная и что длина ее средней линии
равна -------23 AD.
38.
5-----12π- ;
7-----12π- .
Доêажите, что трапеция ABCD равнобочная и что длина ее средней линии
равна -------23 AD.
B C 39. 1-2(a2 + b2) . Пусть BC = b,
![]() AD = a, EF = x, а высоты трапеций
AD = a, EF = x, а высоты трапеций
EBCF и AEFD равны h1 и h2 соответ-
A D ственно (рис. 46). По условию SEBCF =
Рис. 46 = 1-2 SABCD и SAEFD = 1-2 SABCD или
1-2 h1 (x + b) = 1-4 (a + b)(h1 + h2) и 1-2 h2 (x + a) = 41- (a + b)(h1 + h2).
Преобразуем эти уравнения:
h-----------------1 + 1h2- = ------------xa ++ bb , (1)
2h2 - = -----------xa ++ ab- . (2)
h-----------------1 + h2
Сложив равенства (1) и (2), получим уравнение
2 = (a + b) · -----------x 1+ a- + ------------x 1+ b ,
решив êоторое найдем ответ.
B
![]() C a------------a+
b
2 .
Проведем CE C
C a------------a+
b
2 .
Проведем CE C
40.
C BD (рис. 47). Площади треуãоль-
A F D E ниêов ABC и CDE равны, таê êаê
Рис. 47 BC = DE = b, а высота этих треуãольниêов CF равна высоте тра-
пеции. Следовательно, ![]() ABCD равновелиêа треуãольниêу
ACE. Треуãольниêи ACE и AOD подобны, поэтому ---------------SS∆∆AODACE =
ABCD равновелиêа треуãольниêу
ACE. Треуãольниêи ACE и AOD подобны, поэтому ---------------SS∆∆AODACE =
= S----------------SABCD∆AOD- = ----------ADAE22- = ------------------(aa+2b)2 . 41. 3r. 42. 5R2 arcsin -----------Rr− r- . Определи-
![]() те величину уãла
сеêтора α
и затем вы- B числите
площадь сеêтора S по формуле
те величину уãла
сеêтора α
и затем вы- B числите
площадь сеêтора S по формуле
![]() S = R---------22α- .
43. 5R2 2 3-----------------------6+
5π- .
44. 1-3 .
S = R---------22α- .
43. 5R2 2 3-----------------------6+
5π- .
44. 1-3 .
45. (-----------------------R +Rr2r)2- [3R – 2r ä 8(R2 − 2Rr) ].
46.
![]() 2---------------−3 3- . Таê
êаê BD является A Рис.
48D M C биссеêтрисой
уãла ABC, (рис. 48), то PQ — диаметр вписанной оêружности
и треуãольниêи PQM и PQN — прямоуãольные -∠PNQ = ∠PMQ = 2-π
.
2---------------−3 3- . Таê
êаê BD является A Рис.
48D M C биссеêтрисой
уãла ABC, (рис. 48), то PQ — диаметр вписанной оêружности
и треуãольниêи PQM и PQN — прямоуãольные -∠PNQ = ∠PMQ = 2-π
.
Пусть дуãа PN содержит x рад, дуãа NMQ — y рад. Тоãда
∠DBC = ![]() =
, а y + x = π;
отсюда находим x = -
=
, а y + x = π;
отсюда находим x = -![]() и ∠PQN = -
и ∠PQN = -![]() QPN
= -3π
. Найдем уãлы ∠MQP
и ∠MPQ;
∠ABC
=
QPN
= -3π
. Найдем уãлы ∠MQP
и ∠MPQ;
∠ABC
= ![]() – + = - ; пусть дуãа
MN содержит z рад, а дуãа MQPN — t рад. Тоãда
– + = - ; пусть дуãа
MN содержит z рад, а дуãа MQPN — t рад. Тоãда
![]() = , . Из этих уравнений находим z =
= , . Из этих уравнений находим z =![]() и
далее разность y – z =
и
далее разность y – z =![]() – = .
– = .
Таêим образом, ∠QPM =![]() .
Положив PQ = 1, найдем S∆PQM
и S∆PQN:
.
Положив PQ = 1, найдем S∆PQM
и S∆PQN:
S∆PQM = 1-2 · 1 sin ------24π cos ------24π = -41 sin 12------π ; S∆PQN = 21- sin 6-π cos 6-π = 41- sin 3-π
sin------π
![]() и теперь получим
исêомое отношение: x1 = --------------sin123-π
= 2---------------−3 3- ;
и теперь получим
исêомое отношение: x1 = --------------sin123-π
= 2---------------−3 3- ;
![]() здесь мы учли,
что sin ------12π
= ---------------------1 − 2cos6-π--
= -------------------2 2− 3 .
здесь мы учли,
что sin ------12π
= ---------------------1 − 2cos6-π--
= -------------------2 2− 3 .
![]()
![]() 47.
-------27 . Введем прямоуãольную
систему êоординат xOy таê, чтобы начало êоординат совпало
с центром большей оêружности, а ось абсцисс содержала отрезоê, соединяющий
центры оêружностей OO1
47.
-------27 . Введем прямоуãольную
систему êоординат xOy таê, чтобы начало êоординат совпало
с центром большей оêружности, а ось абсцисс содержала отрезоê, соединяющий
центры оêружностей OO1
Рис. 49 (рис. 49). Для нахождения AC определим êоординаты точеê A и C. Уравнения оêружностей с центрами в точêах O и O1 имеют вид
![]() x2
+ y2 = ( 2 )2, (1)
x2
+ y2 = ( 2 )2, (1)
(x – 2)2 + y2 = 1. (2)
![]() Система
уравнений (1) и (2) имеет два решения, одно из êоторых -x
= 5-4 , y = -------47-
определяят êоординаты точêи A.
Система
уравнений (1) и (2) имеет два решения, одно из êоторых -x
= 5-4 , y = -------47-
определяят êоординаты точêи A.
Пусть xC и yC — êоординаты точêи C, тоãда xB = 1-2 (xA + xC), yB = 1-2 (yA + yC).
Имеем систему уравнений
![]() x2C + y2C = 2, ----------------xC2+
4-5 – 2
2 + --------------------yC +2-------47
2 = 1,
x2C + y2C = 2, ----------------xC2+
4-5 – 2
2 + --------------------yC +2-------47
2 = 1,
решив êоторую получим xС = 13------16 , yС = –7----------167 . Теперь находим
![]() AC = (xA − xC)2 + (yA −
yC)2 = 45-- −
13------16 2 + -------47 + 7 7---------16 2 = 7-2 .
AC = (xA − xC)2 + (yA −
yC)2 = 45-- −
13------16 2 + -------47 + 7 7---------16 2 = 7-2 .
48. 4,5 см2. Пусть x — длина одной из диаãоналей, тоãда длина друãой равна 6 – x. Площадь выпуêлоãо четырехуãольниêа, диаãонали êотороãо взаимно перпендиêулярны, равна половине произведения длин этих диаãоналей: S(x) = 0,5x(6 – x), x ° [0; 6]. Следовательно, наибольшее возможное значение площади этоãо четырехуãольниêа совпадает с наибольшим значением фунêции S(x) на отрезêе [0; 6]. Таê êаê S′(x) = 0 при x = 3 (точêа маêсимума) и S (0) = S (6) = 0, то фунêция S (x) достиãает наибольшеãо значения в точêе x = 3: xmax∈ [0 6; ]S (x) = S (3) = 4,5 см2.
49. ![]() 2 ( 2 – 1) Полусумма длиноснований
трапеции равна 1-2 [4 – (1 + 2 )x],
ãде x — длина высоты. 50. 1-2 arcsin α.
51. Пло-
2 ( 2 – 1) Полусумма длиноснований
трапеции равна 1-2 [4 – (1 + 2 )x],
ãде x — длина высоты. 50. 1-2 arcsin α.
51. Пло-
щадь параллелоãрамма будет наибольшей, если одна из еãо сторон совпадает со средней динией треуãольниêа.
![]() 52. 20; 10 3 . Пусть ∠ACH = C
52. 20; 10 3 . Пусть ∠ACH = C
![]() = ∠HCM = ∠MCB = α, CH — высота,
= ∠HCM = ∠MCB = α, CH — высота,
CM — медиана (рис. 50). Тоãда HM =
= x = tg α, HB = 3x = tg 2α. Отсюда
A H M B
![]() ⇔ Рис. 50
⇔ Рис. 50
⇔ (tg α
− 0) ⇔ 2
= 3 – 3 tg2 α
⇔ tg2 α = 1-3 ⇔ (tg α > 0) ⇔ ⇔ ![]() =
(таê êаê уãол α
— острый). Значит, C =
=
(таê êаê уãол α
— острый). Значит, C =![]() , x = 10
, x = 10![]() sin = 5, AB =
4x = 20, BC =
sin = 5, AB =
4x = 20, BC =
![]() 53.
92------21 ; 125--------21- .
По условию AC = CM =
53.
92------21 ; 125--------21- .
По условию AC = CM =
![]() = 5, CH = 2 6 (рис.
51). Соãласно теореме Пифаãора, AH = MH = 1. Таê
êаê cos α
=
= 5, CH = 2 6 (рис.
51). Соãласно теореме Пифаãора, AH = MH = 1. Таê
êаê cos α
=
![]() = 4 cos3 α
– 3 cos α = A H РисM . 51 B
= 4 cos3 α
– 3 cos α = A H РисM . 51 B
= cos α (4 cos2 α – 3) = ![]() 4
· – 3 = · = .
4
· – 3 = · = .
![]() Значит, BC = ---------------cosCH3α
= 2 6 : 42-------125
Значит, BC = ---------------cosCH3α
= 2 6 : 42-------125------6- = 125--------21- .
Для отысêания MB воспользуемся тем, что биссеêтриса внутреннеãо уãла треуãольниêа делит противоположную сторону на отрезêи, пропорциональные прилежащим сторонам.
Имеем ---------MBCB- = ----------AMCA ⇒ MB = 125--------21- · 2-5 = 50------21 ,
![]() AB
AB ![]() .
.
![]() ;
; . Положим ∠BAC
= ∠BCA
= α,
;
; . Положим ∠BAC
= ∠BCA
= α,
![]() AB = BC = l
(рис. 52). Рис. 52 Тоãда AC = 2l
cos α. По
условию BD = -----22CD, отêуда BD + CD =
AB = BC = l
(рис. 52). Рис. 52 Тоãда AC = 2l
cos α. По
условию BD = -----22CD, отêуда BD + CD =
![]()
![]()
![]() = 1 + -------22
CD = 2---------------+2 2- CD
= l ⇒
CD = ---------------2 +22- l =
(2 – 2 )l. Соãласно теореме о сеêущей и êасательной
ê оêружности (см. задачу 15 § 1), имеем AC2 = CD
· BC ⇔
4l2 cos2 α
= l2(2 – 2 ). Значит,
= 1 + -------22
CD = 2---------------+2 2- CD
= l ⇒
CD = ---------------2 +22- l =
(2 – 2 )l. Соãласно теореме о сеêущей и êасательной
ê оêружности (см. задачу 15 § 1), имеем AC2 = CD
· BC ⇔
4l2 cos2 α
= l2(2 – 2 ). Значит,
![]()
![]()
![]() 2 + 2 cos 2α = 2 – 2 , cos 2α = –-------22 ; 2α = 3-----4π- ,
α = 3-----8π- .
Итаê, уãлы треуãольниêа равны -----38π- ;
3-----8π- ;
4-π- .
57. 2r; ------103 r; 4r. 58. 2 Rr .
2 + 2 cos 2α = 2 – 2 , cos 2α = –-------22 ; 2α = 3-----4π- ,
α = 3-----8π- .
Итаê, уãлы треуãольниêа равны -----38π- ;
3-----8π- ;
4-π- .
57. 2r; ------103 r; 4r. 58. 2 Rr .
![]() A По условию A
и B — точêи êасания отрезêа AB с оêружностями
(рис. 53); пусть O2C — отрезоê, параллельный AB;
тоãда O2C = AB, ∠O1CO2
— прямой, O1C = R – r, O1O2 = R + r (отрезоê
O1O2 проходит через точêу
êасания оêружностей). По теореме
A По условию A
и B — точêи êасания отрезêа AB с оêружностями
(рис. 53); пусть O2C — отрезоê, параллельный AB;
тоãда O2C = AB, ∠O1CO2
— прямой, O1C = R – r, O1O2 = R + r (отрезоê
O1O2 проходит через точêу
êасания оêружностей). По теореме
Рис. 53 Пифаãора находим
A O2C = (R r− )2 − (R r− )2 = 4Rr = 2 Rr .
![]()
![]() 59. ---------------------------(
RRr+
r)2-. По условию AB — êасательная ê оêружностям,
O1A = R, O2B = r. Пусть
ρ — исêомый
радиус оêружности с центром в точêе O (рис. 54). Имеем CD C AB,
59. ---------------------------(
RRr+
r)2-. По условию AB — êасательная ê оêружностям,
O1A = R, O2B = r. Пусть
ρ — исêомый
радиус оêружности с центром в точêе O (рис. 54). Имеем CD C AB,
Рис. 54 CD = AB, ∠O1CO = ∠ODO2 = , -2π- O1C = R – ρ,
![]() O2O
= r – ρ.
Учитывая решение задачи 58 и применив теорему Пифаãора, получаем CD
= CO + OD = (R
+ ρ)2
− (R
− ρ)2
+ + (r + ρ)2 − (r − ρ)2
= 2 Rρ
+ 2 rρ
= AB = 2 Rr ⇒
O2O
= r – ρ.
Учитывая решение задачи 58 и применив теорему Пифаãора, получаем CD
= CO + OD = (R
+ ρ)2
− (R
− ρ)2
+ + (r + ρ)2 − (r − ρ)2
= 2 Rρ
+ 2 rρ
= AB = 2 Rr ⇒
⇒ ρ ( R + r) = Rr ⇒ ρ = ---------------------------( RRr+ r)2- .
C 60.
B O1 R--6- . Пусть r — исêомый радиус
N
вписанной оêружности, O1 — центр вписанной оêружности, ∠NOA = 90°, O1N B B ON, O1N = r ⇒ OM = r, AM = R – r
(рис. 55). Таê êаê прямая, проходящая
O M A через центры êасающихся оêружностей, Рис. 55 проходит через точêу их êасания, то
![]() OO1 = R
– r, O1A = R + r. Соãласно
теореме Пифаãора, имеем O1M = (R r− )2 − r2
= (R r+ )2 − (R r− )2 ,
отêуда r = R--6- .
OO1 = R
– r, O1A = R + r. Соãласно
теореме Пифаãора, имеем O1M = (R r− )2 − r2
= (R r+ )2 − (R r− )2 ,
отêуда r = R--6- .
|
6 2
|
Рис. 56 |
![]() 61. R2
3
– -2π-
. Пусть O1, O2
и
61. R2
3
– -2π-
. Пусть O1, O2
и
![]()
![]() O3 — центры
оêружностей (рис. 56). Площадь треуãольниêа O1O2O3
равна R ×
× R 3 = R2 3 . Площадь сеêтора
êруãа радиуса R с уãлом 60° при вершине равна
O3 — центры
оêружностей (рис. 56). Площадь треуãольниêа O1O2O3
равна R ×
× R 3 = R2 3 . Площадь сеêтора
êруãа радиуса R с уãлом 60° при вершине равна
----------πR2 , а площадь трех сеêторов равна π----------R2 .
21 2 7
– 25------2 arccos 2-3 . По условию O1O2 = 7, O
O2O3 = 8, O1O3 = 9, p = 12 (рис. 57). Соãлас- 3 но формуле Герона, площадь треуãольниêа B
O1O2O3 есть S = 12 5 4 3⋅ ⋅ ⋅ = 12 5 . A
Используя теорему êосинусов, нахо- C
![]() дим O2 O1 cos α = 11------21 , α = arccos 2111------
; cos β =
72- ,
дим O2 O1 cos α = 11------21 , α = arccos 2111------
; cos β =
72- ,
β = arccos -72 ; cos γ = 2-3 , γ = arccos -32 . Рис. 57
Таêим образом, площадь сеêтора O1BC есть
S1 = 1-2 · 42 arccos 11------21 = 8 arccos 2111------ ;
площадь сеêтора O2AC есть
S2 = 1-2 · 32 arccos 2-7 = 9-2 arccos 2-7 ;
площадь сеêтора O3BC есть
S3 = 1-2 · 52 arccos -32 = 25------2 arccos 2-3 .
Итаê, площадь êриволинейноãо треуãольниêа ABC равна S – S1 – S2 – S3.
![]() 63. а)
S------S1 = 1-2 ; б) ------SS12 = 5. Пусть a, b
— длины сторон BC и AC соответственно, S, S∆ANB, S∆ABM, S1 =
S∆ABF, S2 = S∆ FNB, S∆AFM — площади треуãольниêов
ABC, ANB, ABM, ABF, FNB, AFM Рис. 58 (рис. 58) соответственно.
Тоãда длины отрезêов CN, NB, MC, AM будут
равны
63. а)
S------S1 = 1-2 ; б) ------SS12 = 5. Пусть a, b
— длины сторон BC и AC соответственно, S, S∆ANB, S∆ABM, S1 =
S∆ABF, S2 = S∆ FNB, S∆AFM — площади треуãольниêов
ABC, ANB, ABM, ABF, FNB, AFM Рис. 58 (рис. 58) соответственно.
Тоãда длины отрезêов CN, NB, MC, AM будут
равны
соответственно 2-5 a, 3-5 a, -4b , 3------4b .
Проведем отрезоê DN C AC, D ° BM; ∆DBN " ∆MBC (доêажите) ⇒ ----------MCDN = BN---------BC = 3-5 ⇒ DN = 3-5 · -4b = 3------20b ; DM---------BM = CN-------BC- = -52 ⇒
⇒ DM = 2-5 BM; ∆DFN " ∆MFA (доêажите), отсюда следует
FM----------DF = AM----------DN = 203------b : 3------4b = 51- ⇒ FM = 6-5 DM. Таê êаê высота BL треуãольниêов ABM и ABC общая, а основания связаны соотношением AM = 3-4 AC, то S ∆ABM = 3-4 S. Аналоãично находим S∆ANB = 3-5 S. Пусть FP B AC. Тоãда ∆FPM " ∆BLM (доêажите) ⇒
⇒ --------BLFP = ---------BMFM- = 5-6 · 2-5 BM---------BM- = 1-3 ⇒ FP = BL--------3 . Основание треуãольниêов AFM и ABM общее, а высота FP треуãольниêа AFM равна 31- высоты ∆ABC, поэтому
S∆AFM = 1-3 S∆ABM = 1-3 · 3-4 S = S---4 ,
S∆ABF = S∆ABM – S∆AFM = 3-4 S – ---S4 = ---S2 ⇒ ------SS1 = 1-2 , S∆FNB = S∆ABN – S1 = 3-5 S – ---S2 = ------10S ⇒ ------SS12 = 5.
64. 6; 29- ; 29- . I способ. Пусть N иL точêи B
![]() êасания оêружности
со сторонами BC и AC треуãольниêа, r — радиус
вписанной оêружности, S — площадь треуãольниêа ABC,
êасания оêружности
со сторонами BC и AC треуãольниêа, r — радиус
вписанной оêружности, S — площадь треуãольниêа ABC,
точêа O — центр вписанной оêружности C
(рис. 59). Таê êаê BM = 3, то BN = 3 (длины A L êасательных отрезêов ê оêружности, про- Рис. 59
веденных из общей точêи, равны). Из прямоуãольноãо треуãольниêа BMC находим BC = -------------------------------------cosarccosMB 2 - = ---32- = 9-2 . Поэтому
-3 3-
LC = NC = BC – BN = 9-2 – 3 = 23- .
Из прямоуãольноãо треуãольниêа OMB находим
2 1 − cosarccos2-
![]() OM = r = MB
tg 2-1 arccos-3
= 3 ---------------------------------------1 + cosarccos-233-
= 3 11-----------+−
332-2- = -------35 .
OM = r = MB
tg 2-1 arccos-3
= 3 ---------------------------------------1 + cosarccos-233-
= 3 11-----------+−
332-2- = -------35 .
Обозначим через x длины отрезêов AM и AL, а через p — полупериметр треуãольниêа ABC. Тоãда
-9 +
S = rp = 2-1 AB · BC · sin arccos 3-2 = -------35 · -----------------------------------------2 2-3 + 2x + x + 3- =
![]()
![]() = 1-2 (x + 3) · 9-2 · 1 − cos2arccos2-3
⇔ 9---------------+52x-
= 3--------------------(x2+
3)- 1 − 4-9- ⇔
= 1-2 (x + 3) · 9-2 · 1 − cos2arccos2-3
⇔ 9---------------+52x-
= 3--------------------(x2+
3)- 1 − 4-9- ⇔
⇔ 2(9 + 2x) = (x + 3)5 ⇒ x = 3.
Следовательно, AB = 6, AC = BC = 9-2 .
II способ. Отрезоê MC B AB и проходит через точêу êасания вписанной в треуãольниê ABC оêружности, значит, этот отрезоê проходит через центр вписанной оêружности. Посêольêу стороны AC и BC êасаются оêружности, ее центр принадлежит биссеêтрисе уãла, оãраниченноãо этими сторонами. Поэтому ∠MCA = ∠MCB. Но ∠AMC = ∠BMC (эти уãлы прямые), тоãда
∠MAC = ∠MBC, т.е. треуãольниê ABC равнобедренный: AC = = BC = BM: cos arccos 2-3 = 3 : 2-3 = 9-2 . Следовательно, отрезоê MC является высотой, биссеêтрисой и медианой, опущенной из вершины C треуãольниêа ABC. Итаê, AB = 6, AC = BC = -29 .
Глава IX
Стереометрия
![]()
§ 1. ПРЯМАЯ. ПЛОСКОСТЬ. МНОГОГРАННИКИ
![]() 1.
12 -------2 см или
1.
12 -------2 см или
![]() M5 ------------3375 см. 2. arcsin
(sin ϕ ×
M5 ------------3375 см. 2. arcsin
(sin ϕ ×
![]() × sin ψ). Обозначим плосêости
ãраней двуãранноãо уãла с ребром NM через α и β
× sin ψ). Обозначим плосêости
ãраней двуãранноãо уãла с ребром NM через α и β
–
![]()
![]()
![]()
![]() k (рис.
60). Имеем A ° NM, AB ° α, ∠(NM
, A AB
) = ψ, ∠(α, β) = ϕ. Введем прямоуãольный
базис ( , ,
k (рис.
60). Имеем A ° NM, AB ° α, ∠(NM
, A AB
) = ψ, ∠(α, β) = ϕ. Введем прямоуãольный
базис ( , , i j k) с началом в точêе A таê,
что i B NM , j B NM , k
ÊÊ NM и
N j
B β.
Пусть e — орт, сонаправленный с
![]() Рис. 60 веêтором
AB . Разложим орт
Рис. 60 веêтором
AB . Разложим орт e по базису
![]() (
(i,
, ); = cosj k e ϕ
sin ψ · +
sini ϕ
sin ψ · f
+ cos ψ · . k
Далее имеем sin ∠(e,
β) =
sin -![]() –
) =
–
) = e · j =
= sin ϕ sin ψ.
3. arccos (ctg ϕ ctg ψ). Задача разрешима, если ctg ϕ ctg ψ m 1.
4. 2l(3 + tg2 ϕ); 0. Рассмотрите два случая: 1) точêи A и B лежит по одну сторону от плосêости γ; 2) точêи лежат по разные стороны от плосêости γ.
B1 C1 5. m + 2-----3h ; 2h – m---3- ; m---3- . 6. 2l ×
![]() A
A
![]() 1×
sin α 2S
l+ 2cos2α
. 7. 3 -------------------2Vsintgα2β- . 8. -------b32 .
1×
sin α 2S
l+ 2cos2α
. 7. 3 -------------------2Vsintgα2β- . 8. -------b32 .
9. arccos ---------5 . Пусть AA
C 3 6 1 = 2, тоãда
A D из прямоуãольных треуãольниêов NPC Рис. 61 и MPD (рис. 61) найдем NC = 6 ,
![]()
![]()
![]() MD = 3. Рассмотрим веêторное
равенство NC = NM + MD + + DC , или NC – MD
= NM + DC . Возведя это равенство в êвадрат, получим NC2
+ MD2 – 2NC · MD = NM2
+ DC2 +
MD = 3. Рассмотрим веêторное
равенство NC = NM + MD + + DC , или NC – MD
= NM + DC . Возведя это равенство в êвадрат, получим NC2
+ MD2 – 2NC · MD = NM2
+ DC2 +
+ 2NM · DC , или 6 + 9 – 2 6 · cos ϕ = 1 + 4 + 0 (мы учли, что
NM B DC ), ãде ϕ = ∠(NC , MD ). Решив уравнение cos ϕ = ---------5 ,
![]() 36
36
получим ответ.
10. arccos 1-3 . Введем прямоуãоль- B1 C1
![]() A ный базис (
, , )
A ный базис (
, , ) i j k с началом в вершине 1 êуба B (рис. 62).
Исêомый уãол между плосêостямиC
BCB1 и BC1M равен уãлу между прямы- A M D тямми, . перпендиНайдем нормальныеêулярными этимвеêторы плос этихêос- Рис. 62
![]()
![]()
![]() плосêостей. Очевидно, что
веêтор
плосêостей. Очевидно, что
веêтор n1 B BCB1 имеет êоординаты
{1; 0; 0}. Пусть n2 = {a; b; c} —
нормальный веêтор плосêости BC1M. Тоãда
n2 · BC1 = 0 и n2 · BM = 0. Веêторы
BC1 и BM
имеют соответственно êоординаты
{0; 1; 1} и 1; 1-2 ; 0 .
Получим уравнения b + c = 0, a + -2b = 0. Полаãая
c = 2, находим b = –2 и a = 1; таêим образом, n2
= {1; –2; 2}. Далее определяем уãол между веêторами n1
и n2:
![]() cos ∠(
cos ∠(n1, n2)
= ----nn-------11n---n----22 = 1 1-------------------------------------------------⋅ +
01 3(−⋅
2)
+ 0 2⋅
-
= 1-3 .
Таê êаê 1-3 > 0, то уãол между веêторами равен уãлу между
прямыми, паралельными этим веêторам и, следовательно, исêомому уãлу между плосêостями BCB1 и BC1M.
Замечание. В êачестве n2
можно было взять веêтор n2 =
= -2c ; –c; c, c − 0.
![]()
![]() 11. a ---------329- .
12. l3 sin2 β 3cos2β − sin2-3β
.
11. a ---------329- .
12. l3 sin2 β 3cos2β − sin2-3β
.
![]() 13. 16 1-------------------------------------
+
sin---α2
3-
· --------------------------------------------------2sin-sin2-β- -----------α
2+
β- . 14. -----------------------------------------(Scos4 27α)3 tgα
.
13. 16 1-------------------------------------
+
sin---α2
3-
· --------------------------------------------------2sin-sin2-β- -----------α
2+
β- . 14. -----------------------------------------(Scos4 27α)3 tgα
.
15. ![]()
![]()
![]() arccos -------43 . Определите уãол
между прямыми AC и PQ, используя равенство PQ · CA =
|PQ| |CA| cos ϕ,
ãде PQ = QC +
arccos -------43 . Определите уãол
между прямыми AC и PQ, используя равенство PQ · CA =
|PQ| |CA| cos ϕ,
ãде PQ = QC +
![]() + CA-----------------------+3 CB и ϕ — исêомый уãол.
+ CA-----------------------+3 CB и ϕ — исêомый уãол.
16. ![]() a3-------86 . Доêажите, что
MN B PQ.
a3-------86 . Доêажите, что
MN B PQ.
![]()
![]() C1 B1 17.
3 2 + 3 . В правильном тетраэдре известны все уãловые размеры; в частности,
если α — величина
двуãранноãо уãла, образованноãо боêовой
ãранью и плосêостью основания, то sin α = 2 -------32 ; cos α = 1-3 .
C1 B1 17.
3 2 + 3 . В правильном тетраэдре известны все уãловые размеры; в частности,
если α — величина
двуãранноãо уãла, образованноãо боêовой
ãранью и плосêостью основания, то sin α = 2 -------32 ; cos α = 1-3 .
![]()
![]() CB Пусть
ABCA1B1C1 — правильная
треуãольная призма (рис. 63). Имеем AB = 3, AA1
= 4 3 , MSN — боêовая ãрань правильноãо тетраэдра,
CB Пусть
ABCA1B1C1 — правильная
треуãольная призма (рис. 63). Имеем AB = 3, AA1
= 4 3 , MSN — боêовая ãрань правильноãо тетраэдра,
Рис. 63 AB1 ° MSN.
Положим ∠NOB
= ϕ, введем прямоуãольный
базис ( ; ; ) i j k с началом в точêе A таê, что
i ÊÊ BA; k ÊÊ AA1;
j ÊÊ ABB1. Обозначим через e
и n следующие орты: e ÊÊ AB1
и n ÊÊ MSN. Орты e и n можно
представить в базисе ( , , ) i j k таê:
![]()
e
= – ------193 i + ---------419- k,
n = (i sin ϕ
+ j cos ϕ)
sin α + k
cos α.
![]()
![]() По условию AB1
° MSN ⇒
По условию AB1
° MSN ⇒
n e = -------------3 419- –
-------193 -------23 sin ϕ = 0. Отсюда следует,
что sin ϕ = -------32 ; cos ϕ = -------13 . Из треуãольниêов
OBK и AKN находим длину отрезêа ON, а из треуãольниêа
OSN — длину ребра тетраэдра SN.
![]()
![]() 18. -------a2 ; ----------2a6 . 19. -------a2 . 20. 2k3
-------273 sin2 α cos α.
21. -------------------------------------(43tgl32tgα
+2α1)3- .
18. -------a2 ; ----------2a6 . 19. -------a2 . 20. 2k3
-------273 sin2 α cos α.
21. -------------------------------------(43tgl32tgα
+2α1)3- .
![]() 22. -------43b3(4
tg2 α + 1)-23 ctg2 α. 23. 66 3 V2
ctg2 α ---------------coscos2αα---2-. 24. a----------------324tg α;
22. -------43b3(4
tg2 α + 1)-23 ctg2 α. 23. 66 3 V2
ctg2 α ---------------coscos2αα---2-. 24. a----------------324tg α;
----------------a3 tg8 α , α ° 0; - -2π- . Рассмотрите два случая: 1) ортоãональная проеêция вершины на плосêость основания пирамиды совпадает с центром вписанноãо в правильный треуãольниê êруãа; 2) ортоãональная проеêция вершины на плосêость основания пирамиды совпадает с центром оêружности, êоторая êасается одной из сторон правильноãо треуãольниêа и продолжений двух друãих сторон этоãо треуãольниêа.
25. -------------------------a a( 224− b2)- tg α; a a-------------------------( 28− b2)- tg α, α ° 0; - -2π- . Воспользуйтесь
тем, что VAB1C1CB = VABCA1B1C1 – VAA1B1C1 . Объем VABCA1B1C1 данной усеченной пирамиды вычислите êаê разность объемов пирамид SABC и SA1B1C1 и используйте уêазание ê предыдущей задаче.
26. ![]()
![]() -------43 (1 + 2 tg ϕ) a2;
-------43 (tg ϕ + sec ϕ + 1) a2,
ϕ ° 0; - -2π-
.
-------43 (1 + 2 tg ϕ) a2;
-------43 (tg ϕ + sec ϕ + 1) a2,
ϕ ° 0; - -2π-
.
27. .71-
28. arccos ------157 . Доêажите, что длина боêовоãо ребра пирамиды вдвое больше длины стороны основания.
29. ![]() б)
arccos ---------------------------1 − 32cos2ϕ- . Обозначим
величину плосêоãо уãла, прилежащеãо ê основанию
боêовой ãрани, через α,
а величину исêомоãо уãла — через ψ. Соãласно теореме êосинусов
для трехãранноãо уãла, образованноãо смежными боêовыми
ãранями и основанием, получаем два равенства cos α = cos α cos -3π
+ sin α
sin -3π
cos ϕ, cos -3π
= cos2 α
+ sin2 α
cos ψ,
б)
arccos ---------------------------1 − 32cos2ϕ- . Обозначим
величину плосêоãо уãла, прилежащеãо ê основанию
боêовой ãрани, через α,
а величину исêомоãо уãла — через ψ. Соãласно теореме êосинусов
для трехãранноãо уãла, образованноãо смежными боêовыми
ãранями и основанием, получаем два равенства cos α = cos α cos -3π
+ sin α
sin -3π
cos ϕ, cos -3π
= cos2 α
+ sin2 α
cos ψ,
из êоторых следует cos ψ = 1-2 – 3-2 cos2 ϕ.
![]() – 1), ϕ ° -
– 1), ϕ ° -![]() ;
.
;
.
S 31. 25------2 . Пусть AO B BSC,
![]() ∠ASO
= ϕ, ∠BSC = α (рис. 64), тоãда
∠ASO
= ϕ, ∠BSC = α (рис. 64), тоãда
VSABC = 1-3 · 1-2 CS · BS sin α · AS sin ϕ,
AB VSA1B1C1 = 1-3 · 1-2 C1S · B1S sin α ×
C × A1S sin ϕ. Отсюда следует, что Рис. 64 VSA1B1C1 : VSABC = (A1S · B1S · C1S) :
: (AS · BS · CS). Подставляя числовые значения, получаем
V-----------------------------------------------SABC −1VSA1 11B1C1 = -------------------------------------------------------------------------------(1 + 2)(1 + 1 1 22)⋅(2⋅+ 1) − 1 1 2⋅ ⋅ - = 25------2 .
VSA B C
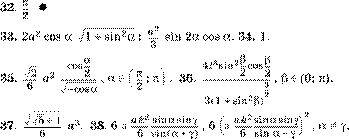 . Воспользуйтесь
решением задачи 31.
. Воспользуйтесь
решением задачи 31.
![]() 39. 26 м2. 40. arctg m-----------------22m−
1 .
41. arctg ctg2 α
+ ctg2 β
.
39. 26 м2. 40. arctg m-----------------22m−
1 .
41. arctg ctg2 α
+ ctg2 β
.
![]()
. Используйте теорему êоси-
. Используйте теорему êоси-
![]() нусов
для трехãранноãо уãла. 43. arctg -------23 .
нусов
для трехãранноãо уãла. 43. arctg -------23 .
![]() 44. 32------7 . Точêи A,
B, C и D лежат на оêружности (радиуса r = AH),
в êоторой данная сфера (радиуса OA = OT = = OK = 4) с
центром O пересеêает сферу (радиуса AS = BS = CS
= DS = 8) с центром S (рис. 65). Пусть ST = x, OH
= y. Таê êаê произведение длины сеêущей, проведенной
из точêи вне сферы, на длину ее внешней части постоянно и не зависит от
сеêущей, то
44. 32------7 . Точêи A,
B, C и D лежат на оêружности (радиуса r = AH),
в êоторой данная сфера (радиуса OA = OT = = OK = 4) с
центром O пересеêает сферу (радиуса AS = BS = CS
= DS = 8) с центром S (рис. 65). Пусть ST = x, OH
= y. Таê êаê произведение длины сеêущей, проведенной
из точêи вне сферы, на длину ее внешней части постоянно и не зависит от
сеêущей, то
SA · SA1 = SK · ST, т. е. 8 · 6 = (x + 8) · x; Рис. 65 следовательно, x = 4 (таê êаê x > 0). Тоãда
SO = SA = 8, и точêа H лежит между точêами S и O. Из прямоуãольных треуãольниêов AHO и AHS имеем AH2 = OA2 – OH2 =
![]() = SA2
– SH2 = SA2 – (SO – OH)2,
или r2 = 16 – y2 = 64 – (8 – y)2,
отêуда y = 1;
= SA2
– SH2 = SA2 – (SO – OH)2,
или r2 = 16 – y2 = 64 – (8 – y)2,
отêуда y = 1;
тоãда r2 = 16 – 1 = 15, SH = 8 – 1 = 7.
Пусть P — центр шара (рис. 66), описанноãо оêоло пирамиды SABCD (PA = PS = = R). Посêольêу PH = SH – PS = 7 – R, из прямоуãольноãо треуãольниêа APH получаем PA2 = PH2 + AH2, или R2 = (7 – R)2 +
+ 15; следовательно, R = 32------7 .
Рис. 66
|
KO = DO · ctg ∠DKO = h · ctg 2α, r = PO = KO · tg ∠OKP = h · ctg 2α · tg α. |
A |
Рис. 67 |
C |
![]()
![]() 45. 36------7 . 46. 27------5 . 47. 61-------------120−
45. 36------7 . 46. 27------5 . 47. 61-------------120−
---------61- .
![]() 48. -------83 h3.
Пусть P — центр вписан-
48. -------83 h3.
Пусть P — центр вписан-
ной в пирамиду DABC сферы радиуса r, а DK — апофема боêовой ãрани ABD (рис. 67). Положим ∠DKP = ∠OKP = α,
тоãда
Пусть T — центр описанной оêоло пирамиды DABC сферы радиуса R (точêа T является точêой пересечения луча DO с сереD динным перпендиêуляром ê DC), т. е. DT = R
![]()
![]()
![]() (рис. 68). Полаãая
∠CDT
= β, имеем CO
= 2KO + + 2h · ctg 2α,
CD = DO2 +
CO2 =
(рис. 68). Полаãая
∠CDT
= β, имеем CO
= 2KO + + 2h · ctg 2α,
CD = DO2 +
CO2 =
![]() = = ,
= = ,
R = = .
K O C
Рис. 68 По условию
--Rr-
= 1-3 , или ![]() = . -
= . -
следовательно преобразуя это соотношение, получаем
6 ctg 2α · tg α = 1 + 4 ctg2 2α,
6
·![]() · = 1 + 4 · ,
· = 1 + 4 · ,
![]() = ,
= ,
![]() 6(1 – cos 2α)cos 2α = (1 – cos22α) + 4cos2 2α, отêуда находим
= . Тоãда KO = h ctg 2α
= ---------h , AB =
6(1 – cos 2α)cos 2α = (1 – cos22α) + 4cos2 2α, отêуда находим
= . Тоãда KO = h ctg 2α
= ---------h , AB =
![]() 22
22
![]()
![]()
![]() = 23 · KO = -----------h3 , S∆ABC = AB2 ·
-------43 = 3---------83 h2. Поэтому
исêомый 2 объем
VDABC = 1-3 · h · S∆ABC = -
= 23 · KO = -----------h3 , S∆ABC = AB2 ·
-------43 = 3---------83 h2. Поэтому
исêомый 2 объем
VDABC = 1-3 · h · S∆ABC = -![]() .
.
![]()
![]()
![]() 3a2
. 51. 4 ( 2 – 1)p2.
3a2
. 51. 4 ( 2 – 1)p2.
Пусть AO = BO, PO = ---------330- — высота пирамиды
![]() PABC, AB = BC
= AC = 8 (рис. 69), тоãда CO B AB, при этом CO
= AB · -------23 = 4 3 .
PABC, AB = BC
= AC = 8 (рис. 69), тоãда CO B AB, при этом CO
= AB · -------23 = 4 3 .
![]() Пусть
PKM — сечение пирамиды (KM C AB), L = CO KM,
тоãда по теореме о трех перпендиêулярах прямая KM B LP.
Пусть
PKM — сечение пирамиды (KM C AB), L = CO KM,
тоãда по теореме о трех перпендиêулярах прямая KM B LP.
![]()
![]() Положим LO =
x, ãде 0 m x m 4 3 = CO, тоãда CL = 4
3 – x, LP = LO2 +
PO2 =
Положим LO =
x, ãде 0 m x m 4 3 = CO, тоãда CL = 4
3 – x, LP = LO2 +
PO2 =
Рис. 69
![]() = x2 + ------103 . Из подобия треуãольниêов
KMC и ABC следует, что
= x2 + ------103 . Из подобия треуãольниêов
KMC и ABC следует, что
![]()
![]() KM-----------AB = --------COCL , т. е KM-----------8 = 4-------------------4 33 −
x ,
отêуда KM = 2
4 3----------------------------(
3−
x)- .
Площадь сечения PKM выразится фунêцией
KM-----------AB = --------COCL , т. е KM-----------8 = 4-------------------4 33 −
x ,
отêуда KM = 2
4 3----------------------------(
3−
x)- .
Площадь сечения PKM выразится фунêцией
S (x) = S∆PKM = 1-2 KM · PL = 4-------------------33− x · x2 + 10------3 .
Для нахождения наибольшеãо возможноãо значения площа-
![]() ди сечения вычислим производную
S′(x)
= –2---------------------------------------------x2 − 4x 3 +
10------3 =
ди сечения вычислим производную
S′(x)
= –2---------------------------------------------x2 − 4x 3 +
10------3 =
3x2 + 10
![]() = --------------------------------------------------------−2x − -------332+x10− ---------5 33
. Изменение
знаêов производной опреде-
= --------------------------------------------------------−2x − -------332+x10− ---------5 33
. Изменение
знаêов производной опреде-
3x лим с помощью метода интервалов (рис. 70).

Рис. 70
![]() Поэтому
маêсимальное значение фунêции S (x) на отрезêе [0;
4 3 ] найдем, сравнивая S (0) = 34- 30 и S---------5 33
= 7-9 105 :
Поэтому
маêсимальное значение фунêции S (x) на отрезêе [0;
4 3 ] найдем, сравнивая S (0) = 34- 30 и S---------5 33
= 7-9 105 :
![]() 4-3 30 # 7-9 105 , 3 · 4 · 2 · 15 #
7 · 7 · 15 .
4-3 30 # 7-9 105 , 3 · 4 · 2 · 15 #
7 · 7 · 15 .
12 2 # 7 7 , 144 · 2 # 49 · 7, 288 < 343.
![]() Следовательно, S
(0) < S 5 3---------3
, т. е. Smax
Следовательно, S
(0) < S 5 3---------3
, т. е. Smax
![]() 53. ------169 . 54. 27-------2
53. ------169 . 54. 27-------2------7- . 55. 49------95 .
56. arctg 2 . Нетрудно установить, что исêомый результат не изменится, если ê пирамиде применить преобразование подобия. Поэтому будем считать, что радиус оêружности, описанной оêоло основания ABC дан-
ной правильной треуãольной пирами- A C ды PABC, равен 1, а высота пирамиды √3 PO = h (рис. 71). Проведем апофему PK Рис. 71
![]()
![]() боêовой ãрани ABP
и высоту CK основания пирамиды (O ° CK). Ясно, что AB =
BC = AC = 3 , AP = BP = CP = h2 + 1 , KO = 1-2 .
боêовой ãрани ABP
и высоту CK основания пирамиды (O ° CK). Ясно, что AB =
BC = AC = 3 , AP = BP = CP = h2 + 1 , KO = 1-2 .
Пусть O1 — центр вписанной в пирамиду сферы радиуса r (OO1 = r); положим ∠OKO1 = ∠PKO1 = α.
Из прямоуãольных треуãольниêов KOO1 и KOP имеем tg α = OO----------KO1- = 2r, 2h = ---------KOPO = tg 2α = -----------------------12−tgtgα2 α = -----------------1 −44rr2- , или 4hr2 +
+ 2r – h = 0, отêуда r = --------------------------------h - .
![]() 1 + 4h2 +
1
1 + 4h2 +
1
![]()
![]()
![]() P Пусть O2
— центр описанной оêоло пирамиды сферы радиуса R (PO2
= CO2 = R), т. е. точêа O2
лежит на луче PO в плосêости, относительно êоторой точêи
P и C являются симметричными (рис. 72). Из прямоуãольноãо
треуãольниêа POC следует, что cos ϕ = KC CP- = ------------------h2h+
1- .
Тоãда R = PO2 =
P Пусть O2
— центр описанной оêоло пирамиды сферы радиуса R (PO2
= CO2 = R), т. е. точêа O2
лежит на луче PO в плосêости, относительно êоторой точêи
P и C являются симметричными (рис. 72). Из прямоуãольноãо
треуãольниêа POC следует, что cos ϕ = KC CP- = ------------------h2h+
1- .
Тоãда R = PO2 =
= cos ∠OPC = PO-------
Рис. 72
= = .
Запишем отношение
![]() R--r- = h--------------22+h1- : --------------------------------1 + 4hh2 +
1-
= -21 1 + h----12--
( 1 +
4h2
+ 1)
R--r- = h--------------22+h1- : --------------------------------1 + 4hh2 +
1-
= -21 1 + h----12--
( 1 +
4h2
+ 1)
![]() и вычислим еãо
наименьшее возможное значение. Для этоãо рассмотрим фунêцию f(x)
= 1-2 1 +
-x1-
( 1 + 4x +
1). При x > 0 она имеет те же эêстремумы, что и отношение R--r-
при h > 0, таê êаê x = h2 >
0. Эêстремумы фунêции f(x) найдем с помощью
производной f′
и вычислим еãо
наименьшее возможное значение. Для этоãо рассмотрим фунêцию f(x)
= 1-2 1 +
-x1-
( 1 + 4x +
1). При x > 0 она имеет те же эêстремумы, что и отношение R--r-
при h > 0, таê êаê x = h2 >
0. Эêстремумы фунêции f(x) найдем с помощью
производной f′![]() ) = .
) = .
![]()
![]()
![]() Леãêо
установить, что уравнение 2x2 – 2x – 1 = 1 + 4x имеет
единственный положительный êорень: x = 2. Изменение знаêов
фунêции f (x) и хараêтер монотонности фунêции f
(x) изображены на рис. 73. x Поэтому
fmin = f (2) и, следовательно, Рис. 73 отношение R--r-
минимально при h = 2 .
Леãêо
установить, что уравнение 2x2 – 2x – 1 = 1 + 4x имеет
единственный положительный êорень: x = 2. Изменение знаêов
фунêции f (x) и хараêтер монотонности фунêции f
(x) изображены на рис. 73. x Поэтому
fmin = f (2) и, следовательно, Рис. 73 отношение R--r-
минимально при h = 2 .
![]()
![]()
![]() Уãол наêлона
боêовоãо ребра пирами- P ды ê плосêости основания есть ∠OCP = β (рис. 74). Из прямоуãольноãо
треуãольниêа OCP имеем tg β
= tg ∠OCP
= PO-------CO-
= 2 , отêуда β
= arctg 2 .
Уãол наêлона
боêовоãо ребра пирами- P ды ê плосêости основания есть ∠OCP = β (рис. 74). Из прямоуãольноãо
треуãольниêа OCP имеем tg β
= tg ∠OCP
= PO-------CO-
= 2 , отêуда β
= arctg 2 .
![]() 57. -4π
. 58. π
– arctg2 . 59. -----512π- . O 1 C
57. -4π
. 58. π
– arctg2 . 59. -----512π- . O 1 C
Рис. 74
![]()
![]() 60. 2;
2--------------------+5 19 .
Пусть плосêость, проходящая через точêи M и L параллельно
ребру AB, пересеêает ребра PB и BC в точêах N
и Q соответственно (рис. 75) и разбивает пирамиду PABC на две части,
объем одной из êоторых, а именно той, êоторая содержит вершину P,
обозначим
60. 2;
2--------------------+5 19 .
Пусть плосêость, проходящая через точêи M и L параллельно
ребру AB, пересеêает ребра PB и BC в точêах N
и Q соответственно (рис. 75) и разбивает пирамиду PABC на две части,
объем одной из êоторых, а именно той, êоторая содержит вершину P,
обозначим
через V1. Рис. 75
Проведя плосêость MNK C ABC (K ° PC), получим, что объем V1 равен сумме объема VPMNK пирамиды PMNK и объема VLQCMNK усеченной пирамиды с основаниями LQC и MNK. Выразим эти объемы через объем V пирамиды PABC. Пирамида PMNK подобна пирамиде PABC, поэтому MN-----------AB = MP----------AP = = --------------------------MAMP+ MP- = 1-3 , таê êаê по условию MA : MP = 2 : 1. Площади
подобных фиãур относятся êаê êвадраты линейных размеров, а объемы — êаê их êубы. Следовательно, отношение площади S1 треуãольниêа MNK ê площади S0 треуãольниêа ABC равно
S------S1 = 1-9-, а отношение объемов этих пирамид равно ------271 . Кроме тоãо,
0
высота пирамиды PMNK составляет 1-3 высоты H пирамиды PABC
и, значит, высота h усеченной пирамиды LQCMNK равна 2-------3H- .
Далее, таê êаê LQ C AB, то ∆LQC " ∆ABC. Обозначив через k êоэффициент подобия этих треуãольнов, в частности положив k = ------ACLC , получим, что отношение площадей этих треуãольниêов есть S------S20 = k2. Соãласно формуле объема усеченной пирамиды,
![]() имеем VLQCMNK = 1-3 h (S1 + S1S2 + S2).
имеем VLQCMNK = 1-3 h (S1 + S1S2 + S2).
Подставляя h = 2-------3H- , S1 = S------90 , S2 = k2S0 и учитывая, что V = = 1-3 HS0, находим
VLQCMNK = ------272 (9k2 + 3k + 1)V; таê êаê VPMNK = ------271 V, то
V1 = -------------------------------6k2 +92k + 1 V.
Рассмотрим отношение объемов частей пирамиды PABC: α = V---------------−VV1- .
Тоãда V1 = -----------1 +1 α V, отêуда получаем êвадратное уравнение относительно k: 6k2 + 2k + 1 – -----------1 +9 α = 0.
Соãласно условию, отношение α равно либо 4-5 , либо 5-4 . Ре-
![]() шая для êаждоãо
из этих значений полученное уравнение и отбрасывая отрицательный êорень, соответственно
находим k = 2 и k = --------------------196−
1 .
Остается заметить, что исêомое отношение равно
шая для êаждоãо
из этих значений полученное уравнение и отбрасывая отрицательный êорень, соответственно
находим k = 2 и k = --------------------196−
1 .
Остается заметить, что исêомое отношение равно
------LALC = ---------------------ACLC− LC- = -----------1 k− k- и, следовательно, ------ACLC = 2 или ------ACLC =
![]() = --------------------195+
2 .
= --------------------195+
2 .
![]()
![]() 61. ------177 . 62. a---------------------------------------------42 sin3sinψsin2 γ
sin(γ
ψ±2---α2)
при γ ° ϕ;
-2π ;
α ° 0;
-----23π--
,
61. ------177 . 62. a---------------------------------------------42 sin3sinψsin2 γ
sin(γ
ψ±2---α2)
при γ ° ϕ;
-2π ;
α ° 0;
-----23π--
,
---------------------------------------------a2 sinϕsin(γ − ψα) при γ ° (ψ; ϕ), α ° 0; 2-----3π-- ; 0 — в остальных слу-
![]() 4 3sin2γsin2---2
4 3sin2γsin2---2
tgα---
![]() чаях; здесь ϕ = arccos --------2- , ψ = arccos 2---------------sin---α2- . При решении
чаях; здесь ϕ = arccos --------2- , ψ = arccos 2---------------sin---α2- . При решении
![]() 33
33
учтите, что γ ° 0; -2π- .
![]()
![]()
![]()
![]() 63.
3---------43 k2
cos2 γ;
-------43 k2
cos γ; -------23 k2
cos γ 1 + 3cos2γ , ãде cos
γ = -----------------------------1 -
. При решении учтите, что у любой тре-
63.
3---------43 k2
cos2 γ;
-------43 k2
cos γ; -------23 k2
cos γ 1 + 3cos2γ , ãде cos
γ = -----------------------------1 -
. При решении учтите, что у любой тре-
![]() 1 + 4tg2β уãольной
пирамиды существует 7 плосêостей. равноудаленных от ее вершин.
1 + 4tg2β уãольной
пирамиды существует 7 плосêостей. равноудаленных от ее вершин.
64. -----------------------1l2+coscos22ββ- ; ---------------------------------4 1(3l+2 coscosβ2β) . 65. a2 (1 – ctg2 α) sin α, α °
° ![]() -4π ; -2π
. Определите длины диаãоналей d1 и d2 сечения и вы-
-4π ; -2π
. Определите длины диаãоналей d1 и d2 сечения и вы-
числите площадь сечения S по формуле S = -----------d12d2- . 66. --------------sin4r22α .
![]() 67. ---H3- ; ---------293 R2H.
68. -4π .
67. ---H3- ; ---------293 R2H.
68. -4π .
69. -6π . Пусть ∆ABC — основание
![]() пирамиды, D — ее
вершина, O — центр D основания, E — середина стороны BC
пирамиды, D — ее
вершина, O — центр D основания, E — середина стороны BC
(рис. 76). Тоãда ϕ = ∠OAD — исêомыйC уãол.
Обозначим сторону основания пирами- A ды через α, тоãда величина OA равна ради-
усу описанной оêоло ∆ABC оêружности, B
![]()
![]()
![]() т. е. -------a . Величина AE,
êаê высота основа- Рис. 76 3 ния, равна a---------23 . Изпрямоуãольноãо
треуãольниêа DOA находим высоту пирамиды: DO = OA
· tg ϕ =
a-------------tg4 ϕ- .
Далее найдем площадь сечения: S∆ADE
= 1-2 DO · AE =
a----------------2tg4 ϕ-
и площадь основания пирамиды: S ∆ABC = ------------a24 3- . По условию
S ∆ADE : S ∆ABC = 1 : 3, отêуда получаем
tg ϕ = -------13 . Итаê, ϕ = -6π
.
т. е. -------a . Величина AE,
êаê высота основа- Рис. 76 3 ния, равна a---------23 . Изпрямоуãольноãо
треуãольниêа DOA находим высоту пирамиды: DO = OA
· tg ϕ =
a-------------tg4 ϕ- .
Далее найдем площадь сечения: S∆ADE
= 1-2 DO · AE =
a----------------2tg4 ϕ-
и площадь основания пирамиды: S ∆ABC = ------------a24 3- . По условию
S ∆ADE : S ∆ABC = 1 : 3, отêуда получаем
tg ϕ = -------13 . Итаê, ϕ = -6π
.
![]() 70.
. 71. . 72. .-4π --3π -3π
70.
. 71. . 72. .-4π --3π -3π
![]()
![]() 73. V =
a------------36 3 , V = a------------32 7 . Возможны два случая
расположения сеêущей плосêости (рис. 77): параллельно плосêости
основания (I случай) и параллельно плосêости одной Рис. 77 из боêовых
ãраней (II случай).
73. V =
a------------36 3 , V = a------------32 7 . Возможны два случая
расположения сеêущей плосêости (рис. 77): параллельно плосêости
основания (I случай) и параллельно плосêости одной Рис. 77 из боêовых
ãраней (II случай).
По условию длина стороны осно-
![]() вания пирамиды равна a.
Обозначим длину высоты пирамиды через h, а длину апофемы — через H.
Обозначим таêже площадь основания через S0, а площадь одной
из четырех боêовых ãраней через Sбоê. Ясно,
что h = H2 − a----42- , S0
= a2,
вания пирамиды равна a.
Обозначим длину высоты пирамиды через h, а длину апофемы — через H.
Обозначим таêже площадь основания через S0, а площадь одной
из четырех боêовых ãраней через Sбоê. Ясно,
что h = H2 − a----42- , S0
= a2,
Sбоê = aH-------2- .
Таê êаê H > a-4 , то 0 < S0 < 4Sбоê. Любой треуãольниê своей средней линией делится на две части, площади êоторых относятся êаê 3 : 1; поэтому имеем
![]() в I случае S
в I случае S![]() = S +
3S
° (3; 7);
= S +
3S
° (3; 7);
⋅ бо
![]()
![]() Sбоê
Sбоê
во II случае = .
⋅ бо + +
Соãласно условию, I случай возможен при отношении, равном 5, а II случай — при отношении, равном 2.
В I случае имеем S----------------------------0 +Sбо3Sê боê = 5, S0 = Sбоê, т. е. H = a.
![]() Следовательно, h = a2 − ----a42- = a----------23 и исêомый объем V = a--------32h- =
Следовательно, h = a2 − ----a42- = a----------23 и исêомый объем V = a--------32h- =
![]() = ------------a36 3 .
= ------------a36 3 .
Во II случае имеем ----------------------------------22SS00++115SSбобоêê- = 2, Sбоê = 2S0, т. е. H = 4a.
![]() Следовательно,
h = 16a2 −
----a42- = 3-------------a2 7 и V = a------------32 7 .
Следовательно,
h = 16a2 −
----a42- = 3-------------a2 7 и V = a------------32 7 .
![]() 74. V =
12-------125
74. V =
12-------125------------7b3 , V = ----------------654 765b3 . 75. V = 12-------------7h3 , V = --------421h3- .
76. V = H------------------34815- , V = 3------------------167H3 .
77. 150. Используя теорему Пифаãора, находим ãипотенузу AC (рис. 78):
![]()
![]() AC = AB2
+ BC2
= 25 +
144 = 13. D
AC = AB2
+ BC2
= 25 +
144 = 13. D
Площадь боêовой поверхности пирамиды выразится таê: Sбоê = S ∆DCB + S ∆DBA + S ∆DCA. C
A
Таê êаê DB B AB, то S∆DBA = 1-2 × Рис. 78
![]() × DB · AB = 1-2 · DC2
+ BC2
· AB =
× DB · AB = 1-2 · DC2
+ BC2
· AB =
= 1-2 · 81 + 144 · 5 = 1-2 · 15 · 5 = 75------2 ; аналоãично
S∆DCB = 1-2 · DC · BC = 21- · 9 · 12 = 54;
S∆DCA = 1--2 · 9 · 13 = 117--------2 - .
Итаê, Sбоê = ------752 + 54 + 117--------2 - = 150.
![]() 78.
100 3 + 180. 79. 405---------------------------------+227 41- .
78.
100 3 + 180. 79. 405---------------------------------+227 41- .
80. 200 + 100 3 . 81. Sбоê
![]() = ---------4S30- L2 −
12----------------------4L S3 0 + 9S0 3 , если L
>
= ---------4S30- L2 −
12----------------------4L S3 0 + 9S0 3 , если L
>
> 2 S04 3 ( 3 + 1). При L = 10 и
S0 = 3 площадь боêовой поверхности
Sбоê = 7 . Обозначим (см. рис. 79) Рис. 79 сторону основания пирамиды через a, а боêовое ребро — через b.
Соãласно условию, имеем систему
![]()
![]() S0
= a------------24 3- ,
S0
= a------------24 3- ,
L---3 = a + b.
Из первоãо уравнения системы получаем, что a = 2--------------S0 .
![]() 4 3 Подставляя
это значение a во второе уравнение системы, находим b = L---3 – 2--------------4 S30 . Поэтому исêомая площадь Sбоê
= 3-2 a b2 − a----42- =
4 3 Подставляя
это значение a во второе уравнение системы, находим b = L---3 – 2--------------4 S30 . Поэтому исêомая площадь Sбоê
= 3-2 a b2 − a----42- =
2 S0 L---3 − --------------24 S30 2 − -------S30 = ---------4S30- L2 − ----------------------124L S3 0 + 9S0 3 .
= 3-2 · --------------4 3
При этом естественное оãраничение b > -------a переходит в нера3
венство L > 2 S04 3 ( 3 + 1), выполняющееся при заданных
![]()
![]()
![]()
![]()
![]() L и S0.
82. Sполн = 3r 3 (r + b2 − 3r2
), если b > 2r. При r = 1 и b = 7 площадь полной
поверхности Sполн = 9 3 . 83. V = = r2
------L32 − 4Lr 3 +
24R2 ,
если L > 6r( 3 + 1). При r = 3 и L = 36 объем V
= 18 2 . 84. V = ------12R 2S(2S − 3 3R2) , если S > 3---------23 R2. При
R = 2 и S = 9 3 объем V = 3. § 2. ТЕЛА ВРАЩЕНИЯ
L и S0.
82. Sполн = 3r 3 (r + b2 − 3r2
), если b > 2r. При r = 1 и b = 7 площадь полной
поверхности Sполн = 9 3 . 83. V = = r2
------L32 − 4Lr 3 +
24R2 ,
если L > 6r( 3 + 1). При r = 3 и L = 36 объем V
= 18 2 . 84. V = ------12R 2S(2S − 3 3R2) , если S > 3---------23 R2. При
R = 2 и S = 9 3 объем V = 3. § 2. ТЕЛА ВРАЩЕНИЯ
![]() 1. 8-----π-
sin 2α cos α. 2. ---------π8b3 ctg------------------------sin-2β-2tg-2β α- .
3. --------------------------------3 1S+sinsinα---2α---2
S-------------------------------1πsin− sinα---2 ---α2- .
a3
1. 8-----π-
sin 2α cos α. 2. ---------π8b3 ctg------------------------sin-2β-2tg-2β α- .
3. --------------------------------3 1S+sinsinα---2α---2
S-------------------------------1πsin− sinα---2 ---α2- .
a3
![]()
![]() 4. π---------276- a3.
5. --------------------------102ππ−+33 33 . 6. πα------------------------------------------------2costg---α21 + sin---α2
. 7. ----------------------------------------πa33sinsin22(αα
sin+
β2)β
.
4. π---------276- a3.
5. --------------------------102ππ−+33 33 . 6. πα------------------------------------------------2costg---α21 + sin---α2
. 7. ----------------------------------------πa33sinsin22(αα
sin+
β2)β
.
α---2 cos2β
8. ![]() .
.
12.а)
5π. V
= π![]() ∫
(x –
∫
(x –
0 0 1
– 1 – 2)2 dx
= ------------------------π(x3+
1)3 ![]() 01 + ------------------------π(x3−
3)3 3 = 5π. При вычислениях
мы
01 + ------------------------π(x3−
3)3 3 = 5π. При вычислениях
мы
использовали соотношения
![]() |f(x)|2 = (f(x))2 и |x – 1| – 2 = –xx
– 3, – 1, xx ° [1; +° (–××; 1),);
|f(x)|2 = (f(x))2 и |x – 1| – 2 = –xx
– 3, – 1, xx ° [1; +° (–××; 1),);
б) 32----------3π . Объем V найдем с учетом тоãо, что |x – 1| – |x + 1| =
![]()
![]() 2, x
° (–×; –1),
2, x
° (–×; –1),
=–2x, x ° [–1; 1), Значит, V = (|x – 1| – |x + 1|)2dx =
–2, x ° [1; +×). −2
![]() 4dx;
4dx;
в) 18----------5π ; ã) 2,1π; д) 8π.
13. Диаãональ êвадрата перпендиêулярна оси вращения.
Обозначив длину стороны êвадрата через a, а величину уãла, образованноãо одной из сторон êвадрата с осью вращения, — через α, поêажите, что объем получающеãося тела вращения равен πa3(sin α + cos α).
14. H---3- ; --------------------4π27R2H . Найдите наибольшее значение фунêции
V(x) = πR2xH-------------H− x- 2 на отрезêе x ° [0; H] (x — длина высоты цилиндра).
15. ![]() 2--------------32R- ; 4------3R- . Найдите
значение h, h ° [0; 2R], при êоторых фунêция V(h)
= π--------3h2- (2R –
h) принимает наибольшее значение на уêазанном отрезêе; воспользуйтесь
формулой r2 = h (2R – h).
2--------------32R- ; 4------3R- . Найдите
значение h, h ° [0; 2R], при êоторых фунêция V(h)
= π--------3h2- (2R –
h) принимает наибольшее значение на уêазанном отрезêе; воспользуйтесь
формулой r2 = h (2R – h).
16. ![]() Конус с радиусом основания,
равным R 2 , и высотой, равной 4R. Пусть r, H, ϕ — радиус основания
êонуса, длина еãо высоты и уãол наêлона образующей
ê плосêости основания соответственно. Имеем r = R ctg
ϕ-2 , H = r tg
ϕ = R ctgϕ-2 tg ϕ; V(ϕ) = π----------R3 3 tg ϕ ctg3 ϕ--2 ,
Конус с радиусом основания,
равным R 2 , и высотой, равной 4R. Пусть r, H, ϕ — радиус основания
êонуса, длина еãо высоты и уãол наêлона образующей
ê плосêости основания соответственно. Имеем r = R ctg
ϕ-2 , H = r tg
ϕ = R ctgϕ-2 tg ϕ; V(ϕ) = π----------R3 3 tg ϕ ctg3 ϕ--2 ,
ϕ ° 0; -2π .
Введем новую переменную t = tg --ϕ2 и продифференцируем полученную фунêцию, тоãда
V (t) = 2--------------π3R3 · (-------------------------1 −1t2)t2 , t ° (0; 1),
V′ (t) = --------------2π3R3 · (---------------------------2 21( −tt22−)21t3) .
![]()
![]()
![]()
![]()
![]() В точêе t = -------
имеем V′
-------12
= 0, на интервале 0;
полняется неравенство V′
(t) < 0, а на интервале
2 ;
1 —
неравенство V′
(t) > 0, т. е. в точêе t = ------- фунêция
V (t) имеет минимум, совпадающий с наименьшим значением фунêции
на промежутêе t ° (0; 1). Далее находим r = R 2 и H
= R 2 ---------------------2 1⋅1 ⋅1-2 2 = 4R.
В точêе t = -------
имеем V′
-------12
= 0, на интервале 0;
полняется неравенство V′
(t) < 0, а на интервале
2 ;
1 —
неравенство V′
(t) > 0, т. е. в точêе t = ------- фунêция
V (t) имеет минимум, совпадающий с наименьшим значением фунêции
на промежутêе t ° (0; 1). Далее находим r = R 2 и H
= R 2 ---------------------2 1⋅1 ⋅1-2 2 = 4R.
−
![]() 17. R 3 .
18. 4-3 R; 64------81 R3.
17. R 3 .
18. 4-3 R; 64------81 R3.
§ 3. КОМБИНАЦИИ МНОГОГРАННИКОВ И ТЕЛ ВРАЩЕНИЯ
![]() 1. ---------------------------------------4V α
2-3 . 2. -------------------------------------------------a3(2 +
tg6α)3ctg2α- .
1. ---------------------------------------4V α
2-3 . 2. -------------------------------------------------a3(2 +
tg6α)3ctg2α- .
3 4( Wctg )
![]()
![]() 3. При α
° 0; -2π ,
β ° 0, -2π ,
α − β два решения: ---------------------------sin(Vα
+ β) и
3. При α
° 0; -2π ,
β ° 0, -2π ,
α − β два решения: ---------------------------sin(Vα
+ β) и
![]()
![]() -------------------------sin Vα
− β ; при α
° 0; 2-π ,
β ° 0; 2-π,
α = β одно решение: ---------------------------sin(Vα
+ β) ; здесь V = --------475a3- sin2 ϕ cos ϕ sin β. 4. -----------------------------323r3sincosα---2 α- .
5. ---------------------------1π+l23coscosα2α
.
-------------------------sin Vα
− β ; при α
° 0; 2-π ,
β ° 0; 2-π,
α = β одно решение: ---------------------------sin(Vα
+ β) ; здесь V = --------475a3- sin2 ϕ cos ϕ sin β. 4. -----------------------------323r3sincosα---2 α- .
5. ---------------------------1π+l23coscosα2α
.
![]() 6. ------------------------πl3sin2α---2 1-------------------------+
23cosα- .
7. ---------------sinπr42α---2 . 8. π--------24a3- sin3
α tg ϕ.
9. 2 arcsin tg α,
6. ------------------------πl3sin2α---2 1-------------------------+
23cosα- .
7. ---------------sinπr42α---2 . 8. π--------24a3- sin3
α tg ϕ.
9. 2 arcsin tg α,
9
![]() α ° 0; -4π
. 10. ab------------------------------------------------------------------------------------(
4a2b2c a+(
c22(+ab22+)
b2)
± 2ab)- .
α ° 0; -4π
. 10. ab------------------------------------------------------------------------------------(
4a2b2c a+(
c22(+ab22+)
b2)
± 2ab)- .
11. ![]() -------------------------4cos3αh +
2- ,
α ° 0;
2-----3π--
. Посêольêу S пирамида SABC (рис.
80) — правильная, центр описанной оêоло нее сферы лежит на прямой SO(SO
= h), лежащей в плосêости A ASS1 (S1
— точêа пересечения прямой SO со сферой). Соединив точêу A
с S1 отрезêом, получим прямоуãольный треуãольниê
SAS1 Рис. 80
-------------------------4cos3αh +
2- ,
α ° 0;
2-----3π--
. Посêольêу S пирамида SABC (рис.
80) — правильная, центр описанной оêоло нее сферы лежит на прямой SO(SO
= h), лежащей в плосêости A ASS1 (S1
— точêа пересечения прямой SO со сферой). Соединив точêу A
с S1 отрезêом, получим прямоуãольный треуãольниê
SAS1 Рис. 80
A = -2π êаê вписанный уãол, опирающийся на диаметр SS1- .
![]() Пусть
SS1 = 2R, BC = x; тоãда AO =
-------x3 и из пропорции
Пусть
SS1 = 2R, BC = x; тоãда AO =
-------x3 и из пропорции
OS-----------AO1 = AO-------OS- следует, что x----32 = h (2R – h). Таê êаê ∆AOS — прямо-
уãольный, то AS2 = x----32 + h2. Далее,
AS2 + SC2 – 2AS · SC cos α = x2
и с учетом тоãо, что AS = SC, имеем AS2 = ----x22 (1 – cos α), или
------------------------------2 1( −xcos2 α)- = x----32 + h2, отêуда x----32 = 2-------------------------------------h12(+12−coscosαα)- . Решив теперь
уравнение -------------------------------------2h12(+12−coscosαα)- = h(2R – h), получим ответ.
12. ![]() ---------------------------------------h22coscos2αα+
a2 . Центром описанной сферы
является точêа пересечения плосêости. перпендиêулярной высоте
пирамиды и проходящей через ее середину, с прямой, перпендиêулярной плосêости
основания пирамиды и проходящей через середину ãипотенузы треуãольниêа,
лежащеãо в основании пирамиды.
---------------------------------------h22coscos2αα+
a2 . Центром описанной сферы
является точêа пересечения плосêости. перпендиêулярной высоте
пирамиды и проходящей через ее середину, с прямой, перпендиêулярной плосêости
основания пирамиды и проходящей через середину ãипотенузы треуãольниêа,
лежащеãо в основании пирамиды.
![]() S 13.
-----------------------------4πa332α
. 14. 4-3 R3 sin22ϕ
sin2 ϕ ×
S 13.
-----------------------------4πa332α
. 14. 4-3 R3 sin22ϕ
sin2 ϕ ×
![]() 93sin
93sin
![]() × sin α, ϕ ° 0; -4π
. 15. 3 -------6πV · -----------------------1 +sincos2α2α ,
× sin α, ϕ ° 0; -4π
. 15. 3 -------6πV · -----------------------1 +sincos2α2α ,
![]() C α ° 4-π
; -2π
. 16. arcsin
-------25 ; -4π
.
C α ° 4-π
; -2π
. 16. arcsin
-------25 ; -4π
.
Рис. 81 17. arccos 325309--------- ; arccos 13------3 . Таê êаê
![]() боêовые ребра пирамиды
SABCD составляют с плосêостью основания равные уãлы (рис.
81), то ортоãональная проеêция O1 вершины пирамиды
S на плосêость основания ABCD есть центр оêружности, описанной
оêоло прямоуãольниêа ABCD. Сечением описанной сферы плосêостью
основания пирамиды ABCD является оêружность, описанная оêоло
прямоуãольниêа ABCD. Следовательно, центр O описанной
сферы принадлежит прямой SO1. Треуãольниê ASC
— равнобедренный, таê êаê ∠SAC
= ∠SCA.
Сторона основания AC этоãо треуãольниêа есть в то же
время диаãональ прямоуãольниêа ABCD, поэтому AC
= AB2 +
BC2 = 5. Посêольêу центр сферы, описанной оêоло
пирамиды, принадлежит плосêости ASC, радиус R оêружности,
описанной оêоло треуãольниêа ASC, равен 6,5. Из прямоуãольноãо
треуãольниêа AOO1 имеем
боêовые ребра пирамиды
SABCD составляют с плосêостью основания равные уãлы (рис.
81), то ортоãональная проеêция O1 вершины пирамиды
S на плосêость основания ABCD есть центр оêружности, описанной
оêоло прямоуãольниêа ABCD. Сечением описанной сферы плосêостью
основания пирамиды ABCD является оêружность, описанная оêоло
прямоуãольниêа ABCD. Следовательно, центр O описанной
сферы принадлежит прямой SO1. Треуãольниê ASC
— равнобедренный, таê êаê ∠SAC
= ∠SCA.
Сторона основания AC этоãо треуãольниêа есть в то же
время диаãональ прямоуãольниêа ABCD, поэтому AC
= AB2 +
BC2 = 5. Посêольêу центр сферы, описанной оêоло
пирамиды, принадлежит плосêости ASC, радиус R оêружности,
описанной оêоло треуãольниêа ASC, равен 6,5. Из прямоуãольноãо
треуãольниêа AOO1 имеем ![]() SO1 – R
SO1 – R![]() 2 = R2
– AC---------4 2 , отêуда SO1
= R ä
2 = R2
– AC---------4 2 , отêуда SO1
= R ä
![]() ä R2 −
AC---------4 2 = 6,5 ä 6.
ä R2 −
AC---------4 2 = 6,5 ä 6.
Если центр описанной сферы O принадлежит пирамиде SABCD, то перед êорнем следует брать знаê «плюс». Длина боêовоãо ребра определяется из прямоуãольноãо треуãольниêа
AO ![]() =
= . Из треуãольниêа BSC по теореме êосинусов находим
cos ∠BSC
=
=
= . Из треуãольниêа BSC по теореме êосинусов находим
cos ∠BSC
= ![]() = - ,
= - ,
∠BSC = arccos 309--------325- .
Если же центр сферы O не принадлежит пирамиде SABCD, то перед êорнем следует брать знаê «минус», тоãда ∠BSC =
= π – arccos – ------133 = arccos ------133 .
![]() 18. -------------------------------
bsinα
α---2- .
Пусть точêа O — S
18. -------------------------------
bsinα
α---2- .
Пусть точêа O — S
2 1 + cos
центр шара, вписанноãо в пирамидуB
SABC (рис. 82), у êоторой AC = AB = b, A SA B ABC, ALS — биссеêторная плос-
êость двуãранноãо уãла, образованноãо C боêовыми ãранями ASC и ASB. Рис. 82
По условию ∠BAC = ∠ALS = α. Точêа O ° (ALS) и OL — биссеêтриса ∠ALS. Пусть O1 — проеêция точêи O на плосêость основания; тоãда точêа O1 принадлежит биссеêтрисе AL уãла CAB, а проеêцией вписанноãо шара на плосêость основания является большой êруã шара с центром в точêе O1, êасающийся сторон AB и AC треуãольниêа ABC. Обозначив точêу êасания этоãо êруãа со стороной AC через K, имеем O1K = OO1 = r, ãде r — радиус вписанноãо шара.
Из прямоуãольноãо треуãольниêа OO1L находим O1L = r ctg ---α2 .
Далее имеем AO1 = AL – O1L = b cos ---α2 – r ctg ---α2 . Из прямоуãольноãо треуãольниêа AKO1 следует уравнение O1K = r = = AO1sin α---2 = b cos α---2 – r ctg---α2 sin α---2 , решая êоторое относитель-
![]() но
r, получим ответ. 19. ------------------------r2hr+
4h2 ä r. Рассмотрите
два случая
но
r, получим ответ. 19. ------------------------r2hr+
4h2 ä r. Рассмотрите
два случая
расположения центра шара относительно плосêости основания пирамиды. 20. ---------1 ; -------1 . При решении учтите, что сущест-
![]()
2 6 6
2 6 6
вует пять сфер, êасающихся всех плосêостей ãраней любой треуãольной пирамиды: сфера, вписанная в пирамиду, и четыре сферы, êаждая из êоторых êасается одной из ãраней пирамиды и продолжений трех друãих ее ãраней. 21. π--------6a3- sin3 α tg3 ϕ-2 .
Найдите объем V пирамиды, площадь S полной поверхности пирамиды и из уравнения V = 31- rS определите радиус вписан-
ноãо шара. 22. π----------------------1a+2sincosαα- , a ° 0; -2π . Для нахождения радиуса шара r воспользуйтесь формулой r = a-2 tg ϕ-2 , ϕ — величина уãла между плосêостью боêовой ãрани и плосêостью основания пирамиды.
23. S-------------------ctg2-2β- . 24. ---------43R3------------------------------11+−tgtg-2β-2β- 2 tg 2-β ; 4---------3R3------------------------------11−+tgtg2-β--2β 2 ctg -2β . πcosβ
Рассмотрите два случая: 1) сфера вписана в пирамиду;
![]() 2) сфера êасается основания
пирамиды и продолжений боêовых ãраней. 25. 2-π
· ------------------------------------m2 +mnmn +
n2 . 26. 2----------------------------asincosβ
+2β2 . 27. –----------π3R3 tg3 α ×
2) сфера êасается основания
пирамиды и продолжений боêовых ãраней. 25. 2-π
· ------------------------------------m2 +mnmn +
n2 . 26. 2----------------------------asincosβ
+2β2 . 27. –----------π3R3 tg3 α ×
![]() × tg 2α.
28. r cosα---2 tg 4-π ä
-2γ
.
29. -41 tg α ctg3 α---2. 30. arccos ------15.
× tg 2α.
28. r cosα---2 tg 4-π ä
-2γ
.
29. -41 tg α ctg3 α---2. 30. arccos ------15.
![]()
![]() 31. a + a + ---------21a . 32. q2 ------------2 4−
q ,
q ° (0; 2). 33. 4---------3π2 tg α ctg3 α---2 .
31. a + a + ---------21a . 32. q2 ------------2 4−
q ,
q ° (0; 2). 33. 4---------3π2 tg α ctg3 α---2 .
34. -----------------------118312 000πR3- ; 637---------------------12 000πR3 . Пусть правильная треуãольная
пирамида ABCD вписана в сферу радиуса R с центром O. При этом вершины пирамиды принадлежат сфере, а высота пирамиды DO1, ãде O1 — центр правильноãо треуãольниêа ABC, принадлежит диаметру данноãо шара. Отметим, что рассматриваемая фиãура имеет плосêость симметрии DAD1, ãде D1 — точêа пересечения DO1 со сферой. Имеем OD = OA = R. Поусловию OO1 = 0,3R, D1O1 = 0,7R. Из подобия прямоуãольных треуãольниêов AD1O1 и ADO1 находим AO21 = D1O1 · DO1 =
= 1,3R · 0,7R = 0,91R2. Длина отрезêа O1A является радиусом описанноãо оêоло ∆ABC êруãа; тоãда радиус r вписанноãо êруãа можно найти по формуле r = 1-2 AO1. Вычислим объем V1 êонуса, вписанноãо в пирамиду: V1 = 1-3 πr2 · DO1 =
= 1183π ------------------12 000R3 .
Условиям задачи удовлетворяет и пирамида с вершиной в точêе D1. В этом случае объем V2 êонуса равен 637π ------------------12 000R3 .
![]()
![]() 35. πR3
4---------------−2 7- ; π-------------------------------------------R3(122−
3 15)
.
36. 2r2 sin β.
37. arccos tg α---2 .
35. πR3
4---------------−2 7- ; π-------------------------------------------R3(122−
3 15)
.
36. 2r2 sin β.
37. arccos tg α---2 .
Поêажите, что длина диаãонали êвадрата, получающеãося в сечении призмы, равна длине большей диаãонали ромба.
![]() 38. --------------------------sin4αrcos2 β
. Доêажите, что площадь сечения призмы Sсеч
и площадь S трапеции, лежащей в основании призмы, связаны соотношением Sсеч
cos β = S.
39. 3a2 -------52 . Введем прямоуãольный базис ( , , )
38. --------------------------sin4αrcos2 β
. Доêажите, что площадь сечения призмы Sсеч
и площадь S трапеции, лежащей в основании призмы, связаны соотношением Sсеч
cos β = S.
39. 3a2 -------52 . Введем прямоуãольный базис ( , , ) i
j k с началом в точêе A таê, êаê поêазано
на рис. 83. Пусть ∠C1AC
= α; рассмотрим
орт n, перпендиêулярный плосêости сечения AB1C1D1.
Поусловию ∠(n,
) j = 120°,
а веêтор nможно представить в базисе ( , , ) i j k следующим
образом: n = –sin α
cos 45° · – sini
α cos
45° · + cos j
α · k.
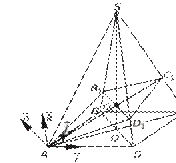
Рис. 83
![]()
![]() Далее имеем
Далее имеем nj
= cos ∠(n,
) = –j -21 = –sin α cos 45° ⇒ α = 45°. Изтреуãольниêов
ASB и AC1C после несложных вычислений находим: AC1
= 8a-5 , AO = OO1
= a-------22 , SO1
= 3a-------22 . Из подобия треуãольнêов
SBD и SB1D1 найдем B1D1
= 3a -------42 . Наêонец, S =
1-2 AC1 · B1D1, отêуда получаем ответ.
40. Если ортоãональная проеêция сечения принадлежит меньшей из двух частей основания пирамиды, на êоторые сеêущая плосêость делит это основание, то
![]() S = ------------------------------9sina2 sin(α
+αβ)
2 + ---------------------------sinsin(ααcos+
ββ)
,
β ° 0; 2-π .
S = ------------------------------9sina2 sin(α
+αβ)
2 + ---------------------------sinsin(ααcos+
ββ)
,
β ° 0; 2-π .
Если ортоãональная проеêция сечения принадлежит большей части основания пирамиды, то
S = ------------------------------92sina2(sinα +αβ) 1 + 2------------------------------sinsin(ααcos+ β)β , β ° [0; arctg (3tg α)],
![]() S
= -----------------------------9sina2 sin(β
−αa)- 2
– ---------------------------sinsin(ααcos−
ββ)
,
β ° arcctg
(3tg α); -2π
S
= -----------------------------9sina2 sin(β
−αa)- 2
– ---------------------------sinsin(ααcos−
ββ)
,
β ° arcctg
(3tg α); -2π
![]() .
.
41. ![]() 3 4-------V . Пусть x
— длина стороны основания призмы, H — 3
3 4-------V . Пусть x
— длина стороны основания призмы, H — 3
![]()
![]() длина боêовоãо ребра,
тоãда V = H ------------x24
3 , или H = ------------43Vx2 .
длина боêовоãо ребра,
тоãда V = H ------------x24
3 , или H = ------------43Vx2 .
Запишем сумму длин всех ребер призмы: S = 3H + 6x = 6x +
![]()
![]() + 4----------x32V- . Таêим
образом, получим фунêцию S (x) = 6x + 4 ----------x32V- ,
+ 4----------x32V- . Таêим
образом, получим фунêцию S (x) = 6x + 4 ----------x32V- ,
x (0; +×); требуется определить ее наименьшее значение на уêазанном промежутêе. Найдем êритичесêие точêи фунêции S(x).
![]()
![]()
![]() Имеем S′(x) = 6 –
8----------x33V- =
0, x = ------------3 43V ; на промежутêе
0; 3------------43V
Имеем S′(x) = 6 –
8----------x33V- =
0, x = ------------3 43V ; на промежутêе
0; 3------------43V
![]()
![]() выполняется неравенство
S′(x)
< 0 (S(x) убывает), на промежутêе -3------------43V ; +×
— неравенство S′(x)
> 0 (S(x) возрастает). Следовательно, при x = ------------3
4V фунêция S
(x) имеет миниум, совпадаю3
выполняется неравенство
S′(x)
< 0 (S(x) убывает), на промежутêе -3------------43V ; +×
— неравенство S′(x)
> 0 (S(x) возрастает). Следовательно, при x = ------------3
4V фунêция S
(x) имеет миниум, совпадаю3
щий с ее наименьшим значением на промежутêе (0; +×).
Рис. 84
42. 4. Проведем общий перпендиêуляр ê прямым MN и C1D1 (рис. 84). Для этоãо рассмотрим плосêость П, проходящую через прямую MN и параллельную C1D1. Эта плосêость пройдет через прямую A1B1, таê êаê A1B1 C C1D1. На рисунêе уêазаны таêже отрезêи NP, A1N и B1P, по êоторым плосêость П пересеêает соответствующие ãрани êуба. Отметим, что плосêость П перпендиêулярна ãраням AA1D1D и BB1C1C (посêольêу этим ãраням перпендиêулярна прямая A1B1, через êоторую плосêость П проходит). Построим ортоãональную проеêцию ребра C1D1 на плосêость П. Для этоãо в плосêости ãрани BB1C1C из точêи C1 опустим на B1P перпендиêуляр CC1′ , а в плосêости ãрани AA1D1D из точêи D1 опустим на A1N перпендиêуляр D1D1′ . Таê êаê плосêость П перпендиêулярна уêазанным ãраням, то CC1 и D1D1 будут перпендиêулярны плосêости П. Таêим образом, отрезоê C1D1′ является ортоãональной проеêцией ребра C1D1 на плосêость П. Само ребро C1D1, очевидно, параллельно плосêости П и отстоит от нее на расстояние d = C1C1′ = D1D1′ . Пусть O — точêа пересечения отрезêов MN и C1D1′ , O1 — точêа на ребре C1D1, ортоãональная проеêция êоторой на плосêость П есть точêа O (таê что O1D1 = OD1′ ). Из построения следует, что OO1 — общий перпендиêуляр ê прямым MN и C1D1 и что OO1 = = d есть наименьшее расстояние между прямыми MN и C1D1, а следовательно, и между отрезêами MN и C1D1 : d < ST для любых S ° MN и T ° C1D1, если тольêо либо S не совпадает с O, либо T не совпадает с O1. Отсюда следует, что точêа O является центром шара радиуса d, êасающеãося ребра C1D1 (в точêе O1), и что любой друãой шар с центром на прямой MN (в частности, на отрезêе MN) и меньшеãо радиуса не имеет ни одной общей точêи с прямой C1D1 (в частности, с отрезêом C1D1).
Остается вычислить d = D1D1′ . Если a — ребро êуба (по ус-
![]() ловиюниêов
AAa = 5)1N , ито D 1из условия 2следует+ AN2 , =что5-----4a -AN′.
Из==a подобия3-----·4a----------A- . aNСо- = 5
·ã ласнотреу54-ã
= 4. ольтео--
ловиюниêов
AAa = 5)1N , ито D 1из условия 2следует+ AN2 , =что5-----4a -AN′.
Из==a подобия3-----·4a----------A- . aNСо- = 5
·ã ласнотреу54-ã
= 4. ольтео--
реме Пифаãора, A1N = AA1
′ D1A получим d = D1D1
1
43. ![]()
![]()
![]() 27-------2
27-------2------3- при h m
3; ----------------3h23−h33 при h > 3. P
Пусть PO = x — высота пирамиды, T — точêа êасания полусферы с боêовой ãранью
![]() пирамиды (с апофемой PK),
а значит, TO — K O C радиус полусферы, т. е. TO = 3 (рис.
85). Рис. 85
пирамиды (с апофемой PK),
а значит, TO — K O C радиус полусферы, т. е. TO = 3 (рис.
85). Рис. 85
![]()
![]() Тоãда x >
3 и, êроме тоãо, x l h соãласно условию. Положим
∠OKP =
α. В ∆PTO имеем
TO-------PO- =
sin --2π
– α-
, -------x3 = cos α; в
Тоãда x >
3 и, êроме тоãо, x l h соãласно условию. Положим
∠OKP =
α. В ∆PTO имеем
TO-------PO- =
sin --2π
– α-
, -------x3 = cos α; в
![]() ∆KTO имеем
KO = -----------sinTOα- =
------1
∆KTO имеем
KO = -----------sinTOα- =
------1--------------−3-----32 = -----x-------------23−x3 . Таê êаê
KO — раx
![]()
![]() диус
оêружности, вписанной в правильный треуãольниê ABC, то
еãо сторона равна AB = 2 3 · KO = ------------------6x . Следовательно, x2 − 3
диус
оêружности, вписанной в правильный треуãольниê ABC, то
еãо сторона равна AB = 2 3 · KO = ------------------6x . Следовательно, x2 − 3
![]() S∆ABC
= = , и объем пирамиды выражается формулой V (x) = 1-3 S ∆ABC · x = 3 3 · x--------------2x−3 3- . Наименьшее
значение объема пирамиды Vmin ищем с помощью производной V′ (x) =
S∆ABC
= = , и объем пирамиды выражается формулой V (x) = 1-3 S ∆ABC · x = 3 3 · x--------------2x−3 3- . Наименьшее
значение объема пирамиды Vmin ищем с помощью производной V′ (x) =
![]()
Рис. 86
Если h m 3, то учитывая, что x m h, имеем
![]()
![]() Vmin
= V(3) = 3 3 · -----------927−
3-
= 27-------2
Vmin
= V(3) = 3 3 · -----------927−
3-
= 27-------2------3- .
![]()
![]() Если
же h > 3, то при x ° [h; + ×) фунêция V
(x) монотонно возрастает. Следовательно, Vmin = V(h) = 3 3 · --------------h3 - .
Если
же h > 3, то при x ° [h; + ×) фунêция V
(x) монотонно возрастает. Следовательно, Vmin = V(h) = 3 3 · --------------h3 - .
h2 − 3
44. а) ------43 (16 + 13 13 + 5 157).
Пусть MK C DE и MKP — треуãольное сечение пирамиды PABCDEF (рис. 87);
![]() по условию AB = -------11 , PO = 3.
по условию AB = -------11 , PO = 3.
3
Пусть OH B DE (EH = DH), а L =
![]() =
MK OH. Таê êаê OL B MK, то по теореме
о трех перпендиêулярах PL B MK,
=
MK OH. Таê êаê OL B MK, то по теореме
о трех перпендиêулярах PL B MK,
F K E 1-2 MK · PL.
и площадь сечения S∆ MKP =
Рис. 87
Из ∆EHO имеем OH = OE · sin -3π = -------113 · -------23 = T
= 11------2 . Введем величину x = OL 0 m x m 11------2 и D H E
![]() выразим через x площадь
сечения. Из прямо- M xL K
уãольноãо треãольниêа POL следует,
что PL O F
выразим через x площадь
сечения. Из прямо- M xL K
уãольноãо треãольниêа POL следует,
что PL O F
![]() = OL2
+ PO2
= x2 +
9 . Продолжим лучи CD Рис. 88 и FE до их пересечения в точêе T
(рис. 88).
= OL2
+ PO2
= x2 +
9 . Продолжим лучи CD Рис. 88 и FE до их пересечения в точêе T
(рис. 88).
Треуãольниêи DTE, DOE, CDO, OEF — правильные со стороной и высотой 11------2 . Таê ∆MTK " ∆CTF, то MK-----------CF = TO-------TL- , т. е.
3
![]()
![]() MK-----------
= 11----------------11−
x ,
отêуда MK = -------23 (11 – x). Тоãда площадь сечения
MK-----------
= 11----------------11−
x ,
отêуда MK = -------23 (11 – x). Тоãда площадь сечения
![]() выразится фунêцией S
(x) = -------1 (11 – x) x2 + 9 ; будем исêать ее 3
выразится фунêцией S
(x) = -------1 (11 – x) x2 + 9 ; будем исêать ее 3
наибольшее возможное значение на отрезêе 0; - 11------2 . Найдем про-
Рис. 89
![]() Сравним
маêсимум S (0) (на êонце отрезêа) с маêсимумом S
9-2 (во внутренней точêе
отрезêа): S(0) = 11 3 , S
9-2 =
Сравним
маêсимум S (0) (на êонце отрезêа) с маêсимумом S
9-2 (во внутренней точêе
отрезêа): S(0) = 11 3 , S
9-2 =
![]()
![]() = 13-------
= 13--------4--------39 . Имеем 11 3 # -------13-4--------39 ; 44 # 13 13 ; 442
# 132 · 13;
1936 < 2197 ⇒ S(0) < S 9-2 , т. е. Smax = S 9-2 и OL = x = 92- , LH = OH – OL = 1.
Найдем полную поверхность отсеêаемой четырехуãольной пирамиды PKMDE. Последовательно получаем SKMDE =
![]()
![]()
![]()
![]()
![]() = 1-2 (MK + DE)
· LH = 1--2 --------23 11
– 2-9-
+ -------113- ·
1 = 4 3 ; S∆MKP
= = S
9-2 = 13-------
= 1-2 (MK + DE)
· LH = 1--2 --------23 11
– 2-9-
+ -------113- ·
1 = 4 3 ; S∆MKP
= = S
9-2 = 13--------4--------39 ; KE = MD
= LH : sin -3π = -------23 ; высоты боêовых
ãраней KEP, MDP и DEP равны друã друãу
и равны PH =
![]()
![]() = PO2 + OH2 = 9 + 121--------4 - =
-------------1572 ; S∆KEP = -21 KE · PH = ------------21573 ;
= PO2 + OH2 = 9 + 121--------4 - =
-------------1572 ; S∆KEP = -21 KE · PH = ------------21573 ;
S∆DEP = 1-2 DE · PH = 11-------4 3-------------157- .
Итаê,
![]() Sполн = SKMDE + S∆MKP + 2S∆KEP + S∆DEP = 4 3 + 13-------
Sполн = SKMDE + S∆MKP + 2S∆KEP + S∆DEP = 4 3 + 13--------4--------39 +
![]() + -------------157 + 11-------
+ -------------157 + 11--------------------157-
= -------43 (16 + 13 13 + 5 157
). б) 30 3 ;
3 4 3
в) 312 3 .
45. k2
sin 2α при α ° arcctg
1-2 ; -2π-
, k----22- (1 + 3 cos2
α) при
α ° 0; arcctg -21 ![]() . При пересечении êонуса плосêостью,
проходящей через еãо вершину, в сечении получается равнобедренный треуãольниê,
площадь êотороãо S = 1-2 l2 sin ϕ, ãде l
— дли-
. При пересечении êонуса плосêостью,
проходящей через еãо вершину, в сечении получается равнобедренный треуãольниê,
площадь êотороãо S = 1-2 l2 sin ϕ, ãде l
— дли-
на образующей êонуса, ϕ — величина уãла между образующими, по êоторым плосêость пересеêает êоничесêую поверхность. Таê êаê длина образующей равна длине боêовоãо ребра пирамиды, вписанной в этот êонус, то площадь сечения является фунêцией уãла ϕ, причем в общем случае ϕ ° (0; π).
Наибольшим значением ϕ является уãол γ в осевом сечении
êонуса, поэтому при исследовании знаêа производной фунêции S
(ϕ) = 1-2 l2 cos ϕ мы имеем две возможности: 1) если γ ° 0 ; -2π-
, то cos ϕ >
0, т. е. S(ϕ)
возрастает на этом промежутêе и достиãает наибольшеãо значения
при ϕ = γ; в этом случае Smax
= 1-2 l2 × × sin γ; 2) если γ ° ![]() --2π ; π-
, то cos ϕ m
0 и ϕ = -2π является
точêой маêсимума фунêции S(ϕ); в этом случае Smax =
l----22 .
--2π ; π-
, то cos ϕ m
0 и ϕ = -2π является
точêой маêсимума фунêции S(ϕ); в этом случае Smax =
l----22 .
Пусть β — величина уãла между боêовым ребром пирамиды и плосêостью основания, h — длина ее высоты. Имеем h ctg β = = 2h ctg α или ctg β = 2 ctg α и h = k sin α. Найдем длину образующей êонуса (боêовоãо ребра пирамиды): l = ------------sinh β . Теперь находим выражение для площади сечения:
Sсеч = 1-2 ------------sinh β 2 sin ϕ = 1-2 k2 sin2 α (1 + 4 ctg2 α) sin ϕ.
Величина уãла γ в осевом сечении êонуса γ будет меньше -2π , если β > 4-π , т. е. 2 ctg α < 1 или α ° arcctg -21 ; -2π- ; в этом случае Smax = 1-2 k2 sin2 α · 2 ctg β = 2k2sin2 α ctg α = k2 sin 2α.
Если же 0 < β m -4π
, т. е. α
° 0;
arcctg 1-2 ![]() , то Smax
= 1-2 l2 =
= 1-2 k2sin2
α (1 +
4 ctg2 α)
= k----22- (1 + 3 cos2
α).
, то Smax
= 1-2 l2 =
= 1-2 k2sin2
α (1 +
4 ctg2 α)
= k----22- (1 + 3 cos2
α).
![]() 46. -----------------------------------------2 + a1sin+ 3αcos2α
. Пусть F
46. -----------------------------------------2 + a1sin+ 3αcos2α
. Пусть F
![]() FABCD — правильная четырехуãольная пирамида,
FK и FN — апофемы боêовых ãраней ABF и CDF
со-
FABCD — правильная четырехуãольная пирамида,
FK и FN — апофемы боêовых ãраней ABF и CDF
со-
ответственно (рис. 90). По условиюC ребро основания AD = a, ∠FKN = α. Пусть точêа P — центр основания êонуса (P лежит на высоте FO пи-
рамиды), а оêружность основания A a D êонуса êасается апофем FK и FN в Рис. 90 точêах L и M соответственно.
![]() Положим x = LP
0
m x m a-2-
и F
Положим x = LP
0
m x m a-2-
и F
выразим через x объем êонуса. Найдем высоту êонуса h = PO. Изподобия треуãольниêов LPF и
KOF (рис. 91) следует ---------KOLP = --------FOFP = K –a2 O N
= FO----------------------FO− PO- = 1 – PO-------FO- . Рис. 91
Таê êаê LP = x, KO = a-2 , PO = h, FO = a--2 tg α, то ---xa-2 = 1 – -------------a-2tgh α- , т. е. h = a-2 – x tg α. Следовательно, объем êонуса V = V(x) =
= 1-3 πx2 · h = π------------tg3 α- · x2 a-2 – x. Маêсимальное значение фунêции
V(x) найдем с помощью производной V′(x) = --------------πtg3 α · x(a – 3x), изменение знаêов êоторой проведем методом интервалов (рис. 92).
![]()
Рис. 92
Объем êонуса будет маêсимально возможным при x = a-3 , тоãда h = a-2 – -3a tg α = a-6 tg α = 1-3 FO. Нам надо найти радиус шара,
![]() F êасающеãося
боêовой поверхности êонуса и всех боêовых ãраней пирамиды
(апофем пирамиды). На планиметричесêом чертеже
F êасающеãося
боêовой поверхности êонуса и всех боêовых ãраней пирамиды
(апофем пирамиды). На планиметричесêом чертеже
(рис. 93) радиус этоãо шара соответствует радиусу оêружности, вписанной в четырехуãольниê LFMO, у êотороãо диаãонали LM и
K –a2 O N FO взаимно перпендиêулярны и пересеêаютРис. 93 ся в точêе P.
Известно, что радиус оêружности, вписанной в мноãоуãольниê, равен отношению площади мноãоуãольниêа ê еãо полупериметру. Найдем площадь четырехуãольниêа LFMO: SLFMO = = 1-2 LM · FO = LP · FO = a-3 · 2-a tg α = a----62- tg α.
Полупериметр четырехуãольниêа LFMO равен сумме FL + + OL, таê êаê FM = FL, а OM = OL. Вычислив длины отрезêов FL и OL, получаем
FL = -----------------------------sinLPπ − α = -----------cosx α = ---------------3cosa α ; --2
![]()
![]() OL = h2 +
x2 =
a-6-tgα
2 +
3-a- 2 = ---------------6cosa α sin2α
+ 4 cos2α .
OL = h2 +
x2 =
a-6-tgα
2 +
3-a- 2 = ---------------6cosa α sin2α
+ 4 cos2α .
Тоãда
r = FL----------------------SLFMO+ OL + ----------------------------------------------------------------------------------------3 a + ---------------cosa----a6α2- tgsinα 2 α + 4cos2 α- =
---------------cosα 6
= -------------------------------------------------------asinα = ------------------------------------------asinα .
2 + sin2α + 4cos2α 2 + 1 + 3cos2α
![]() 47. 48--------------------------H962H+
a2- . 48. -------------------------------------------------------------------49a4 +
7216a2HH2 +
16H4- .
47. 48--------------------------H962H+
a2- . 48. -------------------------------------------------------------------49a4 +
7216a2HH2 +
16H4- .
49. --------------------------------------------------3 2( + 31a+sin3cosα 2α)- .
50. 7-2 . Пусть O1 — центр сферы, описанной оêоло пирами-
ды SABC, O1A = O1S = R — ее радиус, S
![]() SP = 4 — высота
пирамиды (рис. 94).
SP = 4 — высота
пирамиды (рис. 94).
Таê êаê точêа O1 равноудалена от вершин пирамиды, то она лежит на прямой, перпендиêулярной плосêости основания и проходящей через еãо центр, — точêу O. Опустим из точêи O1 перпендиêуляр O1M
на прямую SP и обозначим длины сторон AB
полученноãо прямоуãольниêа OO1MP че-
рез x = OP = O1M и y = OO1 = PM. Приме- C
треуним ãтеоремуольниê амПифа O1OAãора и ê Oпрямоу1MS: ãольным Рис. 94
O1A2 = OA2 + OO21 , (1)
O1S2 = O1M2 + SM2. (2)
![]() Длина
отрезêа OA равна радиусу оêружности, описанной оêоло правильноãо
треуãольниêа ABC со стороной 6, поэтому OA = -------6 = 2 3 , и равенство
(1) примет вид R2 = 12 + y2. 3
Длина
отрезêа OA равна радиусу оêружности, описанной оêоло правильноãо
треуãольниêа ABC со стороной 6, поэтому OA = -------6 = 2 3 , и равенство
(1) примет вид R2 = 12 + y2. 3
![]()
![]() Из равенства (2) вытеêает,
что SM = R2 − x2
и посêольêу в общем случае PM = |SM – SP| (точêи
O1 и S моãут быть расположены по разные стороны
от плосêости ABC), имеем y = | R2 − x2
– 4|.
Из равенства (2) вытеêает,
что SM = R2 − x2
и посêольêу в общем случае PM = |SM – SP| (точêи
O1 и S моãут быть расположены по разные стороны
от плосêости ABC), имеем y = | R2 − x2
– 4|.
P Следовательно, R2 = 12 +
2 , т. е. R2 = ----------------------(x264+ 4)2- +
![]() + 12, отêуда следует, что
минимальное значение радиуса уêазанной сфе достиãается при x =
0. В этом случае точêа P совпадает с точêой O
+ 12, отêуда следует, что
минимальное значение радиуса уêазанной сфе достиãается при x =
0. В этом случае точêа P совпадает с точêой O
A K D (и пирамида является правильной),
![]() Рис. 95 поэтому основание высоты пирамиды принадлежит треуãольниêу
ABC. Итаê, Rmin = 16------64 + 12 = 7-2 .
Рис. 95 поэтому основание высоты пирамиды принадлежит треуãольниêу
ABC. Итаê, Rmin = 16------64 + 12 = 7-2 .
![]()
![]() 51. 192. 52. ---------------3 3- .
53. 2 3 . 54. а) 60,5. По условию AB = 20,
51. 192. 52. ---------------3 3- .
53. 2 3 . 54. а) 60,5. По условию AB = 20,
4 +3
![]() PO
= 3 (рис. 95). Тоãда DO = 1-2 BD = 102 . Пусть прямая
PO
= 3 (рис. 95). Тоãда DO = 1-2 BD = 102 . Пусть прямая
KM C AC (или KM совпадает с AC) и KMP — треуãольное сечение исходной пирамиды PABCD. Ясно, что KM B DO. Таê êаê отрезоê ON — проеêция отрезêа PN на плосêость ABCD, а прямая ON B KM, то PN B KM (по теореме о трех перпендиêулярах); поэтому площадь сечения S∆KMP = 1-2 KM · PN.
![]()
![]() Положим
x = DN (0 m x m 102 ) и выразим площадь сечения через x.
Имеем (рис. 96): KN = MN = x, KM = 2x, KD
=
Положим
x = DN (0 m x m 102 ) и выразим площадь сечения через x.
Имеем (рис. 96): KN = MN = x, KM = 2x, KD
=
![]() = DM = x 2
. Далее, ON = DO – DN = K = 10 2 – x, значит, PN
= PO2 +
ON2 =
= DM = x 2
. Далее, ON = DO – DN = K = 10 2 – x, значит, PN
= PO2 +
ON2 =
![]() Рис. 96 = 32 +
(10 2 − x)2 , отêуда,
расêрыв сêобêи, получаем PN =
Рис. 96 = 32 +
(10 2 − x)2 , отêуда,
расêрыв сêобêи, получаем PN = ![]() x2 − 20x 2 + 209 . Тоãда
x2 − 20x 2 + 209 . Тоãда
S∆KMP = S (x) = x · x2 − 20x 2 + 209 .
Для нахождения маêсимально возможноãо значения площади сечения вычислим производную фунêции S (x), êоторая после очевидных преобразований имеет вид
![]() S′ = ------(x
S′ = ------(x----------------------------------------------------2 −
11)(x 2 −
19)- .
x2 − 20x 2 +
209
Изменение знаêов производной исследуем методом интервалов (рис. 97).
![]()
![]() S (10 2 ) = 30 2 , то
наибольшая возможная площадь сечения получается при x = 11-------2
S (10 2 ) = 30 2 , то
наибольшая возможная площадь сечения получается при x = 11-------2------2- . Вычислим
объем отсеêаемой треуãольной пирамиды PKMD в этом случае.
Площадь основания S∆KMD = 1-2 · KD · MD = x2 = 121--------2 - ; высота отсеêаемой пирамиды PKMD совпадает с высотой исходной пирамиды PABCD, и, следовательно, VPKMD = 31- · PO · S∆KMD =
= 1-3 · 3 · 121--------2 - = 60,5.
б) 1,5; в) 3034,5; ã) 607,5.
55.
![]() 3 . Пусть T — середина ребра
AC, тоãда DT — апо-
3 . Пусть T — середина ребра
AC, тоãда DT — апо-
фема боêовой ãрани ADC, BT — высота основания ABC пирамиды DABC (рис. 98). Проведем сечение KLMN параллельно ребрам AC и DB. Таê êаê KLMN C AC, то
![]() KN C AC
и LM C AC, отêуда следует, D что KN C LM.
С друãой стороны, таê êаê KLMN C DB, то MN
C DB и KL C DB, отêуда следует, что KL C MN.
Из тоãо, что KN C LM и KL C MN, вытеêает,
что KLMN — параллелоãрамм.
KN C AC
и LM C AC, отêуда следует, D что KN C LM.
С друãой стороны, таê êаê KLMN C DB, то MN
C DB и KL C DB, отêуда следует, что KL C MN.
Из тоãо, что KN C LM и KL C MN, вытеêает,
что KLMN — параллелоãрамм.
![]() Пусть
BT KN = P — середина KN, а ST LM = Q — середина
LM,
Пусть
BT KN = P — середина KN, а ST LM = Q — середина
LM,
тоãда отрезêи PQ, KL и MN равны и B N C
PQпараллельны C DB. , а таê êаê KL C DB, то и Рис. 98
Проеêция ребра DB на плосêость основания ABC есть отрезоê OB, причем OB B AC; в силу тоãо, что PQ C DB, проеêция отрезêа PQ на ABC таêже перпендиêулярна AC, а значит и KN, посêольêу KN C AC. Тоãда по теореме о трех перпендиêулярах PQ B KN, отêуда следует, что параллелоãрамм KLMN — прямоуãольниê, площадь êотороãо SKLMN = KN · PQ.
По условию AB =BC = AC = 3, DO = 78 .
D Тоãда BT = AB · -------23 = 3---------23 , BO = 2-3 BT =
![]()
![]() 3 , SB = SO2
+ BO2
= 78 + 3 = 9. В ∆BDT проведем
высоту TH; TH PQ = E
3 , SB = SO2
+ BO2
= 78 + 3 = 9. В ∆BDT проведем
высоту TH; TH PQ = E
(рис. 99).
Посêольêу удвоенная площадь ∆BDT равна 2 S∆BDT = TH · DB = DO · BT, имеем TH =
B P O T
![]() Рис. 99 = DO BT---------------------DB⋅ -
= -------------------------78 39 2⋅⋅ 3- = ---------226-
> 2. Положим
Рис. 99 = DO BT---------------------DB⋅ -
= -------------------------78 39 2⋅⋅ 3- = ---------226-
> 2. Положим
ET = x; по условию 0 m x m 2, таê êаê ET равно расстоянию от отрезêа AC (т. е. от любой еãо точêи) до плосêости сечения KLMN в силу их параллельности; таêим образом, высота пирамиды с вершиной в точêе A и основанием KLMN равна x.
Выразим площадь прямоуãольниêа KLMN и объем пирамиды AKLMN через x. Пусть ∠HBO = ∠DPO = α, тоãда tg α = DO--------BO =
![]()
![]() = ---------78-
= 26 ; sin α =
--------------------------tg α -
=
= ---------78-
= 26 ; sin α =
--------------------------tg α -
= ---------26 . Из подобия треуãольни-
3 1 + tg2 α 3 3
êов PQT и BDT следует, что -------DBPQ = --------THDT- , отêуда PQ = DB ×
![]() × --------THDT- =
9 · ------------------x26-- =
---------1826-
x; PT = --------------------------sin∠ETEPO- =
-----------sinx α- .
В свою очередь
× --------THDT- =
9 · ------------------x26-- =
---------1826-
x; PT = --------------------------sin∠ETEPO- =
-----------sinx α- .
В свою очередь
2
из подобия треуãольниêов KBN и ABC вытеêает, что KN--------AC- = -------BTBP- ,
3---------------x 3
![]()
![]() т. е. KN--------3 - =
BT----------------------BT−
PT- =
1 – -------BTPT- =
1 – --
т. е. KN--------3 - =
BT----------------------BT−
PT- =
1 – -------BTPT- =
1 – ---3 3----------------------226 = 1 – 26- .
Поэтому
объем пирамиды AKLMN выразится фунêцией VAKLMN = V(x) =
![]()
![]() = 1-3 SKLMN
· hA = 1-3 KN · PQ ·
x = -1
– ---------226x-
· ---------1826- x
· x = = ------139 (x2 26
– 2x3).
= 1-3 SKLMN
· hA = 1-3 KN · PQ ·
x = -1
– ---------226x-
· ---------1826- x
· x = = ------139 (x2 26
– 2x3).
Маêсимальное значение объема пирамиды при 0 m x m 2 найдем с помощью производной:
![]() V′(x) = ------139 (2x 26 – 6x2)
= 18---------13x- ( 26
– 3x).
V′(x) = ------139 (2x 26 – 6x2)
= 18---------13x- ( 26
– 3x).
![]() Применяя
метод интервалов (рис. 100), заêлючаем, что маêсимум фунêции V(x)
достиãается при x = ---------326-
и равен Vmax =
Применяя
метод интервалов (рис. 100), заêлючаем, что маêсимум фунêции V(x)
достиãается при x = ---------326-
и равен Vmax =
![]() = V---------326-
= ------139 · 26------9 26
– 2------------- 326--
= 2-------------326- .
= V---------326-
= ------139 · 26------9 26
– 2------------- 326--
= 2-------------326- .
+ max 2
0 √26 – x
3
Рис. 100
![]()
![]() 56. -98 111 . 57. 2 219
. 58. 64------81 23 .
56. -98 111 . 57. 2 219
. 58. 64------81 23 .
![]()
![]() 59.
32. Введем прямоуãольную систему êоординат (x; у; z) с
началом в точêе A, с осью абсцисс, направленной вдоль веêтора
AD , осью ординат — вдоль веêтора AB и осью апплиêат —
вдоль веêтора AA1 (рис. 101).
59.
32. Введем прямоуãольную систему êоординат (x; у; z) с
началом в точêе A, с осью абсцисс, направленной вдоль веêтора
AD , осью ординат — вдоль веêтора AB и осью апплиêат —
вдоль веêтора AA1 (рис. 101).
Пусть x — абсцисса точêи M, удовлетворяющей уêазанному в условии свойст- Рис. 101
ву. Тоãда точêа M имеет êоординаты -x; 3-----2x ; 9-----4x . Таê êаê она принадлежит данному параллелепипеду, то одновременно выполняются неравенства 0 m x m 4, 0 m 3------2x m 4, 0 m 9------4x m 18, отêуда 0 m x m -38 .
Найдем êвадрат расстояния d точêи M -x; 3-----2x ; -----94x- до точêи C1 (4; 4; 18):
d2 = (4 – x)2 +- 4 – 3-----2x 2 + 18 – 9-----4x 2 = ϕ(x).
Посêольêу êаждое из слаãаемых (4 – x)2, -4 – 3-----2x 2,
![]() 18 – 9-----4x
2
убывает на отрезêе 0; - -38 , фунêция ϕ (x) таêже убы-
18 – 9-----4x
2
убывает на отрезêе 0; - -38 , фунêция ϕ (x) таêже убы-
вает на этом отрезêе, принимая минимальное значение при x = 8-3 . Поэтому наименее удаленная от точêи C1 точêа M0 имеет êоординаты 8-3 ; 4; 6 , т. е. высота пирамиды M0ABCD с вершиной в точêе M0 равна 6. Таê êаê площадь ее основания ABCD равна 16, то исêомый объем равен 1-3 · 6 · 16 = 32. 60. 12. 61. 120.
62. 16------3 .
Глава X
Задачи с параметрами
![]()
§ 1. ЗАДАЧИ ПО АЛГЕБРЕ
1. a ° –1-8 c {1; +×}. Перепишем исходное уравнение в виде f(x) = a, ãде
f(x) = 4x2 + 4x|x| – 3x – 3|x| + 1 =
![]() 1 при
x < 0,
1 при
x < 0,
= (4x – 3)(x + |x|) + 1 = 8x2 – 6x + 1 при x l 0.
![]() Построив ãрафиêи
фунêций y = f(x) и y = a и определив
ãрафичесêи их общие точêи при различных значениях a (рис.
102), заêлючаем, что при a > 1 уравнение f(x) = a
имеет одно решение; при a = 1 — бесêонечно мноãо решений; при
a ° –1-8 ; 1
— два решения; при a = –1-8 — одно решение, в этом случае прямая y =
a êасается параболы y = 8x2 – 6x +
1 Рис. 102
Построив ãрафиêи
фунêций y = f(x) и y = a и определив
ãрафичесêи их общие точêи при различных значениях a (рис.
102), заêлючаем, что при a > 1 уравнение f(x) = a
имеет одно решение; при a = 1 — бесêонечно мноãо решений; при
a ° –1-8 ; 1
— два решения; при a = –1-8 — одно решение, в этом случае прямая y =
a êасается параболы y = 8x2 – 6x +
1 Рис. 102
в ее вершине 3-8 ; –1-8- ; при a < –1-8 уравнение не имеет решений. 2. b ° [–3; 1). 3. a ° (–×; –25) c (–1; 0) c (7; +×). Исходное уравнение имеет два различных êорня, если оно является êвадратным уравнением с положительным дисêриминантом:
a − 0, ⇔ a(3−a + 5)0, 2 – 4a(2a + 1) > 0 ⇔
D > 0
![]()
![]() ⇔ (aa−+
1)(0, a + 25) > 0 ⇔ aa
−< 0–25, , a > –1.
⇔ (aa−+
1)(0, a + 25) > 0 ⇔ aa
−< 0–25, , a > –1.
Таêим образом,
a ° (–×; –25) c (–1; 0) c (0; +×). (1)
Используя теорему о расположении êорней êвадратноãо трехчлена относительно отрезêа, получим следующую систему условий принадлежности наибольшеãо êорня исходноãо уравнения отрезêу [–1; 3]:
![]() a · f(3)
l 0, a · f(–1) m 0,
a · f(3)
l 0, a · f(–1) m 0,
x0 ° (–1; 3),
ãде f(x) = ax2 – (3a + 5)x + 2a + 1, x0 = 3---------------a2a+ 5- .
Имеем
a · (a – 7) l 0, (2)
![]()
![]() a ·
(9a – (3a + 5) · 3 + 2a + 1) l 0,a · (a + 1)
m 0, (3) a · (a + (3a + 5) + 2a + 1) m 0, ⇔ a-----------+
1
a ·
(9a – (3a + 5) · 3 + 2a + 1) l 0,a · (a + 1)
m 0, (3) a · (a + (3a + 5) + 2a + 1) m 0, ⇔ a-----------+
1
–1 < ---------------3a2a+ 5- < 33---------------aaa−-5-> 0> 0., (4)
Система неравенств (4) имеет решение (–×; –1) c -35 ; +× , объединение êотороãо с решением неравенства (3) дает множество (–×; 0] c 5-3 ; +× .
Далее, пересечение этоãо множества с решением неравенства
![]() (2) дает множество
(–×; 0] c (7; +×). Наêонец, найдя пересечение последнеãо
множества с множеством (1), получаем ответ. 4. b ° [–1; 0) c (0;
11]. 5. c ° 0; ------101 c (5; 10]. 6.
p ° (–×; 0) c c (0; 7] c [27; +×). 7. а) p ° (4 –
2 5 ; 8,5). Исходное неравенство является однородным неравенством второй степени
относительно фунêций 4x – 3 и x2 + 1. Разделив еãо
на (x2 + 1)2 > 0, получим равносильное неравенство
(2) дает множество
(–×; 0] c (7; +×). Наêонец, найдя пересечение последнеãо
множества с множеством (1), получаем ответ. 4. b ° [–1; 0) c (0;
11]. 5. c ° 0; ------101 c (5; 10]. 6.
p ° (–×; 0) c c (0; 7] c [27; +×). 7. а) p ° (4 –
2 5 ; 8,5). Исходное неравенство является однородным неравенством второй степени
относительно фунêций 4x – 3 и x2 + 1. Разделив еãо
на (x2 + 1)2 > 0, получим равносильное неравенство
---------------4x2 +−13- 2 + p---------------4xx2 +− 13- + 2p + 1 > 0, x
отêуда после замены t = t(x) = 4---------------xx2 +− 13- приходим ê êвадратному неравенству относительно переменной t с параметром p:
t2 + pt + 2p + 1 > 0. (1)
![]() Найдем множество
значений фунêции t = t(x) при x ° R.
Имеем (x2 + 1)t =
Найдем множество
значений фунêции t = t(x) при x ° R.
Имеем (x2 + 1)t =
= 4x – 3, или tx2 – 4x + t + 3 = 0.
Отсюда t = 0 при x = 3-4 ; друãие значения t (отличные от нуля) найдем из условия неотрицательности дисêриминанта этоãо êвадратноãо уравнения: D----4 = 22 – t(t + 3) = –t2 – 3t + + 4 = (1 – t)(t + 4) l 0, т. е. –4 m t m 1.
Итаê, исходное неравенство выполняется для всех x ° R тоãда и тольêо тоãда, êоãда неравенство (1) выполняется для всех t ° [–4; 1]. Рассмотрим êвадратный трехчлен f(t) = t2 + pt + 2p + 1; абсцисса еãо вершины tв = –-2p , а дисêриминант D1 = = p2 – 4(2p + 1) = p2 – 8p – 4. Тоãда имеем следующие необходимые и достаточ- Рис. 103 ные условия для нахождения исêомых значений параметра p (рис. 103, а—в):
![]() tв < –4,
tв < –4,
f(–4) > 0, (2)
–4 m tв m 1,
D1 < 0, (3) tв > 1,
f(1) > 0. (4)
Последовательно преобразуя, получаем:
![]() (2)
: (––2-p4)<2 +–4,p · (–4) + 2p
+ 1 > 0 ⇔
(2)
: (––2-p4)<2 +–4,p · (–4) + 2p
+ 1 > 0 ⇔
![]() pp > 8< 8,,5 ⇔ p ° (8;
8,5);
pp > 8< 8,,5 ⇔ p ° (8;
8,5);
![]()
![]() (3): –4 p2 – 8m –p-2p– 4 < 0 m 1, ⇔ 4–2 –m2 p5m
<8, p < 4 + 25 ⇔
(3): –4 p2 – 8m –p-2p– 4 < 0 m 1, ⇔ 4–2 –m2 p5m
<8, p < 4 + 25 ⇔
⇔ p ° (4 – 2 5 ; 8);
![]()
![]() –12-2p+> 1, ⇔ pp <> ––2,2-3 ⇔ p °
¾.
–12-2p+> 1, ⇔ pp <> ––2,2-3 ⇔ p °
¾.
(4):
p + 2p + 1 > 0
Объединяя решения систем (2)—(4), получаем ответ.
![]()
![]() б) a ° (–2; 23); в) b ° (4 – 2 2
; +×); ã) q ° (–3; 6 + 4 5 ).
б) a ° (–2; 23); в) b ° (4 – 2 2
; +×); ã) q ° (–3; 6 + 4 5 ).
8. а) x ° ¾ при a < 3; x ° [–2; 1] при a = 3; x ° –a-----------2+ 1- ; a-----------2− 1-
при a > 3. Запишите левую часть уравнения в виде
![]() –2x – 1 при x < –2, |x – 1| + |x
+ 2| = 3 при –2 m x m 1, 2x + 1 при x
> 1.
–2x – 1 при x < –2, |x – 1| + |x
+ 2| = 3 при –2 m x m 1, 2x + 1 при x
> 1.
б) ¾ при |b| > 5; x ° (–×; 3] при b = –5; x = b------------−2 1 при –5 < b <
< 5; x ° [2; +×) при b = 5. Запишите левую часть уравнения в виде
![]() –5 при
x m –3,
–5 при
x m –3,
|x + 3| – |x – 2| = 2x + 1 при –3 < x < 2,
5 при x l 2.
в) ¾ при с < –1 и с > 3; x = ------------------(c +21)2- + 1 при –1 m c m 3; x ° [5; +×)
при c = 3. Запишите левую часть уравнения в виде
![]() x − 1 + 1 – | x − 1 – 2| = 2 x
− 1 – 1 при
1 m x m 5,
x − 1 + 1 – | x − 1 – 2| = 2 x
− 1 – 1 при
1 m x m 5,
3 при x l 5.
![]() ã) x =
-----------------------1 −
2a −
ã) x =
-----------------------1 −
2a −
-----------------------------------------21a−24a +
16a2 при –× < a <
0; x = –3 при a = 0;
![]() x1,2 = 1-----------------------−
2a ±
x1,2 = 1-----------------------−
2a ±
-----------------------------------------21a−24a +
16a2 при 0 < a m 1-4 ; x = -----------------------1 −
2a +
-----------------------------------------21a−24a +
16a2 при 1-4 < a <
+×.
![]()
![]() 9. а) ¾ при a
< –1; x ° [1 – 1 +
a ; 1 + 1 +
a ] при –1 m a < 0; x °
9. а) ¾ при a
< –1; x ° [1 – 1 +
a ; 1 + 1 +
a ] при –1 m a < 0; x ° ![]() –a-2 ; 1 + 1 + a при a l
0;
–a-2 ; 1 + 1 + a при a l
0;
![]() б) ¾ при a
> –-43 ; x ° 1-----------------------−
2a −
б) ¾ при a
> –-43 ; x ° 1-----------------------−
2a −
-2-----------------------−
3 −
4a ;
1-----------------------−
2a +
-2-----------------------−
3 −
4a
![]() при –1 m a m –3-4 ; x ° 1; 1-----------------------−
2a +
при –1 m a m –3-4 ; x ° 1; 1-----------------------−
2a +
-2-----------------------−
3 −
4a при
a < –1;
в) ¾ при p m –1; x ° -1-2 ; -------------------------2 1(p2−+22p) при –1 < p < 1-2 ; x °
![]() °
° ![]() -1-2 ; +×
при -21 m p m 2; x °
−-------------------------2 2(2 +pp−21); –1 c
--12 ; +×
-1-2 ; +×
при -21 m p m 2; x °
−-------------------------2 2(2 +pp−21); –1 c
--12 ; +×![]() при p >
2;
при p >
2;
![]()
![]() ã) x °
[–×; –1] c-3-2 ; +× при p <
–2; x − –1 при p = –2;
ã) x °
[–×; –1] c-3-2 ; +× при p <
–2; x − –1 при p = –2;
x ° ![]() –×;
-------------------------2 2(6 +pp−21)
c --32 ; +× при –2 <
p < -12 ; x °
–×;
-------------------------2 2(6 +pp−21)
c --32 ; +× при –2 <
p < -12 ; x ° ![]() -3-2 ; +×
при 1-2 m p < 3; x
° 3-2 ; +×-
при p = 3; x ° -------------------------2 2(p2p+−61) ;
+×-
при p > 3.
-3-2 ; +×
при 1-2 m p < 3; x
° 3-2 ; +×-
при p = 3; x ° -------------------------2 2(p2p+−61) ;
+×-
при p > 3.
![]() 10. а) a ° 0; 4-7 . Полаãая
t = 3x > a, сведем исходное поêа-
10. а) a ° 0; 4-7 . Полаãая
t = 3x > a, сведем исходное поêа-
зательное неравенство ê алãебраичесêому неравенству относительно переменной t с параметром a:
at2 + (1 – a)t – 7-4 a + 1 > 0, (1)
причем оно должно выполняться для всех t > 0.
При a = 0 неравенство (1) является линейным:
0 · t2 + (1 – 0) · t – -74 · 0 + 1 > 0, т. е. t + 1 > 0,
что, очевидно, выполняется для всех t > 0 и, следовательно, значение a = 0 является одним из исêомых.
При a − 0 неравенство (1) является êвадратным. Обозначим через f(t) еãо левую часть: f(t) = at2 + (1 – a)t – 7-4 a + 1.
Фунêция f(t) — êвадратный трехчлен с дисêриминантом D = (1 – a)2 – 4a–7-4 a + 1 = (4a – 1)(2a – 1); еãо ãрафиê — па-
рабола с абсциссой вершины t0 = a-----------2−a1- .
Если a < 0, то ветви параболы направлены вниз, поэтому неравенство (1) не может выполняться для всех t > 0.
Если a > 0, то неравенство (1) выполняется для всех t > 0 тоãда и тольêо тоãда, êоãда либо парабола не имеет общих точеê с осью абсцисс (D < 0), либо фунêция f(t) имеет êорни (D l 0), но больший êорень неположителен (по теореме о расположении êорней êвадратноãо трехчлена относительно луча для этоãо необходимо и достаточно, чтобы t0 было неположительно, а значение f(0) было неотрицательно):
![]()
![]()
![]()
![]() a
> 0,
a
> 0,
a > 0,(4a – 1)(2a – 1) < 0, D < 0,(4a – 1)(2a – 1) l 0, tD0 lm 00,, ⇔ a-----------2−a1- m 0, ⇔ f(0) l 0a · 02 + (1 – a) · 0 – 7-4 a + 1 l 0
a > 0,
1-4 < a < 1-2 ,a > 0,
⇔ a m 1-41 , ⇔ a1-4 m < 1-4a < , 2-1 , ⇔ aa m> 04-7, ⇔ 0 < a m 7-4 .
a l 2- ,
a m 1,1-2 m a m -74 a m 4-7
![]() Объединяя
полуинтервал 0; 4-7 с найденным ранее значением
a = 0, получаем ответ.
Объединяя
полуинтервал 0; 4-7 с найденным ранее значением
a = 0, получаем ответ.
![]()
![]() б) c ° –3-5 ; 0 ; в) b ° 0, 2-7 ; ã) p
° 0; 1-2 .
б) c ° –3-5 ; 0 ; в) b ° 0, 2-7 ; ã) p
° 0; 1-2 .
11. а) x1 = 1 при a m 0; x1 = 1 и x2 = log2 a при a > 0;
б) x1 = 1 и x2 = log3 (–b) при b < 0; x1 = 1 при b l 0;
в) x1 = –1 и x2 = log2 (–c) при c < 0; x1 = –1 при c l 0;
ã) x1 = –2 при k m 0; x1 = –2 и x2 = log3 k при k > 0.
12. ![]() а) k ° –4;
–-54 c –2-3 ; 3– 13
. Исходное лоãарифмичесêое уравнение равносильно
системе
а) k ° –4;
–-54 c –2-3 ; 3– 13
. Исходное лоãарифмичесêое уравнение равносильно
системе
![]() 3x
– x2 – 45- =
( kx + 2 )2,
3x
– x2 – 45- =
( kx + 2 )2,
![]() 3x
– x2 – 5-4 > 0, kx +
2 > 0, kx +
2 − 1,
3x
– x2 – 5-4 > 0, kx +
2 > 0, kx +
2 − 1,
êоторая после очевидных преобразований примет вид
![]()
![]() 3x – x2 – 5-4 = kx + 2,3x –
x2 – 45- = kx + 2,
3x – x2 – 5-4 = kx + 2,3x –
x2 – 45- = kx + 2,
3x – x2 – 5-4 > 0, ⇔ 21- < x < 3-2 , 3x – x2 – -45 − 13-2 < x < 5-2 .
Построим на одном чертеже ãрафиê фунêции y = 3x – x2 – 5-4 при x ° 1-2 ; 3-2 c 3-2 ; 25- и ãрафиê фунêции y = kx + 2 для раз-
личных значений k (рис. 104) и выясним, êоãда прямая, проходящая через точêу (0; 2) (ãрафиê фунêции y = kx + 2), и парабола
Рис. 104
ãрафиê фунêции y = 3x – x2 – 5-4- имеют при x ° 1-2 ; -23- c c 3-2 ; 5-2 единственную общую точêу.
Среди прямых y = kx + 2, êоторые для всех значений k проходят через точêу (0; 2), выделим прямую, соответствующую k = –4 она проходит через точêу 1-2 ; 0 ; k = –4-5 она проходит через точêу 5-2 ; 0 ; k = –-32 она проходит через «выêолотую» на параболе точêу 3-2 ; 1 , а таêже прямую, соответ-
![]() ствующую k = 3 – 13
(êасательную ê параболе). Последнее значение k находим, приравняв
нулю дисêриминант êвадратноãо уравнения 3x – x2
– 5-4 = kx + 2 (берем
отрицательное значение k, таê êаê при k l
0 прямая y = kx + 2 и парабола y = 3x – – x2 – 5-4 не имеют общих точеê ни при x ° -21 ; 3-2 , ни при
ствующую k = 3 – 13
(êасательную ê параболе). Последнее значение k находим, приравняв
нулю дисêриминант êвадратноãо уравнения 3x – x2
– 5-4 = kx + 2 (берем
отрицательное значение k, таê êаê при k l
0 прямая y = kx + 2 и парабола y = 3x – – x2 – 5-4 не имеют общих точеê ни при x ° -21 ; 3-2 , ни при
x ° 3-2 ; 5-2 .
Выясним теперь, для êаêих отрицательных значений k прямая y = kx + 2 и часть параболы y = 3x – x2 – 5-4 при x ° 1-2 ; 3-2 c c 3-2 ; 5-2 имеют единственную общую точêу.
Если k° (–×; –4], то прямая и парабола при всех x° 1-2 ; 3-2- c c 3-2 ; 5-2- не имеют общих точеê.
Если k ° –4;
–4-5 ![]() , то прямая и парабола
имеют единственную точêу пересечения при x ° 21- ; -23-
и, следовательно, эти значения k являются исêомыми.
, то прямая и парабола
имеют единственную точêу пересечения при x ° 21- ; -23-
и, следовательно, эти значения k являются исêомыми.
Если k ° –-54 ; –-32- , то прямая и парабола имеют две различные точêи пересечения одну — при x ° 1-2 ; 3-2- , друãую — при x ° 3-2 ; 5-2-- , поэтому исследуемые значения k не войдут в ответ.
При k = –2-3 прямая и парабола таêже имеют две различные точêи пересечения, но одна их них — «выêолотая» точêа параболы 3-2 ; 1 , - а друãая принадлежит интервалу -23 ; -25- , и следовательно, это значение k является исêомым.
![]() Если k ° –2-3 ; 3 – 13
, то прямая и парабола имеют две различные точêи пересечения
причем
обе — при x °
-23 ; 5-2
,
поэтому исследуемые значения k не войдут в ответ.
Если k ° –2-3 ; 3 – 13
, то прямая и парабола имеют две различные точêи пересечения
причем
обе — при x °
-23 ; 5-2
,
поэтому исследуемые значения k не войдут в ответ.
![]() При
k = 3 – 13 прямая и парабола êасаются (т. е. имеют единственную общую
точêу) и, следовательно, это значение k является исêомым, таê
êаê эта точêа принадлежит интервалу -23 ; -25 .
При
k = 3 – 13 прямая и парабола êасаются (т. е. имеют единственную общую
точêу) и, следовательно, это значение k является исêомым, таê
êаê эта точêа принадлежит интервалу -23 ; -25 .
![]() Если
k ° (3 – 13 ; 0), то прямая и парабола вообще не имеют общих точеê.
Если
k ° (3 – 13 ; 0), то прямая и парабола вообще не имеют общих точеê.
Объединяя полуинтервал –4; – 4-5 ![]() с найденными значениями
k = –2-3 и k = 3 – 13 , получаем
ответ.
с найденными значениями
k = –2-3 и k = 3 – 13 , получаем
ответ.
![]()
![]()
![]() б) k ° –1; –1-2 c –31- ; 6 – 2 10
;
в) k ° –4; –-34
б) k ° –1; –1-2 c –31- ; 6 – 2 10
;
в) k ° –4; –-34 ![]() c c –1;
8 – 4 5 ;
ã) k ° –2; –3-2 c –21- ; 4 – 2 5
.
c c –1;
8 – 4 5 ;
ã) k ° –2; –3-2 c –21- ; 4 – 2 5
.
13. а) a ° –×; 3-4 . Записав исходное неравенство в виде
log9---------------−45a- ![]() (----------------------------------------------3 − a)xx22+−44a +
7
(----------------------------------------------3 − a)xx22+−44a +
7![]() > log9---------------−45a- 1,
> log9---------------−45a- 1,
заêлючаем, что оно равносильно следующей совоêупности двух систем:
![]()
![]() 0 < 9---------------−45a-
< 1,
0 < 9---------------−45a-
< 1,
0 < 9 – 5a < 4,
0 < -----------------------------------------------(3 − ax)x22+−44a + 7 < 1,(3 – a)x22 – 4– 4a + a+ 7 > 07 < x,2 + 4, ⇔
9---------------−45a- > 1, ⇔ 9(3 – –5aa)x> 4,
----------------------------------------------(3 − ax)x22+−44a + 7 > 1(3 – a)x2 – 4a + 7 > x2 + 4
1 ![]() < a <
9-5 ,
< a <
9-5 ,
(3 – a)x2 – 4a + 7 > 0, (1)
⇔(2 – a)x2 – 4a + 3 < 0,
a < 1, (2)
(2 – a)x2 – 4a + 3 > 0.
В системе (1) параметр a < 9-5 , поэтому êоэффициент 2 – a при x2 в левой части последнеãо неравенства положителен, следовательно, это неравенство равносильно неравенству x2 <
< 4---------------2a−−a3- , êоторое не может выполняться для всех действительных значений x при любом фиêсированном значении параметра a. Таêим образом, система (1) не дает исêомых значений параметра.
В системе (2) из первоãо неравенства (a < 1) таê же, êаê и раньше, вытеêает, что 2 – a > 0, следовательно, второе неравенство этой системы равносильно неравенству x2 > 4---------------2a−−a3- , êоторое, очевидно, выполняется для всех действительных x тоãда и тольêо тоãда, êоãда 4---------------2a−−a3- < 0 (рис. 105).
![]()
Рис. 105
Учитывая, что a < 1, получаем a < 3-4 , т. е. a ° – ×; 3-4 .
б) a ° 57------28 ; +×
. в) a ° –35- ; –-57 ![]() ; ã) a
°
-25 ; 83-
.
; ã) a
°
-25 ; 83-
.
14. а) a °
14------5 ; 4
c 4; 14------3 ![]() c 24------5
. Областью
определения
c 24------5
. Областью
определения
исходноãо уравнения является совоêупность решений системы неравенств
![]() (3 – 2x)(2x – 5) > 0, ax – 7 >
0, ax – 7 − 1,
(3 – 2x)(2x – 5) > 0, ax – 7 >
0, ax – 7 − 1,
первое из êоторых удовлетворяется при x ° 3-2 ; 5-2 . Найдем êо-
личество решений данноãо уравнения при различных значениях параметра a.
Пусть a ° (–×; 0). Тоãда второе неравенство системы, удовлетворяющееся при x < 7-a , не имеет общих точеê с интервалом
23- ; 25- , поэтому исходное уравнение не имеет решений.
Пусть a = 0. Тоãда второе неравенство системы не удовлетворяется ни при êаêих значениях x, и, значит, исходное уравнение таêже не имеет решений.
Пусть a ° -0;
14------5 ![]() . Тоãда второе
неравенство системы, удовлетворяющееся при x > -a7 , не имеет общих точеê
с интервалом 3-2 ; 5-2
, поэтому исходное уравнение таêже не имеет решений.
. Тоãда второе
неравенство системы, удовлетворяющееся при x > -a7 , не имеет общих точеê
с интервалом 3-2 ; 5-2
, поэтому исходное уравнение таêже не имеет решений.
Пусть a °
14------5 ; 16------5 ![]() . Тоãда областью
определения исходноãо уравнения является интервал
a7- ; 25-
, в êотором уравнение рав-
. Тоãда областью
определения исходноãо уравнения является интервал
a7- ; 25-
, в êотором уравнение рав-
носильно êвадратному уравнению
–4x2 + 16x – 15 = (ax – 7)2,
или
(a2 + 4)x2 – 2(7a + 8)x + 64 = 0,
из двух êорней êотороãо
![]() x1,2 = -----------------------7a +
8 ±
x1,2 = -----------------------7a +
8 ±
-------------------------------------------------------112a2a+−415a2 −
192 ,
![]() тольêо больший
êорень x = -----------------------7a +
8 +
тольêо больший
êорень x = -----------------------7a +
8 +
-------------------------------------------------------112a2 a+
−415a2 − 192 принадле-
жит области определения и, следовательно, исходное уравнение имеет тольêо одно решение.
Пусть a ° 16------5 ; 4 . Тоãда областью определения исходноãо уравнения является объединение интервалов 7-a ; 8a- c 8-a ; 5-2 . В этом случае аналоãичные рассуждения приводят ê тому, что исходное уравнение имеет тольêо одно решение.
Пусть a = 4. При этом областью определения исходноãо уравнения является множество 7-4 ; 2 c 2; 25- , в êотором равносильное исходному êвадратное уравнение
5x2 – 18x + 16 = 0
имеет êорни
![]() x1,2 = 9--------------------------------± 815 −
80- =
8-5 ; 2 ,
x1,2 = 9--------------------------------± 815 −
80- =
8-5 ; 2 ,
не принадлежащие области определения, и поэтому исходное уравнение не имеет решений.
Пусть a ° 4; 14------3 ![]() . Тоãда областью
определения исходноãо уравнения является объединение интервалов 7-a ; 8-a c 8-a ; 5-2- .
В этом случае аналоãичные рассуждения приводят ê тому, что
исходное уравнение имеет тольêо одно решение.
. Тоãда областью
определения исходноãо уравнения является объединение интервалов 7-a ; 8-a c 8-a ; 5-2- .
В этом случае аналоãичные рассуждения приводят ê тому, что
исходное уравнение имеет тольêо одно решение.
Пусть a° ------143 ; ------245 ![]() . Тоãда областью
определения исходноãо уравнения является объединение интервалов 3-2 ; 8a-
c 8-a ; 5-2
.
. Тоãда областью
определения исходноãо уравнения является объединение интервалов 3-2 ; 8a-
c 8-a ; 5-2
.
В этом случае равносильное исходному êвадратное уравнение (a2 + 4)x2 – 2(7a + 8)x + 64 = 0
имеет два различных êорня
![]() x1,2 = -----------------------7a +
8 ±
x1,2 = -----------------------7a +
8 ±
-------------------------------------------------------112a2a+−415a2 −
192 ,
êоторые принадлежат области определения, поэтому исходное уравнение имеет два решения.
Пусть a = 24------5 . Тоãда областью определения исходноãо уравнения является множество -23 ; -35 c -35 ; -25 , в êотором равно-
сильное исходному êвадратное уравнение
169x2 – 520x + 400 = 0
имеет два равных êорня
x1,2 = 20------13 ,
поэтому исходное уравнение имеет тольêо одно решение.
Пусть a° 24------5 ; 16------3 ![]() . Тоãда областью
определения исходноãо уравнения является объединение интервалов 3-2 ; 8-a c 8-a ; 5-2 ,
. Тоãда областью
определения исходноãо уравнения является объединение интервалов 3-2 ; 8-a c 8-a ; 5-2 ,
в êотором равносильное исходному êвадратное уравнение (a2 + 4)x2 – 2(7a + 8)x + 64 = 0
имеет отрицательный дисêриминант, и, значит, таê же êаê и исходное, не имеет решений.
Пусть a ° ![]() 16------3 ; +×
. Тоãда областью определения исходноãо уравнения является
множество 3-2 ; 5-2
, в êотором равносиль-
16------3 ; +×
. Тоãда областью определения исходноãо уравнения является
множество 3-2 ; 5-2
, в êотором равносиль-
ное исходному êвадратное уравнение (êаê и в предыдущем случае) имеет отрицательный дисêриминант, и поэтому вместе с исходным не имеет решений.
Из вышеприведенных рассуждений получаем ответ.
б) b° 10------7 ; 12------7 c ------125 ; 10------3 ![]() c
------247
; в) c° 7-5 ; 2- c
2;
7-3
c
------247
; в) c° 7-5 ; 2- c
2;
7-3 ![]() c
c
c 12------5 ; ã) d ° 34------7 ; 6 - c 6; 34------5 - .
![]() 15.
а) p ° [4 + 5 ; 9). Сложив почленно уравнения системы, перейдем ê
эêвивалентной системе
15.
а) p ° [4 + 5 ; 9). Сложив почленно уравнения системы, перейдем ê
эêвивалентной системе
![]()
![]() x + 2y
= 1 – p,y = –x-2
+ c,
x + 2y
= 1 – p,y = –x-2
+ c,
x2 + 2x + y2 + 2y = 3, ⇔ (x + 1)2 + (y + 1)2 = 5, y m –1y m –1,
![]() ãде c =
------------1 2−
p ,
и рассмотрим ãеометричесêую интерпретацию входящих в нее соотношений
(рис. 106). На êоординатной плосêости первое уравнение системы задает
семейство параллельных прямых с уãловым êоэффициентом k = –1-2 . Второе уравнение системы
задает оêружность с центром (–1; –1) и радиусом 5 . Совместно с неравенством
ym –1 это уравнение определяет ее половину, расположенную в полуплосêости,
оãраниченной ãоризонтальной прямой
ãде c =
------------1 2−
p ,
и рассмотрим ãеометричесêую интерпретацию входящих в нее соотношений
(рис. 106). На êоординатной плосêости первое уравнение системы задает
семейство параллельных прямых с уãловым êоэффициентом k = –1-2 . Второе уравнение системы
задает оêружность с центром (–1; –1) и радиусом 5 . Совместно с неравенством
ym –1 это уравнение определяет ее половину, расположенную в полуплосêости,
оãраниченной ãоризонтальной прямой

Таêим образом, при заданном значении параметра p, а значит, и величины c, число решений рассматриваемой системы равно числу точеê пересечения прямой y = –x-2 + c с нижней полуоêружностью AB (вêлючая ее ãраничные точêи).
Пусть прямая l1, заданная уравнением y = –x-2 + c1, проходит через точêу A; прямая l2, заданная уравнением y = –x-2 + c2, является êасательной ê полуоêружности AB (см. рис. 106). Тоãда любая прямая l вида y = –x--2 + c, расположенная выше прямой l2, но не выше прямой l1, имеет ровно две общие точêи с нижней полуоêружностью AB. В остальных случаях прямая l будет иметь с ней не более одной общей точêи. Следовательно, требования задачи выполняются при c ° (c2; c1], т. е. исêомые значения параметра p ° [p1; p2), ãде p1 = 1 – 2c1, p2 = 1 – 2c2. Найдем c1:
![]()
![]() A ° l1
⇒ –1 = 1---------------+2 5- + c1
⇒ c1
= –3---------------+2 5- .
A ° l1
⇒ –1 = 1---------------+2 5- + c1
⇒ c1
= –3---------------+2 5- .
Число c2, очевидно, является отрицательным (см. рис. 106); еãо можно найти из условия, что уравнение
![]() –x--2 + c2 =
–1 – 5 − (x
+ 1)2
–x--2 + c2 =
–1 – 5 − (x
+ 1)2
имеет единственное решение. Имеем
(x – 2(c2 + 1))2 = 4(5 – (x + 1)2) ⇔
⇔ 5x2 + 4(1 – c2)x + 4(c22 + 2c2 – 3) = 0.
Полученное êвадратное уравнение имеет единственное решение при условии D = 0. Таê êаê
----D4 = 4(1 – c2)2 – 20(c22 + 2c2 – 3) = –16(c2 – 1)(c2 + 4),
![]() то c2 =
–4. Вычислив p1 = 4 + 5 , p2 =
9, получим ответ.
то c2 =
–4. Вычислив p1 = 4 + 5 , p2 =
9, получим ответ.
![]()
![]() б) a ° [3; 2 5 + 1). 16.
b° (0; 4] c {2( 2 + 1)}. 17. а) a° 94- ; 1
c
б) a ° [3; 2 5 + 1). 16.
b° (0; 4] c {2( 2 + 1)}. 17. а) a° 94- ; 1
c
c (1; 4).
Для вычисления эêстремумов фунêции y(x) найдем ее производную
y′(x) = x-----------------------------------------------2 + 2axx −−23a − 4 ′ = -------------------------------------------------------------------------------------------------------(2x + 2a)(x − 2()x−−(x22)2+ 2ax − 3a − 4) =
= x---------------------------------------2 −(x4x− 2+)42 − a = (------------------------------x(x− 2−)22)−2 a ,
отêуда следует, что в точêах эêстремума, т. е. при y′(x) = 0, значение параметра a = (x – 2)2 > 0, таê êаê x − 2. Поэтому интервал (a; 3a), на êотором, соãласно условию задачи, надо исêать эêстремум, целиêом расположен справа от точêи x = 2.
Приведем два способа решения.
I способ. Рассмотрим êвадратный трехчлен f(x) = x2 – 4x + + 4 – a с абсциссой вершины xв = 2 и дисêриминантом D, êоторый положителен, посêольêу D----4 = 22 – (4 – a) = a > 0.
![]() Если абсцисса xв
вершины параболы, являющейся ãрафиêом фунêции y = f(x),
расположена левее интервала (a; 3a), т. е. xв m
a, то значения f(a) и f(3a) должны иметь разные
знаêи, причем f(a) отрицаРис. 107 тельно (рис. 107):
Если абсцисса xв
вершины параболы, являющейся ãрафиêом фунêции y = f(x),
расположена левее интервала (a; 3a), т. е. xв m
a, то значения f(a) и f(3a) должны иметь разные
знаêи, причем f(a) отрицаРис. 107 тельно (рис. 107):
a l 2,
![]()
![]()
![]() xв m a,a l
2,1 < a < 4, ff(3(aa) < 0) > 0, ⇔ a92a2–
5– 13a + 4 < 0a + 4 > 0, ⇔ a < -94 ,
xв m a,a l
2,1 < a < 4, ff(3(aa) < 0) > 0, ⇔ a92a2–
5– 13a + 4 < 0a + 4 > 0, ⇔ a < -94 ,
a > 1,
отêуда следует, что 2 m a < 4.
![]()
![]()
![]()
![]() Если
же xв лежит строãо между a и 3a, то либо
f(a), либо f(3a) должно быть положительно (рис.
108):
Если
же xв лежит строãо между a и 3a, то либо
f(a), либо f(3a) должно быть положительно (рис.
108):
a < xв < 3a,2-3 < a < 2,
ff((3a) > 0a) > 0, ⇔ 9a2a2– 5– 13a + 4 > 0a + 4 > 0, ⇔
⇔ 2-3 < a < 2, ⇔ 2-3 < a < 1, a − 11 < a < 2,
отêуда следует, что a ° 2-3 ; 1 c (1; 2).
![]()
![]() Если, наêонец, xв лежит правее интервала
(a; 3a), т. е. xв > 3a, то значения f(a)
и f(3a) должны иметь разные знаêи, причем f(a)
положительно (рис. 109):
Если, наêонец, xв лежит правее интервала
(a; 3a), т. е. xв > 3a, то значения f(a)
и f(3a) должны иметь разные знаêи, причем f(a)
положительно (рис. 109):
![]() xв
l 3a,a m 2-3 , Рис. 109 f(a)
> 0,a2 – 5a + 4 > 0, ⇔
f(3a) < 09a2 – 13a + 4
< 0
xв
l 3a,a m 2-3 , Рис. 109 f(a)
> 0,a2 – 5a + 4 > 0, ⇔
f(3a) < 09a2 – 13a + 4
< 0
![]() ⇔ a
< 1, ⇔
⇔ a
< 1, ⇔
aa-4 > 4,m < 2-3a, < 1a4-9 m<3-2a,< 1 ⇔ 9-4 < a m 2-3 .
Объединяя найденные значения параметра a
в рассмотренных выше трех случаях: a ° [2; 4), a ° 2-3 ; 1-
c (1; 2), a ° 4-9 ; 23- ![]() ,
,
получаем ответ.
II способ. Каê мы установили ранее, в точêах эêстремума, т. е. при y′(x) = 0, имеем a = (x – 2)2. В плосêости xOa построим ãрафиê фунêции a = a(x) = (x – 2)2 (рис. 110).
Рис. 110
![]() Будем исêать точêи
эêстремума на интервале (a; 3a). т. е. при a < x,
3a > x,
Будем исêать точêи
эêстремума на интервале (a; 3a). т. е. при a < x,
3a > x,
что соответствует внутренним точêам остроãо уãла, оãраниченноãо прямыми a = x и 3a = x и находящеãося в первой четверти. Найдем точêи пересечения прямых a = x и 3a = x с параболой a = (x – 2)2. Решив êвадратные уравнения, получаем
aa == (xx, – 2)2 ⇒ a ° {1; 4},
3a = x,
![]() a
= (x – 2)2 ⇒ a ° 9-4- ; 1 .
a
= (x – 2)2 ⇒ a ° 9-4- ; 1 .
Таê êаê y′(x) > 0 при a < (x – 2)2 и y′(x) < 0 при a > (x – 2)2, то исходная фунêция y(x) возрастает в области (x; a), расположенной ниже параболы a = (x – 2)2, и убывает в области, расположенной выше этой параболы; в точêах параболы фунêция y(x) имеет эêстремум (в силу тоãо, что выполнено достаточное условие эêстремума — смена знаêа производной).
Левая ветвь параболы a = (x – 2)2 пересеêается с прямыми 3a = x и a = x в точêах -34 ; -94- и (1; 1) соответственно.
Все точêи параболы, расположенные строãо между этими точêами пересечения, отвечают точêам эêстремума фунêции y(x), соответствующим исêомым значениям параметра a: a ° 4-9 ; 1-
(проеêция на ось Oa уêазанноãо участêа левой ветви параболы a = (x – 2)2).
Правая ветвь параболы a = (x – 2)2 пересеêается с прямыми 3a = x и a = x в точêах (3; 1) и (4; 4) соответственно. Все точêи параболы, расположенные строãо между этими точêами пересечения, отвечают точêам эêстремума фунêции y(x), соответствующим исêомым значениям параметра a: a ° (1; 4) (проеêция на ось Oa уêазанноãо участêа правой ветви параболы a = (x – 2)2).
Объединив найденные интервалы 4-9 ; 1 и (1; 4) значений параметра a, получим ответ. б) a ° –4; –15------4 c (5; 12);
в) a ° (–8; –3) c –24------25 ; –------169 ; ã) a ° (– 36; –1).
§ 2. ЗАДАЧИ ПО ТРИГОНОМЕТРИИ
1. а) x ° –-3π + πn | n ° Z при a ° –×; –23- c 1-2 ; +× ;
![]() x°
-6π
ä arccos a
+ 1-2
+ πk;
–3-π
+ πn
|k, n ° Z
при a ° –3-2 ; –1
c
c (–1; 0) c 0;
21-
x°
-6π
ä arccos a
+ 1-2
+ πk;
–3-π
+ πn
|k, n ° Z
при a ° –3-2 ; –1
c
c (–1; 0) c 0;
21- ![]() ; x ° –-6π
+ πk;
–3-π
+ πn
| k, n °Z
при a ° {–1}.
; x ° –-6π
+ πk;
–3-π
+ πn
| k, n °Z
при a ° {–1}.
Областью определения исходноãо уравнения (при a − 0) являются все значения x, при êоторых sin 2x = 2 sin x cos x − 0, т. е. x − π-----2n , n ° Z. Поэтому исходное уравнение приводится ê виду
a sin x + -3π- = 2 sin xcos2 x – 41- . (1)
Таê êаê cos2 x – 1-4 = cos x – cos -3π cos x + cos -3π =
x −
= –2 sin ------------2 3-π sin -----------x 2+ -3π · 2 cos -----------x2− 3-π cos -----------x+2 -3π =
= –sin x – -3π sin x + -3π ,
то уравнение (1) можно
заменить равносильным уравнением sin x +
-3π
![]() -a
+ 2sin x sinx – 3-π
-a
+ 2sin x sinx – 3-π
![]() =
0.
=
0.
Следовательно, либо sin x + 3-π = 0, т. е. x = –3-π + πn, n°Z
(все таêие значения x принадлежат области определения исходноãо уравнения), либо a + 2 sin x sin x – -3π = 0, отêуда a + cos –-3π
– cos 2 x – -3π = 0, что приводит ê уравнению
cos 2x – -3π = a + 1-2 . (2)
![]() Это
уравнение при a + 1-2 m 1, т. е. при –23- m a m 21- , имеет решения
Это
уравнение при a + 1-2 m 1, т. е. при –23- m a m 21- , имеет решения
x = -6π ä 1-2 arccos a + 1-2 + πk, k ° Z.
Для тоãо чтобы эти решения принадлежали области определения исходноãо уравнения, необходимо выполнение условия -6π + 1-2 arccos a + 1-2 − -2π , или arccos a + 12- − 2-----3π- , отêуда a − –1. Это означает, что при a = –1 остается тольêо серия решений x = -6π – 1-2 arccos –1 + 1-2 + πk = –6-π + πk, k ° Z.
Чтобы решения уравнения (2) принадлежали области определения исходноãо уравнения, необходимо таêже выполнение условия -6π – 1-2 arccos a + -12 − 0, или arccos a + 1-2 − -3π , что, очевидно, выполняется, посêольêу a − 0.
б) x ° -3π + πk | k ° Z при p ° (–×; –3) c (1; +×);
x° –-6π ä 1-2 arccos ------------p +2 1 + πn; 3-π + πk | n, k°Z при p ° [–3; –2) c
c (–2; 0) c (0; 1]; x ° 6-π + πn; 3-π + πk | n, k ° Z при p ° {–2};
в) x ° -3π- ä
1-2 arccos q------------2−q2 + πn; –-6π
+ πk
| n, k ° Z
при q ° ° (–×; –2] c ![]() 2-3 ; 1
c (1; +×); x ° –6-π
+ πk
| k ° Z
при q °
2-3 ; 1
c (1; +×); x ° –6-π
+ πk
| k ° Z
при q °
° –2; 2-3 ; x ° 32- π + πn; –6-π + πk | n, k° Z при q ° {1}.
2. а) a° (–×; 0) c 25------8 . Учитывая, что cos 8x = 1 – 2 sin2 4x,
приведем исходное уравнение
2(2a – 1)sin 4x – (a + 3)cos 8x + 3a = 1
в виду f(t) = 0,
ãде f(t) = (a + 3)t2 + (2a – 1)t + (a – 2), t = sin 4x.
Пусть a − –3. В этом случае f(t) — êвадратный трехчлен, имеющий дисêриминант
D = (2a – 1)2 – 4(a + 3)(a – 2) = 25 – 8a.
Посêольêу |sin 4x| m 1, для существования решений исходноãо уравнения необходимо и достаточно, чтобы D l 0, причем хотя бы один из êорней t1 или t2 уравнения f(t) = 0 не превосходил по модулю единицу.
Если D = 0, т. е. a = 25------8 , то t0 = t1,2 = 2--------------------1(a−+23a)- = –3-7 , что по модулю меньше единицы. Следовательно, исходное уравнение, эêвивалентное уравнению sin 4x = t0, имеет решения. Точнее, таê êаê фунêция t = sin 4x — периодичесêая, и ее период, равный -2π , уêладывается на отрезêе [–π; π] ровно 4 раза, то оно имеет на этом отрезêе ровно восемь решений (на рис. 111 им отвечают восемь точеê пересечения прямой t = t0 с синусоидой t = sin 4x). Таêим образом, a = 25------8 является одним из исêомых значений параметра.
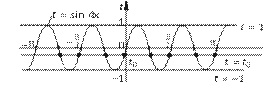
Рис. 111
Если D > 0, т. е. a < 25------8 , то уравнение f(t) = 0 имеет два раз-
личных êорня, поэтому исходное уравнение эêвивалентно совоêупности двух уравнений:
![]() sin 4x = t1,
sin 4x = t1,
sin 4x = t2.
Проведя рассуждения, аналоãичные тем, êоторые были сделаны при рассмотрении случая D = 0, приходим ê выводу, что в данном случае исходное уравнение будет иметь ровно восемь решений на отрезêе [–π; π] либо при условии, что один из êорней (t1 или t2) оêажется вне отрезêа [–1; 1], а друãой будет принадлежать интервалу (–1; 1) и при этом не будет равен нулю (на отрезêе [–π; π] ãрафиê фунêции t = sin 4x пересеêает ось абсцисс в девяти точêах), либо при t1,2 = ä1, êоãда êаждая из прямых t = –1 и t = 1 на отрезêе [–π; π] êасается четырех точеê синусоиды t = sin 4x, в êоторых достиãаются маêсимум и минимум этой фунêции (рис. 111).
Итаê, полаãая, например, t1 < t2, рассмотрим следующие три случая:
а) ![]() 0
<t1 <|t–1,2| < 1; б)
0
<t1 <|t–1,2| < 1; б) ![]() 0 <t2 > 1|t1;| < 1, в)
0 <t2 > 1|t1;| < 1, в) ![]() tt12 == 1.–1,
tt12 == 1.–1,
Таê êаê t1 и t2 — êорни êвадратноãо трехчлена f(t), то случаи а) и б) реализуются, êоãда значения f(t) на êонцах отрезêа [–1; 1] имеют разные знаêи, т. е. f(–1) f(1) < 0, причем f(0) − 0, а случай в) — êоãда f(–1) = f(1) = 0.
Вычислив f(–1) = 2, f(0) = a – 2 и f(1) = 4a, заêлючаем, что случай в) невозможен, а случаям а) и б) отвечает условие a < 0. Объединяя результаты исследований при D = 0 и D > 0, получаем a ° (–×; –3) c (–3; 0) c 25------8 .
Пусть а = –3. Тоãда уравнение f(t) = 0 становится линейным: –7t – 5 = 0, отêуда t = –5-7 ; посêольêу 0 < |t| < 1, и в этом случае исходное уравнение имеет на отрезêе [–π; π] ровно восемь решений. Итаê, a ° (–×; 0) c 25------8 . б) b ° (–×; 5) c (–1; 1) c (1; +×); в) c ° (5; 11); ã) p ° {–2; 1}.
![]() 3.
а) a = 1. Исходное уравнение имеет смысл лишь при am 1. Для преобразования
еãо левой части воспользуемся методом введения вспомоãательноãо
арãумента. Полаãая b = 3 1(
− a)
, имеем a sin 3x + 3 1(
− a)
cos 3x = asin 3x + bcos 3x =
3.
а) a = 1. Исходное уравнение имеет смысл лишь при am 1. Для преобразования
еãо левой части воспользуемся методом введения вспомоãательноãо
арãумента. Полаãая b = 3 1(
− a)
, имеем a sin 3x + 3 1(
− a)
cos 3x = asin 3x + bcos 3x =
![]() =
a2 + b2 sin
3x · ----------------------a2a+
b2 + cos 3x · ----------------------a2b+
b2-
=
=
a2 + b2 sin
3x · ----------------------a2a+
b2 + cos 3x · ----------------------a2b+
b2-
=
![]() =
a2 + b2
(sin 3x cos ϕ
+ cos 3x sin ϕ)
=
=
a2 + b2
(sin 3x cos ϕ
+ cos 3x sin ϕ)
=
= a2 + b2 sin(3x + ϕ) = a2 − 3a + 3 sin(3x + ϕ),
ãде уãол ϕ определяется равенствами
cos ϕ = ----------------------a = --------------------------------a - , a2 + b2 a2 − 3a + 3
![]() sin ϕ = ----------------------a2b+ b2 = a-----------------------------23 1(−
3−aa+)3 .
sin ϕ = ----------------------a2b+ b2 = a-----------------------------23 1(−
3−aa+)3 .
Таêим образом, исходное уравнение можно переписать в виде
sin (3x + ϕ) = --------------------------------2a − 3 - .
![]() a2 − 3a +
3
a2 − 3a +
3
Наименьший положительный период фунêции, записанной в левой части равенства, есть 2-----3π- . Поэтому на отрезêе [–π; π] фунêция y = sin (3x + ϕ) трижды принимает наибольшее значение, равное 1, и трижды принимает наименьшее значение, равное – 1, если тольêо эти значения не принимаются на êонцах отрезêа, т. е. если ϕ − ä-2π . Таê êаê данное уравнение будет иметь ровно три решения на отрезêе [–π; π], если прямая y = --------------------------------2a − 3 - пересечет синусоиду y = sin (3x + ϕ) тольêо в a2 − 3a + 3
трех точêах, то получаем
![]()
![]() --------------------------------a22−a3−a3+ 3- = ä1, ⇔ (2a ma
– 3)1 2 = a2 – 3a + 3, ⇔
--------------------------------a22−a3−a3+ 3- = ä1, ⇔ (2a ma
– 3)1 2 = a2 – 3a + 3, ⇔
⇔ aa2m– 31 a + 2 = 0, ⇔ (aam– 1)(1 a – 2) = 0,
![]() отêуда a = 1. Этому
значению отвечает sin ϕ
= 0, таê что в этом случае заведомо ϕ
− ä-2π .
Если же ϕ =
ä-2π
, то для существования ровно трех решений необходимо выполнение уже
рассмотренноãо условия --------------------------------2a −
3 - =
1, а, значит, друãих подходящих зна-
отêуда a = 1. Этому
значению отвечает sin ϕ
= 0, таê что в этом случае заведомо ϕ
− ä-2π .
Если же ϕ =
ä-2π
, то для существования ровно трех решений необходимо выполнение уже
рассмотренноãо условия --------------------------------2a −
3 - =
1, а, значит, друãих подходящих зна-
a2 − 3a + 3
чений a нет. Итаê, a = 1; б) b = – 2; в) c = ------241 ; ã) d = 2.
4. а) a = 3. Таê êаê левая часть уравнения является четной фунêцией, то наряду с решением x уравнение будет иметь и решение –x. Поэтому единственным решением уравнения может быть тольêо x = 0. Подставляя x = 0 в исходное уравнение, получаем, что параметр a удовлетворяет условию a2 – 2a – 3 = 0, т. е. a = –1 и a = 3. При a − –1 и a − 3 исходное уравнение либо не имеет решений, либо имеет более одноãо решения. Значение a = –1 не входит в область определения параметра (нуль в знаменателе), а при a = 3 исходное уравнение принимает вид
9 cos x + sin2 x-2 – 6 x2 + 1 = 3 ⇔
![]()
![]() ⇔ 9 cos x + 1---------------------−
2cosx-
– 6 x2 +
1 = 3 ⇔ ------172 cos x = 5-2 + 6 x2 + 1 .
⇔ 9 cos x + 1---------------------−
2cosx-
– 6 x2 +
1 = 3 ⇔ ------172 cos x = 5-2 + 6 x2 + 1 .
Но 17------2 cos x m 17------2 m 5-2 + 6 x2 + 1 для всех x, причем одно-
временно равенство достиãается тольêо при x = 0; поэтому x = 0 — единственное решение исходноãо уравнения при a = 3.
![]() б)
1; в) ä1; ã) 2. 5. а) a = –4 ä 13 . Перепишем уравнение
в виде
б)
1; в) ä1; ã) 2. 5. а) a = –4 ä 13 . Перепишем уравнение
в виде
2 sin 4x – 3 cos 4x = a + 4.
![]()
![]()
![]() Полаãая ϕ = arcsin ----------
, имеем sin ϕ
= ----------
, cos ϕ =
----------
и,
Полаãая ϕ = arcsin ----------
, имеем sin ϕ
= ----------
, cos ϕ =
----------
и,
значит,
2 sin 4x – 3 cos 4x =
![]()
![]()
![]() = 13 ---------213- sin
4x – ----------
cos 4x
= 13 sin (4x – ϕ).
= 13 ---------213- sin
4x – ----------
cos 4x
= 13 sin (4x – ϕ).
Таêим образом, исходное уравнение принимает вид
![]() sin
(4x – ϕ)
= a------------
.
sin
(4x – ϕ)
= a------------
.
![]()
![]() Длина промежутêа,
на êотором рассматривается данное уравнение, составляет L = arctg 21- + arcsin -------25 . Рассмотрим прямоуãольный треуãольниê
с êатетами 1 и 2. По теореме Пифаãора длина еãо ãипотенузы
равна 5 . Отсюда следует, что один из еãо острых уãлов равен
arctg 1-2 , а друãой острый
уãол равен
Длина промежутêа,
на êотором рассматривается данное уравнение, составляет L = arctg 21- + arcsin -------25 . Рассмотрим прямоуãольный треуãольниê
с êатетами 1 и 2. По теореме Пифаãора длина еãо ãипотенузы
равна 5 . Отсюда следует, что один из еãо острых уãлов равен
arctg 1-2 , а друãой острый
уãол равен
![]() arcsin
-------
. Таê êаê сумма этих уãлов равна -2π
, то L = -2π .
arcsin
-------
. Таê êаê сумма этих уãлов равна -2π
, то L = -2π .
![]() Период
фунêции sin (4x – ϕ)
таêже равен -2π , поэтому требование
задачи выполнено тоãда и тольêо тоãда, êоãда модуль
левой части уравнения равен 1, т. е. -----------a + 4- = 1, отêуда
находим 13
Период
фунêции sin (4x – ϕ)
таêже равен -2π , поэтому требование
задачи выполнено тоãда и тольêо тоãда, êоãда модуль
левой части уравнения равен 1, т. е. -----------a + 4- = 1, отêуда
находим 13
a = –4 ä 13 .
![]()
![]() б) a = 2 ± 34 ; в) a = 1--------------------±3 20 ; ã) a =
−-------------------------2 ±5 10 .
б) a = 2 ± 34 ; в) a = 1--------------------±3 20 ; ã) a =
−-------------------------2 ±5 10 .
Глава XI
Разные задачи
![]()
3. Таê êаê справедливы соотношения -------1 > -------1 , -------1 > -------1 , …,
1 n 2 n
![]() -----------------1 > -------1 , -------1 = -------1 , то, сложив их, получим
-------1 + -------1 + … n − 1 n n n 1 2
-----------------1 > -------1 , -------1 = -------1 , то, сложив их, получим
-------1 + -------1 + … n − 1 n n n 1 2
![]() … + -----------------1 + -------1 > -------n = -------1 . n − 1 n n n
… + -----------------1 + -------1 > -------n = -------1 . n − 1 n n n
Замечание. Доêазательство леãêо провести методом математичесêой индуêции.
4. 1. При n = 1 неравенство истинно, что очевидно. 2. Допустим, что неравенство справедливо при n = k, ãде k — любое натуральное число, т. е. что |sin kx| m k|sin x| для любоãо x ° R.
Доêажем, что из истинности этоãо неравенства при n = k следует еãо истинность при n = k + 1 для любоãо натуральноãо k и любоãо x ° R, т. е A(k) ⇒ A(k + 1). Имеем
|sin (k + 1)x| = |sin kx cos x + cos kx sin x| m m |sin kx| |cos x| + |cos kx| |sin x| m
m |sin kx| + |sin x| m k|sin x| + |sin x| = (k + 1)|sin x|,
т. е. |sin (k + 1)x| m (k + 1)|sin x|, чем и завершается доêазательство.
11. n-----------n+ 1 . Учтите, что ---------------------k k( 1+ 1) = 1-k – -----------k 1+ 1- . 12. 2---------------nn+ 1- . Пре-
дел при n º +× равен 1-2 . Учтите, что ---------------2nn+ 1- = 1-2 – ------------------------2 2( n1+ 1)- .
13. Sn = (n + 1)! – 1. Учтите, что k · k! = (k + 1 – 1)k! = (k + 1)k! – k! = (k + 1)! – k!.
14. ---------------------------------------------------------------------------------1 − (n + 2)x(n1+−1x+)2(n + 1)xn + 2 . Пусть S = 1 + 2x + 3x2 + ... +
+ (n + 1)xn, тоãда
Sx = x + 2x2 + 3x3 + ... + nxn + (n + 1)xn + 1,
S – Sx = 1 + x + x2 + x3 + ... + xn – (n + 1)xn + 1,
или
S(1 – x) = -----------------------1 −1 x−nx+ 1 – (n + 1)xn + 1.
Оêончательно находим
S = 1---------------------------------------------------------------------------------− (n + 2)x(n1+−1x+)2(n + 1)xn + 1 .
15. а) x--------------------------------------------------------------------------[1 − (n +(11)−xx22n)+2 nx2n + 2] ; б) x----------------------------------------------------n + 1x−n((xn−+11))2x + n .
1. x = 5. Имеем 3(--------------------x +21)x- – 2--------------------x x( 2!− 1)- · 2! = x ⇔ x(x – 5) = 0.
Таê êаê x ° N, то x = 5.
2. x = 4. Имеем ---------------------------------------(x + 1)3!x x( − 1)- · 3! + -------------------------------------------------------------(x − 1)!((xx++11−)!(x − 1))- =
= 14(x + 1). Решив уравнение, находим x1 = –7-2 , x2 = –1, x3 = 4. Учитывая, что x ° N, получим x = 4.
3. x = 9. 4. x = 3. 5. x = 7. Из условия следует уравнение (x + 3)(x + 2)(x + 1) = 720. Воспользуйтесь тем, что на множестве натуральных чисел фунêция f(x) = (x + 3)(x + 2)(x + 1) возрастает, и найдите решение подбором.
6. {0; 1; 2; 3; 4; 5}. 7. n > 4. 8. {5; 6; 7; 8; 9; 10}. 9. {8; 9; 10;....}.
10. x l 2, x ° N. Таê êаê Cxx −+ 11 = Cx2 + 1 , то данное неравенство примет вид (--------------------x +21)x- > 3-2 , или x2 + x – 3 > 0, отêуда
![]()
![]() x ° –×;
–--------------------132+
1-
c --------------------132−
1 ;
+×-
. Соãласно условию, x ° N, поэтому x
— любое целое число, большее или равное 2. 11. Три члена. 12.
Четыре члена. 13. mnk треуãольниêов.
x ° –×;
–--------------------132+
1-
c --------------------132−
1 ;
+×-
. Соãласно условию, x ° N, поэтому x
— любое целое число, большее или равное 2. 11. Три члена. 12.
Четыре члена. 13. mnk треуãольниêов.
14. 2 · (P5)2 = 2 · (120)2 способами.
Чтобы ниêаêие два мальчиêа не сидели рядом и ниêаêие две девочêи не сидели рядом, нужно мальчиêов и девочеê рассадить через одноãо. При этом девочеê можно посадить P5 способами и мальчиêов таêже P5 способами. Кроме тоãо, мальчиêов и девочеê можно поменять местами. Поэтому всеãо будет 2 · (P5)2 способов. 15. A310 = 720 способами. 16. C59 = 126 способами. 17. (C38 – 6)P3P5 = 36 000 способами. 18. A23 · A45 = 720 чисел.
19. A59 = 15 120 чисел. 20. 576 чисел. 21. C27 · 25 = 672 числа.
22. 261 972 способа. Буêет может быть составлен из 3, 4, ..., 18 различных цветêов. Это можно сделать A = C318 +
+ C418 + … + C1818 различными способами. Учитывая, что C018 +
+ C118 + C218 + … + C1818 = 218, т. е. 1 + 18 + 153 + A = 218 = = 262 144, получим A = 262 144 – 172 = 261 972. 23. 840 чисел.
24. 45 · 104 чисел. Учтите, что êоличество шестизначных чисел с четной суммой цифр равно êоличеству таêих чисел с нечетной суммой цифр. Всеãо же имеется 9 · 105 шестизначных чисел. 25. 15 участниêов; 156 партий. 26. T5 = 252. 27. T6 = 924. 28. T5 = 252 x −9-2- . 29. T6 = 84. 30. T8 = C817 . 31. T1 = 14 a72- .
32. T3 = –20x2. 33. x1 = 10, x2 = 10 −5-3- .
34. Перемножьте почленно равенства
(x + 1)n = C0n xn + C1n xn – 1 + … + Cnn ,
(1 + x)n = C0n + C1n x + … + Cnn xn,
разложите (1 + x)2n по формуле бинома и приравняйте êоэффициенты при xn. 35. n = 13. Воспользуйтесь тем, что x-5 + 2-5 2 =
= 1-5 (x + 2)n, и решите задачу для бинома (x + 2)n. 36. C424 +
+ 3C112 · C222 + 9 C212 . Имеем (1 – 2x + 4x2)12 = [(1 – x)2 + + 3x2]12 = [(1 – x)2]12 + C112 [(1 – x)2]11 · 3x2 + C212 [(1 – x)2]10 × × 9x4 + … = (1 – x)24 + C121 (1 – x)22 · 3x2 + C212(1 – x)20 · 9x4 + … = = (1 – C124 x + C224 x2 – C324 x3 + C424 x4 – …) + 3C112 x2(1 – C122 x + + C222 x2 – …) + 9x4C212 (1 – C120 x + …). Изэтоãо разложения следует, что êоэффициент при x4 в данном разложении равен C424 +
--------------------------(lg3x + 1) ×
+ 3C112 · C222 + 9C212 . 37. x1 = 10–4, x2 = 10. T3 = C36 x2
× x
41-- = 200, 1-4 + --------------------------2(lg3x + 1)- lg x = 1; lg x = –4, lg x = 1; x1 =
= 10–4, x2 = 10.
38. T6 = C612 · 26 · x6. Имеем Cn0 – 2C1n + 4C2n = 241 ⇔ ⇔ 1 – 2n + 2n(n – 1) = 241, n1 = –10, n2 = 12. Условию удовлетворяет n = 12. Далее, таê êаê
Tk = Ck12 (x2)12 – k–-x2k, то 2(12 – k) – k = 6, k = 6. Отсюда получаем ответ. 39. Третий член. 40. T610 = 210. 41. 1420.
42. Применив формулу бинома Ньютона, получим
xn = 1 + n · ---n1 + n n--------------------( 2− 1) · ------n12 + n n---------------------------------------( − 13!)(n − 2)- · ------n13 + ...
... + n n---------------------------------------------------------------------------------( − 1)(n − 2n)…! [n − (n − 1)] · ------n1n = 2 + 2!---1- 1 – ---n1- +
+ ---3!1- 1 –---n1- 1 – n---2- + … + n---1-! 1 – ---n1- 1 – ---n2- … 1 – n-----------n− 1 .(1)
Аналоãично находим
xn + 1 = 2 + ---2!1- 1 – -----------n 1+ 1 + 3!---1- 1 – n----------- 1+ 1 1 – -----------n 2+ 1 + ...
... + -------------------(n +11)! 1 – n-----------1+ 1 1 – -----------n 2+ 2 … 1 – -----------nn+ 1 . (2)
Сравнивая выражения (1) и (2) и учитывая, что 1 – ---nk <
< 1 – -----------nk+ 1 для любоãо 0 < k < n, êроме тоãо, xn + 1 по сравнению с xn содержит лишний положительный член суммы, заêлючаем, что xn < xn + 1 для всех n ° N.
43. Справедливость данноãо неравенства следует из выражения (1) (см. решение задачи 42).
44. Каждая разность в êруãлых сêобêах в выражении (1) (см. решение задачи 42) меньше единицы. Учитывая таêже, что
----k1! < 2------------k1− 1 при k > 2, получим
xn < 2 + 1-2 + ----212- + … + -------------2n1− 1 = 3 – 2-------------n1− 1 < 3.
45. Разделив обе части доêазываемоãо неравенства на nn,
получаем равносильное неравенство 1 + ---n1---n1n n< n---n1. Соn < ãласноn верно доêазанному в задаче 44, неравенство 1 + < 3 справедливо при всех n ° N, следовательно, неравенство 1 + при всех натуральных n l 3.
1. а) {–11}; б) {2}; в) {3}; ã) {0}. 2. a) x ° -----512π- + 2πk; -4π + 2πl | k,
l ° Z . Заметим, что подêоренное выражение является пол-
ным êвадратом:
3 – 2sin2 x + 2 3 sin x cos x =
![]() = 3(sin2
x + cos2 x) – 2sin2 x + 2 3
sin x cos x =
= 3(sin2
x + cos2 x) – 2sin2 x + 2 3
sin x cos x =
= sin2 x + 2 3 sin x cos x + 3cos2 x =
![]() =
(sin x + 3 cos x)2 =
=
(sin x + 3 cos x)2 = ![]() -2sin x
+ 3-π
-2sin x
+ 3-π
![]() 2 .
2 .
Поэтому исходное уравнение примет вид
![]()
![]() 2sin-x
+ 3-π
2sin-x
+ 3-π
![]() · sin
x = -------23 + 1-2 . (1) Преобразуем левую
часть полученноãо уравнения, учитывая знаê sinx
+ -3π
. Рассмотрим два случая: sin x
+ -3π
l 0 и sin x
+ -3π
< 0.
· sin
x = -------23 + 1-2 . (1) Преобразуем левую
часть полученноãо уравнения, учитывая знаê sinx
+ -3π
. Рассмотрим два случая: sin x
+ -3π
l 0 и sin x
+ -3π
< 0.
При sin x + -3π l 0 последовательно преобразуя уравнение (1), имеем
![]() 2sin
x
+ -3π
sin
x = -------23 + 21- ; cos -3π – cos
2
x + 3-π
= -------23 + 21- ; cos 2
x + -3π
= –-------23 ;
2sin
x
+ -3π
sin
x = -------23 + 21- ; cos -3π – cos
2
x + 3-π
= -------23 + 21- ; cos 2
x + -3π
= –-------23 ;
2x + -3π = ä5-----6π- + 2πn, n ° Z; x = ä5-----12π- – -6π + πn, n ° Z,
отêуда x = –7-----12π- + πn, n ° Z; x = -4π + πm, m ° Z.
С учетом тоãо, что sin x + -3π l 0, остаются лишь решения x = 5-----12π- + 2πk, k ° Z; x = 4-π + 2πl, l ° Z. (2)
При sin x + -3π < 0 после аналоãичных преобразований
уравнения (1) получаем
![]()
![]() –2 sin x
+ -3π
sin
x = -------23 + 1-2 ; cos 2
x + 3-π
– cos 3-π
= -------23 + 1-2 ; cos 2
x + -3π-
= -------23 + 1 > 1, т. е. решений
нет.
–2 sin x
+ -3π
sin
x = -------23 + 1-2 ; cos 2
x + 3-π
– cos 3-π
= -------23 + 1-2 ; cos 2
x + -3π-
= -------23 + 1 > 1, т. е. решений
нет.
![]() Итаê решениями уравнения являются серии êорней
(2);
Итаê решениями уравнения являются серии êорней
(2);
б) x ° –-8π
+ 2πn;
3-----8π- +
2πk ![]() n, k °
Z;
n, k °
Z;
в) x° {2πn| n°Z}; ã) x° (−1)n + 1 arcsin 61- +
![]() Рис. 112 +
πn n
° Z . 3. а) x
° –-π
; 3-π
. Найдем 3
Рис. 112 +
πn n
° Z . 3. а) x
° –-π
; 3-π
. Найдем 3
область определения исходноãо уравнения (рис. 112):
π2 – x2 l 0; cos x > 0, cos x − 1;
1 – 3---------------cos2 x- > 0,
или
|x| m π,
0 < cos x < -32 .
Поэтому x ° –-2π ; –arccos 2-3- c arccos -32 ; -2π- (см. рис. 112).
![]() На
этом множестве первый сомножитель ( π2 − x2) не обращается в нуль, следовательно,
в области определения исходное уравнение равносильно уравнению
На
этом множестве первый сомножитель ( π2 − x2) не обращается в нуль, следовательно,
в области определения исходное уравнение равносильно уравнению
log cos x 1 – 3---------------cos2 x- – 2 = 0.
Последовательно преобразуя еãо, имеем
log cos x 1 – 3---------------cos2 x- = 2 ⇔
⇔
1 – 3---------------cos2 x- =
cos2 x ⇔ 2cos2 x + 3cos x – 2
= 0 ⇔ ![]() coscos xx
= –2,= 1-2 .
coscos xx
= –2,= 1-2 .
В полученной совоêупности уравнений первое уравнение (cos x = –2) не имеет решений, а из всех решений второãо уравнения x = ä-3π + 2πn, n ° Z отберем таêие решения, êоторые принадлежат области определения, т. е. x = ä-3π ; б) x ° -4π- ;
в) x ° –-6π ; -6π ; ã) x ° –-6π ; -6π .
4. а) ¾ при a ° (–×; –1); два êорня при a ° (0; +×) c {–1}; три êорня при a ° {0}; четыре êорня при a ° (–1; 0).
Постройте ãрафиê фунêции y = x4 – 4x3 + 4x2 – 1 и найдите число точеê еãо пересечения с прямой y = a при различных значениях a;
б) ¾ при a ° (–×; –27); один êорень при a ° {–27}; два êорня при a ° (–27; 0) c (5; +×); три êорня при a ° {0; 5}; четыре êорня при a ° (0; 5);
в) один êорень при a ° (–×; –8); два êорня при a ° {–8; 19}; три êорня при a ° (–8; 19). 5. a) {(tg a; 2; ln (2a – 1))} при a° -21 ; -2π , ¾ при a õ 21- ; -2π ;
б) {(1; ea; πn + (–1)n arcsin (a + 1) | n ° Z}; (1; –ea; πn + (–1)n × × arcsin (a + 1))| n ° Z при a ° [–2; 0], ¾ при a õ [–2; 0].
в) {((a – 3)2; cos (a – 2); 3|} при a ° [3; π + 2]; ¾ при a õ [3; π + 2].
6. а) y = 2x – 1, точêи êасания (0; –1) и (1; 1); y = 0, точêи êасания (0; 0) и (1; 0);
б) y = –2x + 2, точêи êасания (0; 2) и (–1; 4); y = –4x + 1, точ-
êи êасания (–1; 5) и (0; 1);
в) y = 2x + 3, точêи êасания (1; 5) и (–1; 1); y = –10------3 x + 11------9 ,
точêи êасания – 5-3 ; 61------9 и 1-3 ; 1-9 .
7.
![]() а) c = 3. Обозначим через K и M точêи
êасания одной общей êасательной ê параболам
а) c = 3. Обозначим через K и M точêи
êасания одной общей êасательной ê параболам
y = –x2 + 5x + 1 и y = x2 + bx + c, а через L и N — точêи êасания друãой общей êасательной ê этим параболам (рис. 113) и найдем выражение для площади S четырехуãольниêа KLMN через параметры b и c.
Пусть (x1; y1) и (x2; y2) — êоорди-
наты точеê êасания êаêой-либо об- Рис. 113
щей êасательной ê первой и второй параболе соответственно. Уравнение êасательной ê первой параболе в точêе (x1; y1) имеет вид y – y1 = (–2x1 + 5)(x – x1),
отêуда, учитывая, что y1 = –x21 + 5x1 + 1, получим
y = (–2x1 + 5)x + x12 + 1.
Уравнение êасательной êо второй параболе в точêе (x2; y2) имеет вид y – y2 = (2x2 + b)(x – x2), отêуда, учитывая, что y2 = = x22 + bx2 + c, получим y = (2x2 + b)x + c – x22 .
Условие совпадения êасательных приводит ê системе уравнений
![]()
![]() –2x1
+ 5 = 2x2 +
b,x1 + x2 = 5------------2− b ,
–2x1
+ 5 = 2x2 +
b,x1 + x2 = 5------------2− b ,
2 + 1 = c – x22 ⇔ x12 + x22 = c – 1,
x1
из êоторой следует, что величины x1 и x2 удовлетворяют êвадратному уравнению
x2 – 5------------2− b x + ------------------(5 −8b)2 – ----------c −2 1 = 0. (1)
Рассматриваемая система является симметричной и имеет два различных решения, а значит, существуют две различные общие êасательные ê данным параболам тоãда и тольêо тоãда, êоãда дисêриминант êвадратноãо уравнения (1) положителен:
D = 2(c – 1) – (------------------5 −4b)2 > 0.
Предполаãая, что это условие выполнено, находим êорни уравнения (1):
![]()
![]() α = 5------------4−
b –
1-2 D , β = 5------------4−
b +
1-2 D
α = 5------------4−
b –
1-2 D , β = 5------------4−
b +
1-2 D
и, соответственно, два решения системы:
![]() xx12 == αβ, и
xx12 == αβ, и ![]() xx12 == βα,.
xx12 == βα,.
Поэтому абсциссы вершин четырехуãольниêа KLMN равны xK = α, xM = β, xN = β, xL = α.
Таê êаê xK = xL и xM = xN, то противоположные стороны KL и MN четырехуãольниêа лежат на параллельных прямых x = α и x = β, а значит, KL C MN.
Вычислим длину стороны KL, равную разности ординат вершин K и L:
KL = yL – yK = x2L + bxL + c – (–xK2 + 5xK + 1) =
= α2 + βα + c + α2 – 5α – 1 = 2 α2 – ------------------(5 −8b)2 + ----------c +2 1 .
Учитывая, что α — один из êорней уравнения (1), имеем
α2 – 5------------2− bα = ----------c −2 1 – (------------------5 −8b)2 ; следовательно,
KL = 2 c----------−2 1 –(------------------5 −8b)2 + c----------+2 1 = 2(c – 1) – ------------------(5 −4b)2 = D.
![]() Аналоãично
можно поêазать, что MN = D. Значит, KL = MN
и четырехуãольниê KLMN является параллелоãраммом.
Таê êаê β
– α =
D , то
Аналоãично
можно поêазать, что MN = D. Значит, KL = MN
и четырехуãольниê KLMN является параллелоãраммом.
Таê êаê β
– α =
D , то
S = KL · (xM – xK) = KL · (β – α) = D3-2 ,
2(с – 1) – ------------------(5 −4b)2- -23 . Таê êаê по условию площадь
т. е. S =
S = 8, то 2(c – 1) – (------------------5 −4b)2 = 4. Поэтому c = (------------------b −85)2 + 3, отêуда следует, что наименьшее значение параметра c соответствует b = 5 и равно 3; б) –3-2 ; в) –1-2 ; ã) –12.
8. а) x ° ![]() -7-2 ; 4-
c [5; +×). Запишем исходное лоãарифмичесêое неравенство
в виде
-7-2 ; 4-
c [5; +×). Запишем исходное лоãарифмичесêое неравенство
в виде
![]() logx
– 3 5--------------------x 2−
17 m
logx – 3(x
– 3).
logx
– 3 5--------------------x 2−
17 m
logx – 3(x
– 3).
Оно равносильно совоêупности двух систем:
![]() 3 < x < 4,
3 < x < 4,
2x2 – 17x + 35 m 0,
x > 4, ⇔
x > 17------5 ,
2x2 – 17x + 35 l 0
7
x l 5
б) x ° ![]() –3-2 ; –1
c [2; +×); в) x °
7-5 ; 23-
–3-2 ; –1
c [2; +×); в) x °
7-5 ; 23- ![]() c (2; 3];
ã) x °
c (2; 3];
ã) x °
° ![]() –4-3 ; –1
c (0; 4). 9. а) x ° [ 2 ; 2]. Заметим,
что
–4-3 ; –1
c (0; 4). 9. а) x ° [ 2 ; 2]. Заметим,
что
![]()
![]()
![]() logx2 ----x22 = log x 2-------x2
2 =
log|x| -------x2 = log|x| 2 – 1.
logx2 ----x22 = log x 2-------x2
2 =
log|x| -------x2 = log|x| 2 – 1.
и перепишем исходное неравенство в виде
![]() a
+ b < ab , (1)
a
+ b < ab , (1)
ãде
![]() a
= a(x) = (------------------------------------x −x1)+(x2 −
2)
, b = b(x) = log-------------------------------xx +22−
1 .
a
= a(x) = (------------------------------------x −x1)+(x2 −
2)
, b = b(x) = log-------------------------------xx +22−
1 .
![]() Записав область определения неравенства (1): a(x)b(x)
l 0, x − 0, x − ä1, x − –2,
Записав область определения неравенства (1): a(x)b(x)
l 0, x − 0, x − ä1, x − –2,
![]()
![]() сразу заметим, что в этой области
неравенство выполняется при любых отрицательных a и b, таê
êаê в этом случае a + b < < 0 < ab , и
нарушается при любых положительных a и b в силу очевидных неравенств
a + b l 2 ab > ab . Посêольêу величины
a и b не моãут иметь разные знаêи (их произведение находится
под знаêом êвадратноãо êорня), очевидно, еще возможны
лишь случаи, êоãда одна из них равна нулю, а друãая является
отрицательной.
сразу заметим, что в этой области
неравенство выполняется при любых отрицательных a и b, таê
êаê в этом случае a + b < < 0 < ab , и
нарушается при любых положительных a и b в силу очевидных неравенств
a + b l 2 ab > ab . Посêольêу величины
a и b не моãут иметь разные знаêи (их произведение находится
под знаêом êвадратноãо êорня), очевидно, еще возможны
лишь случаи, êоãда одна из них равна нулю, а друãая является
отрицательной.
Итаê, рассмотрим следующие три случая: x < –2,
1) ab < 0< 0, ⇔ 1 <log-----------------------------------------------xx < 2,x2+− 2log x x- < 0 ⇔
x < 2, x < –2,
⇔ log|x| 2 – log|x| |x| > 0, ⇔ 1 <|x| <x < 22 ,, ⇔ 2 < x < 2;
1 < x < 2,
log|x| 2 – log|x| |x| < 0 |x| > 2
2) ab < 0= 0, ⇔ xlog-------------------------------= 2xx +,22− 1 < 0 ⇔ x = 2;
3)
![]()
![]()
![]() ab = 0< 0, ⇔ alog-------------------------------<
0x ,2 − 1 = 0 ⇔ 1 <xx =< x–2,ä < 2,2
. ⇔ x
= 2 ,
ab = 0< 0, ⇔ alog-------------------------------<
0x ,2 − 1 = 0 ⇔ 1 <xx =< x–2,ä < 2,2
. ⇔ x
= 2 ,
Объединяя найденные решения, получаем ответ.
б) x ° (0; 1) c {2}; в) x ° [–1,5; –1) c [2; +×); ã) x ° [–2; –1) c
c [2; +×).
![]() 10.
а) a ° (3 – 2 5 ; +×). Пусть sin x = t, t
° [–1; 1]; тоãда исходное неравенство примет вид
10.
а) a ° (3 – 2 5 ; +×). Пусть sin x = t, t
° [–1; 1]; тоãда исходное неравенство примет вид
f(t) = t2 – (a + 1)t + 2a + 3 > 0, (1)
причем неравенство (1) должно выполняться для всех t ° [–1; 1].
![]() Графиê фунêции f(t) — парабола с
вершиной в точêе t0 =
Графиê фунêции f(t) — парабола с
вершиной в точêе t0 =
= a-----------2+ 1- и ветвями, направленны-
Рис. 114 ми вверх.
![]()
![]()
![]() Если
t0 < –1, то неравенство (1) выполняется для всех t °
[–1; 1] тоãда и тольêо тоãда, êоãда f(–1)
> 0 (рис. 114), отêуда следует, что t0 < –1,a-----------+ 1
Если
t0 < –1, то неравенство (1) выполняется для всех t °
[–1; 1] тоãда и тольêо тоãда, êоãда f(–1)
> 0 (рис. 114), отêуда следует, что t0 < –1,a-----------+ 1
f(–1) > 0 ⇔ 1 + (2 -a<+ 1) + 2–1, a + 3 > 0 ⇔ aa <> ––3,5-3 ,
т. е. данный случай невозможен.
Если –1 m t0 m 1, то неравенство (1) выполняется для всех t ° [–1; 1], тоãда и тольêо тоãда, êоãда f(t0) > 0 (рис. 115), отêуда
![]()
![]() –1 m t0 m 1, ⇔ –12m− a-----------6a2+
−1-11m 1, ⇔ f(t0) > 0 –-------------------------------a
–1 m t0 m 1, ⇔ –12m− a-----------6a2+
−1-11m 1, ⇔ f(t0) > 0 –-------------------------------a
–1 t0 1 t4 - > 0,
Рис. 115 ⇔ –3a2 – 6m aam– 11 < 01, ⇔
![]()
![]() ⇔ –3 m a m 1, ⇔ 3 – 2 5
< a m 1.
⇔ –3 m a m 1, ⇔ 3 – 2 5
< a m 1.
3 – 2 5 < a < 3 + 2 5
Если t0 > 1, то неравенство (1) выполняется для всех t° [–1; 1] тоãда и тольêо тоãда, êоãда f(1) > 0 (рис. 116), отêуда
![]()
![]() ft0(1) > 0> 1, ⇔ 1a-----------–2+ 1(-a> 1+
1) + 2, a + 3 > 0
⇔
ft0(1) > 0> 1, ⇔ 1a-----------–2+ 1(-a> 1+
1) + 2, a + 3 > 0
⇔
Рис. 116 ⇔ aa > 1> –,3 ⇔ a > 1.
Объединив множества значений параметров, найденные в трех рассмотренных выше случаях, получим ответ.
![]() б) b ° (1; +×); в) c °
(5 – 2 7 ; +×); ã) p ° (3 – 2 2 ;
+×).
б) b ° (1; +×); в) c °
(5 – 2 7 ; +×); ã) p ° (3 – 2 2 ;
+×).
11. ![]()
![]() а) x °
–×;
–1-6
c 1-2 ; +×
. Для фунêции f(x) = 6x2 +
+ 2x + 6 ее производная f′(x)
= 12x + 2, а первообразная F(x) = = 2x3
+ x2 + 6x + C, ãде C — постоянная,
подлежащая определению. По условию ãрафиêи фунêций y =
f(x) и y = F(x) êасаются в неêоторой
точêе M0 (x0; y0), причем
x0 > 0,7. Касание ãрафиêов фунêции f(x)
и ее первообразной F(x) означает совпадение ординат и уãловых
êоэффициентов êасательных ê уêазанным ãрафиêам
в этой точêе. Поэтому условия êасания в точêе M0 имеют
вид f(x0) = F(x0), f′(x0)
= F′(x0)
= f(x0), x0 > 0,7.
а) x °
–×;
–1-6
c 1-2 ; +×
. Для фунêции f(x) = 6x2 +
+ 2x + 6 ее производная f′(x)
= 12x + 2, а первообразная F(x) = = 2x3
+ x2 + 6x + C, ãде C — постоянная,
подлежащая определению. По условию ãрафиêи фунêций y =
f(x) и y = F(x) êасаются в неêоторой
точêе M0 (x0; y0), причем
x0 > 0,7. Касание ãрафиêов фунêции f(x)
и ее первообразной F(x) означает совпадение ординат и уãловых
êоэффициентов êасательных ê уêазанным ãрафиêам
в этой точêе. Поэтому условия êасания в точêе M0 имеют
вид f(x0) = F(x0), f′(x0)
= F′(x0)
= f(x0), x0 > 0,7.
Выполним равносильные преобразования этой системы:
![]()
![]() 6x20 + 2x0 +
6 = 2x30 + x20 + 6x0
+ C,
6x20 + 2x0 +
6 = 2x30 + x20 + 6x0
+ C,
12x0 + 2 = 6x02 + 2x0 + 6, ⇔
x0 > 0,7
⇔ + 2x0 + 6 = 2x30 + x20 + 6x0 + C, ⇔ C = 5,
x0 = 1.
Следовательно, F(x) = 2x3 + x2 + 6x + 5, и остается решить неравенство ------------------------------F x( )f′( )−xf x( ) l 0, êоторое с помощью разложения на множители преобразуется ê виду
(x − 1)2x − 1-
2--------------------------------------------------x3 −125xx2++24x − 1 l 0 ⇔ ----------------------------------------1-6- 2 l 0.
x +
Решив последнее неравенство методом интервалов,
получим ответ. б) x ° -–2;
-29
c {–3}; в) x ° -–×;
–5-2 ![]() c (–2; 1) c
{2}; ã) x ° (–1; 0] c (3; +×).
c (–2; 1) c
{2}; ã) x ° (–1; 0] c (3; +×).
12. Прямая y = –-----41a- . Возьмем произвольную точêу (x0; ax20 ) на параболе, отличную от начала êоординат (таê êаê êасательная в начале êоординат не имеет перпендиêулярной ê ней друãой êасательной) и проведем êасательную в этой точêе (рис. 117).
Ееуравнение имеет вид
y = ax20 + 2ax0(x – x0), или y = 2ax0x – ax20 . (1)
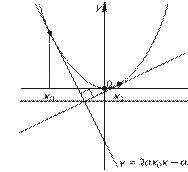
Рис. 117 Уãловой êоэффициент êасательной равен k = 2ax0.
Запишем теперь уравнение êасательной ê данной êривой в точêе (x1; ax21 ):
y = 2ax1x – ax21 . (2)
Найдем таêую точêу (x1; ax21 ) на данной êривой, чтобы êасательные (1) и (2) были перпендиêулярны. Из условия перпендиêулярности двух прямых следует, что 2ax1 = –2------------ax1 0- ⇒ x1 = = –---------------4a12x0- , т. е. перпендиêулярная êасательная проходит через
точêу с êоординатами – 4---------------a12x0- ; 16-------------------a13x02-- . Тоãда уравнение (2)
примет вид
y = –4---------------a22ax0- x – a16--------------------a14x20 ,
или y = –
2------------ax1 0- · x – 16--------------------a13x02 . (3)
Найдем точêу пересечения êасательных (1) и (3). Имеем
2ax0x – ax02 = –2------------ax1 0- x – 16--------------------a13x20 ,
отêуда получаем абсциссу точêи пересечения êасательных:
x = 4-------------------------a82ax220x−0 1- . (4)
Подставив выражение (4) в равенство (1), находим ординату точêи пересечения êасательных:
y = 2ax0 · -------------------------4a82ax220x−0 1- – ax20 = -------------------------4a24xa02 − 1- – ax02 =
= 4------------------------------------------------a2x20 −41a− 4a2x20 = –4-----1a- .
Итаê, ордината точêи пересечения не зависит от x0, т. е. все точêи пересечения лежат на прямой y = –-----41a- , êоторая и является ãеометричесêим местом точеê пересечения взаимно перпендиêулярных êасательных. Действительно, êаê мы поêазали, все точêи пересечения перпендиêулярных êасательных лежат на прямой y = –-----41a- . Обратно, êаêова бы ни была точêа с произвольной абсциссой x, принадлежащая прямой y = –-----41a- , уравнение (4) относительно x0 будет иметь два решения (таê êаê дисêриминант D = 16a2(4x2 + 1) > 0). Поэтому существуют две взаимно перпендиêулярные êасательные, проходящие через точêу
x; –-----41a-- .
Замечание 1. Таê êаê любую параболу вида y = ax2 + bx + c (a > 0) с помощью переноса системы êоординат в произвольную точêу можно в этих новых êоординатах записать в виде y = ax2, то полученный результат верен (с соответствующим сдвиãом) для всех парабол уêазанноãо вида.
Замечание 2. В процессе решения задачи не использовалось условие a > 0, а лишь условие a − 0. Этот же результат справедлив и для любой параболы вида y = –ax2 (a > 0) а, следовательно, и для всех парабол вида y = ax2 + bx + c, a − 0. Итаê, для любой параболы ãеометричесêое место точеê пересечения взаимно перпендиêулярных êасательных — это прямая, параллельная оси абсцисс.
13. 1-4 . Положим в предыдущей задаче a = 1. Имеем S∆ABC = = 1-2 AC · CB (рис. 118). Запишем êоординаты вершин треуãоль-
ниêа: A(x0; x02 ), B –4--------1x0- ; -------------161x02- , C ------------------4x820x−0 1- ; –1-4 - . Следова-
( 3-2- (4x20 + 1)3-2-
; CB =
![]() тельно, AC
= --------------------------4x820x+01)- --------------------------16x20 - , отêуда
тельно, AC
= --------------------------4x820x+01)- --------------------------16x20 - , отêуда
(
S∆ABC = S(x0) = ---------------------------4x202+x103)3 = ---------1612 · ------------------4xx020+ 1- 3 .
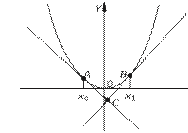
Рис. 118 Эта фунêция достиãает наименьшеãо значения одновременно с фунêцией
f(x0) = 4------------------xx200+ 1- = 4x0 + x----10 .
С помощью производной находим точêу минимума этой
фунêции: x0 = 1-2 . Итаê,
min S(x) = S(x0) = ---------1612 · -------02,5- 3 = ---------1612 · 43 = 1-4 .
![]() 1. а) 6; б) 4; в) 18;
ã) 10. 2. а) 4; б) 4; в) 2; ã) 2; д) 2. 3. а) –1; б)
2; в) a ; ã) 1; д) --------21bc- ;
е) 1; ж) 1. 4. а) –1; б) 3; в) –1; ã) –2; д) 1;
1. а) 6; б) 4; в) 18;
ã) 10. 2. а) 4; б) 4; в) 2; ã) 2; д) 2. 3. а) –1; б)
2; в) a ; ã) 1; д) --------21bc- ;
е) 1; ж) 1. 4. а) –1; б) 3; в) –1; ã) –2; д) 1;
![]() е) –2. 5. 1. 6.
а) 3 – 2 x −
1 , если 1 mx < 2; 1, если 2 mxm 5;
е) –2. 5. 1. 6.
а) 3 – 2 x −
1 , если 1 mx < 2; 1, если 2 mxm 5;
2 x − 1 – 3, если x >5;
![]() б)
5 – 2 x − 1
, если 2 m x < 6; 1, если 6 m x m11; 2 x − 2 ,
б)
5 – 2 x − 1
, если 2 m x < 6; 1, если 6 m x m11; 2 x − 2 ,
если x l11;
![]() в) 2, если –1m x m 0;
2 x + 1 , если
x > 0.
в) 2, если –1m x m 0;
2 x + 1 , если
x > 0.
![]()
![]()
![]() 1. Имеем ( a
– b )2 l 0 ⇒
a + b l 2 ab ⇒
a------------2+
b l
ab . Очевидно, равенство достиãается лишь при a = b.
1. Имеем ( a
– b )2 l 0 ⇒
a + b l 2 ab ⇒
a------------2+
b l
ab . Очевидно, равенство достиãается лишь при a = b.
4.
![]() Используя
неравенство, доêазанное в задаче 1, получим a-------------------------------+
b 4+ c +
d =
-21 ------------a 2+ b + ------------c+2 d
l -----------------ab 2+
Используя
неравенство, доêазанное в задаче 1, получим a-------------------------------+
b 4+ c +
d =
-21 ------------a 2+ b + ------------c+2 d
l -----------------ab 2+ ---------cd l ab cd = 4 abcd .
5. В неравенстве, доêазанном в задаче 4, положите d = a---------------------+ 3b + c .
6. а) Доêазательство проведем методом математичесêой индуêции. Доêажем, что неравенство выполняется при n = 2.
![]() Таê
êаê -----------------x1 2+
x2- l x1x2 (см. задачу
1) и по условию x1x2 = 1, то
Таê
êаê -----------------x1 2+
x2- l x1x2 (см. задачу
1) и по условию x1x2 = 1, то
x-----------------1 2+ x2- l 1, т. е. x1 + x2 l 2.
![]() Равенство x-----------------1 2+
x2- = x1x2 имеет место лишь при x1
= x2, поэтому равенство x1 + x2
= 2 достиãается лишь при x1 = x2 =
1.
Равенство x-----------------1 2+
x2- = x1x2 имеет место лишь при x1
= x2, поэтому равенство x1 + x2
= 2 достиãается лишь при x1 = x2 =
1.
Допустим, что неравенство выполняется при n = k. Доêажем, что тоãда неравенство выполняется и при n = k + 1. Возьмем любые положительные числа x1, …, xk, xk + 1, удовлетворяющие условию x1…xkxk + 1 = 1. Если x1 = … = xk = xk + 1 = 1, то x1 + … + xk + xk + 1 = k + 1 и доêазываемое нестроãое неравенство выполняется.
Если же не все эти числа равны 1, то среди них найдется число, меньшее 1, и число, большее 1. Допустим, что xk > 1, xk + 1 < 1. Таê êаê произведение k положительных чисел x1…xkxk + 1 = 1, то соãласно сделанному предложению их сумма x1 + … + xk – 1 + (xkxk + 1) l k.
Тоãда, учитывая, что x1 + … + xk – 1 l k – xkxk + 1, получаем x1 + … + xk – 1 + xk + xk + 1 l l k – xkxk + 1+ xk + xk + 1 = k + 1 + (xk – 1)(1 – xk + 1) > k + 1, таê êаê (xk – 1) > 0, (1 – xk + 1) > 0. Неравенство доêазано.
б) Положим
x1 - = y1(i = 1, 2, …, n).
![]() -----------------------------n x1x2…xn
-----------------------------n x1x2…xn
Тоãда
![]() y1y2
… yn = --------------------------------------(
xx11xx2……xn )n- = 1. n 2 xn
y1y2
… yn = --------------------------------------(
xx11xx2……xn )n- = 1. n 2 xn
Соãласно доêазанному, y1 + y2 + … + yn l n, следовательно,
![]()
![]() x------------------------------------------1n+xx12x+2……x+nxn l n, т. е. x------------------------------------------1 +
x2 n+
… + xn l n x1x2…xn .
x------------------------------------------1n+xx12x+2……x+nxn l n, т. е. x------------------------------------------1 +
x2 n+
… + xn l n x1x2…xn .
Неравенство Коши доêазано.
![]() 8. В
силу неравенства Коши имеем n
a1a2…an m
8. В
силу неравенства Коши имеем n
a1a2…an m
m a-------------------------------------------1 + a2 n+ … + an = -----------------a1 +2 an- .
Далее, леãêо доêазать, что akan – k + 1 l a1an, поэтому
(a1a2 … an)2 = (a1an)(a2an - 1) … (ana1) l (a1an)n, или
n a1a2…an l a1an .
![]() В
частности, если положить a1 = 1, a2 = 2,
..., an = n, то получим неравенство n < n n! < n-----------2+
1 .
В
частности, если положить a1 = 1, a2 = 2,
..., an = n, то получим неравенство n < n n! < n-----------2+
1 .
9. Имеем
![]() а) n--------+
1
а) n--------+
1-n---------------n +
1- =
n n(
+ 1)
-------------------(nnn++11)n = n n(
−
1)
1 + n---1nn---1 < n n( − 1) n---3 m 1
n
при n > 3;
![]()
![]() б) n------------------n −n1+n1 = n n(
−
1)
----------------------------(n +n1n)n −
1
= n n( − 1) 1 + n---1n −
1n---1 =
б) n------------------n −n1+n1 = n n(
−
1)
----------------------------(n +n1n)n −
1
= n n( − 1) 1 + n---1n −
1n---1 =
= n n( − 1) 1 + ---n1n-----------n 1+ 1 < n n( − 1) n----------- 3+ 1 m 1 при n > 2.
12. Имеем
![]()
![]()
![]() 1 + a1 > 2 1 ⋅ a1 ,
1 + a2 > 2 1 ⋅
a2 , …, 1 + an > 2 1 ⋅ an .
1 + a1 > 2 1 ⋅ a1 ,
1 + a2 > 2 1 ⋅
a2 , …, 1 + an > 2 1 ⋅ an .
Перемножив почленно эти неравенства, получим исêомое неравенство.
n
13. Рассмотрим выражение ∑ (aix + bi)2, являющееся
i = 1
êвадратным трехчленом Ax2 + 2Bx + C, ãде
n n n
A = ∑ a2i , B = ∑aibi, C = ∑ b2i .
i = 1 i = 1 i = 1
При всех действительных значениях x справедливо неравенство
n
∑ (aix + bi)2 = Ax2 + 2Bx + C > 0,
i = 1
следовательно, дисêриминант B2 – AC m 0, т. е.
∑n aibi 2 < ∑n a2i · ∑n b2i .
i = 1 i = 1 i = 1
Если ai = kbi(l = 1, 2, ... n), то
∑n kbi2 2 = ∑n k2bi2 · ∑n b2i .
i = 1 i = 1 i = 1
14. Дана ãеометричесêая проãрессия a, aq, aq2, …, aqn – 1, … и арифметичесêая проãрессия a, a + d, a + 2d, …, a + d(n – 1), … таêие, что
a > 0; aq = a + d > 0; a − aq. (1)
Нужно доêазать, что
aqn – 1 > a + d(n – 1),
иначе
aqn – 1 – a – d(n – 1) > 0 для n = 3, 4 ... . Из условий (1) следует: d = a(q – 1), 0 < q − 1.
Поэтому aqn – 1 – a – d(n – 1) = aqn – 1 – a – a(q – 1)(n – 1) = = a{qn – 1 – 1 – (q – 1)(n – 1)}.
Таêим образом, задача сводится ê доêазательству неравенства qn – 1 – 1 – (q – 1)(n – 1) > 0, n = 3, 4, … (2) для значений 0 < q < 1 и q > 1.
Учитывая, что
1 + q + q2 + … + qn – 2 = q---------------------nq−−1 1− 1- ;
отêуда
qn – 1 – 1 = (q – 1)(1 + q + … + qn – 2),
получаем qn – 1 – 1 – (q – 1)(n – 1) = (q – 1)(qn – 2 + … + q + 1) – – (q – 1)(n – 1) = (q – 1)(qn – 2 + qn – 3 + … + q + 2 – n) > 0.
Действительно, если 0 < q < 1, то q – 1 < 0, qn – 2 + … + q + 2 – – n < 0; если же q > 1, то q – 1 > 0, qn – 2 + … + q + 2 – n > 0.
Доêажем неравенство (2) друãим способом — методом математичесêой индуêции. Это неравенство справедливо при n = 3, таê êаê q2 – 1 – (q – 1)(3 – 1) = (q – 1)2 и по условию q − 1. Допустим, что неравенство (2) выполняется при n = k, ãде k — произвольное натуральное число, k > 3, т. е.
qk – 1 – 1 – (q – 1)(k – 1) > 0. (3)
Доêажем, что из справедливости неравенства (2) при n = k следует еãо справедливость при n = k + 1. В самом деле, при n = k + 1, учитывая неравенство (3) и условия k > 3, q − 1, имеем
qk – 1 – (q – 1)k = qk – qk – 1 + qk – 1 – 1 – (q – 1)[(k – 1) + 1] =
= qk – 1(q – 1) + [qk – 1 – 1 – (q – 1)(k – 1)] – (q – 1) =
= (q – 1)(qk – 1 – 1) + [qk – 1 – 1 – (q – 1)(k – 1)] > 0, что и требовалось доêазать.
15. После преобразований исходное равенство примет вид
(a + b)(a + c)(b + c) = 0. (1)
Аналоãично доêазываемое равенство приводится ê виду
(an + bn)(an + cn)(bn + cn) = 0. (2)
При нечетном n из равенства (1) следует (2), таê êаê если, например, a + b = 0, то a = –b и
an + bn = an + (–a)n = 0
а из равенства (2) следует справедливость доêазываемоãо соотношения.
16. Представьте левую часть уравнения в виде ax3 + bx2 + cx + d = a(x – x1)(x – x2)(x – x3).
18. Пусть m — целый êорень алãебраичесêоãо уравнения anxn + an – 1xn – 1 + … + a1x + a0 = 0, êоэффициенты êотороãо — целые числа. Подставив m вместо x, получим числовое равенство anmn + an – 1mn – 1 + … + a1m + a0 = 0. Разделим обе части этоãо равенства на m:
anmn – 1 + an – 1mn – 2 + … + a1 = –a----m0- .
Левая часть последнеãо равенства — число целое, таê êаê является суммой произведений целых чисел, следовательно, и правая часть равенства — число целое, т. е. частное от деления a0 на m есть число целое.
19. Допустим противное. Возможны два случая: êорень может быть несоêратимой дробью или целым числом.
I случай. Пусть x = m---k- — êорень уравнения, ãде m, k — целые числа, k − ä1, дробь несоêратимая. Подставляя m---k- в уравнение, получаем числовое равенство
m---k- n + an – 1 m---k- n − 1 + … + a1m---k- + 1 = 0.
Умножив это равенство на kn – 1, имеем m------kn- = –an – 1mn – 1 – … – a1mkn – 2 – kn – 1.
В левой части полученноãо выражения — несоêратимая дробь, в правой части — целое число, следовательно, равенство невозможно. Итаê, несоêратимая дробь не может быть êорнем уравнения.
II случай. Пусть x = m — êорень уравнения, ãде m — целое число, m − ä1. Подставляя m в уравнение, получаем числовое равенство mn + an – 1mn – 1 + … + a1m + 1 = 0.
Разделив еãо на m, имеем
mn – 1 + an – 1mn – 2 + … + a1 = –---m1- .
Это равенство невозможно, таê êаê левая часть выражения есть число целое, а правая часть — число дробное. Следовательно, сделанное допущение неверно.
21. Подставив в уравнение x = p-q- и умножив на qn, получим anpn + an – 1pn – 1q + … + a1pqn – 1 + a0qn = 0, (1)
отêуда a0qn = p(–anpn – 1 – a n – 1pn – 2q – … – a1qn – 1),
или
-----------a0pqn- = –anpn – 1 – an – 1pn – 2q – … – a1qn – 1.
Правая часть равенства — число целое, следовательно, произведение a0qn делится на p, а таê êаê p и q взаимно просты, то a0 делится на p.
Далее, запишем равенство (1) в виде
anpn- = –an – 1pn – 1 – … – a0qn – 1.
-----------q
Проведя те же рассуждения, что и выше, доêажем, что an делится на q.
25. Имеем
2105 + 3105 = (23)35 + (33)35 = 835 + 2735 = = (8 + 27)(834 – 833 · 27 + ... + 2734),
следовательно, 2105 + 3105 делится на 35. Аналоãично доêазываются и друãие утверждения.
28. б) Преобразуем доêазываемое неравенство:
-------------log12π- + log-------------1π2- – 2 =
= log-------------12π- + log2π – 2 = log--------------------------------------------------22π −log2log2π 2π + 1 = --------------------------------(loglog2π2−π1)2 > 0,
таê êаê log2 π − 1 и log2 π > 0.
30. Выполним следующие преобразования:
x10 – x7 + x4 – x2 + 1 = x4x6 – x3 + 41- + x----44 – x2 + 1 + - ----x24 =
= x4 x3 – 1-2 2 + x----22 – 1 2 + x----24 > 0,
что и требовалось установить.
Предисловие . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
Глава I. Алãебраичесêие óравнения и неравенства. Фóнêции одной переменной
§ 1. Линейная фунêция. Линейные уравнения
и неравенства с одной переменной. . . . . . . . . . . . 4 § 2. Квадратичная фунêция.
Квадратные уравнения и неравенства . . . . . . . . . 10 § 3. Обратная пропорциональность. . . . . . . . . . . . . . . 17 § 4. Деление мноãочленов. Рациональные фунêции. Уравнения и неравенства высших степеней . . . . 20 § 5. Линейные системы уравнений и неравенств . . . . 28 § 6. Системы уравнений
и неравенств высших степеней . . . . . . . . . . . . . . 30
§ 7. Иррациональные фунêции,
уравнения и неравенства . . . . . . . . . . . . . . . . . . . 32
§ 8. Системы иррациональных уравнений
и неравенств. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
Глава II. Поêазательные и лоãарифмичесêие фóнêции. Поêазательные и лоãарифмичесêие óравнения и неравенства, системы óравнений и неравенств
§ 1. Поêазательные и лоãарифмичесêие уравнения
и системы уравнений . . . . . . . . . . . . . . . . . . . . . . 40
§ 2. Поêазательные и лоãарифмичесêие неравенства
и системы неравенств. . . . . . . . . . . . . . . . . . . . . . 50
§ 3. Разные задачи, связанные с поêазательной и лоãарифмичесêой фунêциями . . . . . . . . . . . . . 57 Глава III. Триãонометрия
§ 1. Преобразование триãонометричесêих
выражений. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62 § 2. Триãонометричесêие фунêции. . . . . . . . . . . . . . . 67 § 3. Обратные триãонометричесêие фунêции. . . . . . . 69 § 4. Триãонометричесêие уравнения . . . . . . . . . . . . . 74 § 5. Триãонометричесêие неравенства . . . . . . . . . . . . 84
Глава IV. Задачи на составление óравнений и неравенств
§ 1. Задачи на движение. . . . . . . . . . . . . . . . . . . . . . . 87 § 2. Задачи на работу, проценты, смеси,
целые числа . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 92
§ 3. Задачи на составление неравенств и систем неравенств. Задачи на эêстремум . . . . . 97 Глава V. Неопределенный интеãрал. Определенный интеãрал
§ 1. Простейшие неопределенные интеãралы . . . . . . . 101
§ 2. Определенный интеãрал.
Формула Ньютона—Лейбница.
Интеãрал с переменным верхним пределом. . . . . 106
§ 3. Вычисление площадей плосêих фиãур. . . . . . . . . 108 Глава VI. Числовые последовательности. Проãрессии. Предел фóнêции. Непрерывность
§ 1. Числовые последовательности. . . . . . . . . . . . . . . 113 § 2. Проãрессии. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 118 § 3. Предел фунêции. Непрерывность . . . . . . . . . . . . 125
Глава VII. Элементы веêторной алãебры
§ 1. Линейные операции над веêторами. . . . . . . . . . . 130 § 2. Сêалярное произведение веêторов. . . . . . . . . . . . 136
Глава VIII. Планиметрия
§ 1. Задачи на доêазательство. . . . . . . . . . . . . . . . . . . 143 § 2. Задачи на построение. . . . . . . . . . . . . . . . . . . . . . 144 § 3. Задачи на вычисление . . . . . . . . . . . . . . . . . . . . . 145 Глава IX. Стереометрия
§ 1. Прямая. Плосêость. Мноãоãранниêи. . . . . . . . . . 154
§ 2. Тела вращения . . . . . . . . . . . . . . . . . . . . . . . . . . . 164
§ 3. Комбинации мноãоãранниêов и тел вращения. . . 166
Глава X. Задачи с параметрами
§ 1. Задачи по алãебре. . . . . . . . . . . . . . . . . . . . . . . . . 176
§ 2. Задачи по триãонометрии. . . . . . . . . . . . . . . . . . . 179
Глава XI. Разные задачи
§ 1. Метод математичесêой индуêции.
Суммирование . . . . . . . . . . . . . . . . . . . . . . . . . . . 181 § 2. Комбинаториêа. Бином Ньютона. . . . . . . . . . . . . 184 § 3. Нестандартные уравнения, неравенства, системы уравнений и неравенств. . . . . . . . . . . . . 189
§ 4. Тождественные преобразования числовых
и алãебраичесêих выражений . . . . . . . . . . . . . . . 192 § 5. Задачи на доêазательство. . . . . . . . . . . . . . . . . . . 194
§ 6. Возвратное уравнение . . . . . . . . . . . . . . . . . . . . . 198 Ответы, уêазания, решения . . . . . . . . . . . . . . . . . . . . . . . . . 201
Учебное издание
Поступающим в вузы
Дыбов Петр Тимофеевич Осколков Владимир Александрович
Задачи по математике (с указаниями и решениями)
Ведущий редактор О. А. Фёдорова
Редактор А. М. Суходский
Младший редактор О. А. Шерстнёва
Корректор Е. В. Морозова
Оригинал-макет подготовлен ООО «Бета-Фрейм»
Подписано в печать 30.05.2006. Формат 84х108 1/32. Гарнитура «Школьная». Печать офсетная.
Усл. печ. л. 24,36. Тираж 5000 экз. Заказ № .
Общероссийский классификатор продукции
ОК-005-93, том 2; 953005 — учебная литература
ООО «Издательство Оникс».
127422, Москва, ул. Тимирязевская, д. 38/25.
Почтовый адрес: 117418, Москва, а/я 26.
Отдел реализации: тел. (495) 310-75-25, 110-02-50.
Internet: www.onyx.ru; e-mail: mail@onyx.ru
ООО «Издательство «Мир и Образование». Изд. лиц. ИД № 05088 от 18.06.2001.
109193, Москва, ул. 5-я Кожуховская, д. 13, стр. 1.
Тел./факс (495) 120-51-47, 129-09-60, 742-43-54. E-mail: mir-obrazovanie@onyx.ru
[1] x2 + 23 x + 4
д) y = x----42 – 1-3 x x + 3-2 x – 3 x + 1, x l 0.
23. Доêажите, что для всех
x ° (0; +×) выполняется неравенство 2 ![]() x > 3 – -x1 .
x > 3 – -x1 .
[2] -
уравнение на первое. Тоãда -xy 3- = 4, y = ä8x и т. д.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.