Законы (свойства) умножения

Третье ноября

Законы умножения

Здравствуйте, мои дорогие юные математики! Надеюсь, вам понравилось заниматься математикой с помощью электронных игр и упражнений.

Начнем урок, как всегда с устного счета. В этом нам опять поможет математическая игра по ссылке: https://learningapps.org/260587.

И, конечно же, повторяем таблицу умножения по ссылке https://learningapps.org/6914333.

Итак, на прошлом уроке мы с вами вспомнили, как называются компоненты при умножении, как правильно умножать числа столбиком. Давайте проверим, насколько хорошо вы усвоили этот материал: https://learningapps.org/13266619.

Получилось?

Вы наверняка знаете, что все в нашем мире существует по определенным законам. Есть законы физические, есть юридические и т.д. Так вот в математике тоже есть свои законы, которых нужно придерживаться. Сегодня мы познакомимся с законами умножения (свойствами умножения).

Умножить число а на натуральное число b – значит, найти сумму а одинаковых слагаемых, каждое из которых равно b. То есть умножить число 3 на число 4 – значит, найти сумму трёх слагаемых, каждое из которых 4.

3·4 = 4 + 4 + 4 = 12

Переместительный закон умножения: от перестановки множителей произведение не изменяется: а·b = b·а. В этом легко убедиться. Перемножим 5 на 3, получим 15. При перемножении 3 на 5 опять получаем 15.

5∙3 = 3∙5 = 15

Выполним проверку на примере вашего уровня знаний и умений:

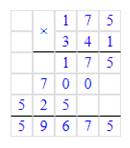Какой знак поставим вместо «?»: 175·341 ? 341·175

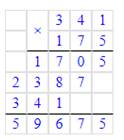341·175=59675;

59675=59675;

175·341=341·175.

(Делаем запись в тетради)

Результат умножения нескольких множителей не зависит от порядка выполнения умножения. Например, чтобы найти произведение чисел 10, 2 и 15, можно сначала перемножить числа 10 и 2, а затем их произведение умножить на число 15. Но удобнее сначала перемножить числа 2 и 15, а затем на их произведение умножить число 10. Порядок умножения чисел указывают при помощи скобок. Для рассматриваемого примера получим:

(10∙2)∙15 = 10∙(2∙15).

Это – сочетательный закон умножения: чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего:

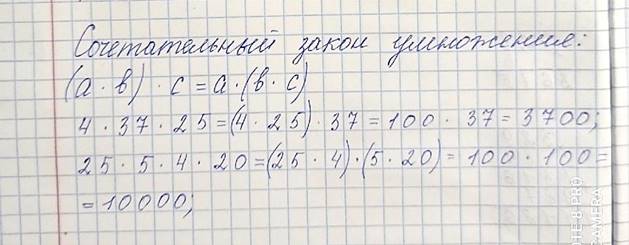Переместительный и сочетательный законы умножения справедливы для любого количества множителей. Применяя эти законы, можно значительно упростить вычисления. Например, найдём произведение.

1) 4 37 25 = (4 25) 37 = 100 37 = 3700;

2) 25 5 4 20 = (25 4) (5 20) = 100 100 = 10000.

(Делаем запись в тетради)

Также с переместительным и сочетательным законами умножения вы можете познакомиться с помощью видео-урока по ссылке https://www.youtube.com/watch?v=qyIzYJT4-ZI&feature=emb_logo

Перед нами есть пример: 69•27+31•27=____

Мы видим, что у нас есть одинаковый множитель 27. Значит, это выражение мы можем записать так: 69•27+31•27=27•(69+31)=27•100=2700

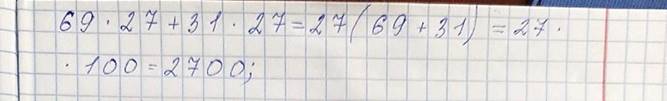a•b+a•c=a•(b+c)

(Делаем запись в тетради)

Или другой пример: 202•87-102•87=____

Это и есть распределительное свойство умножения относительно вычитания:

a•c-b•c=c•(a-b)

(Делаем запись в тетради)

Распределительный закон умножения также представлен на видео по ссылке: https://vk.com/video-114367496_456239084

Закрепим полученные знания с помощью игр: https://learningapps.org/7853329 и https://learningapps.org/13530225

В этом тренировочном варианте 7 карточек с заданиями, которые вам нужно будет выполнить письменно в тетради. Карточку №3 «Соедини выражения с равными значениями и соответствующий им прямоугольник» записывать в тетрадь не нужно.

Напоминаю, что словосочетание «Домашняя работа» вам писать не нужно, просто продолжаете работать дальше. После чего ответ ввести в форму для отправки ответа, чтобы увидеть, правильно ли вы его решили. Данное упражнение является не проверочным, а обучающим. То есть, в нем нет таймера с ограничением времени. На ответ вам дается 3 попытки. Результаты видны после каждой попытки. Если решение не верное, то система сайта выдаст вам алгоритм, как решать правильно.

Успехов! Если возникли какие-то вопросы, вы можете обратиться ко мне в ВК https://vk.com/elena__borodina или на почту virgo.gelena@gmail.com

Скачано с www.znanio.ru