Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Ярославский государственный педагогический университет им. К.Д. Ушинского»

           

 

 

Кафедра Математического анализа, теории и методики обучения математике

(наименование кафедры)

Направление 44.03.05 Педагогическое образование

(наименование направления)

 

 

 

 

 

 

 

 

 

Курсовая работа

 

на тему «Замощение плоскости многоугольниками и их приложения».

 

 

 

Выполнила:              Борисова Полина Алексеевна, 3 курс              _____________

                                         (фамилия, имя, отчество студента, курс)                              (личная подпись)

Научный

руководитель: Смирнов Евгений Иванович, кандидат физико-математических наук, доктор педагогических наук, профессор

                                               (фамилия, имя, отчество, ученая степень, ученое звание)

 

Заключение научного руководителя о допуске к защите:                                    Е.И.Смирнов

(подпись научного руководителя)

 

Оценка публичной защиты работы:

________  ______________________Е.И.Смирнов

   (оценка, подпись научного руководителя)

 

 

 

 

 

 

Ярославль

2019 г.

Оглавление

Введение. 4

Глава I. Теоретическое изучение замощения плоскости многоугольниками. 6

1.1.   Определения и историогенез замощения плоскости. 6

1.1.1.   Примеры замощения плоскости. 10

1.2.   Паркеты.. 12

1.3.   Виды паркетов. 14

1.3.1.   Полуправильные паркеты.. 14

1.3.2.   Квазиправильные паркеты.. 15

1.3.3.   Неоднородные паркеты.. 16

1.3.4.   Непериодические паркеты и апериодические множества плиток. 16

1.4.   Мозаика Роджера Пенроуза. 20

1.4.1.   Типы мозаики Пенроуза. 20

1.4.1.1.   Исходная мозаика Пенроуза (P1) 21

1.4.1.2.   Мозаика Пенроуза из дельтоидов (P2) 21

1.4.1.3.   Мозаика Пенроуза из ромбов (P3) 22

1.4.2.   Свойства мозаик Пенроуза. 23

Глава II. Замощение плоскости многоугольниками. 25

2.1. Замощение плоскости правильными многоугольниками. 25

2.2. Замощение плоскости произвольными многоугольниками. 27

2.2.1. Замощение плоскости треугольниками. 27

2.2.2.   Замощение плоскости четырехугольниками. 28

2.2.3.   Замощение плоскости пятиугольниками. 31

2.2.3.1.   Типы 1,2,3,4,5 (Карл Рейнхардт, 1918) 33

2.2.3.2.   Типы 6,7,8 (Роберт Киршнер, 1968) 33

2.2.3.3.   Тип 10 ( Ричард Джеймс, 1975) 34

Типы 9, 11, 12, 13 (Марджори Райс, 1977) 35

2.2.3.4.   Тип 14 (Рольф Штайн, 1985) 35

2.2.3.5.   Тип 15 (Кейси Манн, Дженниффер Маклауд, Дэвид фон Дюрей, 2015) 36

2.2.4.   Замощение плоскости шестиугольниками. 37

Глава III. Невозможные замощения. 39

3.1.   Раскраски. Замощение шахматной доски доминошками. 39

3.1.1. Постановка задачи. 39

3.1.2. Решение задачи о шахматной доске с вырезанными углами. 39

3.1.3. Вариация замощения шахматной доски доминошками. 40

3.2.   Замощения без раскрасок. 42

3.3.   Замощение квадратами и электрической цепи. 47

3.4.   Замощение прямоугольниками с целочисленными сторонами. 50

3.5.   Замощения треугольниками равной площади. 54

Глава IV. Приложение замощения плоскости многоугольниками. 55

4.1.   Знакомство с понятием ацтекского бриллианта. 55

4.2.   Теорема об ацтекском бриллианте. 58

4.2.1.   Совершенные паросочетания и замощения. 59

4.2.2.   Взвешенные суммы.. 60

4.2.3.   Лемма о расширении площадей. 61

4.2.4.   Подсчет числа совершенных паросочетаний ацтекского бриллианта. 62

4.3.   Связанные понятия с ацтекским бриллиантом. 65

4.3.1.   Ранг разбиения. 65

4.3.2.   Функция высоты.. 65

4.3.3.   Стандартная нотация плиток в разбиении. 66

4.4.   Алгоритм генерации случайного разбиения. 67

4.5.   Теорема о полярном круге. 68

4.6.   Математическое содержание замощения. 70

Заключение. 71

Библиографический список. 72

Приложение 1. 74

Приложение 2. 76

Приложение 3. 78

Приложение 4. 80

Приложение 5. 82

 

 

Введение

Вопрос о замощении плоскости многоугольниками является неновым. Данную проблему исследовали десятки ученых разного времени, но ответов на все поставленные вопросы так и не было найдено. Паркеты (именно такое второе название имеет замощение) имеют очень интересную историю, ведь ими занимались не только математики, то и люди других профессий и даже видов деятельности.

Еще древние художники создавали удивительные геометрические орнаменты. Для создания своих узоров они применяли не простые, случайно придуманные контуры, а фигуры, которые были расположены в определённом порядке. А самое удивительное, что люди снова встретились с ними позже.

Самое серьезное внимание проблеме замощения плоскости в пространстве стали уделять в последние пятьдесят лет, после открытий в физике кристаллов - твердых металлических сплавов. В кристаллографии поворотная симметрия 5-го порядка наиболее эффективно представлена в мире растений и в простейших живых организмах, в частности в некоторых разновидностях вирусов, в некоторых обитателях морей [1].

В настоящей работе исследуется сама математика, присутствующая в паркетах, а также приложения замощения плоскости многоугольниками.

Актуальность данной работы состоит в том, что замощение плоскости достаточно часто встречается в повседневной жизни, а также активно изучается в физике, геометрии и естественных науках.

Цель исследования: выявить математические основания процессов замощения плоскости паркетами и показать разнообразие и сложность геометрических объектов для развития интеллектуальных операций мышления.

Для достижения поставленной цели были выявлены следующие задачи:

-Дать определение замощению плоскости геометрическим фигурами на основе феноменологического подхода;

-Изучить динамику и выявить этапы историогенеза процессов замощения плоскости, описать вклад ученых и исследователей в развитие теории и практики замощения;

-Изучить и систематизировать виды паркетов, их свойства и способы построения;

-Обосновать и изучить геометрию возможных замощений многоугольниками на основе математического моделирования;

- Визуализировать и обосновать на основе наглядного моделирования невозможность замощения плоскости некоторыми видами многоугольников;

-Выявить аспекты приложения процессов замощения плоскости многоугольниками: ацтекский бриллиант, его доказательство и другие способы построения. 

Структура работы: данная курсовая работа состоит из 4 глав и 18 параграфов. I глава будет посвящена общим представлениям о замощении плоскости многоугольниками: паркетам, их видам и свойствам. II глава будет содержать информацию о непосредственном замощении плоскости многоугольниками, алгоритме их построения. III глава будет посвящена невозможным построениям. IV глава  будет рассказывать о приложении замощения плоскости многоугольниками – ацтекском бриллианте, его свойствах, а также способах построения.

 

 

Глава I. Теоретическое изучение замощения плоскости многоугольниками

1.1.          Определения и историогенез замощения плоскости

Замощения иначе называются паркетами, мозаиками, разбиениями плоскости, паркетажами. Замощения трёхмерного пространства и пространств высших размерностей часто называют сотами.

Если объединение нескольких фигур содержит данную фигуру Ф, то говорят, что эти фигуры образуют покрытие фигуры Ф. При этом покрывающие фигуры могут перекрываться, но покрывают фигуру Ф без пробелов.

Упаковка — это размещение внутри данной фигуры нескольких фигур, не имеющих общих точек, кроме, быть может, граничных (т.е. без перекрытий).

Замощение — это разбиение фигуры на части. Замощение является одновременно покрытием и упаковкой.

Другие определения понятия:

Замощение — это покрытие всей плоскости неперекрывающимися фигурами.

Замощение — разбиение плоскости или пространства на фигуры без общих внутренних точек или покрытие всей плоскости неперекрывающимися фигурами [3].

Можно предположить, что интерес человека к замощению плоскости своими корнями уходит к первобытному строю, когда человек свои представления об окружающем мире изображал в виде знаков (рис. 1).

Рис. 1.Изображения первобытного человека

Позднее замощение плоскости геометрическими фигурами уже четко можно проследить в орнаментах, мозаиках и других узорах, которыми люди стремились украсить предметы быта, одежду, украшения и свое жилище (рис. 2).

 

Рис. 2. Древние геометрические узоры в быту

Уже древние пифагорейцы   установили тот факт, что замостить плоскость без пробелов и перекрытий можно только тремя правильными многоугольниками, – треугольником, квадратом и шестиугольником (рис. 3).

Рис. 3. Правильные многоугольники, которыми можно замостить плоскость

Поражают своей красотой и сложностью узоры, которыми в средневековье покрывали мечети Средней и Центральной Азии (рис. 4).

 

Рис. 4. Узоры на стенах мечетей Средней и Центральной Азии

 Оказывается, что для создания этих узоров применяли не простые узоры, расположенные в случайном порядке, а фигуры, которые располагались в строго определенном порядке согласно чертежам. Удивителен тот факт, что математики обратили внимание на данные узоры только спустя столетия в связи с открытием решеток Пенроуза. Именно эти древние узоры есть ничто иное, как мозаики Пенроуза. В свою очередь, физики увидели эти узоры в структуре квазикристаллов [3, 4].

Еще один поразительный факт в истории замощения плоскости связан с деятельностью голландского художника Мориса Эшера (1898-1972), который никогда не понимал математику, но утверждал: «Все мои произведения — это игры. Серьезные игры». Однако математики всего мира в этих играх видят абсолютно серьезное подтверждение многих математических идей (рис. 5) [2].

Рис. 5.Рисунки М. Эшера

Самое серьезное внимание проблеме замощения плоскости стали уделять лишь в конце 20 века. И связано это с развитием физики квазикристаллов – сплавов металлических элементов (рис.6). Дело в том, что атомную структуру квазикристалла можно понять с помощью математической теории замощения.

Рис.6. Атомная модель Al-Pd-Mn квазикристалла

Более ста лет математики всего мира были увлечены решением задачи о замощении плоскости выпуклыми многоугольниками. А именно: необходимо описать все выпуклые многоугольники, которыми можно замостить плоскость. Было доказано, что у такого многоугольника может быть только 3, 4, 5 или 6 сторон. Причем плоскость можно замостить любым трех- или четырехугольником. Были описаны 3 класса выпуклых шестиугольников, которыми можно замостить плоскость.

Самый сложный случай оказался с описанием пятиугольников. В решении этого вопроса принимали участие, как великие математики, так и математики-любители, и даже американская домохозяйка. Только в августе 2015 года математики Вашингтонского университета с помощью компьютерной программы открыли 15-ый класс таких пятиугольников, а французский математик Михаэль Рао - математик из Национального центра научных исследований и Высшей нормальной школы Лиона (Франция) -  только в 2017 году показал, что больше таких классов не существует. То есть с этого времени считается, что задача о замощении плоскости решена [5, 6].

 

1.1.1.   Примеры замощения плоскости

Замощение плоскости можно представить в виде набора склеенных по границам фигур. Один из простейших примеров - так называемое гексагональное замощение (рис. 7), когда плоскость, как соты, составлена из шестиугольников, соединенных по сторонам. [3]

Рис. 7. Гексагональное замощение

В каждом из этих замощений любые два мно­гоугольника имеют либо общую сторону, либо только общую вершину, либо вовсе не имеют общих точек. Замощения плоскости многоугольниками, удовлетворяющие этому требованию, называют паркетами.

Математическая проблема непериодичного замощения плоскости существует уже около полувека. Самое известное решение этой проблемы - мозаика Пенроуза (рис. 8), которая появилась в семидесятых годах прошлого века, и в которой используется всего две различные фигуры.

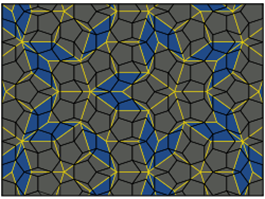
Рис. 8. Мозаика Пенроуза

Первый набор плиток, состоящий из 20426 фигур, представил в 1966 году математик Роберт Бергер [4].

Роберт Бергер (род. 1938) - прикладной математик, известный тем, что изобрел первую апериодическую плитку, используя набор из 20 426 различных форм плитки Вана. Бергер сделал свои студенческие исследования в политехническом институте  им. Ренсселера  и изучал прикладную физику в Гарвардском университете, получив степень магистра, до перехода к прикладной математике для его докторской диссертации. Работа Бергера по плитке была опубликована как «Неразрешимость проблемы домино» в «Memoirs of the AMS» в 1966 году. Эта статья по сути является перепечаткой диссертации Бергера 1964 года в Гарвардском университете. [7] 

Через некоторое время он, впрочем, сумел сократить число необходимых плиток до 104 (рис. 9). Автору рассматриваемой работы для решения задачи хватило одной фигуры — правильного шестиугольника. При укладке таких плиток черные линии не должны прерываться, а флажки в вершинах шестиугольников, которые находятся на расстоянии, равном длине одной стороны плитки (на рисунке отмечены стрелками), должны смотреть в одну сторону [4].

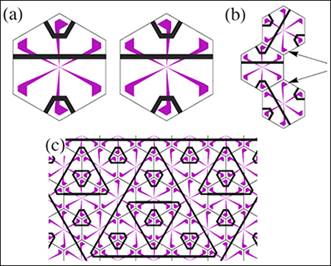
Рис. 9. Набор плиток, представленный Робертом Бергером

 

1.2.          Паркеты

В каждом из замощений, где используются квадрат, правильный треугольник и правильный шестиугольник любые два многоугольника имеют либо общую сторону, либо только общую вершину, либо вовсе не имеют общих точек. Замощения плоскости многоугольниками, удовлетворяющие этому требованию, называют паркетами. Паркеты иначе называются мозаиками, разбиениями плоскости, паркетажами.

Убедиться в том, что никакой другой правильный многоугольник паркета не образует, совсем просто. И здесь нам понадобится формула суммы углов многоугольника.

Если паркет составлен из n-угольников, то в каждой верши­не паркета будет сходиться  k = многоугольников, где n — угол правильного n-угольника. Легко найти, что a₃ = 60°, a₄ = 90°, a₅ = 108°, a₆ = 120° и                   120° < a_n < 180° при п > 7. Поэтому 360° делится нацело на a_n только при п = 3; 4; 6. 

Паркеты из правильных многоугольников сами правильные в том смысле, что они «одинаково устроены» относительно всех своих вершин и всех составляющих паркеты кусочков-многоугольников. (Эти кусочки называются гранями замощения или просто плитками.) Другими словами, для любых двух вершин правильного паркета можно указать такое его самосовмещение, при котором одна из вершин попадает на другую. То же верно для любых двух плиток паркета. 

Можно потребовать, чтобы паркет был правильным только «по вершинам», но разрешить использовать разные виды правильных многоугольников. Тогда к трём исходным паркетам добавятся ещё восемь (рис. 10).

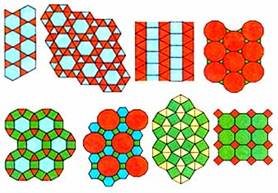
Рис. 10. Правильные «по вершинам» паркеты

Рассматривают и другое обобщение — паркеты из копий произвольного многоугольника, правильные «по граням» (т. е. допускающие самосовмещения, которые переводят любую за­данную плитку в любую другую). Число таких паркетов — 46, включая и первые три (рис. 11). Рис. 11. Правильные «по граням» паркеты Многоугольники, которые могут быть плитками в этих паркетах, называются планигонами. Ясно, что плоскость можно уложить копиями произвольного треугольника, но менее очевидно, что произвольный четырёхугольник — планигон. То же верно и для любого шестиугольника, противоположные стороны которого равны и параллельны.

Все рассмотренные выше паркеты периодичны, т. е. в каждом из них можно выделить (и даже многими способами) составленную из нескольких плиток область, из которой параллельными сдвигами получается весь паркет. Интерес учёных к таким конструкциям объясняется тем, что периодические замощения, особенно замощения пространства, моделируют кристаллические структуры [3].

1.3.          Виды паркетов

Как уже говорилось ранее существуют правильные, периодические паркеты. Но это не единственный вид паркетажей. Какие же еще виды замощения существуют? 

1.3.1.   Полуправильные паркеты

Паркеты, состоящие из правильных многоугольников двух или более типов, такие, что для любых двух вершин паркета существует преобразование симметрии (самосовмещение), переводящее одну из них в другую, называются полуправильными паркетами или архимедовыми паркетами.

Существует 8 полуправильных паркетов. Один из восьми полуправильных паркетов (курносый тришестиугольный паркет) является хиральным, то есть не совпадает с собственным зеркальным отражением [Приложение 1].

Существует два определения, приводящих к одному и тому же набору из 8 полуправильных паркетов на плоскости.

Первое, «локальное» определение, заключается в том, что вершинные конфигурации всех вершин должны совпадать. Иными словами, последовательности граней вокруг любых двух вершин паркета должны быть одинаковыми: одни и те же многоугольники должны идти в одном и том же (или в противоположном) порядке.

Второе, «глобальное» определение, требует, чтобы для любых двух вершин паркета существовало преобразование симметрии (самосовмещение паркета), переводящее одну из них в другую.

Бранко Грюнбаум и Алан Шепард разделяют термины «архимедов паркет» и «однородный паркет» (англ. uniform tiling): к первой группе относятся паркеты, соответствующие «локальному» определению, а ко второй — «глобальному». Хотя на евклидовой плоскости два этих множества совпадают, в других пространствах существуют архимедовы паркеты, не являющиеся однородными [3].

Бранко Грюнбаум (2 октября 1929, Осиек, Хорватия — 14 сентября 2018, Сиэтл, США) — израильский и американский математик, автор более 200 научных работ, в основном в области комбинаторной геометрии, один из создателей теории абстрактных многогранников. В 1948 году начал изучать математику в университете Загреба. В 1949 году эмигрировал в Израиль. В 1957 году получил докторскую степень в Еврейском университете в Иерусалиме. Работал в Институте перспективных исследований, Мичиганском и Вашингтонском университете. В 1995 году нашёл и исправил ошибку в прежнем доказательстве теоремы Эрдёша — Сёкефальви-Надя. Внёс вклад в исследование остроугольных множеств [8].

Алан Бартлетт Шепард Родился 18 ноября 1923 года в городе Ист-Дерри (штат Нью-Гэмпшир, США) в семье кадрового армейского офицера. Начальное образование получил в поселковой школе в Ист-Дерри. В математике был лучшим. Еще в школьные годы увлекся авиацией и по выходным ездил на велосипеде за 10 миль в аэропорт, где помогал обслуживать самолёты в обмен на полёты. Затем он поступил в Академию Пинкертона в г.Дерри.

21.07.1998 - умер во сне в госпитале г.Монтеррей (шт.Калифорния) [9].

В математической литературе значения терминов «архимедов паркет», «полуправильный паркет» и «однородный паркет» варьируются [3].

1.3.2.   Квазиправильные паркеты

Квазиправильный паркет (или многогранник) — однородный паркет (или многогранник), состоящий из граней двух видов, чередующихся вокруг каждой вершины. Иными словами, каждая грань окружена гранями другого типа.

На Евклидовой плоскости существует лишь один квазиправильный паркет — тришестиугольный паркет с вершинной конфигурацией 3.6.3.6. На сфере существует два квазиправильных паркета (сферических многогранника) — кубооктаэдр и икосододекаэдр (рис. 12).

Рис. 12. Квазиправильные паркеты

На плоскости Лобачевского существует бесконечное множество квазиправильных паркетов вида , где  [3].

1.3.3.   Неоднородные паркеты

Существует бесконечное множество неоднородных паркетов, состоящих из правильных многоугольников.

Периодические неоднородные паркеты можно классифицировать по числу орбит вершин, рёбер и граней. Если число орбит вершин равно n, паркет называется n-однородным или n-изогональным. Если число орбит рёбер равно n, то паркет называется n-изотоксальным (рис. 13) [3].

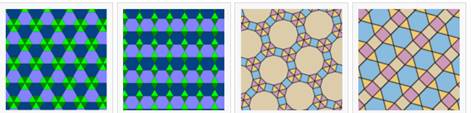
Рис. 13. Неоднородные паркеты

1.3.4.   Непериодические паркеты и апериодические множества плиток

Разбиение T называется периодическим, если среди симметрий Т существуют два параллельных переноса в непараллельных направлениях. В этом случае мозаику можно считать состоящей из повторений небольшого фрагмента, выложенного из элементов в узлах некоторой решётки. Множество прототипов (протомножество) P называется  апериодическим, если оно реализуется в каких-то разбиениях плоскости, но ни одно из этих разбиений не является периодическим.

Первый пример апериодического множества плиток был найден Робертом Бергером  в 1966 году и включал в себя 20 426 плиток Вана. Плитки Вана представляют собой квадраты одного размера с окрашенными сторонами; при построении мозаики разрешено совмещать плитки лишь одноцветными сторонами и запрещено переворачивать плитки (рис. 14) [3].

 

 

 

 

 

 

Плитки Вана (или домино Вана), впервые предложенные математиком, логиком и философом Хао Ваном в 1961, — это класс формальных систем. Они моделируются визуально с помощью квадратных плиток с раскрашиванием каждой стороны. Определяется набор таких плиток (например, как на иллюстрации), затем копии этих плиток прикладываются друг к другу с условием согласования цветов сторон, но без вращения или симметрического отражения плиток .

Хао Ван (20 мая 1921 — 13 мая 1995) — китайский и американский учёный, математик, логик и философ. Родился в 1921 году в урбанизированной части уезда Личэн (провинция Шаньдун, Китайская Республика), впоследствии выделенной в город Цзинань. В 1943 году получил степень бакалавра математики в Государственном Юго-западном объединённом университете. В 1945 году Ван Хао получил степень магистра философии в Университете Цинхуа. Одним из важнейших вкладов Ван Хао в современную науку являются «плитки Вана» [10].

Позднее были найдены апериодические протомножества с меньшим числом плиток. Роджер Пенроуз обнаружил апериодические протомножества, состоящие из двух плиток (рис. 15).

 

 

 

Роджер Пенроуз (род. 8 августа 1931 года, г. Колчестер, Англия) — английский физик и математик, работающий в различных областях математики, общей теории относительности и квантовой теории; автор теории твисторов [12, 13].

В 2010 году Джошуа Соколар и Джон Тэйлор предложили апериодическое множество, состоящее из единственной плитки, которая представляет собой правильный шестиугольник с нанесённой разметкой в виде цветных линий и с дополнительными ограничениями, связанными с взаимным расположением не касающихся друг друга плиток (рис. 16) [3].

 

 

 

 

Плитка Соколара-Тейлор - одна плитка , которая является апериодической на евклидовой плоскости. Базовая версия плитки - это простой шестиугольник с печатными рисунками для обеспечения соблюдения локального правила сопоставления относительно того, как плитки могут быть размещены. 

Существует модификация, не использующая подобных ограничений, но использующая несвязную плитку, то есть, плитку, не являющуюся топологическим диском. Существование единственной связной плитки без дополнительной разметки и ограничений, способной покрыть плоскость только апериодически, остаётся открытой проблемой [11].

 

 

1.4.          Мозаика Роджера Пенроуза

Долгое время предполагали, что не существует плиток и даже наборов из нескольких различных плиток, копии которых могли бы устилать плоскость только непериодически. Однако в середине  60-х гг. XX века эта гипотеза была опровергнута, для чего понадобился набор из более чем 20 000 разных видов плиток. Шаг за шагом число плиток удавалось уменьшить, и, наконец, через десять лет английскому математику Роджеру Пенроузу удалось обойтись всего двумя очень простыми фигурками.

Английский математик Роджер Пенроуз придумал в 1973 году особенную мозаику из геометрических фигур. Называться она стала, соответственно, мозаикой Пенроуза.

Мозаика Пенроуза представляет собой узор, собранный из многоугольных плиток двух определённых форм (немного различающихся ромбов). Ими можно замостить бесконечную плоскость без пробелов.

Получающееся изображение выглядит так, будто является неким "ритмическим" орнаментом – картинкой, обладающей трансляционной симметрией. Такой тип симметрии означает, что в узоре можно выбрать определённый кусочек, который можно "копировать" на плоскости, а затем совмещать эти "дубликаты" друг с другом параллельным переносом (проще говоря, без поворота и без увеличения).

Однако, если присмотреться, можно увидеть, что в узоре Пенроуза нет таких повторяющихся структур – он апериодичен. Но дело вовсе не в оптическом обмане, а в том, что мозаика не хаотична: она обладает вращательной симметрией пятого порядка. Это значит, что изображение можно поворачивать на минимальный угол, равный  градусам, где n –порядок симметрии, в данном случае n = 5. Следовательно, угол поворота, который ничего не меняет, должен быть кратен  градусам [3, 12].

1.4.1.   Типы мозаики Пенроуза

Существует три типа мозаики Пенроуза. Все они имеют много общих черт: формы плиток во всех трёх типах связаны с правильным пятиугольником и золотым сечением. Основные формы при этом должны быть дополнены правилами сочетаний, чтобы гарантировать апериодичность. Правила сочетаний указывают, как соседние плитки могут сочетаться друг с другом, и могут быть реализованы пометками на вершинах, рёбрах или небольшими изменениями формы (добавление соответствующих выступов и впадин к рёбрам) [3, 12].

1.4.1.1.        Исходная мозаика Пенроуза (P1)

Этот тип мозаики Пенроуза строится из плиток шести типов: три из них имеют форму правильного пятиугольника(они различаются между собой правилами сочетаний), остальные имеют форму пятиконечной звезды, «лодочки» (похожа на звезду с отрезанными двумя лучами) и ромба (рис. 17) [3, 12].

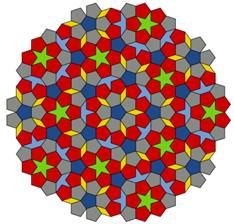
Рис. 17. Исходная мозаика Пенроуза

1.4.1.2.        Мозаика Пенроуза из дельтоидов (P2)

Второй тип мозаики Пенроуза строится из плиток двух типов: выпуклого дельтоида («змея») и вогнутого дельтоида («дротика»). Эти формы могут быть соединены, образуя ромб, однако правила сочетания запрещают такое соединение плиток в мозаике Пенроуза (рис. 18).

•                   Выпуклый дельтоид имеет углы в 72°, 72°, 72° и 144°. Ось симметрии разбивает его на два равных равнобедренных треугольника с углами 36°, 72° и 72° (так называемый «золотой треугольник»).

•                   Вогнутый дельтоид имеет углы в 36°, 72°, 36° и 216°. Ось симметрии разбивает его на два равных равнобедренных треугольника с углами 36°, 36° и 108° (так называемый «тупоугольный золотой треугольник»).

 

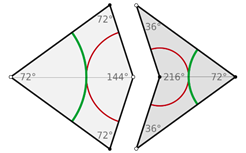
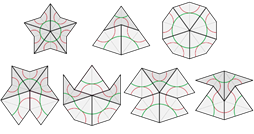
Рис. 18. Мозаика Пенроуза из дельтоидов и правила их сочетания

Правила сочетаний можно обозначить несколькими способами. Можно раскрасить вершины плиток в два цвета и потребовать, чтобы смежные вершины имели один и тот же цвет. Можно нанести на плитки узор, как на рисунке слева, и потребовать, чтобы узоры на соседних плитках были согласованы (для случая цветных дуг слева, чтобы кривые не обрывались).

В мозаике Пенроуза типа P2 может быть семь типов вершин. Конвей дал каждой своё название: симметричные вершины по своей форме были названы «солнце» и «луна», а остальные вершины — в честь достоинств игральных карт: «туз», «двойка», «валет», «дама» и «король» [3, 12].

1.4.1.3.                    Мозаика Пенроуза из ромбов (P3)

Третий тип строится также из плиток двух типов. Оба типа плиток имеют форму ромба. У них одинаковая длина стороны, но разные углы. Правила сочетаний предотвращают использование плиток для периодического замощения (рис. 19).

•                   Узкий ромб имеет острый угол 36°. Короткая диагональ разбивает его на два «золотых треугольника».

•                   Широкий ромб имеет острый угол 72°. Длинная диагональ разбивает его на два тупоугольных «золотых треугольника».

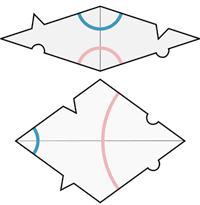
Рис. 19. Правила сочетаний мозаики Пенроуза из ромбов

В мозаике Пенроуза типа P3 может быть восемь типов вершин. Они были названы де Брёйном по первым буквам названий вершин типа P2 [3, 12].

1.4.2.   Свойства мозаик Пенроуза

Все три типа мозаики Пенроуза, как и любые апериодические мозаики, обладают следующими свойствами:

•                   Непериодичность — отсутствие трансляционной симметрии;

•                   Повторяемость (также называемая самоподобием, что, однако, не связано с одноимённым свойством фракталов) — любой сколь угодно большой фрагмент мозаики Пенроуза встречается в мозаике бесконечное число раз, хоть и через неравные расстояния;

•                   Квазикристалличность — при дифракции на мозаике, как на физической структуре, дифракционная картина показывает наличие дальнего порядка и симметрии пятого порядка;

•                   Операции измельчения и укрупнения (Разрезав все плитки мозаики Пенроуза по определённым правилам, а затем объединив некоторые фрагменты, можно получить мозаику Пенроуза с плитками, подобными исходным с коэффициентом:

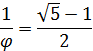
Такая операция называется измельчением. Правила в общем случае следующие: каждый тип плитки разрезается на плитки меньшего размера и части плиток. В случае P2 и P3 частями будут половинки плиток (золотые треугольники), в случае P1 это могут быть золотые треугольники, а также трапеция. При применении этих правил к мозаикам Пенроуза, за счёт соблюдения правил сочетаний, части плиток будут расположены так, что могут быть объединены, образуя целую плитку.

Обратная операция, называемая укрупнением, определена однозначно. Однозначность укрупнения влечёт апериодичность замощения [3, 12].

 

 

Глава II. Замощение плоскости многоугольниками

2.1. Замощение плоскости правильными многоугольниками

Несложно замостить плоскость паркетом из правильных треугольников, квадратов или шестиугольников (под замощением мы понимаем такую укладку, при которой вершины каждой фигуры прикладываются только к вершинам соседних фигур и не возникает ситуации, когда вершина приложилась к стороне). Никакими другими правильными n-угольниками покрыть плоскость без пробелов и наложений не получится (рис. 20).

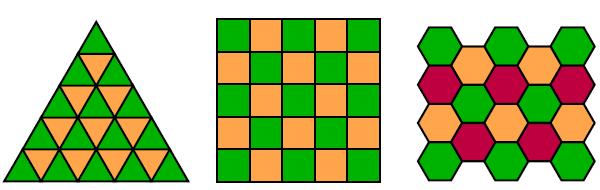
Рис. 20. Замощение правильными многоугольниками

Проверим утверждение о том, что никакими другими правильными n-угольниками покрыть плоскость без пробелов и наложений не получится. Как известно, сумма внутренних углов любого n-угольника равна (n – 2) · 180°. Поскольку все углы правильного n-угольника одинаковые, то градусная мера каждого угла есть . Если плоскость можно замостить такими фигурами, то в каждой вершине сходится k многоугольников (для некоторого k). Сумма углов при этой вершине должна составлять 360°, поэтому . После нескольких простых преобразований это равенство превращается в такое: . Но, как легко проверить, последнее уравнение имеет только три пары решений, если считать, что n и k натуральные числа: k = 3, n = 6; k = 4, n = 4 или k = 6, n = 3. Этим парам чисел как раз и соответствуют замощения из правильных треугольников, четырехугольников и шестиугольников [14, 15].

Также данные утверждения можно доказать с помощью программы GeoGebra.

Идея доказательства: с помощью построения опорных точек A и B и ползунка n (n=1, 2,…, 30) строим правильные треугольники (рис. 21) и правильные четырехугольники (рис. 22), тем самым, замощая плоскость [24].

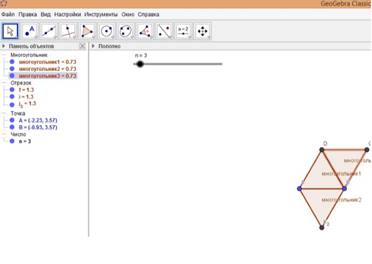
Рис. 21. Замощение правильными треугольниками

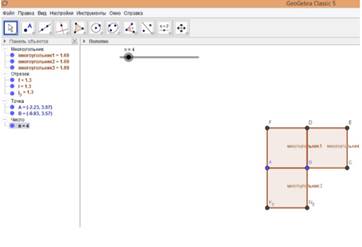
Рис. 22. Замощение правильными четырехугольниками

 

2.2. Замощение плоскости произвольными многоугольниками

2.2.1. Замощение плоскости треугольниками

Теорема 1.

Любым треугольником можно замостить плоскость.

Доказательство:

1.                 Рассмотрим произвольный треугольник ABC, в котором угол АВС=α, угол ВАС=β, угол ВСА=, где α, β, - любые углы (рис. 23).

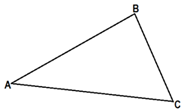
Рис. 23. Произвольный треугольник

2.                 Продлим все стороны треугольника, тогда внешние углы АВС будут равны сумме двух других углов, несмежных с ним (по свойству): внешний угол, смежный с углом α равен β+ Внешний угол, смежный с углом β равен α + Внешний угол, смежный с углом  равен α +(рис. 24).

                                                  

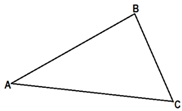
Рис. 24. Внешние углы произвольного треугольника

3.                 Так как внешние углы равны сумме двух других углов, то мы можем совместить внутренний угол треугольника с другим внутренним углом, входящим во внешний угол (рис. 25).

 

 

 

Рис. 25. Построение второго треугольника

4.                 Аналогично проделываем для других внешних углов.

5.                 После построения других треугольников для внешних углов получается аналогичная ситуация пункту 1. Затем мы переходим к пункту 2,3 и т.д.. Мы получаем повторение, которое можно проделывать бесконечное количество раз. Следовательно, любым треугольником можно замостить плоскость.

Что и требовалось доказать.

Алгоритм замощения плоскости треугольниками (рис. 26):

1.                 Достраиваем треугольник до параллелограмма;

2.                 Пристраиваем данный новый параллелограмм к имеющемуся.

[Приложение 3]

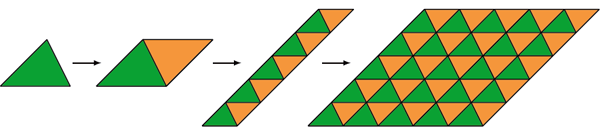
Рис. 26. Алгоритм замощения плоскости произвольными треугольниками

2.2.2.   Замощение плоскости четырехугольниками

Теорема 2.

Плоскость можно замостить любым четырехугольником

Доказательство для выпуклого четырехугольника:

1.         Рассмотрим произвольный выпуклый четырехугольник ABCD, где угол А=, угол В=, угол С=, угол D= (рис. 27).

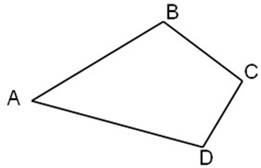
Рис. 27. Произвольный выпуклый четырехугольник

1.                 Сумма внутренних углов выпуклого четырехугольника равна 360˚ (по теореме). Следовательно,   .

2.         Внешний угол АВС = = (по пункту 2). Следовательно к данному углу можно приложить углы  так, что они будут плотно прилегать друг к другу.

3.                 Аналогично пункту 3 получаются и оставшиеся углы. После построения других четырехугольников мы возвращаемся к пункту 1. Затем мы переходим к пункту 2, 3 и т.д.. Мы получаем повторение, которое можно проделывать бесконечное количество раз. Следовательно, любым выпуклым четырехугольником можно замостить плоскость.

Что и требовалось доказать.

[Приложение 4]

Доказательство для невыпуклого четырехугольника:

1.     Рассмотрим произвольный невыпуклый четырехугольник (рис. 28)

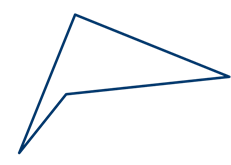
Рис. 28. Произвольный невыпуклый четырехугольник

2.                 Соединим две его вершины внутри так, чтобы получились два  произвольных треугольника (рис. 29)

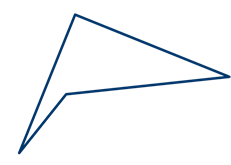
Рис. 29. Внутренняя диагональ невыпуклого четырехугольника

3.                 По теореме 1 – любым треугольником можно замостить плоскость. Следовательно, можно к любому из имеющихся треугольников пристроить точно такой же треугольник и продолжить его до данного невыпуклого четырехугольника (рис. 30).

 

 

 

 

 

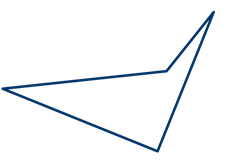
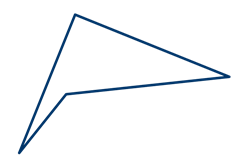
4.                 Затем проделываем те же действия со вторым получившимся треугольником (рис. 31).

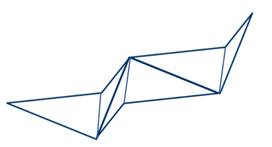
Рис. 31. Построение третьего невыпуклого четырехугольника

5.                 Описанные в пункте 3 действия можно делать бесконечно много. Следовательно любым невыпуклым четырехугольником можно замостить плоскость. Что и требовалось доказать.

Идея замощения плоскости произвольным четырехугольником: укладка четырехугольников диагоналями друг к другу (рис. 32, 33).

·        Выпуклый четырехугольник

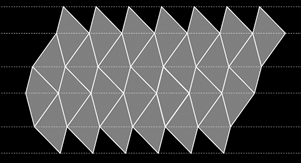
Рис. 32. Идея замощение выпуклым четырехугольником

·        Вогнутый четырехугольник

Рис. 33. Идея замощения невыпуклым четырехугольником

[Приложение 5]

2.2.3.   Замощение плоскости пятиугольниками

Пятиугольный паркет  — в геометрии: замощение, составленное из выпуклых пятиугольников. Замощение из правильных пятиугольников в евклидовом пространстве невозможно, поскольку общий угол правильного пятиугольника равен 108° и не делит ни 180°, ни 360° нацело. Однако, ими можно замостить гиперболическую плоскость и сферу.

Для плоскости же задача о полном описании всех возможных замощений неправильными пятиугольниками (описания всех видов пятиугольников, для которых возможно такое замощение) является очень сложной и исследования по ней ведутся больше века.

Более простой задачей является отыскание всех паркетов, составляющих замощение «ребро к ребру», то есть когда ни одна сторона ни одной плитки не совпадает сразу с двумя сторонами двух других (или, другими словами, когда никакая из вершин многоугольников замощения не лежит посреди некоторой стороны другого многоугольника).

Всего существует 8 пятиугольных паркетов «ребро к ребру» из выпуклых плиток. Тот факт, что остальных таких паркетов, кроме уже найденных, не существует, был доказан Ольгой Багиной на Омском алгебраическом семинаре в 2011 году.

Выпуклый пятиугольник тогда и только тогда замощает плоскость нормально, когда он относится к одному из следующих типов:

1. 𝑥0 + 𝑥1 = 180∘ , 𝐶0 = 𝐶2 или 𝐶3 = 𝐶4;

2. 𝑥0 + 𝑥2 = 180∘ , 𝐶1 = 𝐶3, 𝐶0 = 𝐶2;

3. 𝑥0 = 𝑥2 = 90∘ , 𝐶0 = 𝐶1, 𝐶2 = 𝐶3;

4. 𝑥2 = 2𝑥0 = 120∘ , 𝐶0 = 𝐶1, 𝐶2 = 𝐶3;

5. 𝑥1 + 𝑥3 = 180∘ , 𝑥0 = 2𝑥3, 𝐶0 = 𝐶1 = 𝐶2, 𝐶3 = 𝐶4;

6. 𝑥0 + 2𝑥3 = 360∘ , 𝑥2 + 2𝑥1 = 360∘ ; 𝐶0 = 𝐶1 = 𝐶2 = 𝐶3;

7. 𝑥1 + 2𝑥0 = 360∘ , 𝑥2 + 2𝑥3 = 360∘ , 𝐶0 = 𝐶1 = 𝐶2 = 𝐶3;

8. 𝑥1 + 2𝑥4 = 360∘ , 𝑥2 + 2𝑥3 = 360∘ , 𝐶0 = 𝐶1 = 𝐶2 = 𝐶3.

Предполагается, что существует всего 15 классов пятиугольников, бесконечные паркеты из которых могут замостить плоскость [Приложение 2]. Поиск всех таких классов продолжался до 2015 года, а 1 мая 2017 года Майкл Рао предъявил доказательство того, что других таких пятиугольников не существует.

Ни один из пятнадцати известных классов доступных для замощения пятиугольников не накрывается полностью объединением других. Тем не менее, некоторые пары классов могут пересекаться. Кроме того, в некоторых классах есть многоугольники, для которых кроме стандартной схемы замощения плоскости плитками этого класса существуют ещё и альтернативные способы замощения [3, 6].

2.2.3.1.        Типы 1,2,3,4,5 (Карл Рейнхардт, 1918)

Первые пять типов замощений описал в 1918 году Карл Рейнхардт.  Все эти пять замощений были изоэдральными, то есть каждую из плиток можно было перевести в каждую другую обычным поворотом и переносом, без применения зеркального отражения [6, 15].

Карл Рейнхард Хугершофф (нем. Carl Reinhard Hugershoff; 5 октября 1882, Лейбниц, Вердау — 24 января 1941, Дрезден) — немецкий геодезист, профессор Технического университета Дрездена. С 1910 года 1910 преподавал математику, геодезию, метеорологию и фотограмметрию в Лесотехнической академии в Тарандте и Дрезденском университете [16].

Бранко Грюнбаум и Алан Шепард показали, что существует ровно 24 типа различных изоэдральных замощений. Все эти 24 типа принадлежали к классам, описанным Рейнхардтом, но иногда требовали добавочных условий. Существует по два изоэдральных замощения для каждого набора из типа 2, и по одному для каждого из четырёх остальных. 15 из 18 остальных типов представляют собой специальные случаи замощения типа 1. 9 из 24 типов относятся к паркетам «ребро к ребру» [15, 25].

2.2.3.2.        Типы 6,7,8 (Роберт Киршнер, 1968)

Роберт Киршнер в 1968 году описал ещё три типа плиток. Он утверждал, что, кроме найденных теперь восьми типов, других не существует, но оказался не прав.

В типах 7 и 8 впервые появляются хиральные плитки (то есть для полного описания орбит симметрии впервые приходится использовать не только вращения, но и отражения) [15, 25].

Роберт Киршнер (Robert  Kirshner, род. 15 августа 1949, Лонг Бранч, Нью-Джерси) —американский астроном, космолог и исследователь сверхновых. Профессор Гарвардского университета, член НАН США и Американского философского общества. Лауреат премии Вольфа. Окончил факультет Гарвард-колледжа по астрономии (1970). Степень доктора философии по астрономии получил в Калифорнийском технологическом институте в 1975 году. В 1974—1976 годах постдок в Национальной обсерватории Китт-Пик. На протяжении девяти лет преподавал в Мичиганском университете [17].

2.2.3.3.        Тип 10 ( Ричард Джеймс, 1975)

Изучив результаты Роберта Киршнера в колонке Мартина Гарднера «Математические игры» журнала Scientific American, Ричард Джеймс нашёл ещё один тип пятиугольников, который сейчас именуется типом 10 [15, 25].

Мартин Гарднер (англ. Martin Gardner; род. 21 октября 1914, Талса, Оклахома, США — 22 мая 2010, Норман, Оклахома, США) — американский математик-любитель, писатель, популяризатор науки, один из основателей Комитета по научному расследованию заявлений о паранормальных явлениях. Опубликовал более 70 книг [18].

Ричард Джеймс «Рик» Хиб (англ. Richard James 'Rick' Hieb, род. 21 сентября 1955) — астронавт НАСА. Совершил три космических полёта на шаттлах, совершил три выхода в открытый космос, инженер. Ричард Хиб родился  в городе Джеймстаун (штат Северная Дакота), где в 1973 году окончил среднюю школу. В 1977 году получил степень бакалавра наук в области физики и математики в частном гуманитарном колледже «Университет Северо-Восточного Назарина» в городе Нампа (штат Айдахо). В 1979 году получил степень магистра наук в области аэрокосмическая техника в Колорадском университете в Боулдере [19].

Типы 9, 11, 12, 13 (Марджори Райс, 1977)

Математик-любитель Марджори Райс в 1976 и 1977 году нашла ещё четыре типа плиток, подходящих для замощения.

Все четыре типа паркетов 2-изоэдральны Из всех четырёх типов только тип 9 даёт замощение типа «ребро к ребру».

Примитивные ячейки везде содержат по 8 плиток [25].

Марджори Райс (16 февраля 1923 - 2 июля 2017) - американский математик-любитель, самые известные ее открытия были сделаны в геометрии . Марджори Райс родилась в Санкт – Петербурге - город в округе Пинеллас, штат Флорида, и умерла в Калифорнии, где она жила с сыном и дочерью [20].

2.2.3.4.        Тип 14 (Рольф Штайн, 1985)

Четырнадцатую мозаику нашёл Рольф Штайн в 1985 году. Найденное им замощение 3-изоэдрально и не относится к типу «ребро к ребру».

Более того, его замощение состоит из строго фиксированных плиток — никакой вариабельности через уравнения на углы, как в предыдущих типах, никаких степеней свободы здесь нет. Вот некоторые параметры этой фиксированной плитки:{\displaystyle b=a{\sqrt {\frac {11{\sqrt {57}}-25}{8}}}}

 

Из  этих значений можно легко вывести остальные.

Примитивная ячейка такого замощения содержит шесть плиток [15, 25].

Рольф Альфред Штайн (нем. Rolf Alfred Stein; 31 июня 1911, Свеце, Польша — 9 октября 1999, Париж, Франция) — известный французский синолог и тибетолог. Он внёс вклад, в частности, в изучение «Гэсэра» и китайских источников по истории Тибета.

Рольф Штайн является создателем коллекции фотодокументов разных стран (Китай, Индокитай, Япония, Тибет, Непал, Индия), хранящейся в Центре истории религий, примыкающем к Музею восточных искусств в Париже. [21]

 {\displaystyle \sin(B)={\frac {{\sqrt {57}}-3}{8}}}{\displaystyle \cos(B)=-{\sqrt {\frac {3{\sqrt {57}}-1}{32}}}}

2.2.3.5.        Тип 15 (Кейси Манн, Дженниффер Маклауд, Дэвид фон Дюрей, 2015)

Исследователи из университета Вашингтона Ботелл, математики Кейси Манн, Дженниффер Маклауд и Дэвид фон Дюрей в 2015 году, используя компьютерные вычисления, нашли пятнадцатый тип паркета. Их работа была опубликована в октябре 2015 года в Cornell University  (точное название: «Convex pentagons that admit i-block transitive tilings» - «Выпуклые пятиугольники, допускающие i-транзитные плитки»). [6, 15, 22]

Эта мозаика не относится к типу «ребро к ребру». Она 3-изоэдральна (это обеспечивается двумя симметриями — поворотом на 180° относительно центра стыка белых плиток одной элементарной ячейки и зеркальным отражением относительно центра стыка белых плиток из двух разных элементарных ячеек). В мозаике есть хиральные плитки. Примитивная ячейка содержит 12 плиток.

Так же, как паркет типа 14, этот паркет может быть построен из одной единственной плитки, никаких степеней свободы для изменения углов и длин сторон нет [6, 15, 23, 25].

«Мы открыли фигуру с помощью компьютерного перебора большого, но ограниченного количества вариантов, — говорит Кейси Манн. — Конечно, мы очень взволнованы и немного удивлены, что удалось открыть новый вид пятиугольника». Открытие кажется чисто абстрактным, но на самом деле оно может найти практическое применение (рис. 34). [23]

Рис. 34. Практическое применение 15 типа пятиугольников

2.2.4.   Замощение плоскости шестиугольниками

Возьмем платоново замощение и начнем его растягивать по одному из направлений. В результате получится паркет из уже неправильных шестиугольников. Оказывается, впрочем, что такое растягивание (как и некоторые, более хитрые преобразования) сохраняет фиксированный набор свойств. 

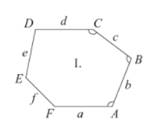Чтобы описать их, обозначим углы шестиугольника как A, B, C, D, E, F, а стороны как a, b, c, d, e, f (рис. 35). При этом считаем, что сторона a примыкает к углу A справа и все стороны и углы названы по часовой стрелке.

 

 

 

 

В 60-е годы прошлого века была доказана замечательная теорема.

Теорема 3.

Шестиугольником можно замостить плоскость тогда и только тогда, когда он принадлежит одному или более из трех классов (классы тут пересекаются, скажем, правильный шестиугольник принадлежит всем трем) :

1.     A + B + C = 360

2.     A + B + D = 360, a = d, c = e

3.     A = C = E = 120, a = b, c = d, e = f.

Теорема 4.

Никаким выпуклым n-угольником с n  6 нельзя замостить плоскость [3, 25].

 

Глава III. Невозможные замощения

3.1.          Раскраски. Замощение шахматной доски доминошками

3.1.1. Постановка задачи

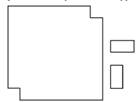Из шахматной доски вырезаны две угловые диагонально противоположные клетки - a1 и h8 (рис. 36).

 

 

 

 

Можно ли замостить полученную «усеченную» шахматную доску доминошками размера 2 × 1?

Типичный фрагмент замощения доминошками показан на рисунке 37.

 

 

 

 

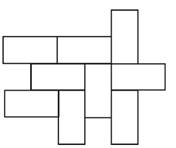
Фигурки, составляющие замощение, не перекрываются (они касаются друг друга только по границе), и при этом каждая точка доски принадлежит какой-либо фигурке. Отметим два момента: во-первых, доминошки разрешается класть как вертикально, так и горизонтально; во-вторых, у соприкасающихся доминошек не обязательно должна быть целая общая сторона. Общая постановка задачи о замощении звучит так: если дан многоугольник P и набор многоугольников Q₁ Q₂ … , возможно ли замостить P копиями многоугольников Q_i? [26]

3.1.2. Решение задачи о шахматной доске с вырезанными углами                

Вспомним, что поля шахматной доски окрашены в черный и белый цвета.

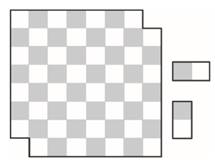Оба вырезанных диагонально противоположных угла черные, т.е. доска состоит из тридцати черных и тридцати двух белых полей (рис. 38).

 

 

 

 

 

С другой стороны, каждая доминошка размера 2 × 1  накрывает одно белое и одно черное поле. Значит, такое замощение невозможно.

Другой способ изложить то же доказательство.

Запишем на каждом белом поле нуль, а на каждом черном – единицу. Общая сумма всех чисел на доске с вырезанными углами составляет 30. Но на каждой доминошке написаны как 0, так и 1, и тридцать одна доминошка дает сумму 31, а не 30. Значит, такого замощения не существует.

Рассмотрим какую-либо область на бумаге в клетку. Замощение доминошками—это способ разбить эту область на прямоугольники 2×1 так, чтобы они покрывали всю область и никакие два прямоугольника не имели бы общих внутренних точек (т.е. не накладывались), а пересекались бы только по границе [26].

3.1.3. Вариация замощения шахматной доски доминошками

Можно ли замостить квадрат 10 × 10 Г-образными фигурками, изображенными на рисунке 39?

 

 

 

 

 

 

 

 

Заметим, что у каждой фигурки может быть восемь различных ориентаций. Ответ снова отрицательный. Запишем в клетках квадрата числа 1 и 5, как показано на рисунке 39. Каждая фигурка накрывает либо три единицы и одну пятерку, либо три пятерки и одну единицу. В любом из этих случаев сумма чисел на фигурке кратна 8. С другой стороны, общая сумма чисел на доске равна 300, что на 8 не делится. Значит, такого замощения не существует [26].

 

3.2.          Замощения без раскрасок

Предположим, что у нас есть два типа фигурок: обычные, положительные, фигурки – и отрицательные фигурки, сделанные из «антивещества». Нам разрешается накладывать фигурки друг на друга, и при этом общие части положительных и отрицательных фигурок взаимно уничтожаются (рис. 40).

 

 

Это можно представить себе по-другому: напишем на каждой положительной фигурке число 1, а на каждой отрицательной число −1 . Кратностью в точке называется сумма этих ±1 по всем фигуркам, взятая в этой точке.

Мы будем говорить, что многоугольник допускает замощение со знаком, если положительные и отрицательные фигурки можно положить так, чтобы кратность в каждой точке внутри P равнялась 1. Ясно, что если рассуждение с использованием раскрасок наподобие того, что обсуждалось в предыдущем разделе, доказывает, что многоугольник нельзя замостить некоторым набором фигурок, то из этого же доказательства следует, что замощения со знаком так- же не существует. Однако бывают задачи, которые имеют решение только для замощений со знаком и неразрешимы для обычных замощений.

Рассмотрим набор точек, расположенных в виде треугольника (рис. 41).

 

 

 

 

 

 

 

Мы хотим замостить этот треугольник прямыми плашками, каждая из которых содержит три точки; каждая такая плашка может быть ориентирована одним из трех возможных способов. Для каких значений n существует такое замощение?

Для начала, чтобы такое замощение было возможным, число точек должно делиться на три. Их общее число равно , и поэтому n ≡ 0 или  .

Теперь «раскрасим» точки так, как показано на рисунке 42.

 

 

 

 

 

 

Сумма чисел, покрытых одной плашкой, будет тогда кратна трем. Общая сумма зависит от n периодическим образом с периодом 9; ее значения по модулю три равны 0, 2, 2, 2, 1, 1, 1, 0, 0.

Поэтому  должно равняться 1, 8 или 0. Мы уже знаем, что n ≡ 0 или , поэтому остаются только последние два случая. Покажем, что если n ≡ 8 или , то треугольник из точек можно замостить со знаком при помощи трехточечных плашек. На рисунке 43 такое замощение показано при n = 8, а на рисунке 44 изображено, как строить треугольники большего размера из треугольников со стороной 8 и рядов трехточечных плашек.

 

 

 

 

 

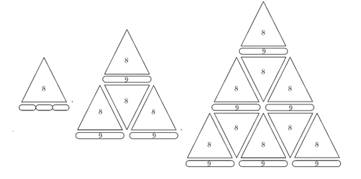
Рис. 44. Построение треугольников большего размера

Из этого получается, что следующую удивительную теорему невозможно доказать каким угодно рассуждением, использующим раскраски.

Теорема 5.

Ни для какого числа n треугольную таблицу точек со стороной n нельзя замостить трехточечными плашками.

Доказательство:

Для доказательства теоремы 5 нам понадобится некоторая предварительная подготовка. Для начала предположим, что все наши многоугольники: и область, которую мы собираемся замостить, и элементы замощения – нарисованы на клетчатой бумаге и составлены из единичных квадратиков. Также условимся, что ни в каком из этих многоугольников не будет дырок: граница каждого из них будет состоять из единой замкнутой кривой.

Путь на клетчатой бумаге будет описываться словом, составленным из букв четырехбуквенного алфавита x, y, х^-1, у^-1: шаг вправо обозначается через x, шаг влево – через х^-1, шаг вверх – через y, и шаг вниз – через у^-1. Пример изображен на рисунке 45.

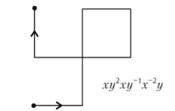
Рис. 45. Пример

Мы будем записывать k символов x или х^-1, идущих подряд, как ; то же самое для y. Тривиальный путь будет обозначаться через e. Также условимся, что идущие подряд символы x и 1 х^-1 (или y и у^-1) сокращаются: например, xyy^-1x^-1=e.

Композиция двух слов a и b будет определяться так: запишем сначала слово a, а потом слово b и сократим в полученном слове все идущие подряд пары, состоящие из x и x^-1 и из y и y^-1. Полученное слово условимся обозначать через ab.

Композиция удовлетворяет закону ассоциативности: (ab)c=a(bc), где через a, b и c обозначены произвольные слова. Слово  обратное к данному слову , получается так: надо прочитать слово  справа налево и заменить все показатели степеней на противоположные. Например, . Ясно, что .

Пусть – полный набор фигурок, разложенных на клетчатой бумаге во всех возможных ориентациях (например, у доминошки различных ориентаций две, а у Г-образной фигурки – восемь). Выберем на границе фигурки  начальную точку и пройдем вдоль границы против часовой стрелки. Полученный замкнутый путь будет соответствовать слову W_i, состоящему из букв x, y, х^-1, у^-1. Разумеется, это слово будет зависеть от выбора начальной точки. Пока что единственным имевшимся у нас правилом работы со словами был набор равенств

Добавим к этому правилу новые равенства: W₁=W₂=…=e.Эти правила значат, что если одно из слов W_i встречается в более длинном слове, то мы можем заменить его на e, и, наоборот, мы можем вставлять в любом месте любого слова какое-либо из слов W_i. Если слово V₁ может быть получено из слова V₂ последовательным применением этих правил, мы будем называть такие слова эквивалентными и записывать это как V₁= V₂.

Нам нужно еще разобраться с неоднозначностью выбора слова W_i, а именно, с его зависимостью от начальной точки. Пусть p′ – другая начальная точка на границе фигурки T_i, и пусть W_i′ – слово, полученное в результате прохождения вдоль границы начиная с точки p′.

Лемма. Имеется равенство W_i′ =e.

Доказательство:

Пусть слово u кодирует путь из p в p′, а слово v – путь из p′ в p (рис.46).

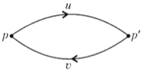
Рис. 46. Пути

Тогда W_i′ =uv и W_i′=vu. Поскольку W_i′ =e, то и uv = e. Тогда vu=(u^-1u)(vu)=u^-1u=e, что и требовалось [26].

 

3.3.          Замощение квадратами и электрической цепи

Рассмотрим замощение прямоугольника квадратами, изображенное на рисунке 47.

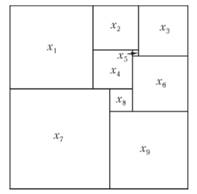
Рис. 47. Замощение прямоугольника квадратами

Пусть х₁,…,х₉ – длины сторон квадратов. Для каждого отрезка на этом рисунке, как горизонтального, так и вертикального, имеется линейное соотношение между переменными x_i: эти соотношения выражают длину отрезка в виде суммы длин сторон квадратов, граничащих по этому отрезку с обеих сторон. Для замощения на рисунке 41 получатся следующие уравнения:

x₂=x₄+x₅, x₃+x₅=x₆, x₁+x₄=x₇+x₈, x₆+x₈=x₉  ()(горизонтальные отрезки) и

x₁=x₂+x₄, x₇=x₈+x₉, x₄+x₈=x₅+x₆ () (вертикальные отрезки). Чтобы такое замощение существовало, эта система линейных уравнений должна быть разрешима в положительных числах. Замощение на рисунке 31 соответствует следующему решению: x₁ = 15, x₂ = 8, x₃ = 9, x₄ = 7, x₅ = 1, x₆ = 10, x₇ = 18,             x₈ = 4, x₉ = 14;

разумеется, весь этот набор чисел можно умножить на произвольный множитель.

Уравнения () и () можно интерпретировать как правила Кирхгофа для электрических цепей. Пример такой цепи показан на рисунке 48.

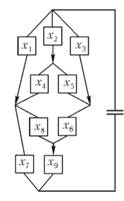
Рис. 48. Пример

Предположим, что все резисторы имеют единичное сопротивление и что сила тока в i-м резисторе равняется x_i. Есть два правила Кирхгофа: первое правило, или закон токов, утверждает, что сумма токов, втекающих в каждый узел, равняется сумме токов, вытекающих из него; второе правило, или закон напряжений, гласит, что сумма падений напряжения по любому замкнутому контуру равна нулю. Поскольку сопротивление всех резисторов единичное, по закону Ома падение напряжения на i-м резисторе равно силе тока x_i. Законы токов для цепи на рисунке 48 – это в точности уравнения (), а законы напряжений – это уравнения (). Контур на рисунке 48 получается из замощения на рисунке 47 следующим образом: всякому горизонтальному отрезку соответствует узел электрической цепи, а каждый квадрат соответствует резистору. Резистор соединяет два узла, если отвечающий ему квадрат примыкает к соответствующим двум отрезкам. Эта конструкция работает для любого замощения прямоугольника квадратами и дает электрическую цепь. Падение напряжения между верхней и нижней вершинами (т.е. напряжение источника ЭДС) единственным образом определяет токи во всех резисторах, и мы получаем решение системы () –       (). В частности, у этой системы имеется единственное решение, с точностью до общего множителя. То же самое верно и для любого замощения прямоугольника квадратами. Недостаток этого метода состоит в том, что у нас нет контроля над знаками силы тока: ток в некоторых резисторах может оказаться отрицательным, и тогда электрическая цепь не будет соответствовать никакому замощению прямоугольника квадратами [26].

 

3.4.          Замощение прямоугольниками с целочисленными сторонами

Теорема 6.

Пусть прямоугольник R замощен прямоугольниками, у каждого из которых есть целочисленная сторона. Тогда и у R есть целочисленная сторона.

У этой теоремы о замощениях известно чрезвычайно много различных доказательств (в журнале «American Mathematical Monthly», 7-й выпуск за 1987 год, опубликована статья, в которой приведено четырнадцать, а кроме них есть и другие). Представим одно из самых красивых.

Доказательство:

Интеграл  по отрезку целой длины равен нулю. Следовательно, двойной интеграл

по каждому из прямоугольников, участвующих в замощении, равен нулю. Значит, этот двойной интеграл по всему прямоугольнику R также равен нулю. Предположим, что левый нижний угол прямоугольника R находится в начале координат, а длины его сторон равны a и b. Тогда

=

Следовательно, либо , либо , т.е. либо a, либо b – целое число. Замена в этом доказательстве функции  на функцию  дает простое доказательство без интегралов.

Аналогичное элементарное доказательство.

Разграфим плоскость на клетки со стороной и раскрасим ее в два цвета – черный и белый, – в шахматном порядке.

Верен такой замечательный факт: как бы мы ни расположили на этой плоскости прямоугольник, стороны которого параллельны линиям сетки и длина одной из сторон целая, в нем будет поровну черного и белого цвета. Это совсем очевидно, если его стороны с целой длиной (пусть они горизонтальны) упираются концами в линии сетки – тогда прямоугольник делится вертикальными линиями сетки на четное число одинаковых по размеру столбиков (для этого мы взяли сторону клетки ), причем в каждом столбике столько белого, сколько в соседнем черного, и наоборот (рис.49).

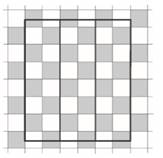
Рис.49. Поделенный прямоугольник

Разбив столбики на пары соседних, видим, что белого и черного в прямоугольнике поровну.

Теперь несложно вывести и саму теорему. Расположим наш большой прямоугольник так, чтобы он весь лежал в первом квадранте, а одна из его вершин совпадала с началом координат. В каждом маленьком прямоугольнике белого и черного будет поровну, а значит и в большом – тоже. Пусть обе стороны большого прямоугольника нецелые. Рассмотрим самую высокую горизонтальную линию сетки с целой ординатой и самую правую вертикальную линию сетки с целой абсциссой, пересекающие наш прямоугольник (рис.50).

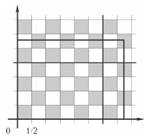
Рис.50. Самая высокая горизонтальная линия сетки с целой ординатой и самая права вертикальная линия сетки с целой абсциссой

Они делят его на четыре прямоугольные части, три из которых имеют сторону с целой длиной и, значит, содержат поровну белого и черного цвета. Тогда и четвертая часть (правая верхняя) содержит поровну черного и белого цвета. Эта часть целиком лежит в квадрате 1×1 и имеет нецелые стороны a и b, где 0 < a, b < 1 (рис.51).

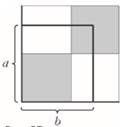
Рис. 51. Квадрат 1×1

Линии сетки делят этот квадрат на четыре квадратика размером ×, раскрашенных в шахматном порядке. Ясно, что стороны a и b не могут быть одновременно меньше  (тогда вся часть лежит в квадратике одного цвета). Пусть a ≥. Будем монотонно увеличивать a до 1. При этом доля одного из цветов в нашей части тоже будет монотонно увеличиваться, но при a = 1 количества цветов сравняются. Значит, их было непоровну. Полученное противоречие доказывает теорему.

У теоремы 6 есть интересное следствие. Предположим, что прямоугольник размера m×n замощен прямоугольниками размера p×q (все числа m, n, p, q целые). Разумеется, отсюда следует, что pq делит mn. Но можно сказать и больше.

Следствие. Число p делит либо m, либо n; то же самое верно и для q.

Доказательство. Домножим все длины на ; получим, что прямоугольник размера  замощен прямоугольниками размера 1. По теореме 6 либо , либо  целое, т.е. p делит либо m, либо n. Аналогично и для q [26].

 

3.5.          Замощения треугольниками равной площади

Теорема 7.

Квадрат нельзя замостить нечетным числом треугольников одинаковой площади (рис. 52).

Рис. 52. Замощение квадрата четным числом треугольников одинаковой площади

 Это достаточно новая теорема – ее доказал Пауль Монски (Paul Monsky) в 1970 году, – и ее доказательство крайне неожиданно. Используя 2-адические числа, строится определённая раскраска точек единичного квадрата в три цвета.

Главные свойства раскраски состоят в следующем:

1.    Площадь любого треугольника с вершинами разных цветов не может быть выражена дробью с нечётными числителем и знаменателем. В частности, если бы существовало разбиение квадрата на нечётное число равновеликих треугольников, то ни один из треугольников не имел бы вершин всех трёх цветов.

2.    Любая прямая окрашена ровно в два цвета [26].

Пауль Монски (17 июня 1936 года) — американский математик и профессор в университете Брандейса. Наиболее известен доказательством теоремы о разрезании квадрата на равновеликие треугольники. Получил степень бакалавра в Свэрсмор-колледже. Защитил диссертацию в 1962 г. в Чикагском университете [27].

 

Глава IV. Приложение замощения плоскости многоугольниками

4.1.          Знакомство с понятием ацтекского бриллианта

Рассмотрим какую-либо область на бумаге в клетку. Замощение доминошками — это способ разбить эту область на прямоугольники 2×1 так, чтобы они покрывали всю область и никакие два прямоугольника не имели бы общих внутренних точек (т. е. не накладывались), а пересекались бы только по границе.

В известной задаче для младших школьников предлагается доказать, что шахматную доску, из которой выброшены две противоположные угловые клетки, замостить доминошками нельзя. Мы будем иметь дело с фигурами, которые замостить доминошками можно; при этом нас будет интересовать, сколькими способами это можно сделать.

Вот самый простой пример. Возьмем прямоугольник размера 2×n. Тогда количество способов замостить его доминошками равно (n+1)-му числу Фибоначчи. Доказать это можно по индукции. Действительно, пусть F(n) — число способов замостить прямоугольник 2×n. Возьмем доминошку, покрывающую левый верхний угол прямоугольника. Тогда она может быть либо вертикальной, и оставшуюся часть прямоугольника можно замостить F(n−1) способами, либо горизонтальной — тогда две клетки под ней тоже будут заняты горизонтальной доминошкой, и останется замостить прямоугольник 2×(n −2). Мы получили рекуррентное соотношение:

А поскольку первые два члена у этой последовательности равны еди- нице: F(0) = F(1) = 1, это и есть последовательность Фибоначчи.

Следующий вопрос, который возникает после этого — сколькими способами можно замостить доминошками прямоугольник произвольного размера m×n? Это уже оказывается весьма непростой задачей, которая была решена в 1961 году Кастелейном и независимо Темперли и Фишером. Они доказали, что число замощений такого прямоугольника задается следующей, довольно замысловатой, формулой:

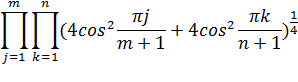
Проанализируем задачу о замощении другой фигуры — квадрата, только повернутого на 45◦ .

Рассмотрим множество квадратиков на клетчатой бумаге, координаты (x, y) центров которых удовлетворяют неравенству |x| + | y|n, где n — целое положительное число. Числа x и y при этом мы считаем полуцелыми. Будем называть такую фигуру ацтекским бриллиантом порядка n; на рис. 53 изображен ацтекский бриллиант порядков 1, 2, 3 и 4, а на рисунке 54 пример замощения ацтекского бриллианта доминошками.

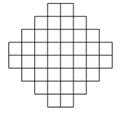
Рис. 53. Ацтекский бриллиант порядков 1, 2, 3, 4

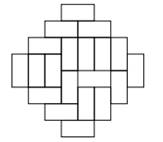
Рис. 54. Замощение ацтекского бриллианта порядка 4 доминошками

Отсюда возникает вопрос - сколько существует способов замостить доминошками ацтекский бриллиант порядка n? Можно попробовать посчитать это количество вручную при малых n. При n = 1 ацтекский бриллиант — это просто квадрат 2 × 2, который, очевидно, можно замостить двумя способами. При n = 2 найти все замощения явно тоже несложно; их оказывается 8. При дальнейшем росте n число замощений очень быстро растет: так, при n = 3 их уже оказывается 64, так что перечислить их все — задача не безнадежная, но при ручном переборе требующая некоторого терпения (или умения программировать). Однако при n = 4 обойтись без компьютера уже значительно сложнее: замощений оказывается 1024.

Итак, в первых примерах число замощений ацтекского бриллианта оказывается степенью двойки: 2, 2³, 2⁶,…, 2¹⁰. По приведенному фрагменту последовательности можно догадаться, чему равны показатели степени: это треугольные числа, т. е. суммы вида 1+2+…‌+ n — иначе говоря, 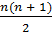. Это и составляет утверждение теоремы об ацтекском бриллианте [28, 29, 30].

 

4.2.          Теорема об ацтекском бриллианте

Теорема 8.

Число замощений ацтекского бриллианта порядка n доминошками размера 1 × 2 равняется

Ниже описаны три способа доказательства данной теоремы.

В первом доказательстве с каждым из замощений ацтекского бриллианта связывается пара квадратных матриц специального вида — так называемых знакочередующихся матриц. Оказывается, что каждая из этих матриц по отдельности позволяет восстановить замощение «почти полностью»: есть лишь несколько участков, на которых замощение не восстанавливается однозначно. Анализируя степень этой неоднозначности, удается найти общее число разбиений. Это первое опубликованное доказательство теоремы об ацтекском бриллианте; оно появилось в 1992 году в работе Ноама Элкиса, Грега Куперберга, Майкла Ларсена и Джима Проппа. Хотя это и не имеет непосредственного отношения к нашему основному сюжету, мы также упоминаем гипотезу о знакочередующихся матрицах, которая долгое время привлекала внимание специалистов по комбинаторике и была доказана независимо Д. Зейльбергером и Г. Купербергом в середине 1990-х гг.

Второе доказательство, принадлежащее Джиму Проппу, основано на подсчете числа так называемых димерных конфигураций, или совершенных паросочетаний графов, — то есть числа способов разбить вершины графа на пары так, чтобы вершины в каждой паре были бы соединены ребром. Ключевым инструментом для этого будет операция расширения площадей (urban renewal), позволяющая сводить графы, для которых мы хотим найти количество совершенных паросочетаний, к более простым. Это рассуждение на несложном примере демонстрирует методы, используемые при работе с димерами в значительно более сложных задачах математической физики. А сама операция расширения площадей, как было недавно показано А. Б. Гончаровым и Р. Кеньоном, неожиданным образом возникает и в других задачах, в частности в таком новом и бурно развивающемся направлении математики, как теория кластерных алгебр.

Третье доказательство теоремы об ацтекском бриллианте, о котором пойдет речь, сводит подсчет числа замощений бриллианта к нахождению числа наборов непересекающихся путей определенного 5 вида на решетке. Число этих наборов выражается как некоторый определитель; для этого используется такой полезный комбинаторный прием, как метод непересекающихся путей Линдстрёма—Гесселя— Вьенно. Это доказательство опубликовали в 2005 году тайваньские математики Сэнь-Пен Эу и Тун-Шань Фу. При этом используемое в доказательстве соответствие между замощениями и наборами путей упоминается и в более ранних работах, в частности, в книге Стенли [29, 30].

4.2.1.   Совершенные паросочетания и замощения

Приведем полное доказательство данной теоремы на основе второго доказательства – совершенных паросочетаниях на графах.

Пусть Γ — произвольный граф (абстрактный, без каких-либо условий на связность, планарность и т.п.). Совершенное паросочетание — это такой способ разбить все вершины на пары, при котором вершины в каждой паре оказываются соединены ребром. Иными словами, совершенное паросочетание—это подмножество M⊂E(Γ) ребер графа, обладающее следующим свойством: из каждой вершины графа исходит ровно одно ребро из подмножества M.

Между замощениями фигур с помощью доминошек и совершенными паросочетаниями на графах существует очевидная связь: для произвольной фигуры на клетчатой бумаге можно рассмотреть ее двойственный граф. Вершины этого графа будут соответствовать клеточкам; в случае, если две клеточки смежны, вершины будут соединены ребром. Тогда замощение фигуры доминошками есть не что иное, как совершенное паросочетание двойственного графа.

В качестве примера на рисунке 55 изображено замощение ацтекского бриллианта порядка 2 и отвечающее ему совершенное паросочетание на двойственном графе.

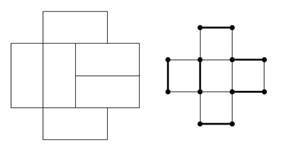
Рис. 55. Замощение ацтекского бриллианта порядка 2

Таким образом, число замощений ацтекского бриллианта порядка n оказывается равным числу совершенных паросочетаний двойственного к нему графа, который мы будем обозначать через AD_n  (на рисунке 56 в качестве примера изображен граф AD₃) [29].

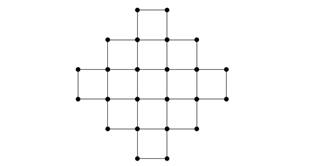
Рис. 56. Граф AD₃

4.2.2.   Взвешенные суммы

Предположим, что граф Γ является взвешенным: на каждом его ребре e∈E(Γ) написан вес, т.е. некоторое выражение wt e (число или многочлен от каких-либо переменных). Весом совершенного паросочетания M будем называть произведение весов всех входящих в него ребер:

Для данного графа Γ определим его статистическую сумму (или, как еще говорят, статсумму) Z(Γ) как сумму весов его всевозможных совершенных паросочетаний:

Пример. Пусть Γ—квадрат, на ребрах которого расставлены веса x, y, z и w, как показано на рисунке 57. Тогда для Γ имеются ровно два совершенных паросочетания, образованные парами противоположных сторон квадрата, и статистическая сумма графа Γ равняется

Z(Γ)= xz+ yw.

Ясно, что если все веса на ребрах графа Γ равны единице, то Z(Γ) равняется числу совершенных паросочетаний. Поэтому наша цель— найти статистическую сумму Z(AD_n) для ацтекского бриллианта AD_n , все веса на ребрах которого равны единице.

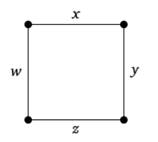
Рис. 57. Пример

Мы сделаем это, сведя вычисление этой функции к вычислению      Z(AD_n-1) при помощи различных манипуляций с исходным графом, при которых статсумма будет меняться контролируемым образом. Для этого нам потребуется вспомогательное утверждение [29].

4.2.3.   Лемма о расширении площадей

Предположим, что в графе Γ имеется подграф из восьми вершин, изображенный на рисунке 58 слева. При этом требуется, чтобы ни одна из вершин внутреннего квадрата (обозначим их через A’, B’, C’ и D’ ) не была бы соединена более ни с какими вершинами; напротив, четыре внешние вершины A, B, C и D могут быть соединены с какими-либо из вершин, не входящих в указанный фрагмент.

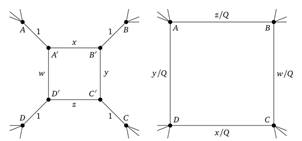
Рис. 58. Подграфы

Также предположим, что между этими восемью вершинами нет никаких других ребер, кроме тех восьми, которые изображены на рисунке. Кроме того, пусть веса на ребрах расставлены так, как указано на рисунке: ребра, соединяющие «внешние» и «внутренние» вершины, имеют вес 1, а веса на ребрах внутреннего квадрата произвольны (обозначим их через x, y, z и w).

Произведем с графом Γ следующие преобразования: заменим в нем этот фрагмент на квадрат ABCD. При этом мы считаем, что все ребра, соединяющие «внешние» вершины с вершинами, не входящими в этот фрагмент, остаются без изменений. Расставим веса на ребрах этого квадрата так, как показано на рисунке 58 справа: поменяем местами веса на противоположных ребрах и поделим все веса на величину Q = xz + yw. Получившийся граф обозначим через Γ’. Следующая лемма утверждает, что статсумма этого графа отличается от Z(Γ) в Q раз:

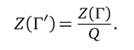 [29].

4.2.4.   Подсчет числа совершенных паросочетаний ацтекского бриллианта

Вычислим Z(AD_n), где AD_n —граф, отвечающий ацтекскому бриллианту порядка n. Все веса на ребрах этого графа мы полагаем равными единице.

Сделаем с графом AD_n   следующее преобразование: заменим каждую его вершину на три вершины, соединенные между собой двумя ребрами, как это показано на рисунке 59. В результате получим «утроенный» граф AD³_n.

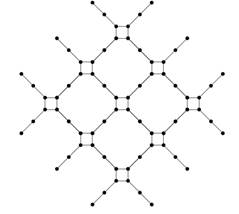
Рис. 59. «Утроенный» граф

Оказывается, «утроение» вершин никак не влияет на статсумму графа: Статсуммы исходного и «утроенного» графа равны: Z(AD_n)=Z(AD³_n).

Теперь настало время применить к «утроенному» графу лемму о расширении площадей. А именно, мы применим ее к каждому из n² маленьких квадратиков, из вершин которого выходят четыре диагональных ребра. Граф, полученный в результате, показан на рисунке 60; обратим внимание, что все его ребра, кроме диагональных «усов», уже будут иметь вес (такие ребра отмечены на рисунке пунктиром; сплошные ребра, как обычно, имеют вес 1).

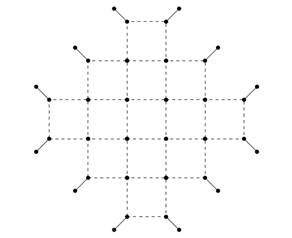
Рис. 60. Применение леммы о расширении площадей

Обозначим этот граф . Лемма о расширении площадей позволяет найти его статсумму. Действительно, каждое применение леммы уменьшает статсумму вдвое, а всего мы ее применили n² раз. Значит, ().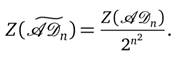

Что можно сказать о совершенных паросочетаниях графа ? Ясно, что в каждое паросочетание будут входить все 4n «усов»—т.е. ребер веса 1. На значение статсуммы они не влияют. Поэтому все эти ребра и смежные с ними вершины можно просто удалить—и статсумма оставшегося графа будет равна Z(). Но граф, который останется при этом, будет ацтекским бриллиантом на единицу меньшего порядка, все ребра которого будут иметь вес .

Теперь выясним, чему равна статистическая сумма ацтекского бриллианта AD_n-1, все ребра в котором имеют вес .

Она меньше Z(AD_n-1) в 2N раз, где N — число ребер в совершенном паросочетании, т.е. половина числа вершин графа. А в ацтекском бриллианте порядка n−1 всего 2n(n−1) вершин—стало быть, интересующая нас сумма равна  Итак,

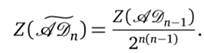
 Сравнив полученное с равенством (), мы получаем, что

Таким образом, число замощений ацтекского бриллианта порядка n в 2ⁿ раз больше числа замощений бриллианта порядка n−1. А отсюда и из равенства Z(AD₁)=2 получается доказательство теоремы об ацтекском бриллианте [29].

 

4.3.          Связанные понятия с ацтекским бриллиантом

4.3.1.   Ранг разбиения

Рангом разбиения {\displaystyle T}T ацтекского бриллианта на домино называется минимальное количество поворотов двух доминошек, имеющих общую длинную грань, вокруг центра их общей грани, необходимое для того, чтобы превратить разбиение в такое, где все плитки лежат горизонтально (такое разбиение, очевидно, существует только одно).

Максимальный возможный ранг разбиения ацтекского бриллианта порядка {\displaystyle n}n достигается при разбиении, в котором все плитки ориентированы вертикально. В этом случае ранг равен  .

4.3.2.   Функция высоты

Для произвольного фиксированного разбиения бриллианта удобно рассматривать функцию высоты. Это функция, определённая на узлах целочисленной решётки, находящихся внутри бриллианта или на его границе, и принимающая целочисленные значения.

Пусть фиксировано некоторое разбиение бриллианта на плитки домино. Рассмотрим раскраску клеток бриллианта в шахматном порядке, в которой верхняя из самых правых клеток – чёрная. На каждой из границ клеток поставим стрелку в таком направлении, чтобы белая клетка была справа от стрелки, а чёрная – слева (рис. 61).

Рис. 61. Разбиение бриллианта на домино со стрелками

Обозначим точку {\displaystyle (-n;0)} как {\displaystyle v_{0}}. Рассмотрим любой путь от  {\displaystyle v_{0}}до {\displaystyle v}, проходящий исключительно по границам разбивающих бриллиант плиток домино. Тогда для точки решётки  {\displaystyle v} функция высоты {\displaystyle H(v)} будет равна разности количества стрелок на этом пути, лежащих, соответственно, сонаправленно и обратно направленно этому пути [28, 30].

4.3.3.   Стандартная нотация плиток в разбиении

Для упрощения иллюстраций и формулировки доказательств часто используется условное деление всех плиток {\displaystyle 1\times 2} конкретного рассматриваемого замощения на четыре класса. Для их описания удобно представить раскраску клеток ацтекского бриллианта по типу шахматной доски такую, что верхняя из двух самых левых клеток - чёрная. Тогда классы определяются так:

·        N (north - север) - горизонтально ориентированная плитка, у которой левая клетка - чёрная;

·        S (south - юг) - горизонтально ориентированная плитка, у которой левая клетка - белая;

·        W (west - запад) - вертикально ориентированная плитка, у которой верхняя клетка - чёрная;

·        E (east - восток) - вертикально ориентированная плитка, у которой верхняя клетка - белая.

Названия классов, как видно, соответствуют сторонам, в которых находятся клетки при двух тривиальных разбиениях (где каждая горизонталь или вертикаль - прямая линия из последовательных плиток). При иллюстрации бриллианта плитки разных классов иногда изображаются разными цветами [28].

 

 

4.4.          Алгоритм генерации случайного разбиения

Известен алгоритм равновероятного выбора случайного разбиения бриллианта заданного размера из всех разбиений такого размера.

Для генерации случайного разбиения размера {\displaystyle n}n алгоритм использует заранее сгенерированное случайное разбиение ацтекского бриллианта размера {\displaystyle n-1}n-1 и специальным образом преобразует его со внесением дополнительной случайности. Таким образом, для генерации случайного разбиения размера {\displaystyle n}n нужно последовательно генерировать разбиения размера 1, 2, …, n-1, n. {\displaystyle 1,2,\dots ,n-1,n}

Преобразование при переходе от размера {\displaystyle n-1}n-1 к {\displaystyle n}n включает в себя три стадии:

1.  Разрушение. 

Из разбиения удаляются следующие пары плиток (если таковые присутствуют):

·  плитка S, соприкасающаяся нижней гранью с клеткой типа N;

·  плитка E, соприкасающаяся правой гранью с плиткой типа W.

2.  Сдвиг. 

Все оставшиеся плитки сдвигаются на одну клетку согласно своему типу в стандартной нотации - N вверх, S вниз, E вправо, W влево. Предшествующая стадия разрушения гарантирует, что при этом не возникнет наложений одной плитки на другую.

3.  Генерация. 

Доказано, что в результате двух предыдущих стадий все пустые клетки в области ацтекского бриллианта размера {\displaystyle n}n можно разбить на квадраты размера 2x2. На стадии генерации каждый такой квадрат отдельно заполняется равновероятно либо двумя вертикальными, либо двумя горизонтальными плитками [28].

 

4.5.          Теорема о полярном круге

Рассмотрим окружность, вписанную в квадрат, ограничивающий ацтекский бриллиант. Она отрезает от квадрата четыре угла. Оказывается, что у случайно выбираемого замощения с очень большой вероятностью почти все доминошки, попадающие в эти углы, т. е. вне этой окружности, будут "заморожены": в нижнем и верхнем углу они все будут горизонтальными, а в левом и правом — вертикальными. Напротив, поведение замощения внутри этой окружности предсказать нельзя — оно является хаотичным. Все вышесказанное составляет утверждение теоремы о полярном круге, доказанной в 1995 году У. Джокушем, Дж. Проппом и П. Шором [28].

Теорема 9.

Пусть {\displaystyle p_{n,\varepsilon }} - вероятность того, что при случайной раскраске бриллианта порядка {\displaystyle n} все плитки вне увеличенной в {\displaystyle 1+\varepsilon } раз вписанной в этот бриллиант окружности будут расположены детерминированным образом, то есть на верхнем краю все клетки будут из класса N, внизу - из класса S, справа - из класса W, слева - из класса E.

Тогда для любого {\displaystyle \varepsilon >0} имеет место   {\displaystyle p_{n,\varepsilon }\to 1} при {\displaystyle n\to \infty } 

Замечание. При стремлении порядка бриллианта к бесконечности граница «замороженной области» стремится ко вписанной в границу бриллианта окружности.

Для доказательства теоремы 9 используются факты о полностью асимметричном процессе исключения на Z, происходящем в дискретное время. Это стохастический процесс, состояния которого представляют собой дважды бесконечные последовательности (..., x_-1, x₀, x₁, ...) из единиц и нулей, чей i-й термин означает наличие или отсутствие частицы в местоположении i в одномерной решетке; на каждом дискретном временном шаге частица, у которого есть свободное место справа от нее, есть 50% шанс сделать один шаг вправо и 50% шанс остаться на месте. (Обратите внимание, что частица с другой частицей, находящейся непосредственно справа от нее, не имеет шансов на перемещение, пока место справа от нее не станет свободным). То есть: если система в момент времени n находится в особом состоянии                 (..., x-1, x0, x1, ...) и вы хотите продвинуть ко времени n + 1, то найти все i такие, что x’_i =1 и x’_i+1 = 0 (эти i обязательно не являются последовательными), и для каждого такого i подбрасывают честную монету (с независимые монеты для разных значений i); когда выпадает решка, положим x’_i = 0 и x’_i+1 = 1, и когда выпадает орел x’_i = 1 и x’_i+1 = 0. Положим x’_i=x_i для всех остальных i. Таким образом, получили новую двойственно – бесконечную последовательность (..., x′_-1 , x′₀ , x′₁ , ...) [31].

Примеры типичных случайных разбиений ацтекских бриллиантов порядков 10, 15, 25 и 40, раскрашенных соответственно стандартной нотацией плиток представлены на рисунке 62. Форма области с хаотичным поведением стремиться к вписанному кругу [28].

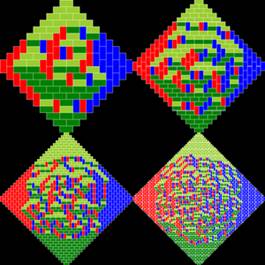
Рис. 62. Случайные разбиения ацтекских бриллиантов

 

4.6.          Математическое содержание замощения

В изучении паркетов оказалось достаточно много математического содержания.

Так, например, при доказательстве теоремы о том, какими правильными многоугольниками можно замостить плоскость, нам потребовались знания из геометрии, а именно то, какова же сумма углов в определенном угольнике, а также элементарные алгебраические операции и алгоритмы выполнения.

Помимо геометрических знаний о сумме углов в треугольнике нам потребовались сведения о сумме углов в четырехугольнике, о внешних углах треугольника, понятии диагонали в четырехугольнике,  знания о сумме углов в пяти- и шестиугольнике, а также тригонометрических функций и площади треугольников.

Также в исследовании паркетов мы пользовались понятиями из теории вероятности: «Золотое сечение», «Золотой треугольник», «Тупоугольный золотой треугольник», рекуррентные соотношения (последовательность Фибоначчи), комбинаторика, графы.

Помимо вышеперечисленных дисциплин мы использовали знания из алгебры и математического анализа. Например, при доказательстве теорем из главы «Невозможные замощения» мы пользовались неопределенными интегралами. Также применяли неравенства, множества и подмножества.

Таким образом, в исследовании паркетов большую роль играет не только художественный взгляд, но и математические формулы, теоремы и понятия.

 

 

 

 

Заключение

Замощение – одна из интереснейших проблем, изучаемых несколько десятилетий. Данная тема затрагивает не только художественную область, но также и математику, и физику, и другие технические науки.

В настоящей работе представлены разнообразные виды замощений, теоремы и их доказательства, примеры правильных паркетов, а также паркетов, состоящих из произвольных многоугольников. Помимо всего перечисленного работа содержит информацию о невозможных замощениях, их доказательства и примеры. В качестве приложения замощения плоскости многоугольниками был взят ацтекский бриллиант, где также доказывались несколько непростых теорем, приводились алгоритм построения данного приложения и примеры его замощения.

В работе было выделено математическое содержание замощения плоскости многоугольниками, что ярко показывает многогранность данной темы.

Главными результатами данной работы являются доказательства теорем, связанных с замощение плоскости многоугольниками, а продуктом – приведенные примеры, описанные пошагово.

Целью дальнейшей работы с данной темой является выделение вероятности, связанной с приведенным приложением – ацтекским бриллиантом. Интерес заключается в том, чтобы отследить ход раскраски бриллианта и попытаться преобразить получаемую в ходе раскрашивания окружность в, например, эллипс.

 

 

Библиографический список

1.            Смирнов Е.И. Фундирование опыта в профессиональной подготовке и инновационной деятельности педагога //Издательство «Канцлер» Ярославль, 2012. – 646 с

2.            http://www.mariatrudler.com/?p=2100 [Электронный ресурс]

3.            https://ru.wikipedia.org/wiki/Замощение_(геометрия) [Электронный ресурс]

4.            http://ezhe.ru/ib/issue719.html [Электронный ресурс]

5.            http://www.pereplet.ru/obrazovanie/stsoros/246.html [Электронный ресурс]

6.            https://wiki2.org/ru/Пятиугольный_паркет [Электронный ресурс]

7.            https://ru.qwertyu.wiki/wiki/Robert_Berger_(mathematician) [Электронный ресурс]

8.            https://ru.wikipedia.org/wiki/Грюбаум,_Бранко [Электронный ресурс]

9.            http://epizodyspace.ru/kosm/s/shepard_alan/shepard_alan-b.html [Электронный ресурс]

10.        https://ru.wikipedia.org/wiki/Ван_Хао_(математик) [Электронный ресурс]

11.        https://ru.wikipedia.org/wiki/Плитка_Соколара_-_Тейлор [Электронный ресурс]

12.        https://ru.wikipedia.org/wiki/Мозаика_Пенроуза [Электронный ресурс]

13.        https://ru.wikipedia.org/wiki/Пенроуз,_Роджер [Электронный ресурс]

14.        https://elementy.ru/problems/42/Zamoshcheniya  [Электронный ресурс]

15.        https://lenta.ru/articles/2015/08/20/pentagon/  [Электронный ресурс]

16.        https://ru.wikipedia.org/wiki/Хугершофф,_Рейнхард [Электронный ресурс]

17.        https://ru.wikipedia.org/Киршнер,_Роберт  [Электронный ресурс]

18.        https://wiki2.org/ru/Гарднер,_Мартин [Электронный ресурс]

19.        https://ru.wikipedia.org/wiki/Хиб,_Ричард_Джеймс [Электронный ресурс]

20.        https://ru.qwertyu.wiki/wiki/Marjorie_Rice [Электронный ресурс]

21.        https://ru.wikipedia.org/wiki/Штайн,_Рольф_Альфред [Электронный ресурс]

22.        https://arxiv.org/abs/1510.01186 [Электронный ресурс]

23.        https://habr.com/ru/post/382747/?mobile=no [Электронный ресурс]

24.        А.М. Нигмедзянова, А. Исмоилова. Замощение плоскости многоугольниками в системе GeoGebra: Системы компьютерной математики и их приложения. Казанский федеральный университет, 2018. - №19.- С. 70-79. [Электронный ресурс]. – Режим доступа: https://elibrary.ru/item.asp?id=35177099

25.        https://nplus1.ru/material/2015/08/21/angles-and-corners [Электронный ресурс]

26.        С. Табачников, Д. Фукс. Невозможные замощения.

27.        https://ru.wikipedia.org/wiki/Монски,_Пауль [Электронный ресурс]

28.        https://ru.wikipedia.org/wiki/Ацтекский_бриллиант  [Электронный ресурс]

29.        Е.Ю. Смирнов. Три взгляда на ацтекский бриллиант. Москва. Издательство: МЦНМО, 2015.

30.        К. Кохась, Разбиение ацтекских диамантов и квадратов на домино, Зап. научн. сем. ПОМИ, 2008, том 360, 180–230;

31.        William Jockusch, James Propp, Peter Shor, Random Domino Tilings and the Arctic Circle Theorem // arXiv:math/9801068. — 1998-01-13

 

 

Приложение 1

Усеченный квадратный паркет
Курносый квадратный паркет
Тришестиугольный паркет
Усеченный шестиугольный паркет
Ромбошетиугольный паркет
Ромбоусечённый тришестиугольный паркет
Изокурносый треугольный паркет
Курносый тришестиугольный паркет

 

 

 

 

 

 

Приложение 2

Приводя классификацию плиток, будем обозначать через A,B,C,D,E углы пятиугольника, а через a, b, c, d, e длины его сторон, где |EA|=a, |AB|=b, |BC|=c, |CD|=d, |DE|=e. Многие из этих классов имеют степени свободы, выражающиеся уравнениями для углов и сторон. В частности, классы 1, 2, 4, 5, 6, 7, 8, 9 и 13 допускают параметры, при которых пятиугольники становятся невыпуклыми.

1	2	3	4	5
B+C=180° A+D+E=360°	c=e B+D=180°	a = b, d = c + e A = C = D = 120°	b = c, d = e B = D = 90°	a = b, d = e A = 60°, D = 120°
6	7	8	9	10
a = d = e, b = c B + D = 180°, 2B = E	b = c = d = e B + 2E = 2C + D = 360°	b = c = d = e 2B + C = D + 2E = 360°	b = c = d = e 2A + C = D + 2E = 360°	a = b = c + e A = 90°, B + E = 180°, B + 2C = 360°
11	12	13	14	15
2a + c = d = e A = 90°, 2B + C = 360° C + E = 180°	2a = d = c + e A = 90°, 2B + C = 360° C + E = 180°	d = 2a = 2e B = E = 90°, 2A + D = 360°	2a = 2c = d = e A = 90°, B ≈ 145,34°, C ≈ 69,32°, D ≈ 124,66°, E ≈ 110,68° (2B + C = 360°, C + E = 180°).	a = c = e, b = 2a A = 150°, B = 60°, C = 135°, D = 105°, E = 90°

 

 

Приложение 3

Пример замощения плоскости произвольным треугольником:

1.   Пусть нам дан произвольный треугольник (рис. 63). Необходимо замостить данным треугольником плоскость.

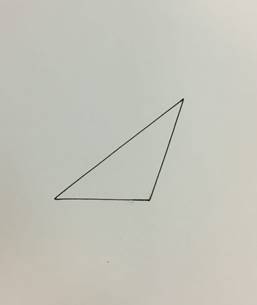
Рис. 63. Произвольный треугольник

2.   Достраиваем треугольник до параллелограмма, используя параллельный перенос его сторон (рис. 64).

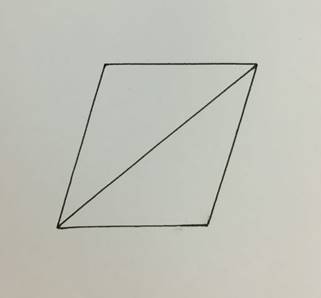
Рис. 64. Построение до параллелограмма

3.   Пристраиваем к получившемуся параллелограмму еще один (точно такой же) параллелограмм (рис. 65).

 

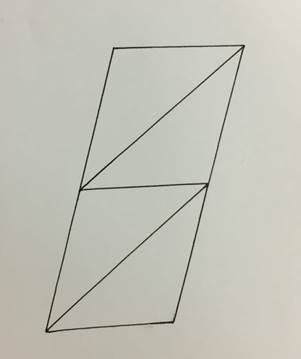
Рис. 65. Построение второго параллелограмма

4.            Аналогично пункту 3 проделываем действия. В итоге мы получили полное замощение плоскости произвольным треугольником (рис. 66).

 

Рис. 66. Замощение плоскости произвольным треугольником

 

Приложение 4

Пример замощения плоскости произвольным выпуклым четырехугольником.

1.   Пусть нам дан произвольный выпуклый четырехугольник, которым необходимо замостить плоскость (рис. 67).

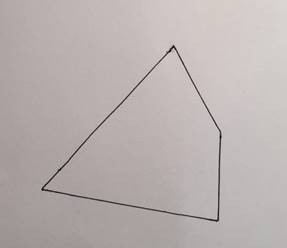
Рис. 67. Произвольный выпуклый четырехугольник

2.   К одному из углов данного четырехугольника пристраиваем другие углы того же четырехугольника так, чтобы их соответствующие стороны не только совпали, но и были равны (рис. 68).

Рис. 68. Построение второго, третьего и четвертого четырехугольника

3.   Аналогично пункту 2 пристраиваем такие же четырехугольники к полученным. В итоге мы получили полное замощение плоскости произвольным выпуклым четырехугольником (рис. 69).

Рис. 69. Замощение плоскости произвольным выпуклым четырехугольником

 

Приложение 5

Примеры замощения плоскости произвольными невыпуклыми четырехугольниками.

Пример 1.

1.   Пусть нам дан произвольный невыпуклый четырехугольник. Необходимо замостить данным невыпуклым четырехугольником плоскость (рис. 70).

Рис. 70. Произвольный невыпуклый четырехугольник

2.   Соединяем внутри две вершины невыпуклого четырехугольника так, чтобы получилось два произвольных треугольника (рис. 71).

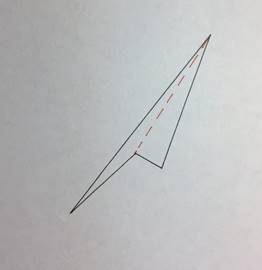
Рис. 71. Проведение диагонали

3.   Так как любым треугольником можно замостить плоскость (по теореме 1), следовательно можно к любому из имеющихся треугольников пристроить точно такой же треугольник и продолжить его до данного невыпуклого четырехугольника (рис. 72).

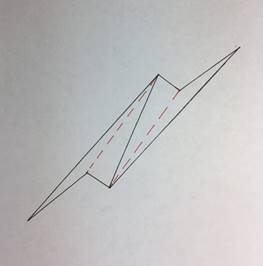
Рис. 72. Построение второго невыпуклого четырехугольника

4.   Аналогично пункту 3 пристраиваем такой же невыпуклый четырехугольник к другому получившемуся треугольнику в пункте 2 (рис.73).

Рис. 73. Построение третьего невыпуклого четырехугольника

5.   Аналогично предыдущим пунктам пристраиваем следующие невыпуклые четырехугольники. В итоге мы получили полное замощение плоскости произвольным невыпуклым четырехугольником (рис. 74).

Рис. 74. Замощение плоскости произвольным невыпуклым четырехугольником

Пример 2.

1.   Пусть нам дан произвольный невыпуклый четырехугольник. Необходимо замостить данным невыпуклым четырехугольником плоскость (рис. 75).

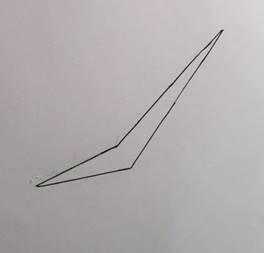
Рис. 75. Произвольный невыпуклый четырехугольник

2.   Аналогично пунктам 2, 3, 4 предыдущего примера пристраиваем к имеющемуся невыпуклому четырехугольнику такие же фигуры (рис. 76).

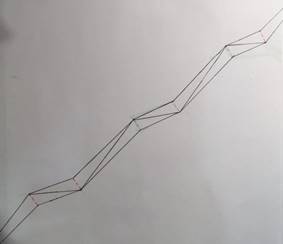
Рис.76. Построение следующих невыпуклых четырехугольников

3.   Аналогично предыдущим пунктам пристраиваем следующие невыпуклые четырехугольники. В итоге мы получили полное замощение плоскости произвольным невыпуклым четырехугольником (рис. 77).

Рис. 77. Замощение плоскости произвольным невыпуклым четырехугольником

 

 

Скачано с www.znanio.ru