МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ - Тема: Решение задач по теме: «Числовая последовательность, способы ее задания, вычисления членов последовательности. Предел последовательности. Бесконечно убывающая геометрическая прогрессия».

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОЙ РАБОТЫ ПО МАТЕМАТИКЕ В СПО

Разработал преподаватель: Игнатьева Елена Сергеевна

Тема:

Решение задач по теме: «Числовая последовательность, способы ее задания, вычисления членов последовательности. Предел последовательности. Бесконечно убывающая геометрическая прогрессия».

Цель работы: 

- применить умения по владению представлений об основных понятиях математического анализа и их свойствах, владение умением характеризовать поведение функций, использование полученных знаний для описания и анализа реальных зависимостей.

Оборудование:

1. Рабочая тетрадь в клетку

2. Раздаточные материалы: карточки-задания, инструкционные карты – 20 штук.

3. Калькулятор простой.

4. Ручка.

Задание:

I Вариант                                                                            II Вариант

1. Последовательность задана словесно. Напишите первые десять членов последовательности

Порядок выполнения:

1.        Внимательно прочитать тему и цель практической работы.

2.        Изучить учебный материал по теме.

3.        Ответить на вопросы.

4.        Выполнить задания.

5.        Подготовить отчет.

Пояснения к работе (учебный материал):

Определение: множество чисел, каждое из которых снабжено своим номером, называется числовой последовательностью.

Элементы этого числового множества называются членами последовательности и обозначают: первый член - а ₁, второй  - а ₂ , n- й член - а _n  и т.д. Вся последовательность обозначается: а _1, а _2, а ₃, …, а _n  или (а _n ).

Числовая последовательность представляет собой не что иное, как множество нумерованных чисел, упорядоченных наподобие натурального ряда, т.е. располагаемое в порядке возрастания номеров. Последовательность может содержать как конечное, так и бесконечное число членов.

Последовательность, состоящая из конечного числа членов, называется конечной, а последовательность, состоящая из бесконечного числа членов, - бесконечной последовательностью.

Иногда бесконечную числовую последовательность вводят, используя понятие функции:

Определение: Функцию у = f(x), xN называют функцией натурального аргумента или числовой последовательностью и обозначают: у = f(n), или у₁, у₂, у₃..., у_n или у(n).

Последовательности можно задавать различными способами, например, словесно, когда правило задавания последовательности описано словами, без указания формулы. Так, словесно задается последовательность простых чисел:

2,3,5,7,11,13,17,19,23,29,...

Особенно важны аналитический и рекуррентный способы задания последовательности.

Говорят, что последовательность задана аналитически, если указана формула ее n-го члена.

Приведем три примера.

1)           у_n = n². Это аналитическое задание последовательности

                 1,4,9,16,…, n², …

Указав конкретное значение n, нетрудно найти член последовательности с соответствующим номером. Если. Например, n= 9, то у₉ = 9² = 81, если

2)           у_n = С. Здесь речь идет о последовательности С, С, С, …., С, …. . Такую последовательность называют постоянной (или стационарной).

3)           у_n = 2ⁿ . Это аналитическое задание последовательности 2, 2², 2³, ….,2ⁿ, …

Рекуррентный способ задания последовательности состоит в том, что указывают правило, позволяющее вычислить n- й член последовательности, если известны ее предыдущие члены. Например, арифметическая прогрессия – это числовая последовательность (а_n), заданная рекуррентно соотношениями:

а _1, = а,  а_n+1 = а_n+ d

(а и d – заданные числа, d – разность арифметической прогрессии)

Геометрическая прогрессия – это числовая последовательность (b_n), заданная рекуррентно соотношениями:

b _1, = b,  b_n+1 = b_n·q

(b и q – заданные числа, b≠0, q ≠ 0; q знаменатель геометрической прогрессии ).

Пример: Выписать первые пять членов последовательности, заданной рекуррентно:у₁ =1; у₂ = 1; у_n = у_n-2 + у_n-1

Решение. n –й член последовательности равен сумме двух предшествующих ему членов. Значит, последовательно получаем:

у₁ =1; у₂ = 1;  у₃ =1+1 = 2; у₄ = 1+ 2 = 3; у₅ =2+3 =5; и т.д.

Ограниченные последовательности.

·                    Последовательность (х_n) называется ограниченной, если существуют такие два числа m и М, что для всех nN выполняется неравенство m≤ х_n ≤М.

·                    Последовательность (х_n) называется ограниченной сверху, если существует такое число М, что для всех nN выполняется неравенство х_n ≤М.

·                    Последовательность (х_n) называется ограниченной снизу, если существует такое число m, что для всех nN выполняется неравенство m≤ х_n

Например: последовательность (х_n), заданная формулой общего члена х_n = n, ограничена снизу (например, число 0) и не ограничена сверху.

Монотонные последовательности.

Последовательность (х_n) называется возрастающей, если каждый ее член, начиная со второго, больше предыдущего, т.е. если для любого натурального n выполняется неравенство х_n+1 > х_n.

Последовательность (х_n) называется убывающей, если каждый ее член, начиная со второго, меньше предыдущего, т.е. если для любого натурального n выполняется неравенство х_n+1 < х_n.

Последовательность (х_n) называется невозрастающей, если каждый ее член, начиная со второго, не более предыдущего, т.е. если для любого натурального n выполняется неравенство х_n+1 ≤ х_n.

Последовательность (х_n) называется неубывающей, если каждый ее член, начиная со второго, не меньше предыдущего, т.е. если для любого натурального n выполняется неравенство х_n+1 ≥ х_n.

Возрастающие, убывающие, невозрастающие и неубывающие последовательности образуют класс монотонных последовательностей.

Предел числовой последовательности.

Рассмотрим для числовые последовательности – (у_n) и (x_n).

(у_n): 1, 3,5, 7, 9, … 2n – 1, …;

(x_n): 1,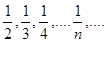

Изобразим члены  этих последовательностей точками на координатной прямой.

0    1      3     5      7      9     11                            у 

0             0,25                 0,5                               1   

Замечаем, что члены последовательности (x_n) как бы «сгущаются» около точки 0 – говорят последовательность сходятся , а у последовательности (у_n) такой точки сгущения нет – и говорят, что последовательность расходится.

Математики не используют термин точка сгущения, а они говорят предел последовательности.

Определение: Число b называется пределом  последовательности (у_n), если в любой заранее выбранной окрестности  точки b содержится все члены последовательности, начиная с некоторого номера.

Пишут так: у_n→b или  читают так: предел последовательности у_n при стремлении n к бесконечности равен b.

На практике используется еще одно истолкование равенства , связанное с приближенными вычислениями: если последовательность у_n = f(_n) сходится к числу b, то выполняется приближенное равенство f(_n)≈b, причем это приближенное равенство тем точнее, чем больше n.

Вопросы для закрепления теоретического материала к практическому занятию:

1. Дайте определение числовой последовательности.

2. Перечислите способы задания последовательностей.

3. Какие последовательности называют ограниченными?

4. Сформулируйте определение предела числовой последовательности.

Содержание отчета:

Название практической работы.

Учебная цель.

Решение заданий практической работы.

Ответы на вопросы для закрепления теоретического материала.

Литература:

1.    Алимов Ш.А. и др. Алгебра и начала математического анализа: Учебник 10—11 классы. — М.И., 2016.

2.    Атанасян Л.С., Бутузов В. Ф., Кадомцев С.Б. и др. Математика: алгебра и начала математического анализа. Геометрия. Геометрия (базовый и углубленный уровни). 10—11 классы. — М., 2016.

3.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: учебник для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

4.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Сборник задач профильной направленности: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

5.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Задачник: учеб. пособие для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

6.    Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия: Электронный учеб.- метод. комплекс для студентов профессиональных образовательных организаций, осваивающих профессии и специальности СПО. – М.,2017

7.    Башмаков М.И. Математика: Учебник. — М., 2016.